Как найти простые числа?

Кубические простые числа

Простые числа вида x3−y3x−y,x=y+1{\displaystyle {\frac {x^{3}-y^{3}}{x-y}},x=y+1}

7, 19, 37, 61, 127, 271, 331, 397, 547, 631, 919, 1657, 1801, 1951, 2269, 2437, 2791, 3169, 3571, 4219, 4447, 5167, 5419, 6211, 7057, 7351, 8269, 9241, 10267, 11719, 12097, 13267, 13669, 16651, 19441, 19927, 22447, 23497, 24571, 25117, 26227, 27361, 33391, 35317 (последовательность A002407 в OEIS).

а также x3−y3x−y,x=y+2{\displaystyle {\frac {x^{3}-y^{3}}{x-y}},x=y+2}

13, 109, 193, 433, 769, 1201, 1453, 2029, 3469, 3889, 4801, 10093, 12289, 13873, 18253, 20173, 21169, 22189, 28813, 37633, 43201, 47629, 60493, 63949, 65713, 69313, 73009, 76801, 84673, 106033, 108301, 112909, 115249

(последовательность A002648 в OEIS).

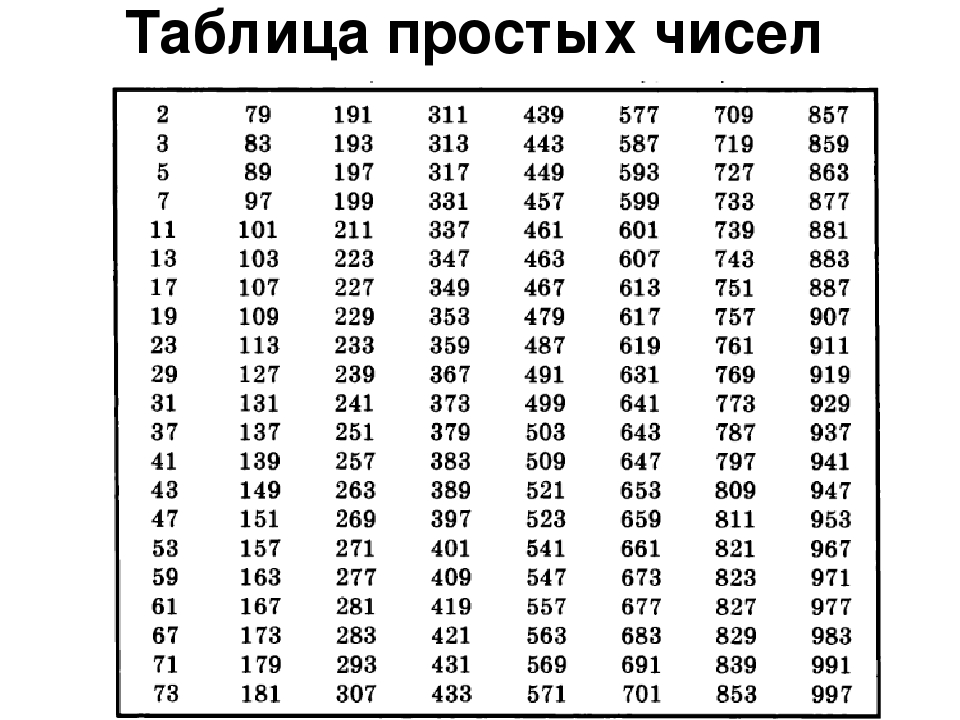
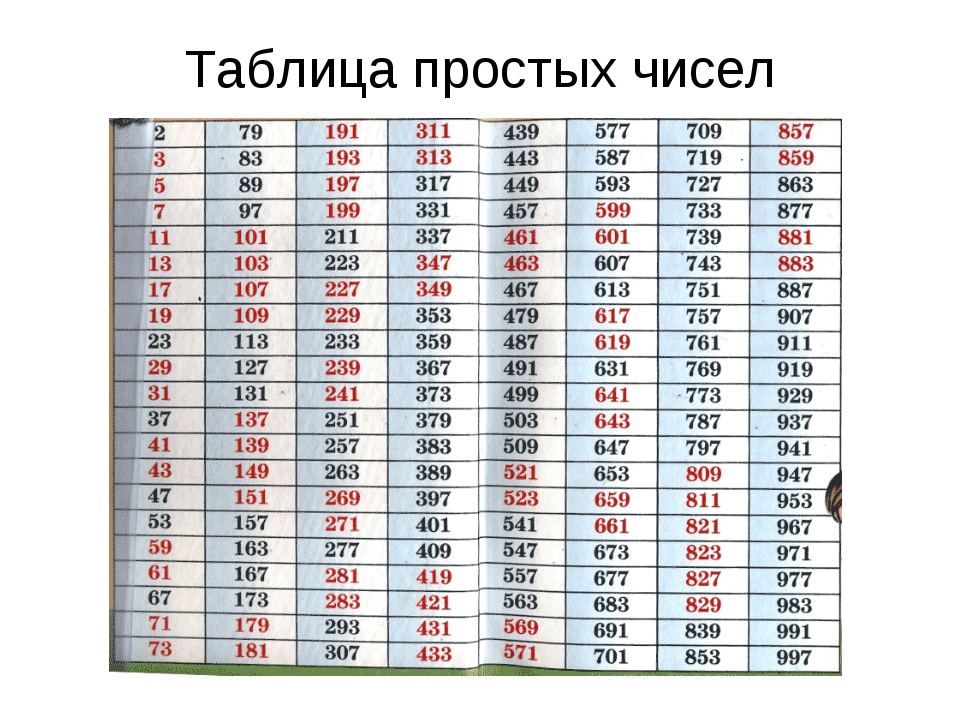
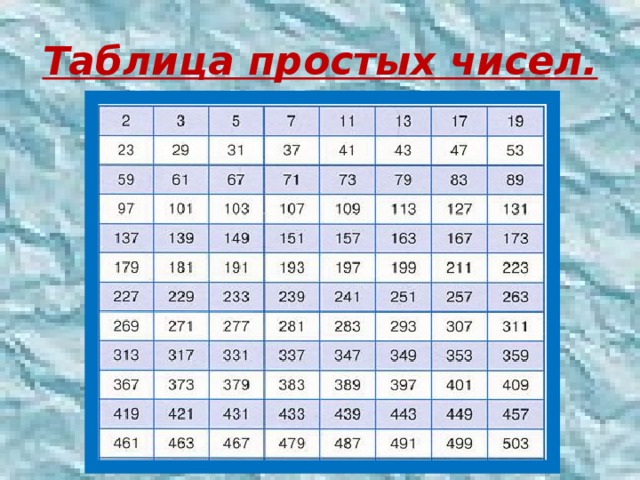
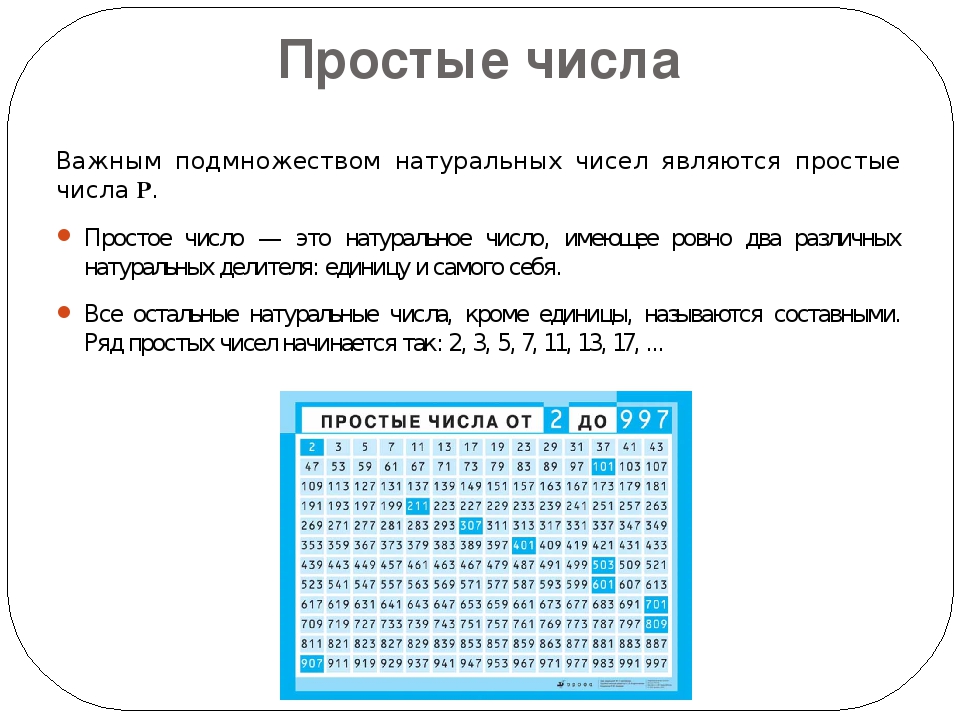
Первые 500 простых чисел

																59		67	71
																157		167
		191				211	223	227	229	233		241	251		263	269	271	277	281
	293	307	311	313		331		347	349		359	367	373	379	383	389	397	401	409
419		431	433	439	443	449	457	461	463	467	479	487	491	499	503	509	521	523	541
547	557		569	571	577	587	593	599	601	607	613	617	619	631	641	643	647	653	659
661	673	677	683	691	701	709	719	727	733	739	743	751	757	761	769	773	787	797	809
811	821	823	827	829	839	853	857	859	863	877	881	883	887	907	911	919	929	937	941
947	953	967	971	977	983	991	997	1009	1013	1019	1021	1031	1033	1039	1049	1051	1061	1063	1069
1087	1091	1093	1097		1109	1117	1123	1129	1151	1153	1163	1171	1181	1187	1193	1201	1213	1217	1223
1229	1231	1237	1249	1259	1277	1279	1283	1289	1291	1297	1301	1303	1307	1319	1321	1327	1361	1367	1373
1381	1399	1409	1423	1427	1429	1433	1439	1447	1451	1453	1459	1471	1481	1483	1487	1489	1493	1499	1511
1523	1531	1543	1549	1553	1559	1567	1571	1579	1583	1597	1601	1607	1609	1613	1619	1621	1627	1637	1657
1663	1667	1669	1693	1697	1699	1709	1721	1723	1733	1741	1747	1753	1759	1777	1783	1787	1789	1801	1811
1823	1831	1847	1861	1867	1871	1873	1877	1879	1889	1901	1907	1913	1931	1933	1949	1951	1973	1979	1987
1993	1997	1999	2003	2011	2017	2027	2029	2039	2053	2063	2069	2081	2083	2087	2089	2099	2111	2113	2129
2131	2137	2141	2143	2153	2161	2179	2203	2207	2213	2221	2237	2239	2243	2251	2267	2269	2273	2281	2287
2293	2297	2309	2311	2333	2339	2341	2347	2351	2357	2371	2377	2381	2383	2389	2393	2399	2411	2417	2423
2437	2441	2447	2459	2467	2473	2477	2503	2521	2531	2539	2543	2549	2551	2557	2579	2591	2593	2609	2617
2621	2633	2647	2657	2659	2663	2671	2677	2683	2687	2689	2693	2699	2707	2711	2713	2719	2729	2731	2741
2749	2753	2767	2777	2789	2791	2797	2801	2803	2819	2833	2837	2843	2851	2857	2861	2879	2887	2897	2903
2909	2917	2927	2939	2953	2957	2963	2969	2971	2999	3001	3011	3019	3023	3037	3041	3049	3061	3067	3079
3083	3089	3109	3119	3121	3137	3163	3167	3169	3181	3187	3191	3203	3209	3217	3221	3229	3251	3253	3257
3259	3271	3299	3301	3307	3313	3319	3323	3329	3331	3343	3347	3359	3361	3371	3373	3389	3391	3407	3413
3433	3449	3457	3461	3463	3467	3469	3491	3499	3511	3517	3527	3529	3533	3539	3541	3547	3557	3559	3571

(последовательность A000040 в OEIS).

Проект по проверке проблемы Гольдбаха сообщает, что были вычислены все простые числа до 1018{\displaystyle 10^{18}}. Это составляет 24 739 954 287 740 860 простых чисел, но они не были сохранены. Существуют известные формулы, позволяющие вычислить количество простых чисел (до заданного значения) быстрее, чем вычисление самих простых чисел. Этот способ был использован, чтобы вычислить, что до 1023{\displaystyle 10^{23}} находится 1 925 320 391 606 803 968 923 простых числа.

Об этой статье

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 60 человек(а). Количество просмотров этой статьи: 143 341.

Категории: Математика

English:Check if a Number Is Prime

Español:saber si un número es primo

Italiano:Riconoscere un Numero Primo

Português:Determinar se um Número é Primo

Deutsch:Überprüfen ob eine Zahl eine Primzahl ist

Nederlands:Controleren of een getal een priemgetal is

Čeština:Jak zjistit, zda je číslo prvočíslem

Печать

Простые и составные числа – определения и примеры

Понятия простые числа и составные числа относятся к , которые больше единицы. Такие целые числа, в зависимости от количества их положительных делителей, подразделяются на простые и составные числа. Таким образом, чтобы понять определения простых и составных чисел, нужно хорошо представлять себе, что такое делители и кратные.

Определение.

Простые числа – это целые числа, большие единицы, которые имеют только два положительных делителя, а именно самих себя и 1.

Определение.

Составные числа – это целые числа, большие единицы, которое имеют, по крайней мере, три положительных делителя.

Отдельно заметим, что число 1 не относится ни к простым, ни к составным числам. Единица имеет только один положительный делитель, которым является само число 1. Этим число 1 отличается от всех остальных целых положительных чисел, которые имеют не менее двух положительных делителей.

Учитывая, что целые положительные числа – это натуральные числа, и что единица имеет только один положительный делитель, можно привести другие формулировки озвученных определений простых и составных чисел.

Определение.

Простыми числами называют натуральные числа, которые имеют только два положительных делителя.

Определение.

Составными числами называют натуральные числа, имеющие более двух положительных делителей.

Отметим, что каждое целое положительное число, большее единицы, есть либо простое, либо составное число. Иными словами, не существует ни одного такого целого числа, которое не являлось бы ни простым, ни составным. Это следует из , которое гласит, что числа 1 и a всегда являются делителями любого целого числа a.

Исходя из информации предыдущего абзаца, можно дать следующее определение составных чисел.

Определение.

Натуральные числа, которые не являются простыми, называются составными.

Приведем примеры простых и составных чисел.

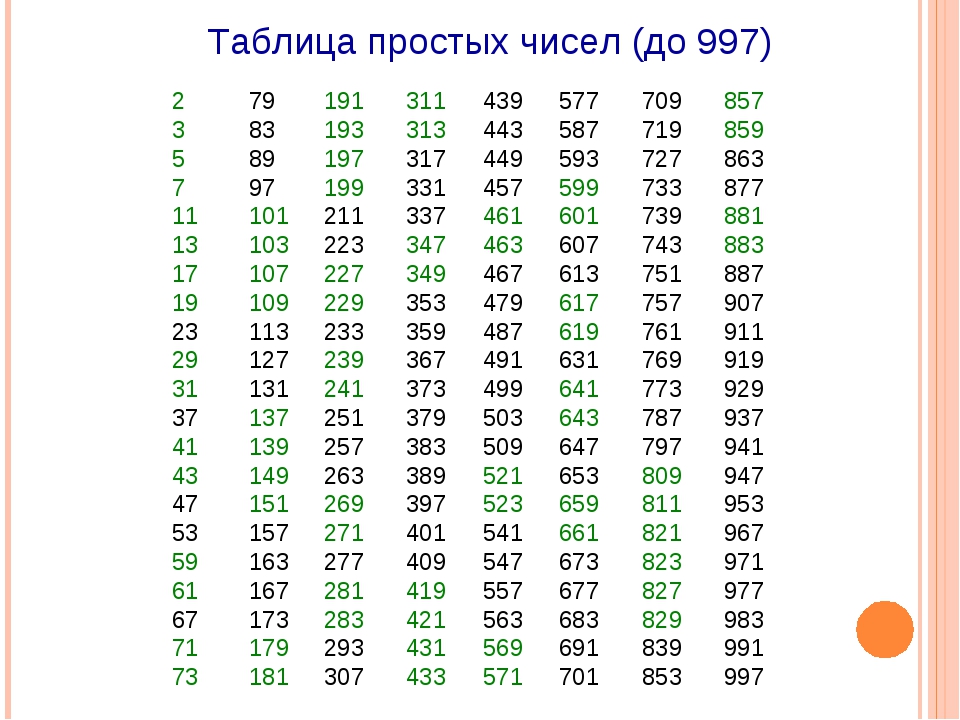
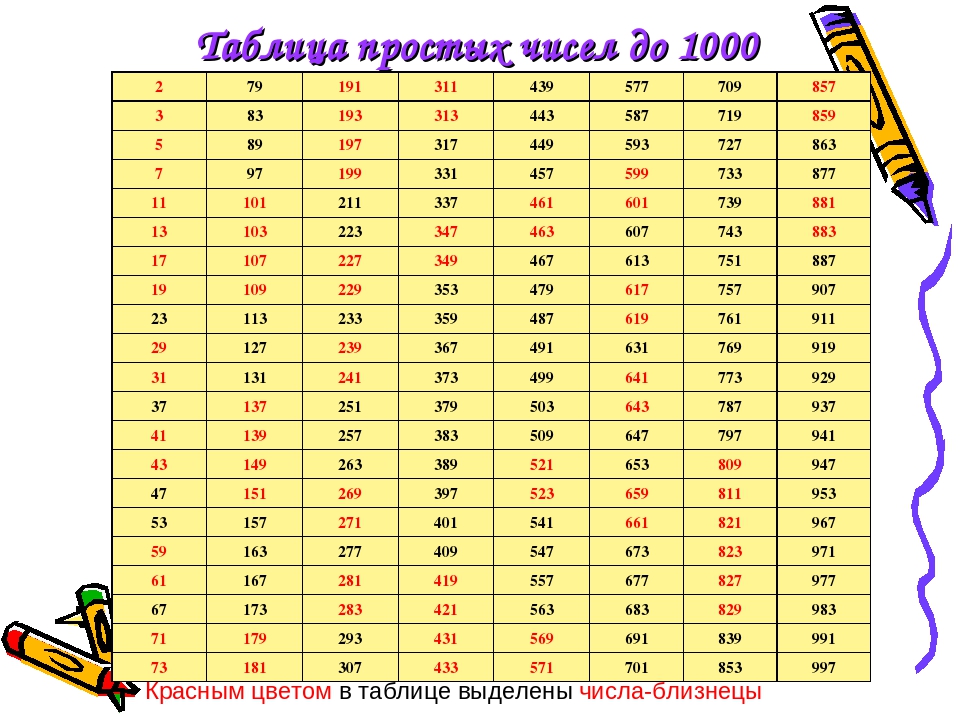
Например, числа 2, 3, 11, 17, 131, 523 являются простыми. Несомненно, это далеко не очевидно. Но все наши попытки подобрать какой-либо положительный делитель любого из этих чисел, отличный от единицы и самих этих чисел, закончатся неудачей. Это свидетельствует о том, что записанные числа являются простыми. В последнем пункте данной статьи мы более подробно поговорим о .

В качестве примеров составных чисел приведем 6, 63, 121 и 6 697. Это утверждение тоже нуждается в пояснении. Число 6 имеет кроме положительных делителей 1 и 6 еще и делители 2 и 3, так как 6=2·3, поэтому 6 – действительно составное число. Положительными делителями 63 являются числа 1, 3, 7, 9, 21 и 63. Число 121 равно произведению 11·11, поэтому его положительными делителями являются 1, 11 и 121. А число 6 697 составное, так как его положительными делителями кроме 1 и 6 697 являются еще и числа 37 и 181.

В заключение этого пункта хочется еще обратить внимание на то, что простые числа и взаимно простые числа – это далеко ни одно и то же.

Что такое простые числа?

Самое техническое определение простых чисел состоит в том, что это натуральное число больше 1 и может быть получено только путем умножения 1 и самого себя. Если бы понимание натуральных чисел было более интуитивным, то можно было бы сказать, что это числа, которые мы используем для подсчета.

Чтобы понять это более точно, давайте выберем два числа — 5 и 6. Теперь 5 — это число, которое можно получить только умножением на 1 и 5 (само число). Однако, когда мы берем число 6, то замечаем, что его можно получить другим способом, кроме умножения 1 и 6 (само число). Его также можно получить умножением чисел 2 и 3, что означает, что это не простое число. Число, которое не является простым, известно как составное число.

Свойства

• Числа a{\displaystyle a} и b{\displaystyle b} взаимно просты тогда и только тогда, когда выполняется одно из эквивалентных условий:
  • наибольший общий делитель a{\displaystyle a} и b{\displaystyle b} равен единице;
  • существуют целые x{\displaystyle x} и y{\displaystyle y} такие, что ax+by=1{\displaystyle ax+by=1} (соотношение Безу).
• Любые два (различных) простых числа взаимно просты.
• Если a{\displaystyle a} — делитель произведения bc{\displaystyle bc}, и a{\displaystyle a} взаимно просто с b{\displaystyle b}, то a{\displaystyle a} — делитель c{\displaystyle c}.
• Если числа a1,…,an{\displaystyle a_{1},\ldots ,a_{n}} — попарно взаимно простые числа, то НОК(a1,…,an)=|a1⋅…⋅an|{\displaystyle (a_{1},\ldots ,a_{n})=|a_{1}\cdot \ldots \cdot a_{n}|}. Например, НОК (9,11)=9⋅11=99{\displaystyle (9,11)=9\cdot 11=99}.
• Вероятность того, что любые k{\displaystyle k} случайным образом выбранных положительных целых чисел будут взаимно просты, равна 1ζ(k){\displaystyle {\dfrac {1}{\zeta (k)}}}, в том смысле, что при N→∞{\displaystyle N\to \infty } вероятность того, что k{\displaystyle k} положительных целых чисел, меньших, чем N{\displaystyle {\textstyle {N}}} (и выбранных случайным образом) будут взаимно простыми, стремится к 1ζ(k){\displaystyle {\dfrac {1}{\zeta (k)}}}. Здесь ζ(k){\displaystyle \zeta (k)} — это дзета-функция Римана.
• Дробь является несократимой тогда и только тогда, когда числитель и знаменатель взаимно просты.