Об аксиомах планиметрии
Что такое планиметрия? Определение в геометрии
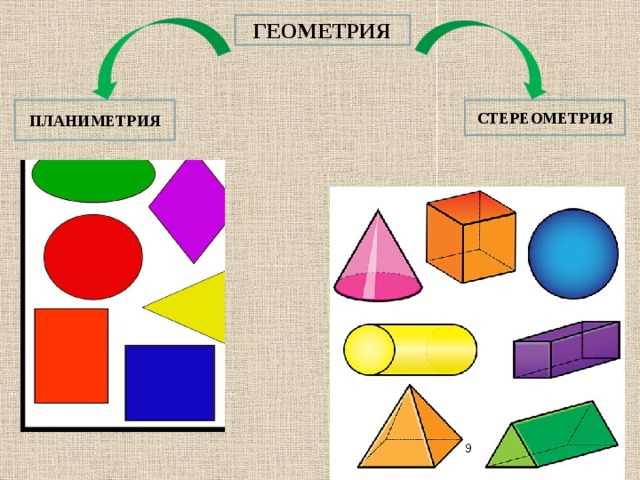
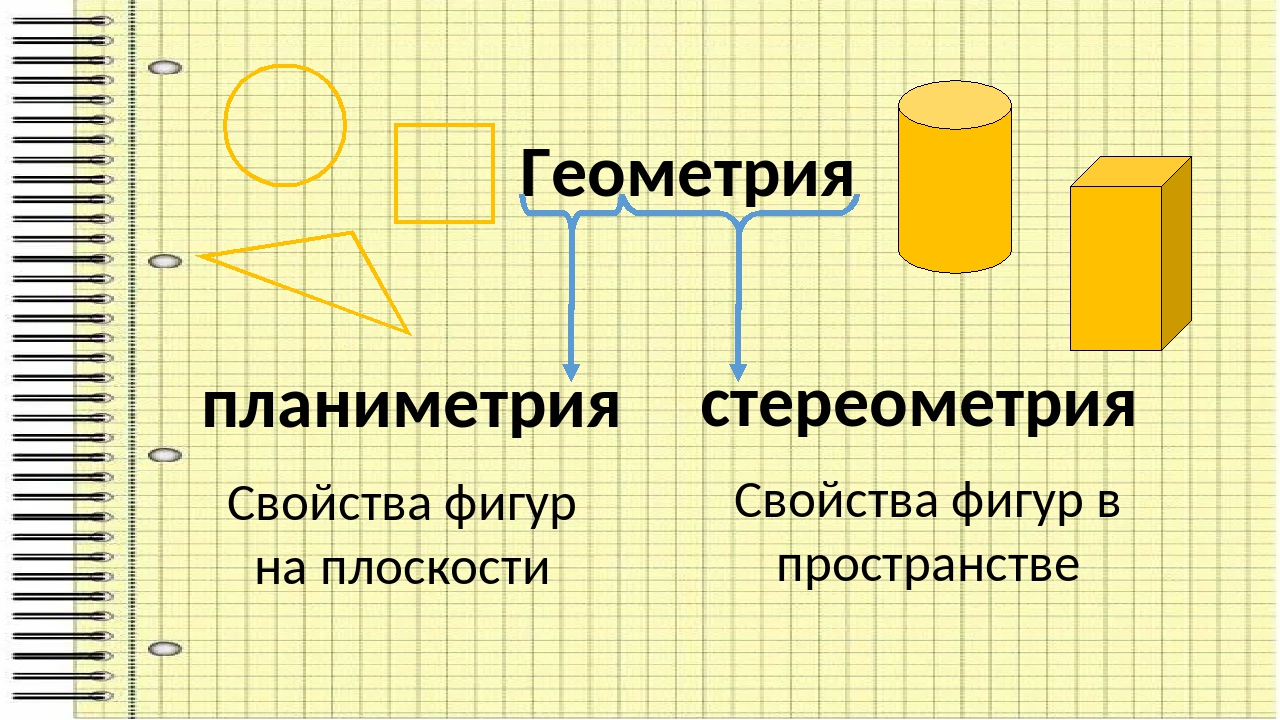
Планиметрия – это раздел геометрии, изучающий фигуры, которые можно расположить в пределах одной плоскости. Например, квадрат, начерченный на листке бумаги, будет относиться к планиметрии.

Планиметрия – это первый шаг школьников к близкому знакомству с геометрией. Именно в планиметрии они узнают о существовании таких понятий, как отрезок, прямая, точка, направление, плоскость и т. д. Для дальнейшего движения в освоении геометрии школьники усваивают, что такое планиметрия. Для них это основа основ. Происходит первое знакомство с теоремами, аксиомами, новыми терминами, явлениями.
Аксиомы и теоремы
Подробнее разберемся с аксиомами. В планиметрии это наиважнейшие правила, по которым работает вся наука. Да и не только в ней. По определению, речь идет об утверждениях, не требующих доказательств.
Аксиомы, которые буду рассмотрены ниже, входят в так называемую Евклидовую геометрию.
- Есть две точки. Через них всегда можно провести единственную прямую.
- Если существует прямая, то есть точки, которые на ней лежат, и точки, не лежащие на ней.
Это 2 утверждения принято называть аксиомами принадлежности, а следующие – порядка:
- Если на прямой расположены три точки, то одна из них обязательно находится между двумя другими.
- Плоскость делится любой прямой на две части. Когда концы отрезка лежат на одной половине, то значит и весь объект принадлежит ей. В ином случае исходная прямая и отрезок имеют точку пересечения.
Аксиомы мер:
- Каждый отрезок имеет длину, отличную от нуля. Если точка разбивает его на несколько частей, то их сумма будет равна полной длине объекта.
- У каждого угла есть определенная градусная мера, которая не равна нулю. Если разбить его лучом, то исходный угол будет равен сумме образованных.
Параллельность:
На плоскости расположена прямая. Через любую точку, не принадлежащую ей, можно провести лишь одну прямую, параллельную данной.
Теоремы в планиметрии — это уже не совсем фундаментальные утверждения. Обычно их принимают как факт, но каждая из них имеет доказательство, построенное на основных понятиях, упомянутых выше. Кроме того, их очень много. Разобрать все будет довольно трудно, но в представленном материале будут присутствовать некоторые из них.
Со следующими двумя стоит ознакомиться пораньше:
- Сумма смежных углов равна 180 градусам.
- Вертикальные углы имеют одинаковую величину.
Эти две теоремы могут пригодиться в решении геометрических задач, связанных с n-угольниками. Они довольно просты и интуитивно понятны. Стоит их запомнить.
Происхождение слова
Как и многие другие термины, слово «планиметрия» берет свое начало в латинском языке. В переводе оно означает «плоскость», «измеряю». Еще древнегреческие философы ввели его в употребление и дали ему определение. Что такое планиметрия, сейчас знает каждый школьник, ведь с нее начинается изучение геометрии.

Планиметрию относят к Евклидовой геометрии или, как ее еще называют, элементарной геометрии. Евклид – древнегреческий философ, а его главный труд – «Начало» – считается вершиной античной математики. Работы этого философа определили ход развития математики и были предметом изучения и обсуждений в течение очень многих лет.
Что изучает планиметрия?
Чтобы подробнее разобраться с тем, что такое планиметрия, следует узнать, что она изучает. Основные фигуры, с которыми имеют дело школьники при освоении базового курса геометрии – это точка, прямая, параллелограмм, окружности, различные многоугольники, треугольники. Они подробно изучают данные фигуры и решают различные геометрические задачи, которые развивают мышление. Конечно, с годами школьная программа меняется, дополняется и корректируется. Но в целом суть остается та же.
Во время учебы школьники знакомятся с понятием параллельности, учатся строить треугольники, четырехугольники. Изучают особенности построения углов, знакомятся с различными теоремами. Узнают многое об окружности и круге, о подобии, начинают первое знакомство с тригонометрическими функциями и еще многое другое. Не стоит пугаться такого объема информации. Лучше отнестись к геометрии как к увлекательному путешествию. Решение геометрических задач – это практически творчество.

Школьникам стоит сразу усвоить, что планиметрия – такой фундамент, который становится подготовкой к более сложным темам. Следующим шагом будет изучение стереометрии, т. е. объемных фигур. И то, насколько хорошо усвоена стереометрия, определит, как легко будет даваться дальнейшее обучение. Чем крепче будет фундамент, тем проще будет по кирпичикам строить новые знания.