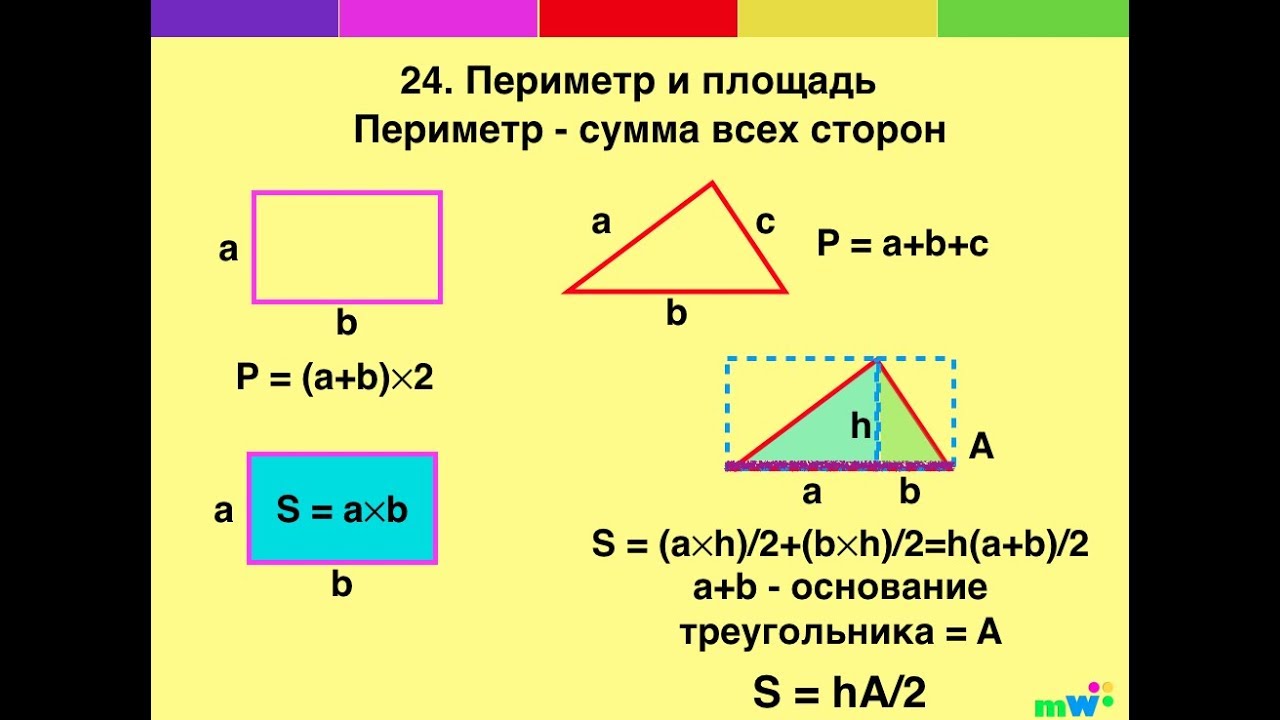
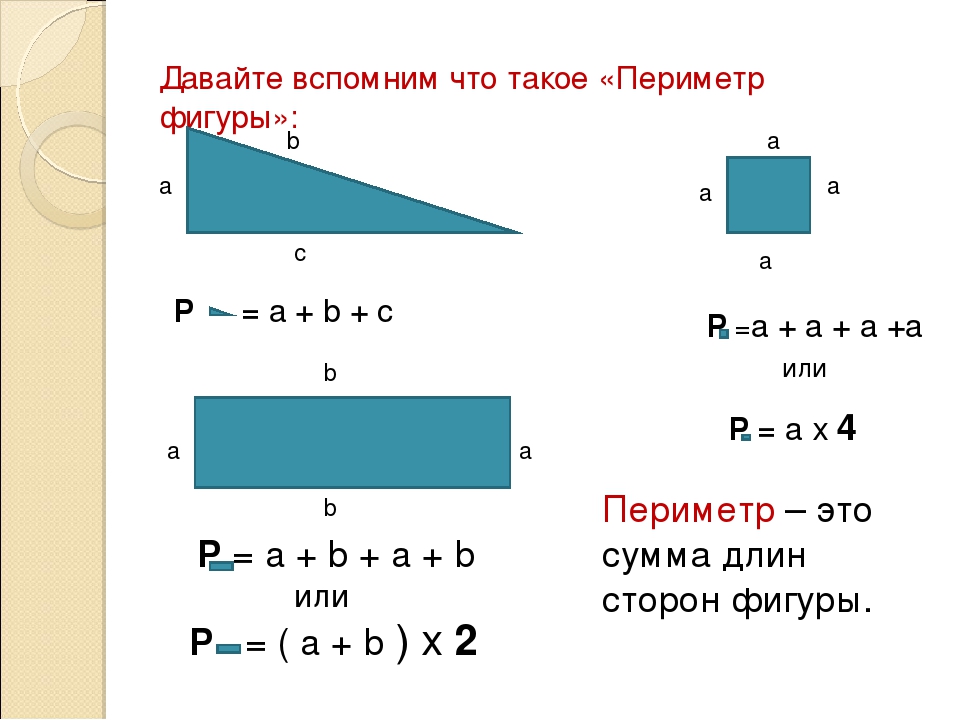
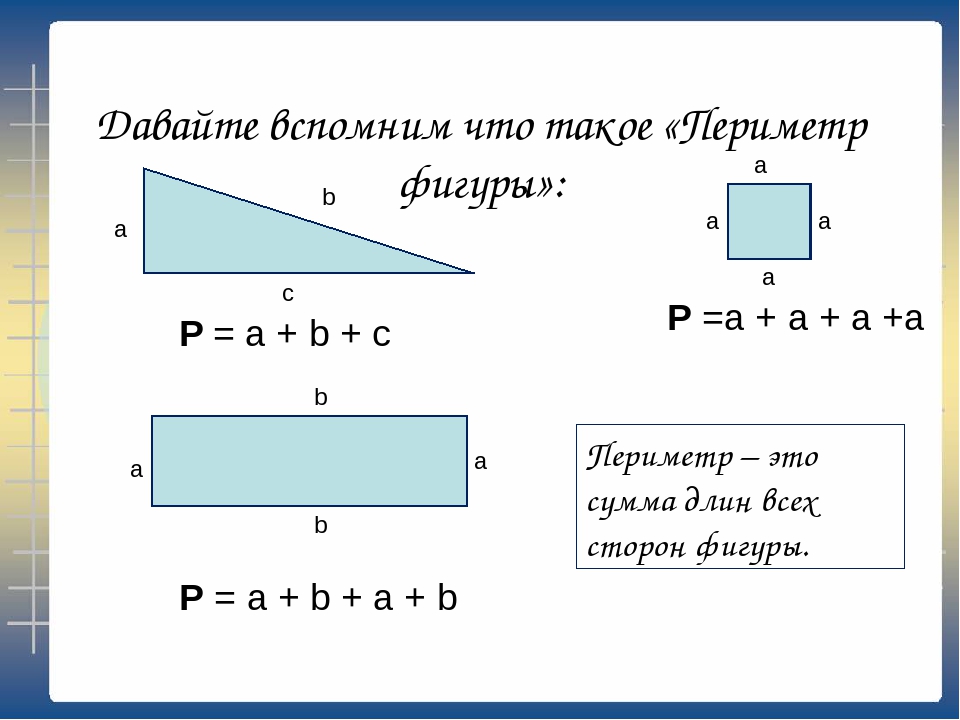
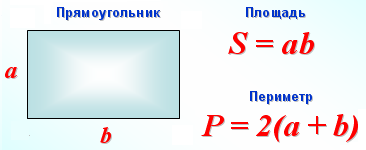
Что такое периметр и площадь

Формулы

фигура	формула	переменные
окружность	2πr=πd{\displaystyle 2\pi r=\pi d}	где r{\displaystyle r} — радиус окружности, а d{\displaystyle d} — диаметр.
треугольник	a+b+c{\displaystyle a+b+c}	где a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c} — длины сторон треугольника.
квадрат/ромб	4a{\displaystyle 4a}	где a{\displaystyle a} — длина стороны.
прямоугольник	2(l+w){\displaystyle 2(l+w)}	где l{\displaystyle l} — длина (основания), а w{\displaystyle w} — ширина.
равносторонний многоугольник	n×a{\displaystyle n\times a}	где n{\displaystyle n} — число сторон, а a{\displaystyle a} — длина сторон.
правильный многоугольник	2nbsin⁡(πn){\displaystyle 2nb\sin \left({\frac {\pi }{n}}\right)}	где n{\displaystyle n} — число сторон, а b{\displaystyle b} — расстояние от центра многоугольника до одной из вершин многоугольника.
общий многоугольник	a1+a2+a3+⋯+an=∑i=1nai{\displaystyle a_{1}+a_{2}+a_{3}+\cdots +a_{n}=\sum _{i=1}^{n}a_{i}}	где ai{\displaystyle a_{i}} — длина i{\displaystyle i}-й (1, 2, 3 … n) стороны n-угольника.

Измерительные приборы на местности

Для вычисления периметра на местности невозможно использование простой ученической линейки. Поэтому специалисты используют специальные приборы. Конечно, самый простой и доступный вариант – это измерение длины границы участка шагами. Размер шага взрослого человека составляет примерно один метр. Иногда один метр и двадцать сантиметров. Но этот способ очень неточный и дает большую погрешность в измерении. Он подходит в том случае, если нет необходимости точного вычисления длины границы, а есть потребность просто прикинуть примерную длину.

Для более точного вычисления длины сторон участка и, соответственно, периметра, существуют специальные приборы. В первую очередь, можно воспользоваться специальной металлической рулеткой или обычным проводом.

Также существуют специальные измерительные устройства, такие как дальномеры. Приборы бывают оптические, лазерные, световые, ультразвуковые. Следует помнить, что чем дальше дальномер способен измерять расстояние, тем выше у него погрешность. Такие приборы используются в геодезических и топографических съемках.

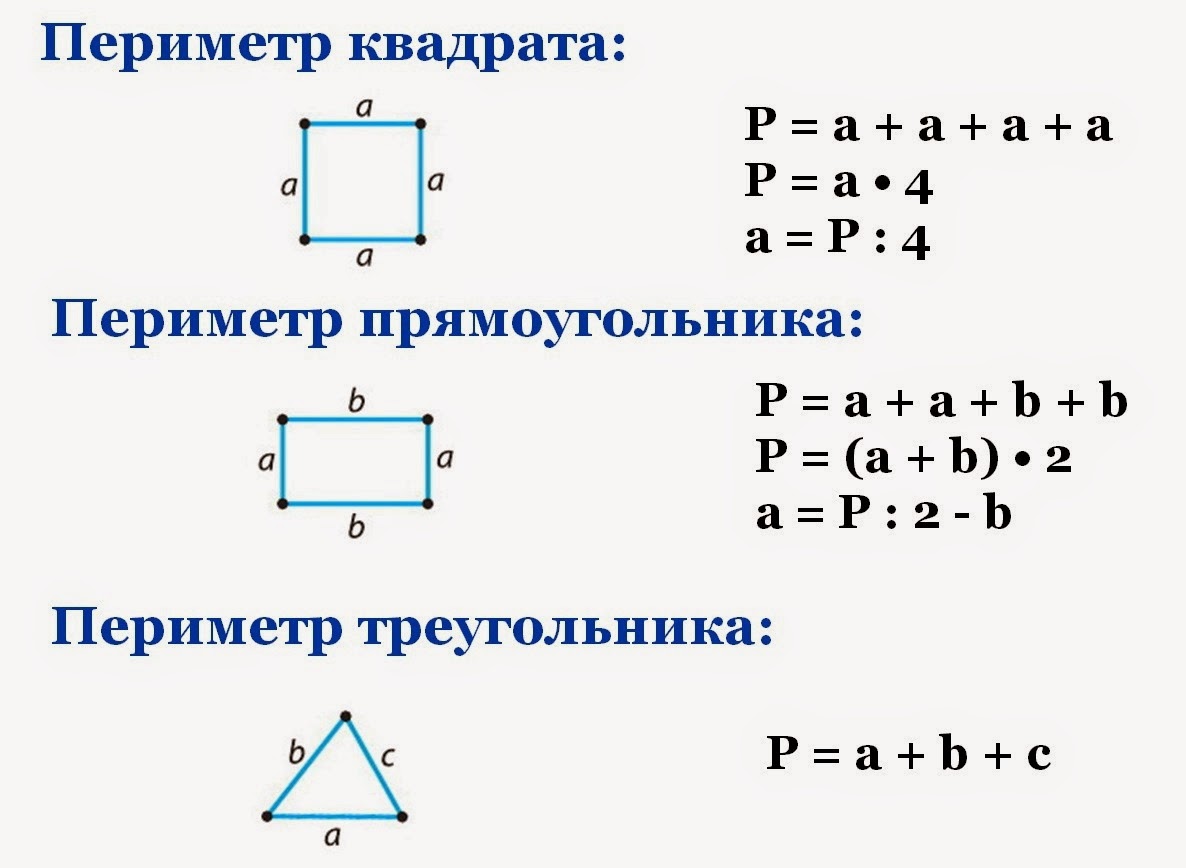
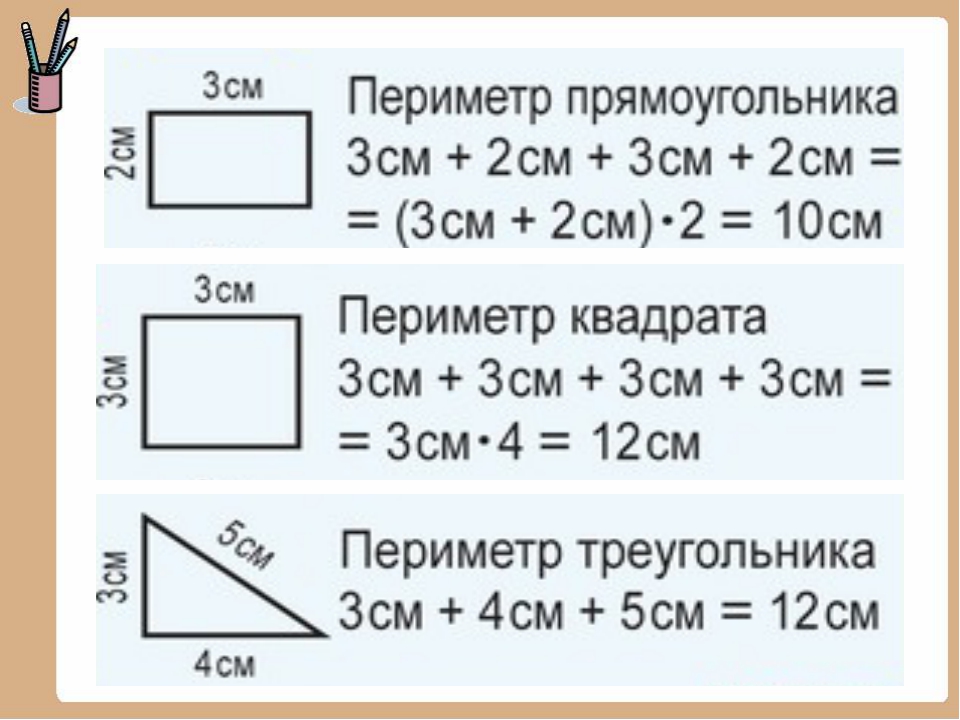
Периметр треугольника

Треугольником следует называть геометрическую фигуру, имеющую три угла (как разного значения, так и одинакового) и состоящую из отрезков, образованных от точек пересечения лучей, образующих углы. Треугольник имеет три стороны и три угла. В нем могут быть из трех равны две стороны. Такой треугольник следует считать равнобедренным. Бывают такие фигуры, в которых равны все три стороны между собой. Принято такие треугольники называть равносторонними.

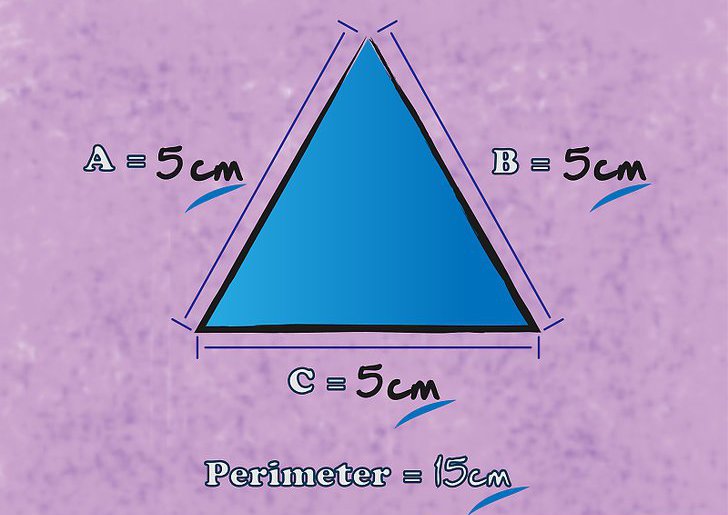
Что такое периметр треугольника? Его вычисление можно провести по аналогии с периметром четырехугольника. Равен периметр треугольника суммарной длине длин его сторон. Вычисление периметра треугольника, в котором две стороны равны – равнобедренного – упрощается умножением одной длины равных сторон на два. К полученному значению необходимо прибавить значение длины третьей стороны. Вычисление периметра треугольника с равными сторонами можно свести к простому вычислению произведения одной длины стороны треугольника на три.

Единицы измерения площади земельных участков

Площади небольших земельных участков удобно измерять в квадратных метрах.

Площади более крупных земельных участков измеряются в арах и гектарах.

Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.

Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:

3 а = 100 м2 × 3 = 300 м2

В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:

1 сотка = 100 м2

2 сотки = 200 м2

10 соток = 1000 м2

Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:

20 га = 10 000 м2 × 20 = 200 000 м2

Площадь геометрической фигуры

Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.

Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.

Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.

Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.

Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:

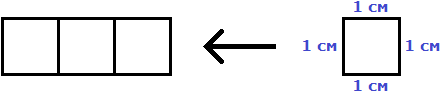
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.

Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:

Допустим, потребовалось измерить площадь следующей комнаты:

Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:

Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:

Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.

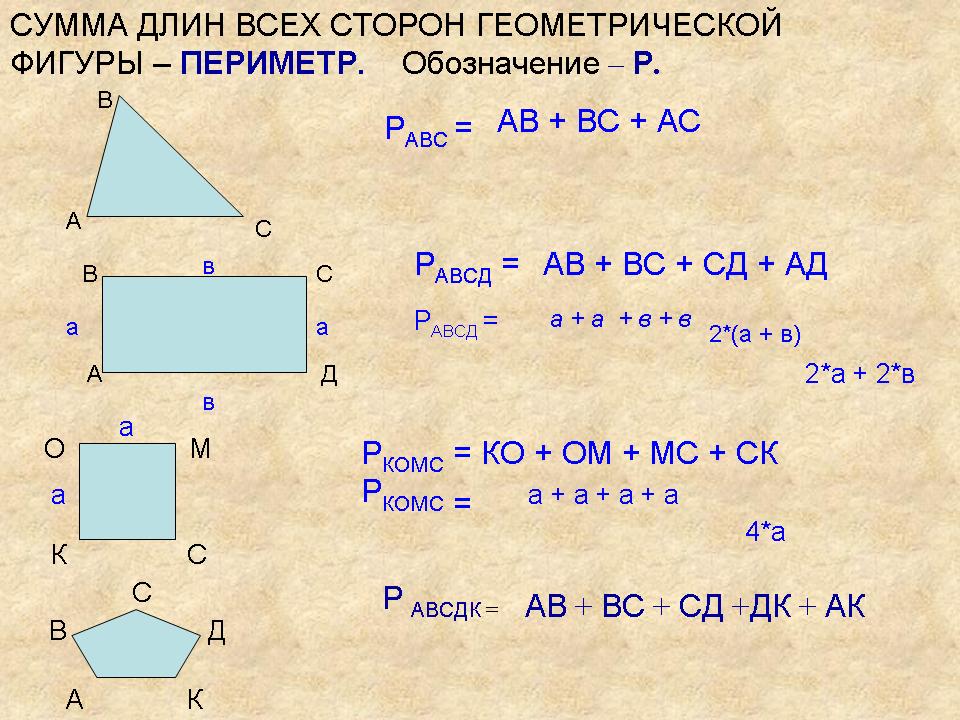
Что такое периметр и площадь

Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».

Периметр обозначается латинской буквой P. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».

Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).

Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.

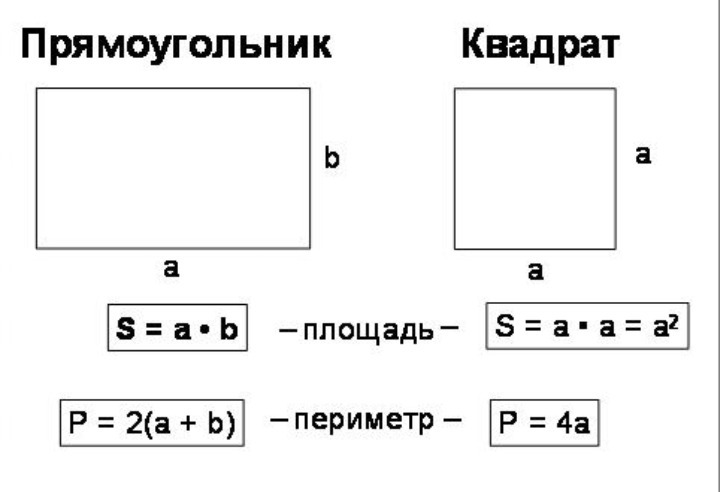
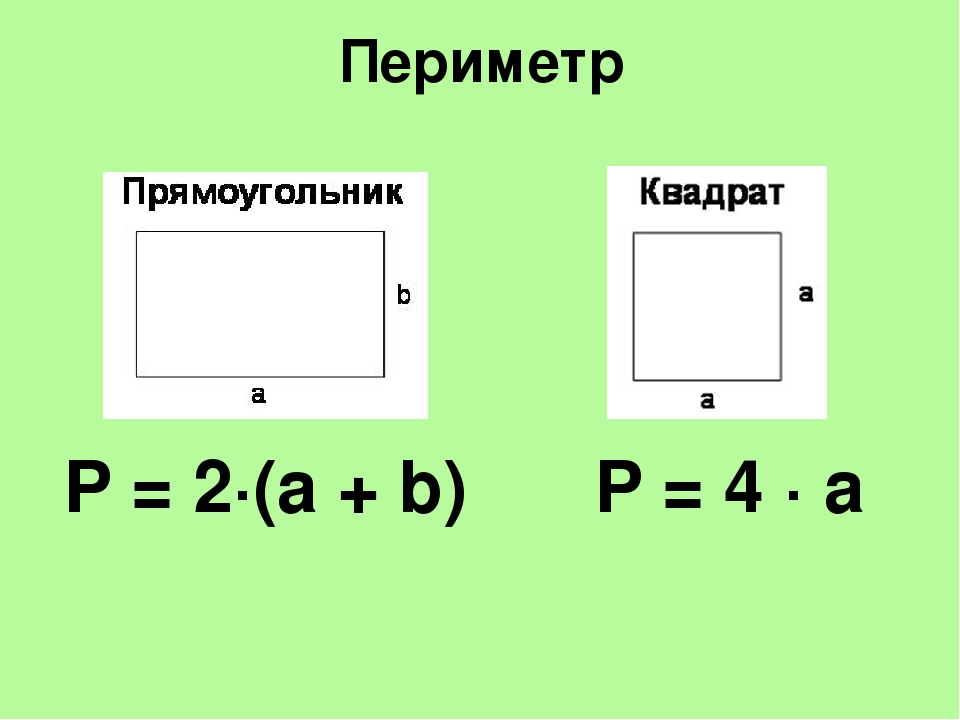
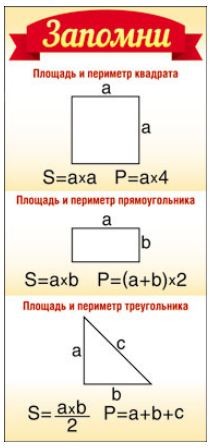
Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.

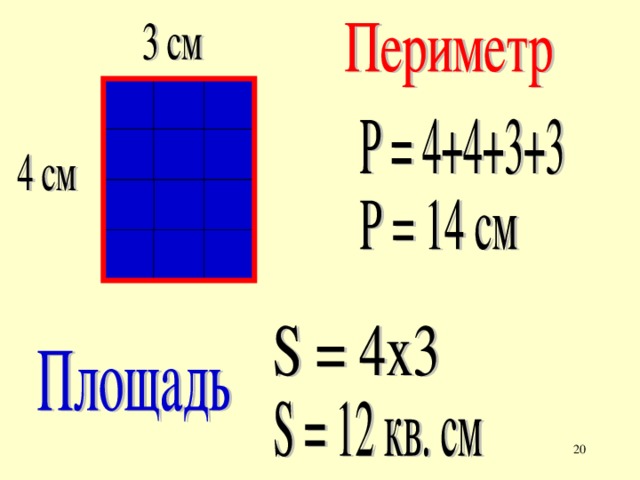
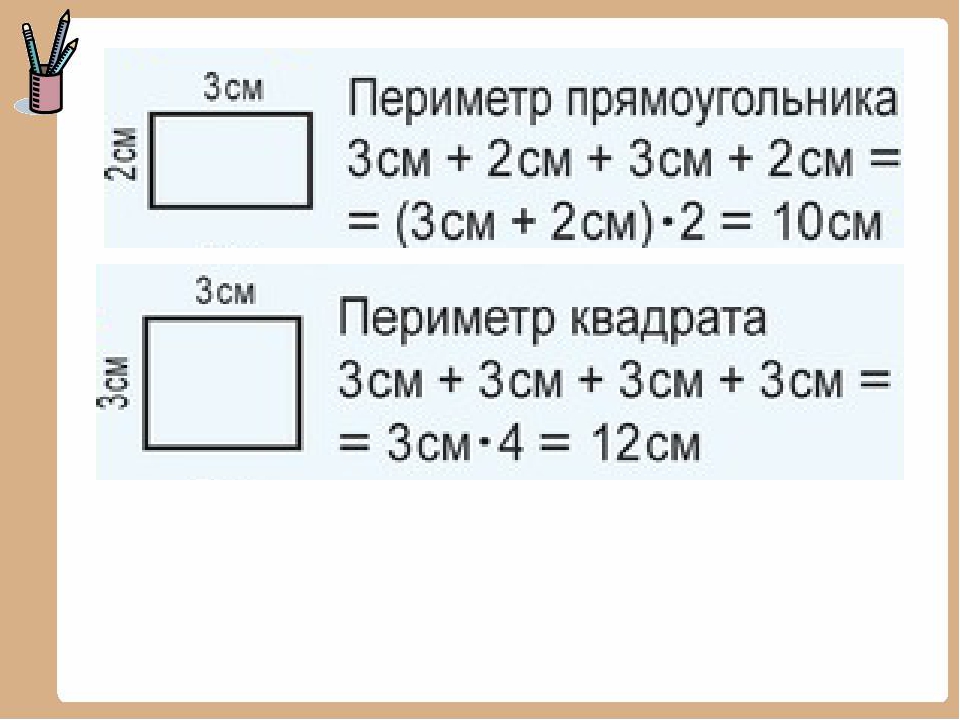
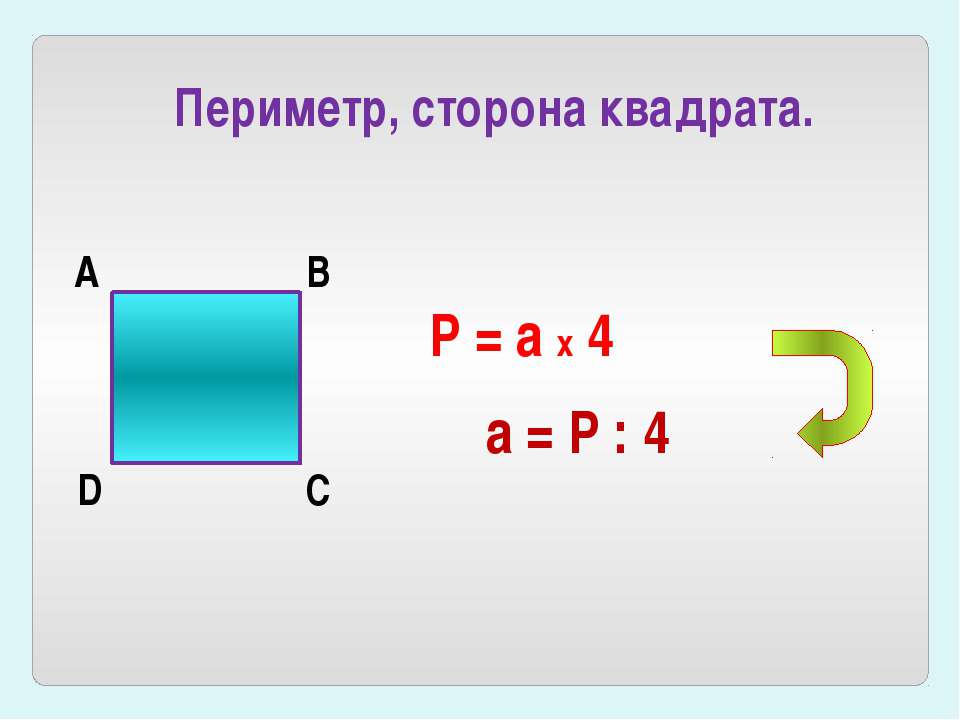
Периметр и площадь квадрата

Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:

P= a*4
P= a+a+a+a

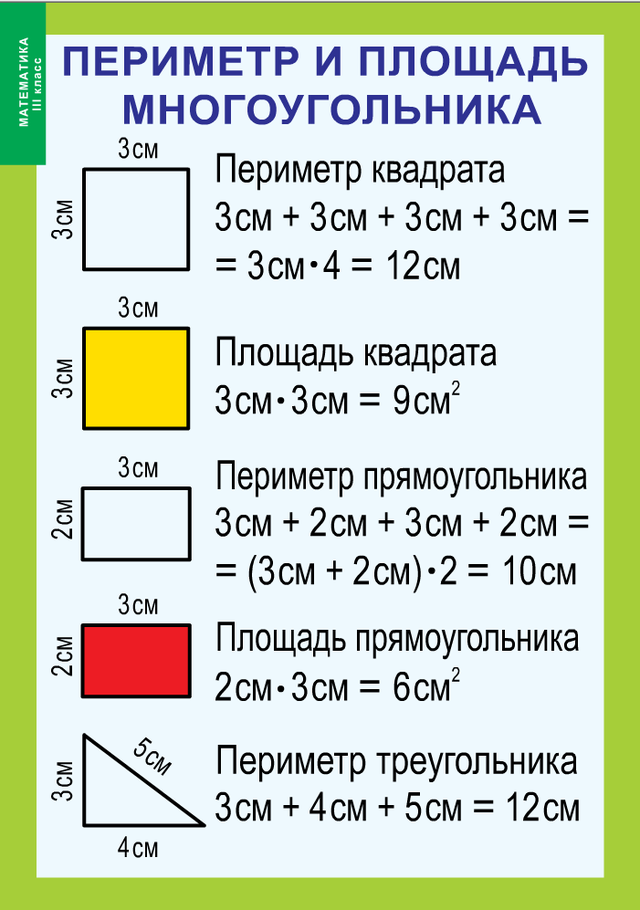
Например, перед нами квадрат со стороной 10 см:

P= 10*4
P=40

Ответ: 40 см

P= 10+10+10+10
P=40

Ответ: 40 см

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.

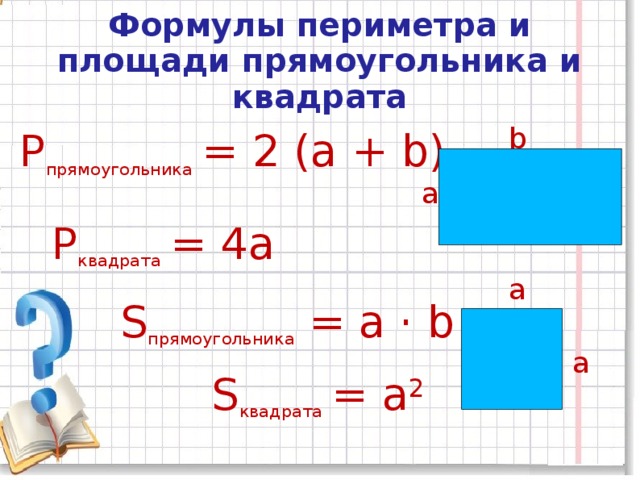
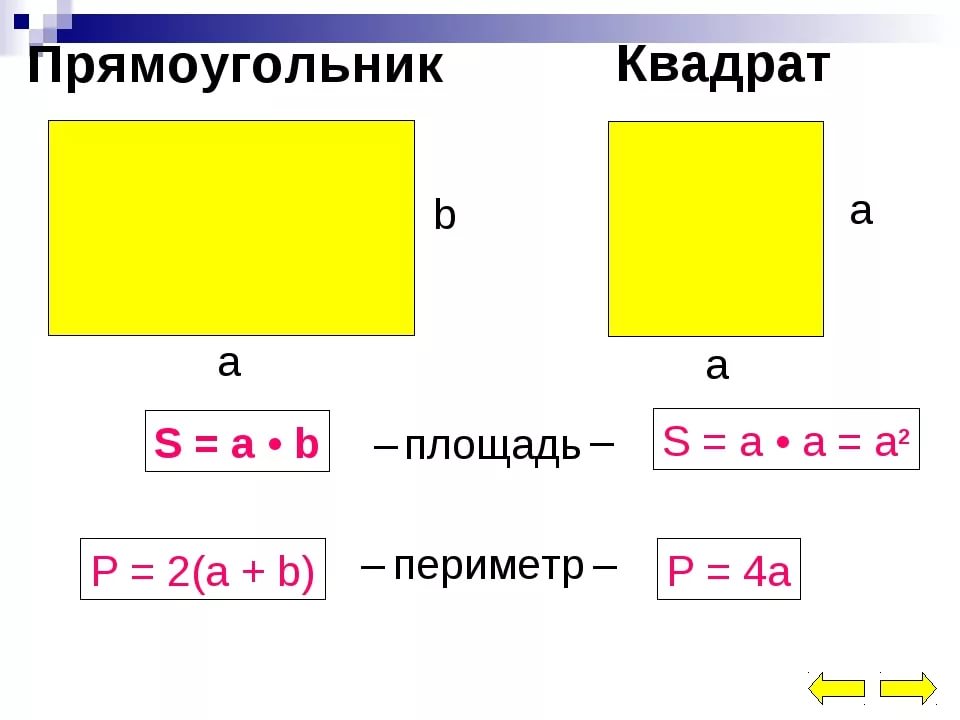
Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:

S= a*a
S=a2

S – это площадь, а – сторона квадрата.

Например, в задаче указано, что длина стороны квадрата составляет 10см.

S=10*10
S= 100см2

Ответ: 100см2

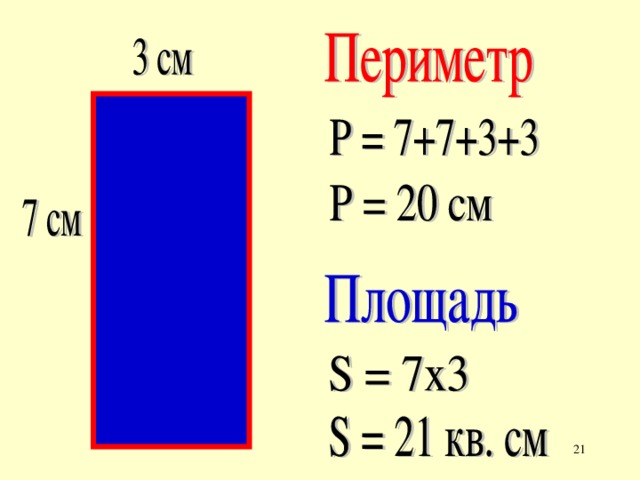
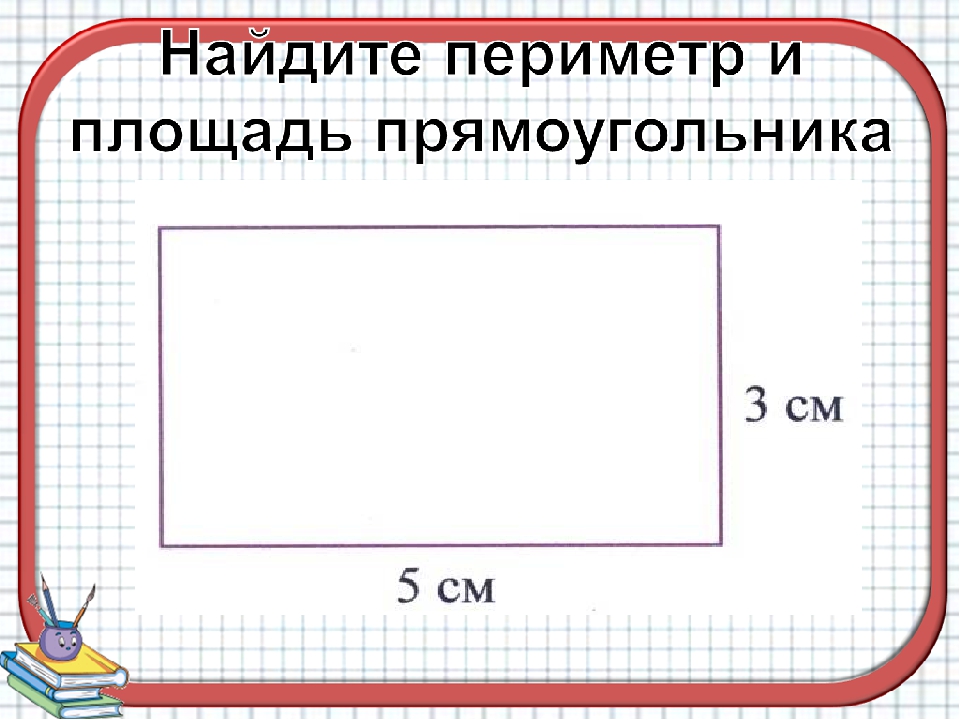
Периметр и площадь прямоугольника

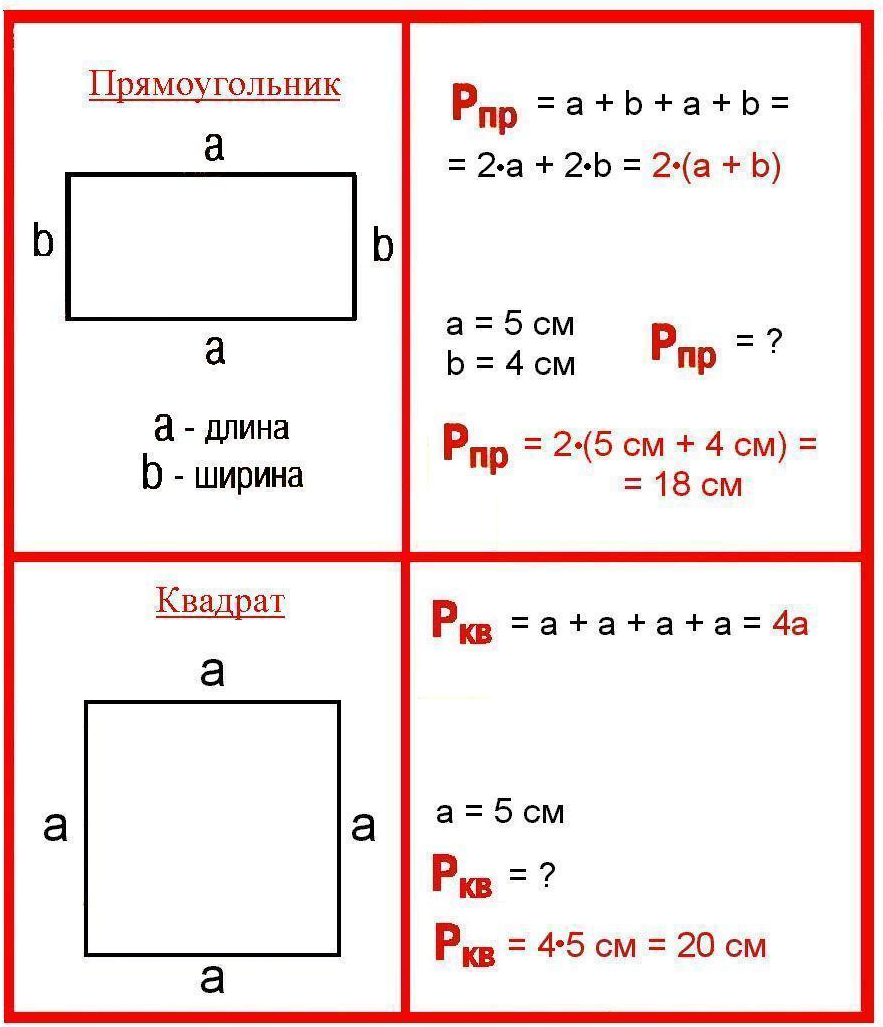
Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:

P= (a+b)*2

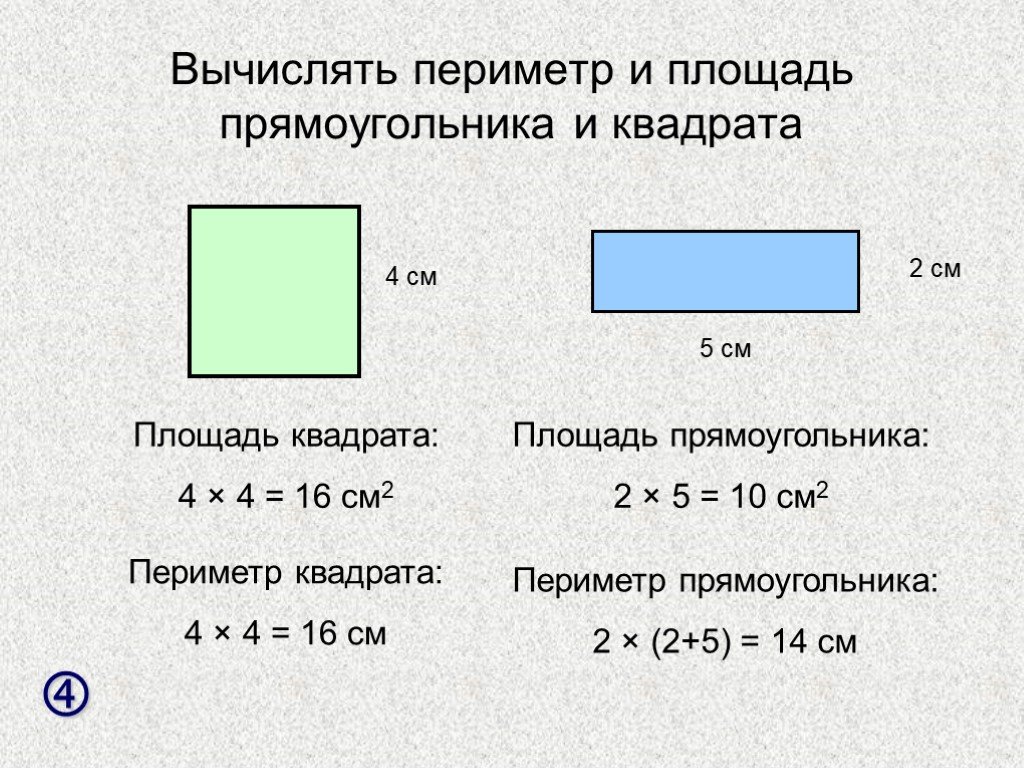
Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два. Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см:

P= (6+2) * 2
P= 16

Ответ: 16 см

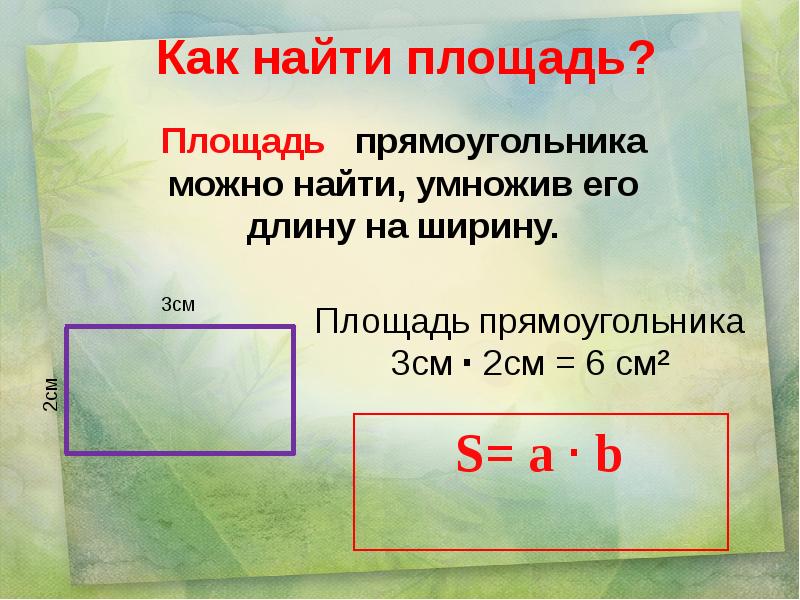
Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:

S= a*b

Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа:

S= 5*2
S=10см2

Ответ: 10 см2

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:

L = 2πr
L= 2πd

L – длина окружности

π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

π = 3.141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R – это радиус окружности

D – Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр:

L= 2*3,14*3
L=6π
L=6*3.14
L = 18.84 см
Pк= 18,84 см

Ответ: 18.84 см

Отличие периметра от площади

Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ. Площадь всегда измеряется в квадратных единицах (см2, м2, мм2). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.

Осмысление периметра

Чем мельче структура фигуры, тем меньше площадь и тем больше периметр. Выпуклая оболочка остаётся той же самой.

Периметр крепости Нёф-Бризах сложный. Кратчайший путь для обхода крепости — по границе выпуклой оболочки.

Основные статьи: Площадь и выпуклая оболочка

Периметр и площадь являются двумя основными измерениями геометрических фигур, их часто путают. Нередко также считают, что увеличение одной из этих величин приводит к увеличению другой. Действительно, увеличение (или уменьшение) размера фигуры приводит к увеличению (или уменьшению) её площади, так же как и её периметра. Так, например, если нарисовать карту поля в масштабе 1/10 000, действительные размеры периметра можно вычислить простым умножением на 10 000. Действительная площадь будет в 10 0002 раз больше площади фигуры на карте.

Тем не менее, нет никакой связи между площадью и периметром фигур. Например, периметр прямоугольника шириной 0,001 и длиной 1000 чуть больше 2000, в то время, как периметр прямоугольника шириной 0,5 и длиной 2 равен 5. Площади обеих фигур равны 1.

Прокл (V-й век) писал, что греческие крестьяне делили поля, опираясь на периметры, однако урожай с поля пропорционален площади, а не периметру, и много наивных крестьян получали поля с большим периметром, но малой площадью.

Если удалить часть фигуры, её площадь уменьшится, а вот периметр может и не уменьшиться. В случае очень неправильных фигур некоторые могут спутать периметр с выпуклой оболочкой. Выпуклую оболочку визуально можно представить как резинку, натянутую вокруг фигуры. На рисунке слева все фигуры имеют одну выпуклую оболочку (шестиугольник).

Периметр окружности

Если диаметр окружности равен 1, её периметр равен π.

Периметр окружности пропорционален её диаметру (и радиусу). То есть, существует константа π такая, что если P — периметр окружности, а D — её диаметр, то:

P=π⋅D.{\displaystyle P=\pi \cdot {D}.}

Для радиуса r окружности формула превращается в

P=2π⋅r.{\displaystyle {P}={2}\pi \cdot {r}.}

Для вычисления периметра окружности знание радиуса или диаметра и числа π достаточно. Проблема заключается в том, что π не является рациональным (его нельзя выразить в виде дроби двух целых чисел) и даже не является алгебраическим (оно не является корнем никакого полиномиального уравнения с рациональными коэффициентами)

Таким образом, получение точного приближения к π важно для вычислений. Нахождение знаков π относится ко многим областям, таким как математический анализ и теория алгоритмов.

Площадь прямоугольника

В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.

Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.

Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.

Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:

Теперь измерим ширину. Пусть она составила 3 метра:

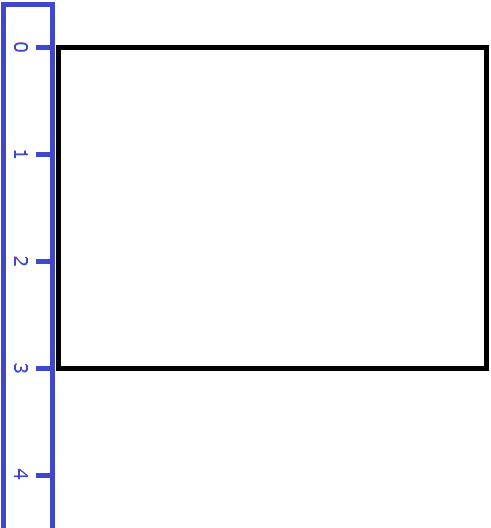
Умножим длину (4 м) на ширину (3 м).

4 × 3 = 12

Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:

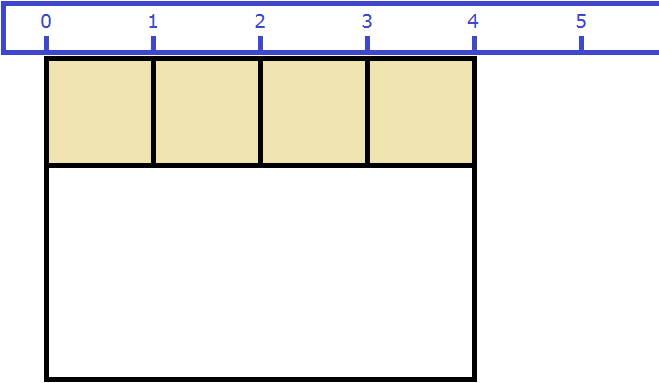
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:

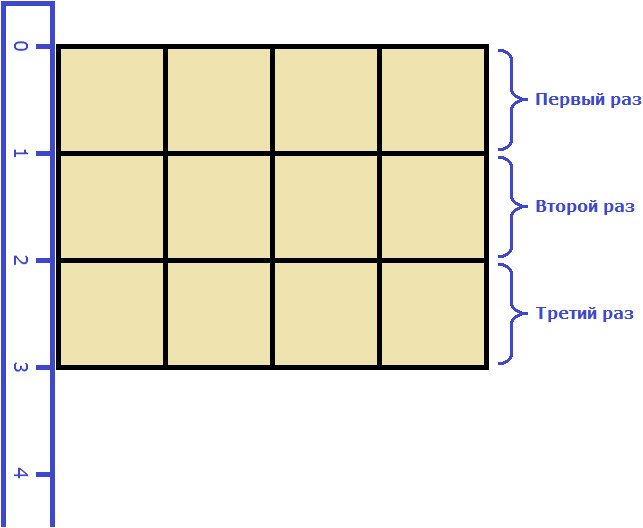
Осмысление периметра

Периметр крепости Нёф-Бризах сложный. Кратчайший путь для обхода крепости — по границе выпуклой оболочки.

Определение и расчет площади застройки

Разделите плоскость на части, которые лучше для расчета площади. Если вы чувствуете, что область не легко найти, то запрашиваемая область может быть нерегулярной. План этажа здания может иметь видные части в разных местах, что может не соответствовать обычной графике. Все, что вам нужно сделать, это разделить его на правильные прямоугольники или треугольники.

Как измерить площадь застройки: определение и расчет площади помещения.

Чтобы узнать площадь плоскости всего пространства, вам нужно знать площадь каждой части, а затем сложить их.

Используйте пунктирные линии, чтобы разделить плоскость на разные части.
Для удобства отметьте A, B и C.

Сначала измерьте длину и ширину первой части. Используя линейку или рулетку, измерьте длину и ширину части A.

Это 12 футов (3,7 метра) в длину и 15 футов (4,6 метра) в ширину.

Умножьте длину первой части на ширину. Чтобы запросить площадь этой части, вам нужно только умножить длину на ширину, как и площадь общего прямоугольника.

Например: 12 футов (3,7 метра) x 15 футов (4,6 метра) = 180 квадратных футов (17 квадратных метров)

Измерьте длину и ширину второй части. Секция B имеет длину 20 футов (6,1 метра) и ширину 10 футов (3,0 метра).

Умножьте длину второй части на ширину. Таким образом, можно получить площадь второй части. Ниже приведен процесс расчета:

Например: 20 футов (6,1 метра) х 10 футов (3,0 метра) = 200 квадратных футов (18 квадратных метров)

Измерьте длину и ширину третьей части.Секция C имеет длину 20 футов (6,1 метра) и ширину 35 футов (10,7 метра).

Умножьте длину третьей части на ширину. Таким образом, можно получить площадь третьей части. Ниже приведен процесс расчета:

Например: 20 футов (6,1 метра) х 35 футов (10,7 метра) = 700 квадратных футов (64 квадратных метра)

Добавьте области трех частей. Когда вы найдете сумму площадей трех частей, вы узнаете площадь плоскости. Вот процесс:

Площадь A + Площадь B + Площадь C = площадь всей плоскости
180 + 200 + 700 = 1080 квадратных футов (100 квадратных метров)

Советы по замерам нестандартных построек

Найдите приблизительную площадь застройки. Если вам необходимо измерить площадь здания по внешним границам, вы можете измерить площадь вне дома, а затем вычесть площадь, которая не является частью дома, например, входную лестницу или гараж.

Найдите площадь застройки полукруглой плоскости. Если часть дома является полукругом, вы можете найти площадь круга, в котором она находится, а затем разделить на 2. Измерьте разделительную линию полукруга, чтобы получить диаметр.

Разделите диаметр на 2, чтобы получить радиус, и затем приведите его в формулу A = πr ^ 2, где r представляет радиус. Разделите результат на 2, чтобы получить площадь полукруга.

Найдите примерную площадь застройки. Если плоскость здания представляет собой почти прямоугольник или треугольник, но отсутствует только небольшая часть прямоугольника или треугольника, то вы можете «наверстать» недостающую часть и затем вычислить площадь всей фигуры. Затем найдите область недостающей части и вычтите ее из предыдущего результата, чтобы получить площадь здания. Этот метод экономит время.

На заметку! Если площадь которую вы хотите замерить не стандартной формы, вы можете разделить ее на несколько частей правильной формы, а затем измерить площадь каждой части отдельно и, суммировать их.

На первый взгляд может показаться, что провести такие замеры проще простого, однако качественно сделать это могут только профессиональные замерщики помещений, с большим стажем работы в области обмеров, в распоряжении которых есть все необходимые для этого инструменты.

Обмер помещений — составление плана, вычисление площади.

Команда профессиональных инженеров «obmer.pro» с большим стажем работы в области обмеров и проектирования, проводят работы со зданиями и сооружениями любого назначения. Обмерные работы включают в себя подготовку точных обмерных чертежей, расчеты площадей для выявления любых неточностей, подробный отчет обследования зданий и конструкций для реконструкции, реставрации и сноса.

Осмысление периметра

Периметр крепости Нёф-Бризах сложный. Кратчайший путь для обхода крепости — по границе выпуклой оболочки.

Помещение неправильной формы

Итак, рассмотрим на конкретных примерах способы вычисления метража:

Кухня. Каждая кухня имеет вентиляционную шахту, радиатор вдоль окна, дверь, окно и встроенную полку для хранения. Посчитаем чистую площадь стен кухни для поклейки обоев.

Данные кухни:

Высота =2,5 м;

Ширина=3 м;

Длина =3,5м.

Размер двери: ширина =0,8 м, высота = 2,0 м;

Размер окна: ширина 1,2 м, высота = 1,5м;

Вентиляционная шахта имеет следующие габариты: ширина =50 см, длина =30 см; высота = 2,5 м;

Габариты радиатора: ширина = 10 см, длина = 100 см, высота = 50 см.

Вычислим чистую площадь:

Сначала находим общую площадь: (3,5 м*2)+(3 м*2)*2,5 м = 32,5 м2;

Далее, определяем площади вычитаемых квадратов:

Окна: S чистая = 1,2 м*1,5 м = 1,8 м2;

Двери: S чистая = 0,8 м*2,0 м = 1,6 м2;

Вентиляционная шахта: S чистая = (50 см * 2) + (30 см *2) *2,5 м = 400 см2 или 0,40 м2;

Встроенная полка: S чистая = (20 см*2) + (50 см * 2) *2,5 м = 350 см2 или 0,35 м2;

Площадь поверхности радиатора: (10 см *2) + (100 см *2) * 0,5 м = 110 см2 или 0, 11 м2.

Теперь определяем количество чистых квадратных метров, путем вычитания их общей площади: S чистая стен кухни = 32,5 м2 — 1,8 м2- 1,6 м2- 0,40 м2- 0,35 м2 – 0,11 м2 = 28,24 м2.

Полезный совет: для подсчета количества трубок обоев, необходимо разделить чистую площадь на количество листов в трубке.

Стандартная трубка имеет следующие размеры: ширина = 50 см, длина полотна = 10 м. Высота стен квартиры составляет 2,5 м, и этого следует, что в одну трубку обоев входит 4 бумажных полотна: 10 м /2,5 м= 4 листа.

Подсчитаем, сколько же нужно трубок, чтобы поклеить кухню:

28,24 м2 /4 = 7,06 трубок. Но так как, бумажное полотно может содержать рисунок с шагом 0,3 или 0,5, то следует округлить количество трубок до 8.

Ванная комната. Рассчитаем количество ящиков плитки для стандартной ванны. Чтобы правильно посчитать квадратуру помещения, необходимо производить измерения с учетом подрезки керамической плитки.

Нам известен стандартный размер двери: ширина =0,8 м; высота = 2,0 м.

Размер типовой ванной комнаты составляет: ширина 2,3 м; длина = 1,6 м, высота= 2,5 м.

Вычисляем чистую площадь ванны:

S ванны = (2,3 м*2) + (1,6 м*2) *2,5 м = 19,5 м2.

Затем, вычитаем следующие значения:

S чистая = 19,5 м2 – 1,6 м2 = 17,9 м2.

Для того, чтобы подсчитать, сколько же ящиков плитки Вам необходимо, следует определиться с размером керамического изделия. Плитка бывает следующих размеров: 10х10; 10х20; 20х30; 30х30. Возьмем более распространенный вариант: 30х30.

В одной упаковке находится 10 штук и, зная размер плитки, можно высчитать количества штук на 1 м2:

Определим, количество целых плиток и количество подрезки:

17,9 м2 / 9= 1,9 — округляем и получаем 20 коробок целых плиток;

20 * 7 = 140 маленьких плиток, размером 10х10.

Если класть плитку по плоскости без подрезки, то следует брать 20 ящиков, а если с подрезкой, то 16.

Балкон. Чтобы получить чистую площадь балкона, необходимо измерить рамы с остеклением. Периметр балкона вымеряется без учета окон.
Гараж. Как правило, гараж представляет собой коробку с маленьким окном. Для подсчета чистой площади, необходимо измерить размеры ворот.

Померить площадь круглого окна, перекрытия, стены здания в виде неправильной формы или восьмигранника, можно с помощью подручных средств.

Возьмите рулетку и вымеряйте максимальный диаметр круга, например, он получился 100 см. Вычисляем радиус: 100 см /2 =50 см — это ¼ круга в виде треугольника.

Если круг зрительно разделить на 4 части, и соединить точки прямыми линиями, мы получим 2 равнобедренных треугольника или 1 квадрат. Нам известна часть равнобедренного треугольника, следовательно, все стороны будут по 50 см. Остается найти площадь квадрата, где все стороны по 50 см. Вычислить общую площадь любой конструкции можно с помощью онлайн – программы.

Смотрите видео, в котором мастер подробно разъясняет, как правильно высчитать площадь стен в квартире: