МЕТОД
К рентгеновским лучам относят излучение, занимающее участок электромагнитного спектра от нескольких сотен до десятых долей ангстрема ( Å) (1 Å = 0,1 нм). Расстояние между атомами в кристаллической решетке твердых тел колеблется от единиц до полутора десятков ангстрем. Прохождение рентгеновских лучей через вещество сопровождается разными видами взаимодействия, одним из которых является рассеяние рентгеновских лучей. Вещество, которое подвергается действию рентгеновского излучения, испускает вторичное излучение, длина волны которого равна длине волны падающих лучей (когерентное рассеяние). Каждый изолированный атом рассеивает излучение равномерно во все стороны в виде концентрических сфер. Если падающая волна рентгеновского излучения перпендикулярна атомному ряду, то все атомы ряда одновременно излучают электромагнитные колебания. Поскольку расстояние между атомами соизмеримо с длиной волны вторичного когерентного излучения, то кристалл может служить для него дифракционной решеткой. Энергия этого излучения рассеивается в разных направлениях с различной интенсивностью: по одним направлениям усиливается, по другим – ослабляется и даже полностью гасится. Усиление колебаний происходит по тем направлениям, где разность хода рентгеновских лучей равна целому числу волн или четному числу полуволн. Это правило (условие интерференции) справедливо для любого излучения. В результате образуется серия плоских волн, которые распространяются в особых направлениях. Дифрагированный луч можно рассматривать как результат отражения от одной из плоскостей атомной решетки. Любая трехмерная решетка рассматривается как совокупность бесконечного числа параллельных атомных плоскостей, расположенных на равном расстоянии друг от друга. Отражение лучей будет происходить не только от внешней поверхности, а от всех атомных плоскостей (их серий), так как рентгеновский луч, в отличие от оптического излучения, проникает вглубь кристалла.
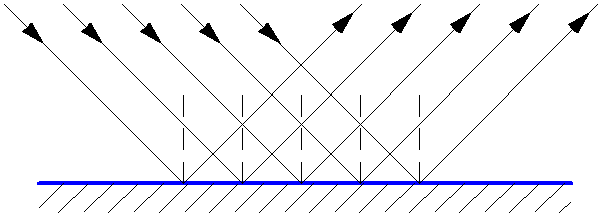
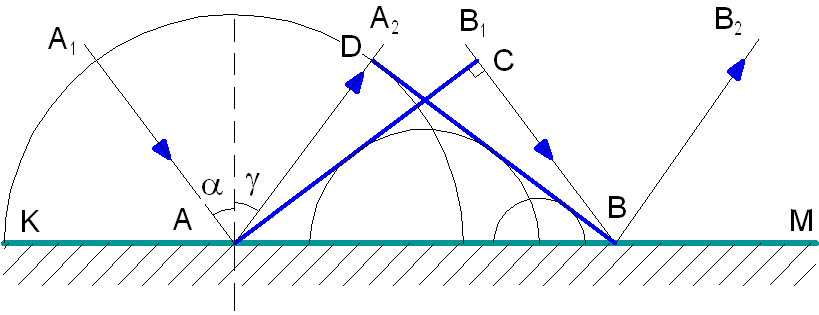
Серия плоскостей характеризуется межплоскостным расстоянием d (рис. 1). Каждая плоскость отражает луч под одним и тем же углом, так как рентгеновские лучи распространяются в веществе практически без преломления. При отражении лучи могут интерферировать в том случае, если их разность хода (АОВ) будет равна целому числу волн Δ (АОВ) = nλ; АОВ = 2d ∙ sin θ.
Рисунок 1 – Иллюстрация отражения лучей от серии плоскостей атомной решетки
Условие дифракции рентгеновских лучей (уравнение Вульфа – Брэгга) имеет вид:
2d ∙ sin θ = nλ,
где
n – порядок отражения (n = 1, 2, 3).
При выполнении условия Вульфа – Брэгга рентгеновский луч регистрируется детектором или на фотопленке. Интенсивность максимума зарегистрированного луча зависит от количества и типов атомов, составляющих данное семейство плоскостей, то есть от «заселенности» атомной плоскости. Поэтому интенсивность отраженного луча также является характеристикой изучаемого объекта.
Широкое распространение из-за простоты и универсальности получил метод порошка (метод Дебая — Шеррера), когда монохроматический пучок рентгеновских лучей направляют на поликристаллический образец. Так как кристаллы, из которых состоит образец, очень малы (микрокристаллы), то в исследуемом объеме образца их оказываются десятки миллионов. Отраженные разными микрокристаллами лучи различной интенсивности фиксируются либо на специальной фотопленке, либо детектором. Рассчитав полученную таким путем рентгенограмму (дифрактограмму), получают сведения о межплоскостных расстояниях в кристалле. Значение межплоскостных расстояний для каждого вещества строго индивидуально, поэтому рентгенограмма (дифрактограмма) однозначно характеризует исследуемое вещество.
8.Поляризация света. Закон Малюса. Поляризация света при отражении и преломлении. Угол Брюстера.
ПОЛЯРИЗАЦИЯ
СВЕТА
Свет,
у которого направления колебаний
вектора упорядочены
каким-то образом, называется поляризованным.
В зависимости от характера колебаний
векторов напряжённости электрического
и магнитного полей плоской монохроматической
электромагнитной волны поляризация
волны может быть линейной, круговой и
эллиптической. В линейно
поляризованной волне колебания
вектора напряжённости электрического
поля совершаются вдоль линии, расположенной
в плоскости, перпендикулярной направлению
распространения волны.Плоскость
поляризации,
обозначенная символом на
рис. 8.1a, определяется направлением
распространения волны и направлением
колебаний вектора напряжённости
электрического поля. В волне,
поляризованной по кругу,
вектор напряжённости электрического
поля вращается
по кругу в плоскости, перпендикулярной
направлению распространения волны,
которое совпадает с осью .
В эллиптически
поляризованной волне,
по мере распространения волны вектор
напряжённости электрического поля
перемещается по эллипсу (рис. 8.1c) в
плоскости, перпендикулярной направлению
волны, распространяющейся, в соответствии
с рис. 8.1c, вдоль оси .Круговую
или эллиптическую поляризацию
электромагнитной волны называют левой,
если вращение вектора напряжённости
электрического поля этой волны происходит
против часовой стрелки, если смотреть
с направления волны. Наоборот, если
вращение вектора напряжённости
электрического поля этой волны происходит
по часовой стрелке, если смотреть с
направления волны, то поляризация
электромагнитной волны называется
правой.
Состояние поляризации произвольной
электромагнитной волны задаётся степенью
поляризации.
Для определения степени поляризации
электромагнитной волы её пропускают
через поляризатор, в котором можно
менять ориентацию плоскости поляризатора,
например, с помощью поворота поляризатора
относительно направления распространения
исследуемой электромагнитной волны. В
двух взаимно ортогональных ориентациях
плоскости поляризатора будут дважды
отмечены максимальное и
минимальное значение
интенсивности проходящей поляризатор
электромагнитной волны. .
ЗАКОН
МАЛЮСА
Интенсивность прошедшей
поляризатор волны,
пропорциональная, как неоднократно
указывалось выше, квадрату модуля
вектора напряжённости её электрического
поля, может быть определена следующим
образом:
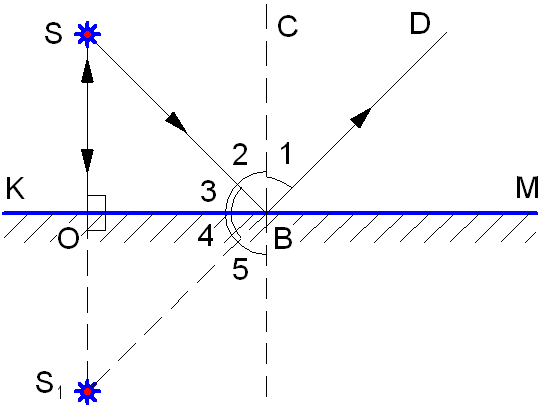
Поляризация
света при отражении и преломлении на
границе двух диэлектриков. Закон
Брюстера.
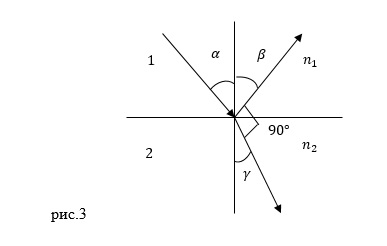
Если
естественный свет падает на границу
раздела двух диэлектриков (например,
воздуха и стекла), то часть его отражается,
а часть преломляется и распространяется
во второй среде. Устанавливая на пути
отраженного и преломленного лучей
анализатор (например, турмалин), убеждаемся
в том, что отраженный и преломленный
лучи частично поляризованы: при
поворачивании анализатора вокруг лучей
интенсивность света периодически
усиливается и ослабевает (полного
гашения не наблюдается!). Дальнейшие
исследования показали, что в отраженном
луче преобладают колебания, перпендикулярные
плоскости падения (на рис. 10.4 они
обозначены точками), в преломленном —
колебания, параллельные плоскости
падения (изображены стрелками).
Степень
поляризации (степень выделения световых
волн с определенной ориентацией
электрического (и магнитного) вектора)
зависит от угла падения лучей и показателя
преломления. Шотландский физик Д.
Брюстер (1781—1868)
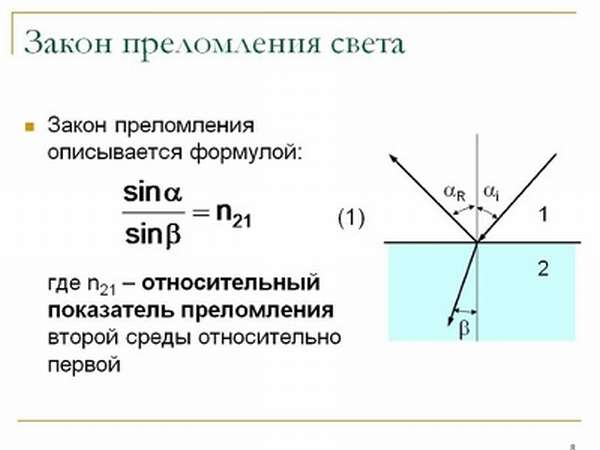
установил закон,
согласно которому при угле падения iB (угол
Брюстера), определяемого соотношением
(n21 —
показатель преломления второй среды
относительно первой), отраженный
луч является плоскополяризованным (содержит
только колебания, перпендикулярные
плоскости падения).
Полное внутреннее отражение в природе и технике
Фата-моргана, эффекты миража, например иллюзия мокрой дороги при летней жаре. Здесь отражения возникают из-за полного отражения между слоями воздуха с разной температурой.
Яркий блеск многих природных кристаллов, а в особенности — огранённых драгоценных и полудрагоценных камней объясняется полным внутренним отражением, в результате которого каждый вошедший в кристалл луч образует большое количество достаточно ярких вышедших лучей, окрашенных в результате дисперсии.
Блеск алмазов, выделяющий их из прочих драгоценных камней, также определяется этим феноменом. Из-за высокого показателя преломления (n ≈ 2) алмаза оказывается большим и число внутренних отражений, которые претерпевает луч света с меньшими потерями энергии, по сравнению со стеклом и другими материалами с меньшим показателем преломления.
Отражение рыбы на поверхности раздела воздух-вода.
Полное внутреннее отражение можно наблюдать, если смотреть из-под воды на поверхность: при определённых углах на границе раздела наблюдается не внешняя часть (то, что в воздухе), а видно зеркальное отражение объектов, которые находятся в воде.
Светоделительный куб
Непосредственно за первой граничной поверхностью, то есть на расстоянии максимум, равной длине волны света, вторая граничная поверхность имеет тот же показатель преломления n1. Электромагнитная волна света проникает через полосу с показателем преломления n2 и попадает во вторую граничную поверхность с показателем преломления n1, но с меньшим значением энергии. Наблюдается раздвоение луча света, часть которого проникла в зону с показателем преломления n2. В конечном результате луч раздваивается : часть распространяется дальше в первоначальном направлении, в то время как другая часть отражается. Потеря интенсивности в среде n2 проходит экспоненциально по формуле:
- I=I⋅exp(−xλ).{\displaystyle I=I_{0}\cdot \exp \!\left(-{\frac {x}{\lambda }}\right).}
Световод
Эффект полного внутреннего отражения используется в оптических волокнах. Осевая часть волокна (сердцевина) формируется из стекла с более высоким показателем преломления, чем окружающая оболочка. Такие световоды используются для построения волоконно-оптических кабелей.