Описанная окружность

Углы

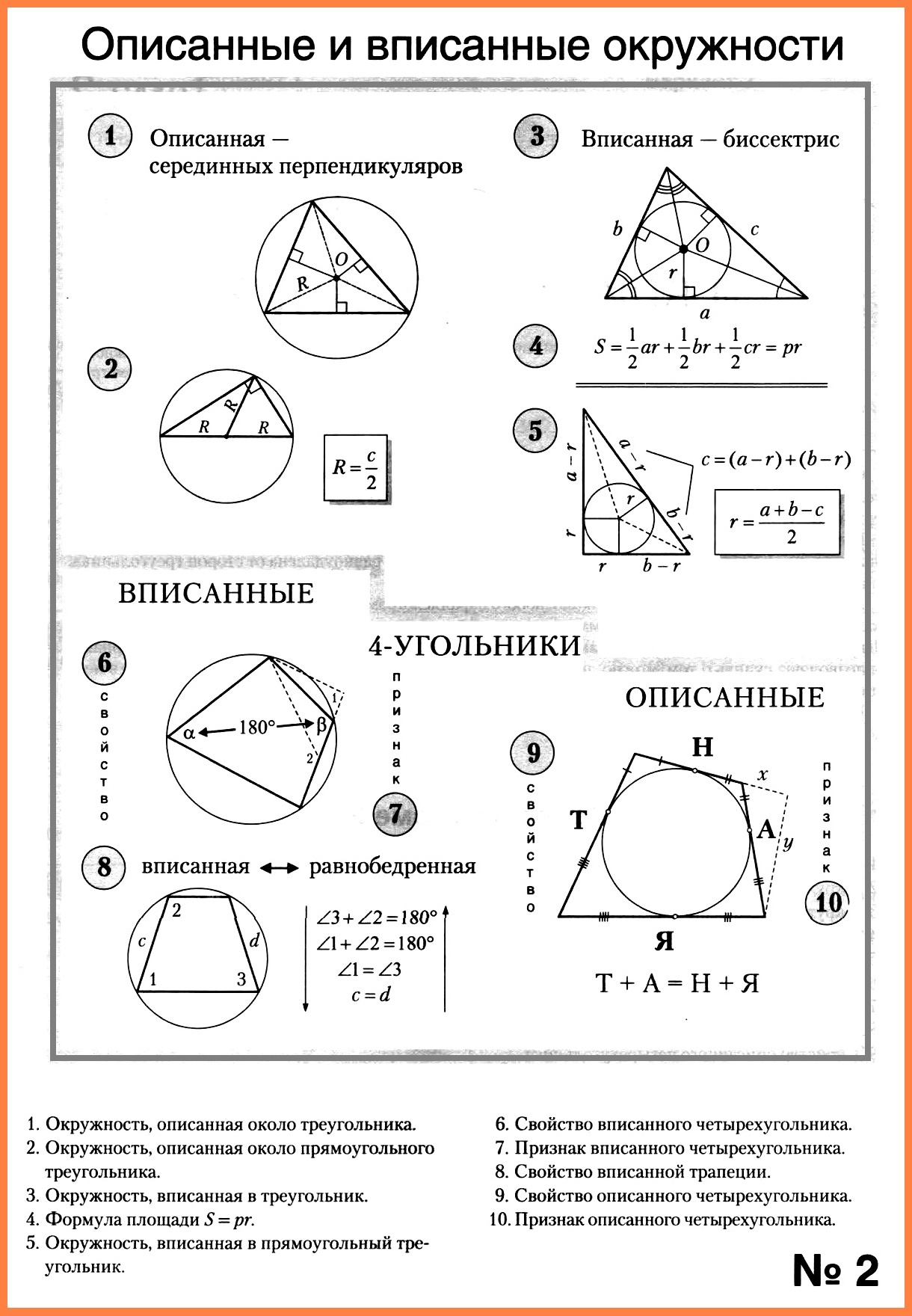
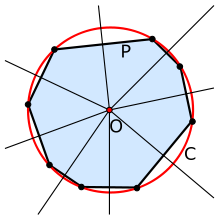
Центральный угол — угол с вершиной в центре окружности. Центральный угол может быть принят как угловая мера дуги, на которую он опирается. Центральный угол, образуемый дугой окружности, равной по длине радиусу, в математике принимается в качестве единицы измерения углов, и называется радиан.

Из определения радиана следует, что длина L{\displaystyle L} любой дуги окружности связана с центральным углом θ{\displaystyle \theta }, опирающимся на эту дугу, простым соотношением: L=Rθ.{\displaystyle L=R\theta .} (при этом длина хорды, стягивающей ту же дугу, равна 2Rsin⁡θ2<L{\displaystyle 2R\sin {\theta \over 2}<L}). Поскольку длина окружности равна 2πR{\displaystyle 2\pi R}, с ростом угла значение его радианной меры меняется от 0 до 2π.{\displaystyle 2\pi .}

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.

Внешний угол для вписанного угла — угол, образованный одной стороной и продолжением другой стороны вписанного угла (угол θ коричневого цвета на рис.). Внешний угол для вписанного угла равен вписанному углу, опирающемуся на ту же хорду с другой стороны.

Угол между окружностью и прямой — угол между секущей прямой и одной из двух касательных к окружности в точке пересечения прямой и окружности.

Свойства вписанных углов:

• Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°. Вписанный угол, опирающийся на дугу длиной в половину окружности, всегда прямой (равен 90°).
• Вписанный угол не меняет своей величины при перемещении его вершины вдоль окружности.
• Два вписанных угла, опирающиеся на одну и ту же дугу, равны.

Другие свойства:

• Угол между двумя секущими, проведёнными из точки, лежащей вне окружности, равен полуразности мер дуг, лежащих между секущими.
• Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле, и дуги напротив неё.
• Угол между касательной и хордой, имеющими общую точку, равен половине угловой меры дуги, стягиваемой хордой.

О городе Орле

Орел – замечательный старый город, который совмещает очарование старой архитектуры и функциональность современных зданий. Расположен он на Среднерусской возвышенности по обеим сторонам реки Оки и её притока Орлика. Население составляет около 341 тысячи жителей. Был основан в 1566 году как крепость для защиты южных границ государства. Статус города Орел получил в 1702 году. Впоследствии город административно входил в состав различных губерний страны, а в 1778 году стал центром Орловской губернии.

За время своего существования Орёл прошёл путь развития от небольшой крепости с примыкавшими к ней слободами до современного культурного и промышленного центра области.

За всю историю Орла ни одна военная кампания не обошла его стороной. Не раз вставал он на пути врагов и давал им сокрушительный отпор. Орел – город воинской славы Российской Федерации. Два года во время Великой Отечественной войны он находился под оккупацией фашистских войск. Город был освобожден во время сражения на Орловско-Курской дуге. Сильные разрушения понес Орел и его восстановление стало одной из главных послевоенных строек СССР. Известным памятным фактом, которым гордятся жители города, стал первый в истории Великой Отечественной войны артиллерийский салют в честь освобождения советскими войсками от немецких фашистов. В честь этого каждый год 5 августа Орел отмечает День города.

Достаточно оперативно Орел был возрожден – уже через три месяца после освобождения города были возрождены 26 предприятий. Появились новые отрасли: коммунальное дорожное и машиностроение, производство тракторных запасных частей и строительных материалов, а также приборостроение . Строилось жилье, школы, больницы, детские сады, вузы, учреждения культуры. На площадях, улицах и скверах города было сооружено тридцать монументов и памятных стел, а также двадцать скульптурный бюстов, монументальных мозаик, барельефов и росписей. Число мемориальных досок в Орле дошло уже до семидесяти, а надгробных кладбищенских памятников, многие из которых являются подлинными произведениями искусства, насчитывается несколько сотен. Расположенные вокруг Орла плодородные земли всегда привлекали в город виднейшие дворянские семьи, благодаря чему он стал средоточием дворянской культуры.

Орел — родина писателей И.С.Тургенева и Л.Н.Андреева, историка Т.Н.Грановского, философа М.М.Бахтина. С городом Орлом связаны жизнь и творчество И.А.Бунина, Н.С.Лескова, А.Н.Апухтина и многих других выдающихся людей. Среди Почётных граждан города – маршал Куликов и Герой Советского Союза летчик Алексей Маресьев, который продолжал воевать с ампутированными ногами.

Современный Орел – научный и промышленный центр, ведущее звено общественно-политической и культурной жизни Черноземья. Город является крупным индустриальным центром одного из важнейших аграрных регионов страны. Там наиболее развиты приборостроение и машиностроение, функционируют предприятия сталепрокатной, легкой и пищевой промышленности.

Хорошо развита в городе торговая инфраструктура.

Орел – студенческий город, там действует 12 высших учебных заведений, в которых обучается около 50 тысяч студентов.

В последние годы Орел заметно помолодеет. Кварталы Орла застраиваются по индивидуальным проектам, чтобы сама архитектура создавала настроение. Город строится, растет вверх этажами, украшается скверами, парками и фонтанами. Бережно хранит он традиции русской духовности. Один за другим восстанавливаются и реставрируются храмы и соборы Орла.

Орел – крупный автомобильный и железнодорожный транспортный узел. Внутригородское транспортное хозяйство Орла составляют: трамвайные пути, троллейбусные линии, автобусные маршруты, городской и пригородный транспорт.

Благодаря тому, что движение в Орле транспортных средств, загрязняющих окружающую среду, неинтенсивное и город утопает в зелени – городской воздух остается не загрязненным и здоровым. Это несомненно привлекает туда туристов. Орел, расположенный в самом сердце центральной России – замечательный город, который достоин посещения. Известен он своим богатым историческим прошлым и литературными традициями.

В Орле находится большое количество развлечений для любого возраста, от мала до велика. Основными туристскими достопримечательностями Орла являются Васильевская, Иверская, Крестительская, Михайло-Архангельская, Николо-Песковская, Смоленская и Троицкая церкви, два действующих монастыря, памятники русским писателям Н.С.Лескову, И.С.Тургеневу и И.А. Бунину. В городе работают 4 театра, филармония, 11 музеев, 4 кинотеатра, несколько парков и другие.

Вблизи различных достопримечательностей располагаются гостиницы, двери которых радушно открыты для гостей города.

Касательные прямые к одной окружности

Касательная прямая t к окружности C пересекает окружность в единственной точке T. Для сравнения, секущие прямые пересекают окружность в двух точках, в то время как некоторые прямые могут не пересекать окружность совсем. Это свойство касательной прямой сохраняется при многих геометрических , таких как подобие, вращение, параллельный перенос, инверсия и картографическая проекция. Говоря техническим языком, эти преобразования не меняют структуру инцидентности касательных прямых и окружностей, даже если сами прямые и окружности деформируются.

Радиус окружности, проведённый через точку касания, перпендикулярен касательной прямой. И обратно, перпендикуляр к радиусу в конечной точке (на окружности) является касательной прямой. Окружность вместе с касательной прямой имеют осевую симметрию относительно радиуса (к точке касания).

По теореме о степени точки произведение длин PM•PN для любого луча PMN равно квадрату PT, длине отрезка от точки P до точки касания (отрезок показан красным цветом).

Никакая касательная прямая не может проходить через точку внутри окружности, поскольку любая такая прямая должна быть секущей. В то же время для любой точки, лежащей вне круга, можно построить две проходящие через неё касательные прямые. Геометрическая фигура, состоящая из окружности и двух касательных прямых, также обладает осевой симметрией относительно прямой, соединяющей точку P с центром окружности O (см. рисунок справа). В этом случае отрезки от точки P до двух точек касания имеют одинаковую длину. По теореме о степени точки квадрат длины отрезка до точки касания равен степени точки P относительно окружности C. Эта степень равна произведению расстояний от точки P до двух точек пересечения окружности любой секущей линией, проходящей через P.

Угол θ между хордой и касательной равен половине дуги, заключённой между концами хорды.

Касательная прямая t и точка касания T обладают свойством сопряжённости друг другу; это соответствие можно обобщить в идею о полюсе и поляре. Такая же взаимосвязь существует между точкой P вне окружности и секущей линией, соединяющей две точки касания.

Если точка P лежит вне окружности с центром O, и если касательные прямые из P касаются окружности в точках T и S, то углы ∠TPS и ∠TOS дают в сумме 180°.

Если хорда TM проведена из точки касания T прямой P T и ∠PTM ≤ 90°, то ∠PTM = (1/2)∠MOT.

Геометрическое построение

Построение касательной прямой к окружности (выделена красным) перпендикулярно радиусу.

Относительно легко построить прямую t, касательную к окружности в точке T на окружности. Для этого следует провести прямую a через центр окружности O и точку T. Тогда прямая t является перпендикуляром к прямой a. Один из способов построения перпендикуляра следующий (см. рисунок). Проводим тем же радиусом (r) окружность с центром в точке T, получаем вторую точку G на прямой a, а точка T становится серединой отрезка OG. Проводим две окружности радиуса R>r с центрами в точках O и G. Прямая, проходящая через точки пересечения этих окружностей, будет касательной.

Построение касательной прямой к окружности

Для построения касательной прямой через точку P к окружности C можно использовать свойство угла, опирающегося на диаметр окружности. Проводится окружность с центром в точке H, середине отрезка OP, где O — центр окружности C. Пересечения T и T‘ являются точками касания прямых, проходящих через точку P, поскольку углы ∠OTP и ∠OT‘P опираются на диаметр OP окружности с центром в H.

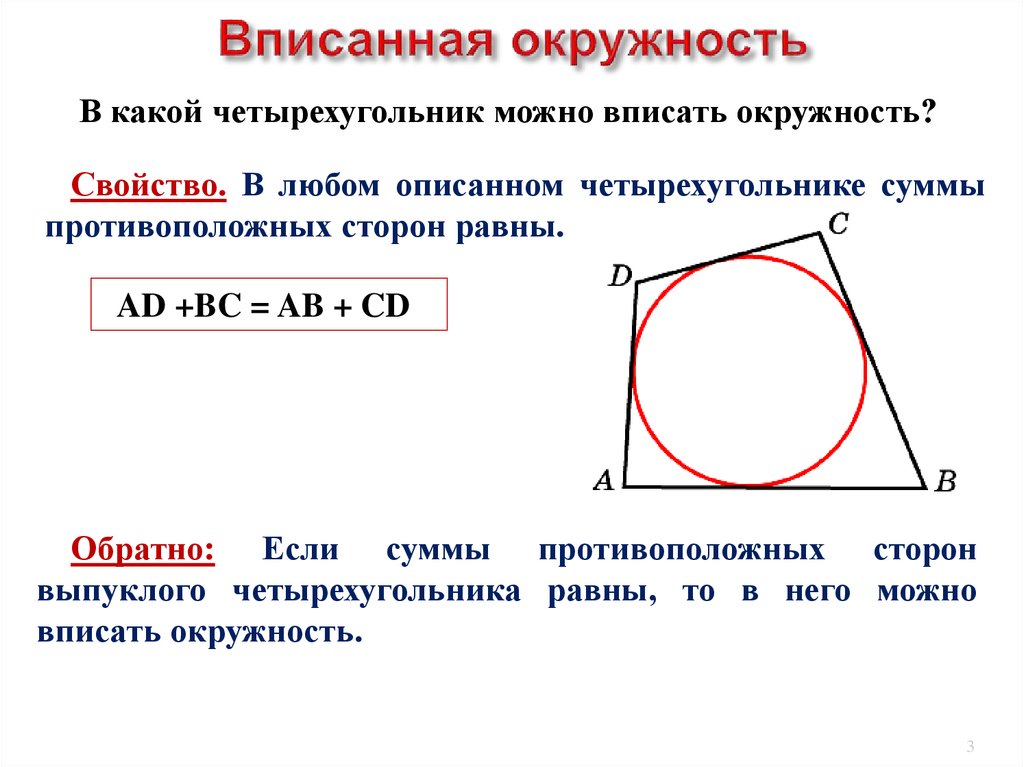
Теорема об описанном четырёхугольнике и вписанные окружности

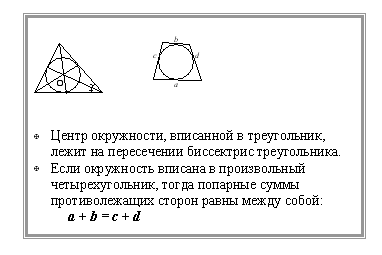
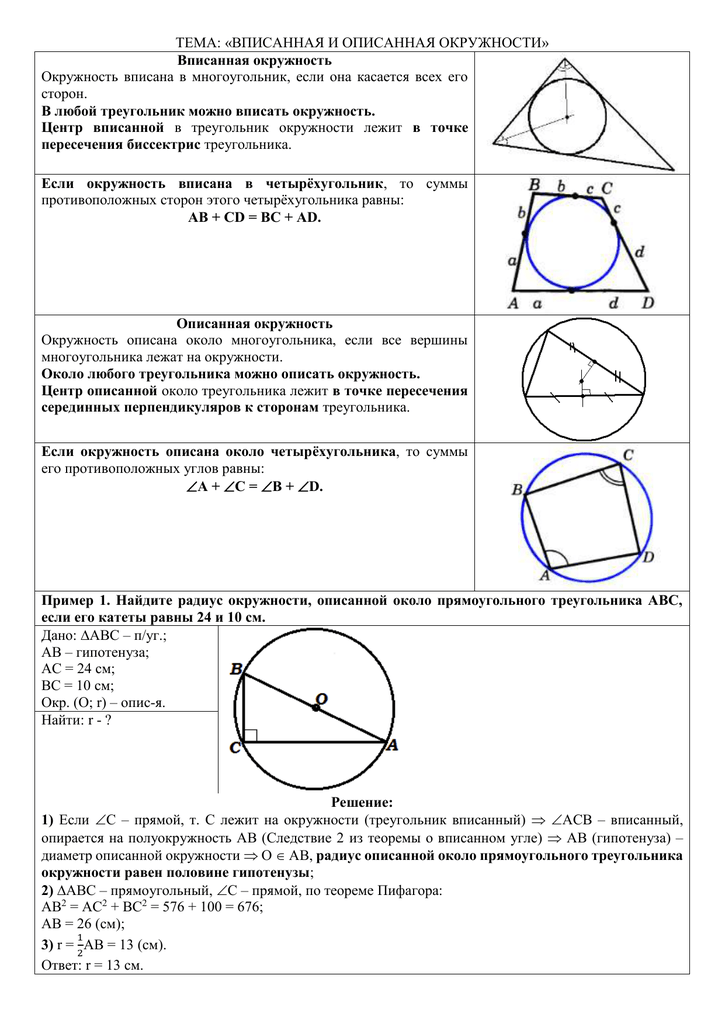
Описанный четырёхугольник ABCD — это замкнутая фигура с четырьмя сторонами, которые касаются окружности C. Соответственно, C — вписанная в четырёхугольник ABCD окружность. По теореме Пито суммы противоположных сторон любого такого четырёхугольника равны, то есть

AB¯+CD¯=BC¯+DA¯.{\displaystyle {\overline {AB}}+{\overline {CD}}={\overline {BC}}+{\overline {DA}}.}

Описанный четырёхугольник

Это заключение следует из равенства отрезков касательных от вершин четырёхугольника. Обозначим точки касания как P (на отрезке AB), Q (на отрезке BC), R (на отрезке CD) и S (на отрезке DA). Симметричные отрезки до точек касания от каждой вершины четырёхугольника ABCD равны, то есть BP=BQ=b, CQ=CR=c, DR=DS=d и AS=AP=a.
Но каждая сторона четырёхугольника состоит из двух таких отрезков

AB¯+CD¯=(a+b)+(c+d)=BC¯+DA¯=(b+c)+(d+a){\displaystyle {\overline {AB}}+{\overline {CD}}=(a+b)+(c+d)={\overline {BC}}+{\overline {DA}}=(b+c)+(d+a)},

что и доказывает утверждение.

Обратное утверждение также верно — окружность можно вписать в любой выпуклый четырёхугольник, у которого суммы длин противоположных сторон равны.

Вариации по теме

Японская теорема (Japanese theorem)

Теорема. Если во вписанном в окружность четырёхугольнике провести диагональ, а в полученные два треугольника вписать две окружности, затем аналогично поступить, проведя вторую диагональ, тогда центры четырёх образовавшихся окружностей являются вершинами прямоугольника (то есть лежат на одной окружности). Эту теорему называют японской теоремой (Japanese theorem). (см. рис.).

Для четырёхугольника

Основная статья: Четырехугольники, вписанные в окружность

Вписанный простой (без самопересечений) четырёхугольник является выпуклым.
Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 180° (π{\displaystyle \pi } радиан).
Можно описать окружность около:

• любого антипараллелограмма
• любого прямоугольника (частный случай квадрат)
• любой равнобедренной трапеции
• любого четырёхугольника, у которого два противоположных угла прямые
• любого четырёхугольника, у которого сумма противоположных углов равна 180 градусов
• любого четырёхугольника, у которого пересекаются в одной точке четыре серединных перпендикуляра его сторон (или медиатрисы его сторон, то есть перпендикуляры к сторонам, проходящие через их середины)
• Первая теорема Птолемея. У четырёхугольника, вписанного в окружность, произведение длин диагоналей равно сумме произведений длин пар противоположных сторон::

|AC|⋅|BD|=|AB|⋅|CD|+|BC|⋅|AD|.{\displaystyle |AC|\cdot |BD|=|AB|\cdot |CD|+|BC|\cdot |AD|.}.

Вторая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство. :

|AC||BD|=|AB|⋅|AD|+|BC|⋅|CD||AB|⋅|BC|+|CD|⋅|AD|.{\displaystyle {\frac {|AC|}{|BD|}}={\frac {|AB|\cdot |AD|+|BC|\cdot |CD|}{|AB|\cdot |BC|+|CD|\cdot |AD|}}.}

Радиус окружности, описанной около четырёхугольника:

R=14(ab+cd)(ad+bc)(ac+bd)(p−a)(p−b)(p−c)(p−d){\displaystyle R={\frac {1}{4}}{\sqrt {\frac {(ab+cd)(ad+bc)(ac+bd)}{(p-a)(p-b)(p-c)(p-d)}}}}

Площадь четырёхугольника, вписанного в окружность, можно вычислить по формуле Брахмагупты:

S=(p−a)(p−b)(p−c)(p−d){\displaystyle S={\sqrt {(p-a)(p-b)(p-c)(p-d)}}}

Та же Формула Брахмагупты для площади вписанного в окружность четырёхугольника может быть записана через определитель:

S=14−|abc−dba−dcc−dab−dcba|{\displaystyle S={\frac {1}{4}}{\sqrt {-{\begin{vmatrix}a&b&c&-d\\b&a&-d&c\\c&-d&a&b\\-d&c&b&a\end{vmatrix}}}}}

Подробнее о четырёхугольниках, вписанных в окружность, можно прочитать в статье «Вписанный четырёхугольник».

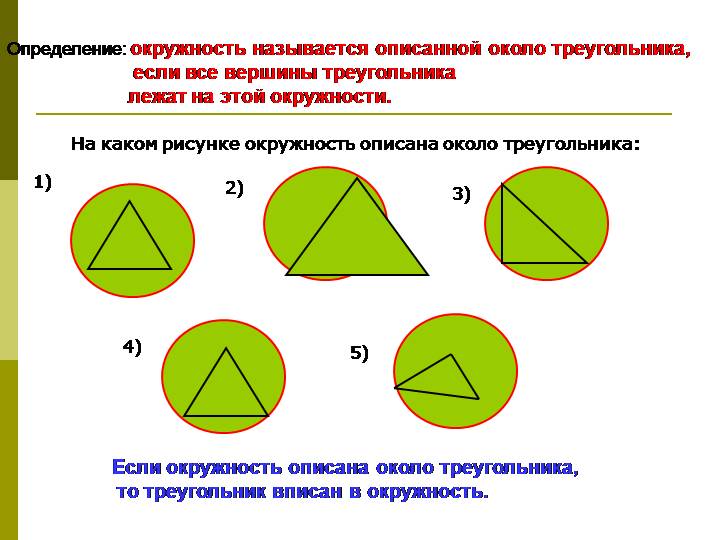
Доказательства теорем о свойствах описанной около треугольника окружности

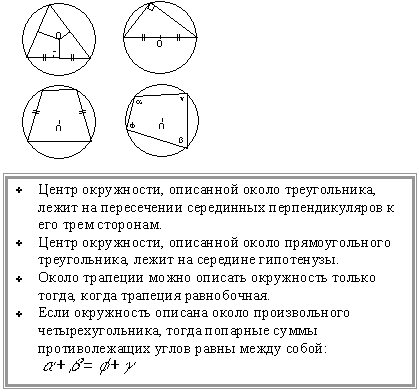
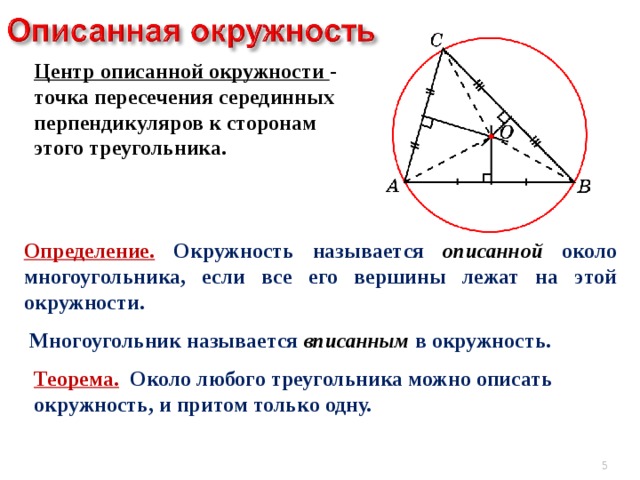
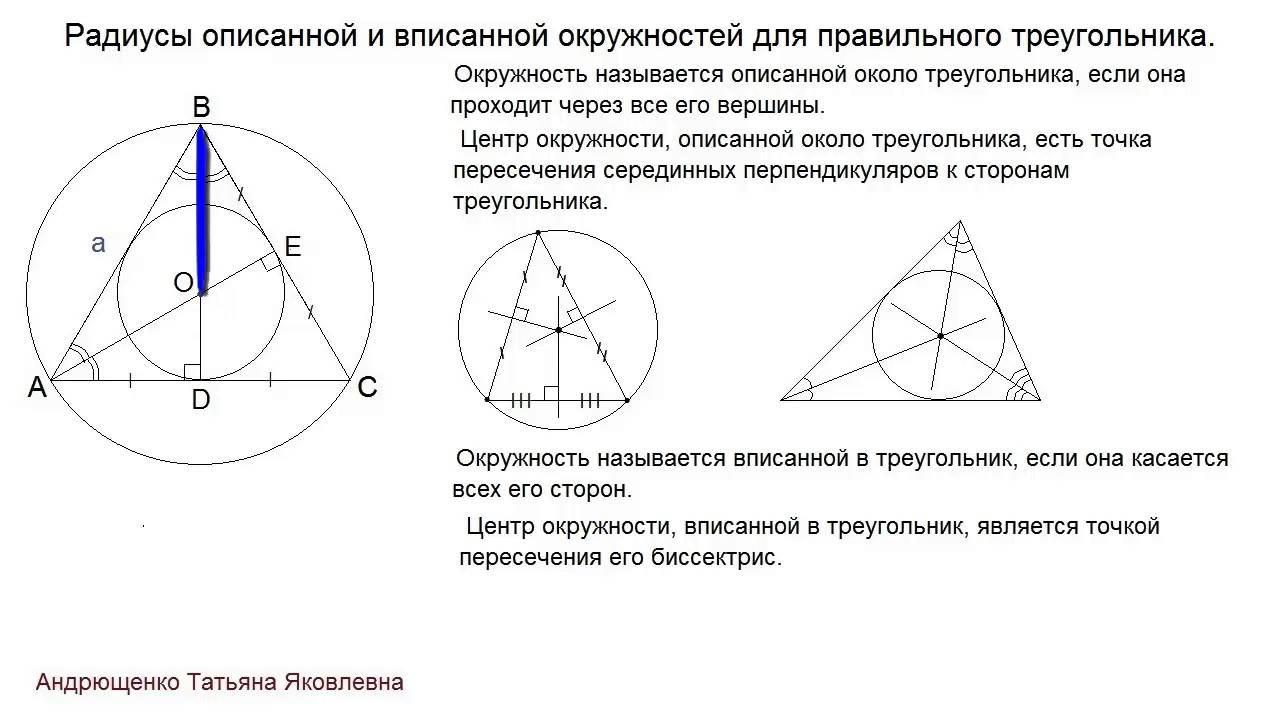
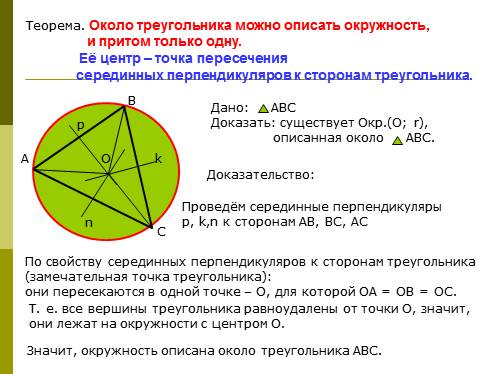
      Теорема 3. Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

      Доказательство. Рассмотрим два серединных перпендикуляра, проведённых к сторонам   AC   и   AB   треугольника   ABC,   и обозначим точку их пересечения буквой   O   (рис. 6).

Рис.6

      Поскольку точка   O   лежит на серединном перпендикуляре к отрезку   AC,   то в силу теоремы 1 справедливо равенство:

CO = AO .

      Поскольку точка O лежит на серединном перпендикуляре к отрезку   AB,   то в силу теоремы 1 справедливо равенство:

AO = BO .

      Следовательно, справедливо равенство:

CO = BO ,

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку   BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

      Следствие. Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

      Доказательство. Рассмотрим точку   O,   в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника   ABC   (рис. 6).

      При доказательстве теоремы 3 было получено равенство:

AO = OB = OC ,

из которого вытекает, что окружность с центром в точке   O   и радиусами   OA,   OB,   OC   проходит через все три вершины треугольника   ABC,   что и требовалось доказать.

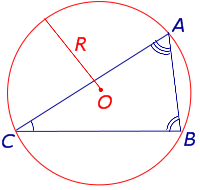
      Теорема 4 (теорема синусов). Для любого треугольника (рис. 7)

Рис.7

справедливы равенства:

.

      Доказательство. Докажем сначала, что длина,   на которую опирается величины   φ ,   вычисляется по формуле:

l = 2Rsin φ .

(1)

      Рассмотрим сначала случай, когда одна из сторон вписанного угла является (рис.8).

Рис.8

      Угол   MPN,   как , и равенство (1) вытекает из определения синуса угла прямоугольного треугольника.

      Поскольку все , то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

      Формула (1) доказана.

      Из формулы (1) для вписанного треугольника   ABC   получаем (рис.7):

      Теорема синусов доказана.

В треугольнике

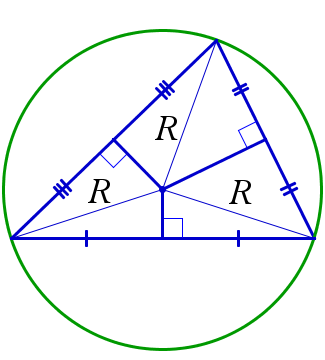
Окружность, вписанная в треугольник со сторонами a, b, c.

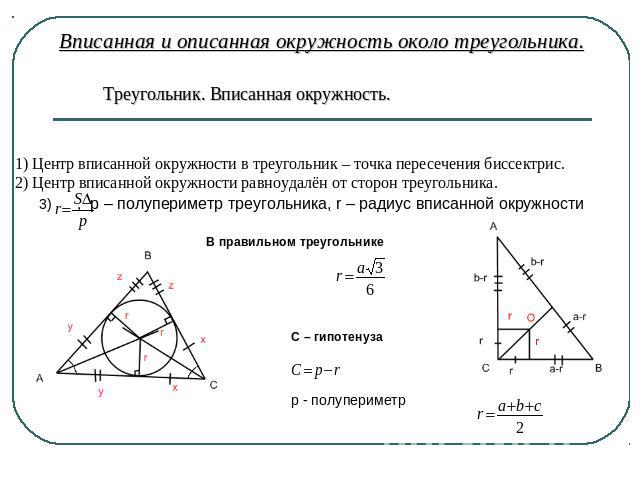
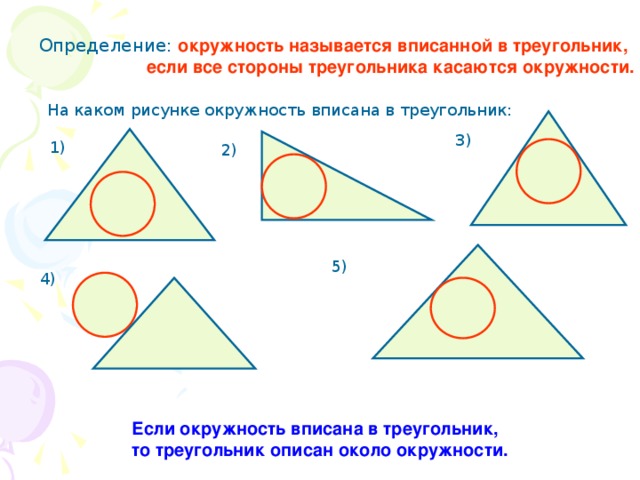
Свойства вписанной окружности:

• В каждый треугольник можно вписать окружность, притом только одну.
• Центр I{\displaystyle I} вписанной окружности равноудалён от всех сторон и является точкой пересечения биссектрис треугольника.
• Радиус r{\displaystyle r} вписанной в треугольник окружности равен:

r=(−a+b+c)(a−b+c)(a+b−c)4(a+b+c);{\displaystyle r={\sqrt {\frac {(-a+b+c)(a-b+c)(a+b-c)}{4(a+b+c)}}};}

1r=1ha+1hb+1hc{\displaystyle {\frac {1}{r}}={\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}}

где a,b,c{\displaystyle a,b,c} — стороны треугольника, ha,hb,hc{\displaystyle h_{a},h_{b},h_{c}} — высоты, проведённые к соответствующим сторонам;

r=Sp=(p−a)(p−b)(p−c)p{\displaystyle r={\frac {S}{p}}={\sqrt {\frac {(p-a)(p-b)(p-c)}{p}}}}

Формула Эйлера

где S{\displaystyle S} — площадь треугольника, а p{\displaystyle p} — его полупериметр.

r=p−actg⁡(α2)=p−bctg⁡(β2)=p−cctg⁡(γ2){\displaystyle r={\frac {p-a}{\operatorname {ctg} (\alpha /2)}}={\frac {p-b}{\operatorname {ctg} (\beta /2)}}={\frac {p-c}{\operatorname {ctg} (\gamma /2)}}}, p{\displaystyle p} — полупериметр треугольника (Теорема котангенсов).

• Если AB{\displaystyle AB} — основание равнобедренного треугольника △ABC{\displaystyle \triangle ABC}, то окружность, касающаяся сторон угла ∠ACB{\displaystyle \angle ACB} в точках A{\displaystyle A} и B{\displaystyle B}, проходит через центр вписанной окружности треугольника △ABC{\displaystyle \triangle ABC}.
• Теорема Эйлера: R2−2Rr=|OI|2{\displaystyle R^{2}-2Rr=|OI|^{2}}, где R{\displaystyle R} — радиус описанной вокруг треугольника окружности, r{\displaystyle r} — радиус вписанной в него окружности, O{\displaystyle O} — центр описанной окружности, I{\displaystyle I} — центр вписанной окружности.
• Если прямая, проходящая через точку I параллельно стороне AB{\displaystyle AB}, пересекает стороны BC{\displaystyle BC} и CA{\displaystyle CA} в точках A1{\displaystyle A_{1}} и B1{\displaystyle B_{1}}, то A1B1=A1B+AB1{\displaystyle A_{1}B_{1}=A_{1}B+AB_{1}}.
• Если точки касания вписанной в треугольник T{\displaystyle T} окружности соединить отрезками, то получится треугольник T1{\displaystyle T_{1}} со свойствами:
  • Биссектрисы T являются серединными перпендикулярами T₁
  • Пусть T₂ — ортотреугольник T₁. Тогда его стороны параллельны сторонам исходного треугольника T.
  • Пусть T₃ — серединный треугольник T₁. Тогда биссектрисы T являются высотами T₃.
  • Пусть T₄ — ортотреугольник T₃, тогда биссектрисы T являются биссектрисами T₄.
• Радиус вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c окружности равен a+b−c2{\displaystyle {\frac {a+b-c}{2}}}.
• Расстояние от вершины С треугольника до точки, в которой вписанная окружность касается стороны, равно d=a+b−c2=p−c{\displaystyle d={\frac {a+b-c}{2}}=p-c}.
• Расстояние от вершины C до центра вписанной окружности равно lc=rsin⁡(γ2){\displaystyle l_{c}={\frac {r}{\sin({\frac {\gamma }{2}})}}}, где r{\displaystyle r} — радиус вписанной окружности, а γ — угол вершины C.
• Расстояние от вершины C до центра вписанной окружности может также быть найдено по формулам lc=(p−c)2+r2{\displaystyle l_{c}={\sqrt {(p-c)^{2}+r^{2}}}} и lc=ab−4Rr{\displaystyle l_{c}={\sqrt {ab-4Rr}}}
• Теорема о трезубце или теорема трилистника: Если D — точка пересечения биссектрисы угла A с описанной окружностью треугольника ABC, I и J — соответственно центры вписанной и вневписанной окружности, касающейся стороны BC, тогда |DI|=|DB|=|DC|=|DJ|{\displaystyle |DI|=|DB|=|DC|=|DJ|}.
• Лемма Веррьера: пусть окружность V{\displaystyle V} касается сторон AB{\displaystyle AB}, AC{\displaystyle AC} и дуги BC{\displaystyle BC} описанной окружности треугольника ABC{\displaystyle ABC}. Тогда точки касания окружности V{\displaystyle V} со сторонами и центр вписанной окружности треугольника ABC{\displaystyle ABC} лежат на одной прямой.

Теорема Фейербаха. Окружность девяти точек касается всех трёх вневписанных окружностей, а также вписанной окружности. Точка касания окружности Эйлера и вписанной окружности известна как точка Фейербаха.

Свойства описанной около треугольника окружности. Теорема синусов

Фигура	Рисунок	Свойство
Серединные перпендикулярык сторонам треугольника		Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Окружность, описанная около треугольника		Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Центр описанной около остроугольного треугольника окружности	Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности		Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.
Центр описанной около тупоугольного треугольника окружности		Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов		Для любого треугольника справедливы равенства (теорема синусов): , где   a , b , c   – стороны треугольника,   A , B , С   – углы треугольника,   R   – радиус описанной окружности.
Площадь треугольника		Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где   A , B , С   – углы треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности.
Радиус описанной окружности		Для любого треугольника справедливо равенство: где   a , b , c   – стороны треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности.

Серединные перпендикуляры к сторонам треугольника

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов): , где   a , b , c   – стороны треугольника,   A , B , С   – углы треугольника,   R   – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где   A , B , С   – углы треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство: где   a , b , c   – стороны треугольника,   S   – площадь треугольника,   R   – радиус описанной окружности.

История

Окружность, наряду с прямой, является самой распространённой кривой практически во всех областях человеческой деятельности

История её исследования и применения уходит в глубокую древность; особенную важность придало этой теме изобретение колеса. Античные учёные рассматривали прямые и окружности как единственный пример «совершенных» кривых, поэтому в геометрии считались допустимыми только построения с помощью циркуля и линейки, а движение планет моделировалось как наложение вращений по окружностям

Теории окружностей посвящена III книга «Начал» Евклида.

Также в древности было открыто, что отношение длины окружности к её диаметру (число π) одно и то же для всех окружностей

Исторически важной темой многовековых исследований было уточнение этого отношения, а также попытки решить проблему «квадратуры круга». В дальнейшем развитие теории окружностей привело к созданию тригонометрии, теории колебаний и многих других практически важных разделов науки и техники.

Окружность получается как сечение конуса плоскостью, перпендикулярной его оси

Связь описанной окружности со вписанной окружностью, с ортоцентром и другими точками

Или через стороны треугольника:

d=OI=Ra3−a2b−ab2+b3−a2c+3abc−b2c−bc2−ac2+c3abc{\displaystyle d=OI=R{\sqrt {\frac {a^{3}-a^{2}b-ab^{2}+b^{3}-a^{2}c+3abc-b^{2}c-bc^{2}-ac^{2}+c^{3}}{abc}}}},

где R{\displaystyle R} — радиус описанной окружности (см. Окружность Фурмана).

Расстояние от центра O до ортоцентра H есть:p. 449

OH=R2−8R2cos⁡Acos⁡Bcos⁡C=9R2−(a2+b2+c2).{\displaystyle OH={\sqrt {R^{2}-8R^{2}\cos A\cos B\cos C}}={\sqrt {9R^{2}-(a^{2}+b^{2}+c^{2})}}.}

Для центроида G и центра девяти точек N имеем:

IG<IO,{\displaystyle IG<IO,}

2IN<IO,{\displaystyle 2IN<IO,}

OI2=2R⋅IN.{\displaystyle OI^{2}=2R\cdot IN.}

Произведение радиусов описанной и вписанной окружностей треугольника связано со сторонами a, b и c в виде: p. 189, #298(d):

rR=abc2(a+b+c).{\displaystyle rR={\frac {abc}{2(a+b+c)}}.}

Если медиана m, высота h и внутренняя биссектриса t выходят из одной и той же вершины треугольника, около которого описана окружность радиуса R, тогда:p.122,#96

4R2h2(t2−h2)=t4(m2−h2).{\displaystyle 4R^{2}h^{2}(t^{2}-h^{2})=t^{4}(m^{2}-h^{2}).}

• Центр описанной окружности изогонально сопряжён с ортоцентром.
• Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности.
• В треугольнике есть три окружности, которые касаются двух сторон треугольника и описанной окружности. Такие окружности называют полувписанными или окружностями Веррьера. Отрезки, соединяющие вершины треугольника и соответствующие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке, называемой точкой Веррьера. Она служит центром гомотетии, которая переводит описанную окружность во вписанную. Точки касания окружностей Веррьера со сторонами лежат на прямой, которая проходит через центр вписанной окружности.

Полувписанная окружность

Теорема Тебо 3 утверждает (см. рис.):

Теорема Тебо 3

Пусть ABC{\displaystyle ABC} — произвольный треугольник, D{\displaystyle D} — произвольная точка на стороне BC{\displaystyle BC}, I1{\displaystyle I_{1}} — центр окружности, касающейся отрезков AD,BD{\displaystyle AD,BD} и описанной около ΔABC{\displaystyle \Delta ABC} окружности, I2{\displaystyle I_{2}} — центр окружности, касающейся отрезков CD,AD{\displaystyle CD,AD} и описанной около ΔABC{\displaystyle \Delta ABC} окружности. Тогда отрезок I1I2{\displaystyle I_{1}I_{2}} проходит через точку I{\displaystyle I} — центр окружности, вписанной в ΔABC{\displaystyle \Delta ABC}, и при этом I1III2=tg2⁡ϕ2{\displaystyle I_{1}I:II_{2}=\operatorname {tg} ^{2}{\frac {\phi }{2}}}, где ϕ=∠BDA{\displaystyle \phi =\angle BDA}.

Формула Карно утверждает, что в треугольнике ABC сумма расстояний от центра D описанной окружности до сторон треугольника ABC, взятых со знаком «-», когда высота из D на сторону целиком лежит вне треугольника (иначе со знаком «+»), будет равна R+r{\displaystyle R+r}, где r и R — радиусы вписанной и описанной окружностей:p.83.

Формула Карно: DG+DH−DF=R+r{\displaystyle DG+DH-DF=R+r}

Например для рисунка формула Карно примет вид: DG+DH−DF=R+r{\displaystyle DG+DH-DF=R+r}.

В другой формулировке формула Карно утверждает, что:

R+r=ka+kb+kc=12(dA+dB+dC),{\displaystyle R+r=k_{a}+k_{b}+k_{c}={\frac {1}{2}}(d_{A}+d_{B}+d_{C}),}

где ka,kb,kc{\displaystyle k_{a},k_{b},k_{c}} — расстояния от центра описанной окружности соответственно до сторон a,b,c{\displaystyle a,b,c} треугольника,
dA,dB,dC{\displaystyle d_{A},d_{B},d_{C}} — расстояния от ортоцентра соответственно до вершин A,B,C{\displaystyle A,B,C} треугольника.

Расстояние от центра описанной окружности например до стороны a{\displaystyle a} треугольника равно:

ka=a(2tgA);{\displaystyle k_{a}=a/(2tgA);}

расстояние от ортоцентра например до вершины A{\displaystyle A} треугольника равно:

dA=2ka=a(tgA).{\displaystyle d_{A}=2k_{a}=a/(tgA).}