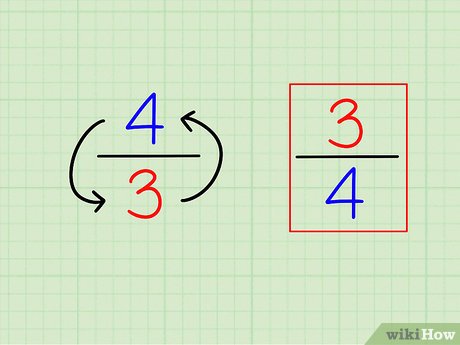
Обратное к действительному числу
Для любого действительного (или комплексного) числа, отличного от нуля, существует число, обратное ему. Обратное к действительному числу можно подать в виде дроби или степени с показателем -1. Но, как правило, используется запись через дробь.
| Число | Обратное | |
| Дробь | Степень | |
| n{\displaystyle n} | 1n{\displaystyle {\frac {1}{n}}} | n−1{\displaystyle n^{-1}} |
То есть 1n=n−1{\displaystyle \ {\frac {1}{n}}=n^{-1}}.
| Примеры | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Число | 3{\displaystyle 3} | 110{\displaystyle {\frac {1}{10}}} | −27{\displaystyle -{\frac {2}{7}}} | 2π{\displaystyle 2\pi } | 2{\displaystyle 2} | −,125{\displaystyle -0,125} | 1{\displaystyle 1} | 3{\displaystyle {\sqrt {3}}} | eπ4{\displaystyle e^{\frac {\pi }{4}}} | 1023{\displaystyle 10^{23}} |
| Обратное | 13{\displaystyle {\frac {1}{3}}} | 10{\displaystyle 10} | −72{\displaystyle -{\frac {7}{2}}} | 12π{\displaystyle {\frac {1}{2\pi }}} | ,5{\displaystyle 0,5} | −8{\displaystyle -8} | 1{\displaystyle 1} | 33{\displaystyle {\frac {\sqrt {3}}{3}}} | e−π4{\displaystyle e^{-{\frac {\pi }{4}}}} | 10−23{\displaystyle 10^{-23}} |
Не стоит путать термины «обратное число» и «противоположное число». Два числа называются противоположными, если их сумма равна нулю. Например, число, противоположное к 3, это -3, а обратное 1/3.
Обратное к нулю
В арифметике, которая оперирует действительными (или комплексными) числами, нет понятия бесконечности (нет числа «бесконечность»). Поэтому в ней считается, что нельзя. Таким образом, ноль не имеет обратного числа. Но, с момента ввода предельного перехода (в математическом анализе), появились такие понятия как бесконечно малая и бесконечно большая величины, которые являются взаимно обратными.
Используя предельный переход, получаем:
- Правый предел: limx→+1x=(1)=+∞{\displaystyle \lim _{x\to +0}{\frac {1}{x}}=\left({\frac {1}{0}}\right)=+\infty } _ или _ (1x)→x→+ +∞{\displaystyle \left({\frac {1}{x}}\right){\xrightarrow{}}\ {+\infty }}
- Левый предел: limx→−1x=(1)=−∞{\displaystyle \lim _{x\to -0}{\frac {1}{x}}=\left({\frac {1}{0}}\right)=-\infty } _ или _ (1x)→x→− −∞{\displaystyle \left({\frac {1}{x}}\right){\xrightarrow{}}\ {-\infty }}
Таким образом, обратной величиной для нуля, в зависимости от того с какой стороны к нему стремиться, формально является бесконечность со знаком «+» или «−». Однако такое определение обратного к нулю бессмысленно — при введении теряется дистрибутивность, что проявляется, в частности, когда предел обратного квадрата также «равен» бесконечности, но при делении предыдущего предела на этот даёт ответ 0, а не 1.
limx→+01×2=+∞{\displaystyle \lim _{x\to +0}{\frac {1}{x^{2}}}={+\infty }}
Но limx→+1x1x2=limx→+x2x={\displaystyle \lim _{x\to +0}{\frac {\frac {1}{x}}{\frac {1}{x^{2}}}}=\lim _{x\to +0}{\frac {x^{2}}{x}}=0}
Обратное к комплексному числу
Числа, обратные к комплексным, выглядят несколько сложнее нежели обратные к действительным. Существует три формы комплексного числа: , и .
| Формы комплексного числа | Число (z){\displaystyle (z)} | Обратное (1z){\displaystyle \left({\frac {1}{z}}\right)} |
| x+iy{\displaystyle x+iy} | xx2+y2−iyx2+y2{\displaystyle {\frac {x}{x^{2}+y^{2}}}-i{\frac {y}{x^{2}+y^{2}}}} | |
| r(cosφ+isinφ){\displaystyle r(\cos \varphi +i\sin \varphi )} | 1r(cosφ−isinφ){\displaystyle {\frac {1}{r}}(\cos \varphi -i\sin \varphi )} | |
| reiφ{\displaystyle re^{i\varphi }} | 1re−iφ{\displaystyle {\frac {1}{r}}e^{-i\varphi }} |
|
Обозначение и доказательство
Доказательство: Алгебраическая форма: 1z=1x+iy=x−iy(x+iy)(x−iy)=x−iyx2+y2=xx2+y2−iyx2+y2{\displaystyle {\frac {1}{z}}={\frac {1}{x+iy}}={\frac {x-iy}{(x+iy)(x-iy)}}={\frac {x-iy}{x^{2}+y^{2}}}={\frac {x}{x^{2}+y^{2}}}-i{\frac {y}{x^{2}+y^{2}}}} Тригонометрическая форма: 1z=1r(cosφ+isinφ)=1rcosφ−isinφ(cosφ+isinφ)(cosφ−isinφ)=1rcosφ−isinφcos2φ+sin2φ=1r(cosφ−isinφ){\displaystyle {\frac {1}{z}}={\frac {1}{r(\cos \varphi +i\sin \varphi )}}={\frac {1}{r}}{\frac {\cos \varphi -i\sin \varphi }{(\cos \varphi +i\sin \varphi )(\cos \varphi -i\sin \varphi )}}={\frac {1}{r}}{\frac {\cos \varphi -i\sin \varphi }{\cos ^{2}\varphi +\sin ^{2}\varphi }}={\frac {1}{r}}(\cos \varphi -i\sin \varphi )} Показательная форма: 1z=1reiφ=1re−iφ{\displaystyle {\frac {1}{z}}={\frac {1}{re^{i\varphi }}}={\frac {1}{r}}e^{-i\varphi }} |
Таким образом, при нахождении обратного к комплексному числу, удобнее пользоваться его показательной формой.
Пример:
| Формы комплексного числа | Число (z){\displaystyle (z)} | Обратное (1z){\displaystyle \left({\frac {1}{z}}\right)} |
| 1+i3{\displaystyle 1+i{\sqrt {3}}} | 14−34i{\displaystyle {\frac {1}{4}}-{\frac {\sqrt {3}}{4}}i} | |
|
2(cosπ3+isinπ3){\displaystyle 2\left(\cos {\frac {\pi }{3}}+i\sin {\frac {\pi }{3}}\right)}
или2(12+i32){\displaystyle 2\left({\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\right)} |
12(cosπ3−isinπ3){\displaystyle {\frac {1}{2}}\left(\cos {\frac {\pi }{3}}-i\sin {\frac {\pi }{3}}\right)}
или12(12−i32){\displaystyle {\frac {1}{2}}\left({\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\right)} |
|
| 2eiπ3{\displaystyle 2e^{i{\frac {\pi }{3}}}} | 12e−iπ3{\displaystyle {\frac {1}{2}}e^{-i{\frac {\pi }{3}}}} |
Обратное к мнимой единице
Существует лишь два числа (), обратное и противоположное числа к которым равны. Это ±i{\displaystyle \pm i}.
| Число | Равенство обратного и противоположного | |
| Запись обратного через дробь | Запись обратного через степень | |
| i{\displaystyle i} | 1i=−i{\displaystyle {\frac {1}{i}}=-i} | i−1=−i{\displaystyle i^{-1}=-i} |
| −i{\displaystyle -i} | −1i=i{\displaystyle -{\frac {1}{i}}=i} | −i−1=i{\displaystyle -i^{-1}=i} |
|
Доказательство Продемонстрируем доказательство для i{\displaystyle i} (для −i{\displaystyle -i} аналогично). |
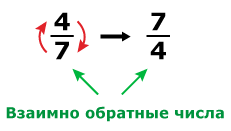
Обратные или взаимно-обратные числа
Обратными – или взаимно-обратными – числами называют пару чисел, которые при перемножении дают 1. В самом общем виде обратными являются числа
. Характерный частный случай взаимно-обратных чисел – пара
. Обратными являются, скажем, числа
;
.
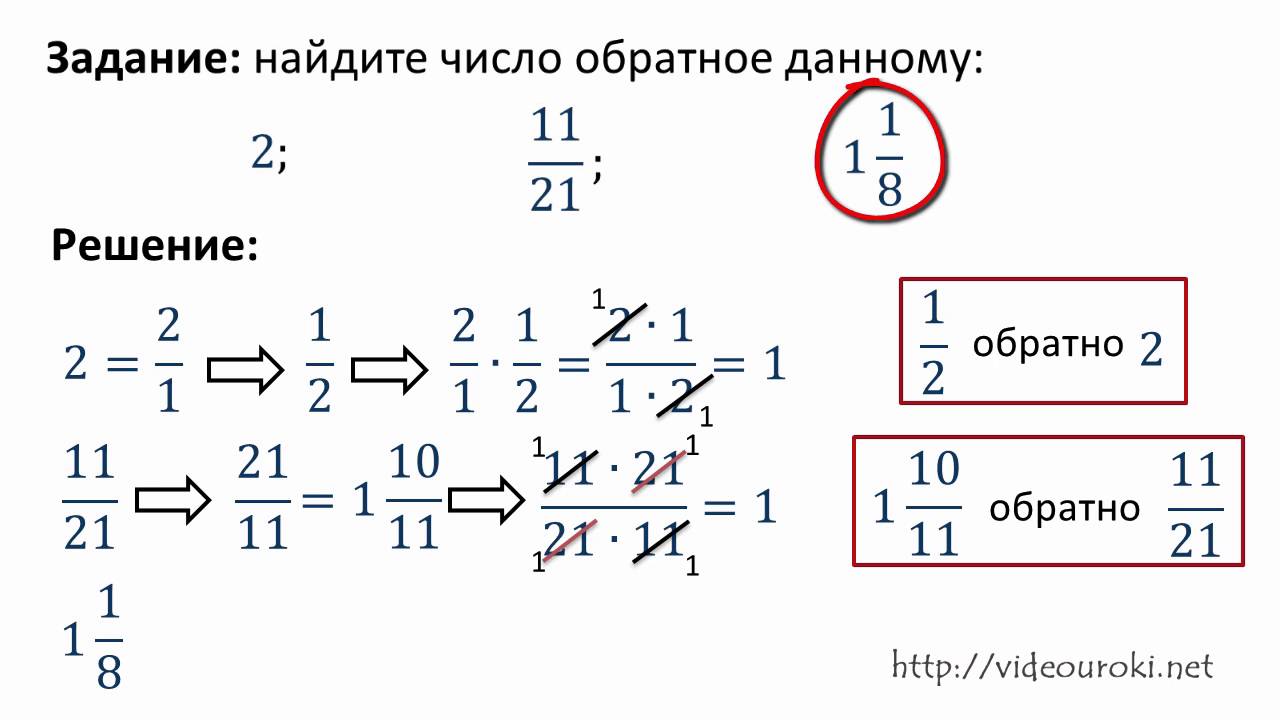
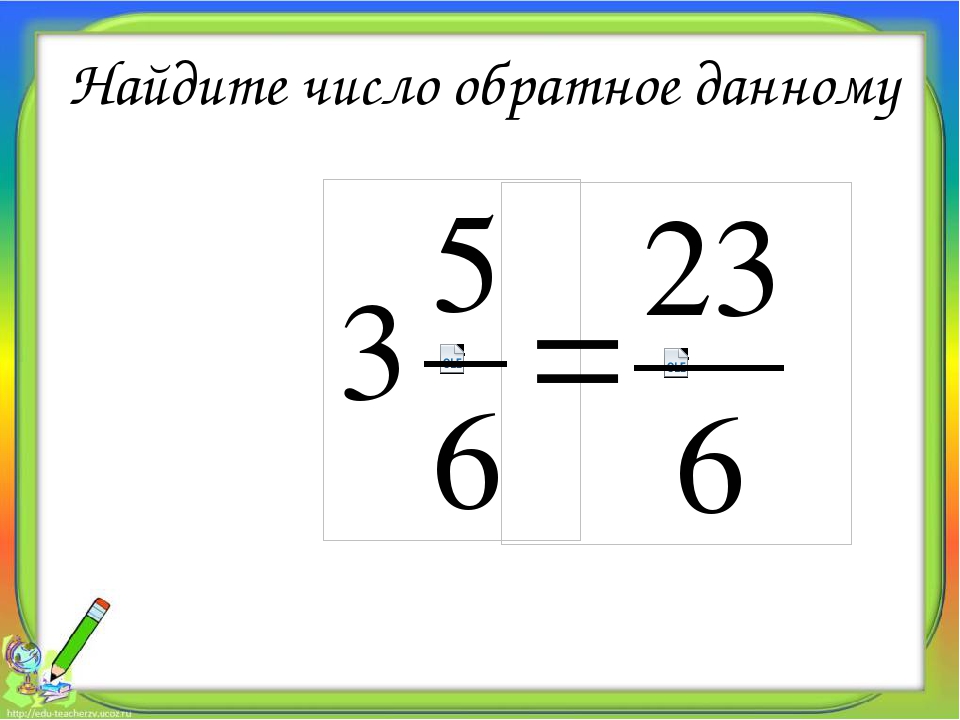
Как найти обратное число
Правило: нужно 1 (единицу) поделить на данное число.
Пример №1.
Дано число 8. Обратное к нему – 1:8 или
(второй вариант предпочтительнее, потому что такая запись математически более корректна).
Когда ищется обратное число для обыкновенной дроби, то делить ее на 1 не очень удобно, т.к. запись получается громоздкой. В этом случае гораздо проще поступать иначе: дробь просто переворачивают, меняя местами числитель и знаменатель. Если дана правильная дробь, то после переворачивания получается дробь неправильная, т.е. такая, из которой можно выделить целую часть. Делать это или нет, решать нужно в каждом конкретном случае особо. Так, если с полученной перевернутой дробью далее придется совершать какие-то действия (к примеру, умножение или деление), то выделять целую часть не стоит. Если же полученная дробь – это конечный результат, то, возможно, выделение целой части и желательно.
Пример №2.
Дана дробь
. Обратная к ней:
.
Если требуется найти обратное число к десятичной дроби, то следует воспользоваться первым правилом (деление 1 на число). В этой ситуации можно действовать одним из 2 способов. Первый – просто разделить 1 на это число в столбик. Второй – сформировать дробь из 1 в числителе и десятичной дроби в знаменателе, а затем домножить числитель и знаменатель на 10, 100 или другое число, состоящее из 1 и такого количества нулей, которое необходимо, чтобы избавиться от десятичной запятой в знаменателе. В результате будет получена обыкновенная дробь, которая и является результатом. При необходимости ее может понадобиться сократить, выделить из нее целую часть или перевести в десятичный вид.
Пример №3.
Дано число 0,82. Обратное число к нему такое:
. Теперь сократим дробь и выделим целую часть:
.
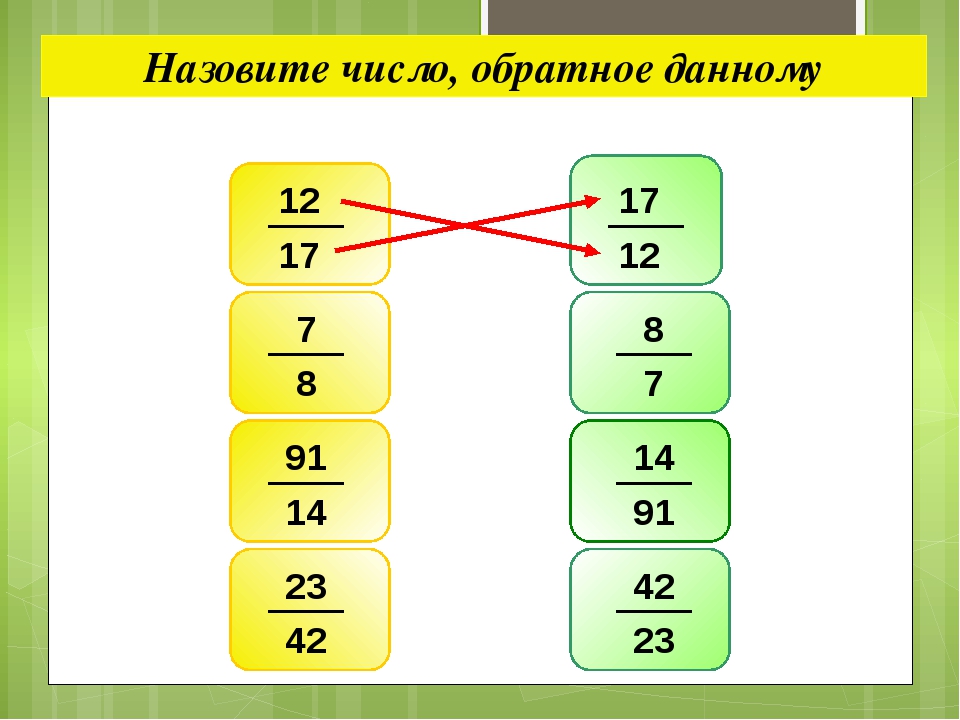
Как проверить, являются ли два числа обратными
Принцип проверки основан на определении обратных чисел. То есть для того, чтобы убедиться, что числа являются обратными друг другу, нужно перемножить их. Если в результате будет получена единица, значит, числа – взаимно обратные.
Пример №4.
Даны числа 0,125 и 8. Являются ли они обратными?
Проверка. Необходимо найти произведение 0,125 и 8. Для наглядности представим данные числа в виде обыкновенных дробей:
(сократим 1-ю дробь на 125)
. Вывод: числа 0,125 и 8 являются обратными.
Свойства обратных чисел
Свойство №1
Обратное число существует для любого числа, кроме 0.
Это ограничение связано с тем, что нельзя делить на 0, а при определении обратного числа для нуля его как раз придется переместить в знаменатель, т.е. фактически делить на него.
Свойство №2
Сумма пары взаимно-обратных чисел всегда не меньше, чем 2.
Математически это свойство можно выразить неравенством:
Свойство №3
Умножение числа на два взаимно-обратных числа равносильно умножению на единицу. Выразим это свойство математически:
.
Пример №5.
Найти значение выражения: 3,4·0,125·8. Поскольку числа 0,125 и 8 являются обратными (см. Пример №4), то умножать 3,4 на 0,125 и затем на 8 нет необходимости. А значит, ответом здесь будет 3,4.
Взаимно-обратными могут быть и числовые выражения.
Пример №6.
Выражения
и
являются обратными. Докажем это: 
.
Свойство №5
Для числа, представленного в виде степени с показателем х, обратным будет число в виде степени с показателем –х. Обоснование:
. Это свойство означает, что и для всякой степени тоже может быть подобрано обратное число.
Пример №7.
Дано число
. Требуется найти обратное к нему.
Решение. Обратное число в данном случае равно:
.
Об этой статье
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 9 человек(а). Количество просмотров этой статьи: 40 665.
Категории: Математика
English:Find the Reciprocal
Português:Achar o Recíproco de um Número
Deutsch:Den Kehrwert bestimmen
Español:encontrar el recíproco
Français:trouver l’inverse
Italiano:Calcolare il Reciproco
Bahasa Indonesia:Mencari Resiprok atau Kebalikan
Nederlands:Het omgekeerde van een getal bepalen
العربية:إيجاد مقلوب عدد
Печать
Google Drive
Не менее популярный сервис — облачное хранилище Google, обходящее DropBox сразу по ряду параметров. Помимо бесплатных 16 Гбайт дискового пространства, Google Drive интегрирован в масштабную экосистему, разработанную поисковым гигантом для своих клиентов. Это и онлайн-фотоальбом Google Фото, и редактор документов Google Docs, и инструмент для работы с формами Google Forms, а также встроенные средства просмотра файлов с поддержкой более 30 форматов, позволяющие открывать их прямо в браузере, а не загружать на ПК или в приложение.
Дополняет набор возможностей собственный магазин приложений, допускающий практически неограниченное расширение функций. Сервис интегрирован в ОС Android, благодаря чему сразу же доступен большинству владельцев смартфонов, и позволяет удобно производить резервирование данных. Из других ОС поддерживаются Windows, macOS и iOS. Правда, Google не раз обвиняли в нарушении конфиденциальности, а документы, находящиеся в общем доступе, периодически индексируются поисковыми системами. Платная подписка стоит 139 рублей в месяц за объем в 100 Гбайт, 699 рублей за 1 Тбайт, 6 990 рублей за 10 Тбайт и 20 990 рублей за 30 Тбайт.