Неравенство треугольника ружа

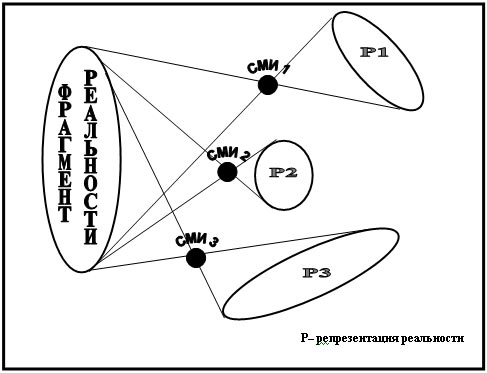
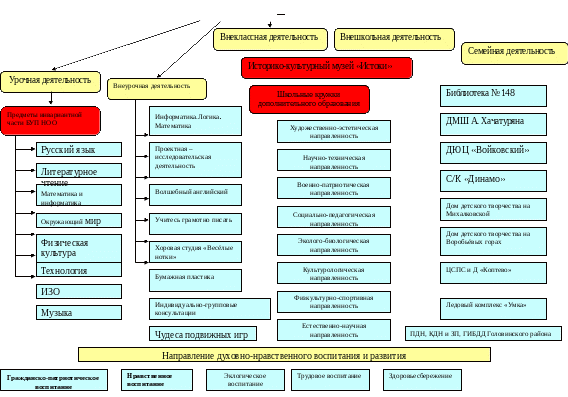
§ 6. Угол между векторами

Вначале заметим,
что на основании неравенства
Коши-Буняковского можно утверждать,
что величина
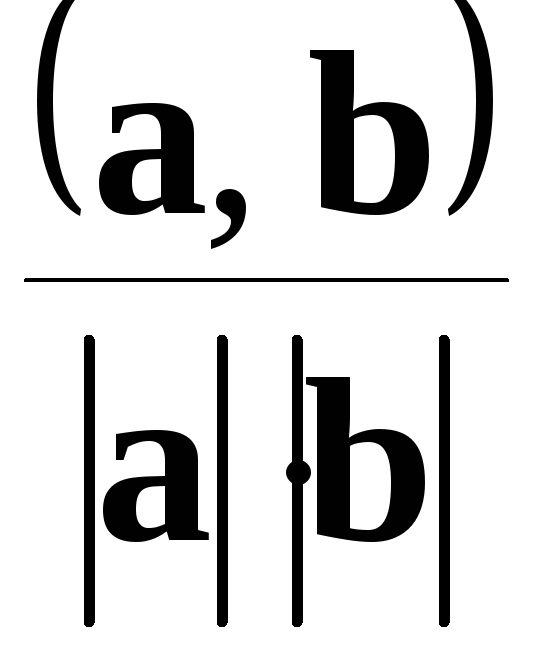меньше
1.

Поэтому можно
ввести следующее определение.

Определение
1. Углом
между векторами

и


называют такое
число

(от
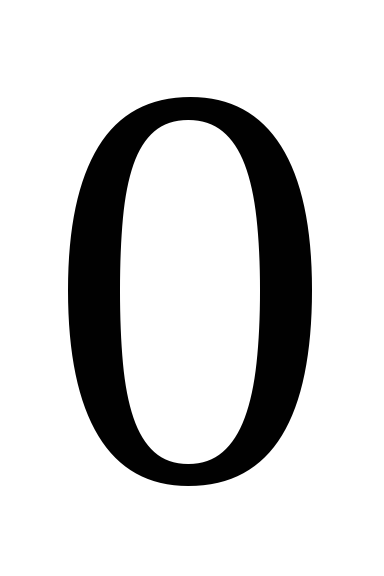до),
для которого выпол­няется равенство

(2.10)

Определение
2. Векторы


и

называются ортогональ­ными,
если выполнено равенство

(2.11)

Если

и

– оба ненулевые, то это определение
означает, что угол между

и

равен
.
Нулевой вектор, по определению, счи­тается
ортогональным любому вектору.

Рассмотрим примеры.

Пример 1. В
пространстве векторов, изученных ранее
в курсе геометрии, скалярное произведение
определено известным образом. Орты

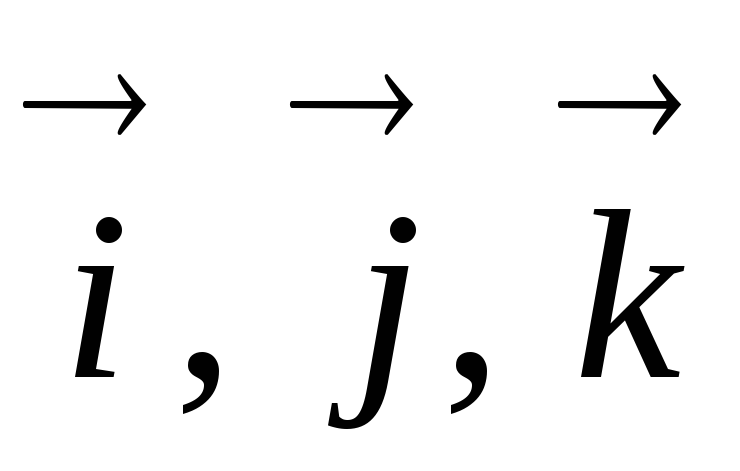
попарно взаимно ортогональны.

Пример 2. В
евклидовом пространстве одностолбцовых
матриц, в котором ска­лярное произведение
определено равенством (2.3), векторы

и

ортогональны.

3.1. Множества связные несвязные

Понятия
относящиеся к множествам точек в
.

Пусть
— отрезокна вещественной оси, переменная на которой обозначается
буквой. Рассмотримфункций

,
заданных на отрезке
. Каждомусоответствует тогда точкапространства. Получаем отображение

сопоставляющее
каждому
соответствующую точку. Это отображениеназывается вектор-функцией, заданной
на отрезке.

Пусть
теперь все функции
, задающие вектор-функцию, непрерывны на отрезке. Тогда и вектор-функциюбудем называть непрерывной. Для такой
непрерывной вектор-функции, при изменениина отрезкеточканепрерывно перемещается из положенияв положение.

        Определение.
  В описанной выше ситуации будем
называть отображение

заданное
формулой
, непрерывным путём, или просто путём,
соединяющим точкус точкойпространства.

Рис.

Множество
всех точек
будем называтьнепрерывной
линией в

, соединяющей точки
и, а ту вектор-функцию, которая порождает линию— параметризацией этой линии.
    Заметим, что одна и та же
линияможет иметь разные параметризации.
Например, на плоскостис координатамиотрезокосиможно параметризовать, положив либо, либо(разумеется, формулы, при любомзадают ещё бесконечное множество
различных параметризации той же линии).

 Определение
:
  Множество
называется связным,
если любые две точки
иэтого множестваможно соединить непрерывной линией, целиком лежащей в множестве, то есть если существует путь, начинающийся ви заканчивающийся в, такой чтопри всех.

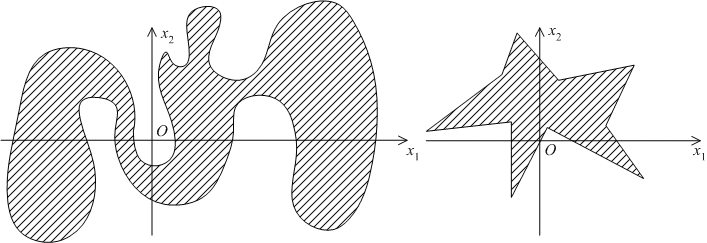
Примеры
связных областей на плоскости.

Связными
областями являются:

1)
всё пространство
;

2)
замкнутые и открытые шары;

3)
гиперплоскости;

4)
замкнутые и открытые полупространства;

5)
замкнутые и открытые параллелепипеды;

6)
положительный и неотрицательный октанты.

3.2. Множества ограниченные, неограниченные.

  Ограниченное
множество —
множество, которое в определенном смысле
имеет конечный размер. Базовым является
понятие ограниченности числового
множества, которое обобщается на
случай произвольногометрического
пространства, а также на случай
произвольногочастично
упорядоченного множества. Понятие
ограниченности множества не имеет
смысла в общихтопологических
пространствах, безметрики.

Ограниченное
числовое множество

Множество
вещественных чисел
называетсяограниченным
сверху,
если существует число

Множество
вещественных
чиселназываетсяограниченным
снизу,
если существует число

Множество
,
ограниченное сверху и снизу, называетсяограниченным.

Множество
,
не являющееся ограниченным, называетсянеограниченным.
Как следует из определения, множество
не ограничено тогда и только тогда,
когда оно не
ограничено сверху
или не
ограничено снизу.

Примеры:

Примером
ограниченного множества является
отрезок
,

неограниченного —
множество всех целых чисел
,

ограниченного
сверху, но неограниченного снизу —
луч

ограниченного
снизу, но неограниченного сверху —
луч

Вариации и обобщения[править | править код]

Обратное неравенство треугольникаправить | править код

Следствием неравенства треугольника в нормированном и метрическом пространствах являются следующие неравенства:

• |‖x‖−‖y‖|⩽‖x−y‖,x,y∈X;{\displaystyle {\bigl |}\|x\|-\|y\|{\bigr |}\leqslant \|x-y\|,\quad x,y\in X;}
• |ρ(x,y)−ρ(x,z)|⩽ρ(y,z),x,y,z∈X.{\displaystyle |\rho (x,y)-\rho (x,z)|\leqslant \rho (y,z),\quad x,y,z\in X.}

Неравенство треугольника для трёхгранного углаправить | править код

См. также: Сферическая геометрия

Каждый плоский угол выпуклого трёхгранного угла меньше суммы двух других его плоских углов.

Произвольное число точекправить | править код

Обозначим ρ(xi,xj){\displaystyle \rho (x_{i},x_{j})} расстояние между точками xi{\displaystyle x_{i}} и xj{\displaystyle x_{j}}. Тогда имеет место следующее неравенство: ρ(x1,xm)⩽ρ(x1,x2)+ρ(x2,x3)+…+ρ(xm−1,xm){\displaystyle \rho (x_{1},x_{m})\leqslant \rho (x_{1},x_{2})+\rho (x_{2},x_{3})+…+\rho (x_{m-1},x_{m})}. Оно получается последовательным применением неравенства треугольника для трех точек: ρ(x1,xm)⩽ρ(x1,x2)+ρ(x2,xm)⩽ρ(x1,x2)+ρ(x2,x3)+ρ(x3,xm)⩽…{\displaystyle \rho (x_{1},x_{m})\leqslant \rho (x_{1},x_{2})+\rho (x_{2},x_{m})\leqslant \rho (x_{1},x_{2})+\rho (x_{2},x_{3})+\rho (x_{3},x_{m})\leqslant …}

Евклидова геометрия

Евклид доказал неравенство треугольника для расстояний в геометрии самолета, используя строительство в числе. Начинаясь с треугольника, равнобедренный треугольник построен с одной стороной, взятой в качестве и другая равная нога вдоль расширения стороны. Тогда утверждается что угол, так сторона. Но так сумма сторон. Это доказательство появляется в Элементах Евклида, Книге 1, Суждении 20.

Математическое выражение ограничения на стороны треугольника

Неравенство треугольника, как заявлено в словах, буквально переводит на три неравенства (учитывая, что длины стороны, все положительные):

Более сжатая форма такого заявления, как могут легко показывать, является

Другим способом заявить его является

допущение

и таким образом что самая долгая длина стороны — меньше, чем полупериметр.

Прямоугольный треугольник

Специализация этого аргумента прямоугольным треугольникам:

:In прямоугольный треугольник, гипотенуза больше, чем любая из этих двух сторон и меньше, чем их сумма.

Вторая часть этой теоремы уже установлена выше для любой стороны любого треугольника. Первая часть установлена, используя более низкое число. В числе рассмотрите прямоугольный треугольник. Равнобедренный треугольник построен с равными сторонами. От постулата треугольника удовлетворяют углы в прямоугольном треугольнике:

Аналогично, в равнобедренном треугольнике, углы удовлетворяют:

Поэтому,

и так, в частности

Это означает сторону, противоположный угол короче, чем сторона напротив большего угла. Но. Следовательно:

Подобное строительство показывает, устанавливая теорему.

Альтернативное доказательство (также основанный на постулате треугольника) продолжается, рассматривая три положения для пункта: (i), как изображено (который должен быть доказан), или (ii) совпадающий с (у того, которое означало бы равнобедренный треугольник, было два прямых угла как, основа удит рыбу плюс угол вершины, который нарушил бы постулат треугольника), или наконец, (iii) интерьер к прямоугольному треугольнику между пунктами и (когда угол — внешний угол прямоугольного треугольника и поэтому больше, чем, означая, что другой основной угол равнобедренного треугольника также больше, чем, и их сумма превышает в нарушении постулата треугольника).

Эти неравенства установления теоремы обострены теоремой Пифагора к равенству, что квадрат длины гипотенузы равняется сумме квадратов других двух сторон.

Некоторые практические примеры использования неравенства треугольника

Рассмотрите треугольник, стороны которого находятся в арифметической прогрессии и позволяют сторонам быть. Тогда неравенство треугольника требует этого

Удовлетворить все эти неравенства требует

Когда выбран таким образом, что, это производит прямоугольный треугольник, который всегда подобен Пифагорейцу трижды со сторонами.

Теперь рассмотрите треугольник, стороны которого находятся в геометрической прогрессии и позволяют сторонам быть. Тогда неравенство треугольника требует этого

Первое неравенство требует, следовательно оно может быть разделено через и устранено. С, среднее неравенство только требует. Это теперь оставляет первые и третьи неравенства, бывшие должные удовлетворить

\begin {выравнивают }\

r^2+r-1 & {}> 0 \\

r^2-r-1 & {}

Первое из этих квадратных неравенств требует, чтобы расположиться в регионе вне ценности положительного корня квадратного уравнения, т.е. где золотое отношение. Второе квадратное неравенство требует, чтобы расположиться между 0 и положительный корень квадратного уравнения, т.е.

§ 7. Ортонормированный базис

Определение
1. Базис
евклидова
простран­ства

называется ортогональным, если векторы
базиса попарно ортогональны,
т. е.

при

.

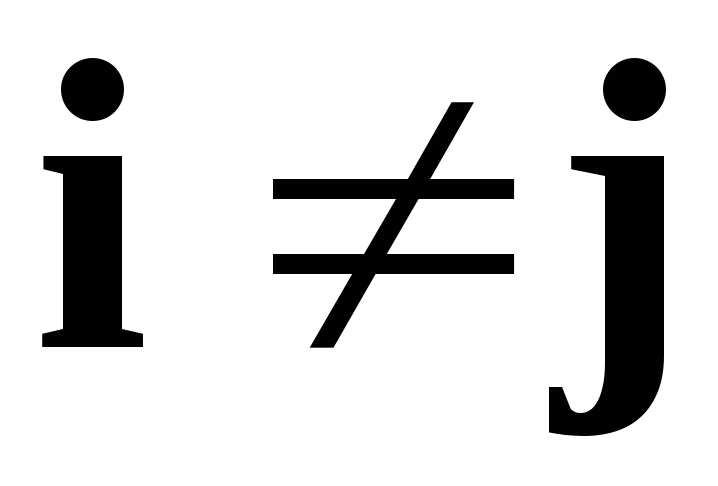Если при этом все
векторы базиса единичные, т. е.

, ,

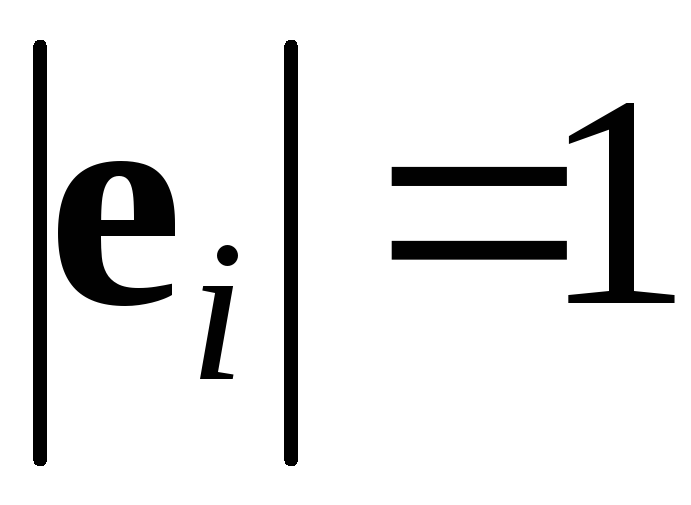то базис называется
ортонормированным.

Теорема.
Во всяком
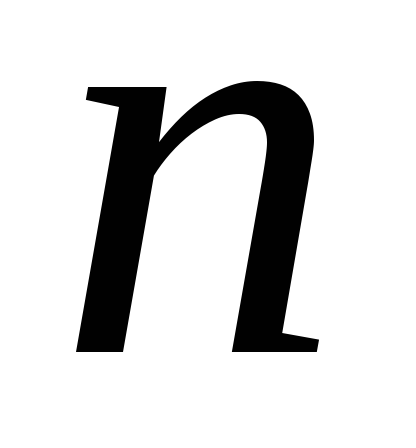-мерном
евклидовом прост­ранстве

имеются ортонормированные базисы.

Доказательство.
Доказательство проведем для слу­чая

.
Пусть
– произвольный базис пространства
.
Докажем, что с его помощью можно построить
ортонормированный базис. Положим
,
где

– некоторое ве­щественное число,
которое мы подберем так, чтобы векторы


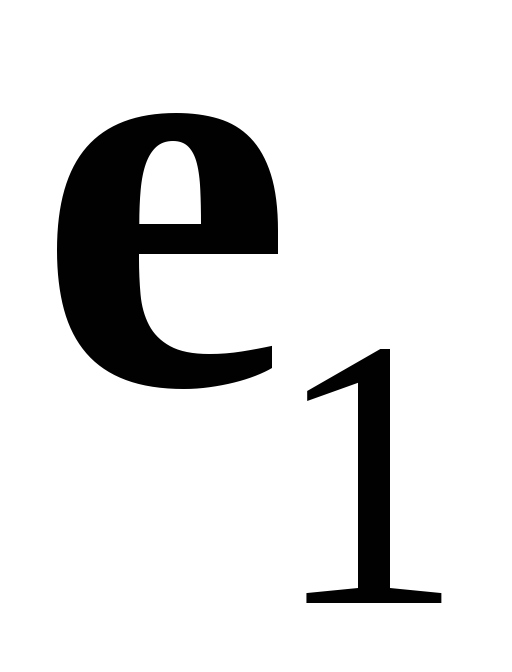
и

были ортогональны, то есть

.

Используя условия
2 и 3 определения евклидова
пространства,
получим

,

откуда получим
(так как
)

.(2.12)

Итак, если в качестве


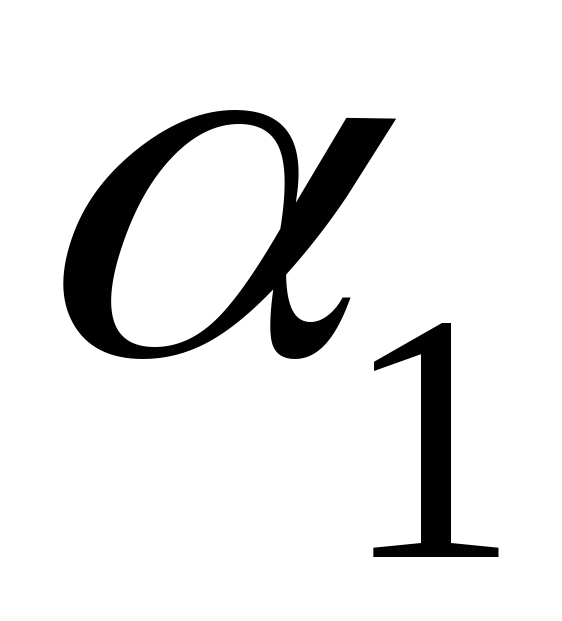
взять число, определяемое равенством
(2.12), то векторы

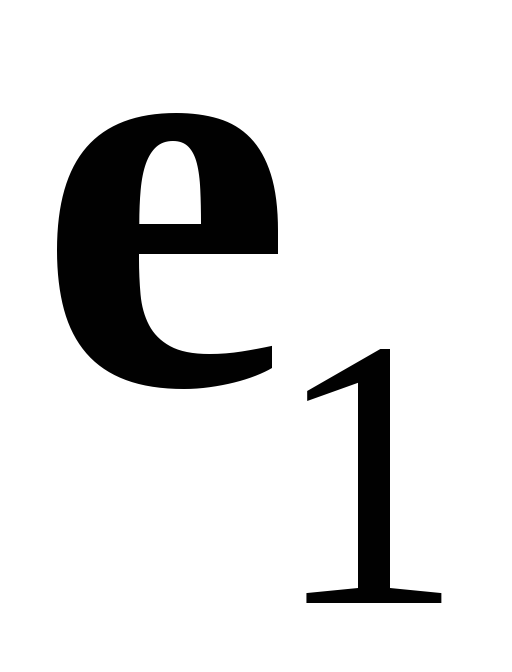
и

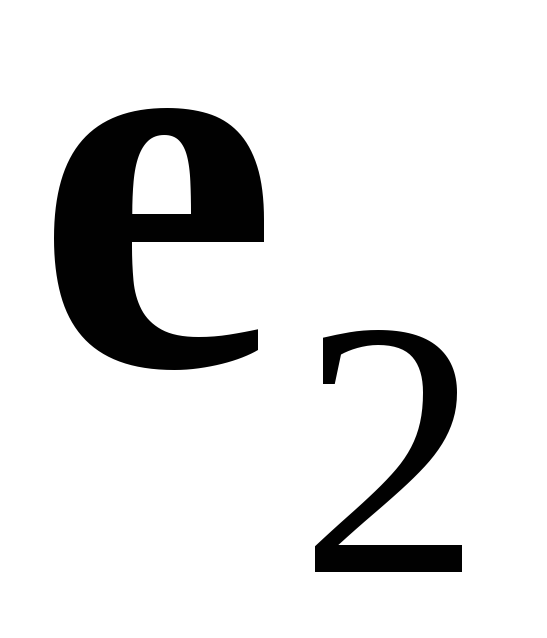
будут ортогональны, а так как векторы


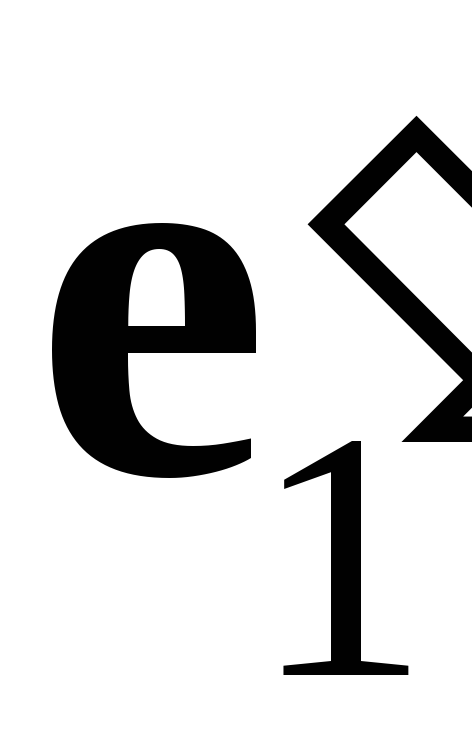
и
линейно
независимы, то из формулы, определяющей
вектор
,
следует, что он не может стать нулевым.
Вектор

опреде­лим с помощью равенства

,
(2.13)

где вещественные
числа

и

определим так, чтобы вектор

был ортогонален к векторам

и
,
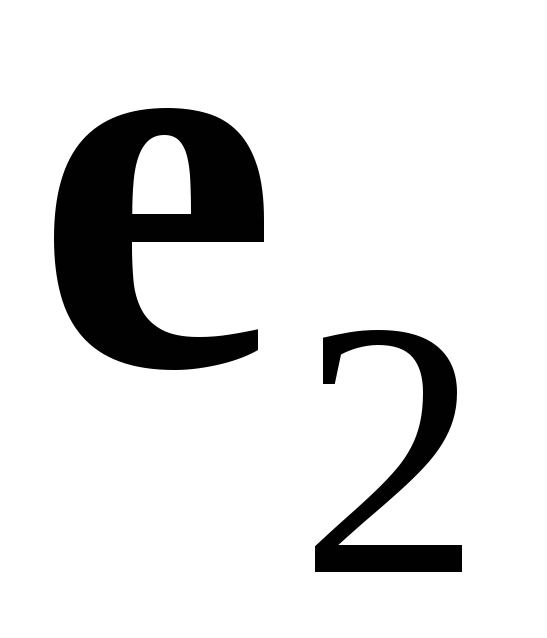т. е. чтобы выполнялись ра­венства

;

.

Используя, как и
выше, условия 2 и 3 определения евклидова
пространства, можем написать

;

,

откуда, учитывая
ортогональность векторов

и

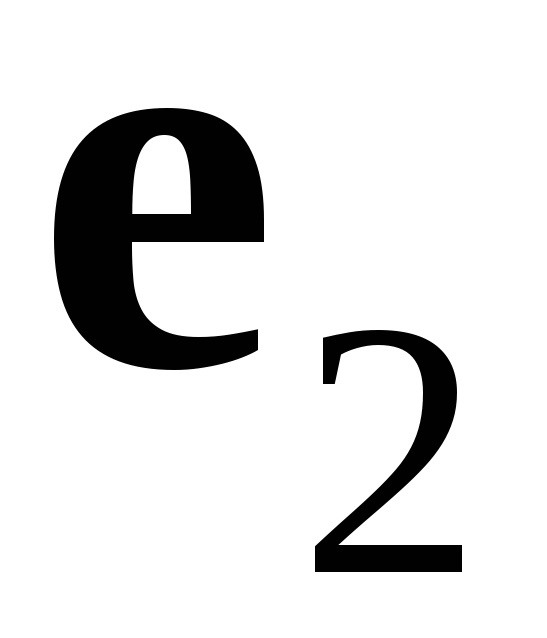
(т. е.
),
получим выражение для

и

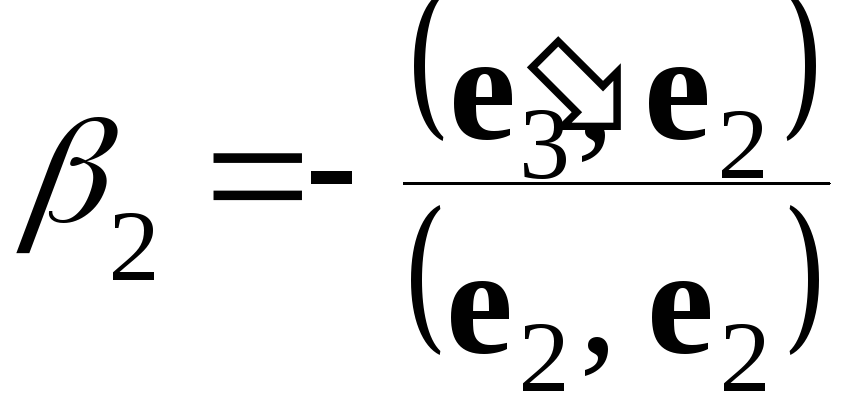, .(2.14)

Итак, если в качестве


и

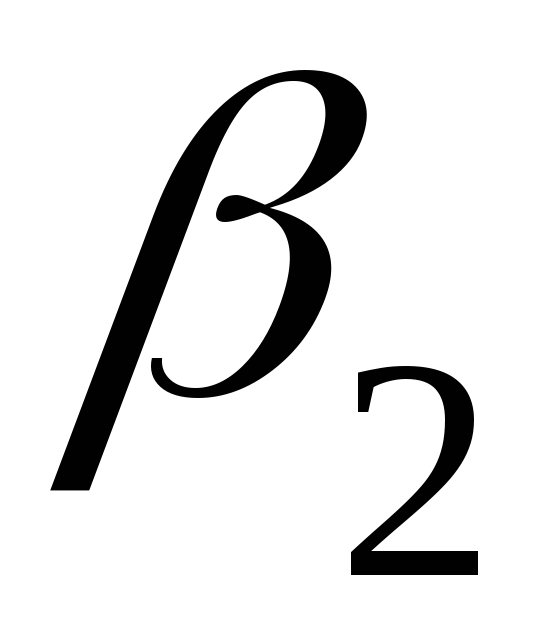
взять числа, определяемые равен­ствами
(2.14), то вектор

будет ортогонален векторам

и
,
так как векторы
,

,


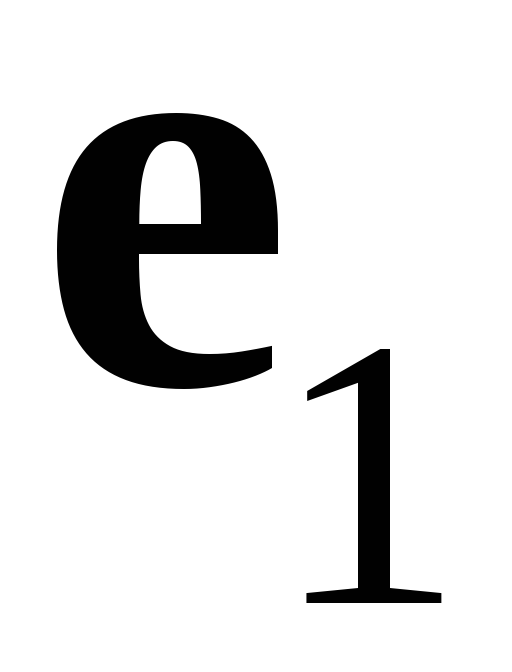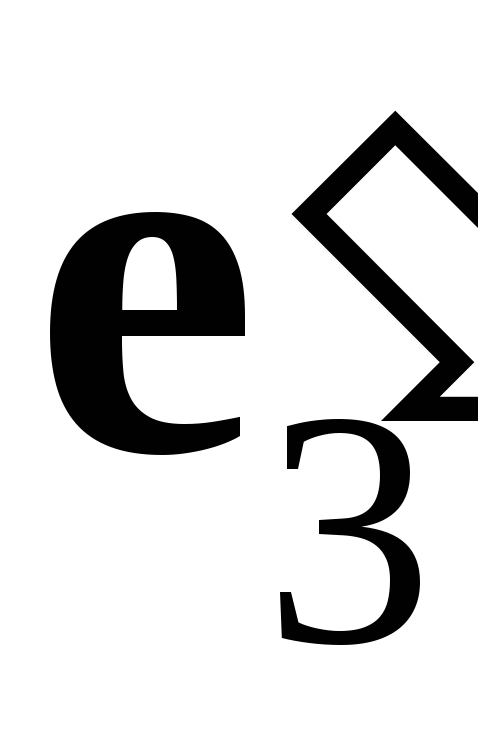
линейно независимы, то вектор

не может быть нулевым (вектор

выражается с помощью (2.13) в виде ли­нейной
комбинации векторов
,

,

).

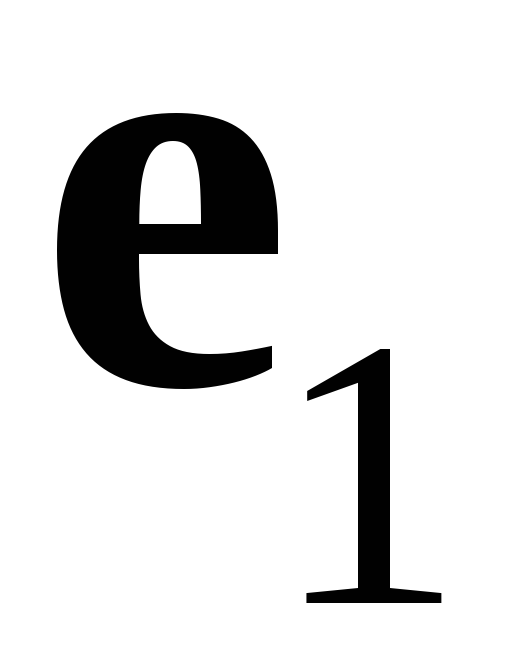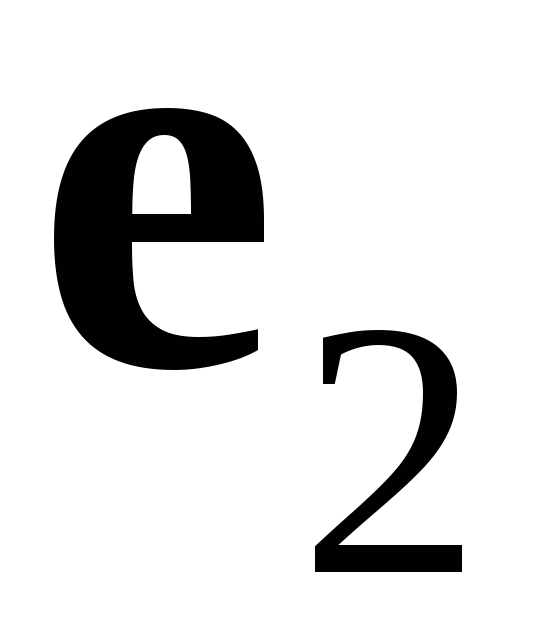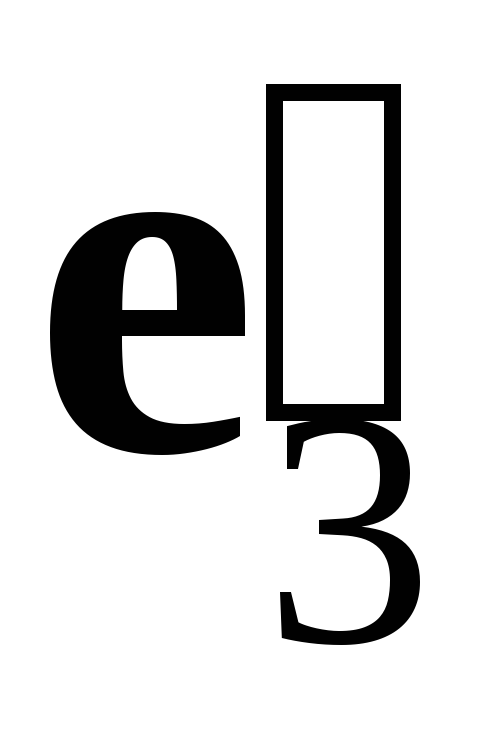Базис
,

,

–
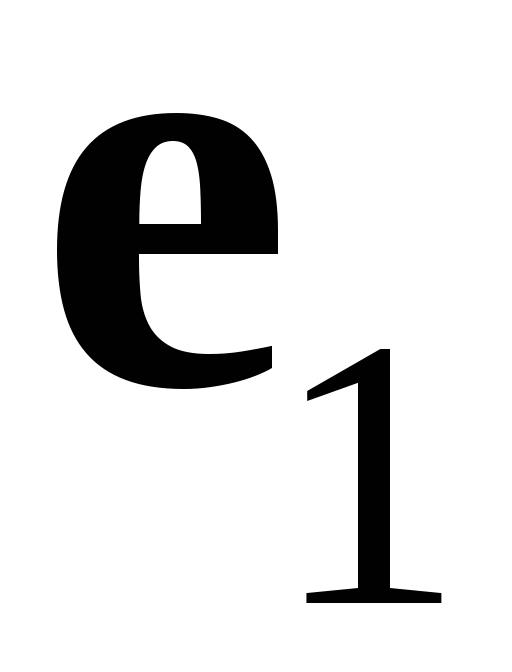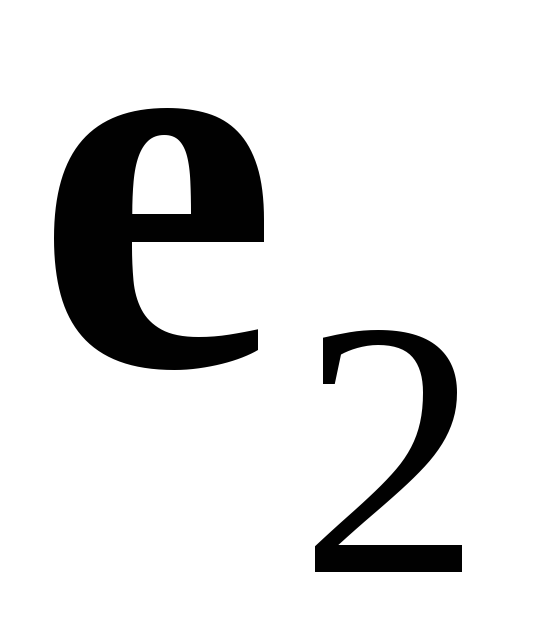ортогональный. Но для того чтобы сделать
его ортонормированным, следует каждый
из векторов
,

,


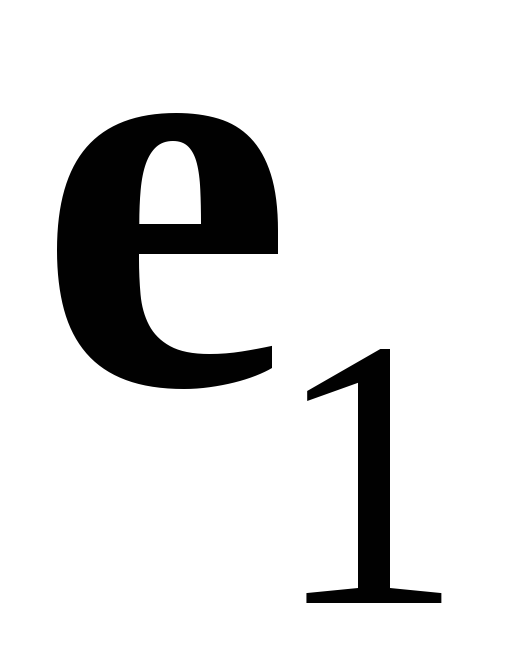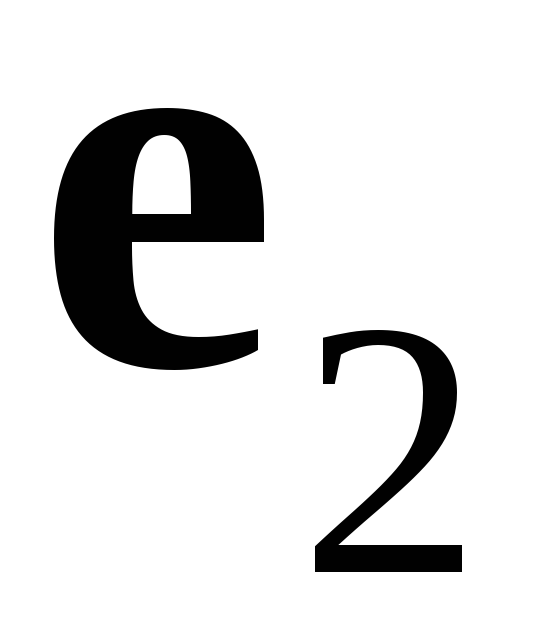поделить на его длину. Векторы

; ;

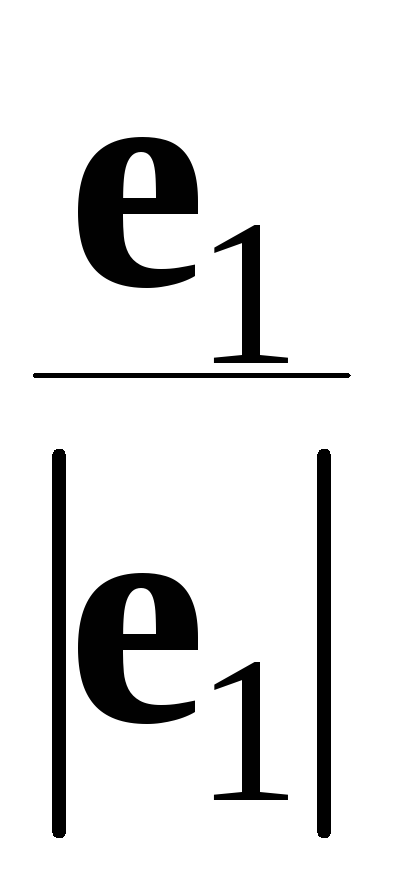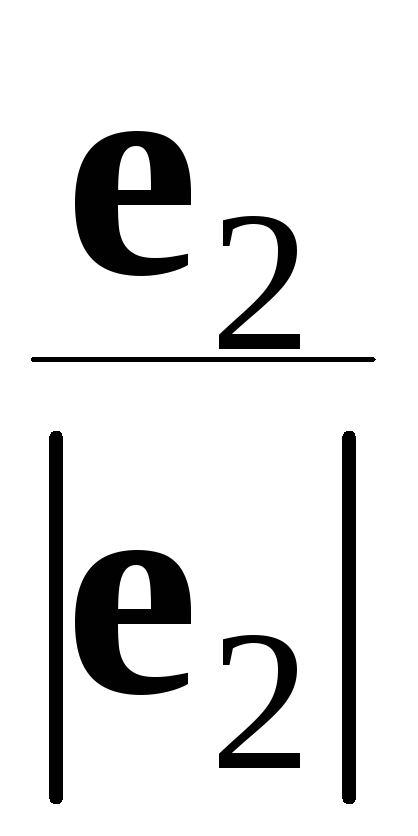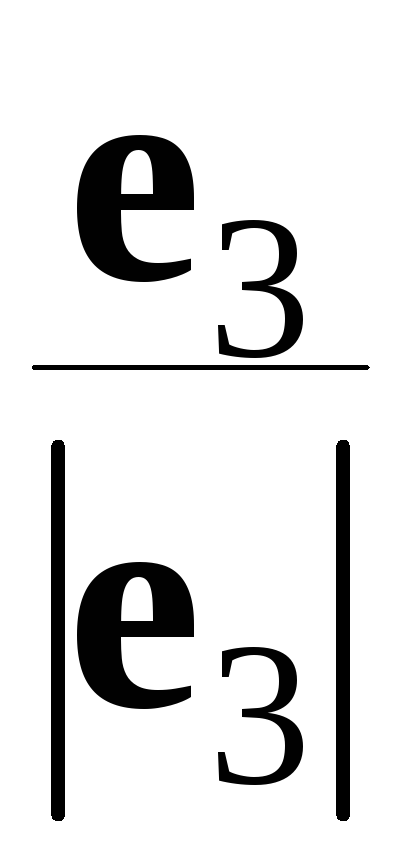
образуют искомый
ортонормированный базис.

Для случая
этот
процесс следует продолжать до тех пор,
пока не найдем последний вектор.

Примененный здесь
способ получения ортонормированного
ба­зиса из произвольного базиса носит
название процесса
ортогонализации.
Естественно, что каждый вектор

в
-мерном
евклидовом пространстве

можно представить в виде

,
(2.15)

где
– некоторый ортонормированный базис,– координаты вектора в этом базисе.
Отметим, что для координатимеют место равенства

, ,

которые получатся,
если умножить обе части равенства (2.15)
на
.

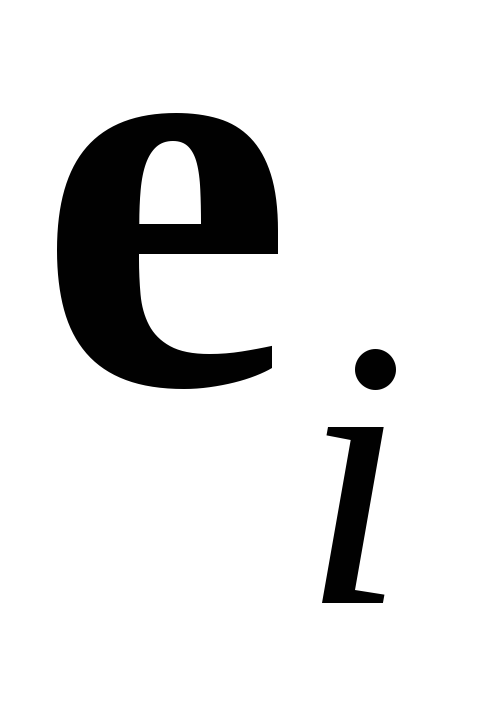Неравенство обратного треугольника

Обратное неравенство треугольника является элементарным следствием неравенства треугольника , что дает нижнюю границу вместо верхних границ. Для плоской геометрии утверждение:

Любая сторона треугольника больше, чем разница между двумя другими сторонами .

В случае нормированного векторного пространства утверждение таково:

|‖Икс‖-‖y‖|≤‖Икс-y‖,{\ Displaystyle {\ bigg |} \ | х \ | — \ | у \ | {\ bigg |} \ leq \ | ху \ |,}

или для метрических пространств | d ( y , x ) — d ( x , z ) | ≤ d ( y , z ) . Это означает , что норма , а также функция расстояния являются липшицируемая с константой Липшица 1 , и , следовательно, в частности , равномерно непрерывна .
‖⋅‖{\ displaystyle \ | \ cdot \ |}d(Икс,⋅){\ Displaystyle д (х, \ cdot)}

Доказательство обратного треугольника использует неравенство правильного треугольника и :
‖y-Икс‖знак равно‖-1(Икс-y)‖знак равно|-1|⋅‖Икс-y‖знак равно‖Икс-y‖{\ Displaystyle \ | Yx \ | = \ | {-} 1 (ху) \ | = | {-} 1 | \ cdot \ | ху \ | = \ | ху \ |}

‖Икс‖знак равно‖(Икс-y)+y‖≤‖Икс-y‖+‖y‖⇒‖Икс‖-‖y‖≤‖Икс-y‖,{\ Displaystyle \ | х \ | = \ | (ху) + у \ | \ leq \ | ху \ | + \ | у \ | \ Rightarrow \ | х \ | — \ | у \ | \ leq \ | ху \ |,}

‖y‖знак равно‖(y-Икс)+Икс‖≤‖y-Икс‖+‖Икс‖⇒‖Икс‖-‖y‖≥-‖Икс-y‖,{\ Displaystyle \ | у \ | = \ | (yx) + x \ | \ leq \ | yx \ | + \ | x \ | \ Rightarrow \ | x \ | — \ | y \ | \ geq — \ | xy \ |,}

Объединение этих двух утверждений дает:

-‖Икс-y‖≤‖Икс‖-‖y‖≤‖Икс-y‖⇒|‖Икс‖-‖y‖|≤‖Икс-y‖.{\ Displaystyle — \ | ху \ | \ leq \ | х \ | — \ | у \ | \ leq \ | ху \ | \ Rightarrow {\ bigg |} \ | x \ | — \ | y \ | {\ bigg |} \ leq \ | xy \ |.}