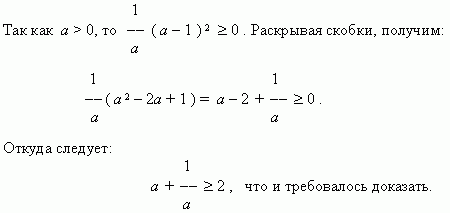Неравенство

3.2.1. document.write(‘Понятие о неравенстве’); window.top.document.title = «3.2.1. Понятие о неравенстве»;

Пусть функции f (x) и g (x) заданы на некоторых числовых множествах X₁ и X₂. Неравенством с одной неизвестной называется отношение вида

(Вместо знака < могут стоять знаки >, ≤, ≥.)


	Областью допустимых значений неравенства (ОДЗ) называется множество значений переменной, на котором обе части неравенства одновременно определены (имеют смысл). Таким образом, то есть пересечение множеств и


	Число a называется решением неравенства (1), если при подстановке его вместо переменной x получаем верное числовое неравенство f (a) < g (a).

Понятно, что a, являясь решением неравенства (1), может лежать только в ОДЗ.

Поскольку проверить решение в неравенствах не так просто, как в уравнениях, искать решения лучше сразу в ОДЗ.

Решить неравенство − это означает найти все его решения или доказать, что их нет. Совокупность всех решений неравенства называется множеством решений неравенства.

Два неравенства,

называются равносильными на множестве X, если на этом множестве неравенства имеют одни и те же решения, то есть, если каждое решение неравенства (2) является решением неравенства (3), и наоборот, каждое решение второго неравенства является решением первого. Два неравенства, не имеющие решений на каком-либо множестве, также считаются равносильными на этом множестве.

Из приведённого определения следует, что если неравенство f₁ (x) < g₁ (x) окажется более простым, чем равносильное ему неравенство f (x) < g (x), то и решать нужно именно его, так как решения у него те же. Остаётся единственная проблема: как от неравенства (2) перейти к равносильному ему неравенству (3) или, как говорят, осуществить равносильный переход? Сформулируем несколько общих правил, позволяющих это делать.

Правило 1. Если функции f (x), g (x) и h (x) определены на множестве X, то неравенства

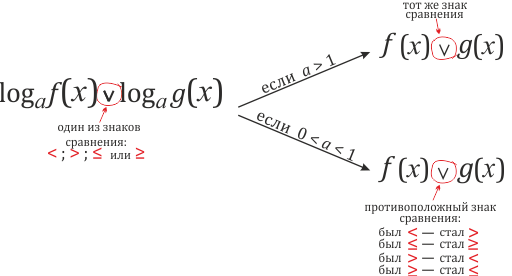
Правило 2. Если h (x) > 0 на множестве X, то неравенства

Вывод. Обе части неравенства можно умножать на положительную функцию, не нарушая равносильности.

Правило 3. Если h (x) < 0 на множестве X, то неравенства

Вывод. Обе части неравенства можно умножать на отрицательную функцию, не нарушая равносильности, меняя при этом знак неравенства на противоположный.

Правило 4. Если f (x) ≥ 0, g (x) ≥ 0 на множестве X, то неравенства

Вывод. Если обе части неравенства
неотрицательны, то возведение в квадрат неравенства не нарушает равносильности. Заметим, что возводить неравенство в квадрат можно, только если обе части этого неравенства неотрицательны. Если хотя бы одна из частей неравенства отрицательна, возведение неравенства в квадрат, вообще говоря, не является равносильным преобразованием. Яснее всего это видно на примере числовых неравенств. Так, если верное неравенство −1 > −4 возвести в квадрат, то получится неверное неравенство 1 > 16. Такое противоречие вызвано именно тем, что части первоначального неравенства не были неотрицательными.

Пример 1

Равносильны ли неравенства

Показать решение

Пример 2

Равносильны ли неравенства
и

Показать решение

Доказательство неравенств

Иногда в неравенствах помимо чисел встречаются переменные величины. При этом некоторые из них верны при любом значении этих переменных

Важно уметь доказывать это. Простейшие случаи связаны с использованием того факта, что квадрат любого числа неотрицателен

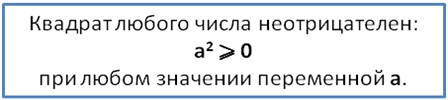
Пример. Докажите, что при любом значении d выполняется неравенство

d2+ 11 >5

Решение. Запишем очевидно верное неравенство

d2⩾ 0

Добавим к нему число 11:

d2 + 11 ⩾ 11

Число 11 больше 5, поэтому можно записать:

d2 + 11 ⩾ 11 > 5

d2 + 11 > 5

Пример. Докажите, что неравенство

n2 – 8n + 19> 0

справедливо для любого n.

Решение.

В левой части стоит квадратный трехчлен, попытаемся преобразовать его с помощью формулы :

n2 – 8n + 19 = n2 – 2•4n + 19 = n2 – 2•4n +16 – 16 + 19 =

= (n2 – 2•4n + 42) – 16 + 19 = (n– 4)2 + 3

Величина (n – 4)2 является неотрицательным числом, поэтому сумма (n – 4)2 + 3 никак не меньше трех, то есть положительна.

Иногда для доказательства числового неравенства можно определить знак разности выражений, стоящих в правой и левой части.

Пример. Докажите, что при любом значении переменных выполняется условие

2ut⩽u2 + t2

Решение. Запишем разность выражений, стоящих в неравенстве, а потом преобразуем ее:

2ut – (u2 + t2) = 2ut – u2 – t2 = – (u2 – 2ut + t2) = – (u – t)2

Разность получилась неположительной. Значит, между уменьшаемым и вычитаемым можно поставить знак «⩽»:

2ut⩽u2 + t2

Полученное выражение означает, что удвоенное произведение двух чисел не превосходит сумму их квадратов. Этот факт мы используем при решении следующего задания.

Пример. Докажите, что

d2 + s2 + m2⩾ds + dm + sm

Решение. В предыдущем примере мы установили, что сумма квадратов чисел больше или равна их двойному произведению, поэтому можно записать:

d2 + s2⩾ 2ds

s2 + m2⩾ 2sm

d2 + m2⩾ 2dm

Сложим полученные неравенства:

(d2 + s2) + (s2 + m2) + (d2 + m2) ⩾2ds + 2sm + 2dm

2d2 + 2s2 + 2m2⩾2ds + 2sm + 2dm

Осталось поделить на два это неравенство:

d2 + s2 + 2m2⩾ds + sm + dm

Примечания

Смелзер Нейл Социология. — М., 1994 стр. 278
Смелзер Нейл Социология. — М., 1994 стр. 282
Масионис Джон Социология. 9-е издание. СПб. 2004 стр. 352
↑
Сорокин Питирим Александрович Человек. Цивилизация Общество. М. 1992. Социальная и культурная мобильность. Стр. 315—322.
Сорокин Питирим Александрович Человек. Цивилизация Общество. М. 1992. Социальная и культурная мобильность. Стр. 334.
Сорокин Питирим Александрович Человек. Цивилизация Общество. М. 1992. Социальная и культурная мобильность. Стр. 330
Смелзер Нейл Социология. — М., 1994 стр. 275
Смелзер Нейл Социология. — М., 1994 стр. 283
Радугин А. А. Радугин К. А. Социология. Курс Лекций. М. «Владос» 1995 стр. 100
Большой толковый социологический словарь в 2 т. (Collins)/ Сост. Джерри Д., Джерри Дж.- М., 1999 Т 2 стр. 242

Коды знаков неравенств

Символ	Изображение	Юникод	Русское название	HTML	LaTeX
Код	Название	Шестнадцатеричное	Десятеричное	Мнемоника
<	<{\displaystyle <}	U+003C	Less-than sign	Меньше	<	<	<	<, \textless
>	>{\displaystyle >}	U+003E	Greater-than sign	Больше	>	>	>	>, \textgreater
⩽	⩽{\displaystyle \leqslant }	U+2A7D	Less-than or slanted equal to	Меньше либо равно	⩽	⩽	отсутствует	\leqslant
⩾	⩾{\displaystyle \geqslant }	U+2A7E	Greater-than or slanted equal to	Больше либо равно	⩾	⩾	отсутствует	\geqslant
≤	≤{\displaystyle \leq }	U+2264	Less-than or equal to	Меньше либо равно	≤	≤	≤	\le, \leq
≥	≥{\displaystyle \geq }	U+2265	Greater-than or equal to	Больше либо равно	≥	≥	≥	\ge, \geq
≪	≪{\displaystyle \ll }	U+226A	Much less-than	Много меньше	≪	≪		\ll
≫	≫{\displaystyle \gg }	U+226B	Much greater-than	Много больше	≫	≫		\gg

Верные и неверные неравенства

Неравенства могут быть верными или неверными.

Определение.

Неравенство является верным, если оно соответствует введенному выше смыслу неравенства, в противном случае оно является неверным.

Приведем примеры верных и неверных неравенств. Например, 3≠3 – это неверное неравенство, так как числи 3 и 3 равные. Другой пример: пусть S – это площадь некоторой фигуры, тогда S<−7 – неверное неравенство, так как известно, что площадь фигуры по определению выражается неотрицательным числом. И еще пример неверного неравенства: |AB|>|AB|. А вот неравенства −3<12, |AB|≤|AC|+|BC| и |−4|≥0 – верные. Первое из них отвечает правилу сравнения чисел с разными знаками, второе – выражает неравенство треугольника, а третье – согласуется с определением модуля числа.

Отметим, что наряду со словосочетанием «верное неравенство» используются такие словосочетания: «справедливое неравенство», «имеет место неравенство» и т.п., означающие одно и то же.

Что такое неравенство?

Понятие неравенства, как и понятие равенства, связано со сравнением двух объектов. И если равенство характеризуется словом «одинаковые», то неравенство, напротив, говорит о различии сравниваемых объектов. Например, объекты и — одинаковые, про них можно сказать, что они равные. А вот два объекта и отличаются, то есть, они не равны или неравные.

Неравенство сравниваемых объектов познается вместе со смыслом таких слов, как выше, ниже (неравенство по высоте), толще, тоньше (неравенство по толщине), дальше, ближе (неравенство по удаленности от чего-либо), длиннее, короче (неравенство по длине), тяжелее, легче (неравенство по весу), ярче, тусклее (неравенство по яркости), теплее, холоднее и т.п.

Как мы уже отмечали при знакомстве с равенствами, можно говорить как о равенстве двух объектов в целом, так и о равенстве их некоторых характеристик. Это же относится и к неравенствам. В качестве примера приведем два объекта и . Очевидно, они не одинаковые, то есть, в целом они неравные. Они не равны по размеру, также они не равны по цвету, однако, можно говорить о равенстве их форм – они оба являются кругами.

В математике общий смысл неравенства сохраняется. Но в ее контексте речь идет о неравенстве математических объектов: чисел, значений выражений, значений каких-либо величин (длин, весов, площадей, температур и т.п.), фигур, векторов и т.п.

Причины социальных различий

Общество — сложный социально-биологический организм, в котором каждому человеку отведена своя роль. Как в человеческом организме ноги не могут выполнять функцию головы, а желудок не может заменить сердце, так и в обществе у каждого своя задача и возможности для ее реализации.

Из-за разных функций, выполняемых отдельными группами людей, сформировались основные отличия в их имущественном и социальном положении.

()

Другие причины социального неравенства:

Разница во врожденных качествах и способностях людей (умственные способности, физические данные, таланты);
Наличие силы воли, целеустремленности у одних, пассивность и лень у других;
Владение частной собственностью;
Неравный доступ к власти.

Таким образом становится ясно, что причины неравенства как природные, так и социальные.

Кроме того, возможность занять определенное положение в обществе зависит от уровня образования, квалификации человека. Представитель популярной востребованной профессии, первоклассный профессионал имеет больше возможностей занять высокое положение в обществе, чем неквалифицированный рабочий.

Формулы основных неравенств

Формулы универсальных неравенств

Универсальные неравенства выполняются при любых значениях входящих в них величин. Ниже перечислены основные виды универсальных неравенств.

1) ; .Доказательство. .

2) .Доказательство. Первое неравенство доказано в пункте 1). Доказываем второе..

3) Равенство имеет место только при .

Доказательство. Докажем, что , где . При имеем:. Применяем метод индукции. Пусть . Тогда.

4) Неравенство Коши — Буняковского Равенство имеет место тогда и только тогда, когда для всех и некоторых .

5) Неравенство Минковского, при

Формулы выполнимых неравенств

Выполнимые неравенства выполняются при определенных значениях входящих в них величин.

1) Неравенство Бернулли:;. В более общем виде:, где , числа одного знака и больше, чем .Лемма Бернулли:. См. «Доказательства неравенств и леммы Бернулли».

2) при .

3) Неравенство Чебышева при и . При и .

4) Обобщенные неравенства Чебышева при и и натуральном. При и .

Исторические формы социального неравенства

Главными видами социального неравенства, известными в истории были: деление общества на касты, сословия, классы.

В Древней Индии общество делилось на 4 основных касты, принадлежность к которым определялась с момента появления человека на свет.

Высшей кастой считались брахманы (священники, жрецы), они могли отдавать распоряжения и приказы даже правителям;
К касте кшатриев (воинов) принадлежали глава государства (император), военачальники, министры, рядовые солдаты;
Вайшьи (торговцы) представляли зажиточный слой населения;
Шудры (рабочие) составляли основную прослойку общества, они подчинялись распоряжениям брахманов, кшатриев, вайшьев.

()

К отдельной полностью бесправной касте относились неприкасаемые, они жили вдалеке от всего остального общества, выполняли самую грязную работу. Считалось, что даже прикосновение или нахождение рядом с неприкасаемым оскверняет представителей других каст.

Вплоть до 19 и начала 20 века, в большинстве стран Европы, России, некоторых государствах Азии общество делилось на сословия. Рассмотрим пример социального неравенства в России в первой половине 18 века.

Высшее положение в российском обществе занимало дворянство. Дворянам принадлежала земля, жившие и работавшие на ней крепостные крестьяне, они имели привилегии при зачислении на государственную службу. В руках дворян была сосредоточена политическая и экономическая власть.

Важно! Только потомственные дворяне передавали свою сословную принадлежность по наследству. Личные дворяне получали свой титул, находясь на службе при государстве, покинув которую они утрачивали свое привилегированное положение

К привилегированным сословиям принадлежало так же белое духовенство — все священнослужители кроме монахов, живших отреченной жизнью вдали от человеческого общества. Священники передавали свой духовный сан от отца к сыну, дети священнослужителей обучались в специальных церковных учебных заведениях.

К полу привилегированным сословиям относились купечество, казачество. Основу городского населения составляли непривилегированные сословия: горожане, ремесленники, небольшая по численности интеллигенция. Но основную часть российского общества – более 80% составляли крестьяне. Самыми бесправными из них были крепостные, которых можно было продавать, обменивать, отправлять на каторгу за малейшую провинность по отношению к помещику.

Постепенно, к концу 19 началу 20 века сословия в России исчезли, общество стало делиться на классы. Классы отличались уровнем дохода и способом заработка на жизнь. Знатное происхождение, родословная утратили свое прежнее значение, теперь, главной ценностью передаваемой по наследству стали деньги, капиталы.

Метод интервалов

При решении сложных неравенств весьма эффективен метод интервалов. Он работает в том случае, если в одной части нер-ва стоит произведение нескольких множителей (обычно линейных полиномов), а в другой ноль. Тогда знак неравенства можно поменять на «=», и получить уравнение. Далее его следует решить и отметить на координатной прямой полученные корни. Эти корни разобьют числовую прямую на несколько интервалов. Далее надо просто определить, на каких интервалах выполняется неравенство. Рассмотрим этот метод на конкретном примере.

Пример. Решите неравенство

(х – 5)(х – 7)(4 – 2х) > 0

Решение.

Первый шаг – заменим знак «>» на «=»:

(х – 5)(х – 7)(4 – 2х) = 0

Получили уравнение. Вспомним правило: произведение множителей равно нулю, если хоть один из них равен нулю. Поэтому

х – 5 = 0 или х – 7 = 0 или 4 – 2х = 0

Решим каждое из трех полученных линейных уравнений:

х – 5 = 0

х = 5

х – 7 = 0

х = 7

4 – 2х = 0

– 2х = – 4

х = 2

Получили корни 2, 5 и 7. Отметим их на координатной прямой:

Эти точки разбивают числовую прямую на 4 промежутка:

(– ∞; 2);
(2; 5);
(5; 7);
(7; + ∞).

В исходном неравенстве слева стоит произведение (х – 5)(х – 7)(4 – 2х). Определим его знак на каждом из этих 4 интервалов. Для этого достаточно взять одно число из интервала и подставить его в выражение:

Из промежутка (– ∞; 2) возьмем х = 0:

(х – 5)(х – 7)(4 – 2х) = (0 – 5)(0 – 7)(4 – 2•0) = (– 5)•(– 7)•4 = 140

Получили число, большее нуля: 140 > 0

Из промежутка (2; 5) возьмем х = 3:

(х – 5)(х – 7)(4 – 2х) = (3 – 5)(3 – 7)(4 – 2•3) = (– 2)•(– 4)•(– 2) = – 16

Получили отрицательное число.

Из промежутка (5; 7) возьмем х = 6:

(х – 5)(х – 7)(4 – 2х) = (6 – 5)(6 – 7)(4 – 2•6) = 1•(– 1)•(– 8) = 8

Получили положительное число

Для последнего промежутка возьмем х = 8:

(х – 5)(х – 7)(4 – 2х) = (8 – 5)(8 – 7)(4 – 2•8) = 3•1•(– 12) = – 36

Теперь поставим на числовой прямой знаки, соответствующие каждому интервалу:

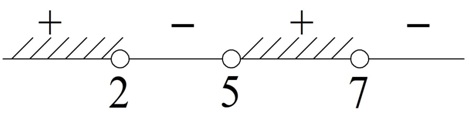
Так как в исходном неравенстве стоял знак «>», то в ответ надо записать объединение тех интервалов, на которых левая часть принимает положительные значения.

Ответ: (– ∞; 2)⋃(5; 7)

В этом примере можно заметить, что знаки в интервалах чередовались. Так и должно происходить в том случае, если каждый из множителей в левой части является первой степени. Напомним, что многочлен 1-ой степени – это выражение вида ах + с, например:

5х + 9
8х – 13
7,56х + 12,35

Пример. Определите, при каких значениях переменной полином

х2 – 8х + 12

принимает отрицательные значения.

Решение. По сути, нам надо решить нер-во

х2 – 8х + 12< 0

Вспомним, что квадратный трехчлен можно разложить на линейные множители. Для этого надо решить уравнение:

х2 – 8х + 12 = 0

D = (– 8)2 – 4•1•12 = 64 – 48 = 16

Зная х₁ и х₂, можем записать, что

х2 – 8х + 12 = (х – х₁)(х – х₂) = (х – 2)(х – 6)

Перепишем исходное нер-во:

(х – 2)(х – 6) > 0

К нему уже можно применить метод интервалов (так как в левой части стоит произведение):

(х – 2)(х – 6) = 0

х – 2 = 0 или х – 6 = 0

х = 2 или х = 6

Естественно, что мы получили те же корни, что и при решении квадратного уравнения выше. Отметим корни на прямой и определим значение трехчлена на каждом из полученных интервалов:

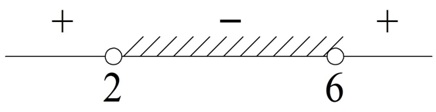
На промежутке (– ∞; 2) при х = 1 имеем (1 – 2)(1 – 6) = (– 1)•(– 5) = 5

Промежуток (2; 6): при х = 3 получаем (3 – 2)(3 – 6) = 1• (– 3) = – 3

На промежутке (6; + ∞) при х = 7 получается (7 – 2)(7 – 6) = 5•1 = 5

В итоге трехчлен отрицателен тогда, когда х принадлежит интервалу (2; 6).

Ответ (2; 6).

Свойства неравенств

Рассмотрим основные свойства числовых неравенств, которые в дальнейшем помогут нам решать некоторые задачи.

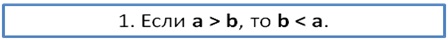
Докажем это. Если а >b, то тогда и разность (a –b) является положительным числом:

а – b = c

умножив части равенства на (– 1), получим:

– (а – b) = – с

(b– a) = – с

Так как разность (b– a)оказалась равна отрицательному числу (– с), тоb<a.

Для доказательства этого очевидного факта используем координатную прямую:

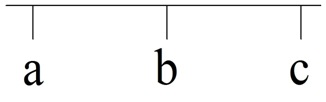
Ясно, что если b>a, то оно располагается правее. Аналогично и с располагается правее b, так как с >b. Видно, что тогда сбудет находиться правее а, то есть оно больше.

Данное свойство называют транзитивностью. Им обладает не только отношение «больше — меньше», но и ряд других отношений. Например, из геометрии известно, что если отрезок АВ параллелен отрезку CD, а тот в свою очередь параллелен ещё одному отрезку EF, то и АВ параллельно ЕF.

Свойство транзитивности позволяет использовать так называемые двойные неравенства. Например, нам надо указать, что 25 меньше 48, а 48 меньше 94. Это можно записать в виде одного неравенства:

25 < 48 < 94

Можно использовать и более двух знаков сравнения:

365 <366 < 367 < 368 < 369

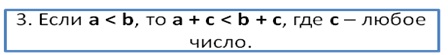
Другими словами, к обеим частям верного неравенства можно добавить одинаковое число, и оно всё равно останется верным. Действительно, пусть нам надо сравнить величины (а + с) и (b + c). Для этого найдем их разность:

(а + с) – (b + c) = a + c – b – с = а – b

Так как a<b, то и разность а – b отрицательна. Значит, отрицательна разность величин (а + с) и (b + c), из чего следует, что

а + с <b + c

Проиллюстрируем это на примере неравенства

73 < 86

Добавим к обеим частям число 11 и получим другое верное равенство:

73 + 11 < 86 + 11

84 < 97

Снова рассмотрим разность величин ac и bc:

ac– bc = (a– b)c

Разность (а – b) отрицательна при условии а <b. Если с – положительное число, то всё произведение (a– b)c остается отрицательным, т тогда

ас <bc

Если же c– отрицательное число, то произведение (a– b)c становится положительным, а потому

ас <bc

Пусть есть неравенство

100< 200

Если умножить его на положительное число, например, на 3, то получим верное равенство

300 < 600

Если же умножить его на (– 3), то придется «перевернуть» знак сравнения, поставить вместо «<»знак «>»:

– 300 >– 600

Следующее свойство неравенств позволяет их складывать:

Докажем эту теорему. Найдем разность чисел (а + c) и (b + d):

(а + c) – (b + d) = а + с – b – d = (a– b) + (b– d)

Получили сумму двух слагаемых, (a– b) и (b– d). Каждое из них является отрицательным числом, так как a<bи c<d. Сумма двух отрицательных чисел также отрицательна, а потому можно утверждать, что

а + c<b + d

Покажем, как с помощью этого правила можно складывать неравенства. Пусть есть два верных неравенства:

59<62

69<75

Теперь сложим отдельно их правые и левые части:

59 + 69<62 + 75

128 < 137

Однако если у неравенств разные знаки, то для их сложения надо в одном из них поменять местами правую и левую часть. Например, даны неравенства

63 < 99

26> 25

В одном стоит знак «меньше», а в другом «больше», поэтому сразу их складывать нельзя. Сначала «перевернем» второе неравенство

25 < 26

теперь в обоих неравенствах стоит знак «<», поэтому их можно сложить:

63 + 25 < 99 + 26

88 < 125

Последнее правило позволяет перемножать неравенства:

Для доказательства утверждения найдем разность величин acи bd. При этом добавим к ней слагаемое bc и тут же его вычтем (это необходимо для того, чтобы мы смогли сгруппировать слагаемые):

ac – bd = ac – bd– bc + bc= (ac – bc) + (bc – bd) =

=c(a– b) + b(c– d)

Так как разности (a– b) и (c– d) являются отрицательными числами, c и b – положительными, то и произведения c(a– b) и b(c– d) – это отрицательные величины. Сумма же двух отрицательных величин также отрицательна, поэтому

ac<bd

Покажем на примере использование этого правила. Пусть есть неравенства

7<8

5<6

Перемножив их, получим:

7•5<8•6

35 < 48

Социальное неравенство – что это?

Социальное классовое неравенство существовало с древних времен эволюции человека. История разных стран служит наглядным доказательством того, к чему приводит угнетение и порабощение людей – это мятежи, голодные бунты, войны и революции. Но этот опыт, прописанный кровью ничему не учит. Да, сейчас это приняло более мягкие, завуалированные формы. В чем выражается социальное неравенство и что оно из себя представляет сегодня?

Социальное неравенство – это разделение или дифференциация людей на классы, общества или группы, согласно их положению в обществе, что предполагает неравное использование возможностей, жизненных благ и прав. Если представить социальное неравенство схематически в виде лестницы, то на самых нижних ее ступенях будут угнетенные, бедные, а вверху угнетатели и богатые, те, у кого в руках власть и деньги. Это основной признак расслоения общества на бедных и богатых. Существуют и другие показатели социального неравенства.

Причины социального неравенства

Каковы причины социального неравенства? Экономисты видят первопричину в неравном отношении к собственности и распределении материальных благ в целом. Р. Михельс (немецкий социолог) видел причину в наделении большими привилегиями и полномочиями аппарат власти, который выбирался самим же народом. Причины возникновения социального неравенства по мнению французского социолога Э. Дюркгейма:

Поощрение людей, приносящих наибольшую пользу для общества, лучших в своем деле.
Уникальные личные качества и таланты человека, выделяющие его из общего социума.

Виды социального неравенства

Формы социального неравенства разные, поэтому существует несколько классификаций. Виды социального неравенства по физиологическим признакам:

возрастное – касается всех людей в определенные возрастные промежутки, это прослеживается при приеме на работу, молодежь не берут из-за отсутствия опыта, пожилых людей при их огромном опыте заменяют молодыми, более перспективными с точки зрения начальства;
социальное сексуальное неравенство – здесь можно рассмотреть такое явление как женская дискриминация, выраженная в том, что мало женщин занимающих ответственные посты, участвующих в экономической жизни страны, женщине отводится роль «за мужем»;
социальное этническое неравенство – малые этносы, те, которые не входят в понятие «белая раса» во многом притесняются из-за такого явлений как ксенофобия и расизм.

Социальное неравенство в связи со статусами в обществе:

отсутствие / наличие богатства;
приближенность к власти.

Проявление социального неравенства

Основные признаки социального неравенства наблюдаются в таком явление как разделение труда. Деятельность человека разнообразна и каждый человек наделен какими-то талантами и умениями, способностями к росту. Социальное неравенство при этом проявляется как отдача привилегий тем, кто более талантлив и перспективен для общества. Расслоение общества или стратификация (от слова «страта» – геологический пласт) это выстраивание иерархической лестницы, деление на классы, и если раньше это были рабы и рабовладельцы, феодалы и челядь, то на современном этапе – это разделение на:

высший класс;
средний класс;
малообеспеченные (социально уязвимые);
за чертой бедности.

Последствия социального неравенства

Социальное неравенство и бедность, порождаемая тем, что основными ресурсами планеты могут пользоваться лишь избранные порождает конфликты и войны среди населения. Последствия развиваются постепенно и выражены в замедленном развитии многих стран, это приводит к тому, что прогресс в экономике тоже замедляется, демократия как система теряет свои позиции, в обществе растет напряжение, недовольство, психологическое давление социальная дисгармония. По данным ООН половиной мировых ресурсов владеет 1% так называемой высшей элиты (мировое господство).

Плюсы социального неравенства

Социальное неравенство в обществе как феномен не носит на себе лишь отрицательные свойства, если рассматривать социальное неравенство с позитивной стороны, то можно отметить важные вещи, присмотревшись к которым возникает мысль, что все «имеет место быть под Солнцем». Плюсы социального неравенства для человека:

стимул стать лучшим в своем деле, проявить по максимуму свои способности и таланты;
мотивация для тех, кто хочет выйти из бедности;
упорядочивание в экономической сфере, у тех, у кого есть капитал производят ресурсы, в отличие от тех, кто не имеет капитала и в состоянии лишь прокормить себя и свою семью.

Решение линейных неравенств

Со школьных уроков мы помним, что у неравенств нет ярко выраженных различий, поэтому рассмотрим несколько определений.

Определение 1. Линейное неравенство с неизвестной переменной x имеет вид ax + b > 0, когда вместо > используется любой знак < , ≤ , ≥ , а и b — действительные числа, a ≠ 0.

Определение 2. Неравенства называют линейными с одной переменной, когда ax < c или ax > c , где x — переменная, a, c — некоторые числа.

Мы не знаем может ли коэффициент равняться нулю, поэтому: 0 * x > c и 0 * x < c можно записать в форме нестрогого неравенства: ax ≤ c, ax ≥ c . Такое уравнение принято называть линейным. Его главные различия:

форма записи ax + b > 0 — в первом и ax > c — во втором;
допустимость равенства нулю: a ≠ 0 — в первом, a = 0 — во втором.

Неравенства ax + b > 0 и ax > c равносильные, так как получены переносом слагаемого из одной части в другую.

Определение 3. Линейные неравенства с одной переменной x выглядят так:

ax + b < 0,
ax + b > 0,
ax + b ≤ 0,
ax + b ≥ 0,

где a и b — действительные числа. А на месте x может быть обычное число.

Социальное неравенство сегодня

В прошлом, переход из одной социальной группы в другую был невозможен. Родившись в определенном сословии, человек принадлежал к нему до конца своей жизни. Запрещены были браки между представителями разных сословий, каст, классов. Такое общество называли закрытым, так как в нем невозможен был переход из одного социального слоя в другой.

Сегодня, у каждого есть возможность, шанс поменять свое социальное положение. Даже родившись в семье бедняков, ребенок может благодаря своему трудолюбию и таланту стать богатым и успешным, повысить свой социальный уровень. Благодаря такой возможности перехода из одного класса в другой, современное общество называют открытым.

Это интересно! Способ, с помощью которого человек может поменять свое имущественное положение, называют социальным лифтом. Лифт движется с высокой скоростью, облегчает передвижение с этажа на этаж. Социальный лифт предоставляет возможности человеку повысить свой социальный уровень. К социальным лифтам относят: высшие учебные заведения, армию, брак.

Социальное неравенство в современном мире проявляется не только между отдельными людьми, общественными группами, но и среди целых стран, народов, государств. Разные страны имеют различный уровень доходов, доступ к природным ресурсам, благам человечества, возможность оказывать влияние на государства мирового сообщества.

()

Так по данным статистики на 2018 год, первые места по уровню жизни в мире занимают страны:

Дания;
Швейцария;
Австрия;
Германия;
Финляндия;
Нидерланды;
Япония.

Румыния занимает в этом рейтинге 37 место, Турция- 44, Индия — 49, Украина — 60, а Россия находится на 56 позиции.