Монотонная функция

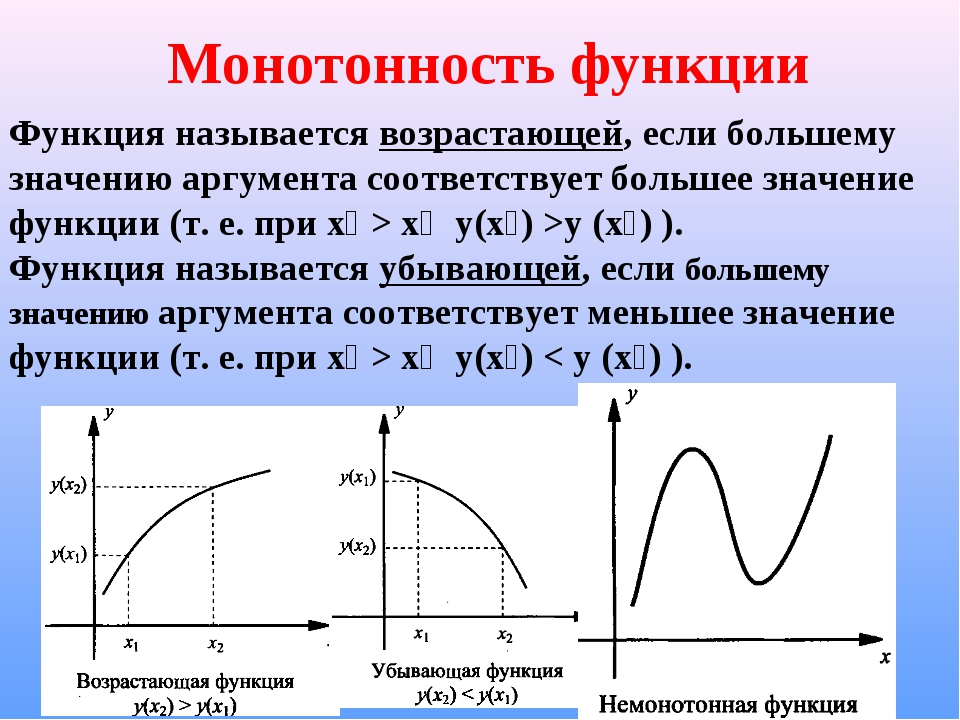
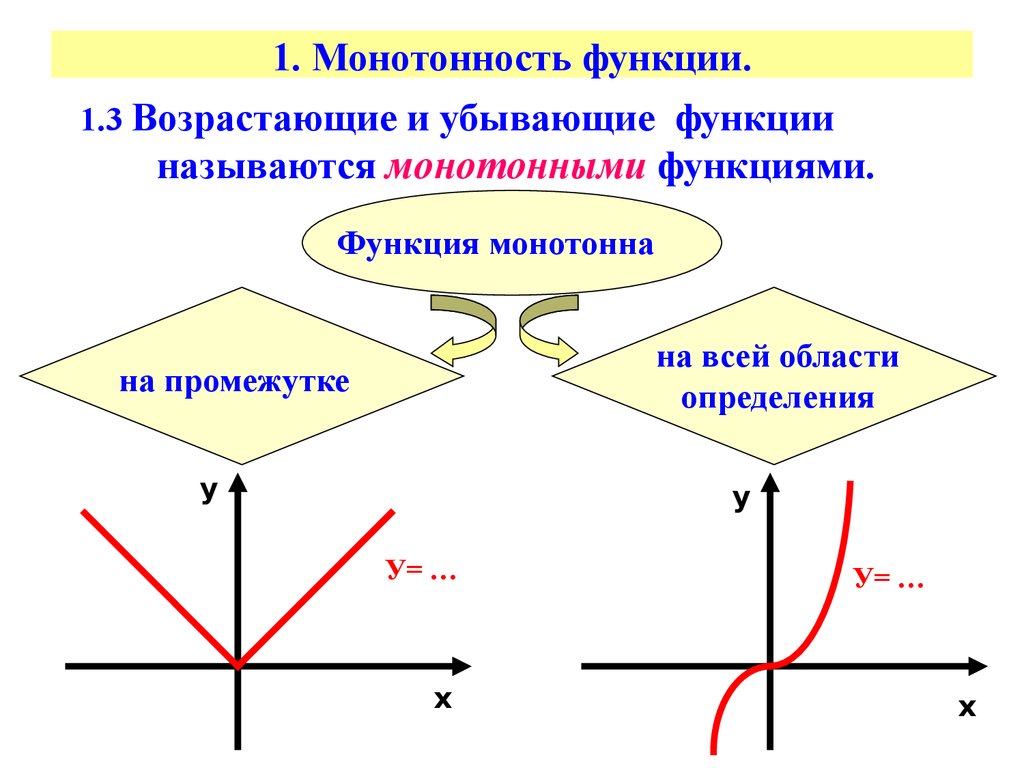
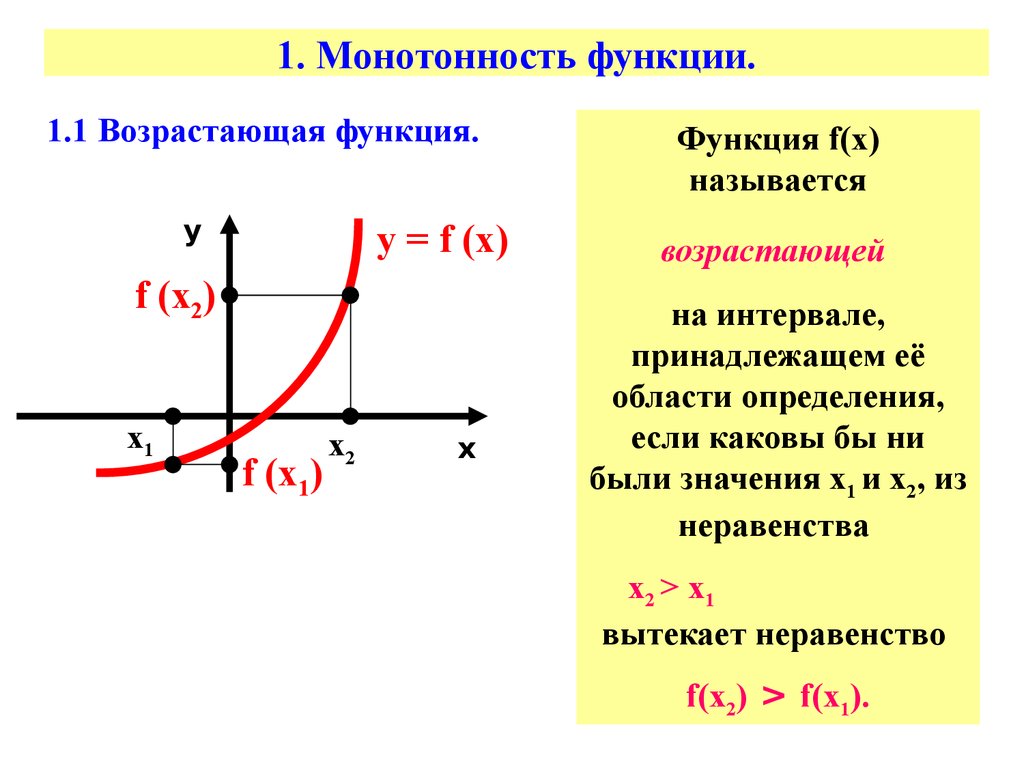
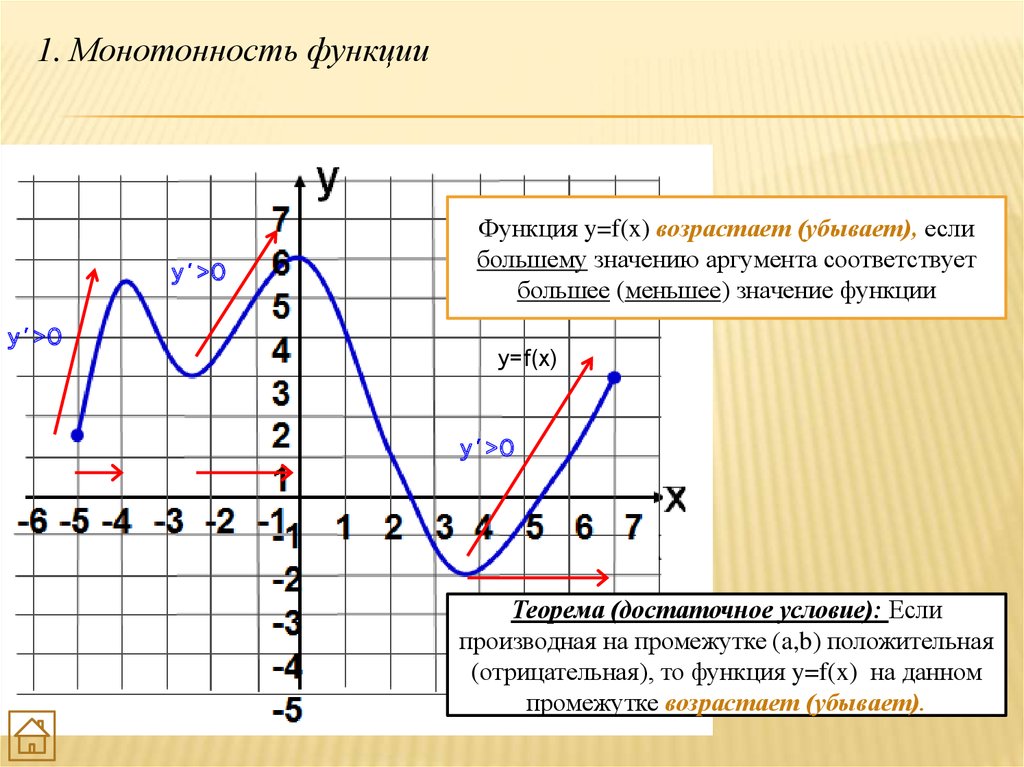
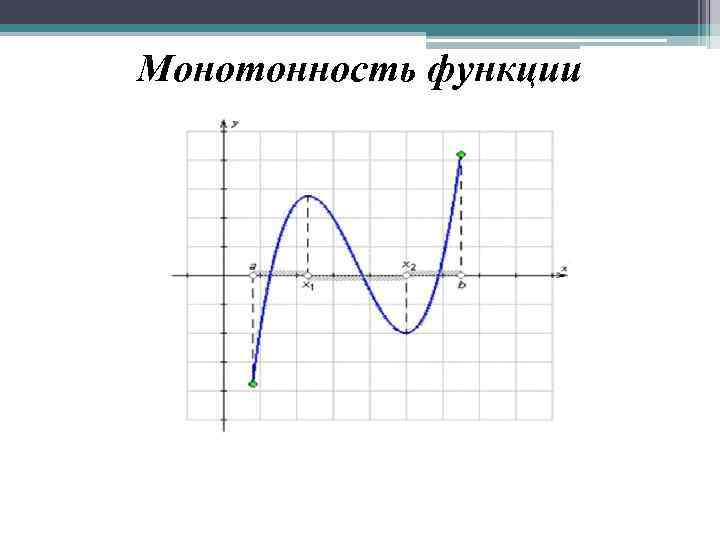
Определения

Пусть дана функция fM⊂R→R.{\displaystyle f:M\subset \mathbb {R} \to \mathbb {R} .} Тогда

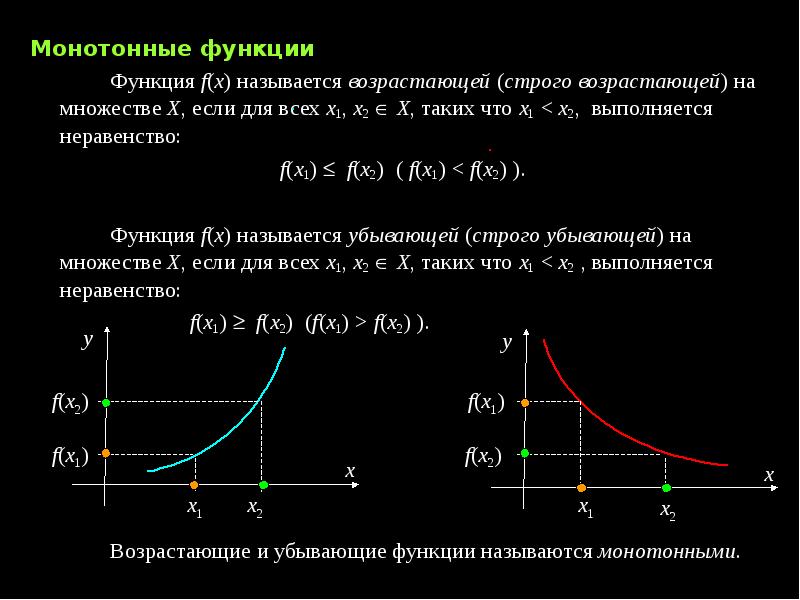
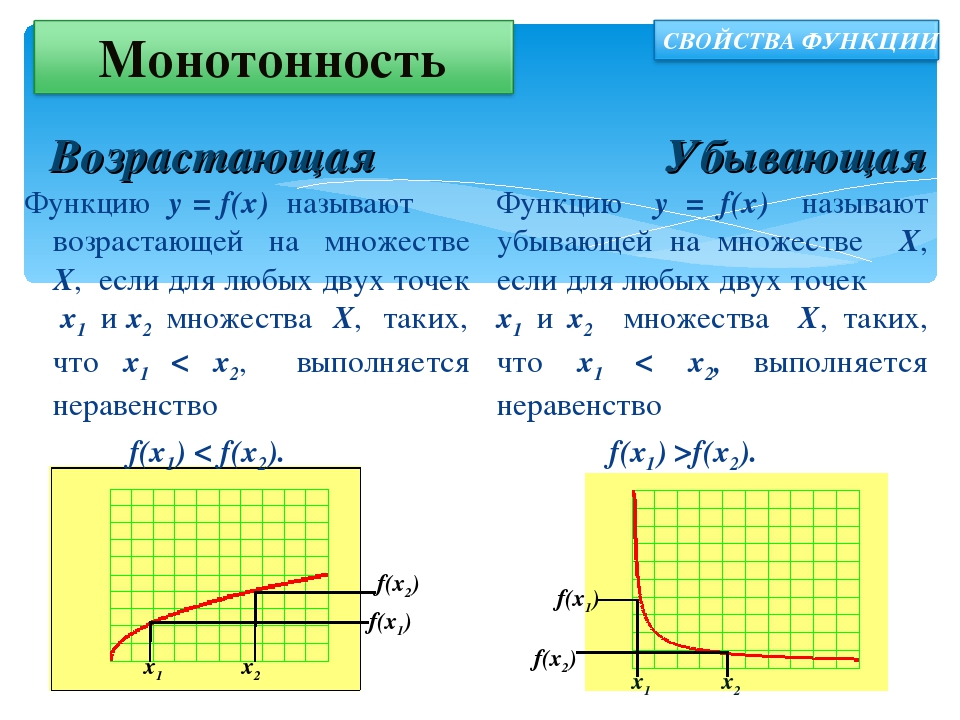
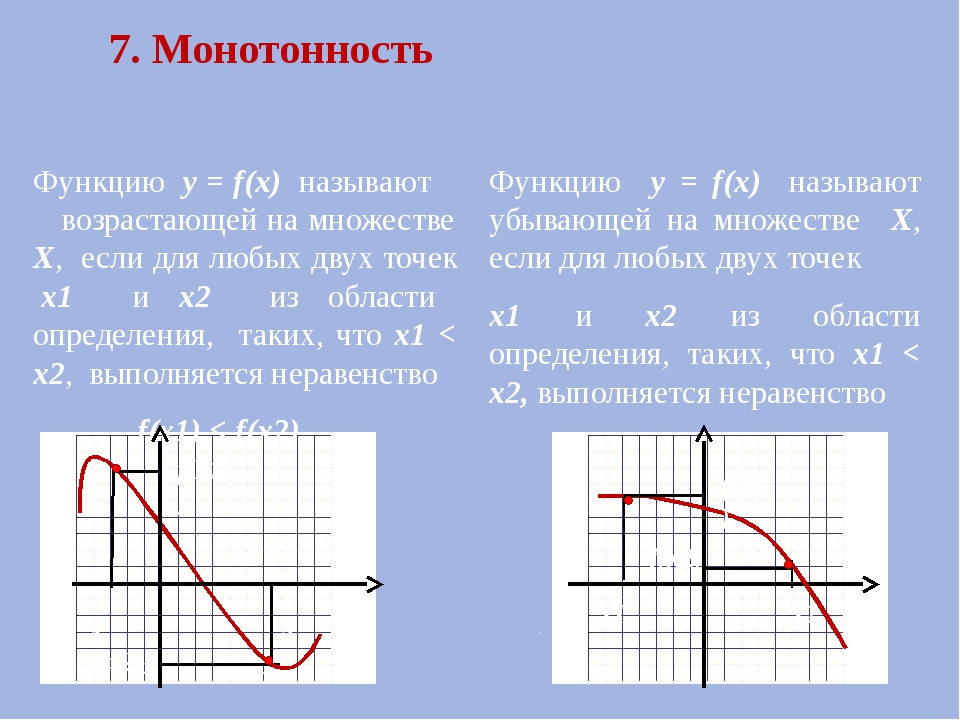
функция f{\displaystyle f} называется возраста́ющей на M{\displaystyle M}, если

∀x,y∈M,x>y⇒f(x)≥f(y){\displaystyle \forall x,y\in M,\;x>y\Rightarrow f(x)\geq f(y)}.

функция f{\displaystyle f} называется стро́го возраста́ющей на M{\displaystyle M}, если

∀x,y∈M,x>y⇒f(x)>f(y){\displaystyle \forall x,y\in M,\;x>y\Rightarrow f(x)>f(y)}.

функция f{\displaystyle f} называется убыва́ющей на M{\displaystyle M}, если

∀x,y∈M,x>y⇒f(x)≤f(y){\displaystyle \forall x,y\in M,\;x>y\Rightarrow f(x)\leq f(y)}.

функция f{\displaystyle f} называется стро́го убыва́ющей на M{\displaystyle M}, если

∀x,y∈M,x>y⇒f(x)<f(y){\displaystyle \forall x,y\in M,\;x>y\Rightarrow f(x)<f(y)}.

(Строго) возрастающая или убывающая функция называется (строго) монотонной.

Решение

Функция f(x)=x^{3}-3x^{2}-9x+5 дифференцируема на R, f'(x)=3x^{2}-6x-9.
Для определения промежутков возрастания и убывания функции решаем уравнение: x^{2}-2x-3=0. Решениями уравнения являются точки: x=-1 и x=3, которые разбивают числовую прямую на три отрезка. Получаем:

x^{2}-2x-3>0 \Leftrightarrow x\in ( -\infty ;-1) \cup (3;+\infty)\Rightarrow f(x) возрастает на отрезках x\in ( -\infty ;-1] \cup [3;+\infty)
x^{2}-2x-3<0\Leftrightarrow x\in \left ( -1;3 \right )\Rightarrow f(x) убывает на отрезке x\in .
Выполним проверку
Для проверки построим график этой функции.

f(x) возрастает на отрезках x\in ( -\infty ;-1] \cup [3;+\infty).
f(x) убывает на отрезке x\in \left .

Источники:

Лысенко З.М. Конспект лекций по курсу математического анализа. (тема «Условия монотонности функции в терминах производной»).
Фихтенгольц Г.М. — Курс дифференциального и интегрального исчисления. Том 1, Глава четвертая, пар. 1, ст. 270-273

Тест по теме: условия монотонности функции в терминах производной

Лимит времени:

из 5 заданий окончено

Вопросы:

Информация

Проверьте себя на знание теоретического и практического материала по теме: Условия монотонности функции в терминах производной.

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Результаты

Правильных ответов: из 5

Ваше время:

Время вышло

Вы набрали из баллов ()

Средний результат
Ваш результат

Ваш результат был записан в таблицу лидеров

Капча:

максимум из 8 баллов
Место	Имя	Записано	Баллы	Результат
Таблица загружается
Нет данных

С ответом
С отметкой о просмотре

Задание 1 из 5

1.

Для доказательства достаточности критерия возрастания и убывания функции мы используем:
- формулу Тейлора
- формулу Маклорена
- формулу Лагранжа
Правильно

Неправильно
Задание 2 из 5

2.

Найдите промежутки убывания данной функции: $latex y=\frac{1}{4}x^{4}-\frac{5}{3}x^{3}-13 $
- $$(-\infty ;0)$$
- $$(0 ;5)$$
- $$(5 ;+\infty)$$
- $$ (-\infty ;+\infty) $$
Правильно

Неправильно
Задание 3 из 5

Правильно

Неправильно
Задание 4 из 5

4.

Допишите формулировку теоремы о достаточном условии строгой монотонности:»Если для любых значений $latex x $ из $latex (a,b)$ $latex f'(x)>0$,то на $latex (a,b)$ $latex f$ …»

Правильно

Неправильно
Задание 5 из 5

Элементы сортировки
- $$ [\frac{3}{2};+\infty ) $$
- $$ (-\infty ;\frac{1}{2}] $$
- $$ (-\infty ;+\infty) $$
- $$ $$
- $$ y=x^{2}-3x+2 $$
- $$ y=-x^{2}+x+6 $$
- $$ y=x $$
- $$ y=-\frac{1}{3}x^{3}+\frac{1}{2}x^{2}+6x-14 $$
Правильно
4 / 4Баллы

Неправильно
/ 4 Баллы

максимум из 8 баллов
Место	Имя	Записано	Баллы	Результат
Таблица загружается
Нет данных

Доказательство:

Пусть, например, функция f(x) монотонно возрастает на . Выберем произвольную внутреннюю точку x_{0}\in (a;b]. Тогда \forall x\in [a;x_{0})\Rightarrow f(x)\leq f(x_{0})\Rightarrow f(x) ограничена сверху на [a;x_{0})\Rightarrow\exists\sup f(x)=M\leqslant f(x_{0}).
Согласно определению:а) \forall x\in [a;x_{0})\Rightarrow f(x) \leqslant Mб) \forall \varepsilon > 0\exists x_{\varepsilon }:M-\varepsilon < f(x_{\varepsilon }), обозначим \delta =x_{0}-x_{\varepsilon }>0.
Если x\in (x_{\varepsilon };x_{0})=(x_{0-\delta };x_{0}), то f(x_{\varepsilon })\leq f(x).Итог: \forall \varepsilon >0\exists \delta>0:\forall x\in (x_{0}-\delta;x_{0}):M-\varepsilon < f(x_{\varepsilon }) < f(x)\leq M< M+\varepsilon \Leftrightarrow |f(x)-M|< \varepsilon
\lim_{x\rightarrow x_{0-0} } f(x) = MИтак f(x_{0}-0)= \sup f(x), a\leqslant x<x_{0} .
Аналогично доказываем, что функция имеет в точке x_{0}\in [a;b) предел справа причем f(x_{0}+0)=\inf f(x), x_{0}<x\leqslant b.Следствие. Если функция f определена и монотонна на интервале (a;b), \forall\ x_{0}\in (a;b)\exists \ предел справа и слева, причем если f возрастает, то
f(x_{0}-0)=\lim\limits_{x\to x_{0}-0} f(x) \leq\lim\limits_{x\to x_{0}+0} f(x)=f(x_{0}+0),
если убывает, то
f(x_{0}-0)=\lim\limits_{x\to x_{0}-0} f(x) \geq\lim\limits_{x\to x_{0}+0} f(x)=f(x_{0}+0).

Литература

Лысенко З.М. Конспект лекций по математическому анализу. Тема «Предел функции»
Вартанян Г. М. Конспект лекций по математическому анализу.
Г.М. Фихтенгольц Курс дифференциального и интегрального исчисления. Глава 2. Функции одной переменной. 2.57. Предел монотонной функции. (с.133-134)

Тест

Лимит времени:

из 2 заданий окончено

Вопросы:

Информация

Тест по теме Пределы монотонных функций.

Желаем удачи!

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Результаты

Правильных ответов: из 2

Ваше время:

Время вышло

Вы набрали из баллов ()

Средний результат
Ваш результат

Ваш результат был записан в таблицу лидеров

Капча:

максимум из 10 баллов
Место	Имя	Записано	Баллы	Результат
Таблица загружается
Нет данных

С ответом
С отметкой о просмотре

Задание 1 из 2

1.

Количество баллов: 5

Дать определение строго монотонно возрастающей функции на отрезке
- $$ \forall x, y\in ,x>y\Rightarrow f(x)\geq f(y)$$
- $$ \forall x, y\in ,x>y\Rightarrow f(x)> f(y) $$
- $$ \forall x, y\in ,x>y\Rightarrow f(x)\leq f(y) $$
- $$ \forall x, y\in ,x>y\Rightarrow f(x)
Правильно

Неправильно
Задание 2 из 2

2.

Количество баллов: 5

Вставьте пропущенные слова.
$$Если~ функция ~ f(x) ~определена ~и~ монотонна~ на ~отрезке ~ ,$$
$$~то~ в ~каждой~ точке ~x ~ из ~ (a;b)$$
$$ эта~ функция~ имеет ~конечные ~пределы ~слева~ и~ справа,~а ~в ~точках~ a~ и~ b$$

(правосторонний) и (левосторонний) пределы.

Правильно

Неправильно

максимум из 10 баллов
Место	Имя	Записано	Баллы	Результат
Таблица загружается
Нет данных

Условия монотонности функции

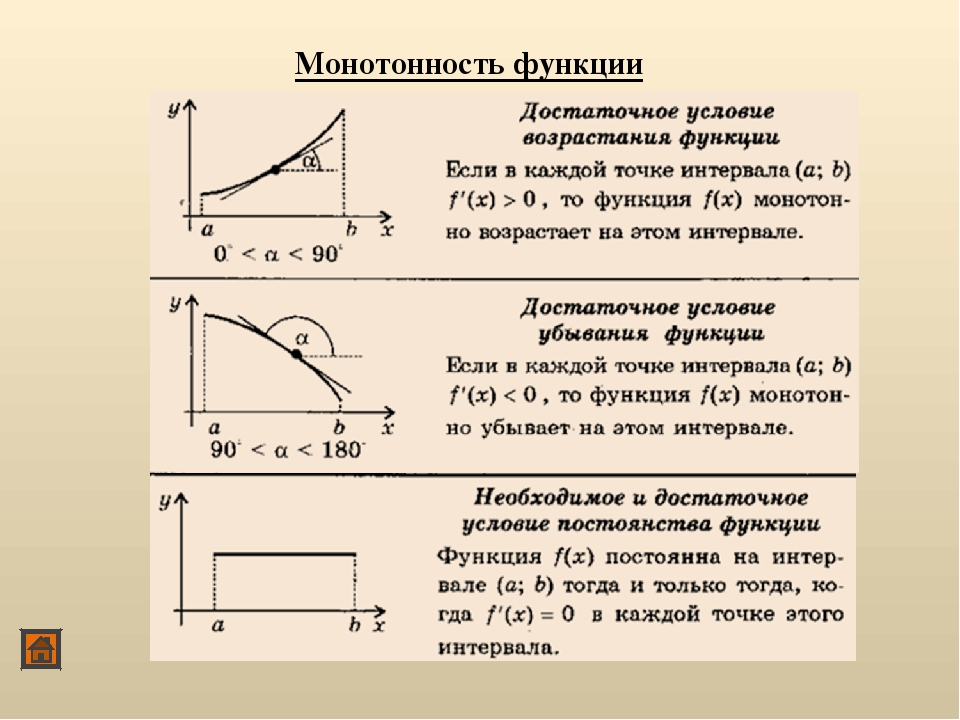
(Критерий монотонности функции, имеющей производную на интервале) Пусть функция f∈C((a,b)){\displaystyle f\in C{\bigl (}(a,b){\bigr )}} непрерывна на (a,b),{\displaystyle (a,b),} и имеет в каждой точке x∈(a,b){\displaystyle x\in (a,b)} производную f′(x).{\displaystyle f'(x).} Тогда

f{\displaystyle f} не убывает на (a,b){\displaystyle (a,b)} тогда и только тогда, когда ∀x∈(a,b)f′(x)≥;{\displaystyle \forall x\in (a,b)\;f'(x)\geq 0;}

f{\displaystyle f} не возрастает на (a,b){\displaystyle (a,b)} тогда и только тогда, когда ∀x∈(a,b)f′(x)≤{\displaystyle \forall x\in (a,b)\;f'(x)\leq 0.}
(Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция f∈C((a,b)){\displaystyle f\in C{\bigl (}(a,b){\bigr )}} непрерывна на (a,b),{\displaystyle (a,b),} и имеет в каждой точке x∈(a,b){\displaystyle x\in (a,b)} производную f′(x).{\displaystyle f'(x).} Тогда

если ∀x∈(a,b)f′(x)>,{\displaystyle \forall x\in (a,b)\;f'(x)>0,} то f{\displaystyle f} строго возрастает на (a,b);{\displaystyle (a,b);}

если ∀x∈(a,b)f′(x)<,{\displaystyle \forall x\in (a,b)\;f'(x)<0,} то f{\displaystyle f} строго убывает на (a,b).{\displaystyle (a,b).}

Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на интервале (a,b).{\displaystyle (a,b).} Точнее имеет место

(Критерий строгой монотонности функции, имеющей производную на интервале) Пусть f∈C((a,b)),{\displaystyle f\in C{\bigl (}(a,b){\bigr )},} и всюду на интервале определена производная f′(x).{\displaystyle f'(x).} Тогда f{\displaystyle f} строго возрастает на интервале (a,b){\displaystyle (a,b)} тогда и только тогда, когда выполнены следующие два условия:

∀x∈(a,b)f′(x)≥;{\displaystyle \forall x\in (a,b)\;f'(x)\geq 0;}
∀(c,d)⊂(a,b)∃x∈(c,d)f′(x)>{\displaystyle \forall (c,d)\subset (a,b)\;\exists x\in (c,d)\;f'(x)>0.}

Аналогично, f{\displaystyle f} строго убывает на интервале (a,b){\displaystyle (a,b)} тогда и только тогда, когда выполнены следующие два условия:

∀x∈(a,b)f′(x)≤;{\displaystyle \forall x\in (a,b)\;f'(x)\leq 0;}
∀(c,d)⊂(a,b)∃x∈(c,d)f′(x)<{\displaystyle \forall (c,d)\subset (a,b)\;\exists x\in (c,d)\;f'(x)<0.}

1.3.5. Монотонность функций

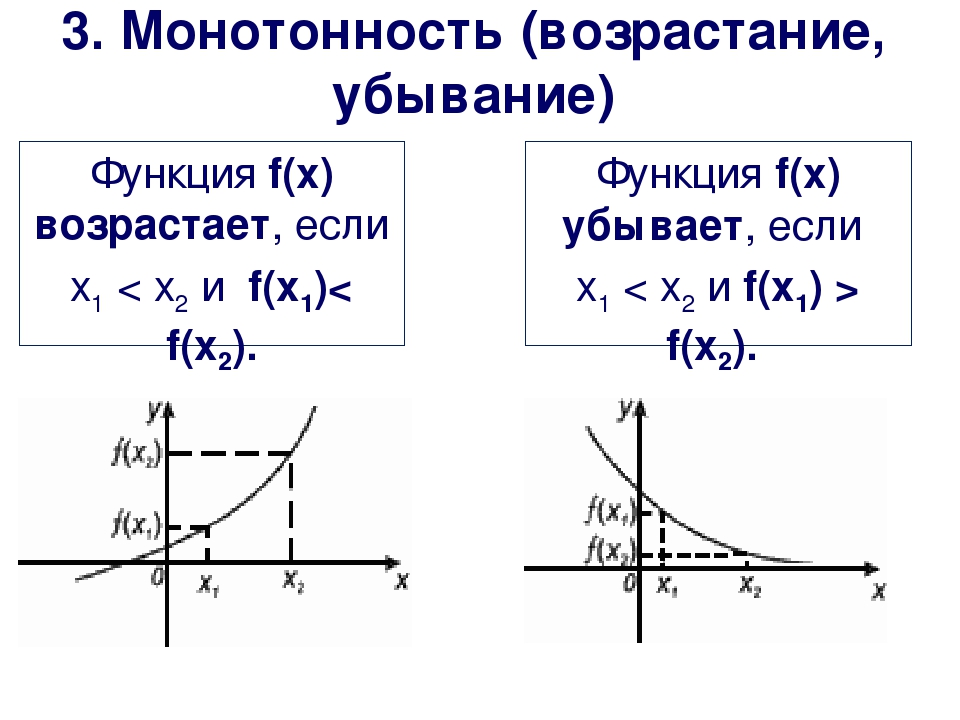
Функция f (x) называется возрастающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ < x₂, выполняется неравенство f (x₁) < f (x₂).

Функция f (x) называется убывающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ < x₂, выполняется неравенство f (x₁) > f (x₂).

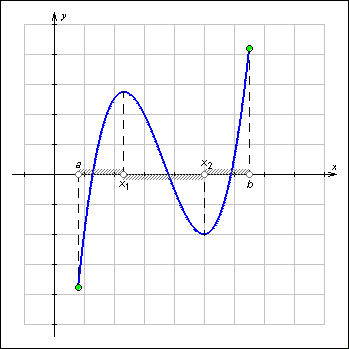Рисунок 1.3.5.1.Промежутки возрастания и убывания функции

y = f (x)[ax₁)(x₂b](x₁x₂)[ax₁)(x₂b]

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.

Заметим, что если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.

Действительно, если x₁ < x₂ – корни этого уравнения на промежутке D (f(x)), то f (x₁) = f (x₂) = 0, что противоречит условию монотонности.

Перечислим свойства монотонных функций (предполагается, что все функции определены на некотором промежутке D).

Сумма нескольких возрастающих функций является возрастающей функцией.
Произведение неотрицательных возрастающих функций есть возрастающая функция.
Если функция f возрастает, то функции cf (c > 0) и f + c также возрастают, а функция cf (c < 0) убывает. Здесь c – некоторая константа.
Если функция f возрастает и сохраняет знак, то функция 1/f убывает.
Если функция f возрастает и неотрицательна, то где

,
также возрастает.
Если функция f возрастает и n – нечетное число, то f n также возрастает.
Композиция g (f (x)) возрастающих функций f и g также возрастает.

Аналогичные утверждения можно сформулировать и для убывающей функции.

Модель 1.9.
Свойства функции

Точка a называется точкой максимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≥ f (x).

Точка a называется точкой минимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≤ f (x).

Точки, в которых достигается максимум или минимум функции, называются точками экстремума.

В точке экстремума происходит смена характера монотонности функции. Так, слева от точки экстремума функция может возрастать, а справа – убывать. Согласно определению, точка экстремума должна быть внутренней точкой области определения.

Если для любого

(x ≠ a) выполняется неравенство f (x) ≤ f (a)

то точка a называется точкой наибольшего значения функции на множестве D:

Если для любого

(x ≠ b) выполняется неравенство f (x) > f (b)

то точка b называется точкой наименьшего значения функции на множестве D.

Точка наибольшего или наименьшего значения может быть экстремумом функции, но не обязательно им является.

Точку наибольшего (наименьшего) значения непрерывной на отрезке функции следует искать среди экстремумов этой функции и ее значений на концах отрезка.

График 1.3.5.1.Функция, ограниченная сверху

График 1.3.5.2.Функция, ограниченная снизу

График 1.3.5.3.Функция, ограниченная на множестве D.

Если существует число C такое, что для любого

выполняется неравенство f (x) ≤ C, то функция f называется ограниченной сверху на множестве D.

Если существует число c такое, что для любого

выполняется неравенство f (x) ≥ c, то функция f называется ограниченной снизу на множестве D.

Функция, ограниченная и сверху, и снизу, называется ограниченной на множестве D. Геометрически ограниченность функции f на множестве D означает, что график функции y = f (x),

лежит в полосе c ≤ y ≤ C.

Если функция не является ограниченной на множестве, то говорят, что она не ограничена.

Примером функции, ограниченной снизу на всей числовой оси, является функция y = x2. Примером функции, ограниченной сверху на множестве (–∞; 0) является функция y = 1/x. Примером функции, ограниченной на всей числовой оси, является функция y = sin x.