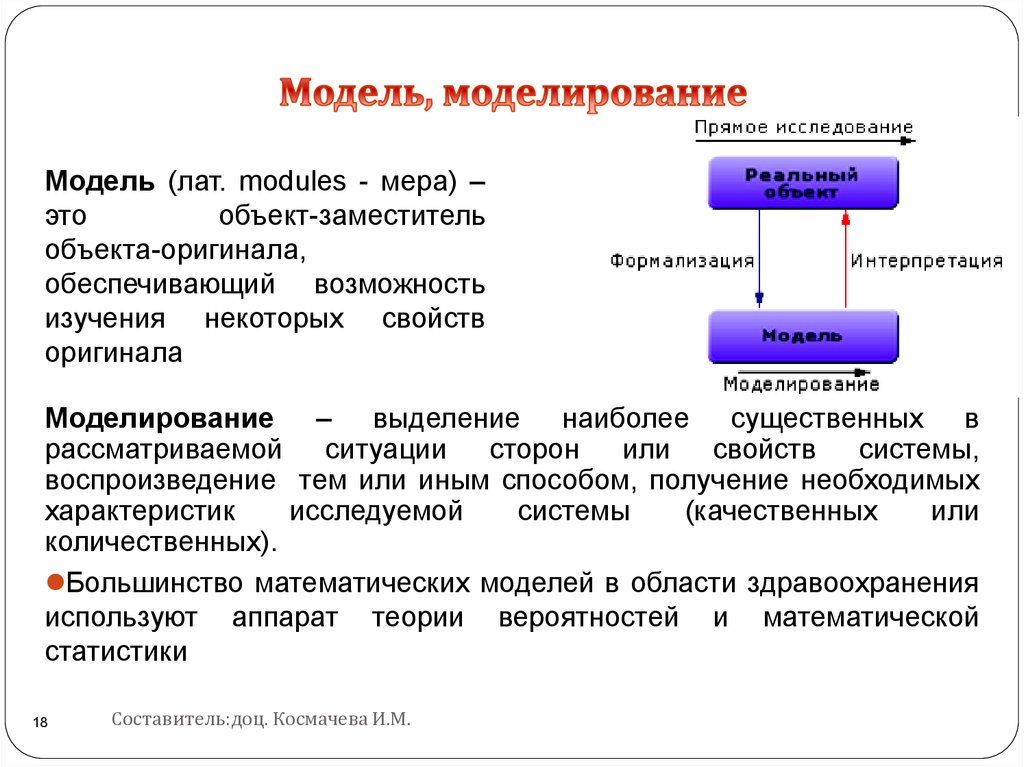
Моделирование в информатике - это что такое? виды и этапы моделирования

Модель

Моделирование в информатике — это составление образа какого-либо реально существующего объекта, который отражает все существенные признаки и свойства. Модель для решения задачи необходима, так как она, собственно, и используется в процессе решения.

В школьном курсе информатики тема моделирования начинает изучаться еще в шестом классе. В самом начале детей необходимо познакомить с понятием модели. Что это такое?

Упрощенное подобие объекта;
Уменьшенная копия реального объекта;
Схема явления или процесса;
Изображение явления или процесса;
Описание явления или процесса;
Физический аналог объекта;
Информационный аналог;
Объект-заменитель, отражающий свойства реального объекта и так далее.

Модель — это очень широкое понятие, как это уже стало ясно из вышеперечисленного

Важно отметить, что все модели принято делить на группы:

материальные;
идеальные.

Под материальной моделью понимают предмет, основанный на реально существующем объекте. Это может быть какое-либо тело или процесс. Данную группу принято подразделять еще на два вида:

физические;
аналоговые.

Такая классификация носит условный характер, ведь четкую границу между двумя этими подвидами провести очень трудно.

Идеальную модель охарактеризовать еще труднее. Она связаны с:

мышлением;
воображением;
восприятием.

К ней можно отнести произведения искусства (театр, живопись, литература и так далее).

Адекватность модели

Поскольку модель является выражением конечного ряда и только важнейших для
конкретного исследования аспектов сущности, то она не может быть абсолютно
идентичной моделируемому объекту. Кроме этого, реальный объект бесконечен для
познания. Поэтому нет смысла стремиться к бесконечной точности при построении
модели. Для выяснения необходимой степени адекватности обычно строят ряд
моделей, начиная с грубых, простых моделей и двигаясь ко все более сложным и
точным. Как только затраты на построение очередной модели начинают превышать
планируемую отдачу от модели, то уточнение модели прекращают. Первоначальные
шаги производятся в каком-либо существующем универсальном моделирующем пакете.
После одобрения модели под неё пишется специализированный пакет. Необходимость
в этом возникает в случае, если функционирование модели в универсальной среде
моделирования не удовлетворяет требованиям быстродействия (или каким-то другим).

В задачи данного курса входит изучение приёмов и способов, необходимых для
формализации, изучения и интерпретации систем.

Моделирование прикладная инженерная наука класса технологических.
Моделирование дисциплина, ставящая целью построение моделей и их
исследование посредством собственных универсальных методов, а также
специфических методов смежных с ней наук (математика, исследование операций,
программирование).

2.Точное моделирование в САПРах

Это моделирование основано на операциях, поочередно совершаемых над телом или поверхностью. Модель задается не полигонами, а математическими формулами (не беспокойтесь — вы как пользователь этих формул не видите, если не захотите задать какую-либо формулу сами). Отличие между полигональным моделированием и моделированием в САПРах аналогично отличию растровой графики от векторной. Чтобы получить гладкую модель полигонами, нужно увеличивать количество полигонов — и все равно на каком-то уровне модель будет иметь неровность, даже если вы добавили столько ребер, что компьютер зависает при попытке просмотреть ее. В САПРах же любая криволинейная поверхность абсолютно гладкая при любом приближении, так как задается математически. В том числе и из-за этого модели под производство не делаются в 3Ds max: было бы не очень хорошо, если бы на компьютерной мыши были бы видны следы низкополигонального моделирования!

Посмотрите на эту картинку. Слева — полигональная модель, заданная координатами точек и гранями между ними. Справа — та же модель, выполненная созданием параболы на плоскости и прокручиванием вокруг своей оси.

Видно, что вторая модель идеально гладкая, а гладкость первой ограничена количеством определяющих ее точек.

Из-за того, что модель задается математически, можно моделировать с точностью до долей миллиметра

Это очень важно при проектировании, например, формы под литье на заводе: из-за отклонения в миллиметр в корпус вполне могут не влезть важные детали прибора. Также это важно, если вы хотите распечатать себе на 3D-принтере предмет, стыкующийся с каким-нибудь другим предметом, например, подставку для ножа или держатель карт памяти

Еще одна особенность САПРов — возможность создавать параметрические модели. Это значит, что модель создается последовательностью действий. В любой момент можно откатить создание модели к самому первому вашему действию и изменить параметры, которые вы задавали в нем (например, высота и диаметр цилиндра):

Это, пожалуй, самое удобное в моделировании в САПРах. При правильно построенной модели можно менять любой параметр и модель автоматически перестроится. По сути, при построении создается алгоритм модели, который можно менять в любом месте. Это очень удобно как просто при проектировании, когда нужно исправить свои ошибки, так и в том случае, когда надо замоделировать много подобных друг другу объектов, например, столов разной высоты или решетки с разным количеством перекладин.

Однако САПРы не предназначены для создания сложных органических моделей, как, например, человеческое тело. Чисто теоретически возможно создать в них простейшего персонажа, но это займет огромное количество времени и усилий, несравнимое с полигональным моделированием и скульптингом.

В САПРе Fusion 360 есть режим скульптинга, в котором можно редактировать модель способом, внешне похожим на полигональное моделирование, и при этом сохранять точные размеры и абсолютную гладкость модели. Но даже в нем создавать персонажа игры крайне нецелесообразно.

Вам стоит выбрать моделирование при помощи САПРов, если:

Вы проектируете что-то, что позже будет выполнено в реальном мире;
Вы не делаете реалистичные модели животных, людей и подобных органических объектов;
Вам нужно создать модель, в которой можно изменить один параметр и получить полностью перестроившуюся под него модель, в остальном такую же.

Какие программы подойдут:

Fusion 360
Catia
Inventor
Rhinoceros+Grasshopper
OpenSCAD – бесплатный редактор с открытым кодом

Еще больше полезных статей — на нашем сайте www.makefabricationstudio.ru

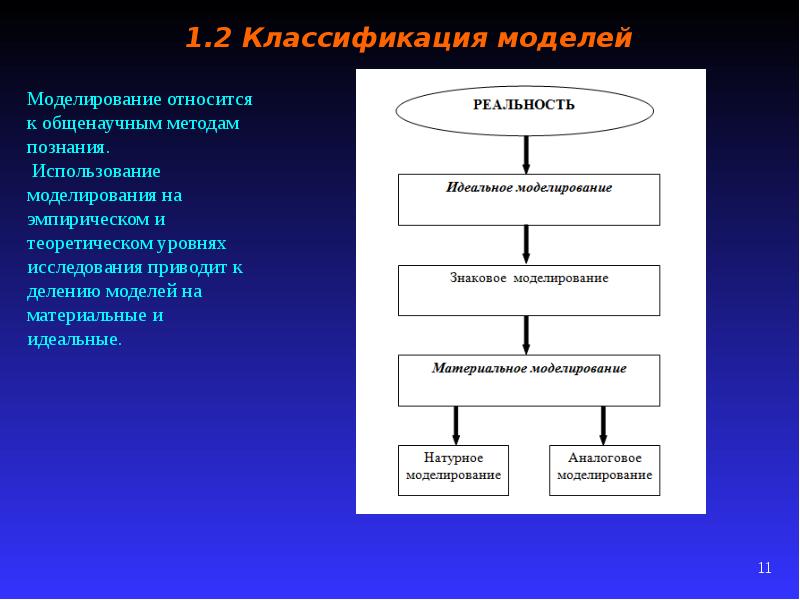
Классификация по характеру моделей

Виды методов моделирования довольно разнообразны, поэтому мы будем рассматривать не одну, а несколько классификаций. Главнейшая из них касается распределения по характеру моделей:

Знаковое моделирование, в котором объектом является чертеж, схема или формула. Такие модели стали довольно популярны после развития ЭВМ.
Мысленное моделирование, которое заключается в том, что мысли становятся наглядными. Для примера можно взять известную модель атома, которую предложил Нильс Бор.
Аналоговое моделирование, при котором оригинал и сама модель описываются при помощи одного и того же математического соотношения. Для примера можно привести электрические модели, которые просто незаменимы при исследовании механических явлений.
Предметное моделирование является самым популярным. Оно заключается в том, что в качестве модели могут выступать физические, геометрические, функциональные или геометрические свойства объекта. Для примера приведем модель корпуса швейной машинки или модель сооружения.
Модельный эксперимент. Этот вид стоит обособленно, так как в таком случае в эксперименте участвует не сам объект, а его модель, наделенная всеми необходимыми качествами. Этот метод идеально демонстрирует, насколько условна грань между эмпирическим и теоретическим познанием.

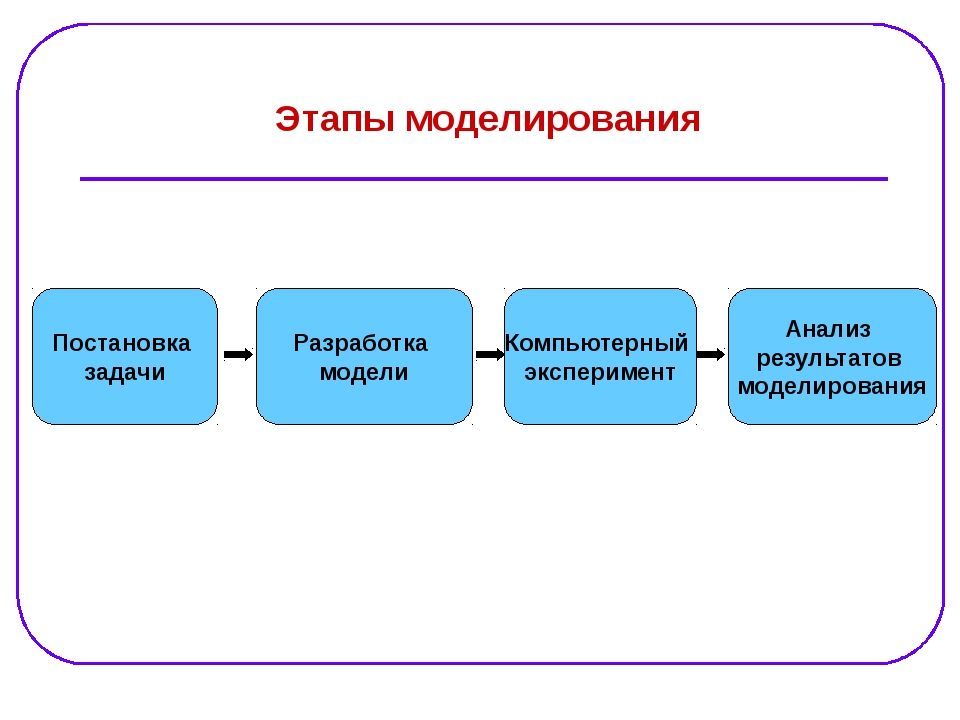
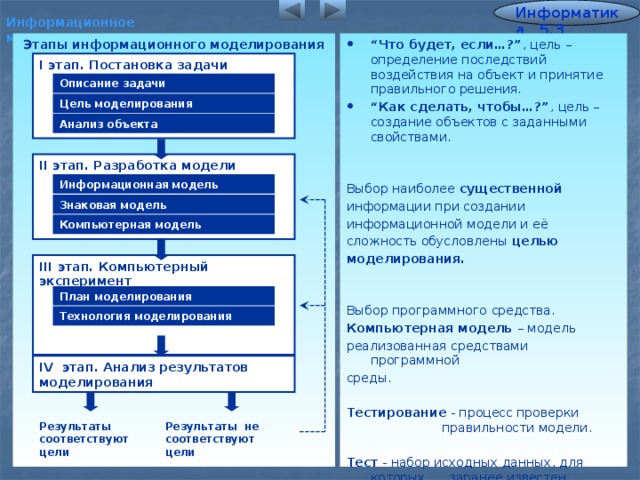
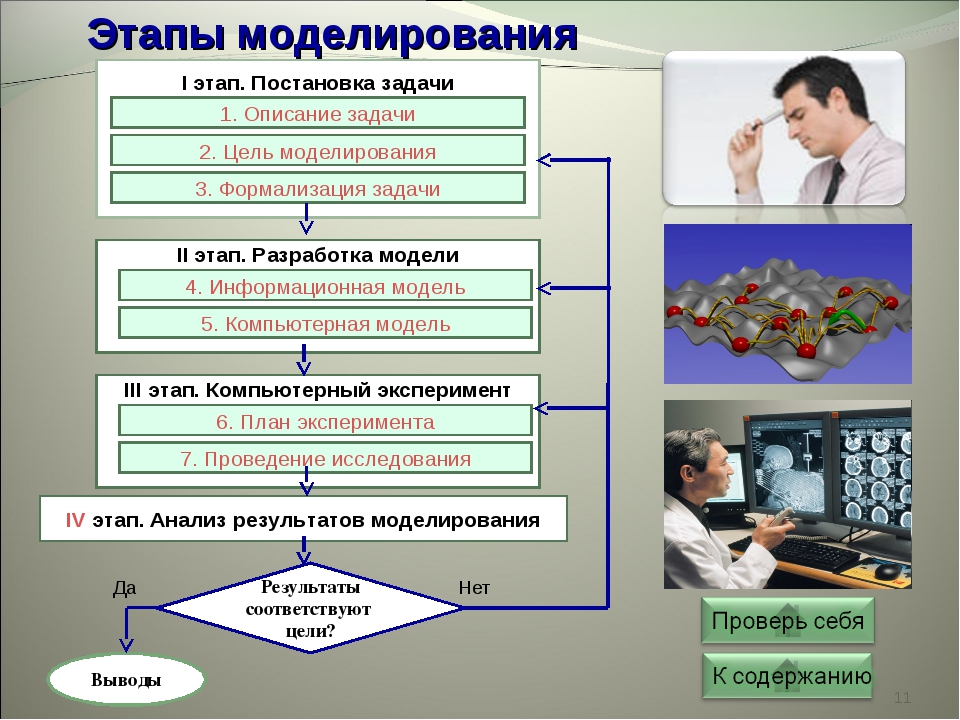
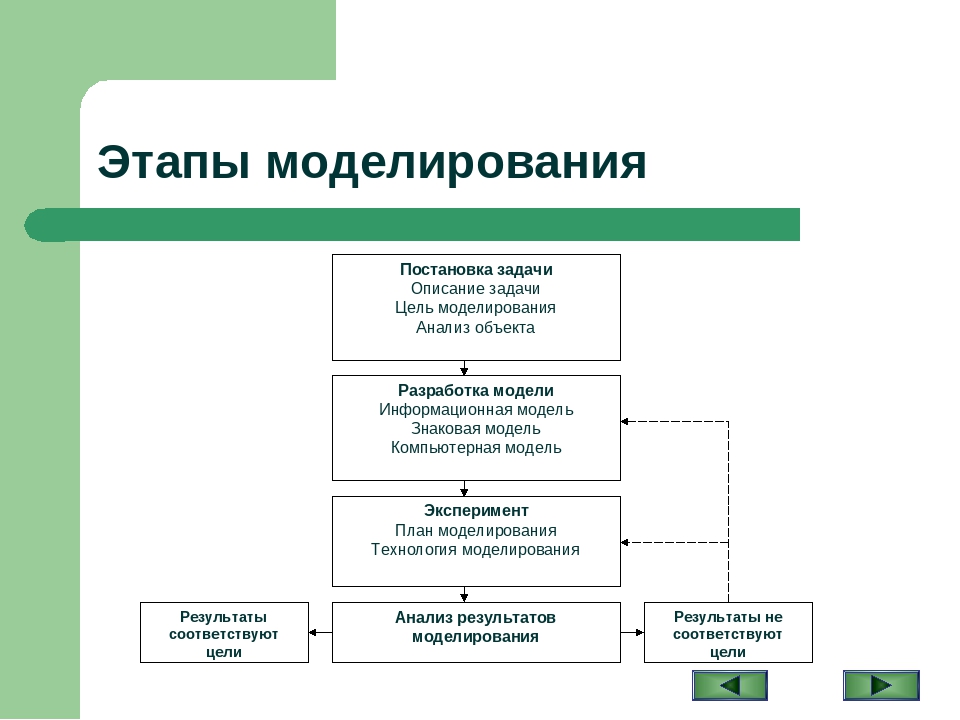
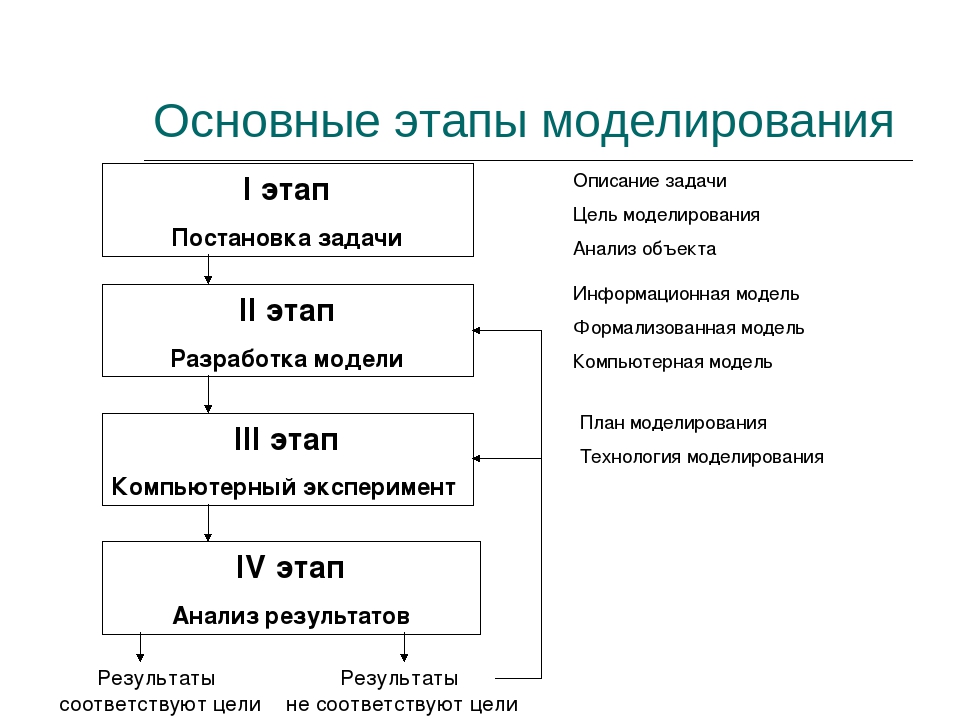
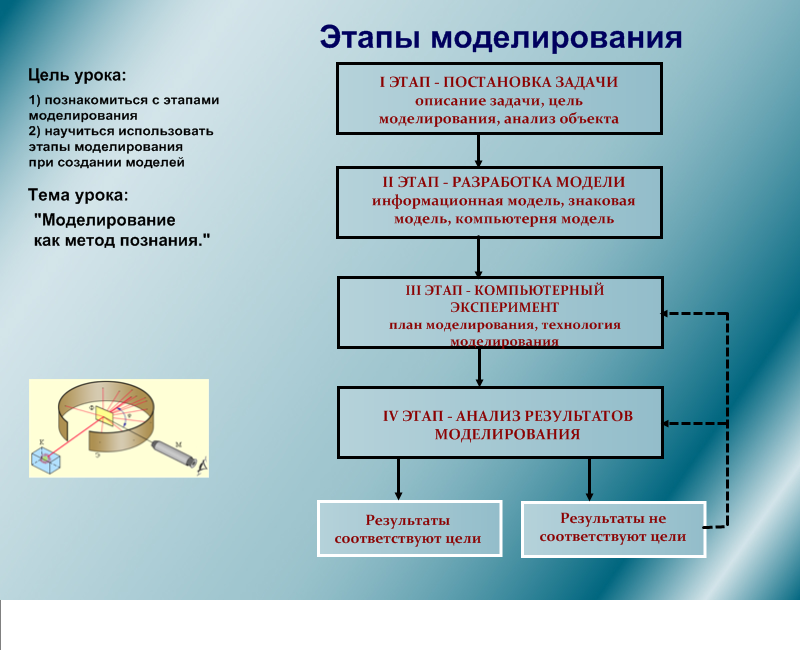
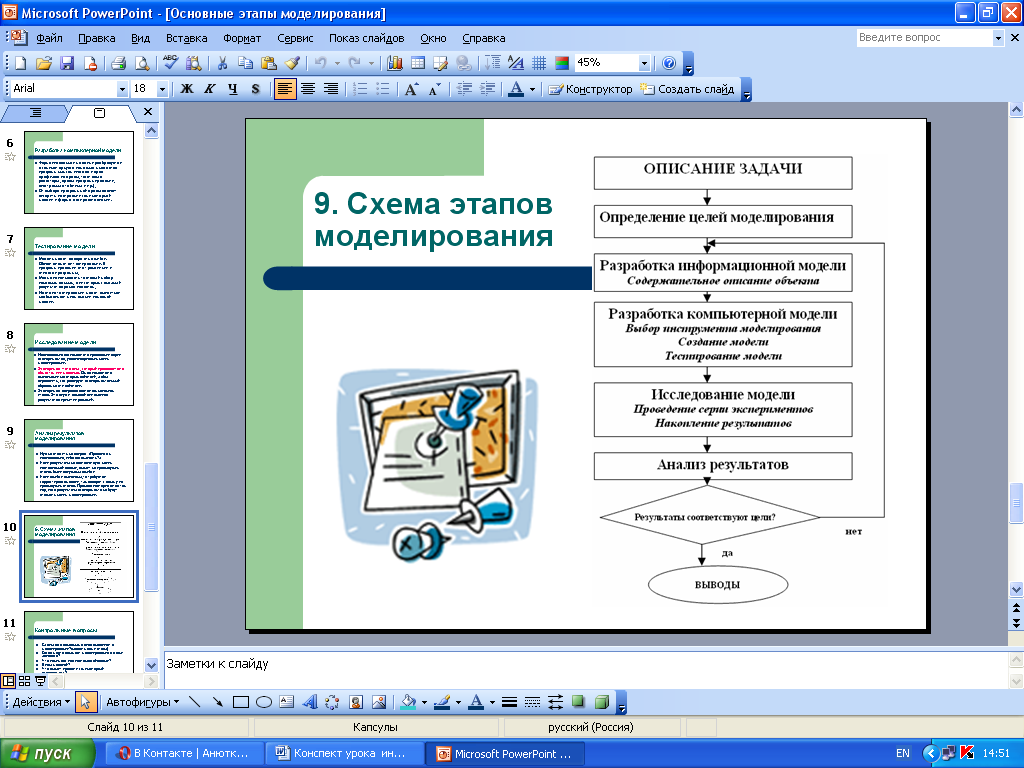
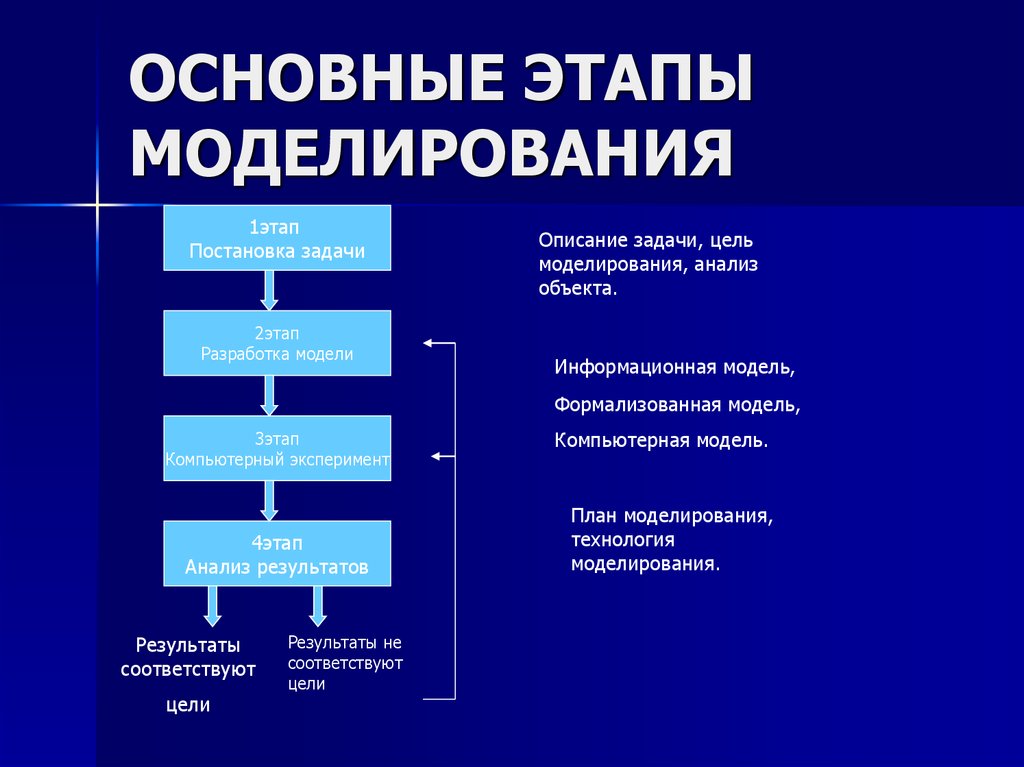
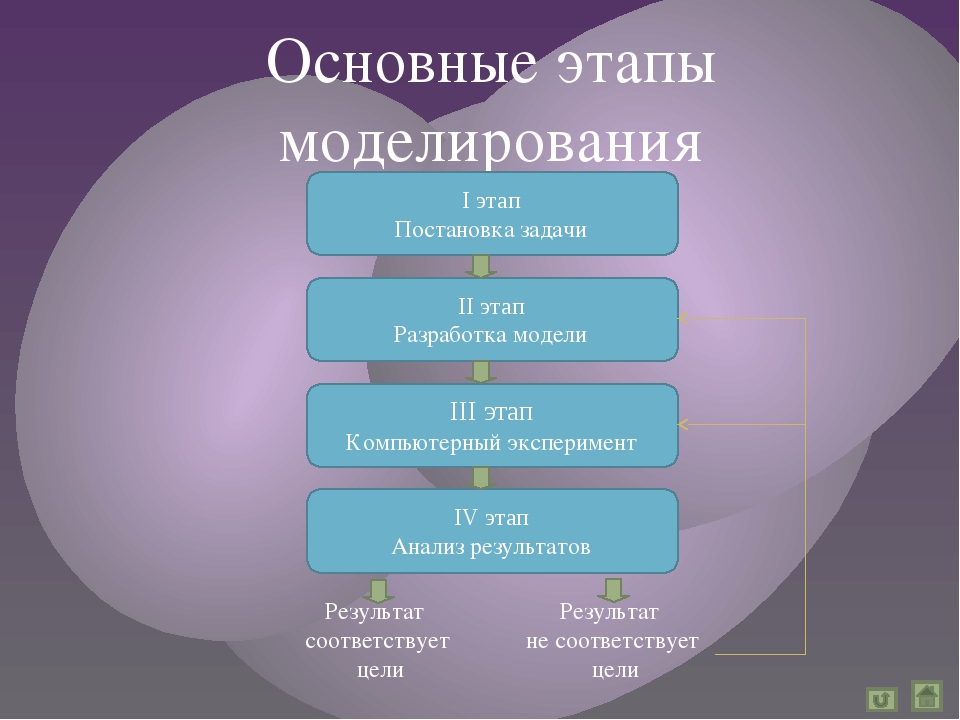
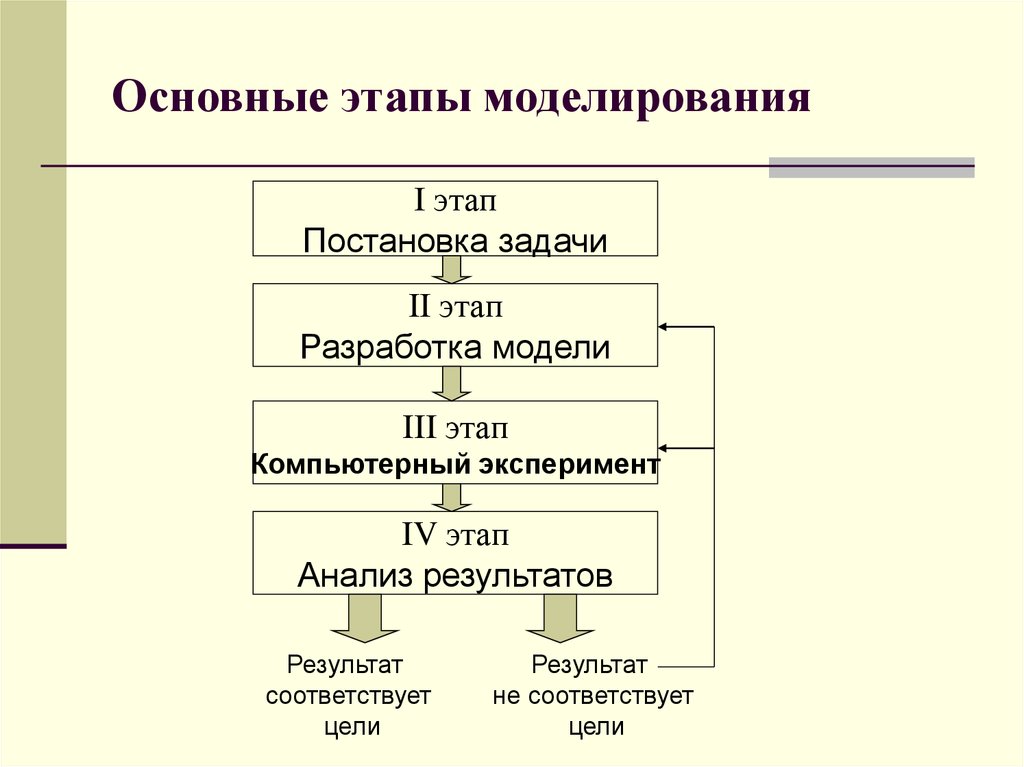
Процесс моделирования

Процесс моделирования включает три элемента:

субъект (исследователь),
объект исследования,
модель, определяющую (отражающую) отношения познающего субъекта и познаваемого объекта.

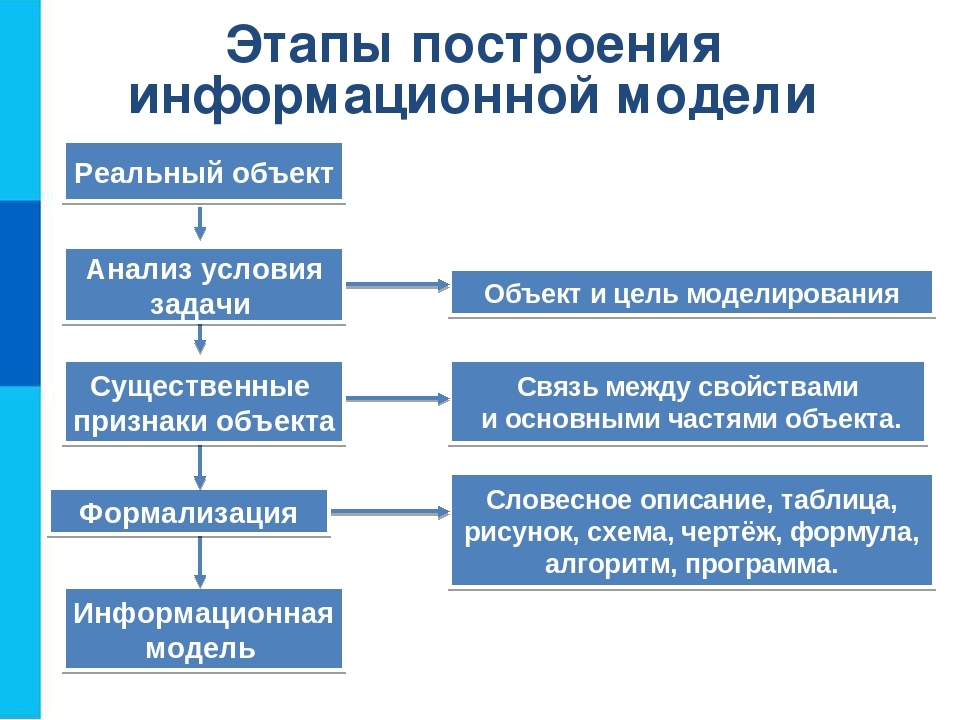
Первый этап построения модели предполагает наличие некоторых знаний об объекте-оригинале. Познавательные возможности модели обусловливаются тем, что модель отображает (воспроизводит, имитирует) какие-либо существенные черты объекта-оригинала. Вопрос о необходимой и достаточной мере сходства оригинала и модели требует конкретного анализа. Очевидно, модель утрачивает свой смысл как в случае тождества с оригиналом (тогда она перестает быть моделью), так и в случае чрезмерного во всех существенных отношениях отличия от оригинала. Таким образом, изучение одних сторон моделируемого объекта осуществляется ценой отказа от исследования других сторон. Поэтому любая модель замещает оригинал лишь в строго ограниченном смысле

Из этого следует, что для одного объекта может быть построено несколько «специализированных» моделей, концентрирующих внимание на определенных сторонах исследуемого объекта или же характеризующих объект с разной степенью детализации.

На втором этапе модель выступает как самостоятельный объект исследования. Одной из форм такого исследования является проведение «модельных» экспериментов, при которых сознательно изменяются условия функционирования модели и систематизируются данные о её «поведении». Конечным результатом этого этапа является множество (совокупность) знаний о модели.

На третьем этапе осуществляется перенос знаний с модели на оригинал — формирование множества знаний. Одновременно происходит переход с «языка» модели на «язык» оригинала. Процесс переноса знаний проводится по определенным правилам. Знания о модели должны быть скорректированы с учетом тех свойств объекта-оригинала, которые не нашли отражения или были изменены при построении модели.

Четвёртый этап — практическая проверка получаемых с помощью моделей знаний и их использование для построения обобщающей теории объекта, его преобразования или управления им.

Моделирование — циклический процесс. Это означает, что за первым четырёхэтапным циклом может последовать второй, третий и т. д. При этом знания об исследуемом объекте расширяются и уточняются, а исходная модель постепенно совершенствуется. Недостатки, обнаруженные после первого цикла моделирования, обусловленные малым знанием объекта или ошибками в построении модели, можно исправить в последующих циклах.

Сейчас трудно указать область человеческой деятельности, где не применялось бы моделирование. Разработаны, например, модели производства автомобилей, выращивания пшеницы, функционирования отдельных органов человека, жизнедеятельности Азовского моря, последствий атомной войны. В перспективе для каждой системы могут быть созданы свои модели, перед реализацией каждого технического или организационного проекта должно проводиться моделирование.

Примечания

Tolk, A. Learning something right from models that are wrong – Epistemology of Simulation (En) // Concepts and Methodologies in Modeling and Simulation. Springer–Verlag. — 2015. — С. pp. 87–106.
Oberkampf, W. L., DeLand, S. M., Rutherford, B. M., Diegert, K. V., & Alvin, K. F. Error and uncertainty in modeling and simulation (En) // Reliability Engineering & System Safety 75(3). — 2002. — № 75(3). — С. 333–57.
Ihrig, M. A New Research Architecture For The Simulation Era (En) // European Council on Modelling and Simulation. — 2012. — С. pp. 715–20.
Pullan Wendy. Structure. — Cambridge: Cambridge University Press. — 2000. — ISBN 0-521-78258-9.
Fishwick PA. Simulation Model Design and Execution: Building Digital Worlds. — Upper Saddle River, NJ: Prentice Hall.. — 1995.
Sokolowski, J.A., Banks, C.M. Principles of Modelling and Simulation. — Hoboken, NJ: John Wiley and Sons.. — 2009.

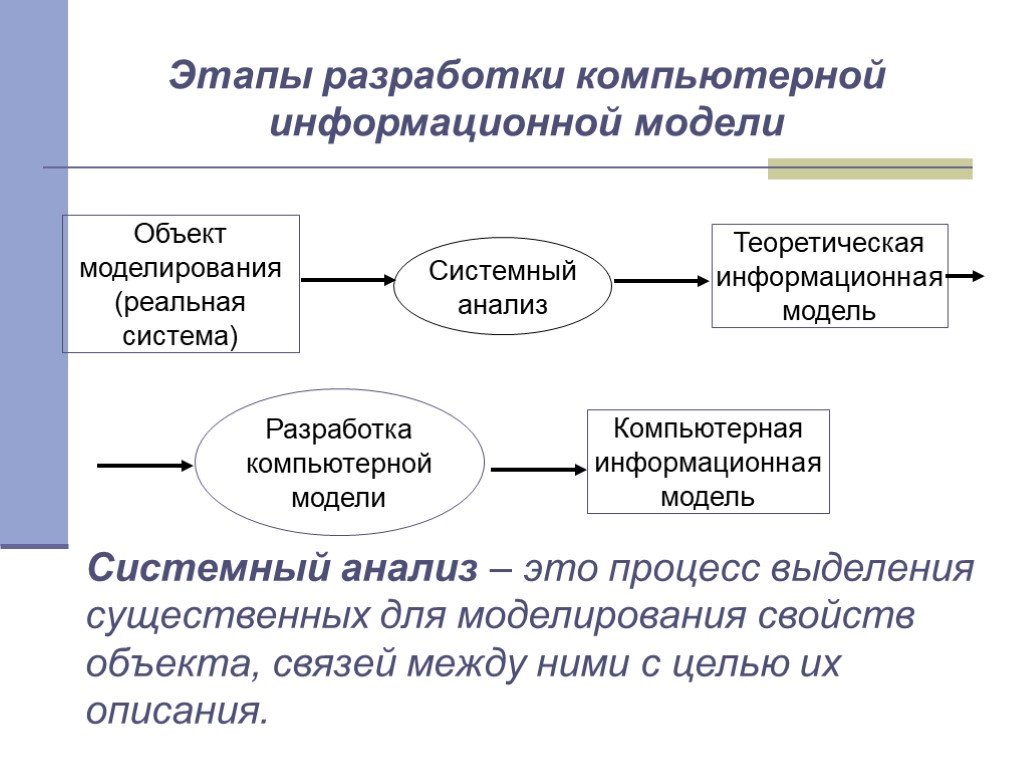
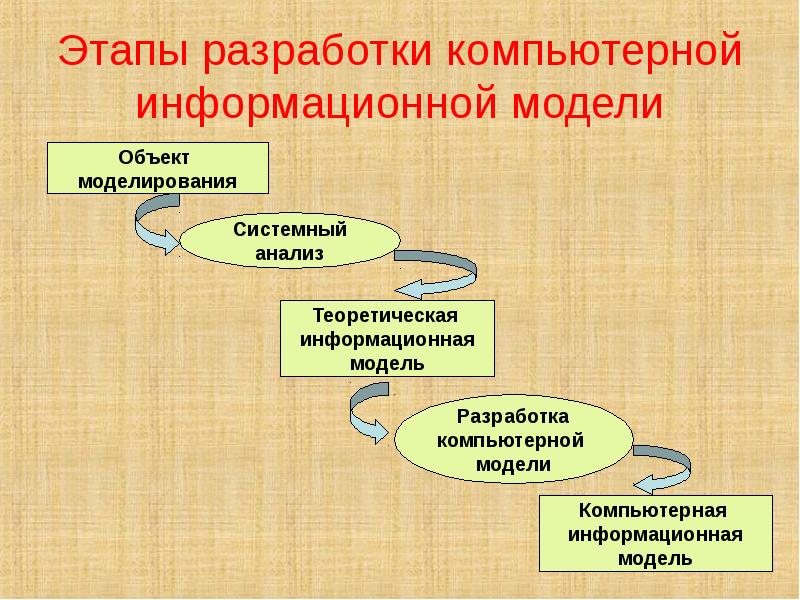
Системный подход к созданию модели

В каком классе школьной программы изучается моделирование? Информатика 9 класса знакомит учеников с данной темой более подробно. Именно в этом классе ребенок узнает о системном подходе моделирования. Предлагаем об этом поговорить немного подробнее.

Начнем с понятия «система». Это группа взаимосвязанных между собой элементов, которые действуют совместно для выполнения поставленной задачи. Для построения модели часто пользуются системным подходом, так как объект рассматривается как система, функционирующая в некоторой среде. Если моделируется какой-либо сложный объект, то систему принято разбивать на более мелкие части – подсистемы.

Модель

Моделирование в информатике – это составление образа какого-либо реально существующего объекта, который отражает все существенные признаки и свойства. Модель для решения задачи необходима, так как она, собственно, и используется в процессе решения.

Упрощенное подобие объекта;
Уменьшенная копия реального объекта;
Схема явления или процесса;
Изображение явления или процесса;
Описание явления или процесса;
Физический аналог объекта;
Информационный аналог;
Объект-заменитель, отражающий свойства реального объекта и так далее.

Модель – это очень широкое понятие, как это уже стало ясно из вышеперечисленного

Важно отметить, что все модели принято делить на группы:

материальные;
идеальные.

физические;
аналоговые.

Идеальную модель охарактеризовать еще труднее. Она связаны с:

мышлением;
воображением;
восприятием.

К ней можно отнести произведения искусства (театр, живопись, литература и так далее).

Задачи моделирования

Мы упомянули в статье, что такое моделирование в информатике. Этот процесс имеет некоторые задачи, о которых мы поговорим в данном разделе.

Что такое задача в моделировании? Предположим, что у нас есть какая-либо проблема, для ее устранения нужно решить ряд задач. То есть, задача – это проблема, с которой необходимо справиться

Важно заметить, что все задачи можно разделить на две большие группы

Вид задач
Пояснение
Прямые
Эти задачи ставят перед нами следующий вопрос: «Что будет, если мы выберем именно это решение из возможного множества?»

При этом стоит обратить внимание на то, что прямая задача дает нам исходные данные, конкретные условия.
Обратные
Обратные задачи ставят перед нами немного другие вопросы: «Как максимизировать критерий эффективности? Какое решение из возможных удовлетворяет данному условию?»

Аналитический способ представления задачи 1

Аналитический явный способ

Эта модель весьма далека от реальности. Что-либо изучить на ней представляется
проблематичным, так как из неё можно найти только время
T
и место встречи
S.
Идеализация заключается в том, что дорога считается идеально прямой, без
уклонов и подъёмов, скорости объектов считаются постоянными, желания объектов
не меняются, силы безграничны, отсутствуют помехи для движения, модель не
зависит от величин
D,
V₁,
V₂
(они могут быть сколь угодно большими или малыми).

T₁ := D/(V₁ + V₂)
S₁ := V₁ · T₁

Реальность обычно не имеет ничего общего с такой постановкой задачи. Но за счёт
большой идеализации (идеализации большого порядка) получается очень простая
модель, которая может быть разрешена в общем виде (аналитически)
математическими способами. Так формулируются чаще всего алгоритмические модели,
где протянута цепочка вычислений от исходных данных к выходу. Поэтому мы
применили в записи знак присваивания
(:=).
После вычисления правой части выражения её значение присваивается переменной,
стоящей в левой части. Далее значение этой переменной применено в правой части
следующего выражения. Схематически это выглядит так, как показано
на
рис. 1.18.

Рис. 1.18. Схема решения задачи о встрече(аналитический явный способ)

Аналитический неявный способ

В данной формулировке за счёт использования знака уравнивания получена связь
переменных
f(T, V₁, V₂, D, S) = 0
в виде системы уравнений. Устанавливая знак «?» на различные
переменные, можно формулировать при необходимости целый ряд произвольных задач,
например так:

T₁ · (V₁ + V₂) = D
S₁ = V₁ · T₁
T₁ = ?

При этом задачи формулируются пользователем и не предусматриваются специально
моделировщиком. То есть модель имеет вид объекта. Мы получили более
качественную модель. Идеализация её велика, но за счёт неявной формы записи
появилась возможность изменения задачи, изучения на ней целого ряда проблем.

Математическая модель

Математическая модель — это в информатике один из главных видов проектирования. Она еще известна, как алгоритмическая. Следует заметить, что между математическим и информационным видами граница максимально условная. Об этом уже говорилось ранее.

Если не задаваться сложными терминами, а попытаться объяснить простым языком, то описываемая модель необходима для того, чтобы решить любую задачу или достигнуть цель при помощи математической точки зрения. Следует заметить, что каждый человек в реальной жизни занимается постоянно проектированием такой модели. Допустим, обычная бытовая задача, например, купить что-то в магазине, требует составления таковой. Человек знает, сколько стоят продукты. Необходимо посчитать, какая сумма в итоге нужна для осуществления покупки, сложив все данные. Это является обычным примером математической модели.