Мгновенная скорость википедия

Скорость при неравномерном движении

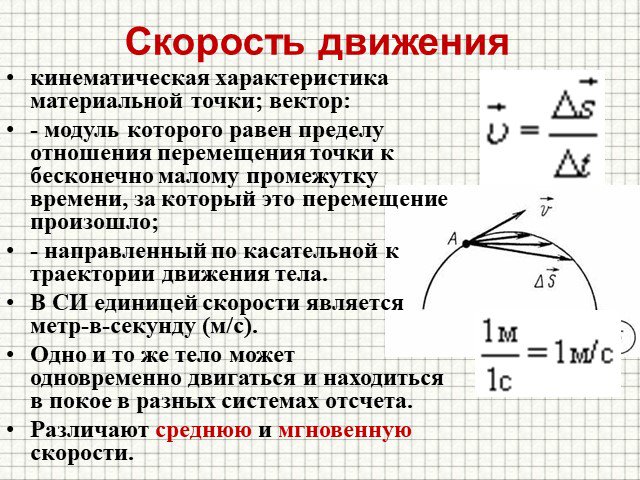
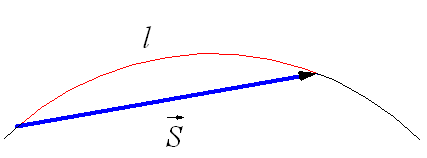
Скорость – величина, показывающая, какое расстояние проходит материальная точка за единицу времени:

$$v= {S\over t}$$

Рис. 1. Скорость равномерного прямолинейного движения.

Однако, для определения положения материальной точки в любой момент времени, во многих случаях эту формулу применять нельзя.

В самом деле, если провести опыт, можно видеть, что на Земле предмет падает с высоты 20м за 2.02с. Откуда следует, что скорость падения составляет:

$$v={20\over 2.02}=9.9(м/с)$$

Выходит, что через полсекунды после начала падения предмет окажется на 5м ниже, чем исходная точка, через секунду – на 9.9м ниже.

Однако, проведя реальное измерение, можно убедиться, что это совсем не так. За первую секунду предмет пройдет только 4.9м. А за первые полсекунды – всего лишь 1.23м ! Если же высота падения будет больше, то за три секунды путь составит не 29.7м, как следует из формулы, а больше 40м !

Рис. 2. Стробоскопическое фото свободного падения.

Причина такого расхождения с расчетом состоит в том, что предмет под действием тяготения Земли движется неравномерно, постоянно изменяя скорость. И на каком бы участке мы не измерили его скорость – полученное значение будет различно, и его невозможно будет использовать в расчетах и уравнениях для других участков.

Свести неравномерное движение к равномерному невозможно.

Сложение скоростей

Скорости движения тела в различных системах отсчёта связывает между собой классический
закон сложения скоростей.

Скорость тела относительно неподвижной системы отсчёта равна сумме
скоростей тела в подвижной системе отсчёта и самой подвижной системы
отсчёта относительно неподвижной.

Например, пассажирский поезд движется по железной дороге со скоростью 60 км/ч.
По вагону этого поезда идет человек со скоростью 5 км/ч. Если считать железную
дорогу неподвижной и принять её за систему отсчёта, то скорость человека относительно
системы отсчёта (то есть относительно железной дороги), будет равна сложению
скоростей поезда и человека, то есть

60 + 5 = 65, если человек идёт в том же направлении, что и поезд

60 – 5 = 55, если человек и поезд движутся в разных направлениях

Однако это справедливо только в том случае, если человек и поезд движутся по одной линии.
Если же человек будет двигаться под углом, то придётся учитывать этот угол, вспомнив о том,
что скорость – это векторная величина.

А теперь рассмотрим описанный выше пример более подробно – с деталями и картинками.

Итак, в нашем случае железная дорога – это неподвижная система отсчёта.
Поезд, который движется по этой дороге – это подвижная система отсчёта.
Вагон, по которому идёт человек, является частью поезда.

Скорость человека относительно вагона (относительно подвижной системы отсчёта) равна 5 км/ч.
Обозначим её буквой _Ч.

Скорость поезда (а значит и вагона) относительно неподвижной системы отсчёта
(то есть относительно железной дороги) равна 60 км/ч. Обозначим её буквой
_В. Иначе говоря, скорость
поезда – это скорость подвижной системы отсчёта относительно неподвижной системы отсчёта.

Скорость человека относительно железной дороги (относительно неподвижной системы отсчёта)
нам пока неизвестна. Обозначим её буквой .

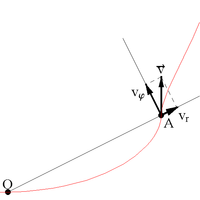
Свяжем с неподвижной системой отсчёта (рис. 1.7) систему координат ХОY,
а с подвижной системой отсчёта – систему координат X_ПО_ПY_П
(см. также раздел ).
А теперь попробуем найти скорость человека относительно неподвижной системы отсчёта,
то есть относительно железной дороги.

За малый промежуток времени Δt происходят следующие события:

Человек перемещается относительно вагона на расстояние _Ч
Вагон перемещается относительно железной дороги на расстояние _B

= _Ч + _B

Это закон сложения перемещений. В нашем примере перемещение человека
относительно железной дороги равно сумме перемещений человека относительно вагона и
вагона относительно железной дороги.

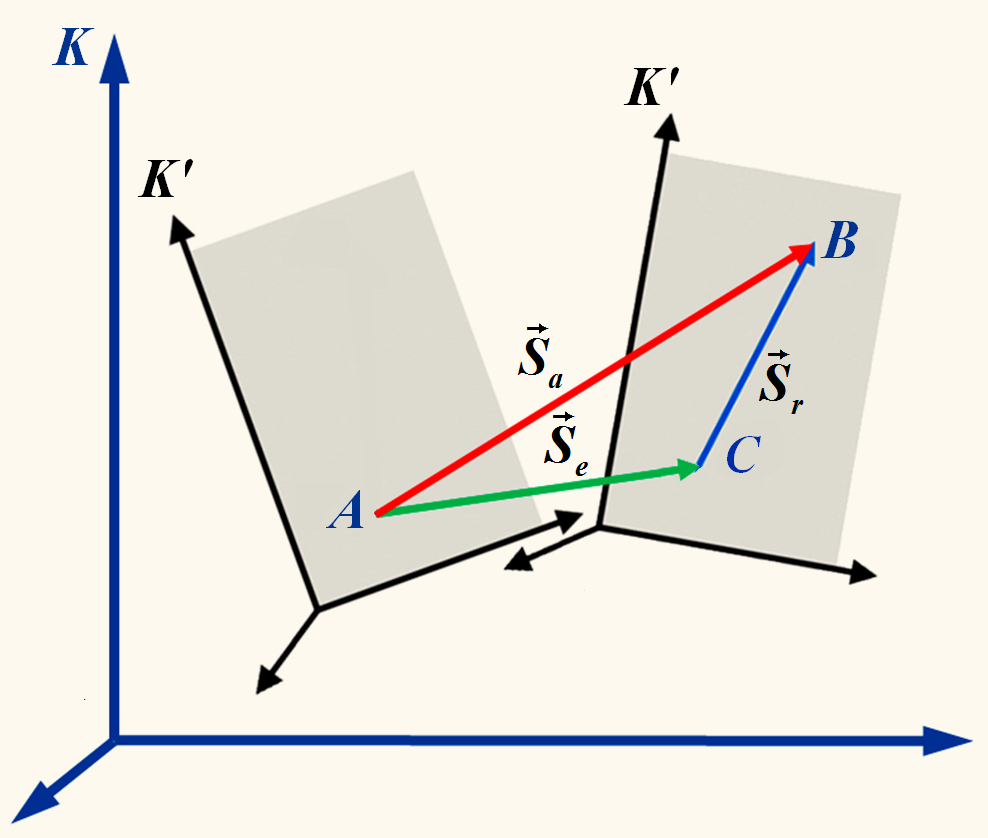
Рис. 1.7. Закон сложения перемещений.

Закон сложения перемещений можно записать так:

_Ч_B

Скорость человека относительно железной дороги равна:

 =  / Δt

= _Ч + _B

то

Скорость человека относительно вагона:

Δ_Ч = _Ч / Δt

Δ_B = _B / Δt

 = Δ_Ч + Δ_B

сложения скоростей
Скорость тела относительно неподвижной системы отсчёта равна сумме скоростей тела в подвижной системе отсчёта и скорости самой подвижной системы отсчёта относительно неподвижной.

Некоторые скорости[ | код]

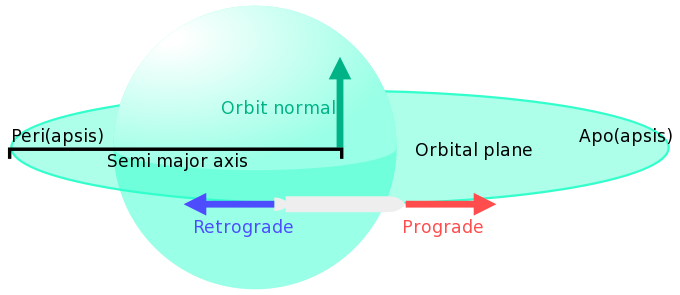
Космические скорости | код

Анализ первой и второй космической скорости по Исааку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D — на эллиптическую. Снаряд E улетает в открытый космос

Небесная механика изучает поведение тел Солнечной системы и других небесных тел. Движение искусственных космических тел изучается в астродинамике. При этом рассматривается несколько вариантов движения тел, для каждого из которых необходимо придание определённой скорости. Для вывода спутника на круговую орбиту ему необходимо придать первую космическую скорость (например, искусственный спутник Земли); преодолеть гравитационное притяжение позволит вторая космическая скорость (например, объект запущенный с Земли, вышедший за её орбиту, но находящийся в Солнечной системе); третья космическая скорость нужна чтобы покинуть звёздную систему, преодолев притяжение звезды (например, объект запущенный с Земли, вышедший за её орбиту и за пределы Солнечной системы); четвёртая космическая скорость позволит покинуть галактику.

В небесной механике под орбитальной скоростью понимают скорость вращения тела вокруг барицентра системы.

Скорости распространения волн | код

Скорость звука | код

Основная статья: Скорость звука

Скорость звука — скорость распространения упругих волн в среде, определяется упругостью и плотностью среды. Скорость звука не является постоянной величиной и зависит от температуры (в газах), от направления распространения волны (в монокристаллах). При заданных внешних условиях обычно не зависит от частоты волны и её амплитуды. В тех случаях, когда это не выполняется и скорость звука зависит от частоты, говорят о дисперсии звука. Впервые измерена Уильямом Дерхамом. Как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях скорость звука меньше, чем в твёрдых телах, поэтому при сжижении газа скорость звука возрастает.

Отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде называется числом Маха по имени австрийского учёного Эрнста Маха. Упрощённо, скорость, соответствующая 1 Маху при давлении в 1 атм (у земли на уровне моря), будет равна скорости звука в воздухе. Движение аппаратов со скоростью, сравнимой со скоростью звука, сопровождается рядом явлений, которые называются звуковой барьер. Скорости от 1,2 до 5 Махов называются сверхзвуковыми, скорости выше 5 Махов — гиперзвуковыми.

Скорость света | код

Основная статья: Скорость света

Время распространения светового луча в масштабной модели Земля-Луна. Для преодоления расстояния от поверхности Земли до поверхности Луны свету требуется 1,255 секунды.

Скорость света в вакууме — абсолютная величина скорости распространения электромагнитных волн в вакууме. Традиционно обозначается латинской буквой «c» (произносится как ). Скорость света в вакууме — фундаментальная постоянная, не зависящая от выбора инерциальной системы отсчёта (ИСО). Она относится к фундаментальным физическим постоянным, которые характеризуют не просто отдельные тела или поля, а свойства пространства-времени в целом. По современным представлениям, скорость света в вакууме — предельная скорость движения частиц и распространения взаимодействий.

Наиболее точное измерение скорости света 299 792 458 ± 1,2 м/с на основе эталонного метра было проведено в 1975 году. Теперь ввиду современного определения метра скорость света считается равной точно 299792458 м/с.

Скорость гравитации | код

Основная статья: Скорость гравитации

Скорость гравитации — скорость распространения гравитационных воздействий, возмущений и волн. До сих пор остаётся не определённой экспериментально, но согласно общей теории относительности должна совпадать со скоростью света.

Рекорды скорости | код

Скорость при равнопеременном движении

Самым простым способом неравномерного движения является равнопеременное перемещение тела, движение с постоянным ускорением. Это движение бывает:

равноускоренным, если скорость и ускорение имеют одинаковые направления, при этом величина скорости увеличивается;
равнозамедленное, при противоположном направлении скорости и ускорения, в этом случае скорость по модулю уменьшается.

При равнопеременном движении скорость в любой момент времени можно вычислить, если использовать выражение:

$\vec v(t)=\vec v_0+\vec a \bullet t (14),$

где $\vec v_0$ — начальная скорость движения точки; $\vec a$ — постоянное ускорения точки.

Сила тяжести

Сила тяжести – это сила, с которой Земля притягивает к себе тела.

Сила тяжести равна произведению массы тела на ускорение свободного падения:

Точка приложения силы тяжести – центр тела.
Сила тяжести всегда направлена вертикально вниз.

Сила тяжести является частным случаем силы всемирного тяготения, поэтому

где $ M $ – масса Земли, $ m $ – масса тела, $ R $ – радиус Земли.

Ускорение свободного падения не зависит от массы тела, зависит от массы Земли и от расстояния от центра Земли до тела.

Важно!
У поверхности Земли ускорение свободного падения не везде одинаково. Оно зависит от географической широты: на полюсах больше, чем на экваторе

Дело в том, что земной шар немного сплюснут у полюсов. Экваториальный радиус Земли больше полярного на 21 километр.

Вес и невесомость

Вес – это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.

Обозначение – $ P $, единица измерения – Н.

Точка приложения веса – точка соприкосновения тела с опорой или подвесом. Вес тела всегда направлен против силы реакции опоры или силы натяжения. Модуль веса находится по третьему закону Ньютона.

Вес тела может изменяться:

если тело покоится или движется прямолинейно и равномерно, то вес равен силе тяжести:

если тело движется с ускорением, направленным вертикально вниз (движение вниз с ускорением или вверх с замедлением), то его вес меньше силы тяжести:

если тело движется вниз с ускорением, равным ускорению свободного падения, то тело находится в состоянии невесомости.Невесомость – это исчезновение веса при движении опоры вниз с ускорением свободного падения:

если тело движется с ускорением, направленным вертикально вверх (движение вверх с ускорением или вниз с замедлением), то его вес больше силы тяжести:

При таком движении тело испытывает перегрузку.Перегрузка – это величина, которая показывает, во сколько раз вес тела, поднимающегося с ускорением или опускающегося с замедлением, больше его веса в состоянии покоя.
Обозначение – $ n $, единиц измерения нет:

Единицы измерения скорости[ | код]

Линейная скорость:

Метр в секунду, (м/с), производная единица системы СИ
Километр в час, (км/ч)
узел (морская миля в час)
Число Маха, 1 Мах равен скорости звука; Max n в n раз быстрее. Как единица, зависящая от конкретных условий, должна дополнительно определяться.
Скорость света в вакууме (обозначается c)

Угловая скорость:

Радианы в секунду, принята в системах СИ и СГС. Физическая размерность 1/с.
Обороты в секунду (в технике)
градусы в секунду, грады в секунду

Соотношения между единицами скорости | код

1 м/с = 3,6 км/ч
1 узел = 1,852 км/ч = 0,514 м/c
Мах 1 ~ 330 м/c ~ 1200 км/ч (зависит от условий, в которых находится воздух)
c = 299 792 458 м/c

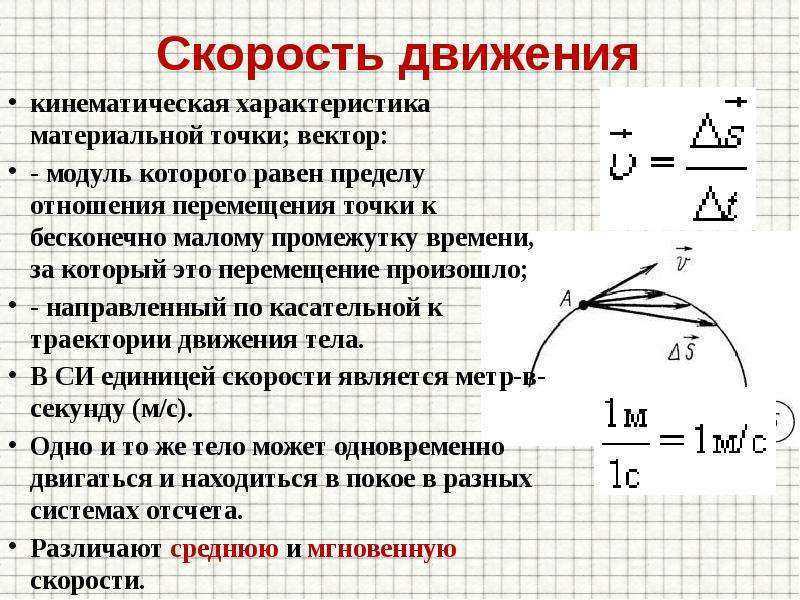
Направление мгновенной скорости

Будем описывать движение материальной точки через параметры траектории. При этом нам известны траектория движения точки и связь пути ($s$) и времени $t$. Путь отмеряется по траектории, от точки траектории, которую мы принимаем за начальную. При этом любая точка траектории характеризуется собственной величиной $s$. Из сказанного выше следует, что радиус-вектор – это функция от $s$, траекторию зададим уравнением:

$\vec r = \vec r(s)(10)$.

Получаем, что в определении мгновенной скорости (3) мы можем считать радиус – вектор как сложную функцию ($\vec r(s(t))$). При этом ее производную найдем, применяя правило дифференцирования сложной функции:

$\vec v=\frac{d\vec r}{dt}=\frac{d\vec r}{ds}\frac{ds}{dt}(11)$,

где по определению мгновенной скорости ее величина равна: $v=\frac{ds}{dt}$.

Обозначим $\Delta s$ — расстояние между парой точек по траектории; $|\Delta \vec r|$– расстояние между рассматриваемыми точками по кратчайшему расстоянию (прямой). При сближении наших точек разница между $\Delta s$ и $|\Delta \vec r|$ уменьшается, запишем:

$\frac{d\vec r}{ds}=\lim_{\Delta s\to 0} (\frac {\Delta \vec r}{\Delta s})=\lim_{\Delta s\to 0}(\frac{\Delta \vec r}{|\Delta r|}\frac {|\Delta r|}{\Delta s})=\vec \tau (12).$

где $\vec \tau$ — единичный вектор, являющийся касательным к траектории движения точки.

Принимая во внимание сказанное выше выражение (12) для мгновенной скорости можно записать как:

$\vec v=v\vec \tau$(13).

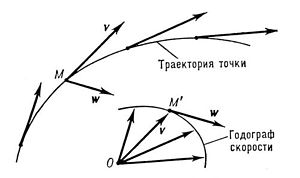
Из формулы (13) становится очевидно, что мгновенная скорость направлена по касательной к траектории движения материальной точки.

Рассматривая направления мгновенной скорости движения материальной точки подчеркнем, что:

Мгновенная скорость материальной точки перемещающейся по прямой — это вектор, который направлен по траектории ее движения.
При перемещении материальной точки по криволинейной траектории вектор мгновенной скорости имеет направление по касательной к траектории движения точки.

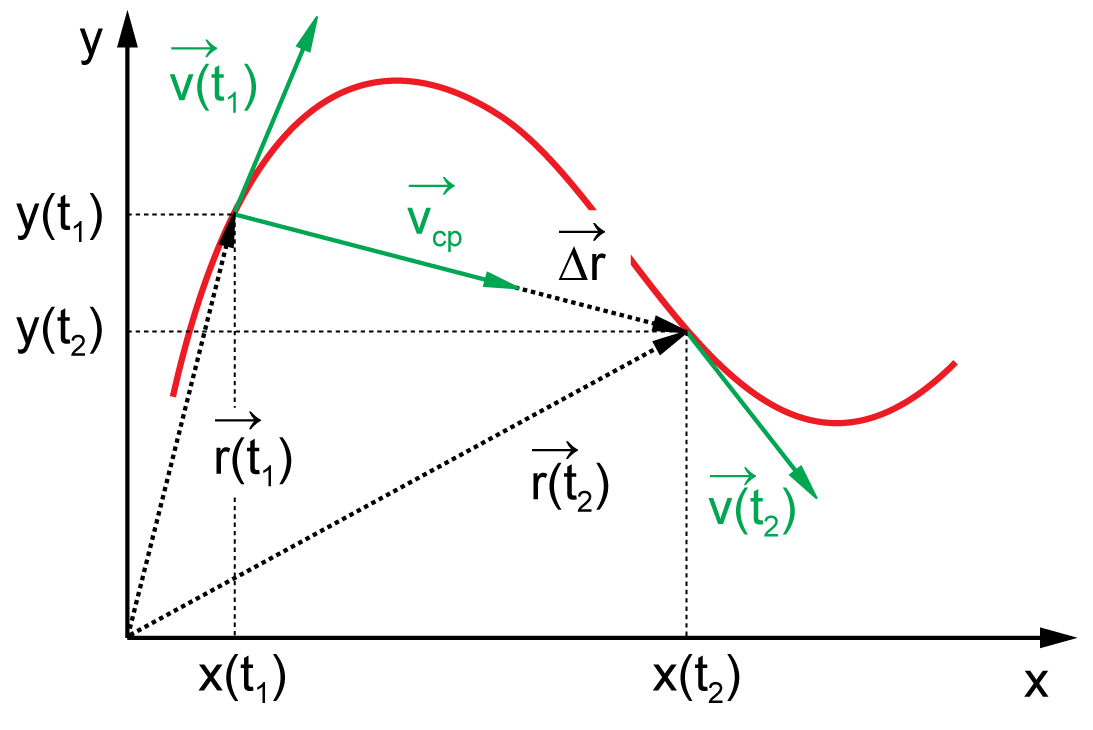
Средняя скорость

Если тело перемещается неравномерно, то описывая его движение в качестве одного из параметров можно воспользоваться средней скоростью движения на отдельных отрезках пути. Но такое описание дает очень приближенную, грубую характеристику перемещения. Поскольку находя средние скорости, мы проводим замену неравномерного движения на движение с постоянной скоростью на избранных отрезках пути, думая, что скорость изменяется скачкообразно при переходе от одного отрезка времени к другому. Графиком пути, отражающем перемещение тела, с постоянной скоростью, отличающейся на разных временных отрезках, станет ломаная линия, имеющая звенья с различным наклоном.

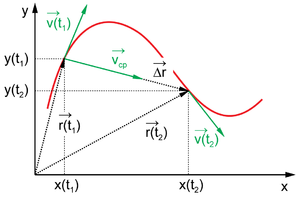
Допустим, что материальная точка перемещается вдоль прямой линии, которая не совпадает с осями координат. При этом ее положение определяет радиус- вектор $\vec r_1$, соответствующий моменту времени $t_1$. В момент времени $t_2$ положение материальной точки в пространстве определяет вектор $\vec r_2$.

Вектор перемещения нашей материальной точки определим как:

$\Delta \vec r=\vec r_2-\vec r_1(1).$

Определение 1

Средняя скорость материальной точки будет определена выражением:

$ \vec v_{sr}=\frac{\Delta \vec r}{\Delta t}=\frac{\vec r_2-\vec r_1}{t_2-t_1}(2).$

Из формулы (2) видно, что в ней происходит деление вектора на скаляр, в результате мы имеем вектор, направление которого совпадает с направлением вектора перемещения.

Векторы скорости и перемещения обладают одинаковыми направлениями.

Упражнения

Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?

Нельзя, так как в общем случае величина средней скорости не равна среднему арифметическому значению величин мгновенных скоростей. А путь и время не даны.

Какую скорость переменного движения показывает спидометр автомобиля?

Близкую к мгновенной. Близкую, так как промежуток времени должен быть бесконечно мал, а при снятии показаний со спидометра так о времени судить нельзя.

В каком случае мгновенная и средняя скорости равны между собой? Почему?

При равномерном движении. Потому что скорость не изменяется.

Скорость движения молотка при ударе равна 8м/с. Какая это скорость: средняя или мгновенная?

Мгновенная

Поезд прошел путь между городами со скоростью 50км/ч. Какая это скорость: средняя или мгновенная?

Средняя

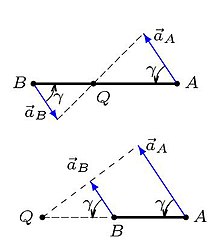
*Два шарика начали одновременно и с одинаковой скоростью двигаться по поверхностям, имеющим форму, изображенную на рисунке. Как будут отличаться скорости и время движения шариков к моменту их прибытия в точку В? Силу трения не учитывать.

Задача решается графическим способом. Скорости будут одинаковы. Время движения второго шарика меньше. Примерные графики движения шариков приведены на рисунке. Так как пути. пройденные шариками, равны, то, как видно из графика (на графике пути численно равны площадям заштрихованных фигур), время второго шарика меньше времени первого.

Мгновенная скорость

Описанное затруднение можно разрешить, если учесть, что движение – процесс непрерывный. Ни координаты точки, ни ее скорость не могут изменяться скачками. Во время движения точка проходит все бесчисленное множество координат пути, на всем пути скорость ее непрерывно изменяется в некотором диапазоне, и при этом, чем меньше рассматриваемый отрезок времени, тем меньше будет изменение координаты и скорости.

Рассмотрим падение предмета, начиная с конца первой секунды. В этот момент координата будет равна 4.905м. Отметим новую координату падающего предмета через небольшое время, и вычислим скорость:

Время	Координата	Скорость
1.000	4.905	–
2.000	19.620	14.715
1.500	11.036	12.263
1.100	5.935	10.301
1.050	5.408	10.055
1.010	5.004	9.859
1.001	4.915	9.815

Можно видеть, что с уменьшением рассматриваемого отрезка времени, изменение вычисленной скорости между строками таблицы также становится меньше.

Приведенный пример показывает главный прием, который используется для изучения непрерывных величин – изучаемый диапазон разбивается на мелкие участки, на которых изменение скорости невелико, и движение мало отличается от непрерывного. В пределе время прохождения каждого такого участка стремится к нулю, а скорость на его протяжении постоянна.

Скорость материальной точки в данный момент времени при прохождении данного малого участка пути называется мгновенной скоростью.

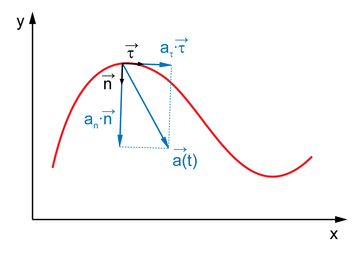
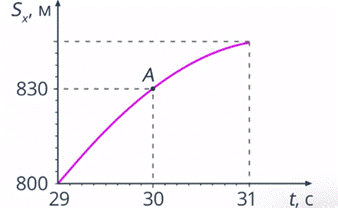
Рис. 3. Мгновенная скорость.

Мгновенная скорость материальной точки равна отношению малого перемещения на пути движения к времени прохождению этого перемещения. Формула мгновенной скорости:

$$v={ΔS\over Δt}, при Δt \rightarrow 0$$

Если для моментов времени, приведенных выше, измерить точные значения мгновенной скорости падающего предмета, то получим следующую таблицу (с отличиями от предыдущей таблицы):

Время	Мгновенная скорость	Отличие,%
2.000	19.620	25.00
1.500	14.715	16.67
1.100	10.791	4.55
1.050	10.301	2.38
1.010	9.908	0.5
1.001	9.820	0.05

Можно видеть, что по мере уменьшения рассматриваемых отрезков времени отличия между первой и второй таблицей уменьшаются.

Что мы узнали?

Мгновенная скорость – это скорость прохождения данного малого участка пути за малый промежуток времени. В идеале мгновенная скорость определяется на текущем бесконечно малом промежутке времени, за который совершается бесконечно малое перемещение.

Вопрос 1 из 10

Начать тест(новая вкладка)

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – $ a_{цс} $, единицы измерения – м/с2.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.Период – это время, за которое тело совершает один полный оборот.
Обозначение – $ T $, единицы измерения – с.

где $ N $ – количество оборотов, $ t $ – время, за которое эти обороты совершены.Частота вращения – это число оборотов за единицу времени.
Обозначение – $ \nu $, единицы измерения – с–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – $ v $, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – $ \omega $, единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к

радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

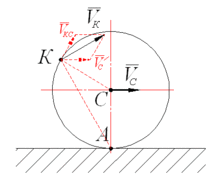
Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью $ v_1 $, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью $ v_1 $, то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки $ (m) $ равна нулю, мгновенная скорость в верхней точке $ (n) $ равна удвоенной скорости $ v_1 $, мгновенная скорость точки $ (p) $, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке $ (c) $ – по теореме косинусов.

Компоненты вектора мгновенной скорости в декартовой системе координат

В декартовой системе координат радиус-вектор запишем как:

$\vec r(t)=x(t)\vec i+y(t)\vec j+z(t)\vec k (4)$,

принимая во внимание, что единичные орты ($\vec i ; \vec j; \vec k$) не изменяются во времени, и используя определение мгновенной скорости (3), получаем:

$\vec v(t)=\frac{dx}{dt}\vec i+\frac{dy}{dt}\vec j+\frac{dz}{dt}\vec k (5).$

Из формулы (5) мы видим, что составляющие вектора скорости в декартовой системе координат задаются выражениями:

$ v_x=\frac{dx}{dt} (6),$

$ v_y=\frac{dy}{dt} (7),$

$ v_z=\frac{dz}{dt} (8).$

При этом величину мгновенной скорости можно найти как:

$ v^2=v_x^2+v_y^2+v_z^2 (9).$

Примечания

, с. 15.
, с. 154.
, с. 15—17.
, с. 154—155.
, с. 163.
, с. 152.
, с. 46—47.
↑ Скорость // : / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
Главный редактор А. М. Прохоров. Импульс // Физический энциклопедический словарь. — Советская энциклопедия (рус.). — М., 1983. Физическая энциклопедия
Главный редактор А. М. Прохоров. Кинетическая энергия // Физический энциклопедический словарь. — Советская энциклопедия (рус.). — М., 1983. Физическая энциклопедия
Главный редактор А. М. Прохоров. Вращательное движение // Физический энциклопедический словарь. — Советская энциклопедия (рус.). — М., 1983. Физическая энциклопедия
Главный редактор А. М. Прохоров. Ускорение // Физический энциклопедический словарь. (рус.). — 1983. Физическая энциклопедия
↑ , с. 21.
, с. 34.
, с. 29.
, с. 31—32.
, с. 32—34.
↑ , с. 35.
, с. 35—36.
, с. 37.
, с. 37—38.
, с. 43.
, с. 45.
, с. 51—52.
, с. 59.
, с. 68.
, с. 77.
, с. 91.
, с. 96.
, с. 72—73.
, с. 64—66.
Кабардин О.Ф., Орлов В.А., Пономарёва А.В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — Тираж 143 500 экз. — С. 44