Кратко о механических и электромагнитных волнах

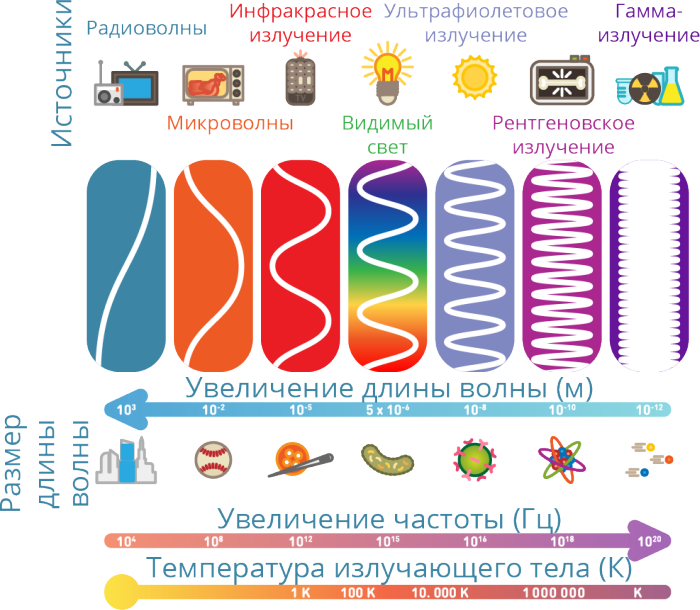
Механические колебания и волны. Звук

Раздел ОГЭ по физике: 1.23. Механические колебания. Амплитуда, период и частота колебаний. Формула, связывающая частоту и период колебаний. Механические волны. Продольные и поперечные волны. Длина волны и скорость распространения волны. Звук. Громкость и высота звука. Скорость распространения звука. Отражение и преломление звуковой волны на границе двух сред. Инфразвук и ультразвук.

Движение, при котором состояния движущегося тела с течением времени повторяются, причём тело проходит через положение своего устойчивого равновесия поочерёдно в противоположных направлениях, называется механическим колебанием.

Условием возникновения колебания является наличие в системе возвращающей силы, всегда направленной к положению устойчивого равновесия. Каждый законченный цикл колебательного движения, после которого оно вновь повторяется, называется полным колебанием.

Смещением х называется отклонение колеблющейся точки от положения равновесия в данный момент времени.

Амплитудой колебаний х_m называется модуль наибольшего смещения тела от положения равновесия при колебательном движении.

Периодом колебания Т называется время, за которое совершается одно полное колебание: Т = tN.

Величину, равную числу колебаний, совершаемых за единицу времени, называют частотой колебаний

Механическое колебание, при котором координата тела меняется по закону синуса или косинуса, называется гармоническим колебанием.

Математическим маятником называют материальную точку, подвешенную на тонкой нерастяжимой нити. Маленький металлический шарик, подвешенный на длинной нити, можно условно считать математическим маятником.

При колебаниях математического маятника (в отсутствие сил трения) выполняется закон сохранения механической энергии и периодически происходит переход потенциальной энергии в кинетическую и обратно.

В положении максимального отклонения от положения равновесия потенциальная энергия маятника максимальна, а кинетическая равна нулю. При приближении к положению равновесия потенциальная энергия уменьшается, а кинетическая увеличивается, достигая максимального значения в положении равновесия, в котором потенциальная становится равной нулю: W_полн = W_п + W_к = const E_полн = E_к_max = Е_п_ma_х.

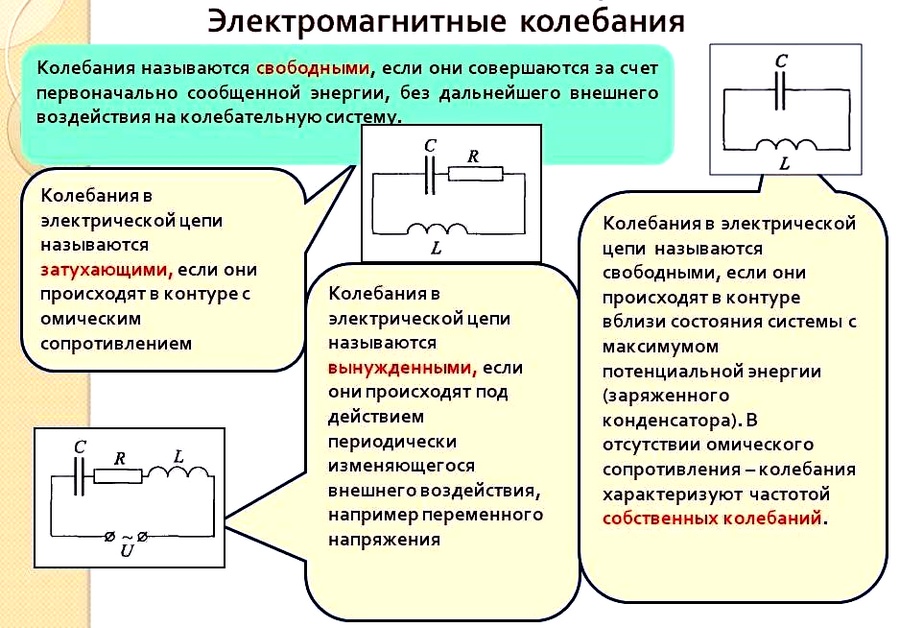
Затухающими называются колебания, амплитуда которых уменьшается с течением времени. Затухание свободных механических гармонических колебаний связано с уменьшением механической энергии колебательной системы за счёт работы сил сопротивления (трения).

Механические волны. Звук

Если в упругой среде (газ, жидкость или твёрдое тело) имеется источник колебаний, то в ней с течением времени происходит процесс распространения колебаний, этот процесс называется волной.

Волны, распространяющиеся в упругой среде, называются механическими волнами. В волне осуществляется перенос энергии колебательного движения без переноса вещества (массы) среды, в которой распространяется волна. Периодом Т волны является период колебаний точек среды при распространении волны. Длиной волны λ называется расстояние, на которое распространяется волна за один период колебаний: λ = ʋT; ʋ = λv.

Продольными волнами называются волны, в которых направление колебаний частиц происходит в направлении распространения волны. Продольные механические волны могут распространяться в твёрдых, в жидких и в газообразных средах.

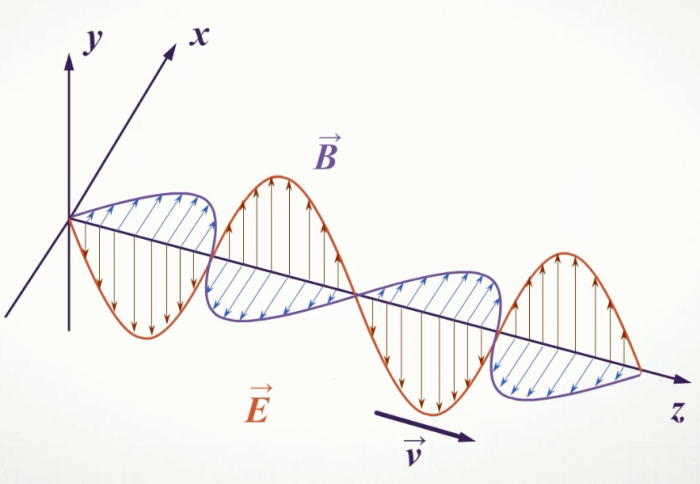
Поперечными называются волны, в которых направление колебаний частиц происходит перпендикулярно направлению распространения волны. Поперечные механические волны могут распространяться только в твёрдых телах и на свободной поверхности жидкости.

Звуковыми волнами называются механические волны, вызывающие у человека ощущение звука: ʋ_зв = (16 ÷ 20 000) Гц.

Характеристики звука

Громкость звука определяется амплитудой колебаний.

Высота тона определяется частотой колебаний.

Скорость звука зависит от плотности среды. Скорость звука в твёрдых телах больше, чем в жидкостях, а в жидкостях больше, чем в газах. Скорость звука увеличивается с ростом температуры среды.

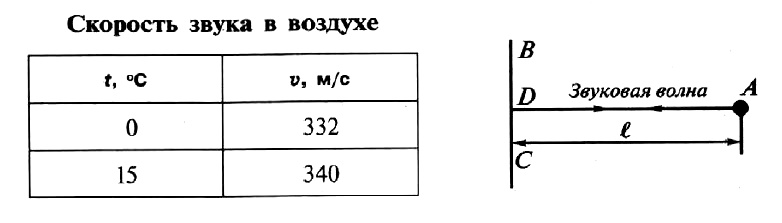
В случае, когда отражающая поверхность перпендикулярна распространению волны, звуковая волна после отражения возвращается обратно к источнику звука. Такой случай отражения называется эхом.

В гидролокации эхо используется для определения глубин, расстояний до преград и других судов.

Конспект урока «Механические колебания и механические волны. Звук».

Следующая тема: «МКТ. Агрегатные состояния вещества».

Что такое продольные волны?

В продольной волне частицы движутся в среде в том же измерении, что и направление движения волны. Другими словами, смещение частицы параллельно направлению движения волны.

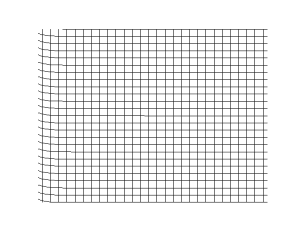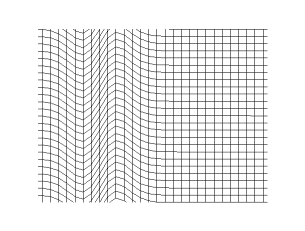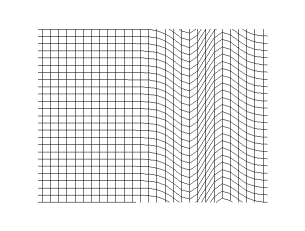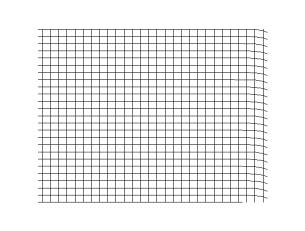
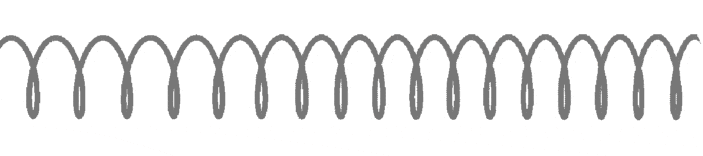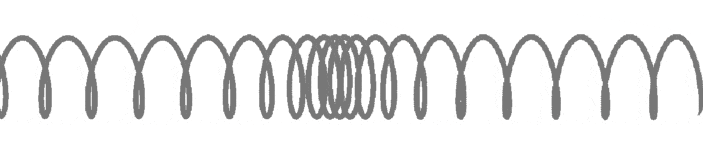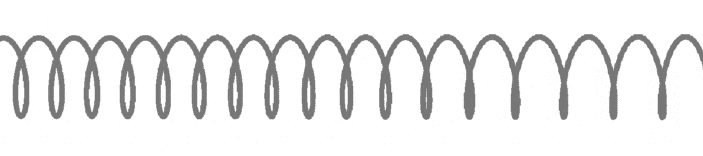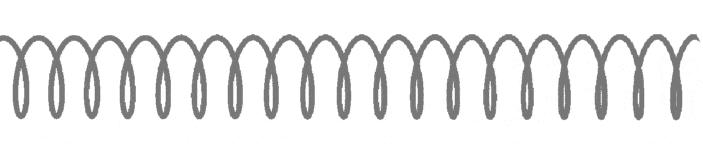Рисунок 1

При прохождении через среду эти волны создают сжатие и разрежение.

Сжатие — это область высокого давления, где волновые частицы находятся близко друг к другу.
Разрежения — это области низкого давления, где частицы распространяются дальше друг от друга.

Как вы можете видеть на рис.1, сжатие перемещается слева направо, и энергия передается в том же направлении. Однако ни одна частица не переносится вдоль продольной волны. Вместо этого все они движутся вперед и назад между сжатием, когда волна проходит через среду.

Расстояние между центрами двух последовательных областей (между сжатиями или разрежениями) определяет длину волны продольной волны. Она может производиться в любой среде, включая твердую, жидкую и газовую среду.

Чтобы лучше объяснить это явление, мы перечислили некоторые из лучших примеров продольных волн, которые люди видят в своей повседневной жизни.

Классификации волн[править | править код]

Имеется множество классификаций волн, различающиеся по своей физической природе, по конкретному механизму распространения, по среде распространения и т.п.

Волны можно классифицировать:

Океанские поверхностные волны, которые являются волнениями, которые образуются посредством воды;
Звук — механическая волна, которая образуется в газах, жидкости, в средах с твердыми частицами и плазме;

По отношению к направлению колебаний частиц среды, в которой распространяется волна, выделяют:

продольные волны (волны сжатия, P-волны) — волна распространяется параллельно колебаниям частиц среды (звук);
поперечные волны (волны сдвига, S-волны) — частицы среды колеблются перпендикулярно направлению распространения волны (электромагнитные волны, волны на поверхностях разделения сред);
волны смешанного типа.

По виду фронта волны (поверхности равных фаз):

плоская волна — плоскости фаз перпендикулярны направлению распространения волны;
сферическая волна — поверхностью фаз является сфера;

Продольные волны:	Поперечные волны:
а) плоская;	а) плоская;
б) сферическая.	б) сферическая.

Рис.1. A = в глубоководном месте; B = в мелкой воде; Краткое движение поверхностной частицы становится более плоским с уменьшающейся глубиной. 1 = Прогрессия волны; 2 = Гребень; *3 = Корыто.

На Рис.1 показаны периодические волны, которые характеризуются гребнями (максимумы) и впадинами (минимумами), и могут обычно категоризироваться как или продольные или поперечные.

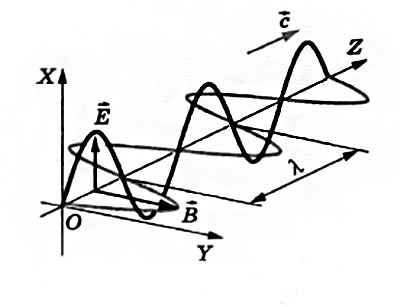
Поперечные волны — волны с напрвлением колебаний, перпендикулярным к вектору распространения волны; примером служат волны в области электромагнитных волн. *Продольные волны — те, крторые имеют колебания, параллельные вектору распространения волны; например, большинство звуковых волн.

Когда объект подпрыгивает на ряби в водоёме, то вектор движения точек волны происходит по орбитальной траектории. Появляющаяся рябь — не простые поперечные синусоидальные волны.

Все волны имеют общее поведение со множеством стандартных ситуаций.

По демонстрируемым волнами физическим проявлениям их можно разделить на:

линейные волны — волны с небольшой амплитудой, свойства которых описываются простыми линейными зависимостями;

По постоянству во времени различают:

одиночная волна — короткое одиночное возмущение (солитоны);

волновой пакет — это ряд возмущений, ограниченных во времени с перерывами между ними. Одно беспрерывное возмущение такого ряда называется цуг волн. В теории волновой пакет описывается как сумма всевозможных плоских волн, взятых с определёнными весами. В случае нелинейных волн, форма огибающей волнового пакета эволюционирует с течением времени;

Подобно сложным колебаниям, волновые цуги и негармонические волны могут быть представлены в виде суммы (суперпозиции) синусоидальных волн разных частот. Когда фазовые скорости всех этих волн одинаковы, то вся их группа (волновой пакет) движется с одной скоростью.
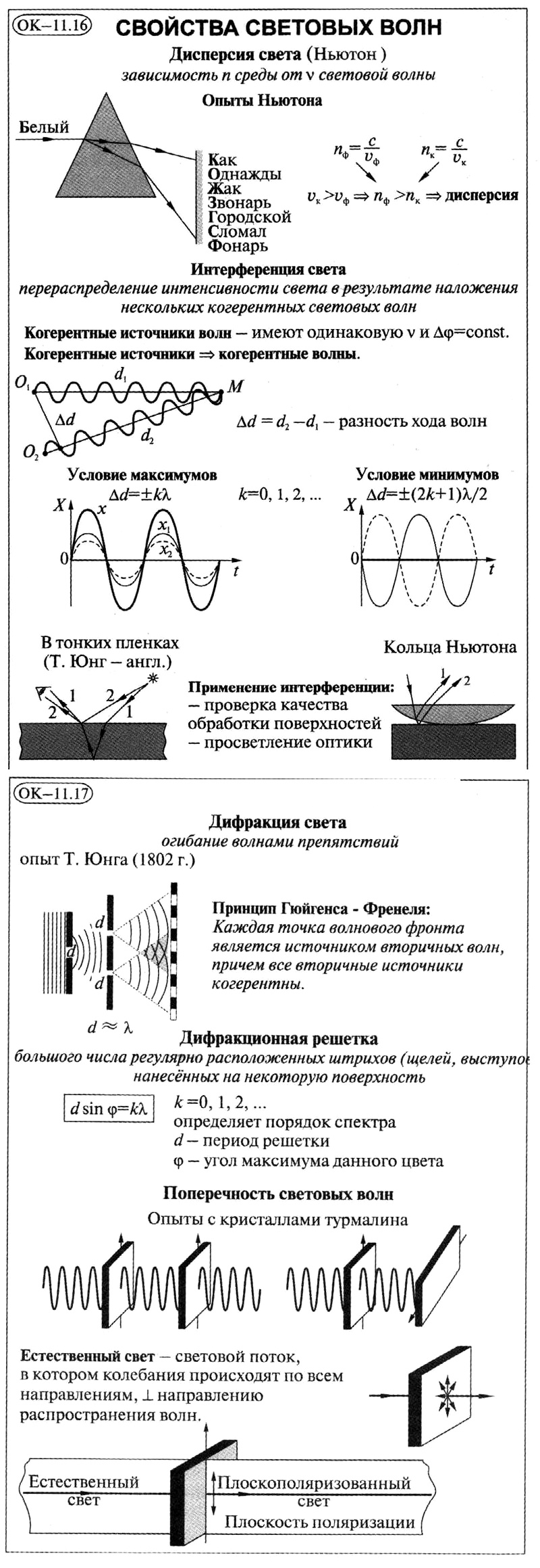
Если же фазовая скорость волны зависит от её частоты w, наблюдается дисперсия – волны различных частот идут с разной скоростью. Нормальная, или отрицательная дисперсия тем больше, чем выше частота волны. За счёт дисперсии, например, луч белого света в призме разлагается в спектр, в каплях воды – в радугу. Волновой пакет, который можно представить как набор гармонических волн, лежащих в диапазоне w0 ± Dw, из-за дисперсии расплывается. Его форма – огибающая амплитуд компонент цуга – искажается, но перемещается в пространстве со скоростью vгр, называемой групповой скоростью. Если при распространении волнового пакета максимумы волн, его составляющих, движутся быстрее огибающей, фазовая скорость сигнала выше групповой: сф > vгр. При этом в хвостовой части пакета за счёт сложения волн возникают все новые максимумы, которые передвигаются вперёд и пропадают в его головной части. Примером нормальной дисперсии служат среды, прозрачные для света – стёкла и жидкости.
В ряде случаев наблюдается также аномальная (положительная) дисперсия среды, при которой групповая скорость превышает фазовую: vгр > сф, причём возможна ситуация, когда эти скорости направлены в противоположные стороны. Максимумы волн появляются в головной части пакета, перемещаются назад и исчезают в его хвосте.

Математические выражения, описывающие волновые процессы

В связи с многообразием, нелинейностью свойств субстанции, особенностями границ и способов возбуждения, пользуются свойством разложения любых, самых сложных колебаний в спектр по частотам отклика субстанции на возбуждение. Для дискретных спектров наиболее общим решением моделирующих уравнений является выражение, которое удобно представлять в комплексной форме:

u=∑j=nAj(r,t)exp⁡i(ωjt−kjr+φj)+Bj(r,t)exp⁡i(ωjt+kjr+ψj),{\displaystyle u=\sum \limits _{j=0}^{n}{A_{j}\left({r,t}\right)\exp i\left({\omega _{j}t-k_{j}r+\varphi _{j}}\right)}+B_{j}\left({r,t}\right)\exp i\left({\omega _{j}t+k_{j}r+\psi _{j}}\right),}

где j{\displaystyle j} — номер моды, гармоники спектра; ψj{\displaystyle \psi _{j}} φj{\displaystyle \varphi _{j}} — постоянные фазы запаздывания колебаний данной моды, определяемые, как правило, различием реакции динамической системы в точке её возбуждения, а также особенностями границ; они могут в общем случае иметь как действительный, так и комплексных вид; n{\displaystyle n} — количество мод в спектре, которое может быть и бесконечным. Мода с j={\displaystyle j=0} называется основной модой, гармоникой. С нею переносится самая большая часть энергии волнового процесса.
Для интегральных спектров вместо сумм записываются интегралы по частотам спектра.
В дискретных структурах имеют место три режима колебательного процесса: периодический, критический, и апериодический.

В идеальной дискретной системе переход от одного режима к другому определяется разностью фаз колебания соседних элементов. При достижении противофазности колебаний система переходит от периодического режима к критическому. В апериодическом режиме противофазность колебаний соседних элементов сохраняется, но от точки возбуждения идёт интенсивное затухание колебательного процесса последующих элементов системы. Данный режим проявляется и в конечных упругих линиях.

В линиях с сопротивлением колебания соседних элементов никогда не достигают противофазности. Тем не менее, особенности колебаний, характерные для апериодического режима, сохраняются и при наличии сопротивления.

Гармоническая волна

Гармонической волной называется линейная монохроматическая волна, распространяющаяся в бесконечной динамической системе.
В распределённых системах общий вид волны описывается выражением, являющимся аналитическим решением линейного волнового уравнения

u=Asin⁡(ωt−kr+φ),{\displaystyle u=A\sin \left({\omega t-kr+\varphi _{0}}\right),}

где A{\displaystyle A} — некоторая постоянная амплитуда волнового процесса, определяемая параметрами системы, частотой колебаний и амплитудой возмущающей силы; ω=2πT=2πf{\displaystyle \omega =2\pi /T=2\pi f} — круговая частота волнового процесса, T{\displaystyle T} — период гармонической волны, f{\displaystyle f} — частота; k=2πλ=ωc{\displaystyle k=2\pi /\lambda =\omega /c} — волновое число, λ{\displaystyle \lambda } — длина волны, c{\displaystyle c} — скорость распространения волны; φ{\displaystyle \varphi _{0}} — начальная фаза волнового процесса, определяемая в гармонической волне закономерностью воздействия внешнего возмущения.

Лучи волны

Лучом волны (геометрическим лучом) называется нормаль к волновому фронту. Например, плоской волне (см. раздел «Классификация волн») соответствует пучок параллельных прямых лучей; сферической волне — радиально расходящийся пучок лучей.

Расчёт формы лучей при небольшой длине волны — по сравнению с препятствиями, поперечными размерами фронта волны, расстояниями до схождения волн и т. п. — позволяет упростить сложный расчёт распространения волны. Это применяется в геометрической акустике и геометрической оптике.

Наряду с понятием «геометрический луч», зачастую удобно использовать понятие «физический луч», который является линией (геометрическим лучом) только в определённом приближении, когда поперечными размерами самого луча можно пренебречь. Учёт физичности понятия луча позволяет рассматривать волновые процессы в самом луче, наряду с рассмотрением процессов распространения луча как геометрического

Особенно это важно при рассмотрении физических процессов излучения движущимся источником.

Видимый свет

Преломление белого света через призму

Форма: электромагнитное излучение

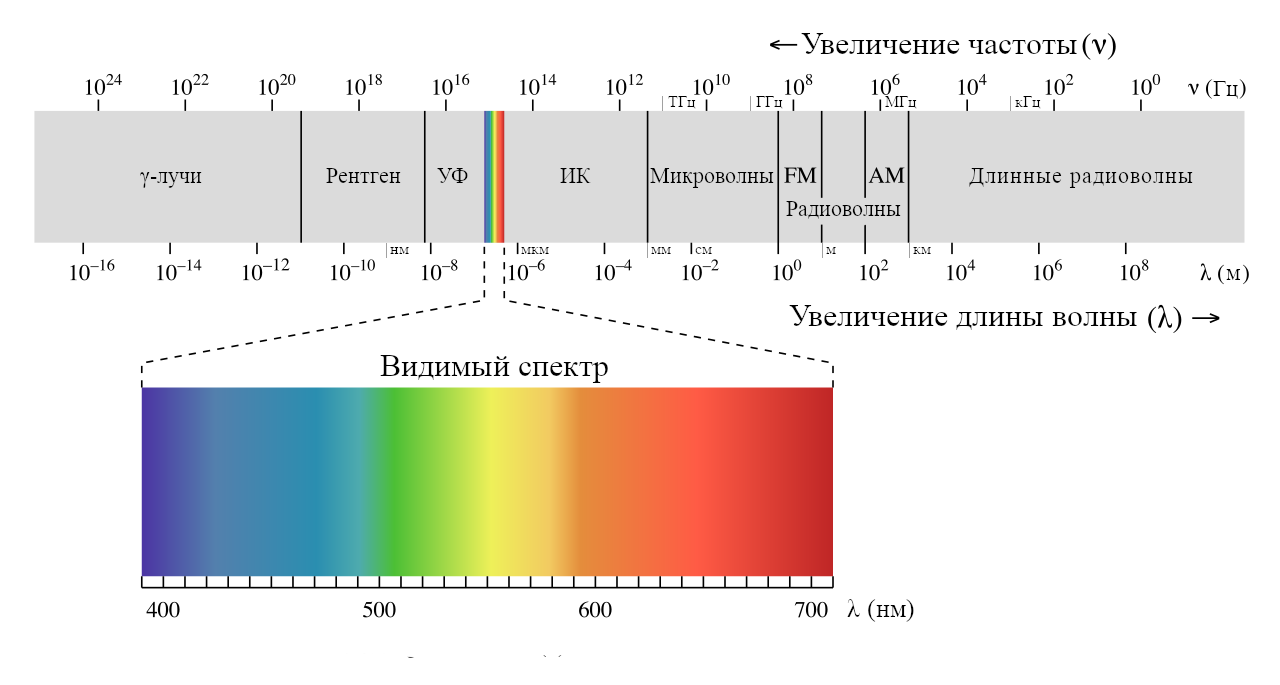
Наиболее распространенным примером поперечной волны является видимый свет, длина волны которого обычно находится в диапазоне от 400 до 700 нанометров. Его также можно описать в терминах потоков фотонов (безмассовых пакетов энергии), каждый фотон движется со скоростью 299 792 458 метров в секунду в вакууме.

Свет — единственный источник пищи для всех живых организмов, за исключением нескольких хемотрофных организмов, таких как бактерии. Есть сотни научных и коммерческих применений световой энергии. Его можно отражать, преломлять или собирать, чтобы видеть объекты.

Свойства света, такие как интенсивность, частота, направление распространения и поляризация, используются для создания оптических устройств, таких как микроскопы и телескопы, которые позволяют людям видеть объекты, которые нельзя увидеть невооруженным глазом.

Естественный свет от солнца собирается для создания электричества. Искусственные источники света, такие как лазер, используются в оптической связи, лазерной хирургии, лечении кожи, приводах оптических дисков, волоконно-оптических, режущих и сварочных материалах, а также в производстве полупроводниковых чипов (фотолитография).

Астрономы также используют свет для понимания структуры и свойств небесных тел. Космические и наземные телескопы улавливают видимый свет для наблюдения и изучения поверхности нашей планеты.

Механическая волна и ее возникновение

Механическая волна – это процесс распространения возмущений в материальной среде (чаще всего в каком-то веществе).

Для возникновения волны необходимо начальное воздействие, при котором колебания (свободные или вынужденные) возникают только в одной или нескольких «начальных» материальных точках среды.

В материальной среде все точки связаны друг с другом, поэтому колебательные движения начальных точек будут влиять на соседние точки, и воздействие будет периодическим, в соответствии с исходными колебаниями. В результате и соседние точки также придут в колебательное движение.

Далее, соседние точки начнут воздействовать (и опять, периодически) на более дальних соседей, и так колебательное воздействие будет распространяться по всем точкам среды. А поскольку воздействие распространяется с какой-то задержкой, то в среде будут точки, которые только начнут движение «вперед», в то время, как начальная точка уже может двигаться «назад», то есть, колебательный процесс «отрывается» от его источника, и распространяется в среде.

Такой процесс называется «волной».

Рис. 1. Волны и их распространение.

Неразрушающий контроль

Форма: высокочастотные звуковые волны

Неразрушающий контроль — это широкий спектр методов контроля, используемых в науке и технике для оценки свойств системы, компонента или материала без их повреждения.

Одной из часто используемых методик является ультразвуковой контроль, основанный на распространении ультразвуковых волн в исследуемом материале или объекте. Очень короткие ультразвуковые импульсы с частотой от 0,1 до 50 МГц передаются на компоненты для обнаружения внутренних дефектов или свойств материала.

Поскольку ультразвуковые волны обладают высокой чувствительностью и высокой проникающей способностью, они позволяют обнаруживать чрезвычайно мелкие дефекты, скрытые глубоко в деталях. Этот метод дает немедленные результаты, поэтому инженеры могут принимать точечные решения. Он в основном используется на металлических сплавах и бетоне.

Ссылки[править | править код]

Горелик Г. С. Колебания и волны. Введение в акустику, радиофизику и оптику. — М.: Гос. издат. ф.— м. лит-ры, 1959, с. 144.
http://en.wikipedia.org/wiki/Wave
http://bse.sci-lib.com/article012647.html
Paul R Pinet. op. cit.. p. 242. ISBN 0763759937. http://books.google.com/books?id=6TCm8Xy-sLUC&pg=PA242.
Paul R Pinet. op. cit.. p. 242. ISBN 0763759937. http://books.google.com/books?id=6TCm8Xy-sLUC&pg=PA242.
Mischa Schwartz, William R. Bennett, and Seymour Stein (1995). Communication Systems and Techniques. John Wiley and Sons. p. 208. ISBN 9780780347151. http://books.google.com/books?id=oRSHWmaiZwUC&pg=PA208&dq=sine+wave+medium++linear+time-invariant&lr=&as_brr=3&ei=u69cSpuKNZDKkASph-GaBw.
See Eq. 5.10 and discussion in A. G. G. M. Tielens (2005). The physics and chemistry of the interstellar medium. Cambridge University Press. pp. 119 ff. ISBN 0521826349. http://books.google.com/books?id=wMnvg681JXMC&pg=PA119. ; Eq. 6.36 and associated discussion in Otfried Madelung (1996). Introduction to solid-state theory (3rd ed.). Springer. pp. 261 ff. ISBN 354060443X. http://books.google.com/books?id=yK_J-3_p8_oC&pg=PA261. ; and Eq. 3.5 in F Mainardi (1996). «Transient waves in linear viscoelastic media». in Ardéshir Guran, A. Bostrom, Herbert Überall, O. Leroy. Acoustic Interactions with Submerged Elastic Structures: Nondestructive testing, acoustic wave propagation and scattering. World Scientific. p. 134. ISBN 9810242719. http://books.google.com/books?id=UfSk45nCVKMC&pg=PA134.
Aleksandr Tikhonovich Filippov (2000). The versatile soliton. Springer. p. 106. ISBN 0817636358. http://books.google.com/books?id=TC4MCYBSJJcC&pg=PA106.
Seth Stein, Michael E. Wysession (2003). An introduction to seismology, earthquakes, and earth structure. Wiley-Blackwell. p. 31. ISBN 0865420785. http://books.google.com/books?id=Kf8fyvRd280C&pg=PA31.
Michael A. Slawinski, Klause Helbig (2003). «Wave equations». Seismic waves and rays in elastic media. Elsevier. pp. 131 ff. ISBN 0080439306. http://books.google.com/books?id=s7bp6ezoRhcC&pg=PA134.
Jalal M. Ihsan Shatah, Michael Struwe (2000). «The linear wave equation». Geometric wave equations. American Mathematical Society Bookstore. pp. 37 ff. ISBN 0821827499. http://books.google.com/books?id=zsasG2axbSoC&pg=PA37.
Karl F Graaf (1991). Wave motion in elastic solids (Reprint of Oxford 1975 ed.). Dover. pp. 13–14. http://books.google.com/books?id=5cZFRwLuhdQC&printsec=frontcover.
Christian Jirauschek (2005). FEW-cycle Laser Dynamics and Carrier-envelope Phase Detection. Cuvillier Verlag. p. 9. ISBN 3865374190
Fritz Kurt Kneubühl (1997). Oscillations and waves. Springer. p. 365. ISBN 354062001X
Mark Lundstrom (2000). Fundamentals of carrier transport. Cambridge University Press. p. 33. ISBN 0521631343
Chin-Lin Chen (2006). «§13.7.3 Pulse envelope in nondispersive media». Foundations for guided-wave optics. Wiley. p. 363. ISBN 0471756873. http://books.google.com/books?id=LxzWPskhns0C&pg=PA363.
Chin-Lin Chen (2006). «§13.7.3 Pulse envelope in nondispersive media». Foundations for guided-wave optics. Wiley. p. 363. ISBN 0471756873. http://books.google.com/books?id=LxzWPskhns0C&pg=PA363.
Stefano Longhi, Davide Janner (2008). «Localization and Wannier wave packets in photonic crystals». in Hugo E. Hernández-Figueroa, Michel Zamboni-Rached, Erasmo Recami. Localized Waves. Wiley-Interscience. p. 329. ISBN 0470108851. http://books.google.com/books?id=xxbXgL967PwC&pg=PA329.

Примечания

↑ Волны // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 1. — С. 315. — ISBN 5-85270-034-7.
Г. Пейн, Физика колебаний и волн, стр. 161
Строго говоря, это равенство справедливо только для гармоничных волн.
Н. И. Калитеевский, Волновая оптика, с. 33
К. А. Самойло, Радиотехнические цепи и сигналы, с. 19
Л. Э. Эльсгольц, Дифференциальные уравнения и вариационное исчисление, с. 113.
Н. И. Калитеевский, Волновая оптика, с. 136.
↑ Н. И. Калитеевский, Волновая оптика, с. 47.
Н. И. Калитеевский, волновая оптика, с. 49.
Н. И. Калитеевский, волновая оптика, с. 314.
Р. В. Поль, Оптика и атомная физика, с. 204.
К. Г. Гусев, Атлас поляризационных параметров эллиптически поляризованных волн, отражённых от сред земной поверхности, Харьков, 1966 г., тип. ХВКИУ, Г-884029

Примеры

Один простой пример для понимания стоячих волн — это два человека, которые трясут один конец скакалки . Если они трясутся синхронно, веревка может образовывать регулярную структуру волн, колеблющихся вверх и вниз, с неподвижными точками вдоль веревки, где веревка почти неподвижна (узлы), и точками, где дуга веревки максимальна (пучности).

Акустический резонанс

Гексагональное облако на северном полюсе Сатурна первоначально считалось стоячими волнами Россби . Однако это объяснение недавно было оспорено.

Стоячие волны также наблюдаются в физических средах, таких как струны и столбы воздуха. Любые волны, движущиеся по среде, будут отражаться назад, когда достигнут конца. Этот эффект наиболее заметен в музыкальных инструментах , где, при различных кратных вибрирующей струне или воздушной колонки «с собственной частотой , создаются стоячая волна, позволяя гармоники , которые будут определены. Узлы возникают на фиксированных концах, а анузлы — на открытых. Если зафиксирован только на одном конце, доступны только гармоники с нечетными номерами. На открытом конце трубы противоузел не будет точно на конце, так как он изменяется из-за его контакта с воздухом, поэтому для его точного размещения используется коррекция конца . Плотность струны влияет на частоту, на которой будут воспроизводиться гармоники; чем больше плотность, тем ниже должна быть частота для создания стоячей волны той же гармоники.

Видимый свет

Стоячие волны также наблюдаются в оптических средах, таких как оптические волноводы и оптические резонаторы . В лазерах используются оптические резонаторы в виде пары обращенных зеркал, которые составляют интерферометр Фабри – Перо . Средний коэффициент усиления в полости (такие как кристалл ) испускает свет когерентны , захватывающие стоячие волны света в полости. Длина световой волны очень мала (в диапазоне нанометров , 10 -9 м), поэтому стоячие волны имеют микроскопические размеры. Одно из применений стоячих световых волн — измерение малых расстояний с помощью оптических плоскостей .

Рентгеновские лучи

Интерференция между рентгеновскими лучами может формировать поле стоячей волны рентгеновского излучения (XSW). Из-за короткой длины волны рентгеновских лучей (менее 1 нанометра) это явление можно использовать для измерения событий атомного масштаба на поверхности материалов . XSW генерируется в области, где рентгеновский луч интерферирует с дифрагированным лучом от почти идеальной поверхности монокристалла или отражением от рентгеновского зеркала . Регулируя геометрию кристалла или длину волны рентгеновского излучения, XSW можно перемещать в пространстве, вызывая сдвиг в рентгеновской флуоресценции или выходе фотоэлектронов из атомов вблизи поверхности. Этот сдвиг может быть проанализирован, чтобы точно определить местоположение конкретного вида атомов относительно кристаллической структуры или поверхности зеркала. Метод XSW использовался для уточнения деталей атомарного масштаба примесей в полупроводниках, атомной и молекулярной адсорбции на поверхности и химических превращений, участвующих в катализе .

Механические волны

Каякеры на стоячей волне в национальном парке Грейт-Фолс .

Стоячие волны можно механически вызвать в твердую среду с помощью резонанса. Один простой для понимания пример — это два человека, которые трясут оба конца скакалки. Если они трясутся синхронно, веревка будет образовывать регулярный узор с узлами и пучностями и будет казаться неподвижной, отсюда и название стоячей волны. Точно так же консольная балка может иметь стоячую волну, наложенную на нее путем применения базового возбуждения. В этом случае свободный конец перемещается на наибольшее расстояние вбок по сравнению с любым местом вдоль балки. Такое устройство можно использовать в качестве датчика для отслеживания изменений частоты или фазы резонанса волокна. Одно из приложений — это измерительный прибор для метрологии размеров .

Волны Фарадея

Волны Фарадея является нелинейной стоячей волны на границе раздела воздух-жидкость , индуцированной гидродинамической неустойчивости. Его можно использовать в качестве шаблона на жидкой основе для сборки микромасштабных материалов.