Средние беспристрастные оценщики
Любой средний беспристрастный оценщик минимизирует риск (ожидаемая потеря) относительно функции брусковой ошибки потерь, как наблюдается Гауссом. Средний беспристрастный оценщик минимизирует риск относительно функции абсолютного отклонения потерь, как наблюдается лапласовским. Другие функции потерь используются в статистической теории, особенно в прочной статистике.
Теория средних беспристрастных оценщиков была восстановлена Джорджем В. Брауном в 1947:
Сообщили о дальнейших свойствах средних беспристрастных оценщиков. В частности средние беспристрастные оценщики существуют в случаях, где средний беспристрастный и оценщики максимальной вероятности не существуют. Средние беспристрастные оценщики инвариантные при непосредственных преобразованиях.
Расчет моды в Excel
В настоящее время большинство вычислений делается в MS Excel, где для расчета моды также предусмотрена специальная функция. В Excel 2013 я таких нашел ажно 3 штуки.

МОДА – пережиток старых изданий Excel. Функция оставлена для совмещения со старыми версиями.
МОДА.ОДН – рассчитывает моду по заданным значениям. Здесь все просто. Вставили функцию, указали диапазон данных и «Ок».
МОДА.НСК – позволяет рассчитать сразу несколько модальных значений (одинаковых максимальных частот) для одного ряда данных, если они есть. Функцию нужно вводить как формулу массива, перед этим выделив количество ячеек равное количеству требуемых модальных значений. Иногда действительно модальных значений может быть несколько. Однако для этих целей предварительно лучше посмотреть на диаграмму распределения.
Моду для интервальных данных одной функцией в Excel рассчитать нельзя. То есть такая функция в готовом виде не предусмотрена. Придется прописывать вручную.
Следующая статья посвящена медиане.
До встречи на statanaliz.info.
Другие связанные с медианой понятия
Псевдомедиана
Для одномерных распределений, которые симметричны об одной медиане, оценщик Ходжеса-Леманна — прочный и очень эффективный оценщик медианы населения; для несимметричных распределений оценщик Ходжеса-Леманна — прочный и очень эффективный оценщик псевдомедианы населения, которая является медианой symmetrized распределения и которая является близко к медиане населения. Оценщик Ходжеса-Леманна был обобщен к многомерным распределениям.
Средний фильтр
В контексте обработки изображения монохромных растровых изображений есть тип шума, известный как соль и перечный шум, когда каждый пиксель независимо становится черным (с некоторой маленькой вероятностью) или белый (с некоторой маленькой вероятностью), и неизменно иначе (с вероятностью близко к 1). Изображение, построенное из средних ценностей районов (как 3×3-Сквер), может эффективно уменьшить шум в этом случае.
Кластерный анализ
В кластерном анализе k-медианы, группирующие алгоритм, обеспечивают способ определить группы, в который критерий увеличения расстояния между средством группы, которое используется в объединении в кластеры k-средств, заменен, максимизировав расстояние между медианами группы.
Средняя средняя линия
Это — метод прочного регресса. Идея относится ко времени Уолда в 1940, который предложил делить ряд двумерных данных на две половины в зависимости от ценности независимого параметра: левая половина с ценностями меньше, чем медиана и правильная половина с ценностями, больше, чем медиана. Он предложил предпринять меры зависимых и независимых переменных левых и правых половин и оценить наклон линии, присоединяющейся к этим двум пунктам. Линия могла тогда быть приспособлена, чтобы приспособить большинство пунктов в наборе данных.
Nair и Shrivastava в 1942 предложили подобную идею, но вместо этого защитили делить образец на три равных части прежде, чем вычислить средства подобразцов. Браун и Настроение в 1951 предложили идею использовать медианы двух подобразцов скорее средства. Tukey объединил эти идеи и рекомендовал делить образец на три равных подобразца размера и оценить линию, основанную на медианах подобразцов.
Пример использования
Предположим, что в одной комнате оказалось 19 бедняков и один миллионер. У каждого бедняка есть $5, а у миллионера — $1 млн (106). В сумме получается $1 000 095. Если мы разделим деньги равными долями на 20 человек, то получим $50 004,75. Это будет среднее арифметическое значение суммы денег, которая была у всех 20 человек в этой комнате.
Медиана в этом случае будет равна $5 (полусумма десятого и одиннадцатого, срединных значений ранжированного ряда). Можно интерпретировать это следующим образом. Разделив нашу компанию на две равные группы по 10 человек, мы можем утверждать, что в первой группе у каждого не больше $5, во второй же не меньше $5. В общем случае можно сказать, что медиана это то, сколько принёс с собой «средний» человек. Наоборот, среднее арифметическое — неподходящая характеристика, так как оно значительно превышает сумму наличных, имеющуюся у среднего человека.
Свойства медианы для случайных величин
Если распределение непрерывно, то медиана является одним из решений уравнения
- F(x)=0.5{\displaystyle F(x)=0.5}
Если распределение является непрерывной строго возрастающей функцией, то решение уравнения однозначно. Если распределение имеет разрывы, то медиана может совпадать с минимальным или максимальным (крайним) возможным значением случайной величины, что противоречит «геометрическому» пониманию этого термина.
Медиана является важной характеристикой распределения случайной величины и, так же как математическое ожидание, может быть использована для центрирования распределения. Поскольку оценки медианы более робастны, её оценивание может быть более предпочтительным для распределений с т. н
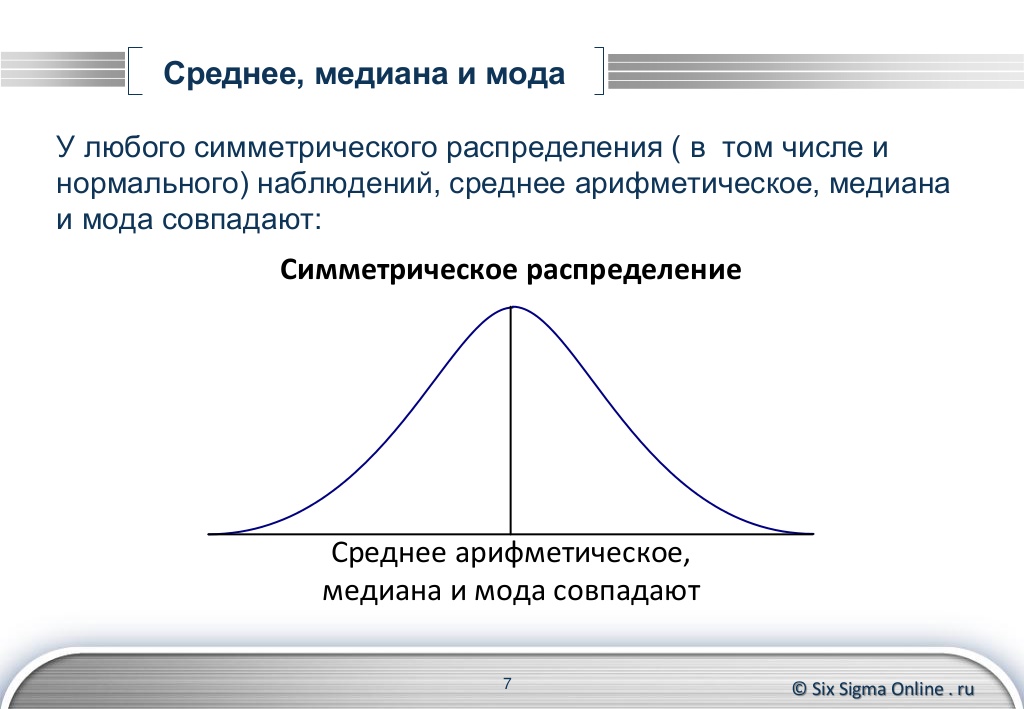
тяжёлыми хвостами. Однако о преимуществах оценивания медианы по сравнению с математическим ожиданием можно говорить только в случае, если эти характеристики у распределения совпадают, в частности, для симметричных функций плотности распределения вероятностей.
Медиана определяется для всех распределений, а в случае неоднозначности, естественным образом доопределяется, в то время как математическое ожидание может быть не определено (например, у распределения Коши).
Медиана
Медиана – число, характеризующее выборку, т.е. если взять все элементы множества, то это число ровно делит множество пополам. Одна половина множества равна или больше этого число, а другая меньше или равна этому числу.
Объясним это на примере. Допустим, дано следующее множество: $\{2, 5, 10, 8, 7\}$. Здесь число $7$ делит это множество пополам. $2$ и $5$ меньше, а $10$ и $8$ больше этого числа. Для удобства нахождения медианы сначала нужно отсортировать выборку в возрастающем или убывающем порядке $\{2, 5, 7, 8, 10\}$. Тогда элемент, стоящий ровно посередине, будет медианой. Как видите, это число $7$.
А как быть, если во множестве четное количество чисел? Например $\{2, 5, 6, 8, 10, 15\}$. Тогда берем среднеарифметическое значение двух чисел, которые стоят посередине. У нас эти числа $6$ и $8$. Значит $(6+8):2=14:2=7$. Среднее значение этих двух чисел, а значит медиана равна $7$.
Пример из практики
Допустим, в стране $1\%$ взрослого населения зарабатывает $1$ млн. у.е. в год (может быть больше, но для примера ограничимся этим числом), $10\%$ населения зарабатывает по $20,000$ у.е. в год. Остальные живут за чертой бедности, зарабатывая всего $100$ у.е. в год. Тогда, несмотря на большие заработки $11\%$ населения, медиана все равно будет равна $100$ у.е. Потому что подавляющее большинство получает всего $100$ у.е. в год. Теперь вычислим среднее значение.
Значит, среднее значение в год составляет
Зная соотношение неработающих людей, на каждого работающего, и поделив полученное на это число, получим доход на душу населения (с учетом детей, стариков и больных без пенсии).
Итак, такая статистика показывает, что народ живет припеваючи, зарабатывая примерно 1,000 у.е. в месяц, а действительность другая. Как раз, так и вычисляется доход на душу населения. Берется национальный доход и делится на численность населения. Теперь вы понимаете, почему в сводках всегда называют эту цифру, потому что она никоим образом не отображает благосостояние большинства, а только является показателем экономического благосостояния страны.
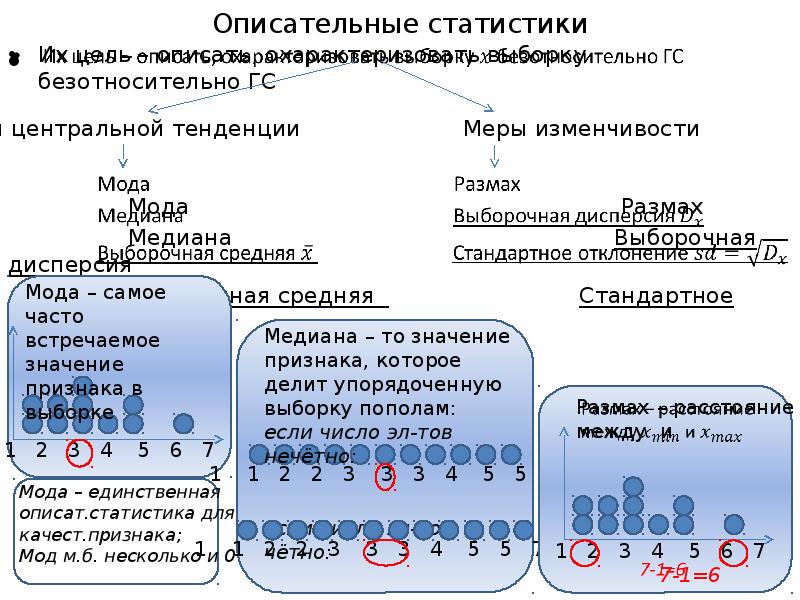
Меры местоположения и дисперсии
Медиана — один из многих способов суммировать типичные ценности, связанные с членами статистического населения; таким образом это — возможный параметр местоположения. Так как медиана совпадает со вторым квартилем, его вычисление иллюстрировано в статье о квартилях.
Когда медиана используется в качестве параметра местоположения в описательной статистике, есть несколько выбора для меры изменчивости: диапазон, диапазон межквартиля, среднее абсолютное отклонение и среднее абсолютное отклонение.
Практически, различные меры местоположения и дисперсии часто сравниваются на основе того, как хорошо соответствующие ценности населения могут быть оценены от образца данных. У медианы, оцененное использование типовой медианы, есть хорошие свойства в этом отношении. В то время как это не обычно оптимально, если данное распределение населения принято, его свойства всегда довольно хороши. Например, сравнение эффективности оценщиков кандидата показывает, что средний образец более статистически эффективен, чем типовая медиана, когда данные не загрязнены данными от распределений с тяжелым хвостом или от смесей распределений, но менее эффективный иначе, и что эффективность типовой медианы выше, чем это для широкого диапазона распределений. Более определенно у медианы есть 64%-я эффективность по сравнению со средним минимальным различием (для больших нормальных образцов), который должен сказать, что различие медианы будет на ~50% больше, чем различие среднего — видит Эффективность (статистика) #Asymptotic эффективность и ссылки там.
Свойства медианы для случайных величин
Если распределение непрерывно, то медиана является одним из решений уравнения
- F(x)=0.5{\displaystyle F(x)=0.5}
Если распределение является непрерывной строго возрастающей функцией, то решение уравнения однозначно. Если распределение имеет разрывы, то медиана может совпадать с минимальным или максимальным (крайним) возможным значением случайной величины, что противоречит «геометрическому» пониманию этого термина.
Медиана является важной характеристикой распределения случайной величины и, так же как математическое ожидание, может быть использована для центрирования распределения. Поскольку оценки медианы более робастны, её оценивание может быть более предпочтительным для распределений с т. н
тяжёлыми хвостами. Однако о преимуществах оценивания медианы по сравнению с математическим ожиданием можно говорить только в случае, если эти характеристики у распределения совпадают, в частности, для симметричных функций плотности распределения вероятностей.
Медиана определяется для всех распределений, а в случае неоднозначности, естественным образом доопределяется, в то время как математическое ожидание может быть не определено (например, у распределения Коши).
Неуникальность значения
Если имеется чётное количество случаев и два средних значения различаются, то медианой, по определению, может служить любое число между ними (например, в выборке {1, 3, 5, 7} медианой может служить любое число из интервала (3,5)). На практике в этом случае чаще всего используют среднее арифметическое двух средних значений (в примере выше это число (3+5)/2=4). Для выборок с чётным числом элементов можно также ввести понятие «нижней медианы» (элемент с номером n/2 в упорядоченном ряду из n{\displaystyle n} элементов; в примере выше это число 3) и «верхней медианы» (элемент с номером (n+2)/2; в примере выше это число 5). Эти понятия определены не только для числовых данных, но и для любой порядковой шкалы.
История
Идея медианы произошла в книге Эдварда Райта по навигации (Ошибки Certaine в Навигации) в 1599 в секции относительно определения местоположения с компасом. Райт чувствовал, что эта стоимость была наиболее вероятна быть правильным значением в ряде наблюдений.
В 1757 Роджер Джозеф Боскович развил метод регресса, основанный на норме L1 и поэтому неявно на медиане.
В 1774, лапласовский предложил, чтобы медиана использовалась в качестве типичного оценщика ценности следующего PDF. Определенные критерии должны были минимизировать ожидаемую величину ошибки; | α — α* то, где α* — оценка и α, является истинным значением. Критерий Лэплэйсеза обычно отклонялся в течение 150 лет в пользу метода наименьших квадратов Гаусса и Леджендгра, который минимизирует>, чтобы получить среднее. Распределение и среднего образца и типовой медианы было определено лапласовским в начале 1800-х.
Антуан Огюстен Курно в 1843 был первым, чтобы использовать термин медиана (valeur médiane) для стоимости, которая делит распределение вероятности на две равных половины. Густав Теодор Фехнер использовал медиану (Centralwerth) в социологических и психологических явлениях. Это ранее использовалось только в астрономии и смежных областях. Густав Фехнер популяризировал медиану в формальный анализ данных, хотя это использовалось ранее лапласовским.
Фрэнсис Гэлтон использовал английскую медиану термина в 1881, ранее использовав термины центральная стоимость в 1869 и среда в 1880.
Многомерная медиана
Ранее, эта статья обсудила понятие одномерной медианы для одномерного объекта (население, образец). Когда измерение равняется двум или выше, есть многократные понятия, которые расширяют определение одномерной медианы; каждая такая многомерная медиана соглашается с одномерной медианой, когда измерение точно один. В более высоких размерах, однако, есть несколько многомерных медиан.
Крайняя медиана
Крайняя медиана определена для векторов, определенных относительно фиксированного набора координат. Крайняя медиана определена, чтобы быть вектором, компоненты которого — одномерные медианы. Крайнюю медиану легко вычислить, и ее свойства были изучены Пури и Сенатором
Пространственная медиана (медиана L1)
В normed векторном пространстве измерения два или больше, «пространственная медиана» минимизирует ожидаемое расстояние
где X и векторы, если у этого ожидания есть конечный минимум; другое определение лучше подходит для общих распределений вероятности. Пространственная медиана уникальна, когда измерение набора данных равняется двум или больше. Это — прочный и очень эффективный оценщик центральной тенденции населения.
Геометрическая медиана — соответствующий оценщик, основанный на типовой статистике конечного множества пунктов, а не статистике населения. Это — пункт, минимизирующий арифметическое среднее число Евклидовых расстояний до данных типовых пунктов вместо ожидания
Обратите внимание на то, что арифметическое среднее число и сумма взаимозаменяемые, так как они отличаются фиксированной константой, которая не изменяет местоположение минимума
Другие многомерные медианы
Альтернативное обобщение пространственной медианы в более высоких размерах, которая не касается особой метрики, является centerpoint.
Неуникальность значения
Если имеется чётное количество случаев и два средних значения различаются, то медианой, по определению, может служить любое число между ними (например, в выборке {1, 3, 5, 7} медианой может служить любое число из интервала (3,5)). На практике в этом случае чаще всего используют среднее арифметическое двух средних значений (в примере выше это число (3+5)/2=4). Для выборок с чётным числом элементов можно также ввести понятие «нижней медианы» (элемент с номером n/2 в упорядоченном ряду из n{\displaystyle n} элементов; в примере выше это число 3) и «верхней медианы» (элемент с номером (n+2)/2; в примере выше это число 5). Эти понятия определены не только для числовых данных, но и для любой порядковой шкалы.
Описательная статистика
Медиана используется прежде всего для перекошенных распределений, которые она суммирует по-другому от среднего арифметического. Рассмотрите мультинабор {1, 2, 2, 2, 3, 14}. Медиана равняется 2 в этом случае, (как способ), и это могло бы быть замечено как лучший признак центральной тенденции (менее восприимчивый к исключительно большой стоимости в данных), чем среднее арифметическое 4.
Вычисление медиан — популярная техника в итоговой статистике и суммирующий статистические данные, так как просто понять и легкий вычислить, также давание меры, которая более прочна в присутствии ценностей изолированной части, чем, является средним.
Подробнее о среднем значении
Иногда вычисляют среднее значение для группы данных. Тогда значения разбивают на группы и вычисляют серединную точку каждой группы. Затем эти значения умножают на количество членов каждой группы (на частотность) и складывают. А результат делят на общее количество. Такое значение называют средним значением группы. Посмотрите на этот пример:
| Группа | Частота | Середина |
|---|---|---|
| 1-20 | 5 | 10.5 |
| 21-40 | 25 | 30.5 |
| 41-60 | 37 | 50.5 |
| 61-80 | 23 | 70.5 |
Здесь середина вычисляется таким образом: $(20+1):2 = 10.5, \ (40+21):2 = 30.5$, и т.д.
Умножаем эти значения на частоты и складываем, затем делим на общее количество:
Как уже показали на примере с доходом населения, экстремумы сильно влияют на среднеарифметическое значение, поэтому иногда полезно их отбрасывать. Тогда среднее значение называется урезанным средним.
Иногда среднее значение вычисляется для дихотомных данных (когда члены множества принимают два значения) используя $0-1$ кодировку. Например, если из $10$ людей $6$ мужчин и $4$ женщины, то обозначив мужчин числом $1$, а женщин числом $0$, можно найти процент мужчин, вычисляя среднее значение.
В симметричном распределении (типа нормального распределения) среднее значение, медиана и мода равны или близки друг другу. В асимметричном же, они отличаются, и число, на которое отличаются эти показатели, дают информацию о “скошенности” распределения относительно нормального.
Надеемся, что нам удалось “на пальцах” объяснить значение терминов среднеарифметическое значение, медиана и мода. Если кто-то из Ваших знакомых до сих пор в недоумении, просвещайте их, поделившись данной статьей в соц. сетях.
Переменные потока и запасы
Все экономические переменные, которые имеют временное измерение, т.е. величины которых можно измерить по истечении времени называем переменными потока. А запас не имеет временное измерение.
Показатели вариации
Чтобы знать, насколько далеко значение совокупности простирается от центральной тенденции, вычисляют вариацию (на английском dispersion или variability, но не путайте с variation). Есть несколько показателей вариации. Это размах, межквартильный размах, среднее линейное отклонение, дисперсия и стандартное отклонение.
Типы выборки
Для расследования генеральной совокупности применяют два вида выборки. Случайную и неслучайную выборку. Простая, систематическая, стратифицированная и кластерная выборка являются случайными выборками. Стихийная, удобная и квотная выборка являются примером неслучайной выборки.
Скользящее среднее значение
Среди наиболее популярных технических индикаторов чаще всего, скользящее среднее значение используются для измерения направления текущего тренда. Самая простая формула скользящей средней, известна как Простое Скользящее Среднее значение.
Генеральная совокупность и выборка
Генеральной совокупностью называют всё исследуемое множество. На английском языке этот термин называется популяцией (population). Выборкой (на английском sample) называют некоторое случайно отобранное подмножество из генеральной совокупности.
Нулевая гипотеза
Нулевая гипотеза утверждает, что между исследуемыми данными никакой закономерности нет. Пока нулевая гипотеза не опровергнута, она в силе. Альтернативная гипотеза является обратной нулевой гипотезе.
Типы данных в статистике
Такие выражения, как минимум, максимум, медиана и процентиль имеют значение лишь для порядковых данных. Порядковые данные делятся на метрические и неметрические.
Что такое тренд?
Термины тренд и тенденция используются в различных целях. Люди часто говорят о тенденции относительно роста цен и падения курса какой-то валюты. Здесь мы раскроем статистическое значение этих терминов.
Ошибка репрезентативности
Стандартная ошибка (standard error) и ошибка репрезентативности часто употребляются, как взаимозаменяемые термины. Ошибка репрезентативности показывает, насколько результаты, полученные при выборочном наблюдении отличаются от результатов, полученных при исследовании генеральной совокупности.
Медиана в статистике
Медиана – середина упорядоченного ряда. Медиана делит этот ряд пополам таким образом, что в одной половине стоят все значения меньшие, а в другой все значения большие медианы.
Население
Собственность Optimality
Средняя абсолютная ошибка реальной переменной c относительно случайной переменной X является
При условии, что распределение вероятности X таково, что вышеупомянутое ожидание существует, тогда m — медиана X, если и только если m — minimizer средней абсолютной ошибки относительно X. В частности m — типовая медиана, если и только если m минимизирует среднее арифметическое абсолютных отклонений.
См. также объединение в кластеры k-медиан.
Распределения Unimodal
Можно показать для unimodal распределения что медиана и средняя ложь в пределах (3/5) ≈ 0,7746 стандартных отклонения друг друга. В символах,
где |. | абсолютная величина.
Подобное отношение держится между медианой и способом: они лежат в пределах 3 ≈ 1,732 стандартных отклонения друг друга:
Средства связи неравенства и медианы
Если у распределения есть конечное различие, то расстояние между медианой и средним ограничено одним стандартным отклонением.
Связанный был доказан Просвирниками, кто использовал неравенство Йенсена дважды, следующим образом. У нас есть
\begin {выравнивают }\
\left | \mu-m\right | = \left |\mathrm {E} (X-m) \right | & \leq \mathrm {E }\\уехал (\left|X-m\right |\right) \\
& \leq \mathrm {E }\\уехал (\left|X-\mu\right |\right) \\
& \leq \sqrt {\\mathrm {E} ((X-\mu)^2)} = \sigma.
\end {выравнивают }\
Первые и третьи неравенства, прибывшие от неравенства Йенсена, относились к функции абсолютной величины и квадратной функции, которые являются каждым выпуклым. Второе неравенство прибывает из факта, что медиана минимизирует абсолютную функцию отклонения
Это доказательство может легко быть обобщено, чтобы получить многомерную версию неравенства, следующим образом:
\begin {выравнивают }\
\left \|\mu-m\right \|
& \leq \mathrm {E} \|X-m \| \\
& \leq \mathrm {E} (\left \| X-\mu \right \|) \\
& \leq \sqrt {\mathrm {E} (\| X-\mu \| ^2) }\
\end {выравнивают }\
где m — пространственная медиана, то есть, minimizer функции
Пространственная медиана уникальна, когда измерение набора данных равняется двум или больше. Альтернативное доказательство использует одностороннее неравенство Чебышева; это появляется в.
Среднее значение
Часто так называют среднеарифметическое значение выборки (или множества чисел). Это, пожалуй, самый распространенный термин, из вышеперечисленных трех. Хотя бы потому, что почти каждый день мы слышим это слово в СМИ. Значение его тоже объясняет само название. Тем не менее, для тех, кому непонятен смысл этого слова, объясним “на пальцах”.
Это сумма данных чисел, деленное на количество. Если написать в виде формулы, это выглядит так.
Здесь $\bar{x}$ – среднее арифметическое значение. Если у Вас имеется $5$ чисел $\{10, 12, 5, 20, 8\}$, то их сумма будет $10+12+3+20+8=55$ . Так как количество равно $5$, то делим $55:5=11$. Это и есть среднеарифметическое значение.
Пример из практики
Допустим, у вас есть магазин, и вы торгуете чем то. В день, выручка составляет от $600$ до $1,200$ у.е. По итогам месяца вы наторговали на сумму $30,000$ у.е. Если условное количество дней в месяце $30$, значит, ваша средняя ежедневная выручка составляет $1,000$ у.е. ($30000:30 = 1000$).
Расчет моды
Теперь посмотрим, как рассчитать моду. Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто. Если данных много, то моду легче всего найти с помощью соответствующей гистограммы. Бывает так, что совокупность данных имеет бимодальное распределение.

Без диаграммы очень трудно понять, что в данных не один, а два центра. К примеру, на президентских выборах предпочтения сельских и городских жителей могут отличаться. Поэтому распределение доли отданных голосов за конкретного кандидата может быть «двугорбым». Первый «горб» – выбор городского населения, второй – сельского.
Немного сложнее с интервальными данными, когда вместо конкретных значений имеются интервалы. В этом случае говорят о модальном интервале (при анализе доходов населения, например), то есть интервале, частота которого максимальна относительно других интервалов. Однако и здесь можно отыскать конкретное модальное значение, хотя оно будет условным и примерным, так как нет точных исходных данных. Представим, что есть следующая таблица с распределением цен.
Для наглядности изобразим соответствующую диаграмму.
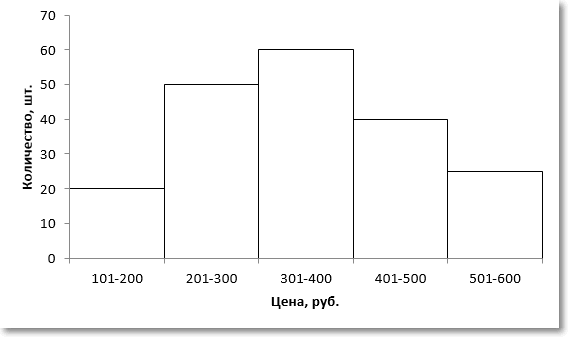
Требуется найти модальное значение цены.
Вначале нужно определить модальный интервал, который соответствует интервалу с наибольшей частотой. Найти его так же легко, как и моду в дискретном ряду. В нашем примере это третий интервал с ценой от 301 до 400 руб. На графике – самый высокий столбец. Теперь нужно определить конкретное значение цены, которое соответствует максимальному количеству. Точно и по факту сделать это невозможно, так как нет индивидуальных значений частот для каждой цены. Поэтому делается допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные вес и как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Давайте еще раз посмотрим на рисунок, чтобы понять формулу, которую я напишу чуть ниже.
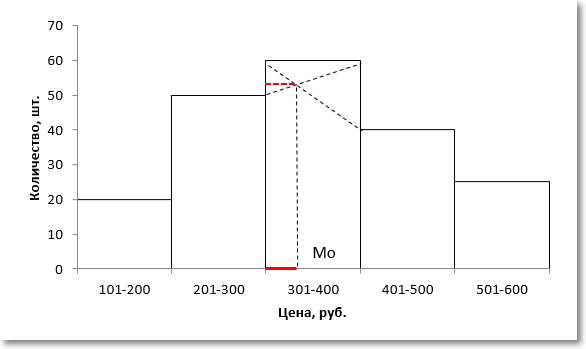
На рисунке отчетливо видно, что соотношение высоты столбцов, расположенных слева и справа от модального определяет близость моды к левому или правому краю модального интервала. Задача по расчету модального значения состоит в том, чтобы найти точку пересечения линий, соединяющих модальный столбец с соседними (как показано на рисунке пунктирными линиями) и нахождении соответствующего значения признака (в нашем примере цены). Зная основы геометрии (7-й класс), по данному рисунку нетрудно вывести формулу расчета моды в интервальном ряду.
Формула моды имеет следующий вид.
Где Мо – мода,
x – значение начала модального интервала,
h – размер модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
Второе слагаемое формулы моды соответствует длине красной линии на рисунке выше.
Рассчитаем моду для нашего примера.
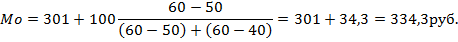
Таким образом, мода интервального ряда представляет собой сумму, состоящую из значения начального уровня модального интервала и отрезка, который определяется соотношением частот ближайших интервалов от модального.