Прямоугольный параллелепипед

Расчетные формулы

Формулы для каждого частного случая параллелепипеда будут свои.

Для произвольного параллелепипеда верно утверждение, что его объем равен абсолютной величине тройного скалярного произведения векторов трех сторон, исходящих из одной вершины. Однако формулы для вычисления объема произвольного параллелепипеда не существует.

Для прямоугольного параллелепипеда действуют следующие формулы:

V=a*b*c;
Sб=2*c*(a+b);
Sп=2*(a*b+b*c+a*c).

Где:

V — объем фигуры;
Sб — площадь боковой поверхности;
Sп — площадь полной поверхности;
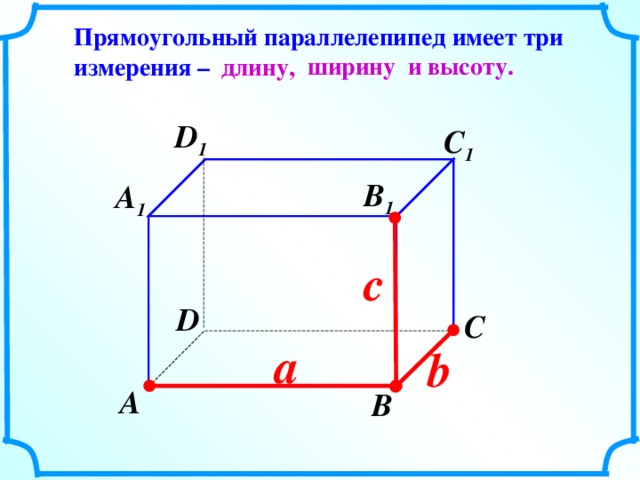
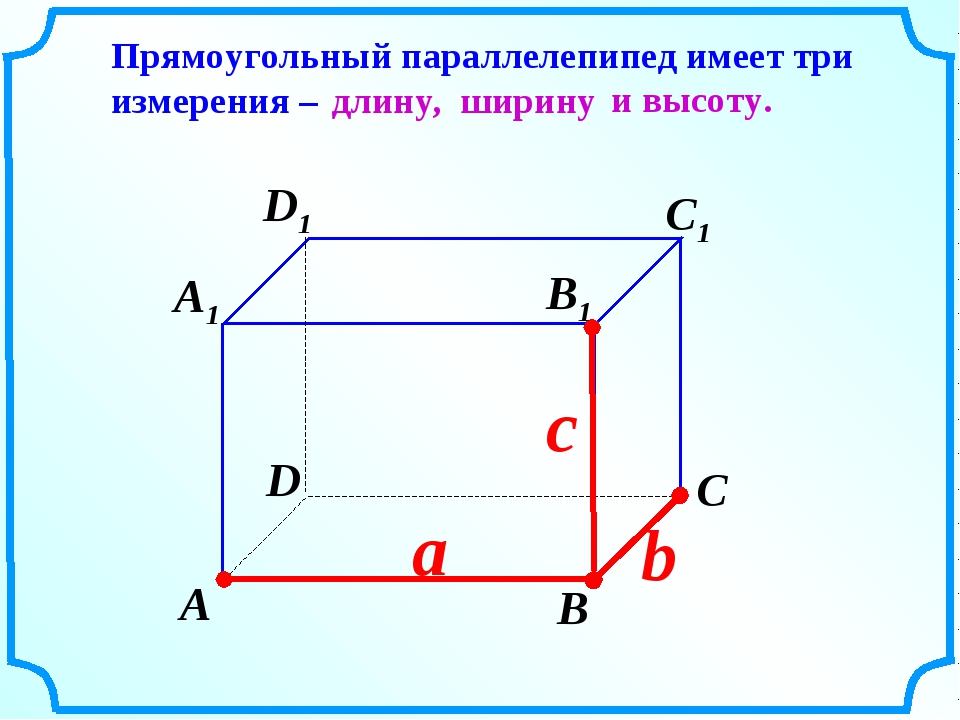
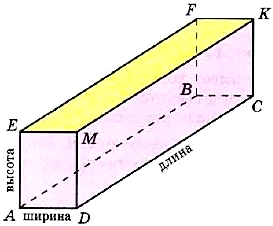
a — длина;
b — ширина;
c — высота.

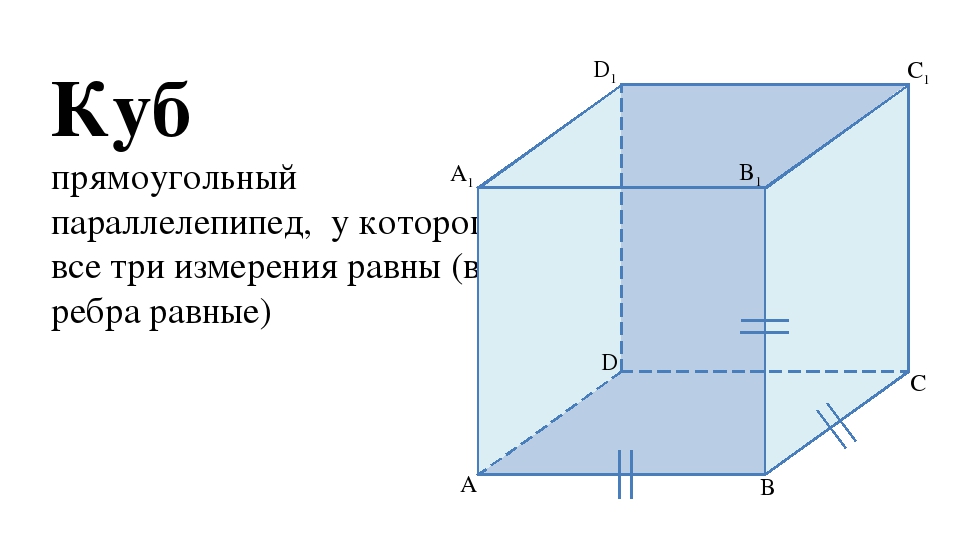
Еще одним частным случаем параллелепипеда, в котором все стороны — квадраты, является куб. Если любую из сторон квадрата обозначить буквой a, то для площади поверхности и объема данной фигуры можно будет использовать следующие формулы:

S=6*a*2;
V=3*а.

Где:

S — площадь фигуры,
V — объем фигуры,
a — длина грани фигуры.

Последняя рассматриваемая нами разновидность параллелепипеда – прямой параллелепипед. В чем разница между прямым параллелепипедом и прямоугольным параллелепипедом, спросите вы. Дело в том, что основанием прямоугольного параллелепипеда может быть любой параллелограмм, а основанием прямого – только прямоугольник. Если обозначить периметр основания, равный сумме длин всех сторон, как Po, а высоту обозначить буквой h, мы имеем право воспользоваться следующими формулами для вычисления объема и площадей полной и боковой поверхностей:

Sб=Ро*h;
Sп=Sб+2Sо;
V=Sо*h.

Вам также могут быть интересные следующие статьи:

Как найти площадь параллелепипеда
Что такое паралелепипет
Геометрические понятия

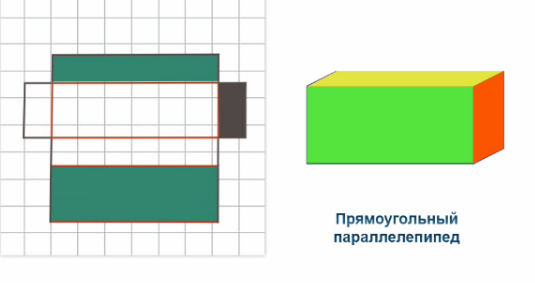
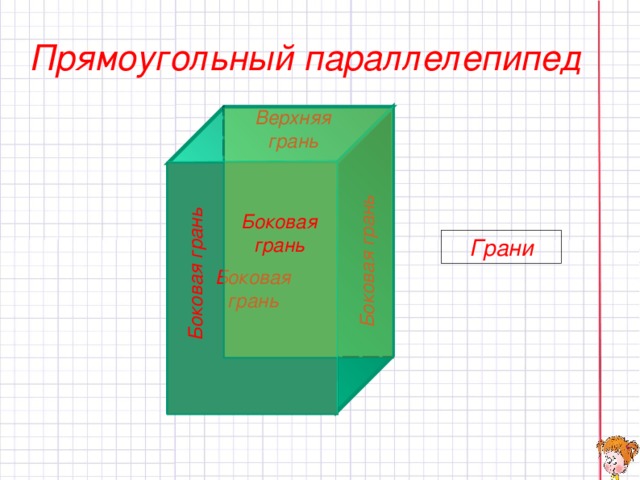
Прямоугольный параллелепипед

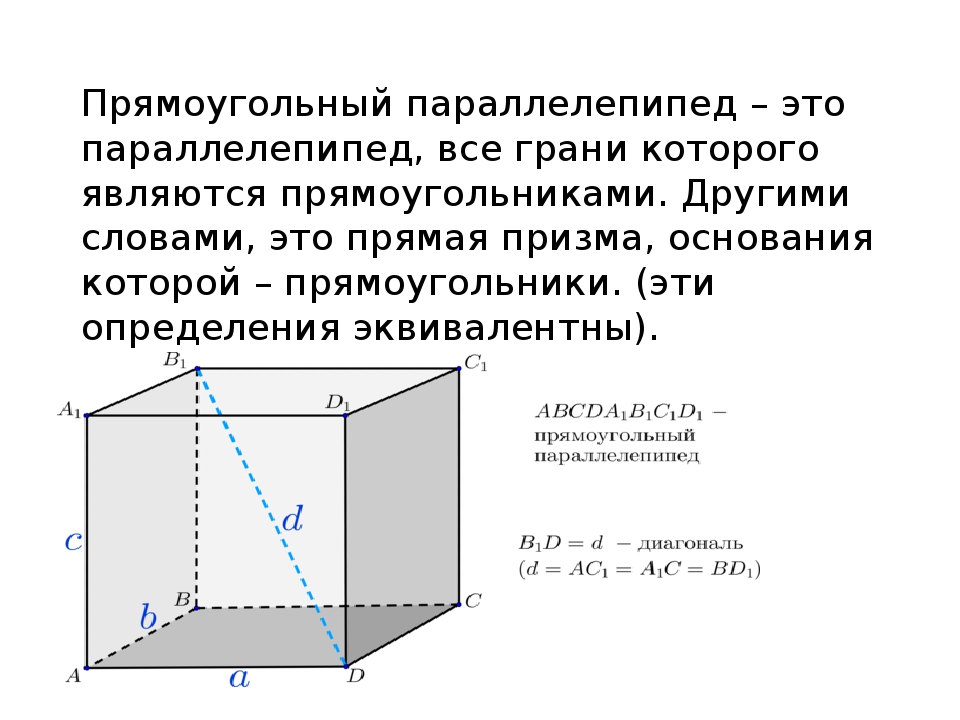
Прямоугольный параллелепипед – это такой прямой параллелепипед, у которого все грани являются прямоугольниками.

Достаточно посмотреть вокруг себя, и мы увидим, что окружающие нас предметы имеют форму похожую на параллелепипед. Они могут отличать по цвету, иметь массу дополнительных деталей, но если эти тонкости отбросить, то можно сказать, что например шкаф, коробка и т.д., имеют приблизительно одинаковую форму.

С понятием прямоугольного параллелепипеда мы сталкиваемся практически каждый день! Оглянитесь вокруг и скажите, где вы видите прямоугольные параллелепипеды? Посмотрите на книгу, ведь она как раз такой формы! Эту же форму имеют кирпич, спичечный коробок, деревянный брусок, и даже прямо сейчас вы находитесь внутри прямоугольного параллелепипеда, ведь классная комната – это ярчайшая интерпретация этой геометрической фигуры.

Задание: А какие примеры параллелепипеда вы можете назвать?

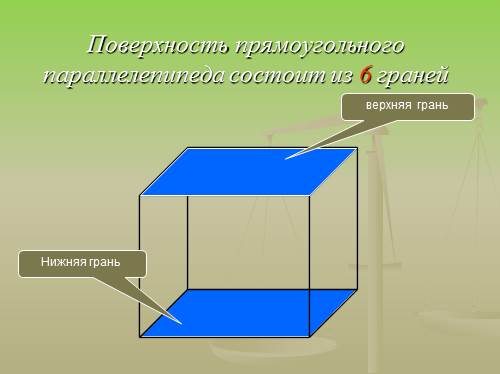
Давайте более тщательно рассмотрим прямоугольный параллелепипед. И что мы видим?

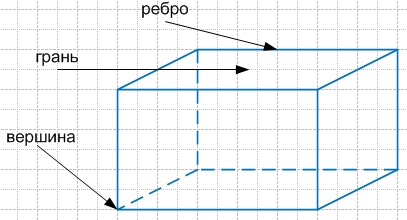
Во-первых, мы видим, что эта фигура образована из шести прямоугольников, которые являются гранями прямоугольного параллелепипеда;

Во-вторых, прямоугольный параллелепипед имеет восемь вершин и двенадцать ребер. Ребра прямоугольного параллелепипеда – это стороны его граней, а вершины параллелепипеда являются вершинами граней.

Задание:

1. Какое название носит каждая из граней прямоугольного параллелепипеда?
2. Благодаря каким параметрам можно измерить параллелограмм?
3. Дайте определение противоположных граней.

Свойства параллелепипеда

1. Противоположные грани параллелепипеда параллельны и равны.

(фигуры равны, то есть их можно совместить наложением)

Например:

АВСD = А1В1С1D1 (равные параллелограммы по определению),

АА1В1В = DD1С1С (так как АА1В1В и DD1С1С – противоположные грани параллелепипеда),

АА1D1D = ВВ1С1С (так как АА1D1D и ВВ1С1С – противоположные грани параллелепипеда).

2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

Диагонали параллелепипеда АС1, В1D, А1С, D1В пересекаются в одной точке О, и каждая диагональ делится этой точкой пополам (рис. 2).

Рис. 2 Диагонали параллелепипеда пересекаются и деляться точкой пересечения пополам.

3. Имеются три четверки равных и параллельных ребер параллелепипеда: 1 – АВ, А1В1, D1C1, DC, 2 – AD, A1D1, B1C1, BC, 3 – АА1, ВВ1, СС1, DD1.

Свойства прямоугольного параллелепипеда

1. В прямоугольном параллелепипеде все шесть граней прямоугольники.

АВСD и А1В1С1D1 – прямоугольники по определению.

2. Боковые ребра перпендикулярны основанию. Значит, все боковые грани прямоугольного параллелепипеда — прямоугольники.

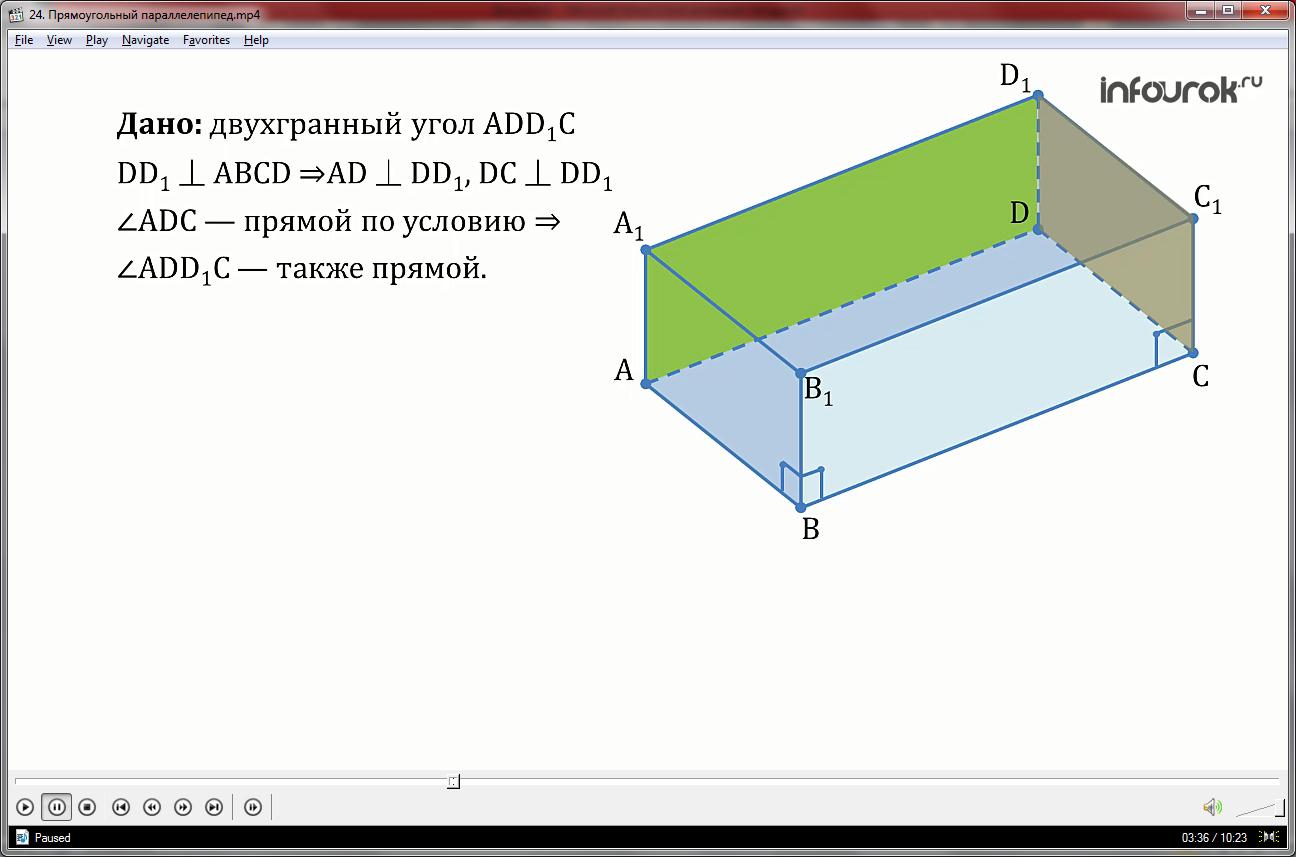
3. Все двугранные углы прямоугольного параллелепипеда прямые.

Рассмотрим, например, двугранный угол прямоугольного параллелепипеда с ребром АВ, т. е. двугранный угол между плоскостями АВВ1 и АВС.

АВ – ребро, точка А1 лежит в одной плоскости – в плоскости АВВ1, а точка D в другой – в плоскости А1В1С1D1. Тогда рассматриваемый двугранный угол можно еще обозначить следующим образом: ∠А1АВD.

Возьмем точку А на ребре АВ. АА1 – перпендикуляр к ребру АВ в плоскости АВВ1, AD перпендикуляр к ребру АВ в плоскости АВС. Значит, ∠А1АD – линейный угол данного двугранного угла. ∠А1АD = 90°, значит, двугранный угол при ребре АВ равен 90°.

∠(АВВ1, АВС) = ∠(АВ) = ∠А1АВD= ∠А1АD = 90°.

Аналогично доказывается, что любые двугранные углы прямоугольного параллелепипеда прямые.

Параллелотоп

Коксетер назвал обобщение параллелепипеда в высших измерениях параллелоэдром .

В частности, в n -мерном пространстве он называется n -мерным параллелоэдром или просто n -параллелоэдром. Таким образом, параллелограмм — это 2-параллелоэдр, а параллелепипед — это 3-параллелоэдр.

В более общем смысле параллелоэдр или параллелоэдр Вороного имеет параллельные и конгруэнтные противоположные грани. Итак, 2-параллелоэдр — это параллелогон, который также может включать в себя определенные шестиугольники, а 3-параллелоэдр — это параллелоэдр , включающий 5 типов многогранников.

В диагоналями из в п -parallelotope пересекаются в одной точке и делятся пополам этим пунктом. Инверсия в этой точке не меняет n -параллелоэдр. См. Также неподвижные точки групп изометрий в евклидовом пространстве .

Ребра, исходящие из одной вершины k -параллелоэдра, образуют k- каркас векторного пространства, и параллелоэдр можно восстановить из этих векторов, взяв линейные комбинации векторов с весами от 0 до 1.
(v1,…,vп){\ displaystyle (v_ {1}, \ ldots, v_ {n})}

П -VOLUME из п -parallelotope встроенное в котором может быть вычислено с помощью определителя Грама . В качестве альтернативы объем — это норма внешнего произведения векторов:
рм{\ Displaystyle \ mathbb {R} ^ {m}}м≥п{\ Displaystyle м \ geq п}

Vзнак равно‖v1∧⋯∧vп‖.{\ Displaystyle V = \ left \ | v_ {1} \ wedge \ cdots \ wedge v_ {n} \ right \ |.}

Если m = n , это составляет абсолютное значение определителя n векторов.

Еще одна формула для вычисления объема с п -parallelotope Р в , которого п + 1 вершины , является
рп{\ Displaystyle \ mathbb {R} ^ {п}}V,V1,…,Vп{\ Displaystyle V_ {0}, V_ {1}, \ ldots, V_ {n}}

Vол(п)знак равно|dет (V 1Т,V1 1Т,…,Vп 1Т)|,{\ Displaystyle {\ rm {Vol}} (P) = | {\ rm {det}} \ ( ^ {\ rm {T}}, ^ {\ rm {T}}, \ ldots, ^ {\ rm {T}}) |,}

где — вектор-строка, образованный конкатенацией и 1. Действительно, определитель не изменяется, если вычитается из ( i > 0 ), а размещение в последней позиции меняет только его знак.
Vя 1{\ displaystyle }Vя{\ displaystyle V_ {i}}V 1{\ displaystyle }Vя 1{\ displaystyle }V 1{\ displaystyle }

Кроме того , объем любого п — симплекс , который разделяет п сходящиеся ребра параллелепипеда имеет объем , равный единице 1 / п ! объема этого параллелоэдра.

Лексикография

Это слово появляется как parallelipipedon в переводе сэра Генри Биллингсли « Элементов» Евклида , датированного 1570 годом. В издании Cursus mathematicus 1644 года Пьер Эригон использовал правописание « параллелепипед» . Оксфордский словарь английского языка приводит современный параллелепипед , как первое появление в Уолтер Чарлтон в хорея gigantum (1663).

Словарь Чарльза Хаттона (1795 г.) показывает параллелепипед и параллелепипед , показывая влияние объединяющей формы параллело- , как если бы второй элемент был трубопроводом, а не эпипедоном . Ной Вебстер (1806 г.) включает орфографический параллелепипед . Оксфордский словарь английского языка издания 1989 г. описывает параллелепипед (и параллелепипед ) явно как неправильные формы, но они перечислены без комментариев в издании 2004 г., и даны только произношения с акцентом на пятый слог пи ( / paɪ / ).

Отказ от традиционного произношения скрыл различное разделение, предложенное греческими корнями, с epi- («он») и pedon («земля»), объединяющимися, чтобы дать epiped , плоскую «плоскость». Таким образом, грани параллелепипеда плоские, а противоположные грани параллельны.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладаем рядом важнейших свойств:

• во-первых, квадрат диагонали этой геометрической фигуры равняется сумме квадратов трех его основных параметров: высоты, ширины и длины.

• во-вторых, все его четыре диагонали абсолютно идентичны.

• в-третьих, если все три параметра параллелепипеда одинаковы, то есть длина, ширина и высота равны, то такой параллелепипед называют кубом, и все его грани будут равны одному и тому же квадрату.

Задание

1. Имеет ли прямоугольный параллелепипед равные грани? Если таковы имеются, то покажите их на рисунке.
2. Из каких геометрических форм состоят грани прямоугольного параллелепипеда?
3. Какое расположение имеют равные грани по отношению друг к другу?
4. Назовите количество пар равных граней данной фигуры.
5. Найдите в прямоугольном параллелепипеде ребра, которые обозначают его длину, ширину, высоту. Сколько вы их насчитали?

Задача

Чтобы красиво оформить подарок на день Рождения маме, Таня взяла коробку в форме прямоугольного параллелепипеда. Размер данной коробки 25см*35см*45см. Чтобы сделать эту упаковку красивой, Таня решила, оклеит ее красивой бумагой, стоимость которой 3 гривны за 1 дм2. Сколько нужно потратить денег на упаковочную бумагу?

Особые случаи по симметрии

Отношения подгруппы октаэдрической симметрии с центром инверсии

Частные случаи параллелепипеда

Форма	Куб	Квадратный кубоид	Тригональный трапецоэдр	Прямоугольный кубоид	Правая ромбическая призма	Правая параллелограммная призма	Косая ромбическая призма
Ограничения	азнак равнобзнак равноc{\ displaystyle a = b = c}αзнак равноβзнак равноγзнак равно90∘{\ Displaystyle \ альфа = \ бета = \ гамма = 90 ^ {\ circ}}	азнак равноб{\ displaystyle a = b}αзнак равноβзнак равноγзнак равно90∘{\ Displaystyle \ альфа = \ бета = \ гамма = 90 ^ {\ circ}}	азнак равнобзнак равноc{\ displaystyle a = b = c}αзнак равноβзнак равноγ{\ Displaystyle \ альфа = \ бета = \ гамма}	αзнак равноβзнак равноγзнак равно90∘{\ Displaystyle \ альфа = \ бета = \ гамма = 90 ^ {\ circ}}	азнак равноб{\ displaystyle a = b}αзнак равноβзнак равно90∘{\ Displaystyle \ альфа = \ бета = 90 ^ {\ circ}}	αзнак равноβзнак равно90∘{\ Displaystyle \ альфа = \ бета = 90 ^ {\ circ}}	азнак равноб{\ displaystyle a = b}αзнак равноβ{\ Displaystyle \ альфа = \ бета}
Симметрия	О _ч порядка 48	D _4ч порядка 16	D _3d заказ 12	D _2h порядка 8	C _2h порядка 4
Образ
Лица	6 квадратов	2 квадрата, 4 прямоугольника	6 ромбов	6 прямоугольников	4 прямоугольника, 2 ромба	4 прямоугольника, 2 параллелограмма	2 ромба, 4 параллелограмма

Параллелепипед с симметрией O _h известен как куб , имеющий шесть одинаковых квадратных граней.
Параллелепипед с симметрией D _4h известен как квадратный кубоид , который имеет две квадратные грани и четыре совпадающие прямоугольные грани.
Параллелепипед с симметрией D _3d известен как тригональный трапецоэдр , который имеет шесть конгруэнтных ромбических граней (также называемых изоэдральным ромбоэдром ).
Для параллелепипедов с симметрией D _{2h возможны} два случая:
- Прямоугольный кубоид : у него шесть прямоугольных граней (также называемых прямоугольным параллелепипедом или иногда просто кубоидом ).
- Правая ромбическая призма : у нее две ромбические грани и четыре конгруэнтных прямоугольных грани.

Примечание: частный случай полностью ромбической формы с двумя ромбическими гранями и четырьмя конгруэнтными квадратными гранями имеет то же имя и одну и ту же группу симметрии (D _2h , порядок 8).(азнак равнобзнак равноc){\ Displaystyle (а = Ь = с)}

Для параллелепипедов с симметрией C _{2h возможны} два случая:
- Правая параллелограммная призма : у нее четыре прямоугольных грани и две параллелограммные грани.
- Косая ромбическая призма : у нее две ромбические грани, а из остальных граней две соседние равны, а две другие тоже (две пары являются зеркальным отображением друг друга).

Задача 2

Рисунок

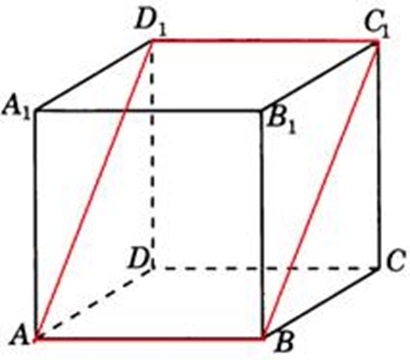
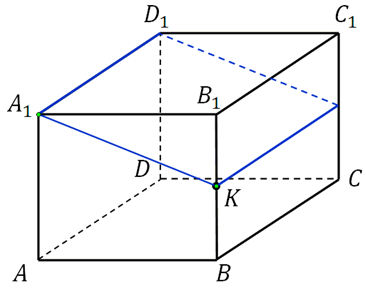
Дан куб АВСDА1В1С1D1 (рис. 8). Докажите, что плоскости АВС1 и А1В1D перпендикулярны.

Рис. 8

Доказательство:

Прямые ВС1 и В1С перпендикулярны как диагонали квадрата ВВ1С1С.

Прямая DC перпендикулярна плоскости ВВ1С1, а значит, и прямой ВС1, которая лежит в этой плоскости.

Имеем, прямая ВС1 перпендикулярна двум пересекающимся прямым В1С и DC плоскости, значит А1В1D. Значит, прямая ВС1 перпендикулярна плоскости А1В1D.

Плоскость АВС1 проходит через перпендикуляр ВС1 ко второй плоскости А1В1D, значит, плоскости АВС1 и А1В1D перпендикулярны по признаку, что и требовалось доказать.

Вред скандинавской ходьбы с палками

Вред может быть нанесен только в 2 случаях: если не соблюдать правильную технику (приведет к неверному распределению нагрузки) или заниматься при наличии медицинских ограничений. Этот любительский спорт имеет свои противопоказания:

сердечная недостаточность с выраженной гипоксией;
до 30 дней с момента перенесенного инфаркта и до 2 месяцев после инсульта;
выраженный варикоз нижних конечностей, тромбофлебит;
болезни легких с тяжелым течением, которые сопровождаются симптомами дыхательной недостаточности, либо объем легких снижен до 50%;
острые вирусные и инфекционные заболевания;
артериальная гипертензия;
стенокардия;
аритмия, сопровождающаяся учащенным сердечным ритмом.

При наличии данных заболеваний занятия финской ходьбой запрещены, т. к. они могут ухудшить состояние человека. Неправильная техника может привести к:

повреждению связочного аппарата и суставов;
чрезмерному перенапряжению мышц, после чего они еще долго будут болеть, могут появиться судороги и спазмы;
нарушениям сердца и сосудистой системы вплоть до появления аритмии и усугубления сердечной ишемии;
приступам головокружения, сильной усталости.

Чтобы не подвергать позвоночник и суставы чрезмерной нагрузке, необходимо постоянно следить за техникой выполнения

Особенно это важно делать новичкам, пока правильная поза и ритмичность движений не дойдут до автоматизма

Объем

Параллелепипед, образованный тремя векторами

Параллелепипед можно рассматривать как наклонную призму с параллелограммом в качестве основания. Следовательно, объем параллелепипеда — это произведение площади основания и высоты (см. Диаграмму). С участием
V{\ displaystyle V}B{\ displaystyle B}час{\ displaystyle h}

Bзнак равно|а→|⋅|б→|⋅грех⁡γзнак равно|а→×б→| {\ displaystyle B = | {\ vec {a}} | \ cdot | {\ vec {b}} | \ cdot \ sin \ gamma = | {\ vec {a}} \ times {\ vec {b}} | ~}(где — угол между векторами и ), иγ{\ displaystyle \ gamma}а→{\ displaystyle {\ vec {a}}}б→{\ displaystyle {\ vec {b}}}

часзнак равно|c→|⋅|потому что⁡θ | {\ displaystyle h = | {\ vec {c}} | \ cdot | \ cos \ theta ~ | ~}(где угол между вектором и нормалью к основанию), получаем:θ{\ displaystyle \ theta}c→{\ displaystyle {\ vec {c}}}

Vзнак равноB⋅часзнак равно(|а→||б→|грех⁡γ)⋅|c→||потому что⁡θ |знак равно|а→×б→| |c→| |потому что⁡θ |знак равно|(а→×б→)⋅c→| .{\ displaystyle V = B \ cdot h = (| {\ vec {a}} || {\ vec {b}} | \ sin \ gamma) \ cdot | {\ vec {c}} || \ cos \ theta ~ | = | {\ vec {a}} \ times {\ vec {b}} | ~ | {\ vec {c}} | ~ | \ cos \ theta ~ | = | ({\ vec {a}} \ раз {\ vec {b}}) \ cdot {\ vec {c}} | ~.}

Смешанное произведение трех векторов называется тройным произведением . Это можно описать определителем . Следовательно, объем равен:
а→знак равно(а1,а2,а3)Т, б→знак равно(б1,б2,б3)Т, c→знак равно(c1,c2,c3)Т,{\ displaystyle {\ vec {a}} = (a_ {1}, a_ {2}, a_ {3}) ^ {T}, ~ {\ vec {b}} = (b_ {1}, b_ {2 }, b_ {3}) ^ {T}, ~ {\ vec {c}} = (c_ {1}, c_ {2}, c_ {3}) ^ {T},}

(V1) .Vзнак равно|Detа1б1c1а2б2c2а3б3c3|{\ displaystyle \ quad V = \ left | \ det {\ begin {bmatrix} a_ {1} & b_ {1} & c_ {1} \\ a_ {2} & b_ {2} & c_ {2} \\ a_ {3} & b_ {3} & c_ {3} \ end {bmatrix}} \; \ right |}

Альтернативное представление объема использует только геометрические свойства (углы и длины кромок):

(V2) ,Vзнак равноабc1+2потому что⁡(α)потому что⁡(β)потому что⁡(γ)-потому что2⁡(α)-потому что2⁡(β)-потому что2⁡(γ){\ displaystyle \ quad V = abc {\ sqrt {1 + 2 \ cos (\ alpha) \ cos (\ beta) \ cos (\ gamma) — \ cos ^ {2} (\ alpha) — \ cos ^ {2 } (\ beta) — \ cos ^ {2} (\ gamma)}}}

где и — длины ребер.
αзнак равно∠(б→,c→),βзнак равно∠(а→,c→),γзнак равно∠(а→,б→), {\ displaystyle \ \ alpha = \ angle ({\ vec {b}}, {\ vec {c}}), \; \ beta = \ angle ({\ vec {a}}, {\ vec {c}} ), \; \ gamma = \ angle ({\ vec {a}}, {\ vec {b}}), \}а,б,c{\ displaystyle a, b, c}

Доказательство (V2)

Доказательство (V2) использует и :

Позвольте быть 3×3-матрицей, столбцы которой — векторы (см. Выше). Тогда верно следующее:
M{\ displaystyle M}а→,б→,c→{\ displaystyle {\ vec {a}}, {\ vec {b}}, {\ vec {c}}}

V2знак равно(DetM)2знак равноDetMDetMзнак равноDetMТDetMзнак равноDet(MТM){\ Displaystyle V ^ {2} = (\ Det M) ^ {2} = \ Det M \ Det M = \ Det M ^ {T} \ Det M = \ Det (M ^ {T} M)}

знак равноDetа→⋅а→а→⋅б→а→⋅c→б→⋅а→б→⋅б→б→⋅c→c→⋅а→c→⋅б→c→⋅c→знак равно а2б2c2(1+2потому что⁡(α)потому что⁡(β)потому что⁡(γ)-потому что2⁡(α)-потому что2⁡(β)-потому что2⁡(γ)).{\ displaystyle = \ det {\ begin {bmatrix} {\ vec {a}} \ cdot {\ vec {a}} и {\ vec {a}} \ cdot {\ vec {b}} и {\ vec { a}} \ cdot {\ vec {c}} \\ {\ vec {b}} \ cdot {\ vec {a}} & {\ vec {b}} \ cdot {\ vec {b}} & {\ vec {b}} \ cdot {\ vec {c}} \\ {\ vec {c}} \ cdot {\ vec {a}} и {\ vec {c}} \ cdot {\ vec {b}} & {\ vec {c}} \ cdot {\ vec {c}} \ end {bmatrix}} = \ a ^ {2} b ^ {2} c ^ {2} \; \ left (1 + 2 \ cos ( \ alpha) \ cos (\ beta) \ cos (\ gamma) — \ cos ^ {2} (\ alpha) — \ cos ^ {2} (\ beta) — \ cos ^ {2} (\ gamma) \ right ).}

(Используется последний шаг )
а→⋅а→знак равноа2,…,а→⋅б→знак равноабпотому что⁡γ,а→⋅c→знак равноаcпотому что⁡β,б→⋅c→знак равнобcпотому что⁡α,…{\ displaystyle \ {\ vec {a}} \ cdot {\ vec {a}} = a ^ {2}, …, \; {\ vec {a}} \ cdot {\ vec {b}} = ab \ cos \ gamma, \; {\ vec {a}} \ cdot {\ vec {c}} = ac \ cos \ beta, \; {\ vec {b}} \ cdot {\ vec {c}} = bc \ cos \ alpha, …}

Соответствующий тетраэдр

Объем любого тетраэдра, который имеет три сходящихся ребра параллелепипеда, равен одной шестой объема этого параллелепипеда (см. ).

Прямоугольный параллелепипед

Определение. Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию. Основания являются прямоугольниками.

Параллелепипед АВСDА1В1С1D1 – прямоугольный (рис. 4), если:

1. АА1⊥ АВСD (боковое ребро перпендикулярно плоскости основания, то есть параллелепипед прямой).

2. ∠ВАD = 90°, т. е. в основании лежит прямоугольник.

Рис. 4 Прямоугольный параллелепипед

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда. Но есть дополнительные свойства, которые выводятся из определения прямоугольного параллелепипеда.

Итак, прямоугольный параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию. Основание прямоугольного параллелепипеда — прямоугольник.

Основные формулы

Прямой параллелепипед

Площадь боковой поверхности
S_б=Р_о*h, где Р_о — периметр основания, h — высота

Площадь полной поверхности
S_п=S_б+2S_о, где S_о — площадь основания

Объём
V=S_о*h

Прямоугольный параллелепипед

Основная статья: Прямоугольный параллелепипед

Площадь боковой поверхности
S_б=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда

Площадь полной поверхности
S_п=2(ab+bc+ac)

Объём
V=abc, где a, b, c — измерения прямоугольного параллелепипеда.

Куб

Площадь поверхности: S=6a2{\displaystyle S=6a^{2}}Объём: V=a3{\displaystyle V=a^{3}}, где a{\displaystyle a} — ребро куба.

Произвольный параллелепипед

Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры. Объём параллелепипеда равен абсолютной величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины. Соотношение между длинами сторон параллелепипеда и углами между ними даёт утверждение, что определитель Грама указанных трёх векторов равен квадрату их смешанного произведения.

Примеры решения типовых заданий ЕГЭ

Задание 1.

Дано: прямоугольный параллелепипед с измерениями 3, 4 и 12 см.Необходимо найти длину одной из главных диагоналей фигуры.Решение: Любое решение геометрической задачи должно начинаться с построения правильного и четкого чертежа, на котором будет обозначено «дано» и искомая величина. На рисунке ниже приведен пример правильного оформления условий задания.

Рассмотрев сделанный рисунок и вспомнив все свойства геометрического тела, приходим к единственно верному способу решения. Применив 4 свойство параллелепипеда, получим следующее выражение:

После несложных вычислений получим выражение b2=169, следовательно, b=13. Ответ задания найден, на его поиск и чертеж необходимо потратить не более 5 минут.

Задание 2.

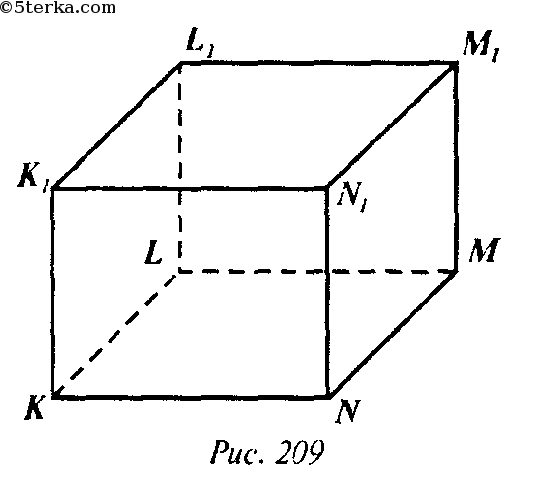
Дано: наклонный параллелепипед с боковым ребром 10 см, прямоугольник KLNM с измерениями 5 и 7 см, являющийся сечением фигуры параллельным указанному ребру.Необходимо найти площадь боковой поверхности четырехугольной призмы.Решение: Сначала необходимо зарисовать дано.

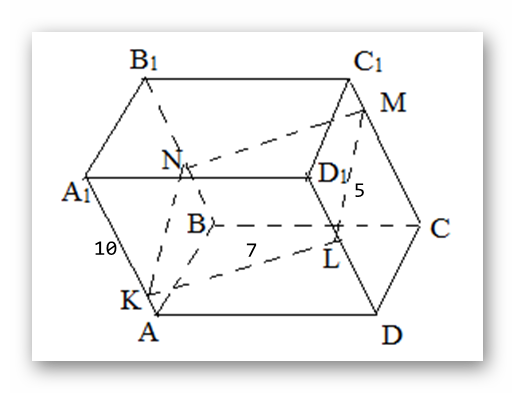
Для решения данного задания необходимо применить смекалку. Из рисунка видно, что стороны KL и AD – неравны, как и пара ML и DC. Однако, периметры данных параллелограммов очевидно равны.

Следовательно, боковая площадь фигуры будет равна площади сечения помноженной на ребро AA1, так как по условию ребро перпендикулярно сечению. Ответ: 240 см2.

Идеальный параллелепипед

Идеально параллелепипед представляет собой параллелепипед с целым числом длиной ребер, гранями диагоналями и пространственными диагоналями . В 2009 году было показано, что существуют десятки идеальных параллелепипедов, что явилось ответом на открытый вопрос Ричарда Гая . В одном примере есть края 271, 106 и 103, второстепенные диагонали лица 101, 266 и 255, диагонали основной грани 183, 312 и 323 и диагонали пространства 374, 300, 278 и 272.

Известны идеальные параллелепипеды с двумя прямоугольными гранями. Но неизвестно, существуют ли такие, у которых все грани прямоугольные; такой случай можно было бы назвать идеальным кубоидом .

Основные формулы

Прямой параллелепипед

Площадь боковой поверхности
S_б=Р_о*h, где Р_о — периметр основания, h — высота

Площадь полной поверхности
S_п=S_б+2S_о, где S_о — площадь основания

Объём
V=S_о*h

Прямоугольный параллелепипед

Основная статья: Прямоугольный параллелепипед

Площадь полной поверхности
S_п=2(ab+bc+ac)

Объём
V=abc, где a, b, c — измерения прямоугольного параллелепипеда.

Куб

Площадь поверхности: S=6a2{\displaystyle S=6a^{2}}Объём: V=a3{\displaystyle V=a^{3}}, где a{\displaystyle a} — ребро куба.

Произвольный параллелепипед

Прямоугольный параллелепипед

Можно выделить два частных случая понятия параллелепипеда. Один из них — понятие прямоугольного параллелепипеда.

Определение 2

Параллелепипед, у которого в основаниях лежат прямоугольники и все двугранные углы равны ${90}^0$ называется прямоугольным (рис. 4).

Рисунок 4. Прямоугольный параллелепипед

Прямоугольный параллелепипед обладает теми же свойствами, что и произвольный, однако он помимо этого обладает отдельным свойством.

Теорема 3

Сумма квадратов трех измерений (высота, длина и ширина) равняется квадрату его диагонали.

Математически это можно записать следующим образом:

Рисунок 5.

Доказательство.

Рассмотрим рисунок 5. Докажем, для примера, что

Рассмотрим треугольник $ADC$. По теореме Пифагора, имеем

Так как $ABCD$ — прямоугольник, то $DC=AB$, следовательно

Рассмотрим треугольник $ACC_1$. По теореме Пифагора, имеем

Так как ${CC}_1=AA_1$, то

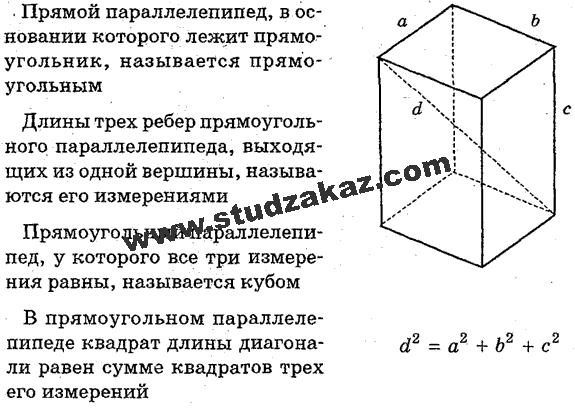
Теорема

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Примечание. Длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда, являются измерениями прямоугольного параллелепипеда. Их иногда называют длина, ширина, высота.

Дано: АВСDА1В1С1D1 – прямоугольный параллелепипед (рис. 5).

Доказать: .

Рис. 5 Прямоугольный параллелепипед

Доказательство:

Прямая СС1 перпендикулярна плоскости АВС, а значит, и прямой АС. Значит, треугольник СС1А – прямоугольный. По теореме Пифагора:

Рассмотрим прямоугольный треугольник АВС. По теореме Пифагора:

Но ВС и AD – противоположные стороны прямоугольника. Значит, ВС = AD. Тогда: