Что такое модель в информатике? виды, примеры

Жёсткие и мягкие модели

Гармонический осциллятор — пример так называемой «жёсткой» модели. Она получена в результате сильной идеализации реальной физической системы. Свойства гармонического осциллятора качественно изменяются малыми возмущениями. Например, если добавить в правую часть малое слагаемое −εx˙{\displaystyle -\varepsilon {\dot {x}}} (трение) (ε>{\displaystyle \varepsilon >0} — некоторый малый параметр), то получим экспоненциально затухающие колебания, если изменить знак добавочного слагаемого (εx˙){\displaystyle (\varepsilon {\dot {x}})} то трение превратится в накачку и амплитуда колебаний будет экспоненциально возрастать.

Для решения вопроса о применимости жёсткой модели необходимо понять, насколько существенными являются факторы, которыми мы пренебрегли. Нужно исследовать мягкие модели, получающиеся малым возмущением жёсткой. Для гармонического осциллятора они могут задаваться, например, следующим уравнением:

mx¨=−kx+εf(x,x˙){\displaystyle m{\ddot {x}}=-kx+\varepsilon f(x,{\dot {x}})}.

Здесь f(x,x˙){\displaystyle f(x,{\dot {x}})} — некоторая функция, в которой может учитываться сила трения или зависимость коэффициента жёсткости пружины от степени её растяжения. Явный вид функции f{\displaystyle f} нас в данный момент не интересует.

Если мы докажем, что поведение мягкой модели принципиально не отличается от поведения жёсткой (вне зависимости от явного вида возмущающих факторов, если они достаточно малы), задача сведётся к исследованию жёсткой модели. В противном случае применение результатов, полученных при изучении жёсткой модели, потребует дополнительных исследований.

Если система сохраняет своё качественное поведение при малом возмущении, говорят, что она структурно устойчива. Гармонический осциллятор — пример структурно-неустойчивой (негрубой) системы. Тем не менее, эту модель можно применять для изучения процессов на ограниченных промежутках времени.

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

Требования

Очень важно знать, что к данному виду модели предъявляют некоторые требования, среди которых — приведенные в таблице ниже

Универсальность
Это свойство позволяет использовать одну и ту же модель при описании однотипных групп объектов

Важно отметить, что универсальные математические модели совершенно не зависят от физической природы исследуемого объекта
Адекватность
Здесь важно понимать, что данное свойство позволяет максимально правильно воспроизводить реальные процессы. В задачах эксплуатации очень важно данное свойство математического моделирования

Примером модели может служить процесс оптимизации использования газовой системы. В данном случае сопоставляются расчетные и фактические показатели, в результате проверяется правильность составленной модели
Точность
Данное требование подразумевает совпадение значений, которые мы получаем при расчете математической модели и входных параметров нашего реального объекта
Экономичность
Требование экономичности, предъявляемое к любой математической модели, характеризуется затратами на реализацию. Если работа с моделью осуществляется ручным способом, то необходимо рассчитать, сколько времени уйдет на решение одной задачи при помощи данной математической модели. Если речь идет об автоматизированном проектировании, то рассчитываются показатели затрат времени и памяти компьютера

Построение экономико-математической модели

Мы уже ранее сказали о том, что такое экономико-математическая модель. Пример решения задачи будет рассмотрен прямо сейчас. Нам необходимо произвести анализ производственной программы для выявления резерва повышения прибыли при сдвиге в ассортименте.

Полностью рассматривать задачу мы не будем, а только построим экономико-математическую модель. Критерий нашей задачи – максимизация прибыли. Тогда функция имеет вид: Л=р1*х1+р2*х2…, стремящееся к максимуму. В данной модели р – это прибыль за единицу, х – это количество производимых единиц. Далее, основываясь на построенной модели, необходимо произвести расчеты и подвести итог.

Понятие «модель»

Мы часто слышим слово «модель». Что же это такое? Данный термин имеет множество определений, вот только три из них:

специфический объект, который создается для получения и хранения информации, отражающий некоторые свойства или характеристики и так далее оригинала данного объекта (этот специфический объект может выражаться в разной форме: мысленный, описание при помощи знаков и так далее);
еще под моделью подразумевается отображение какой-либо конкретной ситуации, жизненной или управленческой;
моделью может служить уменьшенная копия какого-либо объекта (они создаются для более подробного изучения и анализа, так как модель отражает структуру и взаимосвязи).

Исходя из всего, что было сказано ранее, можно сделать небольшой вывод: модель позволяет подробно изучить сложную систему или объект.

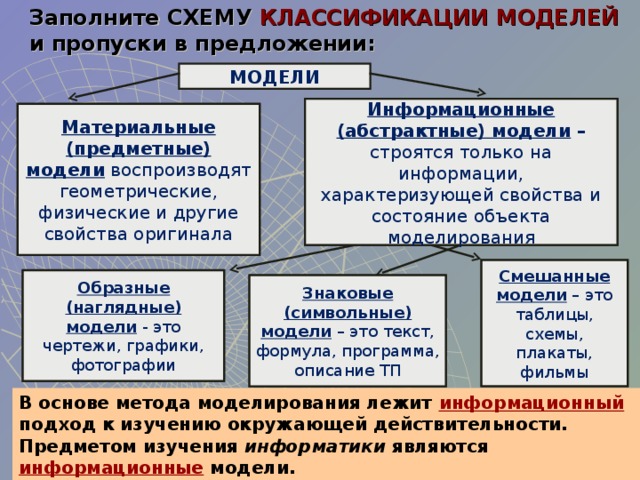
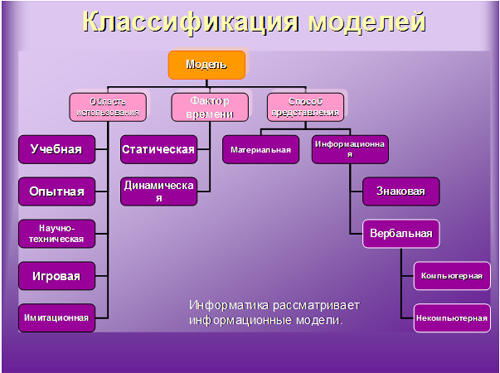
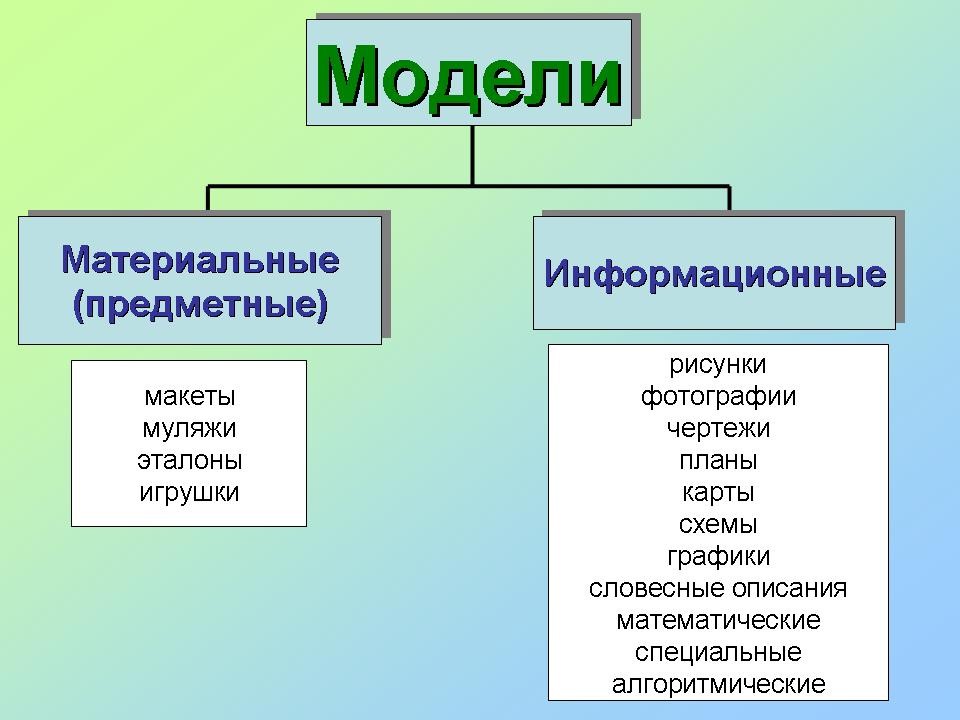
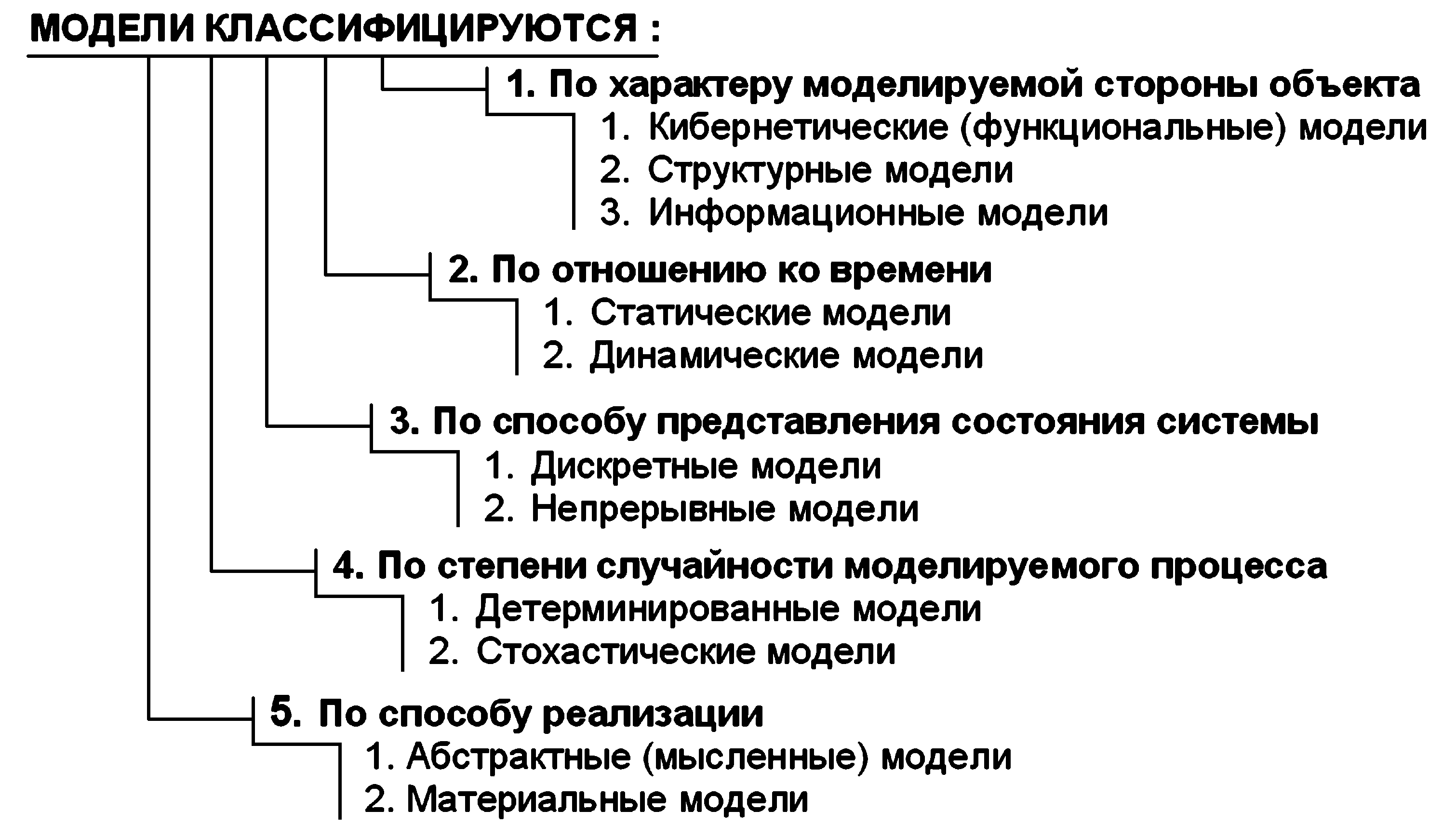
Все модели можно классифицировать по ряду признаков:

по области использования (учебные, опытные, научно-технические, игровые, имитационные);
по динамике (статические и динамические);
по отрасли знаний (физические, химические, географические, исторические, социологические, экономические, математические);
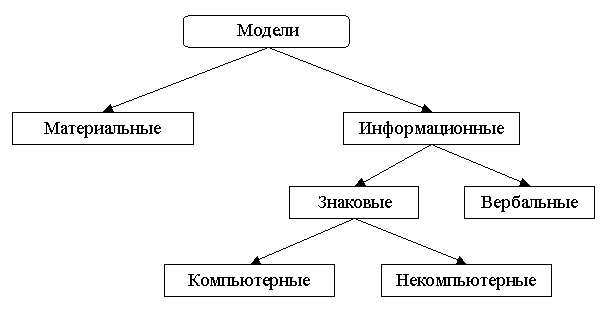
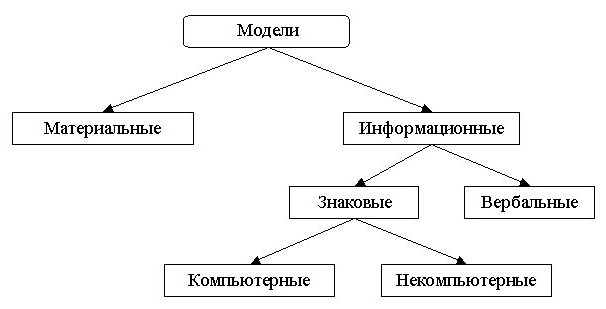
по способу представления (материальные и информационные).

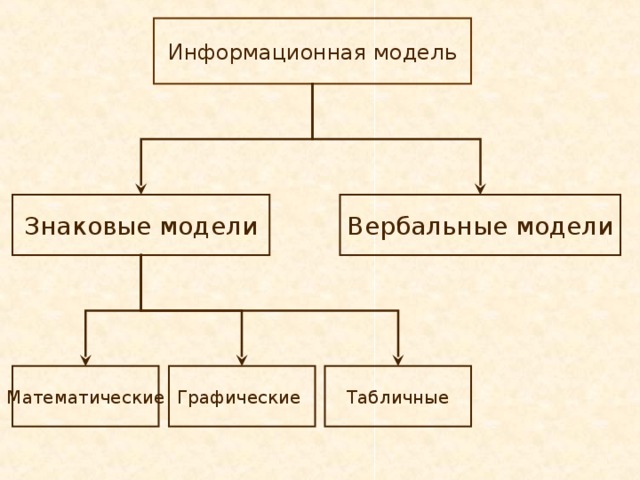
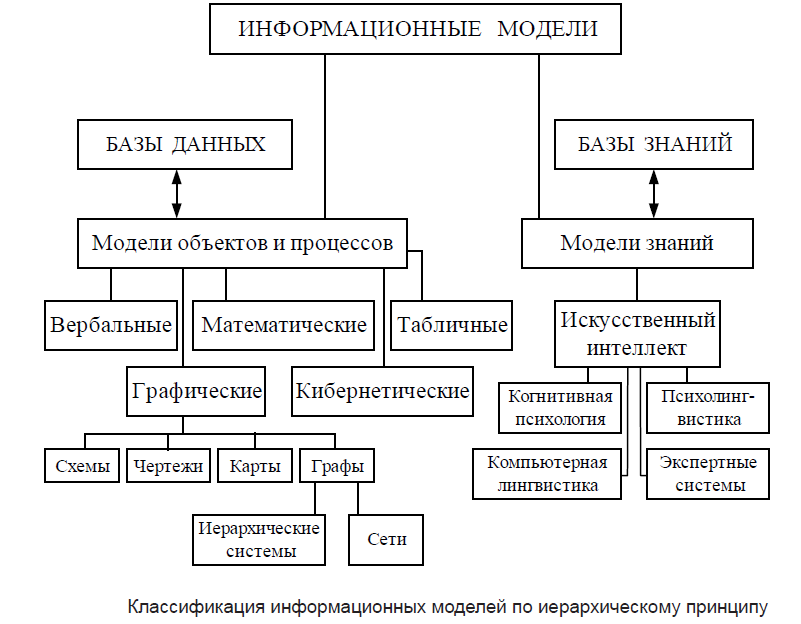
Информационные модели, в свою очередь, делятся на знаковые и вербальные. А знаковые — на компьютерные и некомпьютерные. Теперь перейдем к подробному рассмотрению примеров математической модели.

Область применения моделей

В процессе моделирования реальные объекты – прототипы заменяются их искусственными образцами – моделями, в которых ярко выражены исследуемые свойства, и не отражены свойства незначительные или не подлежащие изучению. Свойства объекта, раскрываемые с помощью модели, называются существенными.

Процесс, в результате которого создаются и исследуются модели, называется моделированием.

К моделированию прибегают, когда исследовать реальный прототип путем измерения или наблюдения нет возможности. Так, моделируют процессы, происходящие в объекте изучения, слишком быстро, такие как газодинамические процессы при определенных условиях, или процессы, которые длятся по времени столько, что не хватит и ста лет, чтобы их наблюдать, например, процессы движения земной коры.

Создают модели также и для объектов мегамира и микромира, например, всем известен глобус – модель планеты Земля, а также модель микроскопичного атома.

Популярным цифровым глобусом, который в реальном виде показывает поверхность Земли, является продукт Google Earth одноименной компании Google. Планета Земля является виртуальной моделью, в которой используются высокоточные изображения, полученные в результате спутниковой и аэрофотосъемки.

Рис. 1. Модель Земли.

Целесообразно создавать модели для реальных объектов, слишком дорогих в производстве, а также объектов, опасных для окружающих.

Дополнительные примеры

Модель Мальтуса

Согласно модели, предложенной Мальтусом, скорость роста пропорциональна текущему размеру популяции, то есть описывается дифференциальным уравнением:

x˙=αx{\displaystyle {\dot {x}}=\alpha x},

где α{\displaystyle \alpha } — некоторый параметр, определяемый разностью между рождаемостью и смертностью. Решением этого уравнения является экспоненциальная функция x(t)=xeαt{\displaystyle x(t)=x_{0}e^{\alpha t}}. Если рождаемость превосходит смертность (α>{\displaystyle \alpha >0}), размер популяции неограниченно и очень быстро возрастает. В действительности этого не может происходить из-за ограниченности ресурсов. При достижении некоторого критического объёма популяции модель перестаёт быть адекватной, поскольку не учитывает
ограниченность ресурсов. Уточнением модели Мальтуса может служить логистическая модель, которая описывается дифференциальным уравнением Ферхюльста:

x˙=α(1−xxs)x{\displaystyle {\dot {x}}=\alpha \left(1-{\frac {x}{x_{s}}}\right)x},

где xs{\displaystyle x_{s}} — «равновесный» размер популяции, при котором рождаемость в точности компенсируется смертностью. Размер популяции в такой модели стремится к равновесному значению xs{\displaystyle x_{s}}, причём такое поведение структурно устойчиво.

Система хищник-жертва

Основная статья: Система «хищник-жертва»

Допустим, что на некоторой территории обитают два вида животных: кролики (питающиеся растениями) и лисы (питающиеся кроликами). Пусть число кроликов x{\displaystyle x}, число лис y{\displaystyle y}. Используя модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имя модели Лотки — Вольтерры:

{x˙=(α−cy)xy˙=(−β+dx)y{\displaystyle {\begin{cases}{\dot {x}}=(\alpha -cy)x\\{\dot {y}}=(-\beta +dx)y\end{cases}}}

Поведение данной системы не является структурно устойчивым: малое изменение параметров модели (например, учитывающее ограниченность ресурсов, необходимых кроликам) может привести к качественному изменению поведения.

При некоторых значениях параметров эта система имеет равновесное состояние, когда число кроликов и лис постоянно. Отклонение от этого состояния приводит к постепенно затухающим колебаниям численности кроликов и лис.

Возможна и противоположная ситуация, когда любое малое отклонение от положения равновесия приведёт к катастрофическим последствиям, вплоть до полного вымирания одного из видов. На вопрос о том, какой из этих сценариев реализуется, модель Вольтерры — Лотки ответа не даёт: здесь требуются дополнительные исследования.

Примеры

Диаграмма состояний для М

M = ( Q , Σ, δ, q , F ), где

Q = { S ₁ , S ₂ },
Σ = {0, 1},
q = S ₁ ,
F = { S ₁ } и
δ определяется следующей таблицей переходов состояний :

	1
S ₁	S ₂	S ₁
S ₂	S ₁	S ₂

Состояние S ₁ означает, что до сих пор на входе было четное количество нулей, а S ₂ означает нечетное число. 1 на входе не меняет состояние автомата. Когда ввод завершается, состояние покажет, содержал ли ввод четное число нулей или нет. Если вход содержал четное количество нулей, M завершит работу в состоянии S ₁ , состоянии принятия, поэтому входная строка будет принята.

Язык, распознаваемый буквой M, — это обычный язык, задаваемый регулярным выражением 1 * (0 (1 *) 0 (1 *)) *, где «*» — звезда Клини , например, 1 * обозначает любое неотрицательное число ( возможно ноль) символов «1».

Многие повседневные действия, выполняемые без мысли, основаны на математических моделях. Проекция географической карты региона Земли на небольшую плоскую поверхность — это модель, которую можно использовать для многих целей, таких как планирование путешествий.
Еще одно простое действие — это прогнозирование положения транспортного средства по его начальному положению, направлению и скорости движения с использованием уравнения, согласно которому пройденное расстояние является произведением времени и скорости. При более формальном использовании это известно как мертвая расплата . Таким образом, математическое моделирование не обязательно требует формальной математики; было показано, что животные используют мертвый счет.
Рост населения . Простая (хотя и приблизительная) модель роста населения — это мальтузианская модель роста . Немного более реалистичной и широко используемой моделью роста населения является логистическая функция и ее расширения.
Модель частицы в потенциальном поле . В этой модели мы рассматриваем частицу как точку массы, которая описывает траекторию в пространстве, которая моделируется функцией, дающей ее координаты в пространстве как функцию времени. Потенциальное поле задается функцией, а траектория, то есть функцией , является решением дифференциального уравнения:Vр3→р{\ Displaystyle V \!: \ mathbb {R} ^ {3} \! \ rightarrow \ mathbb {R}}рр→р3{\ Displaystyle \ mathbf {r} \!: \ mathbb {R} \ rightarrow \ mathbb {R} ^ {3}}

-d2р(т)dт2мзнак равно∂Vр(т)∂ИксИкс^+∂Vр(т)∂yy^+∂Vр(т)∂zz^,{\ displaystyle — {\ frac {\ mathrm {d} ^ {2} \ mathbf {r} (t)} {\ mathrm {d} t ^ {2}}} m = {\ frac {\ partial V } {\ partial x}} \ mathbf {\ hat {x}} + {\ frac {\ partial V } {\ partial y}} \ mathbf {\ hat {y}} + {\ frac {\ partial V } {\ partial z}} \ mathbf {\ hat {z}},}

это можно также записать как:

мd2р(т)dт2знак равно-∇Vр(т).{\ displaystyle m {\ frac {\ mathrm {d} ^ {2} \ mathbf {r} (t)} {\ mathrm {d} t ^ {2}}} = — \ nabla V .}

Обратите внимание, что эта модель предполагает, что частица является точечной массой, что, как известно, неверно во многих случаях, когда мы используем эту модель; например, как модель движения планет.

Модель рационального поведения потребителя . В этой модели мы предполагаем, что потребитель сталкивается с выбором из n товаров, обозначенных 1,2, …, n, каждый с рыночной ценой p 1 , p 2 , …, p n . Предполагается, что потребитель имеет порядковую функцию полезности U (порядковую в том смысле, что имеет значение только знак различий между двумя полезностями, а не уровень каждой полезности), зависящую от количества товаров x 1 , x 2 , …, x n израсходовано. Модель также предполагает, что у потребителя есть бюджет M, который используется для покупки вектора x 1 , x 2 , …, x n таким образом, чтобы максимизировать U ( x 1 , x 2 , …, x п ). Тогда проблема рационального поведения в этой модели становится проблемой математической оптимизации , а именно:

МаксимумU(Икс1,Икс2,…,Иксп){\ Displaystyle \ макс. U (x_ {1}, x_ {2}, \ ldots, x_ {n})}

при условии:

∑язнак равно1ппяИкся≤M.{\ displaystyle \ sum _ {i = 1} ^ {n} p_ {i} x_ {i} \ leq M.}

Икся≥∀я∈{1,2,…,п}{\ displaystyle x_ {i} \ geq 0 \; \; \; \ forall i \ in \ {1,2, \ ldots, n \}}

Эта модель использовалась в самых разных экономических контекстах, например, в теории общего равновесия, чтобы показать существование и эффективность экономического равновесия по Парето .

Модель определения соседей — это модель, которая объясняет образование грибов из изначально хаотической грибковой сети.
В информатике математические модели могут использоваться для моделирования компьютерных сетей.
В механике математические модели могут использоваться для анализа движения модели ракеты.

Модель

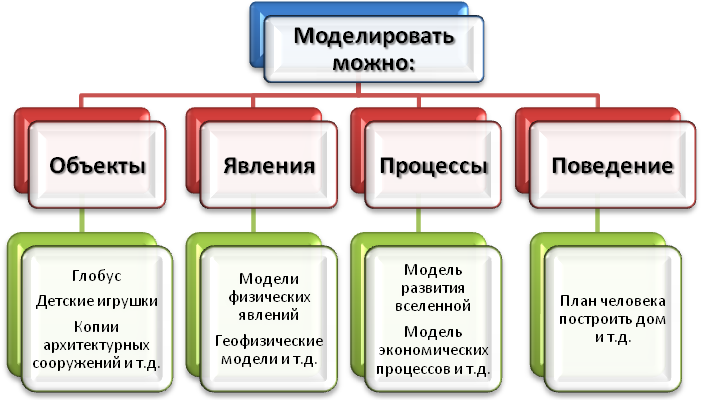
Моделирование в информатике – это составление образа какого-либо реально существующего объекта, который отражает все существенные признаки и свойства. Модель для решения задачи необходима, так как она, собственно, и используется в процессе решения.

В школьном курсе информатики тема моделирования начинает изучаться еще в шестом классе. В самом начале детей необходимо познакомить с понятием модели. Что это такое?

Упрощенное подобие объекта;
Уменьшенная копия реального объекта;
Схема явления или процесса;
Изображение явления или процесса;
Описание явления или процесса;
Физический аналог объекта;
Информационный аналог;
Объект-заменитель, отражающий свойства реального объекта и так далее.

Модель – это очень широкое понятие, как это уже стало ясно из вышеперечисленного

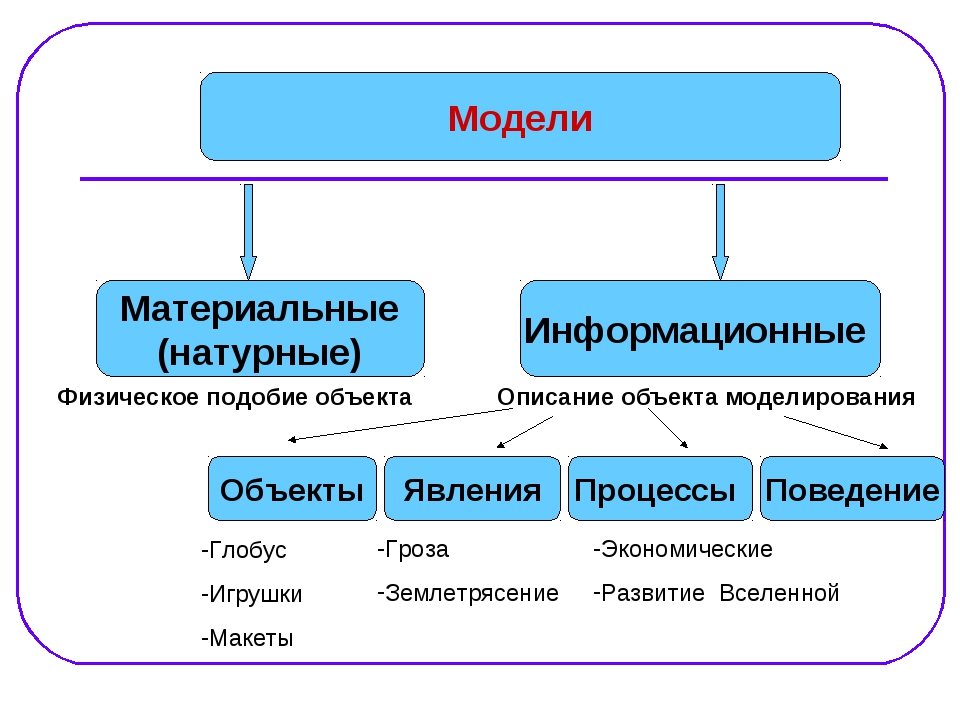
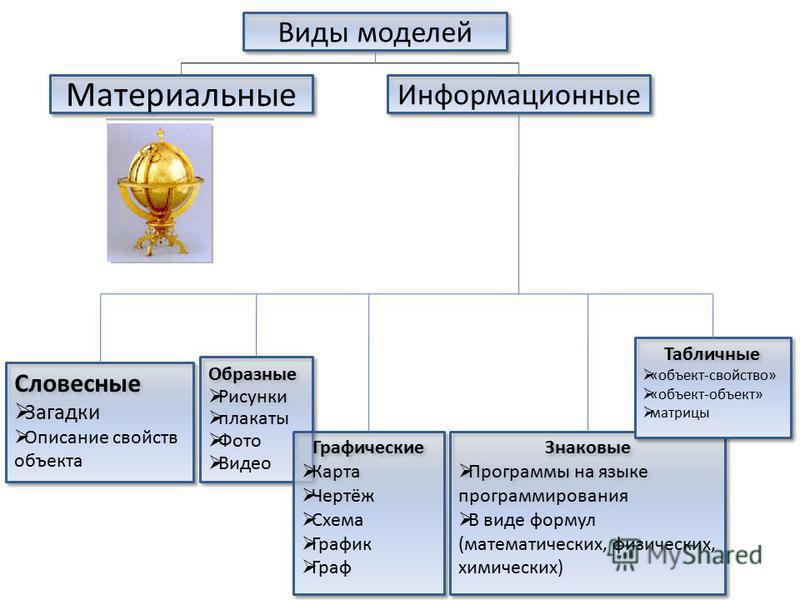
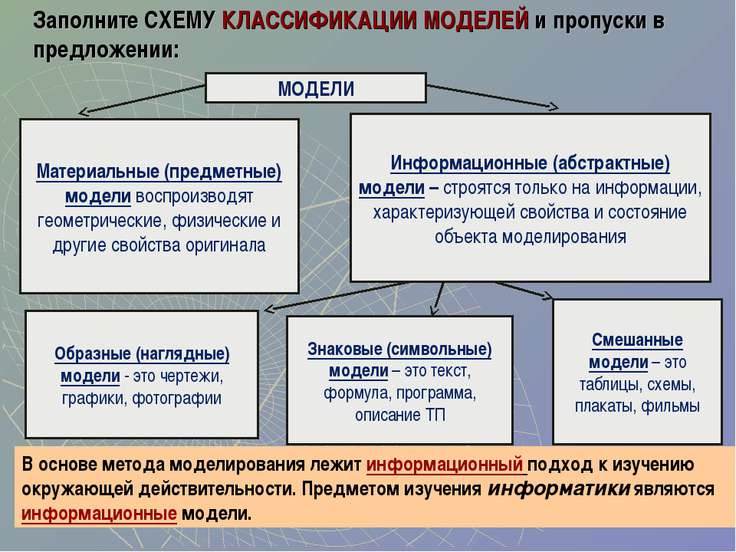
Важно отметить, что все модели принято делить на группы:

материальные;
идеальные.

Под материальной моделью понимают предмет, основанный на реально существующем объекте. Это может быть какое-либо тело или процесс. Данную группу принято подразделять еще на два вида:

физические;
аналоговые.

Такая классификация носит условный характер, ведь четкую границу между двумя этими подвидами провести очень трудно.

Идеальную модель охарактеризовать еще труднее. Она связаны с:

мышлением;
воображением;
восприятием.

К ней можно отнести произведения искусства (театр, живопись, литература и так далее).

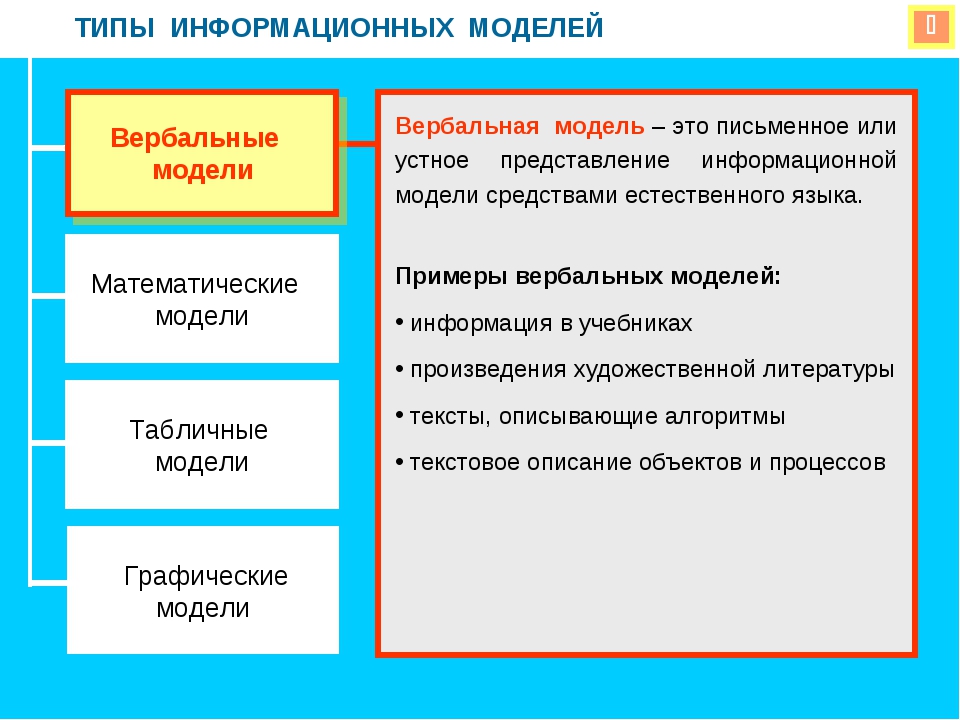
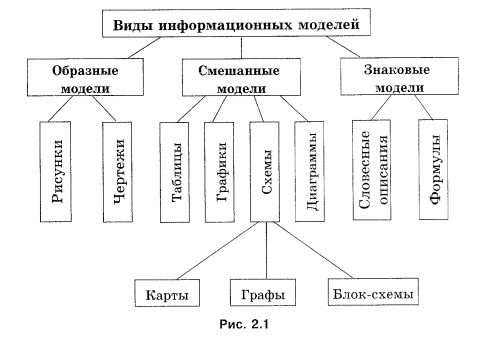
Информационная модель

Далее рассмотрим информационную модель в информатике. Ее проектирование изучается в школе. Преподается как базовый тип.

Следует заметить, что с этим видом моделирования нужно ознакомиться любому человеку, который видит свое будущее в IT-сфере. Как правило, все информационные модели создаются при помощи компьютерной техники. Причем речь идет не только конкретно о проектировании каких-то диаграмм, но используются еще и таблицы, рисунки, чертежи, схемы и так далее.

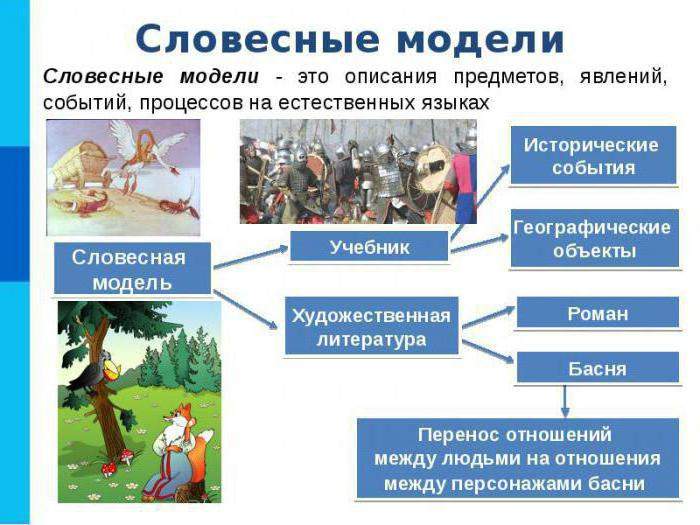
В целом информационная модель представляет собой свойства того объекта, который мы отображаем, максимально описывая его состояние, а также то, насколько он связан с окружающим миром, отношение к другим внешним предметам и влияние на них. Следует отметить, что информационной моделью может служить обычный текст, рисунок, словесное описание, чертеж, формула и так далее.

Такой вид отличается от других вышеперечисленных тем, что он является данными. То есть модель не имеет материального воплощения, так как считается примитивным комплексом информации, представленной в разном виде.

Оптимизационные модели

Сейчас мы немного поговорим об экономико-математических моделях, примерами которых могут служить разные сложившиеся ситуации. В данном случае речь идет о моделях, которые помогают найти верный ответ в определенных условиях. Они обязательно имеют некие параметры. Чтобы стало предельно понятно, рассмотрим пример из аграрной части.

У нас есть зернохранилище, но зерно очень быстро портится. В этом случае нам необходимо правильно подобрать температурный режим и оптимизировать процесс хранения.

Таким образом, мы можем дать определение понятию «оптимизационная модель». В математическом смысле это система уравнений (как линейных, так и нет), решение которой помогает найти оптимальное решение в конкретной экономической ситуации. Пример математической модели (оптимизационной) мы рассмотрели, но хочется еще добавить: данный вид относится к классу экстремальных задач, они помогают описать функционирование экономической системы.

Отметим еще один нюанс: модели могут носить разный характер (см. таблицу ниже).

детерминированный	В данном случае результат зависит от входных данных
стохастический	Описание случайных процессов. В данном случае результат остается неопределенным

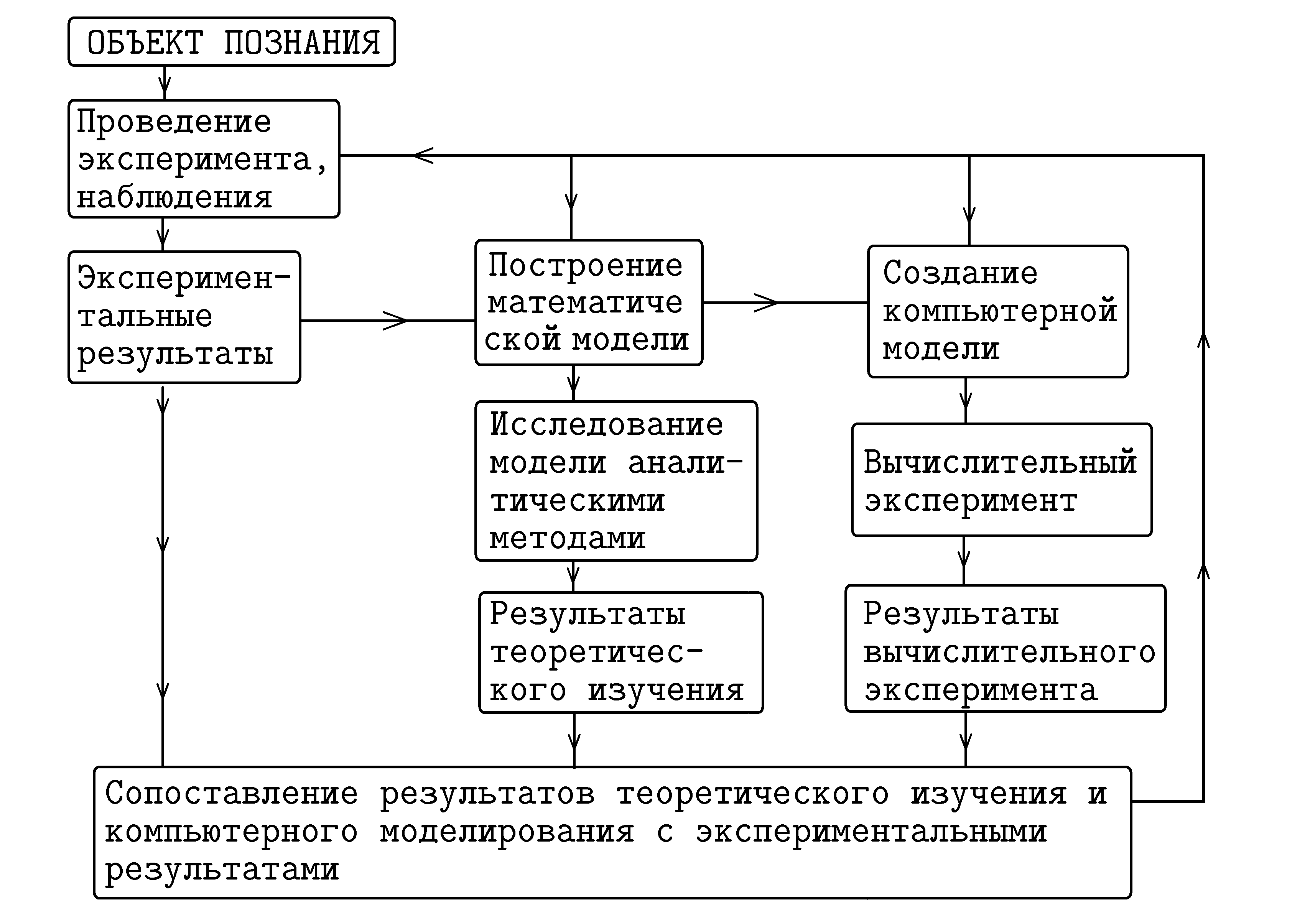
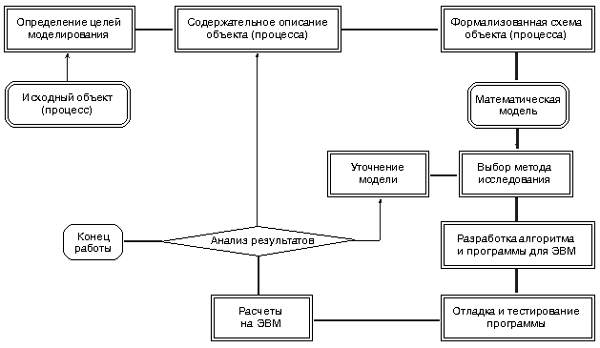
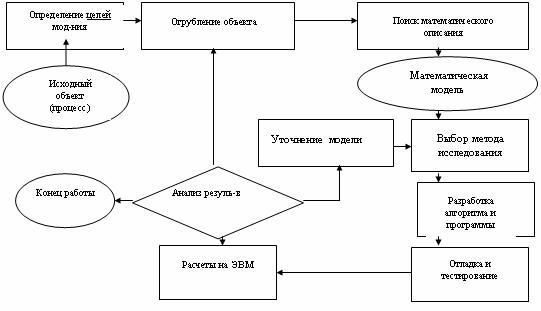
2.2. ЭТАПЫ И ЦЕЛИ КОМПЬЮТЕРНОГО МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

Здесь мы рассмотрим процесс компьютерного математического моделирования, включающий численный эксперимент с моделью (рис. 7.1).

Первый этап — определение целей моделирования. Основные из них таковы:

1)модель нужна для того, чтобы понять как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия с окружающим миром (понимание);

2)модель нужна для того, чтобы научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях (управление);

3)модель нужна для того, чтобы прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект (прогнозирование).

Поясним это на примерах. Пусть объект исследования — взаимодействие потока жидкости или газа с телом, являющимся для этого потока препятствием. Опыт показывает, что сила сопротивления потоку со стороны тела растет с ростом скорости потока, но при некоторой достаточно высокой скорости эта сила скачком уменьшается с тем, чтобы с дальнейшим увеличением скорости снова возрасти. Что же произошло, обусловив уменьшение силы сопротивления? Математическое моделирование позволяет получить четкий ответ: в момент скачкообразного уменьшения сопротивления вихри, образующиеся в потоке жидкости или газа позади обтекаемого тела, начинают отрываться от него и уноситься потоком.

Пример совсем из другой области: мирно сосуществовавшие со стабильными численностями популяции двух видов особей, имеющих общую кормовую базу, «вдруг» начинают резко менять численность — и здесь математическое моделирование позволяет (с известной долен достоверности) установить причину (или, по крайней мере, опровергнуть определенную гипотезу).

Рис. 7.1. Общая схема процесса компьютерного математического моделирования

2.1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И КОМПЬЮТЕРЫ

Математическая модель выражает существенные черты-объекта или процесса языком уравнений и других математических средств. Собственно говоря, сама математика обязана своим существованием тому, что она пытается отразить, т.е. промоделировать, на своем специфическом языке закономерности окружающего мира.

Путь математического моделирования в наше время гораздо более всеобъемлющ, нежели моделирования натурного. Огромный толчок развитию математического моделирования дало появление ЭВМ, хотя сам метод зародился одновременно с математикой тысячи лет назад.

Математическое моделирование как таковое отнюдь не всегда требует компьютерной поддержки. Каждый специалист, профессионально занимающийся математическим моделированием, делает все возможное для аналитического исследования модели. Аналитические решения (т.е. представленные формулами, выражающими результаты исследования через исходные данные) обычно удобнее и информативнее численных. Возможности аналитических методов решения сложных математических задач, однако, очень ограниченны и, как правило, эти методы гораздо сложнее численных. В данной главе доминируют численные методы, реализуемые на компьютерах. Это связано с тем, что моделирование здесь рассматривается под углом зрения компьютерных (информационных) технологий. Такой подход несколько сужает возможности метода в целом; его достоинство — некоторое снижение барьера необходимой математической подготовки (хотя, разумеется, и в численные методы при профессиональном занятии математическим моделированием приходится углубляться настолько, что при этом требуется значительное математическое образование). Наконец, отметим, что понятия «аналитическое решение» и «компьютерное решение» отнюдь не противостоят друг другу, так как

а) все чаще компьютеры при математическом моделировании используются не только для численных расчетов, но и для аналитических преобразований;

Литература

Введение в математическое моделирование. Учебное пособие. Под ред. П. В. Трусова. — М.: Логос, 2004. — ISBN 5-94010-272-7.
Краснощёков П. С., Петров А. А. Принципы построения моделей. — издание второе, пересмотренное и дополненное. — М.: ФАЗИС; ВЦ РАН, 2000. — xii + 412 с. — (Математическое моделирование; Вып.1). — ISBN 5-7036-0061-8.
Петров А. А., Поспелов И. Г., Шананин А. А. Опыт математического моделирования экономики. — М.: Энергоатомиздат, 1996. — 544 с. — 1500 экз. — ISBN 5-7036-0061-8.
Дьяконов В. П. Matlab R2006/2007/2008. Simulink 5/6/7. Основы применения. Серия: Библиотека профессионала. — М.: Солон-Пресс, 2008. — 800 с. — ISBN 978-5-91359-042-8
Огибалов П. М., Мирзаджанзаде А. Х. Механика физических процессов. — МГУ, 1976. — 370 с. — 3330 экз.

Игровые модели

Говоря об игровых моделях, необходимо понимать понятие «теория игр». Если говорить просто, то данные модели отражают математические модели настоящих конфликтов. Только стоит понимать, что, в отличие от реального конфликта, игровая математическая модель имеет свои определенные правила.

Сейчас будет приведен минимум информации из теории игр, которая поможет вам понять, что такое игровая модель. И так, в модели обязательно присутствуют стороны (две или более), которых принято называть игроками.

Все модели имеют некие характеристики.

Субъекты	Количество игроков
Стратегия	Варианты возможных действий
Платеж	Исход конфликта (выигрыш или проигрыш).

Игровая модель может быть парной или множественной. Если у нас есть два субъекта, то конфликт парный, если больше – множественный. Также можно выделить антагонистическую игру, ее еще называют игрой с нулевой суммой. Это модель, в которой выигрыш одного из участников равняется проигрышу другого.

Определения

Никакое определение не может в полном объёме охватить реально существующую деятельность по математическому моделированию. Несмотря на это, определения полезны тем, что в них делается попытка выделить наиболее существенные черты.

По Ляпунову, математическое моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель), находящаяся в некотором объективном соответствии с познаваемым объектом, способная замещать его в определённых отношениях и дающая при её исследовании, в конечном счёте, информацию о самом моделируемом объекте.

В других вариантах, математическая модель определяется как объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала, как «„эквивалент“ объекта, отражающий в математической форме важнейшие его свойства — законы, которым он подчиняется, связи, присущие составляющим его частям», как систему уравнений, или арифметических соотношений, или геометрических фигур, или комбинацию того и другого, исследование которых средствами математики должно ответить на поставленные вопросы о свойствах некоторой совокупности свойств объекта реального мира, как совокупность математических соотношений, уравнений, неравенств, описывающих основные закономерности, присущие изучаемому процессу, объекту или системе.

Некоторые приложения

С доисторических времен использовались простые модели, такие как карты и диаграммы .

Часто, когда инженеры анализируют систему, которую нужно контролировать или оптимизировать, они используют математическую модель. В процессе анализа инженеры могут построить описательную модель системы в качестве гипотезы того, как система может работать, или попытаться оценить, как непредвиденное событие может повлиять на систему. Точно так же, управляя системой, инженеры могут опробовать различные подходы к управлению в симуляциях .

Математическая модель обычно описывает систему набором переменных и набором уравнений, которые устанавливают отношения между переменными. Переменные могут быть разных типов; действительные или целые числа, логические значения или строки , например. Переменные представляют некоторые свойства системы, например, измеряемые выходные данные системы, часто в форме сигналов , данных синхронизации , счетчиков и возникновения события (да / нет). Фактическая модель — это набор функций, которые описывают отношения между различными переменными.

Способ представления

Подытоживая все вышесказанное о моделях данных в информатике, необходимо разузнать, как же представляется созданная запись.

Она бывает материальная и нематериальная. К первому виду нужно отнести все копии, которые были сняты с существующих объектов. Таким образом, их можно взять в руки, потрогать, понюхать и так далее. Они даже способны имитировать какие-либо свойства оригинального объекта, а также его действия. Данные материальные модели являются опытным методом проектирования.

К нематериальным относятся те, которые работают на теории. Они идеальные либо же абстрактные. Эта категория также имеет несколько типов. Речь идет об информационных, а еще воображаемых вариантах. Первый представляет собой перечень данных, который касается определенного объекта. Таковыми можно назвать таблицы, рисунки, схемы и так далее.

Однако многих их интересует, почему же данная модель класса информатики считается нематериальной. Текст хоть и напечатан, таблица составлена, но его потрогать нельзя. Именно поэтому данная модель является абстрактной. К слову, среди информационных вариантов записи имеются наглядные примеры.

К воображаемой модели относят то, что называется творческим процессом, то есть все происходящее в сознании человека. Это побуждает его создать на основе данной схемы оригинальный объект.

Что такое модель в информатике? Виды, примеры на News4Auto.ru.

Наша жизнь состоит из будничных мелочей, которые так или иначе влияют на наше самочувствие, настроение и продуктивность. Не выспался — болит голова; выпил кофе, чтобы поправить ситуацию и взбодриться — стал раздражительным. Предусмотреть всё очень хочется, но никак не получается. Да ещё и вокруг все, как заведённые, дают советы: глютен в хлебе — не подходи, убьёт; шоколадка в кармане — прямой путь к выпадению зубов. Мы собираем самые популярные вопросов о здоровье, питании, заболеваниях и даем на них ответы, которые позволят чуть лучше понимать, что полезно для здоровья.

Пример

Рассмотрим механическую систему, состоящую из пружины, закреплённой с одного конца, и груза массой m{\displaystyle m}, прикреплённого к свободному концу пружины. Будем считать, что груз может двигаться только в направлении оси пружины (например, движение происходит вдоль стержня). Построим математическую модель этой системы. Будем описывать состояние системы расстоянием x{\displaystyle x} от центра груза до его положения равновесия. Опишем взаимодействие пружины и груза с помощью закона Гука (F=−kx{\displaystyle F=-kx}), после чего воспользуемся вторым законом Ньютона, чтобы выразить его в форме дифференциального уравнения:

mx¨=−kx{\displaystyle m{\ddot {x}}=-kx},

где x¨{\displaystyle {\ddot {x}}} означает вторую производную от x{\displaystyle x} по времени: x¨=d2xdt2{\displaystyle {\ddot {x}}={\frac {d^{2}x}{dt^{2}}}}.

Полученное уравнение описывает математическую модель рассмотренной физической системы. Эта модель называется «гармоническим осциллятором».

По формальной классификации эта модель линейная, детерминистская, динамическая, сосредоточенная, непрерывная. В процессе её построения мы сделали множество допущений (об отсутствии внешних сил, отсутствии трения, малости отклонений и т. д.), которые в реальности могут не выполняться.

По отношению к реальности это, чаще всего, модель типа 4 упрощение («опустим для ясности некоторые детали»), поскольку опущены некоторые существенные универсальные особенности (например, диссипация). В некотором приближении (скажем, пока отклонение груза от равновесия невелико, при малом трении, в течение не слишком большого времени и при соблюдении некоторых других условий), такая модель достаточно хорошо описывает реальную механическую систему, поскольку отброшенные факторы оказывают пренебрежимо малое влияние на её поведение

Однако модель можно уточнить, приняв во внимание какие-то из этих факторов. Это приведёт к новой модели, с более широкой (хотя и снова ограниченной) областью применимости.

Впрочем, при уточнении модели сложность её математического исследования может существенно возрасти и сделать модель фактически бесполезной. Зачастую более простая модель позволяет лучше и глубже исследовать реальную систему, чем более сложная (и, формально, «более правильная»).

Если применять модель гармонического осциллятора к объектам, далёким от физики, её содержательный статус может быть другим. Например, при приложении этой модели к биологическим популяциям её следует отнести, скорее всего, к типу 6 аналогия («учтём только некоторые особенности»).

Цели моделирования

Рассматривая, что такое модель в информатике, необходимо также сказать и о целях ее создания.

Моделирование — довольно важный этап, так как он позволяет осуществить большое количество задач. Именно об этом мы далее и поговорим.

Для начала, моделирование позволит человеку больше узнать о том, что его окружает. Если говорить в обширном смысле, то в самой древности люди собирали какие-то данные, информацию, факты и передавали из поколения в поколение. Примером можно назвать модель нашего мира, которая называется “глобус”. В прошлые века, как правило, моделирование было построено на несуществующих объектах, с трудом познаваемыми человеком, которые на данный момент уже имеют свою реализацию в качестве материального предмета. Большинство из них прочно закрепились в нашей жизни. Речь может идти о зонтах, мельницах и так далее.

На данный момент модели систем информатики касаются путей достижения максимального эффекта от принимаемых решений, а также обращают внимание на последствия какого-либо процесса или же действия. Если говорить о последнем подпункте, то в пример можно привести модель, которая выясняет, какие последствия будут в результате повышения стоимости проезда либо после утилизации каких-либо отходов под землей