Лемма

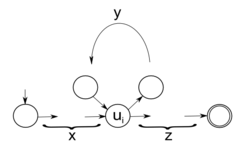
Примеры не КС-языка, для которого выполняется лемма[править]

Следует обратить особое внимание на то, что лемма содержит лишь необходимые условия принадлежности КС языку.

Пример править

Утверждение:

Можно построить такой язык, для которого будет выполняться лемма Огдена, однако язык не будет контекстно-свободным.

При анализе этого языка следует использовать алгебраические свойства множества. Выберем — подмножество и Языки над . Очевидно, что — КС, если контекстно-свободен. является рекурсивно-перечислимым, если и им является. Для будет выполняться лемма Огдена при . Выбрав таким образом, чтобы он был рекурсивно-перечислимым, мы создадим язык для которого будет выполняться лемма Огдена, однако язык не будет контекстно-свободным. (Такие языки существуют)

Пример править

Утверждение:

Язык , где — попарно различны, не является КС-языком.

Предположим, что данный язык контекстно-свободный. Возьмем цепочку , где — константа из леммы Огдена, выделив в ней все вхождения символа . Тогда при представлении цепочки в виде цепочка (по условию (1) леммы) обязательно «зацепит» хотя бы один символ . Cледовательно, цепочка состоит только из символов (как и цепочка ). А именно, , . Тогда, если цепочка содержит и другие символы, кроме , цепочка может входить либо в «зону» символов (целиком), либо в «зону» символов (целиком), так как расположение накачиваемых цепочек на стыках зон, очевидно, невозможно. В первом случае «кратность» накачки цепочки , которая уравняет числа символов и , определяется из соотношения: , то есть Во втором случае — кратная накачка цепочки уравняет числа вхождений символов и . Не исключено, наконец, что обе накачиваемые цепочки расположены в «зоне» символов . Но тогда одним из указанных выше способов накачки можно уравнять числа либо символов и , либо и . Заметим, что возможность выделения символов существенно упрощает анализ данного языка, так как позволяет считать, что цепочка может расположиться единственным способом. Иначе, т.е. при использовании леммы о разрастании для кс-языков, решение задачи было бы, по меньшей мере, сильно затруднено.

Вариации и обобщения

Теорема Тужрона

В окрестности критической точки {\displaystyle 0} конечной кратности μ{\displaystyle \mu } существует система координат, в которой гладкая функция f(x){\displaystyle f(x)} имеет вид многочлена Pμ+1(x){\displaystyle P_{\mu +1}(x)} степени μ+1{\displaystyle \mu +1} (в качестве Pμ+1(x){\displaystyle P_{\mu +1}(x)} можно взять многочлен Тейлора функции f(x){\displaystyle f(x)} в точке {\displaystyle 0} в исходных координатах). В случае невырожденной критической точки кратность μ=1{\displaystyle \mu =1}, и теорема Тужрона превращается в лемму Морса.

Лемма Морса с параметрами

Пусть f(x1,…,xn,y1,…,ym)Rn+m→R{\displaystyle f(x_{1},\ldots ,x_{n},y_{1},\ldots ,y_{m}):\mathbb {R} ^{n+m}\to \mathbb {R} } — гладкая функция, имеющая начало координат {\displaystyle 0} своей критической точкой, невырожденной по переменным x1,…,xn{\displaystyle x_{1},\ldots ,x_{n}}. Тогда в окрестности точки {\displaystyle 0} существуют гладкие координаты, в которых

f(x,y)=α1×12+⋯+αnxn2+f(y1,…,ym),αi=±1,{\displaystyle f(x,y)=\alpha _{1}x_{1}^{2}+\cdots +\alpha _{n}x_{n}^{2}\,+\,f_{0}(y_{1},\ldots ,y_{m}),\quad \alpha _{i}=\pm 1,}

где f{\displaystyle f_{0}} — некоторая гладкая функция.
Это утверждение позволяет свести исследование особенности (критической точки) функции от n+m{\displaystyle n+m} переменных к исследованию особенности функции от меньшего числа переменных (а именно, от числа переменных, равного корангу гессиана исходной функции).

Доказательство этого утверждения может быть проведено индукцией по n с использованием леммы Адамара или другим способом.

Морфология

Форма слова, выбранная для использования в качестве леммы, обычно является наименее отмеченной формой, но есть несколько исключений, например, для некоторых языков использование инфинитива для глаголов.

В английском языке форма цитирования существительного — единственное число : mouse, а не mice . Для многословных лексем, содержащих притяжательные прилагательные или возвратные местоимения , форма цитирования использует форму неопределенного местоимения one : делать все возможное , лжесвидетельствовать . В европейских языках с грамматическим родом форма цитирования обычных прилагательных и существительных обычно — мужского рода в единственном числе. Если в языке также есть падежи , в форме цитирования часто используется именительный падеж единственного числа мужского рода.

Для многих языков форма цитирования глагола — инфинитив : французский , немецкий , испанский . В английском языке это обычно совпадает с неотражаемой, наименее отмеченной формой глагола (то есть «бегать», а не «бегать» или «бегать»), но настоящее время используется для некоторых дефектных глаголов ( должен , может и должен иметь только одну форму). Однако для латинского , древнегреческого и новогреческого языков традиционно используется первое лицо единственного числа в настоящем времени , но в некоторых современных словарях вместо этого используется инфинитив. (Для в древнегреческом языке несогласованное первое лицо единственного числа в настоящем времени используется для раскрытия контрактной гласной: φιλέω philéō для φιλῶ philō «я люблю» ; ἀγαπάω agapáō для ἀγαπῶ agapō «я люблю» ). Финские словари перечисляют глаголы не под их корнем, а под первым инфинитивом, отмеченным — (t) a , — (t) ä .

В японском языке используется непрошедшее (настоящее и будущее) время. Для арабского языка , в котором нет инфинитива, мужской род единственного числа третьего лица прошедшего времени является наименее заметной формой и используется для записей в современных словарях. В более старых словарях, которые все еще широко используются, используется трехбуквенное слово — глагол или существительное. В иврите часто используется мужское совершенство от третьего лица, например ברא bara ‘ создавать, כפר kaphar deny. В грузинском языке используется глагольное существительное . Для корейского , -da прикрепляется к стеблю.

В ирландском языке слова сильно изменяются падежем (родительный, именительный, дательный и звательный) и их местом в предложении из-за начальных мутаций . Существительное cainteoir , лемма для существительного, означающего «говорящий», имеет множество форм: chainteoir , gcainteoir , cainteora , chainteora , cainteoirí , chainteoirí и gcainteoirí .

Некоторые фразы цитируются в своего рода лемме: Carthago delenda est (буквально «Карфаген должен быть разрушен») — распространенный способ цитирования Катона , но то, что он сказал, было ближе к censeo Carthaginem esse delendam («Я считаю, что Карфаген находится в необходимость разрушения »).

Общий случай леммы

В произвольной (локально малой) категории для данного объекта A можно рассмотреть ковариантный функтор Hom, обозначаемый

hA=Hom(A,−).{\displaystyle h^{A}=\mathrm {Hom} (A,-).}

Пусть F — произвольный функтор из C в Set. Лемма Йонеды утверждает, что:

для любого объекта A категории C, естественные преобразования из hA в F находятся во взаимно-однозначном соответствии с элементами F(A):

Nat(hA,F)≅F(A).{\displaystyle \mathrm {Nat} (h^{A},F)\cong F(A).}

Для данного естественного преобразования Φ из hA в F соответствующий элемент F(A) — это u=ΦA(idA){\displaystyle u=\Phi _{A}(\mathrm {id} _{A})}, то есть естественное преобразование однозначно определяется образом тождественного морфизма.

Контравариантная версия леммы Йонеды рассматривает контравариантный функтор

hA=Hom(−,A),{\displaystyle h_{A}=\mathrm {Hom} (-,A),}

отправляющий X во множество Hom(X, A). Для произвольного контравариантного функтора G из C в Set

Nat(hA,G)≅G(A).{\displaystyle \mathrm {Nat} (h_{A},G)\cong G(A).}

Замечание: для запоминания индексов удобно использовать мнемоническое правило «падать во что-то» при рассмотрении морфизмов в зафиксированный объект.

Доказательство

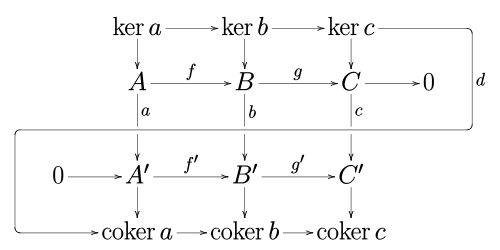
Доказательство леммы Йонеды представлено на следующей коммутативной диаграмме:

Диаграмма показывает, что естественное преобразование Φ полностью определяется ΦA(idA)=u{\displaystyle \Phi _{A}(\mathrm {id} _{A})=u}, так как для любого морфизма f : A → X

ΦX(f)=(Ff)u.{\displaystyle \Phi _{X}(f)=(Ff)u.}

Более того, эта формула задаёт естественное преобразование для любого u∈F(A) (так как диаграмма коммутативна). Доказательство контравариантного случая совершенно аналогично.

Что такое аксиома

Слово аксиома произошло от древнегреческого слова «axioma» — утверждение, положение.

Запомните!

Аксиома —
утверждение, которое не требует доказательств.

С точки зрения учащихся, аксиома — лёгкий способ получить отличную оценку. Достаточно просто выучить формулировку.
Ведь никаких доказательств для аксиомы учить не требуется.

Всего в геометрии насчитывается около 15 аксиом.
В школьном курсе используются далеко не все.
Некоторые из них используются в школьном курсе как само собой разумеющееся для нас.
Приведем некоторые примеры довольно известных аксиом из школьного курса геометрии:

• через любые две точки проходит прямая, и притом только одна;
• через точку, не лежащую на данной прямой, проходим только одна прямая, параллельная данной;
• если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки;
• любая фигура равна самой себе.

Что такое теорема

Совсем по-другому обстоят дела с теоремами. Слово теорема происходит
от древнегреческого слова «theorema» — смотреть, рассматривать какое-либо утверждение.

Запомните!

Теорема — утверждение,
которое требует доказательства.

Теоремы менее «любимы» учащимися, чем аксиомы. Если учитель попросит рассказать теорему, будет недостаточно,
как для аксиомы, сообщить только её формулировку. Потребуется также дать доказательство теоремы.

Примеры формулировок теорем:

• сумма углов треугольника равна 180 градусов;
• площадь прямоугольника равна произведению его смежных сторон;
• теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Важно!

Формулировки аксиом и теорем необходимо учить строго наизустьбез искажений.

Каждое слово или предлог в формулировке играет существенную роль в передаче смысла выражения.
Даже просто поменяв порядок слов можно сильно изменить смысл утверждения.

Помните, что все формулировки в геометрии были выверены несколькими тысячами лет развития математики лучшими умами планеты и не терпят
никаких словесных изменений.

Что такое лемма

Среди теорем выделяют такие теоремы, которые сами по себе не используются в решениях задач.
Но их используют для доказательства других теорем.

Лемма происходит от древнегреческого слова «lemma» – предположение.

Запомните!

Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы.

Пример леммы:

если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.

Что такое следствие в геометрии

Запомните!

Следствие — утверждение, которое выводится непосредственно из аксиомы или теоремы.
Следствие, как и теорему, необходимо доказывать.

Приведем примеры следствий из аксиомы о параллельности прямых:

• если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую;
• если две прямые параллельны третьей прямой, то они параллельны.

Если подытожить все вышесказанное, то сравнивая геометрию с высотным домом, можно представить, что:

• аксиомы — фундамент дома;
• теоремы — основные кирпичи дома;
• леммы и следствия — вспомогательные кирпичи для упрочнения конструкции.

Каждая доказанная теорема служит основанием доказательства для следующей теоремы.
Именно поэтому так важно изучать геометрию последовательно, переходя с самых основ (аксиом) к теоремам. Невозможно понять геометрию 9 и 10 класса, не выучив аксиомы и теоремы 7 и 8 класса

Невозможно понять геометрию 9 и 10 класса, не выучив аксиомы и теоремы 7 и 8 класса.

Лемма[править]

Лемма:

Для каждой контекстно-свободной грамматики существует такое , что для любого слова длины не менее и для любых выделенных в не менее позиций, может быть представлено в виде , причем: содержит выделенную позицию; либо и , либо и обе содержат выделенные позиции; содержат не более выделенных позиций; существует , такой что . (т.е. )

Доказательство:

Введем следующие обозначения: и — длина самой длинной правой части правила из . Тогда в качестве возьмем . Рассмотрим дерево разбора для произвольного слова , у которого . В силу выбора в будет по крайне мере один путь от корня до листа длины не менее . Произвольным образом выделим в не менее позиций. Соответствующие этим позициям листья дерева будем называть выделенными. Пусть — корень , а — сын , который имеет среди своих потомков наибольшее число выделенных листьев (если таких несколько, то самый правый из них). Рассмотрим — путь от корня до листа. Будем называть ветвящейся ту вершину, у которой по крайне мере два сына имеют выделенных потомков. Докажем по индукции, что если среди вершин есть ветвящихся, то имеет хотя бы выделенных потомков. База индукции: . Тогда и имеет по крайне мере выделенных потомков, поскольку является корнем. Индукционный переход. Если не является ветвящейся вершиной, то имеет такое же число ветвящихся потомков, как и . Если — ветвящаяся вершина, то имеет не более чем в раз меньшее число выделенных потомков. Поскольку имеет хотя бы выделенных потомков, то содержит по крайне мере ветвящиеся вершин. Заметим, что — лист, поэтому . Дерево вывода Будем называть левой ветвящейся вершиной, если ее сын, не принадлежащий пути , имеет выделенного потомка, лежащего слева от . В противном случае назовем правой ветвящейся вершиной. Рассмотрим последние вершины, принадлежащие пути . Предположим, что хотя бы вершины — левые ветвящиеся (случай, когда хотя бы вершины — правые ветвящиеся, разбирается аналогично). Пусть — последние левые ветвящиеся вершины. Поскольку , то среди них можно найти как минимум две вершины, соответствующие одному нетерминалу. Обозначим эти вершины и , причем — потомок . Тогда на рисунке показано, как представить в требуемом виде. Условие выполнено, поскольку содержит выделенную вершину, а именно . Очевидно, что условие выполнено в силу предложенного разбиения . Кроме того, содержит выделенную вершину, а именно потомка некоторого сына вершины . Аналогично, выделенный потомок некоторого сына вершины содержится в . Таким образом, условие выполнено. Поскольку между и не более вершин, вершина имеет не более выделенных потомков, поэтому условие выполнено.

Разница между основанием и леммой

Стебель является частью слова , которое никогда не меняется , даже когда морфологический изменяемым; лемма — это основная форма слова. Например, от «произведено» лемма будет «производить», а основа — «производи-». Это потому, что есть такие слова, как производство . и производство. В лингвистическом анализе основа определяется в более общем смысле как анализируемая базовая форма, из которой могут быть образованы все флективные формы

Когда фонологию принимаются во внимание, определение неизменяемой части слова не является полезным, как можно видеть в фонологических формах слов в предыдущем примере: «произведенных» против. «производство» .

У некоторых лексем несколько основ, но одна лемма. Например, глагол « » (лемма) имеет основы «идти» и «пошел» из-за дополнения : прошедшее время было заимствовано из другого глагола « ».