Логические операции и их свойства

Классическая логика

В классическом исчислении высказываний свойства конъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства конъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для конъюнкции:
a∧b→a{\displaystyle a\land b\to a}
a∧b→b{\displaystyle a\land b\to b}
a→(b→(a∧b)){\displaystyle a\to (b\to (a\land b))}

С помощью этих аксиом можно доказать другие формулы, содержащие операцию конъюнкции

Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.

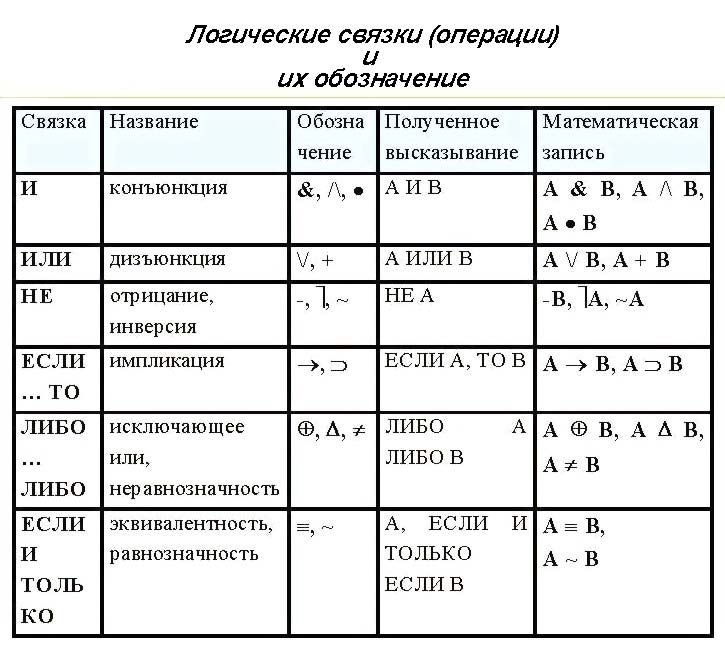
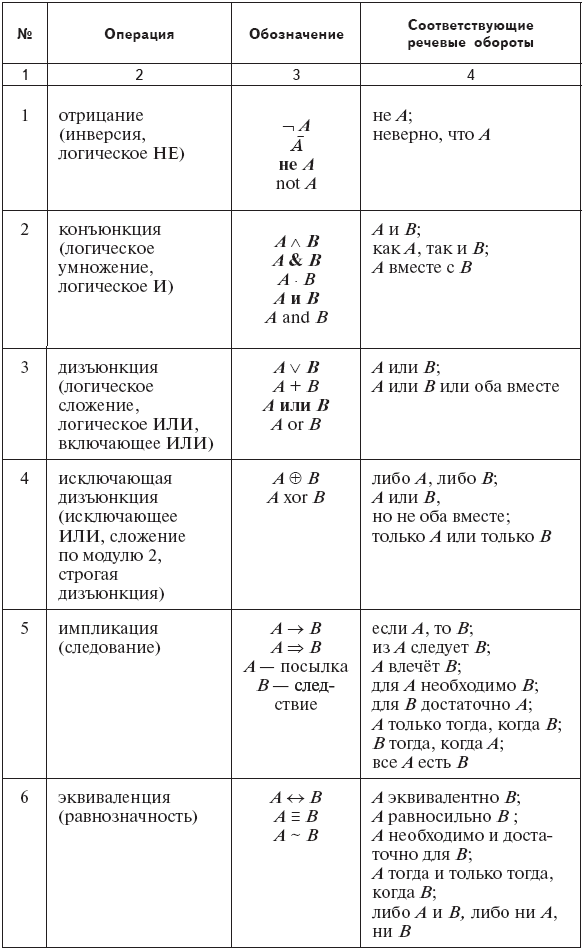
Обозначения

Наиболее часто встречаются следующие обозначения для операции конъюнкции:

a∧b,a&&b,a&b,a⋅b,aANDb,min(a,b){\displaystyle a\land b,\quad a\And \And b,\quad a\And b,\quad a\cdot b,\quad a\,\,\mathrm {AND} \,\,b,\quad \min(a,b)}

(в случае использования точки как знака логического умножения этот знак — как и при обычном умножении в алгебре — может быть опущен: ab{\displaystyle ab}).

При этом обозначение a∧b{\displaystyle a\land b} наиболее широко распространено в современной математике и математической логике, где оно, впрочем, конкурирует со знаком амперсанда &; последний, появившись ещё в I веке до н. э. как графическое сокращение (лигатура) латинского союза et ‘и’, уже Якобом и Иоганном Бернулли в 1685 году использовался в качестве логической связки (у них он, однако, связывал не высказывания, а понятия). Джордж Буль (а за ним — и другие пионеры систематического применения символического метода к логике: У. С. Джевонс, Э. Шрёдер, П. С. Порецкий) обозначал конъюнкцию знаком ⋅{\displaystyle \cdot } — как обычное умножение. Символ ⋀ (перевёрнутый знак дизъюнкции) в качестве обозначения конъюнкции был предложен Арендом Гейтингом (1930).

Обозначение для конъюнкции было использовано и в раннем языке программирования Алгол 60. Однако из-за отсутствия соответствующего символа в стандартных наборах символов (например, в ASCII или EBCDIC), применявшихся на большинстве компьютеров, в получивших наибольшее распространение языках программирования были предусмотрены иные обозначения для конъюнкции. Так, в Фортране IV и PL/I применялись соответственно обозначения и (с возможностью замены последнего на ключевое слово ); в языках Паскаль и Ада используется зарезервированное слово ; в языках C и C++ применяются обозначения для побитовой конъюнкции и для логической конъюнкции).

Наконец, при естественном упорядочении значений истинности двузначной логики (когда полагают, что <1{\displaystyle 0<1}), оказывается, что (a∧b)=min(a,b).{\displaystyle (a\land b)\,=\,\min(a,b).} Таким образом, конъюнкция оказывается частным случаем операции вычисления минимума; это открывает наиболее естественный способ определить операцию конъюнкции в системах многозначной логики (хотя иногда рассматривают и другие способы обобщения конъюнкции — например, такой: (a∧b)=ab(mod⁡k){\displaystyle (a\land b)\,=\,ab\;(\operatorname {mod} k)} в случае k-значной логики, в которой множество значений истинности представлено начальным отрезком {,…,k−1}{\displaystyle \{0,\dots ,k-1\}} полугруппы N{\displaystyle \mathbb {N} } натуральных чисел).

Штрих Шеффера

Булева функция двух переменных или бинарная логическая операция. Введена в рассмотрение Генри Шеффером в 1913 г.

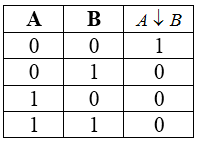
Обозначения: $|$, эквивалентно операции И-НЕ.

Таблицей истинности для функции штрих Шеффера

Рисунок 8.

Свойства:

Штрих Шеффера образует базис для всех булевых функций двух переменных. Применяя штрих Шеффера можно построить остальные операции, например,

$X \mid X = ¬X$ — отрицание

$(X \mid Y) \mid (X \mid Y) = (X \wedge Y)$ — конъюнкция

$(X \mid X) \mid (Y \mid Y) = X \vee Y$ — дизъюнкция

$X \mid ¬X$ — константа 1

Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).

Связь с естественным языком

Часто указывают на сходство между конъюнкцией и союзом «и» в естественном языке. Составное утверждение «A и B» считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как {\displaystyle 0}. При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз «и» может нести дополнительный оттенок «и тогда», «и поэтому», «и потом». Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке «Мэри вышла замуж и родила ребенка» — не то же самое, что «Мэри родила ребенка и вышла замуж».

Программирование

В компьютерных языках используется два основных варианта конъюнкции: логическое «И» и побитовое (поразрядное) «И». Например, в языках C/C++ логическое «И» обозначается символом «&&», а побитовое — символом «&». В терминологии, используемой в C#, операцию «&» принято называть логическим «И», а операцию «&&» — условным «И», поскольку значения операндов являются условиями для продолжения вычисления. В языках Pascal/Delphi оба вида конъюнкции обозначаются с использованием ключевого слова «and», а результат действия определяется типом операндов. Если операнды имеют логический тип (например, Boolean) — выполняется логическая операция, если целочисленный (например, Byte) — поразрядная.

Логическое «И» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата false{\displaystyle false} или true{\displaystyle true}. Например:

if (a & b & c) 
{
    /* какие-то действия */
};

Сравнение в данном случае будет продолжаться до конца выражения, независимо от промежуточных результатов.
Принцип работы условного «И» в аналогичной ситуации:

a = false; b = true; c = true;
if (a && b && c) 
{
    /* какие-то действия */ 
};

Проверка истинности выражения в данном случае остановится после проверки переменной a, так как дальнейшее сравнение не имеет смысла.

Результат будет равен true{\displaystyle true}, если оба операнда равны true{\displaystyle true} (для числовых типов не равны {\displaystyle 0}). В любом другом случае результат будет равен false{\displaystyle false}.

При этом применяется стандартное соглашение: если значение левого операнда равно false{\displaystyle false}, то значение правого операнда не вычисляется (вместо b{\displaystyle b} может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Компилятор Delphi поддерживает специальную директиву, включающую

{$B-}

или выключающую

{$B+}

подобное поведение. Например, если левый операнд проверяет возможность вычисления правого операнда:

if (a !=  && b  a > 3) 
{
    /* какие-то действия */
};

В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет деления на ноль.

Побитовое «И» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,

если
a =	011001012{\displaystyle 01100101_{2}}
b =	001010012{\displaystyle 00101001_{2}}
то
a И b =	001000012{\displaystyle 00100001_{2}}

Классическая логика

В классическом исчислении высказываний свойства конъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства конъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для конъюнкции:
a∧b→a{\displaystyle a\land b\to a}
a∧b→b{\displaystyle a\land b\to b}
a→(b→(a∧b)){\displaystyle a\to (b\to (a\land b))}

С помощью этих аксиом можно доказать другие формулы, содержащие операцию конъюнкции

Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.

Обозначения

Наиболее часто встречаются следующие обозначения для операции конъюнкции:

a∧b,a&&b,a&b,a⋅b,aANDb,min(a,b){\displaystyle a\land b,\quad a\And \And b,\quad a\And b,\quad a\cdot b,\quad a\,\,\mathrm {AND} \,\,b,\quad \min(a,b)}

(в случае использования точки как знака логического умножения этот знак — как и при обычном умножении в алгебре — может быть опущен: ab{\displaystyle ab}).

При этом обозначение a∧b{\displaystyle a\land b} наиболее широко распространено в современной математике и математической логике, где оно, впрочем, конкурирует со знаком амперсанда &; последний, появившись ещё в I веке до н. э. как графическое сокращение (лигатура) латинского союза et ‘и’, уже Якобом и Иоганном Бернулли в 1685 году использовался в качестве логической связки (у них он, однако, связывал не высказывания, а понятия). Джордж Буль (а за ним — и другие пионеры систематического применения символического метода к логике: У. С. Джевонс, Э. Шрёдер, П. С. Порецкий) обозначал конъюнкцию знаком ⋅{\displaystyle \cdot } — как обычное умножение. Символ ⋀ (перевёрнутый знак дизъюнкции) в качестве обозначения конъюнкции был предложен Арендом Гейтингом (1930).

Обозначение для конъюнкции было использовано и в раннем языке программирования Алгол 60. Однако из-за отсутствия соответствующего символа в стандартных наборах символов (например, в ASCII или EBCDIC), применявшихся на большинстве компьютеров, в получивших наибольшее распространение языках программирования были предусмотрены иные обозначения для конъюнкции. Так, в Фортране IV и PL/I применялись соответственно обозначения и (с возможностью замены последнего на ключевое слово ); в языках Паскаль и Ада используется зарезервированное слово ; в языках C и C++ применяются обозначения для побитовой конъюнкции и для логической конъюнкции).

Наконец, при естественном упорядочении значений истинности двузначной логики (когда полагают, что <1{\displaystyle 0<1}), оказывается, что (a∧b)=min(a,b).{\displaystyle (a\land b)\,=\,\min(a,b).} Таким образом, конъюнкция оказывается частным случаем операции вычисления минимума; это открывает наиболее естественный способ определить операцию конъюнкции в системах многозначной логики (хотя иногда рассматривают и другие способы обобщения конъюнкции — например, такой: (a∧b)=ab(mod⁡k){\displaystyle (a\land b)\,=\,ab\;(\operatorname {mod} k)} в случае k-значной логики, в которой множество значений истинности представлено начальным отрезком {,…,k−1}{\displaystyle \{0,\dots ,k-1\}} полугруппы N{\displaystyle \mathbb {N} } натуральных чисел).

Связь с естественным языком

Часто указывают на сходство между конъюнкцией и союзом «и» в естественном языке. Составное утверждение «A и B» считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как {\displaystyle 0}. При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз «и» может нести дополнительный оттенок «и тогда», «и поэтому», «и потом». Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке «Мэри вышла замуж и родила ребенка» — не то же самое, что «Мэри родила ребенка и вышла замуж».

Программирование

В компьютерных языках используется два основных варианта конъюнкции: логическое «И» и побитовое (поразрядное) «И». Например, в языках C/C++ логическое «И» обозначается символом «&&», а побитовое — символом «&». В терминологии, используемой в C#, операцию «&» принято называть логическим «И», а операцию «&&» — условным «И», поскольку значения операндов являются условиями для продолжения вычисления. В языках Pascal/Delphi оба вида конъюнкции обозначаются с использованием ключевого слова «and», а результат действия определяется типом операндов. Если операнды имеют логический тип (например, Boolean) — выполняется логическая операция, если целочисленный (например, Byte) — поразрядная.

Логическое «И» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата false{\displaystyle false} или true{\displaystyle true}. Например:

if (a & b & c) 
{
    /* какие-то действия */
};

Сравнение в данном случае будет продолжаться до конца выражения, независимо от промежуточных результатов.
Принцип работы условного «И» в аналогичной ситуации:

a = false; b = true; c = true;
if (a && b && c) 
{
    /* какие-то действия */ 
};

Проверка истинности выражения в данном случае остановится после проверки переменной a, так как дальнейшее сравнение не имеет смысла.

Результат будет равен true{\displaystyle true}, если оба операнда равны true{\displaystyle true} (для числовых типов не равны {\displaystyle 0}). В любом другом случае результат будет равен false{\displaystyle false}.

При этом применяется стандартное соглашение: если значение левого операнда равно false{\displaystyle false}, то значение правого операнда не вычисляется (вместо b{\displaystyle b} может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Компилятор Delphi поддерживает специальную директиву, включающую

{$B-}

или выключающую

{$B+}

подобное поведение. Например, если левый операнд проверяет возможность вычисления правого операнда:

if (a !=  && b  a > 3) 
{
    /* какие-то действия */
};

В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет деления на ноль.

Побитовое «И» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,

если
a =	011001012{\displaystyle 01100101_{2}}
b =	001010012{\displaystyle 00101001_{2}}
то
a И b =	001000012{\displaystyle 00100001_{2}}

Логические операции

Операции логического типа очень часто применяются при построении выражений, используемых в программировании. К ним относятся следующие:

Конъюнкция.
Дизъюнкция.
Инверсия.

Однако булева алгебра не ограничивается только ими, поскольку существуют и другие их производные. Для каждой из трех составляются определенные таблицы истинности, которые каждый раз необходимо строить для получения результата вычисления логических выражений. Специалисты рекомендуют отдельно на листе картона перечертить таблицы всех логических операций.

Функция конъюнкции

Конъюнкция — операция логического умножения, которая будет истинным при достоверности каждого выражения. Ее обозначение — символ конъюнктора «&”. Записывается следующим образом: S&T, где S и T — логические тождества или конкретные значения. Операция имеет такие особенности: только при равенстве всех элементов 1 значение выражения является истинным, а в других случаях — ложью. Для проверки необходимо составить таблицу значений логического тождества:

S	T	S&T
F
1	F
1	F
1	1	T

Таблица 1. Значение функции в зависимости от логических переменных.

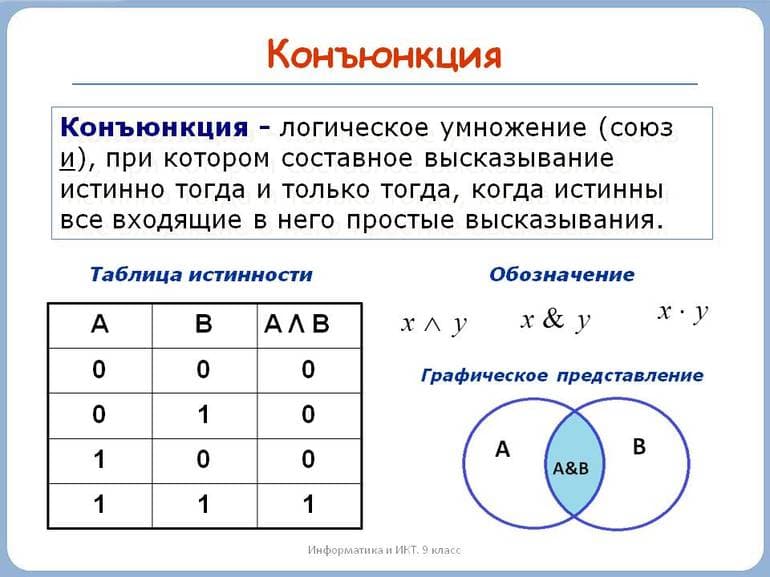
Из таблицы 1 видно, что выражение S&T принимает только TRUE при всех истинных значениях переменных. Если рассматривать алгебру, то можно провести аналогию между логическим и обыкновенным умножениями. Например, произведение двух чисел S*T, которые для удобства сравнения принимают значения 0 или 1.

Информация о дизъюнкции

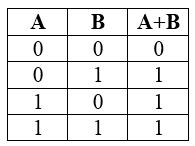
В булевой алгебре операция логического сложения называется дизъюнкцией. Обозначается она символом, который называется дизъюнктором (V или I). Логическое тождество, содержащее два элемента, имеет такой вид: SVT. Операция имеет только ложное значение при равенстве S и T нулю. Для нее нужно также строить специальную таблицу:

S	T	Результат — S|T
1	1
1	1
1	1	1

Таблица 2. Истинность операции дизъюнкции SVT.

Операция аналогична сложению в алгебре, хотя имеются некоторые отличия. Чтобы убедиться в этом, требуется выполнить определенное действие — построить специальную таблицу результатов для алгебраического сложения нулей и единиц.

Если рассмотреть результаты в последнем случае, то можно сделать вывод о схожести сложения и дизъюнкции. Однако в последней строке алгебраической суммы есть некоторое несоответствие — 2. Это показывает, какое переполнение разряда происходит в булевой алгебре. В последней происходит переход с одного разряда в другой.

Булево отрицание

В алгебре логики применяется также операция отрицания, которую также называют инверсией. Суть ее заключается в том, что при истинном значении выражения под знаком инверсии получается ложный результат, а при ложном — истина. Обозначается она символом инверсии «¬”, а записывается в таком виде ¬(S). Для демонстрации операции необходимо ознакомиться с таблицей:

Исходное выражение, S	Результат, ¬(S)
T
1	F

Таблица 3. Истинность ¬(S).

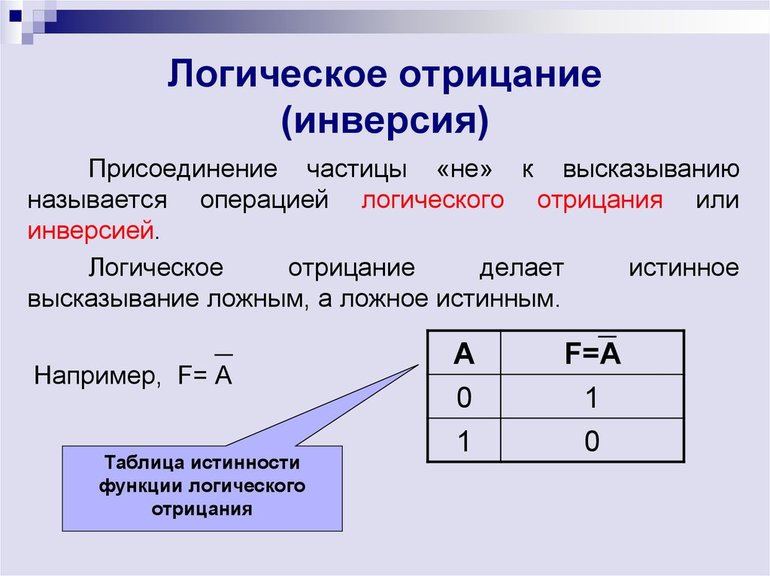
Следует отметить, что операция инверсии функции прибавляет к искомому выражению частицу «НЕ». Очень часто используется при построении логических условий. В алгоритмах и языках программирования отрицание записывается в виде комбинации следующих символов: «<!» (не меньше), «=!» (не равно) и «>!» (не больше).

Например, если необходимо указывать несколько тождеств логического вида, то при помощи отрицания можно использовать только одно. Для примера необходимо написать, что число не равно 0: (t<0)&(t>0). При использовании логического отрицания условие выглядит короче: t=!0.

Приоритеты вычислений

При решении выражений булевского типа, как и в алгебре, существуют определенные приоритеты. Каждая операция обладает определенным из них. Наибольшей степенью пользуется конъюнкция, средней — дизъюнкция. Наименьшим приоритетом обладает логическое отрицание. Однако эту особенность можно поменять при помощи группировки элементов в выражениях, которая производится скобками. С учетом этих особенностей алгоритм решения тождества имеет следующий вид:

Написать выражение: S&T|S|.
Определить последовательность вычислений: , S&T, |S и v.
Составить обобщенную таблицу.

Иногда бывают задачи, в которых следует упрощать выражение. Для этой цели следует знать некоторые особенности:

¬(0)=1.
¬(1)=0.
¬(¬(0))=0.
¬(¬(1))=1.
¬(S&T)=¬(S)&¬(T).
S&(S|T)=S|T.

Этих правил достаточно для упрощения булевского выражения. Следует отметить, что перед построением булевской таблицы требуется с самого начала упростить исходное тождество.

Операторы сравнения

Для формирования логических условий применяются соответствующие знаки. К ним относятся следующие: более (>), менее (<), более либо равно (>=), менее или равно (<=), равно (==) и не равно (==!). Чтобы понять их смысловое значение, нужно разобрать примеры на практике:

>: 5>4.
<: 3<9.
>=: 5>=5 и 6>=8.
<=: 3<=3 и 6<=11.
<> <>

Следует отметить, что в этих примерах получается истинное значение, поскольку условие выполняется. Однако в информатике при построении алгоритмов используются методы ветвления. Они представляют собой такую конструкцию: ЕСЛИ (a>b), ТО a+b. ИНАЧЕ (a*b). Читается запись следующим образом: в том случае, когда значение а больше b, нужно сложить оба числа, а иначе (a<b) — их перемножить.

Связь с естественным языком

Часто указывают на сходство между конъюнкцией и союзом «и» в естественном языке. Составное утверждение «A и B» считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как {\displaystyle 0}. При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз «и» может нести дополнительный оттенок «и тогда», «и поэтому», «и потом». Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке «Мэри вышла замуж и родила ребенка» — не то же самое, что «Мэри родила ребенка и вышла замуж».

Дизъюнкция

Нестрогая
дизъюнкция
2
– это суждение, полученное из любых
двух суждений при помощи логического
союза «или».

В
повседневном языке слово «или» имеет
два разных смысла. Иногда оно означает
«одно или другое или оба», а иногда «одно
или другое, но не оба вместе». В логике
и математике слово «или» всегда
употребляется в неисключающем значении.

Итак,
дизъюнкция является нестрогой, если ее
члены не исключают друг друга.

Пример
.
Суждение «В этом сезоне я хочу пойти на
“Пиковую даму” или на “Аиду”» является
нестрогой дизъюнкцией.

Строгая
дизъюнкция ‒ это суждение
,
полученное
из любых двух суждений при помощи
логического союза «либо
…,
либо
….

Пример
.В
суждении «Он учится в Московском или в
Саратовском университете» подразумевается,
что упоминаемый человек учится только
в одном из этих университетов.

Нестрогая
дизъюнкция означает, что, по крайней
мере, одно из этих суждений истинно,
независимо от того, истинны они оба или
нет. Строгая дизъюнкция означает, что
одно из них истинно, а второе – ложно.

Символ
«v» обозначает нестрогую дизъюнкцию,
символ «V» – строгую дизъюнкцию.
Применяются также другие обозначения.

Нестрогая
дизъюнкция истинна
,
когда хотя бы одно из входящих в нее
суждений истинно
,
и ложна тогда
,
когда
оба ее члена ложны
.

Строгая
дизъюнкция истинна
,
когда
истинным является только один из ее
членов
,
и она ложна
,
когда оба ее члена истинны или оба ложны
.

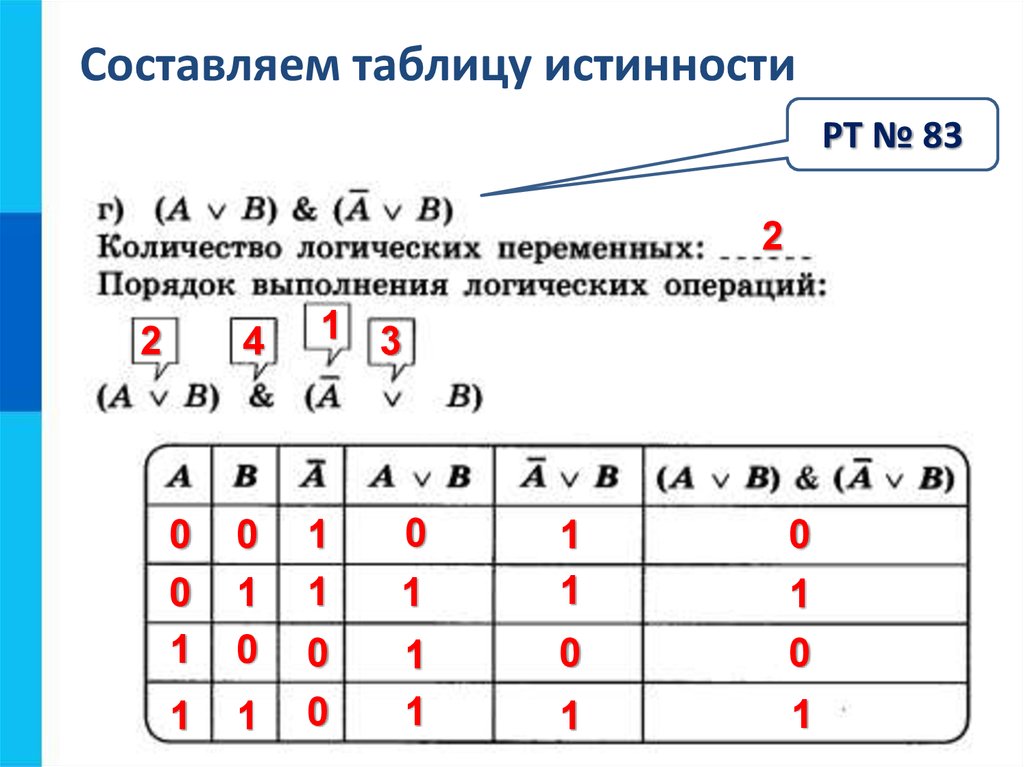
Таблица
истинности для дизъюнкции такова.

		A v В	A V B

Примечания

1. ↑ , с. 264—266, 534—536.
2. , с. 67.
3. Стяжкин Н. И.  Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 321, 348, 352, 368.
4. , с. 30.
5. Пратт Т.  Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
6. Грогоно П.  Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
7. Вегнер П.  Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
8. Эллис М., Строуструп Б.  Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
9. Яблонский С. В.  Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
10. Рвачёв В. Л.  Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.
11. ↑ Словарь по кибернетике. 2-е изд / Под ред. В. С. Михалевича. — Киев: Украинская советская энциклопедия, 1989. — 751 с. — ISBN 5-88500-008-5.

Примечания

1. ↑ , с. 264—266, 534—536.
2. , с. 67.
3. Стяжкин Н. И.  Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 321, 348, 352, 368.
4. , с. 30.
5. Пратт Т.  Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
6. Грогоно П.  Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
7. Вегнер П.  Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
8. Эллис М., Строуструп Б.  Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
9. Яблонский С. В.  Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
10. Рвачёв В. Л.  Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.
11. ↑ Словарь по кибернетике. 2-е изд / Под ред. В. С. Михалевича. — Киев: Украинская советская энциклопедия, 1989. — 751 с. — ISBN 5-88500-008-5.

Связь с естественным языком

Часто указывают на сходство между конъюнкцией и союзом «и» в естественном языке. Составное утверждение «A и B» считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как {\displaystyle 0}. При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз «и» может нести дополнительный оттенок «и тогда», «и поэтому», «и потом». Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке «Мэри вышла замуж и родила ребенка» — не то же самое, что «Мэри родила ребенка и вышла замуж».