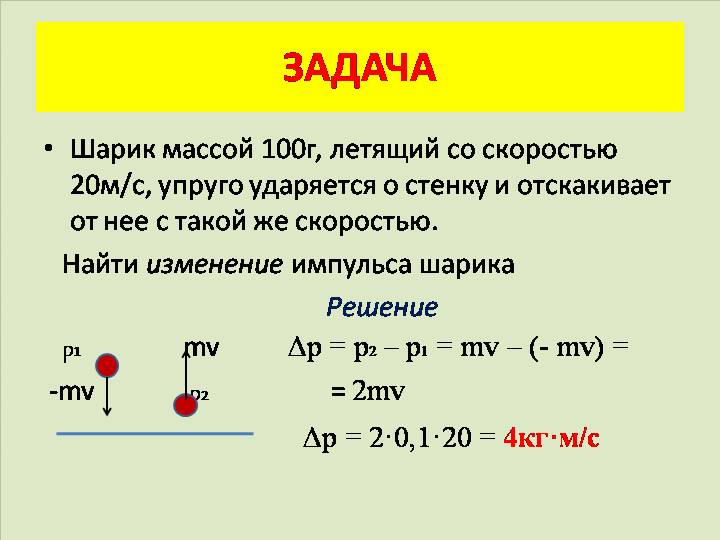
Импульс тела. импульс силы. закон сохранения импульса

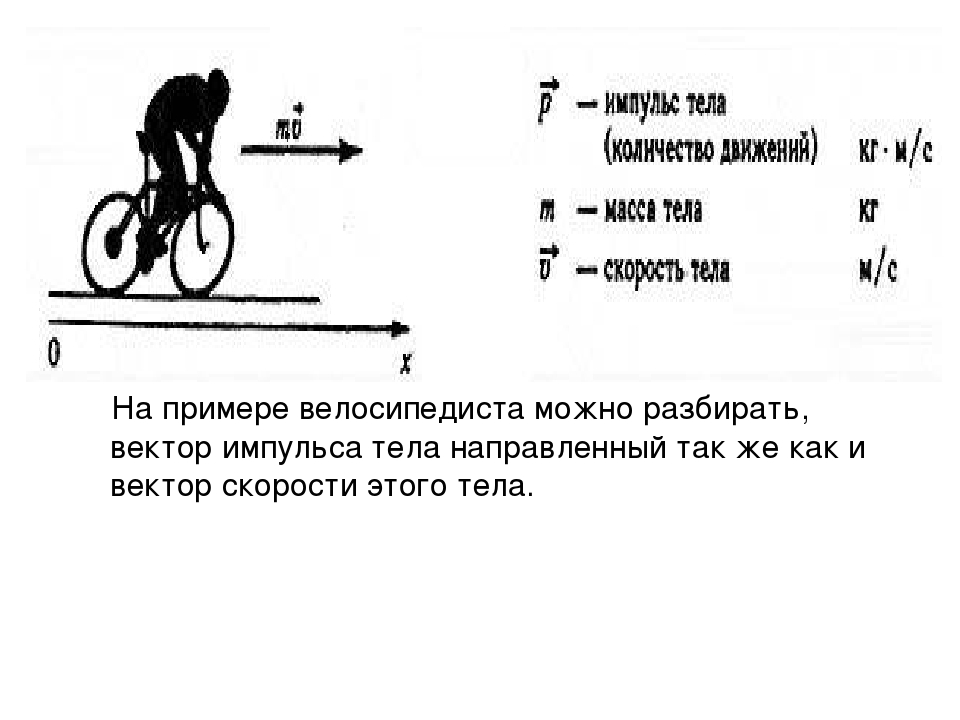
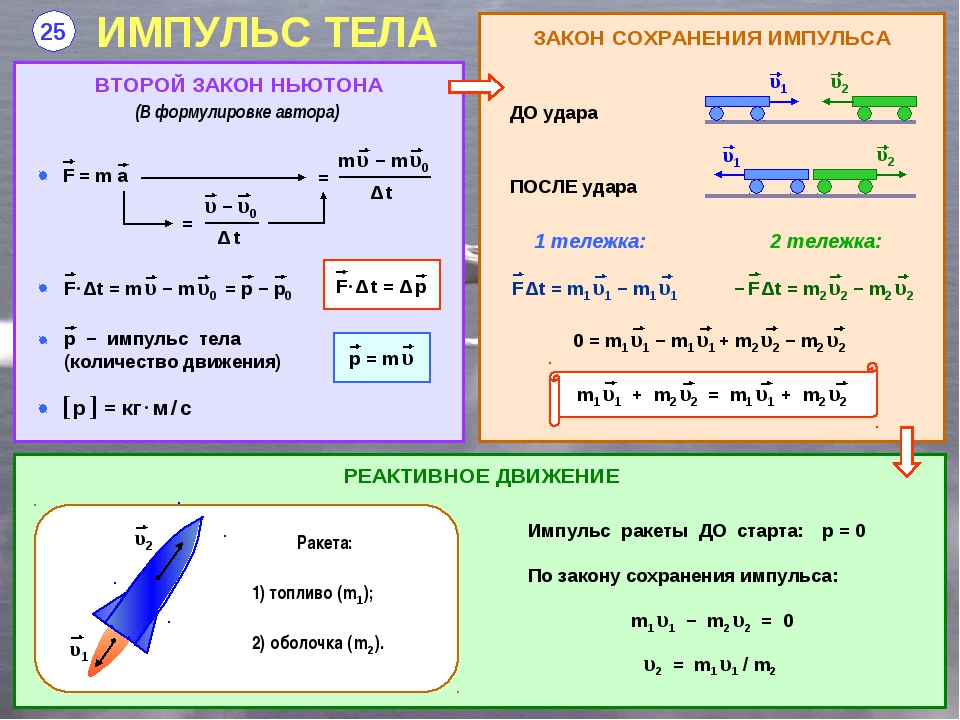
Импульс в гидродинамике

В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа ρ{\displaystyle \ \rho }. А вместо импульса фигурирует вектор плотности импульса, совпадающий по смыслу с вектором плотности потока массы

p→=ρv→.{\displaystyle {\vec {p}}=\rho {\vec {v}}.}

Поскольку в турбулентном потоке характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса. Если, в согласии с методом Рейнольдса, представить ρ=ρ¯+ρ′{\displaystyle \ \rho ={\overline {\rho }}+\rho ‘}, v→=v→¯+v→′{\displaystyle \ {\vec {v}}={\overline {\vec {v}}}+{\vec {v}}’}, где черта сверху — знак осреднения, а штрих — отклонения от среднего, то вектор осреднённой плотности импульса приобретёт вид:

p→¯=ρv→¯=ρ¯ v→¯+S→,{\displaystyle \ {\overline {\vec {p}}}={\overline {\rho {\vec {v}}}}={\overline {\rho }}~{\overline {\vec {v}}}+{\vec {S}},}

где S→=ρ′v→′¯{\displaystyle \ {\vec {S}}={\overline {\rho ‘{\vec {v}}’}}} — вектор плотности флуктуационного потока массы (или «плотность турбулентного импульса»).

Основные теоретические сведения

Импульс тела

Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р. Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:

Направление вектора импульса совпадает с направлением вектора скорости тела (направлен по касательной к траектории). Единица измерения импульса – кг∙м/с.

Изменение импульса одного тела находится по формуле (обратите внимание, что разность конечного и начального импульсов векторная):

где: p_н – импульс тела в начальный момент времени, p_к – в конечный. Главное не путать два последних понятия.

Абсолютно упругий удар – абстрактная модель соударения, при которой не учитываются потери энергии на трение, деформацию, и т.п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется. Может поменяться только его направление. При этом угол падения равен углу отражения.

Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Например, пластилиновый шарик при падении на любую поверхность полностью прекращает свое движение, при столкновении двух вагонов срабатывает автосцепка и они так же продолжают двигаться дальше вместе.

Закон сохранения импульса

При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.

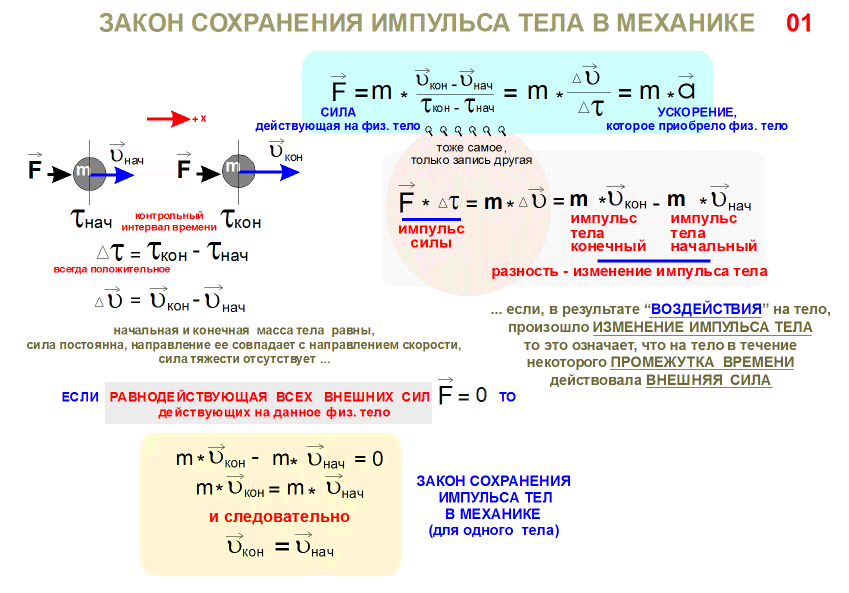
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения импульса (ЗСИ). Следствием его являются законы Ньютона. Второй закон Ньютона в импульсной форме может быть записан следующим образом:

Как следует из данной формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:

Аналогично можно рассуждать для равенства нулю проекции силы на выбранную ось. Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:

Аналогичные записи можно составить и для остальных координатных осей. Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.

Сохранение проекции импульса

Возможны ситуации, когда закон сохранения импульса выполняется только частично, то есть только при проектировании на одну ось. Если на тело действует сила, то его импульс не сохраняется. Но всегда можно выбрать ось так, чтобы проекция силы на эту ось равнялась нулю. Тогда проекция импульса на эту ось будет сохраняться. Как правило, эта ось выбирается вдоль поверхности по которой движется тело.

Многомерный случай ЗСИ. Векторный метод

В случаях если тела движутся не вдоль одной прямой, то в общем случае, для того чтобы применить закон сохранения импульса, нужно расписать его по всем координатным осям, участвующим в задаче. Но решение подобной задачи можно сильно упростить, если использовать векторный метод. Он применяется если одно из тел покоится до или после удара. Тогда закон сохранения импульса записывается одним из следующих способов:

Из правил сложения векторов следует, что три вектора в этих формулах должны образовывать треугольник. Для треугольников применяется теорема косинусов.

Определение импульса

Классическая механика

В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:

p→=∑imiv→i,{\displaystyle {\vec {p}}=\sum _{i}m_{i}{\vec {v}}_{i},}

соответственно величина p→i=miv→i{\displaystyle {\vec {p}}_{i}=m_{i}{\vec {v}}_{i}} называется импульсом одной материальной точки. Это векторная величина, направленная в ту же сторону, что и скорость частицы. Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с).

Если мы имеем дело с телом конечного размера, не состоящим из дискретных материальных точек, для определения его импульса необходимо разбить тело на малые части, которые можно считать материальными точками, и просуммировать по ним, в результате получим:

p→=∫ρ(x,y,z)v→(x,y,z)dxdydz.{\displaystyle {\vec {p}}=\int \rho (x,y,z){\vec {v}}(x,y,z)dxdydz.}

Импульс системы, на которую не действуют никакие внешние силы (или они скомпенсированы), сохраняется во времени:

dp→dt={\displaystyle {\frac {d{\vec {p}}}{dt}}=0.} (*)

Сохранение импульса в этом случае следует из второго и третьего закона Ньютона: написав второй закон Ньютона для каждой из составляющих систему материальных точек и просуммировав по всем материальным точкам, составляющим систему, в силу третьего закона Ньютона получим равенство (*).

Релятивистская механика

В релятивистской механике трёхмерным импульсом системы невзаимодействующих материальных точек называется величина

p→=∑imiv→i1−vi2c2,{\displaystyle {\vec {p}}=\sum _{i}{\frac {m_{i}{\vec {v}}_{i}}{\sqrt {1-v_{i}^{2}/c^{2}}}},}

где mi{\displaystyle m_{i}} — масса i{\displaystyle i}-й материальной точки, v→i{\displaystyle {\vec {v}}_{i}} — её скорость.

Для замкнутой системы не взаимодействующих материальных точек эта величина сохраняется. Однако трёхмерный импульс не есть релятивистски инвариантная величина, так как он зависит от системы отсчёта.
Более осмысленной величиной будет четырёхмерный импульс, который для одной материальной точки определяется как

pμ=(Ec,p→)=(mc1−vi2c2,mv→1−vi2c2).{\displaystyle p_{\mu }=(E/c,{\vec {p}})=\left({\frac {m_{0}c}{\sqrt {1-v_{i}^{2}/c^{2}}}},{\frac {m_{0}{\vec {v}}}{\sqrt {1-v_{i}^{2}/c^{2}}}}\right).}

На практике часто применяются следующие соотношения между массой, импульсом и энергией частицы:

E2−p2c2=m2c4 p=Ec2v.{\displaystyle E^{2}-\mathbf {p} ^{2}c^{2}=m^{2}c^{4}~~~~~~~~~~~~~~~~\mathbf {p} ={\frac {E}{c^{2}}}\,\mathbf {v} .}

В принципе, для системы невзаимодействующих материальных точек их 4-импульсы суммируются. Однако для взаимодействующих частиц в релятивистской механике следует учитывать импульсы не только составляющих систему частиц, но и импульс поля взаимодействия между ними. Поэтому гораздо более осмысленной величиной в релятивистской механике является тензор энергии-импульса, который в полной мере удовлетворяет законам сохранения.

Импульс в квантовой механике

Формальное определение

В квантовой механике оператором импульса частицы называют оператор — генератор группы трансляций. Это эрмитов оператор, собственные значения которого отождествляются с импульсом системы частиц. В координатном представлении для системы нерелятивистских частиц он имеет вид

P^=∑jp^j=∑j−iℏ∇j,{\displaystyle {\hat {\mathbf {P} }}=\sum _{j}{\hat {\mathbf {p} }}_{j}=\sum _{j}-i\hbar \nabla _{j},}

где ∇j{\displaystyle \nabla _{j}} — оператор набла, соответствующий дифференцированию по координатам j{\displaystyle j}-ой частицы. Гамильтониан системы выражается через оператор импульса:

H^=∑i12mip^i2+U(r1,…).{\displaystyle {\hat {H}}=\sum _{i}{\frac {1}{2m_{i}}}{\hat {\mathbf {p} }}_{i}^{2}+U(\mathbf {r_{1}} ,\dots ).}

Для замкнутой системы (U={\displaystyle U=0}) оператор импульса коммутирует с гамильтонианом и импульс сохраняется.

Определение через волны де Бройля

Формула де Бройля связывает импульс и длину волны де Бройля.

Модуль импульса обратно пропорционален длине волны λ{\displaystyle \lambda }:

p=hλ,{\displaystyle p={\frac {h}{\lambda }},}

где h{\displaystyle h} — постоянная Планка.

Для частиц не очень высокой энергии, движущихся со скоростью v≪c{\displaystyle v\ll c} (скорости света), модуль импульса равен p=mv{\displaystyle p=mv} (где m{\displaystyle m} — масса частицы), и

λ=hp=hmv.{\displaystyle \lambda ={\frac {h}{p}}={\frac {h}{mv}}.}

Следовательно, длина волны де Бройля тем меньше, чем больше модуль импульса.

В векторном виде это записывается как:

p→=h2πk→=ℏk→,{\displaystyle {\vec {p}}={\frac {h}{2\pi }}{\vec {k}}=\hbar {\vec {k}},}

где k→{\displaystyle {\vec {k}}} — волновой вектор.

Основные понятия и законы динамики

Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой

Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией. Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.

Принцип относительности Галилея:во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законамМасса — это мера инертности телаСила — это количественная мера взаимодействия тел.

Второй закон Ньютона:Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F{→} = m⋅a{→}$

Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.

Третий закон Ньютона: Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
$F_1{→} = -F_2{→} $

III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело
A (см. рис.).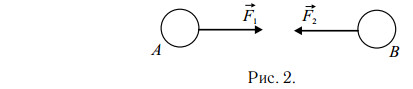
Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.
Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости.

Закон Гука записывают в виде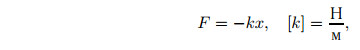
где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.

При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения подсчитывается по формуле
где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.

Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значенияГравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.

Закон всемирного тяготения:Весом телаСила тяжестиНевесомостьюИскусственный спутник ЗемлиПервая космическая скорость

1.3. Основные понятия и законы статики и гидростатики

устойчивое, неустойчивое и безразличное.устойчивое равновесие.неустойчивое положениебезразличное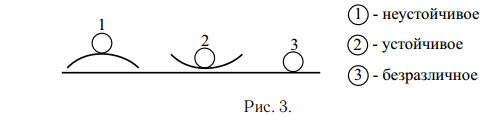Плечом силыУсловие равновесия рычага:Давлениемзакон Паскаля:Гидравлический прессA1 = A2.силой Архимедазакон Архимеда_жидк_погрУсловие плавания тела

1.4. Законы сохранения

Импульсом телаимпульсом силы.закон сохранения импульсаМеханической работойМощностьэнергией.кинетическую и потенциальную.кинетической энергией.потенциальной энергией.Энергия сжатой пружины:механическую энергию.закон сохранения механической энергии

1.5. Механические колебания и волны

КолебаниямиГармоническими колебаниямиамплитудой колебанийПериодом TЧастотой периодических колебаний-1Математическим маятникомПериод колебаний математического маятникаПериод колебаний груза на пружинеРаспространение колебаний в упругих средах.поперечнойпродольнойДлиной волныЗвуковыми волнами

Литература

Арнольд В. И. Математические методы классической механики. — 5-е изд., стереотипное. — М.: Едиториал УРСС, 2003. — 416 с. — 1500 экз. — ISBN 5-354-00341-5.
Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 4-е, исправленное. — М.: Наука, 1988. — 215 с. — («Теоретическая физика», том I). — ISBN 5-02-013850-9.
Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
Сивухин Д. В. Общий курс физики. — Издание 4-е. — М.: Физматлит, 2002. — Т. I. Механика. — 792 с. — ISBN 5-9221-0225-7.
Айзерман М. А. Классическая механика. — М.: Наука, 1980. — 368 с.

Определение импульса

Классическая механика

p→=∑imiv→i,{\displaystyle {\vec {p}}=\sum _{i}m_{i}{\vec {v}}_{i},}

p→=∫ρ(x,y,z)v→(x,y,z)dxdydz.{\displaystyle {\vec {p}}=\int \rho (x,y,z){\vec {v}}(x,y,z)dxdydz.}

dp→dt={\displaystyle {\frac {d{\vec {p}}}{dt}}=0.} (*)

Релятивистская механика

p→=∑imiv→i1−vi2c2,{\displaystyle {\vec {p}}=\sum _{i}{\frac {m_{i}{\vec {v}}_{i}}{\sqrt {1-v_{i}^{2}/c^{2}}}},}

где mi{\displaystyle m_{i}} — масса i{\displaystyle i}-й материальной точки, v→i{\displaystyle {\vec {v}}_{i}} — её скорость.

pμ=(Ec,p→)=(mc1−vi2c2,mv→1−vi2c2).{\displaystyle p_{\mu }=(E/c,{\vec {p}})=\left({\frac {m_{0}c}{\sqrt {1-v_{i}^{2}/c^{2}}}},{\frac {m_{0}{\vec {v}}}{\sqrt {1-v_{i}^{2}/c^{2}}}}\right).}

На практике часто применяются следующие соотношения между массой, импульсом и энергией частицы:

E2−p2c2=m2c4 p=Ec2v.{\displaystyle E^{2}-\mathbf {p} ^{2}c^{2}=m^{2}c^{4}~~~~~~~~~~~~~~~~\mathbf {p} ={\frac {E}{c^{2}}}\,\mathbf {v} .}

Обобщённый импульс в теоретической механике

В теоретической механике обобщённым импульсом называется частная производная лагранжиана системы по обобщённой скорости

pi=∂L∂q˙i.{\displaystyle p_{i}={{\partial {\mathcal {L}}} \over {\partial {\dot {q}}_{i}}}.}

В случае, если лагранжиан системы не зависит от некоторой обобщённой координаты, то в силу уравнений Лагранжа dpidt={\displaystyle dp_{i}/dt=0.}

Для свободной частицы в релятивистской механике функция Лагранжа имеет вид: L=−mc21−v2c2{\displaystyle {\mathcal {L}}=-mc^{2}{\sqrt {1-v^{2}/c^{2}}}}, отсюда:

p→=mv→1−v2c2.{\displaystyle {\vec {p}}={\frac {m{\vec {v}}}{\sqrt {1-v^{2}/c^{2}}}}.}

Независимость лагранжиана замкнутой системы от её положения в пространстве следует из свойства однородности пространства: для хорошо изолированной системы её поведение не зависит от того, в какое место пространства мы её поместим. По теореме Нётер из этой однородности следует сохранение некоторой физической величины. Эту величину и называют импульсом (обычным, не обобщённым).

Обобщённый импульс в электромагнитном поле

В электромагнитном поле обобщённый импульс частицы равен:

p=mv1−v2c2+qA,{\displaystyle \mathbf {p} ={\frac {m\mathbf {v} }{\sqrt {1-v^{2}/c^{2}}}}+q\mathbf {A} ,}

где A{\displaystyle \mathbf {A} } — векторный потенциал электромагнитного поля.

Литература

Арнольд В. И. Математические методы классической механики. — 5-е изд., стереотипное. — М.: Едиториал УРСС, 2003. — 416 с. — 1500 экз. — ISBN 5-354-00341-5.
Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 4-е, исправленное. — М.: Наука, 1988. — 215 с. — («Теоретическая физика», том I). — ISBN 5-02-013850-9.
Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
Сивухин Д. В. Общий курс физики. — Издание 4-е. — М.: Физматлит, 2002. — Т. I. Механика. — 792 с. — ISBN 5-9221-0225-7.
Айзерман М. А. Классическая механика. — М.: Наука, 1980. — 368 с.

Импульс в гидродинамике

p→=ρv→.{\displaystyle {\vec {p}}=\rho {\vec {v}}.}

p→¯=ρv→¯=ρ¯ v→¯+S→,{\displaystyle \ {\overline {\vec {p}}}={\overline {\rho {\vec {v}}}}={\overline {\rho }}~{\overline {\vec {v}}}+{\vec {S}},}

Импульс в квантовой механике

Формальное определение

P^=∑jp^j=∑j−iℏ∇j,{\displaystyle {\hat {\mathbf {P} }}=\sum _{j}{\hat {\mathbf {p} }}_{j}=\sum _{j}-i\hbar \nabla _{j},}

H^=∑i12mip^i2+U(r1,…).{\displaystyle {\hat {H}}=\sum _{i}{\frac {1}{2m_{i}}}{\hat {\mathbf {p} }}_{i}^{2}+U(\mathbf {r_{1}} ,\dots ).}

Для замкнутой системы (U={\displaystyle U=0}) оператор импульса коммутирует с гамильтонианом, и импульс сохраняется.

Определение через волны де Бройля

Формула де Бройля связывает импульс и длину волны де Бройля.

Модуль импульса обратно пропорционален длине волны λ{\displaystyle \lambda }:

p=hλ,{\displaystyle p={\frac {h}{\lambda }},}

где h{\displaystyle h} — постоянная Планка.

λ=hp=hmv.{\displaystyle \lambda ={\frac {h}{p}}={\frac {h}{mv}}.}

Следовательно, длина волны де Бройля тем меньше, чем больше модуль импульса.

В векторном виде это записывается как:

p→=h2πk→=ℏk→,{\displaystyle {\vec {p}}={\frac {h}{2\pi }}{\vec {k}}=\hbar {\vec {k}},}

где k→{\displaystyle {\vec {k}}} — волновой вектор.

Астрология имени Эми

Между управителем именоформы и планетой имеется очень тесная связь

Поэтому знать астрологическое влияние не менее важно, чем происхождение имени Эми, тотемы и талисманы Эми, национальность Эми и т.д

Происхождение имени Эми таково, что управляющей планетой является Марс. Эта планета наделяет носителя имени рядом преимуществ и недостатков.

Преимущества, которые получает имя Эми от Марс: Отвага, смелость, любовь к действиям, познанию, быстрота реакции, жизнестойкость

Недостатки, которыми наделяет Марс имя Эми: Инстинкт разрушения, необузданность, нетерпеливость, эгоцентризм, эгоизм

Также той или иной планете соответствует и имеет непосредственное влияние на судьбу каждая буква, из которой состоит имя Эми. Если в именоформе присутствует несколько одинаковых букв, влияние соответствующей планеты усиливается во столько раз, сколько раз повторяется эта буква. Доминирующая планета для Эми:

Особое значение имени Эми придается согласно планете, управляющей завершающей буквой. В ряде случаев, независимо от того, какую имя имеет национальность и значение, завершающая планета определяет продолжительность и особенности завершения жизни. Последняя планета по имени: Плутон

Совместимость с именем Эми

Наибольшую совместимость в любви, работе, дружбе составляют имена, покровителями которых являются планеты: Луна, Меркурий, Уран, Прозерпина.

Астрологический цвет имени: Золотисто-Оранжевый

Сторона света: Восток

Астрологический камень: Бриллиант, Цитрин, Турмалин

Олицетворяющее животное: Баран, Сорока, Барсук, Лошадь, Осел

Планетарное число и значение имени Эми

Читателям сайта aznaetelivy.ru, наверняка, будет интересно узнать, что за имя Эми с точки зрения планетарных чисел. Значение имени Эми и происхождение имени Эми указывает на планетарное число 4. Управляет этим именем Меркурий.

Четверка как итоговое число имени выводит на мистерию обретения защиты с помощью знаний, информации, умения различать истину и ложь

Зодиакальное и Сакральное число имени Эми

Происхождение имени Эми определяет Зодиакальное число 1, что соответствует знаку-зодиака Овен. Обладатель имени — Овна вовлекается в борьбу, активные действия. В худшем случае вокруг него может быть поле войны, в которую будут втягиваться окружающие. В лучшем — он станет первопроходцем и бесстрашным рыцарем, защищающим других. В коллективном бессознательном с этими именами связаны образы воинственных и активных людей.

Сакральным числом, которое определяет значение имени Эми, является 7, что соответствует знаку-зодиака Весы. Имена — Весы создают поле равновесия и справедливости. Они вовлекают в решение различных двойственных ситуаций, требующих выбора и умения все объективно оценить. Такие имена призывают к спокойствию и соблюдению во всем меры, к миру и гармонии в отношениях с окружающими.

Редакция сайта aznaetelivy.ru постаралась собрать самую полную информацию, которая описывает происхождение имени Эми, чье имя, что значит имя Эми, имя какой национальности Эми, талисманы Эми… Используйте эту информацию правильно и вы обязательно почувствуете всю скрывающуюся в нем энергетику.

1.16. Импульс тела

Пусть на тело массой m в течение некоторого малого промежутка времени Δt действовала сила Под действием этой силы скорость тела изменилась на Следовательно, в течение времени Δt тело двигалось с ускорением

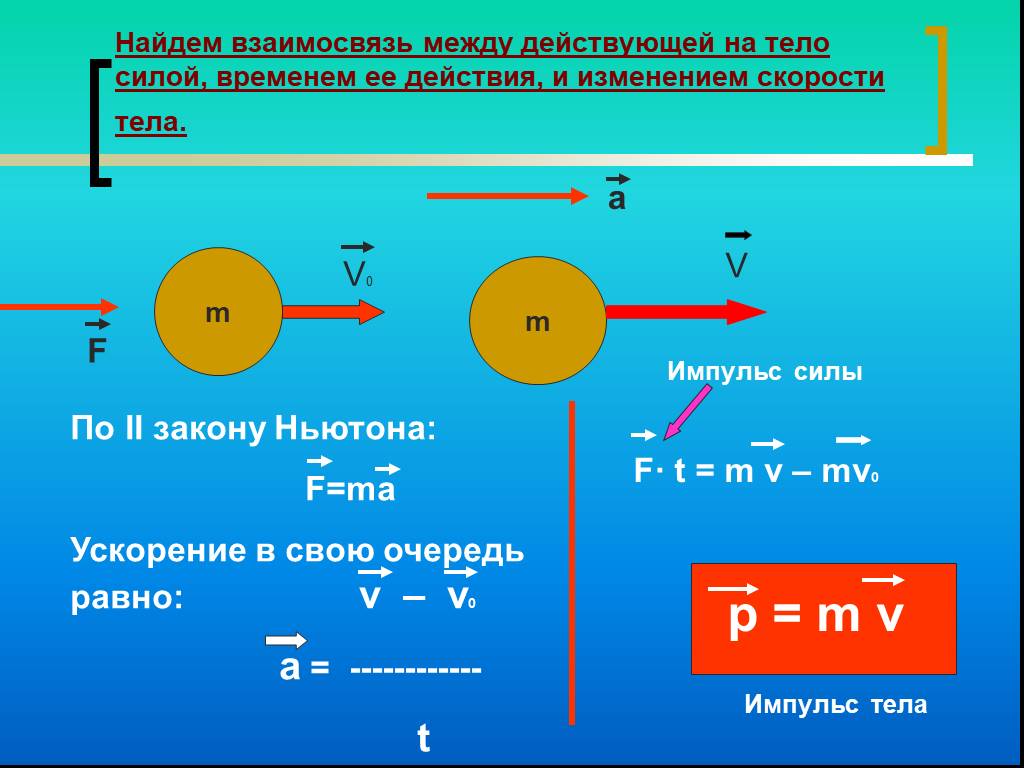
Из основного закона динамики (второго закона Ньютона) следует:

Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения). Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с).

Физическая величина, равная произведению силы на время ее действия, называется импульсом силы. Импульс силы также является векторной величиной.

В новых терминах второй закон Ньютона может быть сформулирован следующим образом: изменение импульса тела (количества движения) равно импульсу силы.

Обозначив импульс тела буквой второй закон Ньютона можно записать в виде

Именно в таком общем виде сформулировал второй закон сам Ньютон. Сила в этом выражении представляет собой равнодействующую всех сил, приложенных к телу. Это векторное равенство может быть записано в проекциях на координатные оси:

Модель.
Импульс тела

Таким образом, изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось. Рассмотрим в качестве примера одномерное движение, т. е. движение тела по одной из координатных осей (например, оси OY). Пусть тело свободно падает с начальной скоростью υ под действием силы тяжести; время падения равно t. Направим ось OY вертикально вниз. Импульс силы тяжести F_т = mg за время t равен mgt. Этот импульс равен изменению импульса тела

Этот простой результат совпадает с кинематической формулой для скорости равноускоренного движения. В этом примере сила оставалась неизменной по модулю на всем интервале времени t. Если сила изменяется по величине, то в выражение для импульса силы нужно подставлять среднее значение силы F_ср на промежутке времени ее действия. Рис. 1.16.1 иллюстрирует метод определения импульса силы, зависящей от времени.

Рисунок 1.16.1.Вычисление импульса силы по графику зависимости F(t)

Выберем на оси времени малый интервал Δt, в течение которого сила F (t) остается практически неизменной. Импульс силы F (t) Δt за время Δt будет равен площади заштрихованного столбика. Если всю ось времени на интервале от до t разбить на малые интервалы Δt_i, а затем просуммировать импульсы силы на всех интервалах Δt_i, то суммарный импульс силы окажется равным площади, которую образует ступенчатая кривая с осью времени. В пределе (Δt_i → 0) эта площадь равна площади, ограниченной графиком F (t) и осью t. Этот метод определения импульса силы по графику F (t) является общим и применим для любых законов изменения силы со временем. Математически задача сводится к интегрированию функции F (t) на интервале .

Импульс силы, график которой представлен на рис. 1.16.1, на интервале от t₁ = 0 с до t₂ = 10 с равен:

В этом простом примере

В некоторых случаях среднюю силу F_ср можно определить, если известно время ее действия и сообщенный телу импульс. Например, сильный удар футболиста по мячу массой 0,415 кг может сообщить ему скорость υ = 30 м/с. Время удара приблизительно равно 8·10–3 с.

Импульс p, приобретенный мячом в результате удара есть:

Следовательно, средняя сила F_ср, с которой нога футболиста действовала на мяч во время удара, есть:

Это очень большая сила. Она приблизительно равна весу тела массой 160 кг.

Если движение тела во время действия силы происходило по некоторой криволинейной траектории, то начальный и конечный импульсы тела могут отличаться не только по модулю, но и по направлению. В этом случае для определения изменения импульса удобно использовать диаграмму импульсов, на которой изображаются вектора и , а также вектор построенный по правилу параллелограмма. В качестве примера на рис. 1.16.2 изображена диаграмма импульсов для мяча, отскакивающего от шероховатой стенки. Мяч массой m налетел на стенку со скоростью под углом α к нормали (ось OX) и отскочил от нее со скоростью под углом β. Во время контакта со стеной на мяч действовала некоторая сила направление которой совпадает с направлением вектора

Рисунок 1.16.2.Отскок мяча от шероховатой стенки и диаграмма импульсов

При нормальном падении мяча массой m на упругую стенку со скоростью после отскока мяч будет иметь скорость Следовательно, изменение импульса мяча за время отскока равно В проекциях на ось OX этот результат можно записать в скалярной форме Δp_x = –2mυ_x. Ось OX направлена от стенки (как на рис. 1.16.2), поэтому υ_x < 0 и Δp_x > 0. Следовательно, модуль Δp изменения импульса связан с модулем υ скорости мяча соотношением Δp = 2mυ.

В словаре Энциклопедии

в физике: 1) мера механического движения (то же , что количество движения). Импульсом обладают все формы материи, в т. ч. электромагнитные и гравитационные поля;..2) импульс силы — мера действия силы за некоторый промежуток времени; равен произведению среднего значения силы на время ее действия;..3) импульс волновой — однократное возмущение, распространяющееся в пространстве или среде, напр.: звуковой импульс — внезапное и быстро исчезающее повышение давления; световой импульс (частный случай электромагнитного) — кратковременное (? 0,01 с) испускание света источником оптического излучения;..4) импульс электрический — кратковременное отклонение напряжения или тока от некоторого постоянного значения.—(от лат. impulsus — удар, толчок), толчок, побуждение, стремление; побудительная причина.