T1ha = fast positive hash / хабр

3.1. Оригинальная rebound-атака

Внутренняя фаза: эта фаза стартует с нескольких выбранных входных/выходных разностей в E_in, которые распространяются через линейный уровень в прямом и обратном направлении. Затем генерируются все возможные пары актуальных значений, которые удовлетворяют требуемой разности и соответствуют разностям после одного уровня табличной замены. Эти фактические пары значений являются стартовыми точками для внешней фазы.
Внешняя фаза: подобранные пары внутренней фазы используются в вычислениях в прямом и обратном направлении через E_fw и E_bw для получения желательных коллизий или почти-коллизий. Обычно E_fw и E_bw имеют низкую вероятность, так что необходимо повторять внутреннюю фазу для получения большего количества стартовых точек.

Что такое хеш-сумма файла

Всё очень и очень просто с этим самым хешем — давайте возьмём два файла, с первого взгляда, совершенно одинаковых…

Допустим, что я их скачал с разных сайтов. У них, как видите, совершенно одинаковое название и расширение, но кроме этого сходства, у этих инсталляторов может быть схожий до последнего байта размер.

Обычные рядовые пользователи даже не догадываются, что подобные «экзешники» являются практически простыми архивами. Так вот, в этот файл (архив) очень легко подсунуть зловреда какого-нибудь (вирус) — они почти всегда маскируются под «правильный» файл, копируют не только название с расширением, но и размер даже.

Такой изменённый файл можно распространять в сети Интернет под видом официального, белого и пушистого. Кстати, идеального антивируса не существует и Ваш защитник может Вас подвести в любой момент, если не знали.

Ещё одна ситуация — выбрали и начали скачивание какой-либо программы, файла или архива через торрент? В таком случае, подсунуть Вам маленький бездомный вирус ещё проще, ведь файл закачивается в Ваш компьютер крохотными частями, от огромного количества человек и собирается в кучу только у Вас.

Как же проверить подлинность любого файла, как его идентифицировать со 100% гарантии? Сравнить его хеш-сумму (контрольную сумму)!

Хеш-сумма файла — это уникальный идентификатор, который задаётся (автором программы или первым владельцем файла) с помощью «перемешивания» и шифрования содержимого файла по специальному алгоритму с последующей конвертацией результата (этой адской смеси) в обычную строчку символов.

На официальных сайтах программ или на торрент-трекерах обычно авторы выкладывают рядом со своими файлами оригинальную (правильную) хеш-сумму, чтоб пользователи могли сравнивать с ней свою после скачивания…

Файлы с одинаковым хешем являются абсолютно идентичными, даже если у них разное название или расширение.

Как пользоваться HashTab

При установке программа HashTab интегрируется в окно свойств Проводника. После установки программы HashTab на ваш компьютер, вы можете проверять хэш-суммы файлов. Для этого кликните по какому-нибудь файлу правой кнопкой мыши.

В контекстном меню выберите пункт «Свойства». После открытия окна, в окне «Свойства» вы увидите новую вкладку «Хеш-суммы файлов».

При нажатии на вкладку «Хеш-суммы файлов» появляется окно со значениями контрольных сумм этого файла.

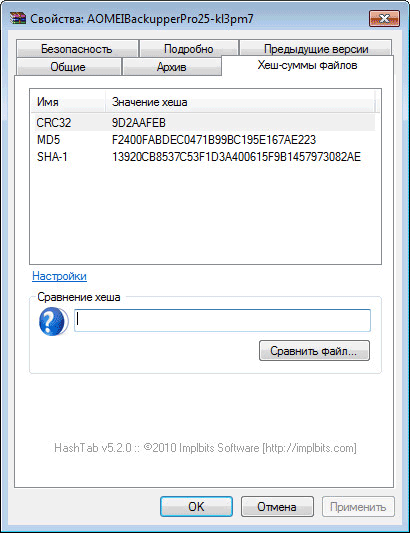
После нажатия на ссылку «Настройки», откроется окно настроек программы HashTab, где во кладке «Отображаемые хеш-суммы» можно выбрать соответствующие пункты алгоритмов проверки.

Для проверки файлов будет достаточно выбрать главные алгоритмы проверки: CRC32, MD5, SHA-1. После выбора алгоритмов проверки нажимаете на кнопку «OK».

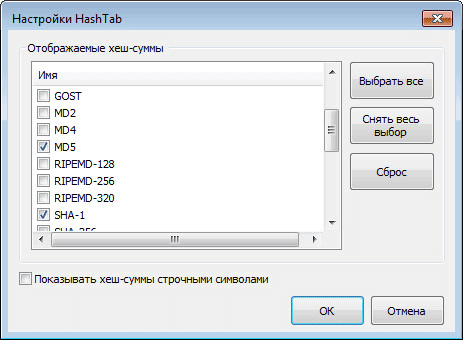
Для сравнения хеш-сумм файлов нужно будет перетянуть файл в поле «Сравнение хеша». Если значения хэша файлов совпадают, то появится зеленый флажок.

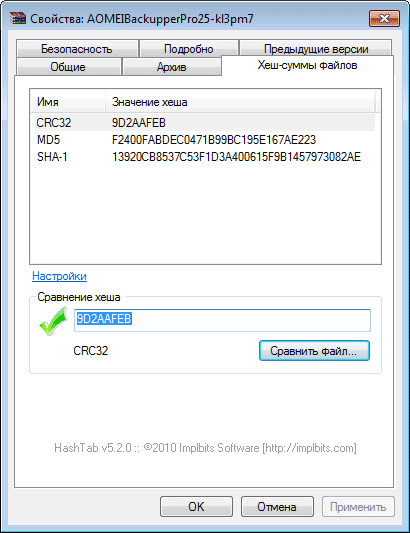
Также можно проверить хеш другим способом. Для этого, нажимаете на кнопку «Сравнить файл…», а затем выбираете в окне Проводника файл для сравнения.

После этого нажимаете на кнопку «Открыть», а потом в открывшемся окне, вы увидите полученный результат сравнения контрольной суммы файла.

Кликнув правой кнопкой мыши по соответствующей контрольной сумме, вы можете скопировать эту сумму или все контрольные суммы, а также перейти к настройкам программы, если выберете в контекстном меню соответствующий пункт.

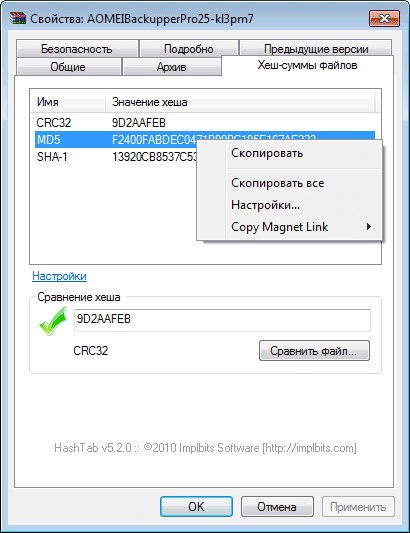
Можно также одновременно проверить два файла поодиночке и сравнить результат в двух окнах. На этом изображении видно, что контрольные суммы двух файлов совпадают.

Зачем нужен хэш

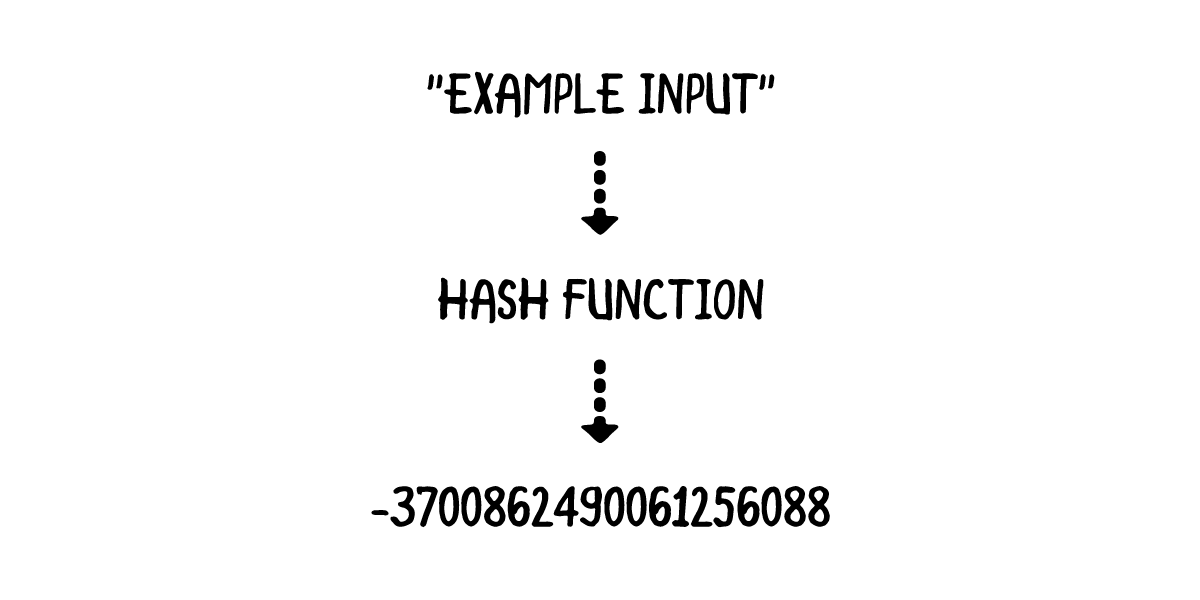
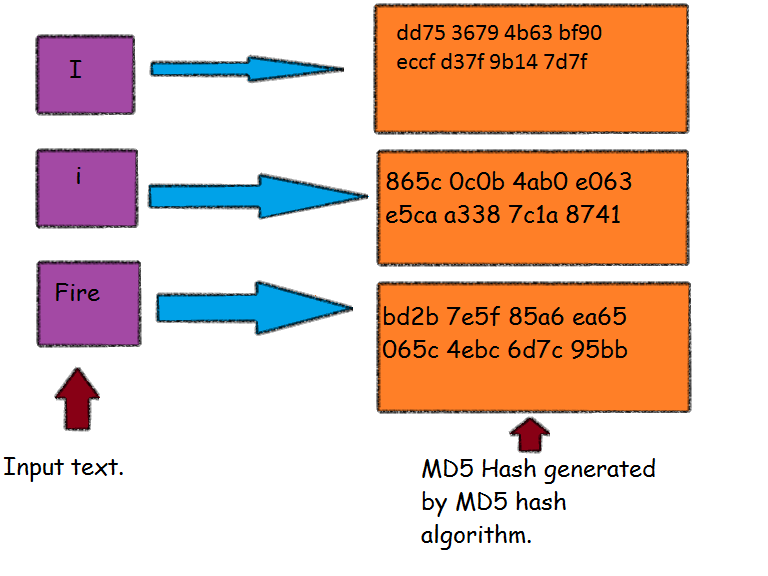
Смотрите, еще пример. Есть у вас текст в файле. Но на самом деле это ведь не текст, а массив цифровых символов (по сути число). Как вы знаете, в компьютерной логике используются двоичные числа (ноль и единица). Они запросто могут быть преобразованы в шестнадцатиричные цифры, над которыми можно проводить математические операции. Применив к ним хеш-функцию мы получим на выходе (после ряда итераций) число заданной длины (хеш-сумму).

Если мы потом в исходном текстовом файле поменяем хотя бы одну букву или добавим лишний пробел, то повторно рассчитанный для него хэш уже будет отличаться от изначального (вообще другое число будет). Доходит, зачем все это нужно? Ну, конечно же, для того, чтобы понять, что файл именно тот, что и должен быть. Это можно использовать в целом ряде аспектов работы в интернете и без этого вообще сложно представить себе работу сети.

Обещанный няш-меш

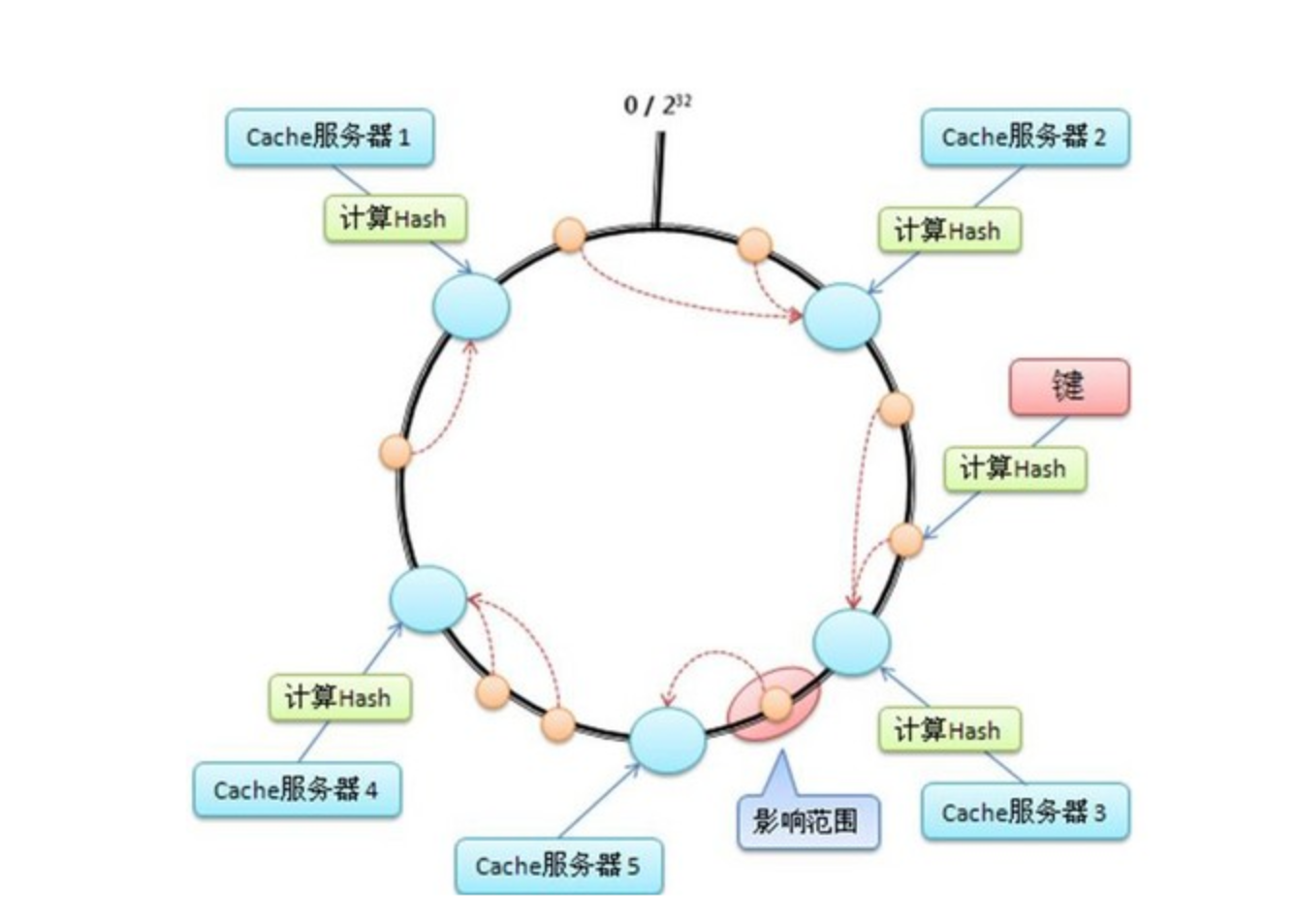
Зная хэш требуемого вспомогательно файла, можно почти смело запрашивать его у кого угодно; основная опасность: если опрашиваемый узел действительно имеет требуемый файл, то он знает его содержимое и, скорее всего, как минимум один URI-адрес, по которому требуемый файл может (или мог) быть получен. Имеем два варианта использования предлагаемой технологии с учётом этой угрозы с целью плавного подхода к няш-меш сети:

Доверенные устройства

Например, в офисе работают программисты, ЭВМ которых объединены в локальную сеть. Программист Вася приходит рано утром, открывает гитхаб и получает в кэш стили от нового дизайна, который выкатили ночью (у нас — ночь, там — день). Когда в офис приходит программист Петя и тоже загружает html-код гитхабовской странички, его ЭВМ спрашивает у всех ЭВМ в сети: «А нет ли у вас файла с таким-то хэшем?» «Лови!» — отвечает Васина ЭВМ, экономя тем самым трафик.
Потом наступает перерыв, Вася и Петя лезут смотреть котиков и пересылают фотографии друг другу. Но каждый котик скачивается через канал офиса только один раз…

Анонимный разделяемый кэш

Аня едет в трамвае с работы и читает новости… например, на Яндекс-Новостях. Встретив очередной тэг , Анин телефон со случайного MAC-адреса спрашивает всех, кого видит: «Ребят, а ни у кого нет файла с таким-то хэшем?». Если ответ получен в разумное время — профит, Аня сэкономила недешёвый мобильный трафик

Важно почаще менять MAC-адрес на случайный да не «орать», когда в поле видимости слишком мало узлов и спрашивающего можно идентифицировать визуально.
Разумность времени ответа определяется исходя из стоимости трафика

История

Шифровка сообщений без возможности однозначной расшифровки, а только с целью подтверждения авторского приоритета, применялась издавна.

Галилео Галилей наблюдал кольца Сатурна, которые принял за «ушки». Не будучи уверен, но желая утвердить свой приоритет, он опубликовал сообщение с перестановленными буквами: smaismrmilmepoetaleumibunenugttauiras. В 1610 году он раскрыл исходную фразу: Altissimum planetam tergeminum obseruaui, что в переводе с латинского языка означает «высочайшую планету тройною наблюдал». Таким образом, на момент публикации первого сообщения исходная фраза не была раскрыта, но была создана возможность подтвердить её позже.

В середине 1650-х Христиан Гюйгенс разглядел кольца и опубликовал сообщение с буквами, расставленными по алфавиту: ааааааа, ссссс, d, еееее, g, h, iiiiiii, lllll, mm, nnnnnnnnn, oooo, pp, q, rr, s, ttttt, uuuuu. Через некоторое время была опубликована и исходная фраза: Annulo cingitur, tenui plano, nusquam cohaerente, ad eclipticam inclinato — «Окружен кольцом тонким, плоским, нигде не подвешенным, наклоненным к эклиптике». От применения хеш-функции, включая и цель позднее подтвердить некоторое нераскрытое сообщение, данный случай отличается только тем, что выходное сообщение не имеет фиксированной длины, а определяется длиной входного. Фактически, расстановка букв исходного сообщения по алфавиту является некоторой хеш-функцией, но только с результатом нефиксированной длины.

В январе 1953 года Ханс Петер Лун (нем. Hans Peter Luhn) (сотрудник фирмы IBM) предложил «хеш-кодирование». Дональд Кнут считает, что Ханс первым выдвинул систематическую идею «хеширования».

В 1956 году Арнольд Думи (англ. Arnold Dumey) в своей работе «Computers and automation» первым описал идею «хеширования» такой, какой её знает большинство программистов сейчас. Думи рассматривал «хеширование» как решение «проблемы словаря», предложил использовать в качестве «хеш-адреса» остаток от деления на простое число.

В 1957 году в журнале «IBM Journal of Research and Development» была опубликована статья Уэсли Питерсона (англ. W. Wesley Peterson) о поиске текста в больших файлах. Эта работа считается первой «серьёзной» работой по «хешированию». В статье Уэсли определил «открытую адресацию», указал на уменьшение производительности при удалении. Спустя шесть лет была опубликована работа Вернера Бухгольца (нем. Werner Buchholz), в которой было проведено обширное исследование «хеш-функций». В течение нескольких последующих лет «хеширование» широко использовалось, однако никаких значимых работ не публиковалось.

В 1967 году «хеширование» в современном значении упомянуто в книге Херберта Хеллермана «Принципы цифровых вычислительных систем». В 1968 году Роберт Моррис (англ. Robert Morris) опубликовал в журнале «Communications of the ACM» большой обзор по «хешированию». Эта работа считается «ключевой» публикацией, вводящей понятие о «хешировании» в научный оборот, и закрепившей термин «хеш», ранее применявшийся только специалистами (жаргон).

До начала 1990-х годов в русскоязычной литературе в качестве эквивалента термину «хеширование» благодаря работам Андрея Петровича Ершова использовалось слово «расстановка», а для «коллизий» использовался термин «конфликт» (А. П. Ершов использовал «расстановку» с 1956 года). В русскоязычном издании книги Никлауса Вирта «Алгоритмы и структуры данных» 1989 года также используется термин «расстановка». Предлагалось также назвать метод другим русским словом: «окрошка». Однако ни один из этих вариантов не прижился, и в русской литературе используется преимущественно термин «хеширование».

Программы для вычисления различных хешей

Кроме перечисленных встроенных в Linux утилит, имеются другие программы, способные подсчитывать контрольные суммы. Часто они поддерживают сразу несколько алгоритмов хеширования, могут иметь дополнительные опции ввода и вывода (поддерживают различные форматы и кодировки), некоторые из них подготовлены для выполнения аудита файловой системы (выявления несанкционированных изменений в файлах).

Список некоторых популярных программ для вычисления хешей:

hashrat
hashdeep
Hasher
omnihash

Думаю, используя русскоязычную справку с примерами использования, вы без труда сможете разобраться в этих программах самостоятельно.

Последовательное хеширование с использованием трубы (|)

К примеру, нам нужно рассчитать sha256 хеш для строки ‘HackWare’; а затем для полученной строки (хеша), рассчитать хеш md5. Задача кажется очень тривиальной:

echo -n 'HackWare' | sha256sum | md5sum

Но это неправильный вариант. Поскольку результатом выполнения в любом случае является непонятная строка из случайных символов, трудно не только обнаружить ошибку, но даже понять, что она есть. А ошибок здесь сразу несколько! И каждая из них ведёт к получению абсолютно неправильных данных.

Даже очень бывалые пользователи командной строки Linux не сразу поймут в чём проблема, а обнаружив первую проблему не сразу поймут, что есть ещё одна.

Очень важно помнить, что в строке вместе с хешем всегда выводится имя файла, поэтому выполняя довольно очевидную команду вроде следующей:

echo -n 'HackWare' | sha256sum | md5sum

мы получим совсем не тот результат, который ожидаем. Мы предполагаем посчитать sha256 хеш строки ‘HackWare’, а затем для полученной строки (хеша) рассчитать новый хеш md5. На самом деле, md5sum рассчитывает хеш строки, к которой прибавлено « -». Т.е. получается совершенно другой результат.

Выше уже рассмотрено, как из вывода удалять « -», кажется, теперь всё должно быть в порядке:

echo -n 'HackWare' | sha256sum | awk '{print $1}' | md5sum

Давайте разобьём это действие на отдельные команды:

echo -n 'HackWare' | sha256sum | awk '{print $1}'

Получаем

353b717198496e369cff5fb17bc8be8a1d8e6e6e30be65d904cd000ebe394833

Второй этап хеширования:

echo -n '353b717198496e369cff5fb17bc8be8a1d8e6e6e30be65d904cd000ebe394833' | md5sum
0fcc41fc5d3d7b09e35866cd6e831085  -

Это и есть правильный ответ.

Попробуем выполнить

echo -n 'HackWare' | sha256sum | awk '{print $1}' | md5sum

Мы получим:

379f867937e7a241f7c7609f1d84d11f —

Проблема в том, что когда выводится промежуточный хеш, к нему добавляется символ новой строки, и второй хеш считается по этой полной строке, включающей невидимый символ!

Используя printf можно вывести результат без конечного символа новой строки:

printf '%s' `echo -n 'HackWare' | sha256sum | awk '{print $1}'` | md5sum

Результат вновь правильный:

0fcc41fc5d3d7b09e35866cd6e831085 —

С printf не все дружат и проблематично использовать рассмотренную конструкцию если нужно хешировать более трёх раз, поэтому лучше использовать tr:

echo -n 'HackWare' | sha256sum | awk '{print $1}' | tr -d '\n' | md5sum

Вновь правильный результат:

0fcc41fc5d3d7b09e35866cd6e831085 —

Или даже сделаем ещё лучше – с программой awk будем использовать printf вместо print (это самый удобный и короткий вариант):

echo -n 'HackWare' | sha256sum | awk '{printf $1}' | md5sum

Варианты t1ha

Разработка t1ha преследовала сугубо практические цели. Первой такой целью было получение быстрой переносимой и достаточно качественной функции для построения хэш-таблиц.

Затем потребовался максимально быстрый вариант хэш-функции, который давал-бы сравнимый по качеству результат, но был максимально адаптирован на целевую платформу. Например, базовый вариант t1ha работает с little-endian порядком байт, из-за чего на big-endian архитектурах требуется конвертация с неизбежной потерей производительности. Так почему-бы не избавиться от лишних операций на конкретной целевой платформе? Таким же образом было добавлено ещё несколько вариантов:

Упрощенный вариант для 32-битных платформ, как little, так и big-endian.
Вариант с использованием инструкций AES-NI, но без AVX.
Два варианта с использованием инструкций AES-NI и AVX.

Чуть позже стало понятно, что потребуются ещё варианты, сконструированные для различных применений, включая разную разрядность результата, требования к качеству и стойкости. Такое многообразие потребовало наведения порядка. Что выразилось в смене схемы именования, в которой цифровой суффикс обозначает «уровень» функции:

— максимально быстрый вариант для текущего процессора.
— базовый переносимый 64-битный вариант t1ha.
— переносимый 64-битный вариант с чуть большей заботой о качестве.
— быстрый переносимый 128-битный вариант для получения отпечатков.
и т.д.

В этой схеме предполагается, что является диспетчером, который реализует перенаправление в зависимости от платформы и возможностей текущего процессора. Кроме этого, не исключается использование суффиксов «_le» и «_be» для явного выбора между little-endian и big-endian вариантами. Таким образом, под «вывеской» t1ha сейчас находится несколько хэш-функций и это семейство будет пополняться, в том числе с прицелом на отечественный E2K «Эльбрус».

Представление о текущем наборе функций и их свойствах можно получить из вывода встроенного теста (). Стоит лишь отметить, что все функции проходят все тесты SMHasher, а производительность вариантов AES-NI сильно варьируется в зависимости от модели процессора:

Спасибо за внимание. Всем добра.English version is here

Какими свойствами должна обладать хеш-функция

Функция должна уметь приводить любой объем данных (а все они цифровые, т.е. двоичные, как вы понимаете) к числу заданной длины (по сути это сжатие до битовой последовательности заданной длины хитрым способом).
При этом малейшее изменение (хоть на один бит) входных данных должно приводить к полному изменению хеша.
Она должна быть стойкой в обратной операции, т.е. вероятность восстановления исходных данных по хешу должна быть весьма низкой (хотя последнее сильно зависит от задействованных мощностей)
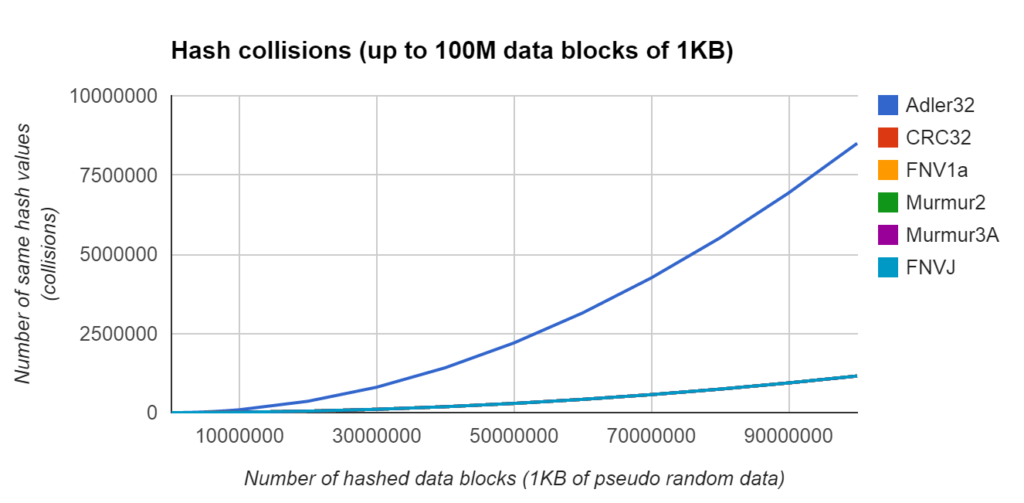
В идеале она должна иметь как можно более низкую вероятность возникновения коллизий. Согласитесь, что не айс будет, если из разных массивов данных будут часто получаться одни и те же значения хэша.
Хорошая хеш-функция не должна сильно нагружать железо при своем исполнении. От этого сильно зависит скорость работы системы на ней построенной. Как я уже говорил выше, всегда имеется компромисс между скорость работы и качеством получаемого результата.
Алгоритм работы функции должен быть открытым, чтобы любой желающий мог бы оценить ее криптостойкость, т.е. вероятность восстановления начальных данных по выдаваемому хешу.

Применения в реальной жизни

Чек-суммы. Простой и быстрый способ проверить целостность большого передаваемого файла — посчитать хэш-функцию на стороне отправителя и на стороне получателя и сравнить.
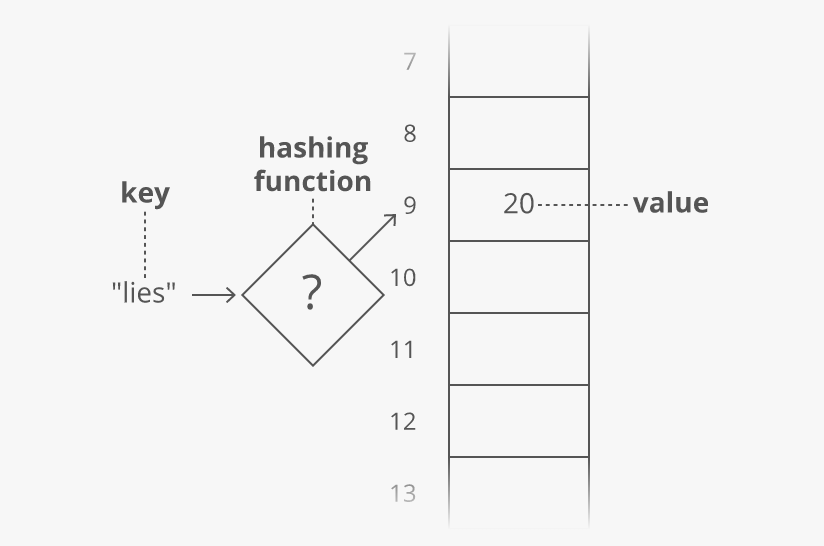
Хэш-таблица. Класс unordered_set из STL можно реализовать так: заведём (n) изначально пустых односвязных списков. Возьмем какую-нибудь хэш-функцию (f) с областью значений ([0, n)). При обработке .insert(x) мы будем добавлять элемент (x) в (f(x))-тый список. При ответе на .find(x) мы будем проверять, лежит ли (x)-тый элемент в (f(x))-том списке. Благодаря «равномерности» хэш-функции, после (k) добавлений ожидаемое количество сравнений будет равно (frac{k}{n}) = (O(1)) при правильном выборе (n).
Мемоизация. В динамическом программировании нам иногда надо работать с состояниями, которые непонятно как кодировать, чтобы «разгладить» в массив. Пример: шахматные позиции. В таком случае нужно писать динамику рекурсивно и хранить подсчитанные значения в хэш-таблице, а для идентификации состояния использовать его хэш.
Проверка на изоморфизм. Если нам нужно проверить, что какие-нибудь сложные структуры (например, деревья) совпадают, то мы можем придумать для них хэш-функцию и сравнивать их хэши аналогично примеру со строками.
Криптография. Правильнее и безопаснее хранить хэши паролей в базе данных вместо самих паролей — хэш-функцию нельзя однозначно восстановить.
Поиск в многомерных пространствах. Детерминированный поиск ближайшей точки среди (m) точек в (n)-мерном пространстве быстро не решается. Однако можно придумать хэш-функцию, присваивающую лежащим рядом элементам одинаковые хэши, и делать поиск только среди элементов с тем же хэшом, что у запроса.

Хэшируемые объекты могут быть самыми разными: строки, изображения, графы, шахматные позиции, просто битовые файлы.

Источники

https://ru.crypto-news.io/articles/heshirovanie-ego-funkcii-i-svoistva.html
https://zen.yandex.ru/media/info_law_society/shifrovanie-heshirovanie-kodirovanie-dannyh-razlichiia-i-primenenie-5d6168b0c31e4900ad8a4614
https://habr.com/ru/post/93226/
https://KtoNaNovenkogo.ru/voprosy-i-otvety/xesh-chto-eto-takoe-xesh-funkciya.html
https://coderlessons.com/tutorials/akademicheskii/izuchite-kriptografiiu/kriptografiia-khesh-funktsii
https://OptimaKomp.ru/chto-takoe-khesh-summa-fajjla-zachem-i-kak-ejo-zameryat/
https://vellisa.ru/hashtab-kontrolnyie-summyi-fayla
https://algorithmica.org/ru/hashing

Методы борьбы с коллизиями

Основная статья: Коллизия хеш-функции

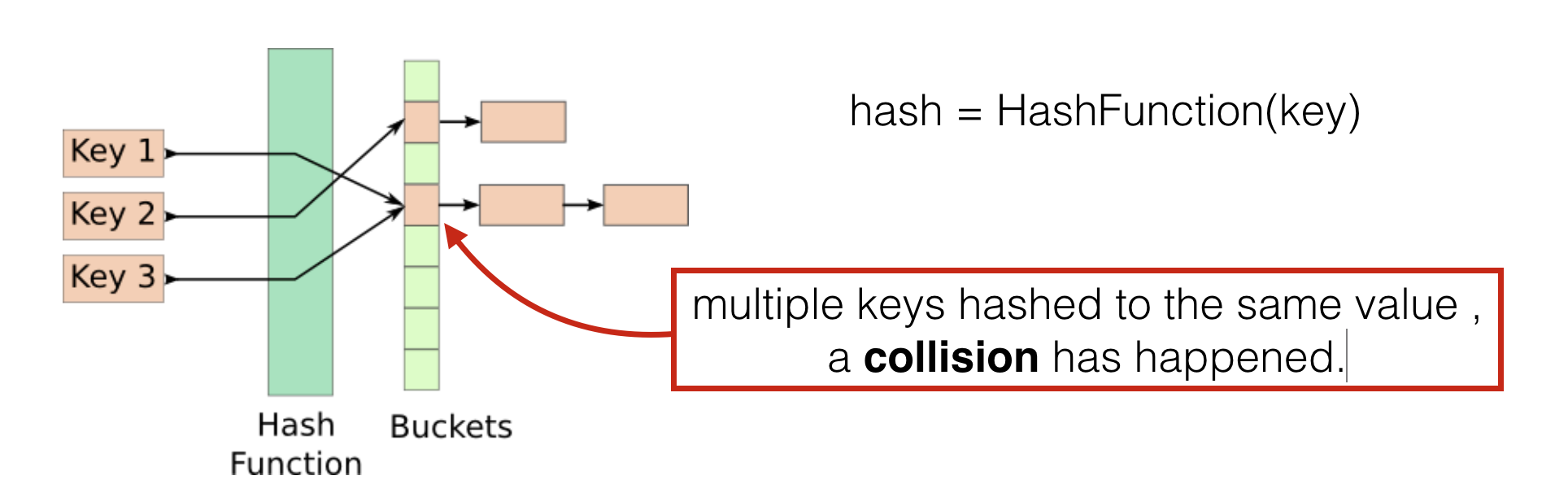
Коллизией (иногда конфликтом или столкновением) называется случай, при котором одна хеш-функция для разных входных блоков возвращает одинаковые хеш-коды.

Методы борьбы с коллизиями в хеш-таблицах

Основная статья: Хеш-таблица

Большинство первых работ, описывающих хеширование, посвящено методам борьбы с коллизиями в хеш-таблицах. Тогда хеш-функции применялись при поиске текста в файлах большого размера. Существует два основных метода борьбы с коллизиями в хеш-таблицах:

метод цепочек (метод прямого связывания);
метод открытой адресации.

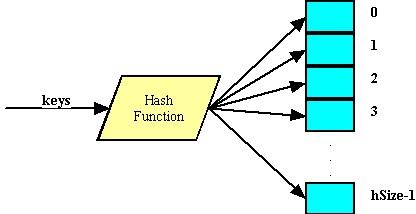
При использовании метода цепочек в хеш-таблице хранятся пары «связный список ключей» — «хеш-код». Для каждого ключа хеш-функцией вычисляется хеш-код; если хеш-код был получен ранее (для другого ключа), ключ добавляется в существующий список ключей, парный хеш-коду; иначе создаётся новая пара «список ключей» — «хеш-код», и ключ добавляется в созданный список. В общем случае, если имеется N{\displaystyle N} ключей и M{\displaystyle M} списков, средний размер хеш-таблицы составит NM{\displaystyle {\frac {N}{M}}}. В этом случае при поиске по таблице по сравнению со случаем, в котором поиск выполняется последовательно, средний объём работ уменьшится примерно в M{\displaystyle M} раз.

При использовании метода открытой адресации в хеш-таблице хранятся пары «ключ» — «хеш-код». Для каждого ключа хеш-функцией вычисляется хеш-код; пара «ключ» — «хеш-код» сохраняется в таблице. В этом случае при поиске по таблице по сравнению со случаем, в котором используются связные списки, ссылки не используются, выполняется последовательный перебор пар «ключ» — «хеш-код», перебор прекращается после обнаружения нужного ключа. Последовательность, в которой просматриваются ячейки таблицы, называется последовательностью проб.

Криптографическая соль

Основная статья: Соль (криптография)

Для защиты паролей и цифровых подписей от подделки создано несколько методов, работающих даже в том случае, если криптоаналитику известны способы построения коллизий для используемой хеш-функции. Одним из таких методов является добавление к входным данным так называемой криптографической «соли» — строки случайных данных; иногда «соль» добавляется и к хеш-коду. Добавление случайных данных значительно затрудняет анализ итоговых хеш-таблиц. Данный метод, к примеру, используется при сохранении паролей в UNIX-подобных операционных системах.

3.6. Нахождение коллизий для 9,5-раундовой функции сжатия ГОСТ Р

19264Рис. 6. Схематичное изображение атаки для 9,5-раундовой функции сжатия ГОСТ Р

3.6.1. Внешняя фаза

R₃R₈-56R₂R₉R₁R₁₀-112112mR₁₀P112+641766464+17624016128176128

5. Мультиколлизии хэш-функции ГОСТ Р

kknn/2kn(k-1)/kttn/2tB₁B₁*B₂B₂*B_tB_t*tb₁b₂b_tb_iB_iB_i*Рис. 7. Схема 2t-коллизии Жуа. 2t сообщений имеют вид (b₁, b₂,…, b_t), где b_i – один из двух блоков B_i и B_i*kth_t

Пусть h будет начальным значением IV алгоритма ГОСТ Р.
Для i от 1 до t выполняем:
- Поиск таких B_i и B_i*, для которых g_N(h_i-1, B_i) = g_N(h_i-1, B_i*), где B_i и B_i* имеют форму 0256 || {0, 1}256. Поскольку всего существует 2256 сообщений такого вида, мы предполагаем найти коллизию с помощью обобщенного парадокса дней рождений .
- Составление результирующих 2t сообщений в форме (b₁,…, b_t), где b_i – это один из двух блоков: B_i или B_i*.

tkktNkkРис. 8. Схематическое изображение конструирования k коллизий для ГОСТ Р256256b₁b₂b_t₂tkt256tt256kk

X. Wang, H. Yu, How to Break MD5 and Other Hash Functions, in: Advances in Cryptology–EUROCRYPT 2005, Springer, 2005, pp. 19–35.
X. Wang, Y. L. Yin, H. Yu, Finding Collisions in the Full SHA-1, in: Advances in Cryptology–CRYPTO 2005, Springer, 2005, pp. 17–36.
V. Dolmatov, Gost R 34.11-94: Hash function algorithm.
P. Barreto, V. Rijmen, The Whirlpool Hashing Function, in: First open NESSIE Workshop, Leuven, Belgium, Vol. 13, 2000, p. 14.
F. Mendel, C. Rechberger, M. Schläffer, S. S. Thomsen, The Rebound Attack: Cryptanalysis of Reduced Whirlpool and Grøstl, in: Fast Software Encryption, Springer, 2009, pp. 260–276.
M. Lamberger, F. Mendel, C. Rechberger, V. Rijmen, M. Schläffer, Rebound Distinguishers: Results on the Full Whirlpool Compression Function, in: Advances in Cryptology–ASIACRYPT 2009, Springer, 2009, pp. 126–143.
H. Gilbert, T. Peyrin, Super-sbox Cryptanalysis: Improved Attacks for AES-like Permutations, in: Fast Software Encryption, Springer, 2010, pp. 365–383.
O. Dunkelman, N. Keller, A. Shamir, Improved Single-Key Attacks on 8-Round AES-192 and AES-256, in: Advances in Cryptology-ASIACRYPT 2010, Springer, 2010, pp. 158–176.
F. Mendel, T. Peyrin, C. Rechberger, M. Schläffer, Improved Cryptanalysis of the Reduced Grøstl Compression Function, Echo Permutation and AES Block Cipher, in: Selected Areas in Cryptography, Springer, 2009, pp. 16–35.
D. Khovratovich, I. Nikolić, C. Rechberger, Rotational Rebound Attacks on Reduced Skein, in: Advances in Cryptology-ASIACRYPT 2010, Springer, 2010, pp. 1–19.
A. Duc, J. Guo, T. Peyrin, L. Wei, Unaligned Rebound Attack: Application to Keccak, in: Fast Software Encryption, Springer, 2012, pp. 402–421.
A. Joux, Multicollisions in Iterated Hash Functions: Application to Cascaded Constructions, in: Advances in Cryptology–CRYPTO 2004, Springer, 2004, pp. 306–316.
D. Wagner, A Generalized Birthday Problem, in: Advances in Cryptology–CRYPTO 2002, Springer, 2002, pp. 288–304.

Что за «зверь» такой это хеширование?

Чтобы в головах читателей не образовался «винегрет», начнем со значения терминологий применительно к цифровым технологиям:

хэш-функция («свертка») – математическое уравнение или алгоритм, предназначенный и позволяющий превратить входящий информационный поток неограниченного объема в лаконичную строчку с заданным количеством парных символов (число зависит от протокола);
хеширование – процесс, описанный в предыдущем пункте;
хэш (хэш-код, хэш-сумма) – та самая лаконичная строчка (блок) из нескольких десятков «случайно» подобранных символов или, другими словами, результат хеширования;
коллизия – один и тот же хэш для разных наборов данных.

Исходя из пояснений, делаем вывод: хеширование – процесс сжатия входящего потока информации любого объема (хоть все труды Уильяма Шекспира) до короткой «аннотации» в виде набора случайных символов и цифр фиксированной длины.

Коллизии

Коллизии хэш-функций подразумевает появление общего хэш-кода на два различных массива информации. Неприятная ситуация возникает по причине сравнительно небольшого количества символов в хэш. Другими совами, чем меньше знаков использует конечная формула, тем больше вероятность итерации (повтора) одного и того же хэш-кода на разные наборы данных. Чтобы снизить риск появления коллизии, применяют двойное хеширование строк, образующее открытый и закрытый ключ – то есть, используется 2 протокола, как, например, в Bitcoin. Специалисты, вообще, рекомендуют обойтись без хеширования при осуществлении каких-либо ответственных проектов, если, конечно же, это возможно. Если без криптографической хэш-функции не обойтись, протокол обязательно нужно протестировать на совместимость с ключами.

Технические параметры

Основополагающие характеристики протоколов хеширования выглядят следующим образом:

Наличие внутрисистемных уравнений, позволяющих модифицировать нефиксированный объем информации в лаконичный набор знаков и цифр заданной длины.
Прозрачность для криптографического аудита.
Наличие функций, дающих возможность надежно кодировать первоначальную информацию.
Способность к расшифровке хэш-суммы с использованием вычислительного оборудования средней мощности.

Здесь стоит так же отметить важные свойства алгоритмов: способность «свертывать» любой массив данных, производить хэш конкретной длины, распределять равномерно на выходе значения функции. Необходимо заметить, любые изменения во входящем сообщении (другая буква, цифра, знак препинания, даже лишний пробел) внесут коррективы в итоговый хэш-код. Он просто будет другим – такой же длины, но с иными символами.

Требования

К эффективной во всех отношениях хэш-функции выдвигаются следующие требования:

протокол должен обладать чувствительностью к изменениям, происходящим во входящих документах – то есть, алгоритм обязан распознавать перегруппировку абзацев, переносы, другие элементы текстовых данных (смысл текста не меняется, просто происходит его коррекция);
технология обязана так преобразовывать поток информации, чтобы невозможно на практике осуществить обратную процедуру – восстановить из значения хэш первоначальные данные;
протокол должен использовать такие математические уравнения, которые исключили или значительно снизили факт появления коллизии.

Данные требования выполнимы исключительно тогда, когда протокол базируется на сложных математических уравнениях.

Описание

В настоящее время практически ни одно приложение криптографии не обходится без использования хэширования.

Хэш-функции – это функции, предназначенные для «сжатия» произвольного сообщения или набора данных, записанных, как правило, в двоичном алфавите, в некоторую битовую комбинацию фиксированной длины, называемую сверткой. Хэш-функции имеют разнообразные применения при проведении статистических экспериментов, при тестировании логических устройств, при построении алгоритмов быстрого поиска и проверки целостности записей в базах данных. Основным требованием к хэш-функциям является равномерность распределения их значений при случайном выборе значений аргумента.

Криптографической хеш-функцией называется всякая хеш-функция, являющаяся криптостойкой, то есть удовлетворяющая ряду требований специфичных для криптографических приложений. В криптографии хэш-функции применяются для решения следующих задач:

построения систем контроля целостности данных при их передаче или хранении,
аутентификация источника данных.

Хэш-функцией называется всякая функция h:X -> Y, легко вычислимая и такая, что для любого сообщения M значение h(M) = H (свертка) имеет фиксированную битовую длину. X — множество всех сообщений, Y — множество двоичных векторов фиксированной длины.Как правило хэш-функции строят на основе так называемых одношаговых сжимающих функций y = f(x1, x2) двух переменных, где x1, x2 и y — двоичные векторы длины m, n и n соответственно, причем n — длина свертки, а m — длина блока сообщения.

Для получения значения h(M) сообщение сначала разбивается на блоки длины m (при этом, если длина сообщения не кратна m то последний блок неким специальным образом дополняется до полного), а затем к полученным блокам M1, M2,.., MN применяют следующую последовательную процедуру вычисления свертки:

Ho = v,Hi = f(Mi,Hi-1), i = 1,.., N,h(M) = HNЗдесь v — некоторая константа, часто ее называют инициализирующим вектором. Она выбираетсяиз различных соображений и может представлять собой секретную константу или набор случайных данных (выборку даты и времени, например).

При таком подходе свойства хэш-функции полностью определяются свойствами одношаговой сжимающей функции.

Выделяют два важных вида криптографических хэш-функций — ключевые и бесключевые. Ключевые хэш-функции называют кодами аутентификации сообщений. Они дают возможность без дополнительных средств гарантировать как правильность источника данных, так и целостность данных в системах с доверяющими друг другу пользователями.

Бесключевые хэш-функции называются кодами обнаружения ошибок. Они дают возможность с помощью дополнительных средств (шифрования, например) гарантировать целостность данных. Эти хэш-функции могут применяться в системах как с доверяющими, так и не доверяющими друг другу пользователями.