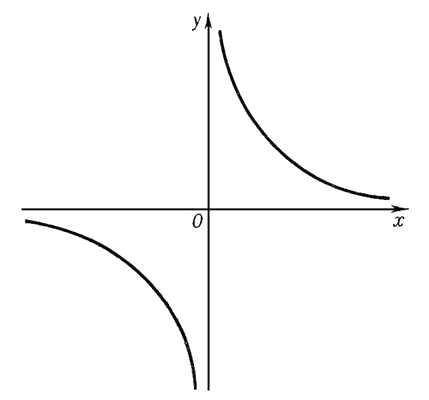Что такое гипербола

Касательная и нормаль

Поскольку гипербола является гладкой кривой, в каждой её точке (x, y) можно провести касательную и нормаль. Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:

xxa2−yyb2=1{\displaystyle {\frac {xx_{0}}{a^{2}}}-{\frac {yy_{0}}{b^{2}}}=1},

или, что то же самое,

y=y+b2xa2y(x−x){\displaystyle y=y_{0}+{\frac {b^{2}x_{0}}{a^{2}y_{0}}}\left(x-x_{0}\right)}.

Вывод уравнения касательной

Уравнение касательной произвольной плоской линии имеет вид y−y=y′(x,y)⋅(x−x){\displaystyle y-y_{0}=y’\left(x_{0},y_{0}\right)\cdot \left(x-x_{0}\right)} Каноническое уравнение гиперболы можно представить в виде пары функций y=±b2a2x2−b2{\displaystyle y=\pm {\sqrt {{\frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}. Тогда производная этих функций имеет вид y′=±b2a2xb2a2x2−b2=b2a2xy{\displaystyle y’=\pm {\frac {{\frac {b^{2}}{a^{2}}}x}{\sqrt {{\frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}={\frac {b^{2}}{a^{2}}}{\frac {x}{y}}}. Подставив это уравнение в общее уравнение касательной, получим y−y=b2a2xy(x−x){\displaystyle y-y_{0}={\frac {b^{2}}{a^{2}}}{\frac {x_{0}}{y_{0}}}\left(x-x_{0}\right)} xxa2−yyb2=x2a2−y2b2=1{\displaystyle {\frac {xx_{0}}{a^{2}}}-{\frac {yy_{0}}{b^{2}}}={\frac {x_{0}^{2}}{a^{2}}}-{\frac {y_{0}^{2}}{b^{2}}}=1}

Уравнение нормали к гиперболе имеет вид:

y=y−a2b2yx(x−x){\displaystyle y=y_{0}-{\frac {a^{2}}{b^{2}}}{\frac {y_{0}}{x_{0}}}\left(x-x_{0}\right)}.

Вывод уравнения нормали

Уравнение нормали произвольной плоской линии имеет вид y−y=1y′(x,y)(x−x){\displaystyle y-y_{0}={\frac {1}{y’\left(x_{0},y_{0}\right)}}\left(x_{0}-x\right)}. Каноническое уравнение гиперболы можно представить в виде пары функций y=±b2a2x2−b2{\displaystyle y=\pm {\sqrt {{\frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}. Тогда производная этих функций имеет вид y′=±b2a2xb2a2x2−b2=b2a2xy{\displaystyle y’=\pm {\frac {{\frac {b^{2}}{a^{2}}}x}{\sqrt {{\frac {b^{2}}{a^{2}}}x^{2}-b^{2}}}}={\frac {b^{2}}{a^{2}}}{\frac {x}{y}}}. Подставив это уравнение в общее уравнение нормали, получим y−y=−a2b2yx(x−x){\displaystyle y-y_{0}=-{\frac {a^{2}}{b^{2}}}{\frac {y_{0}}{x_{0}}}\left(x-x_{0}\right)}.

В словаре Словарь иностранных слов

I

ы, ж.

Стилистическая фигура, состоящая в образном преувеличении. Гиперболический — характеризую-щийся гиперболой, свойственный гиперболе. Гиперболизировать — преувеличивать. | Примеры гипер-болы в художественной и бытовой речи: «В сто сорок солнц закат пылал» (Маяковский); «Тыщу раз тебе говорили!»||Ср. ЛИТОТА» title=’ЛИТОТА, ЛИТОТА это, что такое ЛИТОТА, ЛИТОТА толкование’>ЛИТОТА.II

ы, ж., мат.

Незамкнутая кривая из двух неограниченно простирающихся ветвей, одно из сечений прямого круго-вого конуса плоскостью, параллельной двум его образующим. Гиперболический — относящийся к ги-перболе.||Ср. ПАРАБОЛА.

Кривизна и эволюта

Синим цветом показана гипербола. Зелёным цветом — эволюта правой ветви этой гиперболы (эволюта левой ветви вне рисунка. Красным цветом показан круг, соответствующий кривизне гиперболы в её вершине)

Кривизна гиперболы в каждой её точке (x, y) определяется из выражения:

K=ab(a2b2y2+b2a2x2)32{\displaystyle K={\frac {ab}{\left({\frac {a^{2}}{b^{2}}}y^{2}+{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}}}.

Соответственно, радиус кривизны имеет вид:

R=1K=(a2b2y2+b2a2x2)32ab{\displaystyle R={\frac {1}{K}}={\frac {\left({\frac {a^{2}}{b^{2}}}y^{2}+{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}{ab}}}.

В частности, в точке (a, ) радиус кривизны равен

R(a,)=b2a=p{\displaystyle R\left(a,0\right)={\frac {b^{2}}{a}}=p}.

Вывод формулы для радиуса кривизны

Формула для радиуса кривизны плоской линии, заданной параметически, имеет вид: Rc=(x′2 +y′2)32|x′y″−x″y′|{\displaystyle R_{c}={\frac {\left(x’^{2}\ +y’^{2}\right)^{3/2}}{\left|x’y»-x»y’\right|}}}. Воспользуемся параметрическим представлением гиперболы: {x=a⋅ch(t)y=b⋅sh(t){\displaystyle {\begin{cases}x=a\cdot \mathrm {ch} \,(t)\\y=b\cdot \mathrm {sh} \,(t)\end{cases}}} Тогда, первая производная x и y по t имеет вид {x′=a⋅sh(t)=abyy′=b⋅ch(t)=bax{\displaystyle {\begin{cases}x’=a\cdot \mathrm {sh} \,(t)={\frac {a}{b}}y\\y’=b\cdot \mathrm {ch} \,(t)={\frac {b}{a}}x\end{cases}}}, а вторая производная — {x″=a⋅ch(t)=xy″=b⋅sh(t)=y{\displaystyle {\begin{cases}x»=a\cdot \mathrm {ch} \,(t)=x\\y»=b\cdot \mathrm {sh} \,(t)=y\end{cases}}} Подставляя эти значения в формулу для кривизны получаем: Rc=(a2b2y2 +b2a2x2)32|ay2b−bx2a|=(a2b2y2 +b2a2x2)32ab|y2b−x2a|=(a2b2y2 +b2a2x2)32ab{\displaystyle R_{c}={\frac {\left({\frac {a^{2}}{b^{2}}}y^{2}\ +{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}{\left|a{\frac {y^{2}}{b}}-b{\frac {x^{2}}{a}}\right|}}={\frac {\left({\frac {a^{2}}{b^{2}}}y^{2}\ +{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}{ab\left|{\frac {y^{2}}{b}}-{\frac {x^{2}}{a}}\right|}}={\frac {\left({\frac {a^{2}}{b^{2}}}y^{2}\ +{\frac {b^{2}}{a^{2}}}x^{2}\right)^{3/2}}{ab}}}.

Координаты центров кривизны задаются парой уравнений:

{xc=x3a2(1+b2a2)yc=−y3b2(1+a2b2){\displaystyle {\begin{cases}x_{c}={\frac {x^{3}}{a^{2}}}\left(1+{\frac {b^{2}}{a^{2}}}\right)\\y_{c}=-{\frac {y^{3}}{b^{2}}}\left(1+{\frac {a^{2}}{b^{2}}}\right)\end{cases}}}

Подставив в последнюю систему уравнений вместо x и y их значения из параметрического представления гиперболы, получим пару уравнений, задающих новую кривую, состоящую из центров кривизны гиперболы. Эта кривая называется эволютой гиперболы.

{x=±ach3t(1+b2a2)y=bsh3t(1+a2b2){\displaystyle {\begin{cases}x=\pm a\,\mathrm {ch} ^{3}\,t\left(1+{\frac {b^{2}}{a^{2}}}\right)\\y=b\,\mathrm {sh} ^{3}\,t\left(1+{\frac {a^{2}}{b^{2}}}\right)\end{cases}}}

Эллиптическая система координат

Свойства

• Оптическое свойство.

  Иначе говоря, если F1{\displaystyle F_{1}} и F2{\displaystyle F_{2}} фокусы гиперболы, то касательная в любой точке X{\displaystyle X} гиперболы является биссектрисой угла ∠F1XF2{\displaystyle \angle F_{1}XF_{2}}.

  Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.

• Для любой точки, лежащей на гиперболе, отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.
• Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.
• Каждая гипербола имеет сопряжённую гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Это соответствует замене a и b друг на друга в формуле, описывающей гиперболу. Сопряжённая гипербола не является результатом поворота начальной гиперболы на угол 90°; гиперболы различаются формой при a≠b{\displaystyle a\neq b}.
• Отрезок касательной в каждой точке гиперболы, заключенный между двумя асимптотами гиперболы, делится точкой касания пополам и отсекает от двух асимптот треугольник постоянной площади.

Асимптоты

Две сопряжённые гиперболы (голубая и зелёная) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так как a = b = 1

Для гиперболы, заданной в каноническом виде

x2a2−y2b2=1{\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}

уравнения двух асимптот имеют вид:

xa±yb={\displaystyle {\frac {x}{a}}\pm {\frac {y}{b}}=0}.

Диаметры и хорды

Диаметры гиперболы

Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряжённый диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.

Угловой коэффициент k{\displaystyle k} параллельных хорд и угловой коэффициент k1{\displaystyle k_{1}} соответствующего диаметра связан соотношением

k⋅k1=ε2−1=b2a2{\displaystyle k\cdot k_{1}=\varepsilon ^{2}-1={\frac {b^{2}}{a^{2}}}}

Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными. Главными диаметрами называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.

Определение центра гиперболы по её графику

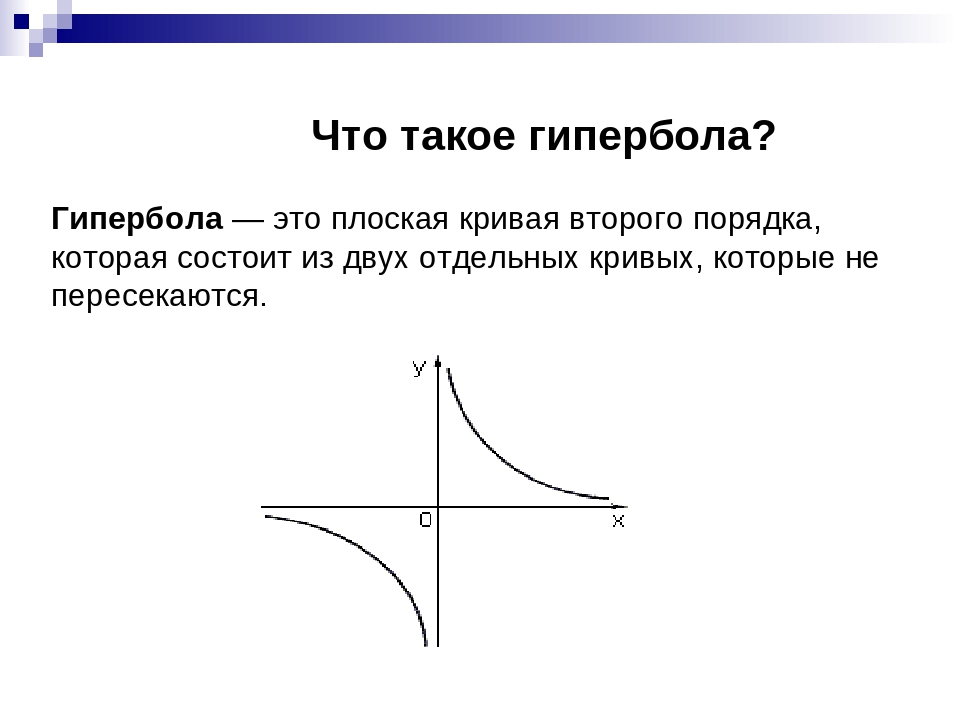
Гипербола — определение

Само это слово греческое – «hyper­bole» и обозначает оно «чрезмерность, избыток, преувеличение».

Гипербола – это одно из средств усиления эмоциональной оценки, заключающееся в чрезмерном преувеличении каких-либо явлений, качеств, свойств или процессов. Благодаря этому создается более впечатляющий образ.

Причем часто преувеличение доходит до совершенно непостижимых понятий, иногда даже граничащих с абсурдом. Любой иностранец, если будет переводить словосочетания дословно, будет явно озадачен. Мы же давно к ним привыкли, и воспринимаем их как совершенно нормальные.

Вот примеры наиболее часто используемых в обиходе гипербол:

• НАПУГАТЬ ДО СМЕРТИ
• ТЫСЯЧА ИЗВИНЕНИЙ
• ХОТЬ ЗАЛЕЙСЯ
• РЕКИ КРОВИ
• ГОРЫ ТРУПОВ
• ЖДУ ЦЕЛУЮ ВЕЧНОСТЬ
• ЕХАТЬ ЗА ТЫСЯЧУ КИЛОМЕТРОВ
• ВЕСЬ ДЕНЬ ПРОСТОЯЛА
• КУЧА ДЕНЕГ
• ПИР НА ВЕСЬ МИР
• МОРЕ СЛЕЗ
• НЕ ВИДЕЛИСЬ 100 ЛЕТ
• ОКЕАН СТРАСТЕЙ
• ВЕСИТ СТО ПУДОВ
• ЗАДУШИТЬ В ОБЪЯТЬЯХ
• ИСПУГАТЬСЯ ДО СМЕРТИ

Все перечисленные выражения мы постоянно используем в разговорной речи. И ради эксперимента просто попробуйте разобрать их дословно и увидите, насколько некоторые из них смешны, а порой и абсурдны.

Ну, например, «хоть залейся» — это должно быть такое количество жидкости, чтобы ее хватило на целый бассейн, в который можно было бы погрузиться с головой. Хотя на самом деле мы этим выражением просто хотим сказать, что напитков у нас много — даже больше чем нужно.

Или фраза «куча денег» на самом ведь деле обозначает просто хорошее финансовое состояние, а не то, что человек собрал все свои сбережения и давай их складывать в одну кучу.

А выражение «ехать за тысячу километров» мы употребляем, ни когда речь идет о реальном расстоянии, например, от Москвы до Волгограда или Ростова-на-Дону. А просто в значении «далеко», хотя на самом деле в реальных цифрах там расстояние может быть всего в несколько километров.

И так можно «развенчать» абсолютно любую гиперболу. Но делать этого не стоит. Они и не должны означать абсолютную правду, их задача – наиболее живописно охарактеризовать конкретную ситуацию или мысль, усиливая ее эмоциональный окрас.

Применения

Гиперболы на вертикальных солнечных часах Дворца великих князей литовских в Вильнюсе, видна круглая тень верхушки гномона, описывающая гиперболу в течение дня

Гиперболы можно видеть на многих солнечных часах. В течение любого дня года Солнце описывает окружность на небесной сфере, и его лучи, падающие на верхушку гномона солнечных часов, описывают конус света. Линия пересечения этого конуса с плоскостью горизонтальных или вертикальных солнечных часов является коническим сечением. На наиболее населённых широтах и в большую часть года это коническое сечение является гиперболой. На солнечных часах часто показаны линии, описываемые тенью от верхушки гномона в течение дня для нескольких дней года (например, дней летнего и зимнего солнцестояний), таким образом, на них часто можно видеть определённые гиперболы, вид которых различен для различных дней года и различных широт.

Примеры гипербол

Текст, содержащий преувеличения, становится более ярким и выразительным. Гипербола усиливает впечатление от персонажей и их действий, а также помогает глубже раскрыть характеры и точнее передать атмосферу.

Слишком частое использование преувеличений подрывает доверие к тексту. Наиболее распространённые гиперболы давно стали штампами: из-за частого употребления они утратили выразительный потенциал и больше не производят должного эффекта. Чтобы придать тексту яркость, необходимо придумывать новые, авторские преувеличения или неожиданно преподносить старые.

В литературе

На самом деле подобные преувеличения – это очень старый литературный прием. Он использовался еще в русских былинах, а это было без малого тысячу лет назад. С помощью гипербол многократно усиливали силу богатырей и их противников.

• Сон богатырский длился 12 ДНЕЙ (ну не может человек спать почти две недели)
• На пути богатыря стояли силы несметные – ВОЛК ИХ ЗА ДЕНЬ НЕ ОБЕЖИТ, ВОРОН ЗА ДЕНЬ НЕ ОБЛЕТИТ (это сколько врагов должно быть – миллион?)
• Махнет богатырь рукой – СРЕДИ ВРАГОВ УЛИЦА, махнет другой – ПЕРЕУЛОК (то есть одним ударом богатырь убивает сразу несколько десятков)
• Взял Илья Муромец палицу ВЕСОМ СТО ПУДОВ (тут надо понимать, что сто пудов – это полторы тонны)
• Соловей-разбойник свистит – ЛЕС К ЗЕМЛЕ КЛОНИТСЯ, а ЛЮДИ МЕРТВЫМИ ПАДАЮТ (ну тут совсем что-то из разряда сказки)

Точно такие же гиперболы встречаются и в «Слове о полку Игореве». Например:

«Русичи червлеными щитами перегородили широкие поля, ища себе честь, а князю славы» или «Войско такое, что можно Волгу веслами расплескать, а Дон вычерпать шлемами».

Среди писателей больше всего гипербол встречается у Николая Васильевича Гоголя. Преувеличения есть практически в каждом его известном произведении. Вот, например, он описывает реку Днепр:

Редкая птица долетит до середины Днепра. Днепр как дорога без конца в длину и без меры в ширину.

Или использует преувеличения в своих сатирических произведениях, вкладывая их в уста героев:

В муку бы вас все стер! (Городничий) Тридцать пять тысяч одних курьеров… Меня сам государственный совет боится. (Хлестаков)

А в «Мертвых душах» есть такие слова: «Бесчисленны человеческие страсти как морские пески».

Гиперболы использует практически любой писатель или поэт. С их помощью они, например, более красочно описывают характер героев произведений или показывают свое авторское отношение к ним.

Причем писатели зачастую не используют уже устоявшиеся выражения, а стараются придумать что-то свое.

Вот еще примеры гипербол в литературе:

1. И ядрам пролетать мешала гора кровавых тел (Лермонтов)
2. Закат пылал во сто сорок солнц (Маяковский)
3. Миллион терзаний (Грибоедов)
4. Порядочный человек за вас за тридевять земель готов убежать (Достоевский)
5. И сосна до звезд достает (Мандельштам)
6. Во сне дворник стал тяжелым как комод (Ильф и Петров)

В рекламе

Конечно, мимо такого интересного приема, который позволяет усилить реальное значение слов, не могли пройти и рекламщики. Масса слоганов основана на этом принципе

Ведь задача – привлечь внимание клиента, обещая при этом «золотые горы» и всячески подчеркивая уникальность товара:

1. Вкус на грани возможного (жевательная резинка «Стиморол»)
2. Контроль над стихией (кроссовки «Адидас»)
3. Король салатов (майонез «Оливьез»)

В создании рекламных роликов также часто используется принцип гиперболы. Например, серия знаменитых видео про батончики «Сникерс» со слоганом «Ты не ты, когда голоден». Там, где различные персонажи превращаются в совершенно других людей и начинают творить всякие глупости, и только шоколадный батончик способен вернуть их в привычную русло.

В этих роликах явно гиперболизировано (сильно преувеличено) чувство голода и «чудодейственная» сила самого «Сникерса».

Ну и самый простой пример гипербол, который применяют в рекламе, это выражения типа «самый лучший», «самый стильный», «самый комфортный» и так далее, а про цены, наоборот, говорят «самые низкие».

В политике

Предвыборные обещания политиков часто бывают невыполнимыми. Неудивительно, что их часто выражают при помощи гипербол. Самый распространённый пример – обещание благосостояния для всех и каждого.

В политической риторике художественное преувеличение также может применяться, чтобы разрядить обстановку или создать неформальную атмосферу. Президент США Джон Кеннеди встретил лауреатов Нобелевской премии в Белом доме шуткой, основанной на преувеличении:

«Я думаю, это самое необычное собрание человеческих талантов и умов в Белом Доме за исключением тех времена, когда Томас Джефферсон обедал здесь в одиночестве».

Связанные определения

Асимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F₁ и F₂. Директрисы гиперболы обозначены линиями двойной толщины и обозначены D₁ и D₂. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зелёным). Вершины гиперболы обозначены как ±a. Параметры гиперболы обозначают следующее: a — расстояние от центра C до каждой из вершинb — длина перпендикуляра к оси абсцисс, восставленного из каждой из вершин до пересечения с асимптотойc — расстояние от центра C до любого из фокусов, F₁ и F₂, θ — угол, образованный каждой из асимптот и осью, проведённой между вершинами

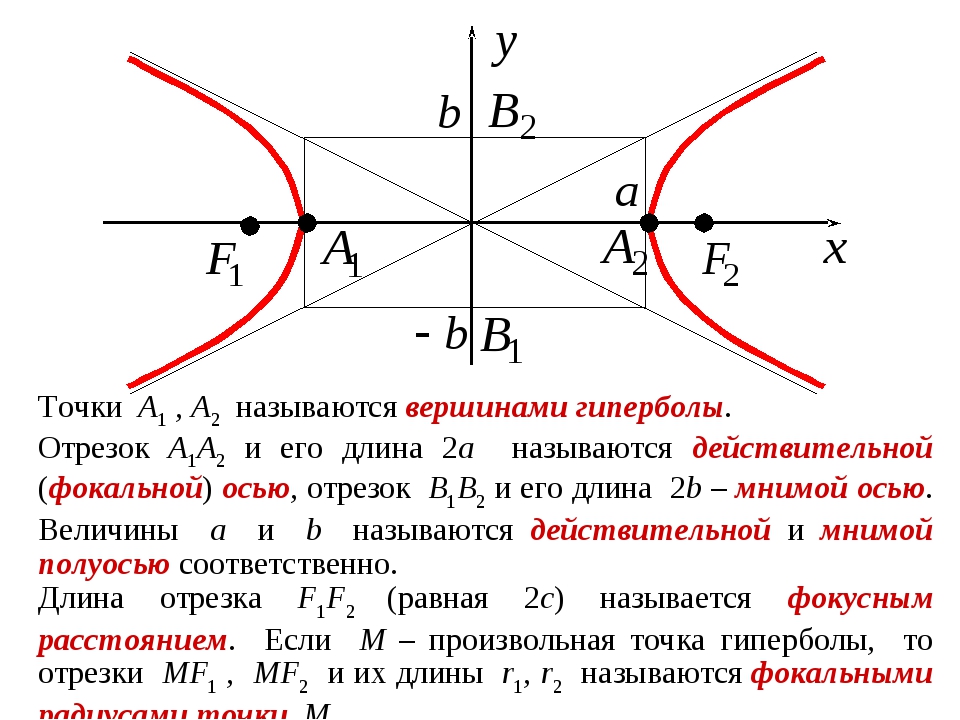
• Гипербола состоит из двух отдельных кривых, которые называют ветвями.
• Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.
• Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.
• Середина большой оси называется центром гиперболы.
• Расстояние от центра гиперболы до одной из вершин называется большой полуосью

  Обычно обозначается a.

  гиперболы.

• Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием

  Обычно обозначается c.

  .

• Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной или поперечной осью гиперболы.
• Прямая, перпендикулярная действительной оси и проходящая через её центр, называется мнимой или сопряжённой осью гиперболы.
• Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется фокальным параметром.
• Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром

  Обычно обозначается b.

  .

• В задачах, связанных с движением тел по гиперболическим траекториям, расстояние от фокуса до ближайшей вершины гиперболы называется перицентрическим расстоянием

  Обычно обозначается rp{\displaystyle r_{p}}.

Соотношения

Для характеристик гиперболы, определённых выше, существуют следующие соотношения

• c2=a2+b2{\displaystyle c^{2}=a^{2}+b^{2}}.
• ε=ca{\displaystyle \varepsilon =c/a}.
• b2=a2(ε2−1){\displaystyle b^{2}=a^{2}\left(\varepsilon ^{2}-1\right)}.
• rp=a(ε−1){\displaystyle r_{p}=a\left(\varepsilon -1\right)}.
• a=pε2−1{\displaystyle a={\frac {p}{\varepsilon ^{2}-1}}}.
• b=pε2−1{\displaystyle b={\frac {p}{\sqrt {\varepsilon ^{2}-1}}}}.
• c=pεε2−1{\displaystyle c={\frac {p\varepsilon }{\varepsilon ^{2}-1}}}.
• p=b2a{\displaystyle p={\frac {b^{2}}{a}}}.

В словаре Энциклопедии

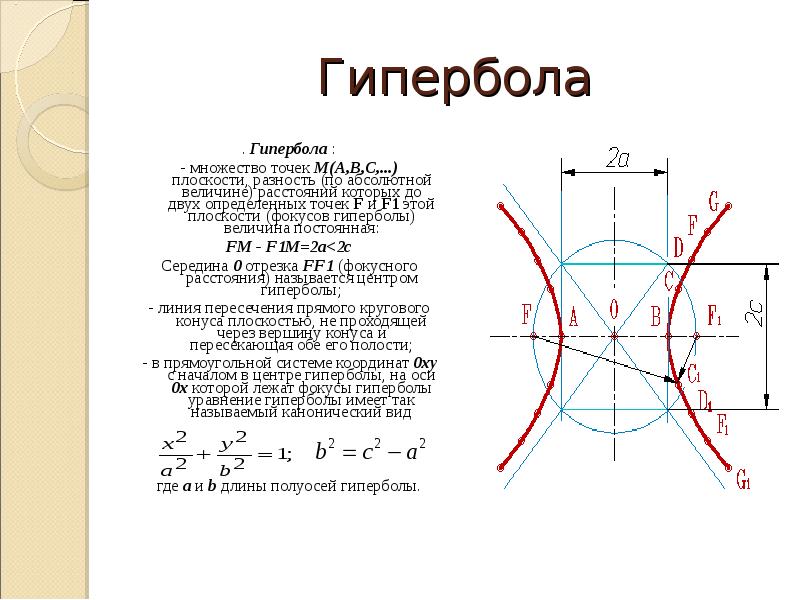
(греч. hyperbole) плоская кривая (2-го порядка), состоящая из двух бесконечных ветвей. Гипербола — множество точек М, разность расстояний которых от двух данных точек (F1, F2) — фокусов гиперболы — постоянна и равна длине действительной оси A1A2, другая ось гиперболы B1B2 называется мнимой. В надлежащей системе координат уравнение гиперболы имеет вид: x2/a2 — y2/b2 = 1, где 2a = F1M — F2M, OF1 = OF2 = c,. Через центр О гиперболы проходят ее асимптоты C1C2 и D1D2. См. также Конические сечения.—(от греч. hyperbole — преувеличение), разновидность тропа, основанная на преувеличении («реки крови»). Ср. Литота.

Для чего нужна гипербола

Гипербола в литературе позволяет авторам передавать читателю свои эмоции, тем самым позволяя красочней представить ситуацию

Эти стилистические фигуры, которые достаточно просто отличить от любого другого речевого приема, нужны, чтобы привлечь внимание, позволить прочувствовать все эмоции, которыми хотел поделиться писатель

Они освобождают читателя от рамок реальности и приписывают сверхъестественные характеристики природным явлениям и людям. Гипербола в литературе играет отнюдь не последнюю роль, так как она делает нашу речь более живой, и позволяет прочувствовать эмоциональное и душевное состояние рассказчика или автора текста.

Это позволяет им четко и правильно передать словесную атмосферу рассказа. Функция гиперболы как приема — придавать яркости, эмоциональности и убедительности тексту. Также ее часто используют писатели-юмористы для создания в своих произведениях комических образов для персонажей, позволяя фантазии читателя оживить их в своем воображении.

Тропы

Гипербола считается тропом. Троп — это выразительный оборот речи, в котором автор использует слово/выражение в переносном значении либо сопоставляет предметы и явления, которые каким-то образом переплетаются между собой по смыслу.

Главные виды тропов, которые существуют в русском языке:

• аллегория (иносказание, выражение абстрактных идей конкретными);
• гипербола (явное преувеличение);
• дисфемизм (замена одного слова другим, более вульгарным);
• ирония (скрытая тонкая насмешка);
• каламбур (шутка с игрой разных значений одного слова либо словами, схожими по звучанию);
• литота (сильное преуменьшение либо двойное отрицание);
• метафора (переносное значение, сравнение и перенос с одного предмета на другой);
• метонимия (переименование одного слова другим; существует логическая связь замены);
• оксюморон (постановка слов противоположного значения бок о бок, создавая парадокс);
• олицетворение (одушевление, сравнение чего-то неодушевлённого с живым);
• перифраз (иносказание);
• сарказм (негативная ирония);
• синекдоха (узкое понятие заменяется более широким или наоборот);
• сравнение (сравниваются два предмета, часто присутствуют союзы «как», «будто» и другие);
• эвфемизм (замена социально непристойных/неудобных слов на более мягкие);
• эпитет (прилагательное, наречие, причастие или глагол, которые выразительно описывают что-то).

Смотрите подробнее про Метафору и Эпитет.