Что такое функция?

Примечания

1. ↑ В. А. Зорич. Глава I. Некоторые общематематические понятия и обозначения. § 3. Функция // Математический анализ. Часть I. — четвертое, исправленное. — М.: МЦНМО, 2002. — С. 13, 22, 25, 31. — 664 с. — ISBN 5-94057-056-9.
2. ↑ Колмогоров А. Н., Абрамов А. М., Дудницын Ю. П. Алгебра и начала анализа. Учебник для 10-11 классов средней школы. — М., Просвещение, 1994. — ISBN 5-09-006088-6. — C. 86-87
3. ↑ Г. Е. Шилов. Глава 2. Элементы теории множеств. § 2.8. Общее понятие функции. График // Математический анализ (функции одного переменного). — М.: Наука, 1969. — С. 69. — 528 с.
4. А. Н. Колмогоров, С. В. Фомин. Глава 1. Элементы теории множеств // Элементы теории функций и функционального анализа. — 3-е изд. — М.: Наука, 1972. — С. 14—18. — 496 с.
5. В. А. Садовничий. Теория операторов. — М.: Дрофа, 2001. — С. 241. — 381 с. — ISBN 5-71-074297-X.

В словаре Ожегова

ФУНКЦИЯ, -и, ас. 1. В философии: явление, зависящее от другого и изменяющееся по мере изменения этого другого явления. 2. В математике: закон, по к-рому каждому значению переменной величины (аргумента) ставится в соответствие нек-рая определенная величина, а также сама эта величина. Линейная ф. (меняющаяся прямо пропорционально изменению своего аргумента). 3. Работа производимая органом, организмом (книжн.). Ф. желез. 4. Роль, значение чего-н. (книжн.). Функции кредита. 5. Обязанность, круг деятельности (книжн.). Служебные функции. Функции профкома. || прил. функциональный, -ая, -ое (к 1, 2, 3 и 4 знач.).

Определение функции.

Наиболее популярное определение функции сводится к следующему:

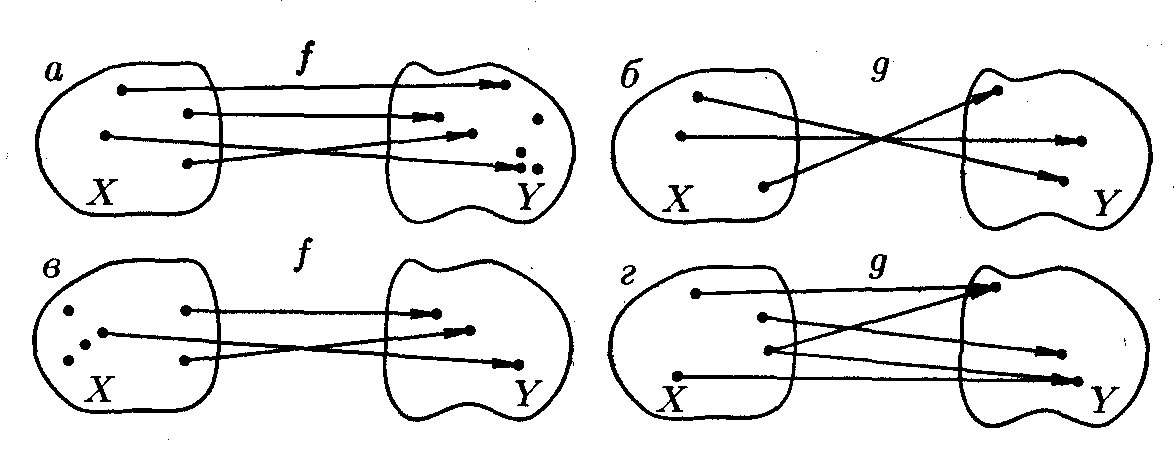
Функцией называется правило f, по которому каждому элементу х множества Х ставится в соответствие единственный элемент у множества У.

Человеку, который не в теме, так просто не понять… Но вы-то уже в теме?)

Множество Х для числовых функций — это просто набор всех возможных значений икса. Элементом х называется любое конкретное число из этого множества. Про правило f я уже говорил, но… Так уж и быть, ещё раз.)

Для функции у = 2х + 3, например, Х — это множество всех чисел. Вообще всех. Элемент х — любое число. 5 — элемент, и 117 — элемент, и -0,34 — элемент.

А правило f — это действие над иксом. В данном случае правило гласит: «Умножить икс на два и к результату прибавить три». Каждому иксу соответствует (т.е. ставится в соответствие) свой игрек именно по этому правилу.

Ну, элемент у, понятно, это конкретное значение для конкретного икса. А множество У — это набор всех возможных значений игрека.

Замечу (на всякий случай), что данные буквы (х, Х, у, У, f) относятся к самой популярной записи функции: y = f(x). Но если будут другие буквы, смысл определения функции сохраняется.)

Вот и все дела. Иногда говорят ещё короче:

Функция есть закон отображения множества Х на множество У.

Суть та же. Только фраза «ставить в соответствие» заменена на понятие «отображать».

Бывает, в голове возникает некоторая путаница… Как так?! Всё время называем игрек функцией, работаем с ним, как с функцией, а в определении функции какое-то правило f прорезалось!?

Вношу ясность.

Дело в том, что функцией называется не только правило, но и сама зависимая переменная у. По той простой причине, что в записи конкретной функции именно игрек и показывает, что надо делать с иксом, показывает это самое правило f. Если, скажем, y=x2, правило — это возведение в квадрат. Если y=5x, правило — умножение на пять. Именно через игрек слова «возведение в квадрат», «умножение на пять» и т.д. переводятся в математическую запись. И никак иначе.

Поэтому игрек — и зависимая переменная, и функция (т.е. правило f). Одновременно.

Очень часто в определении функции присутствуют названия множеств Х и У. Множество Х — область определения функции, множество У — область значений функции. Это очень важные понятия. И вполне заслуживают отдельных уроков.)

Но, прежде всего, имеет смысл разобраться: какие же бывают эти самые правила f, о которых говорится в определении функции? Об этом — в следующем уроке.

Обозначения функции

Если на множестве X{\displaystyle X} задана функция f{\displaystyle f}, принимающая значения из множества Y{\displaystyle Y}, то

• этот факт записывают в виде fX→Y{\displaystyle f\colon X\to Y} или X⟶fY{\displaystyle X{\stackrel {f}{\longrightarrow }}Y};
• множество X{\displaystyle X} — область задания функции f{\displaystyle f} — обозначается символом D(f){\displaystyle D(f)} или domf;{\displaystyle \mathrm {dom} \,f;}
• множество Y{\displaystyle Y} — область значений функции f{\displaystyle f};
• множество значений {y}{\displaystyle \{y\}} функции f{\displaystyle f} обозначается символом E(f){\displaystyle E(f)} или codf{\displaystyle \mathrm {cod} \,f} (ranf{\displaystyle \mathrm {ran} \,f}).
• Если область значений Y{\displaystyle Y} и множество значений E(f){\displaystyle E(f)} совпадают, то говорят, что f{\displaystyle f} отображает множество X{\displaystyle X} на Y{\displaystyle Y}.
• Функция, заданная на множестве X{\displaystyle X}, наиболее часто обозначается как соответствие между элементами x∈X{\displaystyle x\in X} и y∈Y{\displaystyle y\in Y}:

  y=f(x){\displaystyle y=f(x)}, или кратко:f(x){\displaystyle f(x)} или f{\displaystyle f};

  x↦y{\textstyle x\mapsto y} или x↦f(x){\displaystyle x\mapsto f(x)};

• для сокращения числа обозначений знак функции, заданной на множестве X{\displaystyle X}, может обозначаться той же буквой, что и каждое значение функции:

  y=y(x){\displaystyle y=y(x)}, z=z(x){\displaystyle z=z(x)};

• функция обозначается и как функция f{\displaystyle f}, которая отображает множество X{\displaystyle X} в Y{\displaystyle Y}с обозначением соответствия между элементами x∈X{\displaystyle x\in X} и y∈Y{\displaystyle y\in Y}:

  fx↦y{\displaystyle f\colon x\mapsto y} или fy=f(x){\displaystyle f\colon y=f(x)};

• реже используется обозначение функции как соответствие между элементами x∈X{\displaystyle x\in X} и y∈Y{\displaystyle y\in Y} без скобок: y=fx{\displaystyle y=fx}, y=f∘x{\displaystyle y=f\circ x} или y=xf{\displaystyle y=xf},
• а там, где необходимо подчеркнуть двойственность, используются обозначения со скобками: y=(f,x){\displaystyle y=(f,x)} или y=(x,f){\displaystyle y=(x,f)};
• также существует и операторное обозначение y=xf{\displaystyle y=x^{f}}, которое можно встретить в общей алгебре.
• В лямбда-исчислении Чёрча используется обозначение λx.y{\displaystyle \lambda x.y} .

Функции нескольких аргументов

График функции двух переменных f(x,y)=sin⁡(x−sin⁡(2y)){\displaystyle f(x,y)=\sin(x-\sin(2y))}

Понятие функции легко обобщается на случай функции многих аргументов.

Если множество X{\displaystyle X} представляет собой декартово произведение множеств X1,X2,…,Xn{\displaystyle X_{1},\;X_{2},\;\ldots ,\;X_{n}}, тогда отображение fX→Y{\displaystyle f\colon X\to Y}, где Y{\displaystyle Y} — множество вещественных чисел, оказывается n{\displaystyle n}-местным отображением, при этом элементы упорядоченного набора x=(x1,x2,…,xn){\displaystyle x=(x_{1},\;x_{2},\;\ldots ,\;x_{n})} называются аргументами (данной n{\displaystyle n}-местной функции), каждый из которых пробегает своё множество:

xi∈Xi{\displaystyle x_{i}\in X_{i}} где i=1,n¯{\displaystyle i={\overline {1,n}}}.

В этом случае запись y=f(x){\displaystyle y=f(x)} означает, что y=f(x1,x2,…,xn){\displaystyle y=f(x_{1},\;x_{2},\;\ldots ,\;x_{n})}.

В словаре Д.Н. Ушакова

ФУ́НКЦИЯ, функции, ·жен. (·лат. functio — выполнение работы).1. Явление, зависящее от другого и изменяющееся по мере изменения этого другого явления (·книж. ).2. Переменная величина, меняющаяся в зависимости от изменения другой величины (мат.). Величина давления газа есть функция величины его объема.3. Работа, производимая органом, организмом (биол., физиол.). Отделение слюны является основной функцией слюнной железы.4. перен. Обязанность, круг деятельности чего-нибудь, подлежащая исполнению работа (·книж. ). Служебные функции. Исполнять свою функцию в обществе. Функции государственного управления.5. Значение, назначение, роль (·книж. ). Функция математического знака. Функция родительного падежа.

В словаре Энциклопедии

в математике -..1) зависимая переменная величина…2) Соответствие y = f (x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента, или независимого переменного) соответствует определенное значение другой величины y (зависимой переменной, или функции). Такое соответствие может быть задано различным образом, напр. формулой, графически или таблицей (типа таблицы логарифмов). С помощью функции математически выражаются многообразные количественные закономерности в природе.—(от лат. functio — исполнение, осуществление),..1) деятельность, обязанность, работа; внешнее проявление свойств какого-либо объекта в данной системе отношений (напр., функция органов чувств, функция денег)…2) Функция в социологии — роль, которую выполняет определенный социальный институт или процесс по отношению к целому (напр., функция государства, семьи и т. д. в обществе)…3) В лингвистике — назначение, роль (иногда и значение) языковой единицы или элемента языковой структуры.

Область определения функции с логарифмом

Третья распространённая функция – логарифм. В качестве образца я буду рисовать натуральный логарифм, который попадается примерно в 99 примерах из 100. Если некоторая функция содержит логарифм , то в её область определения должны входить только те значения «икс», которые удовлетворяют неравенству . Если логарифм находится в знаменателе: , то дополнительно накладывается условие  (так как ).

Пример 9

Найти область определения функции

Решение: в соответствии с вышесказанным составим и решим систему:

Графическое решение для чайников:Ответ: область определения:

Остановлюсь ещё на одном техническом моменте – у меня ведь не указан масштаб и не проставлены деления по оси. Возникает вопрос: как выполнять подобные чертежи в тетради на клетчатой бумаге? Отмерять ли расстояние между точками по клеточкам строго по масштабу? Каноничнее и строже, конечно, масштабировать, но вполне допустим и схематический чертёж, принципиально отражающий ситуацию.

Пример 10

Найти область определения функции

Для решения задачи можно использовать метод предыдущего параграфа – проанализировать, как парабола расположена относительно оси абсцисс. Ответ в конце урока.

Как видите, в царстве логарифмов всё очень похоже на ситуацию с квадратным корнем: функция  (квадратный трёхчлен из Примера №7) определена на интервалах , а функция  (квадратный двучлен из Примера №6) на интервале . Неловко уже и говорить, функции типа  определены на всей числовой прямой.

Полезная информация: интересна типовая функция , она определена на всей числовой прямой кроме точки . Согласно свойству логарифма , «двойку» можно вынести множителем за пределы логарифма, но, чтобы функция не изменилась, «икс» необходимо заключить под знак модуля: . Вот вам и ещё одно «практическое применение» модуля = ). Так необходимо поступать в большинстве случаев, когда вы снОсите чётную степень, например: .  Если же основание степени  заведомо положительно, например, , то в знаке модуля отпадает необходимость и достаточно обойтись круглыми скобками: .

Чтобы не повторяться, давайте усложним задание:

Пример 11

Найти область определения функции

Решение: в данной функции у нас присутствует и корень и логарифм.

Подкоренное выражение должно быть неотрицательным: , а выражение под знаком логарифма – строго положительным: . Таким образом, необходимо решить систему:

Многие из вас прекрасно знают или интуитивно догадываются, что решение системы должно удовлетворять каждому условию.

Исследуя расположение параболы  относительно оси , приходим к выводу, что неравенству  удовлетворяет интервал  (синяя штриховка):
Неравенству , очевидно, соответствует «красный» полуинтервал  .

Поскольку оба условия должны выполняться одновременно, то решением системы является пересечение данных интервалов. «Общие интересы» соблюдены на полуинтервале .

Ответ: область определения:

Типовое неравенство , как демонстрировалось в Примере №8,  нетрудно разрешить и аналитически.

Найденная область определения не изменится для «похожих функций», например, для  или .  Также можно добавить какие-нибудь непрерывные на  функции, например: , или так: , или даже так: . Как говорится, корень и логарифм – вещь упрямая. Единственное, если одну из функций «сбросить» в знаменатель, то область определения изменится (хотя в общем случае это не всегда справедливо). Ну а в теории матана по поводу этого словесного… ой… существуют теоремы.

Пример 12

Найти область определения функции

Это пример для самостоятельного решения. Использование чертежа вполне уместно, так как функция не самая простая.

Ещё пару примеров для закрепления материала:

Пример 13

Найти область определения функции

Решение: составим и решим систему:
Все действия уже разобраны по ходу статьи. Изобразим на числовой прямой интервал, соответствующий неравенству  и, согласно второму условию, исключим две точки:
Значение  оказалось вообще не при делах.

Ответ: область определения

Небольшой математический каламбур на вариацию 13-го примера:

Пример 14

Найти область определения функции

Это пример для самостоятельного решения. Кто пропустил, тот в пролёте 😉

Завершающий раздел урока посвящен более редким, но тоже «рабочим» функциям:

Представление о функции.

Ключевое слово в понятии функции — зависимость. Или — взаимосвязь. В повседневной жизни вы часто сталкиваетесь с функциональными зависимостями. И умело пользуетесь ими, да-да! Сомневаетесь? Тогда пара житейских примеров.

Допустим, вы идёте на встречу с приятелем. И чувствуете, что опаздываете. Что будете делать? Видимо, двигаться шустрее.) Вы твёрдо знаете: быстрей идёшь — меньше время на дорогу. Это общий закон. Время в пути зависит от скорости передвижения. Или, говоря более научно: время в пути есть функция скорости передвижения.

Ещё пример. Вы бросаете камешек в воду. На дальность. Разумеется, стараетесь швырнуть его посильнее. Вы знаете закон: дальность полёта зависит от силы броска. Другими словами: дальность полёта есть функция силы броска.

Вот вам и самое общее, житейское понятие о функции. Если какая-то величина А зависит от другой величины В, говорят, что величина А есть функция величины В. Зачем всё так трудно?! — слышу возмущённый вопрос. Ну зависит, и пусть зависит себе…

Конечно, камешек бросить и без функции можно. Но в обоих примерах есть незаметный, но оч-чень важный момент

Обратите внимание: зная закон зависимости, вы знаете, что нужно делать сейчас, чтобы получить нужный результат потом

Это не очень важно при бросании камешков. А если это не камешек, а ракета? Тогда очень желательно знать, куда она попадёт, да…) Причём, знать безошибочно! Ракета — не камешек, на берегу не валяется..

А если это не камешек, а ракета? Тогда очень желательно знать, куда она попадёт, да…) Причём, знать безошибочно! Ракета — не камешек, на берегу не валяется…

Оказывается, знание функциональных зависимостей позволяет просчитывать результат заранее. Заманчивые возможности, правда?)

В случае с ракетой, в любых технических (и не только!) применениях, люди просто обязаны просчитывать результат. Причём, безошибочно! Следовательно, на всякие взаимосвязи и зависимости требуется строгая математика. И она есть! Этот раздел математики называется «Математический анализ». Для студентов — просто «матан».) Элементы этого раздела — графики, функции, производные, интегралы — начинают осваивать ещё в школе.

Представление о функции — вещь полезная. Но, для строгой математики — недостаточная.

Двигаемся дальше.

Похожие слова

ФункцииФункционалФункционерФункционалкаФункция койкиФункционалистФункционализмФункциональноФункциональныйФункции ладовыеФункционирующийФункционироватьФункциональностьФункционированиеФункции тональныеФункция барьернаяФункционировавшийФункциональная пробаФункция генеративнаяФункция распределенияФункциональный анализФункциональная группаФункциональная кроватьФункциональная нагрузкаФункциональное зонированиеФункциональная подвижностьФункция врачебной должностиФункциональное пространствоФункциональное подразделениеФункция адаптационно-трофическая

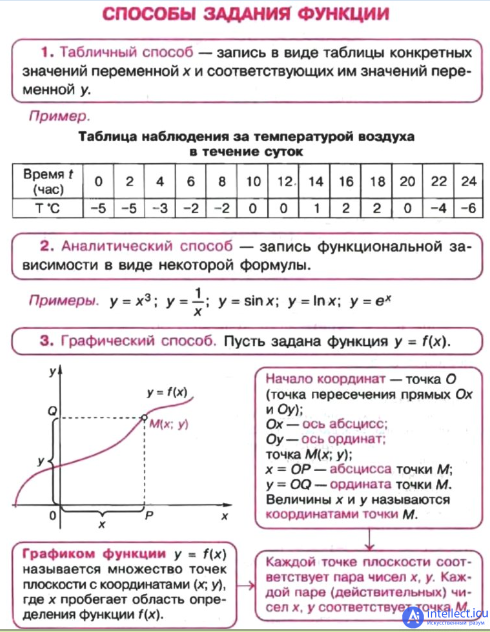
Способы задания функции

Аналитический способ

Функцию можно задать с помощью аналитического выражения (например, формулой). В этом случае её обозначают как соответствие в форме равенства записью y=f(x),{\displaystyle y=f(x),} где x{\displaystyle x} есть переменная, пробегающая область задания функции, а соответствующие значения переменной y{\displaystyle y} (или, что то же самое, значения выражения f(x){\displaystyle f(x)} ) принадлежат области значений функции. Например, равенство y=x2{\displaystyle y=x^{2}}, где x{\displaystyle x} пробегает множество вещественных чисел, задает числовую функцию y=f(x).{\displaystyle y=f(x).\;}

Само по себе равенство y=f(x){\displaystyle y=f(x)}, без указания что это функция, заданная на некотором множестве, функцией не является.

Например, y=x2{\displaystyle y=x^{2}} есть равенство выражений, содержащих разные переменные. Аналогично, если f(x){\displaystyle f(x)} является другим обозначением переменной y{\displaystyle y}, то f(x)=x2{\displaystyle f(x)=x^{2}} также есть равенство выражений, содержащих разные переменные. Если же в равенстве f(x)=x2{\displaystyle f(x)=x^{2}}слева стоит обозначение выражения, содержащего переменную x{\displaystyle x}, то имеется равенство двух выражений, содержащих одну переменную.

Однако высказывание функция y=x2{\displaystyle y=x^{2}\;}(или функция f(x)=x2{\displaystyle f(x)=x^{2}}) на множестве задания обозначает именно функцию. Более того, часто функцию x↦f(x){\displaystyle x\mapsto f(x)} (или y=f(x){\displaystyle y=f(x)\;} ) для краткости обозначают как функцию f(x){\displaystyle f(x)} на множестве задания. Это соглашение является удобным и оправданным.

Графический способ

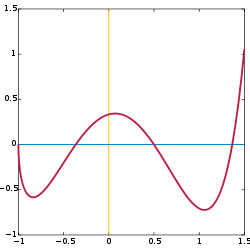
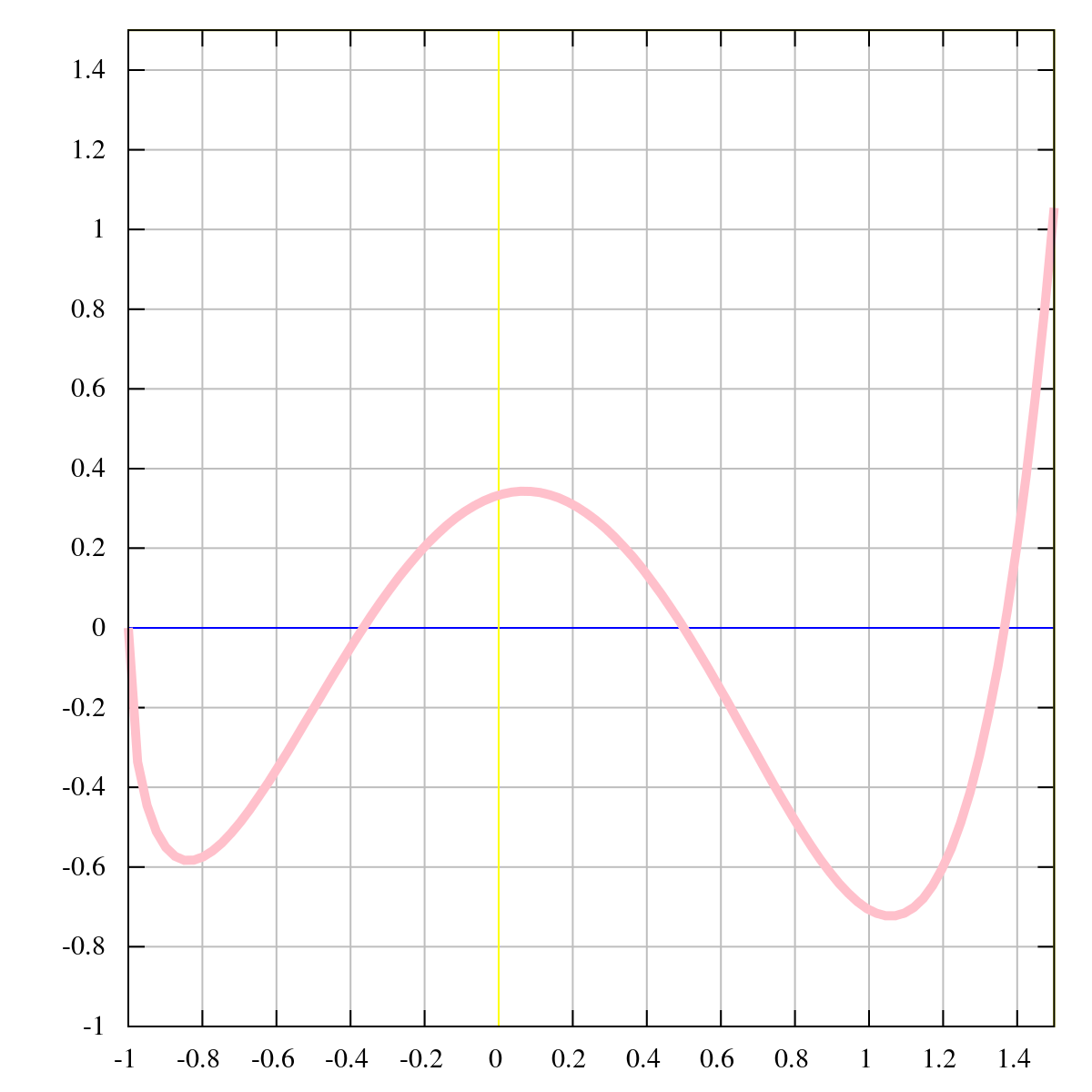
График f(x)=x3−3x{\displaystyle f(x)=x^{3}-3x}

Числовые функции можно также задавать с помощью графика. Пусть y=f(x1,x2,…,xn){\displaystyle y=f(x_{1},x_{2},\ldots ,x_{n})\;} — вещественная функция n переменных.
Тогда её графиком является множество точек в n+1{\displaystyle n+1}-мерном пространстве:{(x1,x2,…,xn,f(x1,x2,…,xn)}{\displaystyle \{(x_{1},x_{2},\ldots ,x_{n},f(x_{1},x_{2},\ldots ,x_{n})\}}.
Это множество точек, часто является поверхностью.
В частности при n=1{\displaystyle n=1}, график функции может в некоторых случаях может быть изображён кривой в двумерном пространстве.

Для функций трёх и более аргументов такое графическое представление не применимо. Однако, и для таких функций можно придумать наглядное полугеометрическое представление (например каждому значению четвёртой координаты точки сопоставить некоторый цвет на графике).

Обобщения

Частично определённые функции

Частично определённая функция f{\displaystyle f} из множества X{\displaystyle X} в множество Y{\displaystyle Y} есть функция fX′→Y{\displaystyle f\colon X’\to Y} с областью задания X′⊂X{\displaystyle X’\subset X}.

Некоторые авторы понимают под функцией частично определённую функцию. Это имеет свои преимущества, например, возможна запись fR→R{\displaystyle f\colon \mathbb {R} \to \mathbb {R} }, где f(x)=1x{\displaystyle f(x)=1/x} в этом случае Dom⁡f=R∖{}{\displaystyle \mathop {\rm {Dom}} f=\mathbb {R} \backslash \{0\}}.

Многозначные функции

В силу определения функции, заданному значению аргумента соответствует ровно одно значение функции. Несмотря на это, нередко можно услышать про так называемые многозначные функции. В действительности, это не более чем удобное обозначение функции, область значений которой сама является семейством множеств.

Пусть fX→B{\displaystyle f\colon X\to \mathbb {B} }, где B{\displaystyle \mathbb {B} } — семейство подмножеств множества Y{\displaystyle Y}. Тогда f(x){\displaystyle f(x)} будет множеством для всякого x∈X{\displaystyle x\in X}.

Функция однозначна, если каждому значению аргумента соответствует единственное значение функции. Функция многозначна, если хотя бы одному значению аргумента соответствует два или более значений функции.

Свойства множеств и функций

В зависимости от того, какова природа области задания и области значений, различают следующие случаи областей:

1. абстрактные множества — множества без какой-либо дополнительной структуры;
2. множества, которые наделены некоторой структурой.

В случае 1 рассматриваются отображения в самом общем виде и решаются наиболее общие вопросы. Таким общим вопросом, например, является вопрос о сравнении множеств по мощности: если между двумя множествами существует взаимно однозначное отображение (биекция), то два данных множества называют эквивалентными или равномощными.
Это позволяет провести классификацию множеств в виде единой шкалы, начальный фрагмент выглядит следующим образом:

• конечные множества — здесь мощность множества совпадает с количеством элементов;
• счётные множества — множества, эквивалентные множеству натуральных чисел;
• множества мощности континуума (например, отрезок вещественной прямой или сама вещественная прямая).

В соответствии с этим, имеет смысл рассматривать следующие примеры отображений:

• конечные функции — отображения конечных множеств;
• последовательности — отображение счётного множества в произвольное множество;
• континуальные функции — отображения несчётных множеств в конечные, счётные или несчётные множества.

В случае 2, основной объект рассмотрения — заданная на множестве структура (дополнительные свойства элементов множества) и то, что происходит с этой структурой при отображении: если при взаимно однозначном отображении сохраняются свойства заданной структуры, то говорят, что между двумя структурами установлен изоморфизм. Таким образом, изоморфные структуры, заданные в различных множествах, невозможно различить, поэтому в математике принято говорить, что данная структура рассматривается «с точностью до изоморфизма».

Существует большое разнообразие структур, которые могут быть заданы на множествах. Сюда относится:

• структура порядка — частичный или линейный порядок элементов множества;
• алгебраическая структура — группоид, полугруппа, группа, кольцо, тело, область целостности или поле, заданные на элементах множества;
• структура метрического пространства — на элементах множества задаётся функция расстояния;
• структура евклидового пространства — на элементах множества задаётся скалярное произведение;
• структура топологического пространства — на множестве задаётся совокупность «открытых множеств»;
• структура измеримого пространства — на множестве задаётся сигма-алгебра подмножеств исходного множества (например, посредством задания меры с данной сигма-алгеброй в качестве области задания функции)

Функции с конкретным свойством могут не существовать на множествах, не обладающих соответствующей структурой. Например, формулировка свойства непрерывности функции, заданной на множестве, требует задания на этом множестве топологической структуры.

История

Термин «функция» (в некотором более узком смысле) был впервые использован Лейбницем (1692 год). В свою очередь, Иоганн Бернулли в письме к тому же Лейбницу употребил этот термин в смысле, более близком к современному.

Первоначально понятие функции было неотличимо от понятия аналитического представления. Впоследствии появилось определение функции, данное Эйлером (1751 год), затем — у Лакруа (1806 год), — уже практически в современном виде. Наконец, общее определение функции (в современной форме, но для числовых функций) было дано Лобачевским (1834 год) и Дирихле (1837 год).

К концу XIX века понятие функции переросло рамки числовых систем. Сначала понятие функции было распространено на векторные функции, вскоре Фреге ввёл логические функции (), а после появления теории множеств Дедекинд () и Пеано () сформулировали современное универсальное определение.