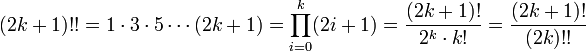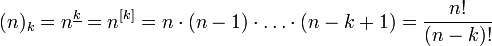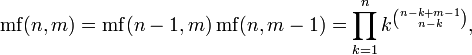Факториал

Скорость роста и приближения для больших n

График натурального логарифма факториала

В п растет, факторный п ! растет быстрее , чем все многочлены и экспоненциальная функция (но медленнее , чем и двойная экспоненциальная функция ) в п .
пп{\ Displaystyle п ^ {п}}

Большинство приближений для n ! основаны на приближении его натурального логарифма

пер⁡п!знак равно∑Иксзнак равно1ппер⁡Икс.{\ Displaystyle \ пер п! = \ сумма _ {х = 1} ^ {п} \ пер х \ ,.}

График функции f ( n ) = ln n ! показан на рисунке справа. Он выглядит приблизительно линейным для всех разумных значений n , но это предположение неверно. Мы получаем одно из простейших приближений для ln n ! путем ограничения суммы интегралом сверху и снизу следующим образом:

∫1ппер⁡ИксdИкс≤∑Иксзнак равно1ппер⁡Икс≤∫ппер⁡(Икс+1)dИкс{\ displaystyle \ int _ {1} ^ {n} \ ln x \, dx \ leq \ sum _ {x = 1} ^ {n} \ ln x \ leq \ int _ {0} ^ {n} \ ln (х + 1) \, dx}

что дает нам оценку

ппер⁡(пе)+1≤пер⁡п!≤(п+1)пер⁡(п+1е)+1.{\ displaystyle n \ ln \ left ({\ frac {n} {e}} \ right) +1 \ leq \ ln n! \ leq (n + 1) \ ln \ left ({\ frac {n + 1}) {e}} \ right) +1 \ ,.}

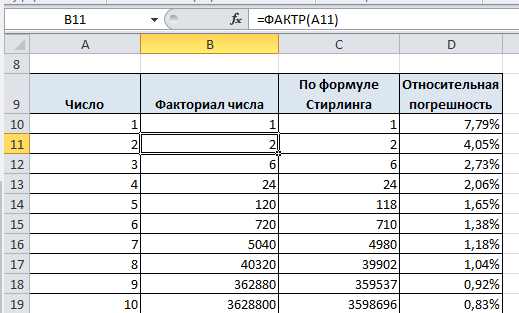
Следовательно, ln n ! ∼ n ln n (см. ). Этот результат играет ключевую роль в анализе вычислительной сложности из алгоритмов сортировки (см сравнения сортировки ). С границ на ln n ! Выведено выше, мы получаем, что

(пе)пе≤п!≤(п+1е)п+1е.{\ displaystyle \ left ({\ frac {n} {e}} \ right) ^ {n} e \ leq n! \ leq \ left ({\ frac {n + 1} {e}} \ right) ^ { п + 1} е \ ,.}

Иногда бывает полезно использовать более слабые, но более простые оценки. Используя приведенную выше формулу, легко показать, что для всех n мы имеем (п3) п < п ! , и для всех n ≥ 6 имеем n ! <(п2) п .

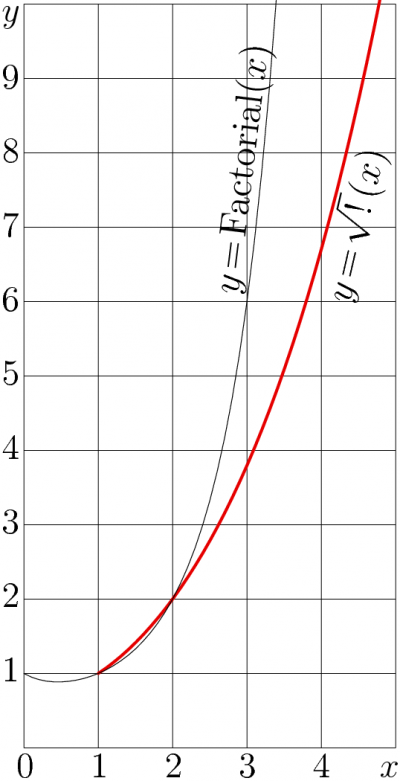
Сравнение приближения Стирлинга с факториалом

Для больших n мы получаем лучшую оценку числа n ! используя приближение Стирлинга :

п!∼2πп(пе)п.{\ displaystyle n! \ sim {\ sqrt {2 \ pi n}} \ left ({\ frac {n} {e}} \ right) ^ {n} \ ,.}

Фактически это происходит из асимптотического ряда для логарифма, а n факториал лежит между этим и следующим приближением:

2πп(пе)п<п!<2πп(пе)пе1(12п).{\ displaystyle {\ sqrt {2 \ pi n}} \ left ({\ frac {n} {e}} \ right) ^ {n} <n! <{\ sqrt {2 \ pi n}} \ left ( {\ frac {n} {e}} \ right) ^ {n} e ^ {1 / (12n)} \ ,.}

Другое приближение для ln n ! дан Шринивасой Рамануджаном ( )

пер⁡п!≈ппер⁡п-п+пер⁡(п(1+4п(1+2п)))6+пер⁡π2⟹п!≈2πп(пе)п(1+12п+18п2)16.{\ Displaystyle {\ begin {align} \ ln n! & \ приблизительно n \ ln n-n + {\ frac {\ ln {\ Bigl (} n {\ bigl (} 1 + 4n (1 + 2n) {\ bigr )} {\ Bigr)}} {6}} + {\ frac {\ ln \ pi} {2}} \\ \ Longrightarrow \; n! & \ Приблизительно {\ sqrt {2 \ pi n}} \ left ({\ frac {n} {e}} \ right) ^ {n} \ left (1 + {\ frac {1} {2n}} + {\ frac {1} {8n ^ {2}}} \ right) ^ {1/6} \,. \ end {align}}}

И это, и приближение Стирлинга дают относительную ошибку порядка 1п 3, но Рамануджан примерно в четыре раза точнее. Однако, если мы используем два поправочных члена в приближении типа Стирлинга, как в приближении Рамануджана, относительная ошибка будет порядка1п 5:

п!≈2πп(пе)пexp⁡(112п-1360п3).{\ displaystyle n! \ приблизительно {\ sqrt {2 \ pi n}} \ left ({\ frac {n} {e}} \ right) ^ {n} \ exp \ left ({{\ frac {1} { 12n}} — {\ frac {1} {360n ^ {3}}}} \ right) \ ,.}

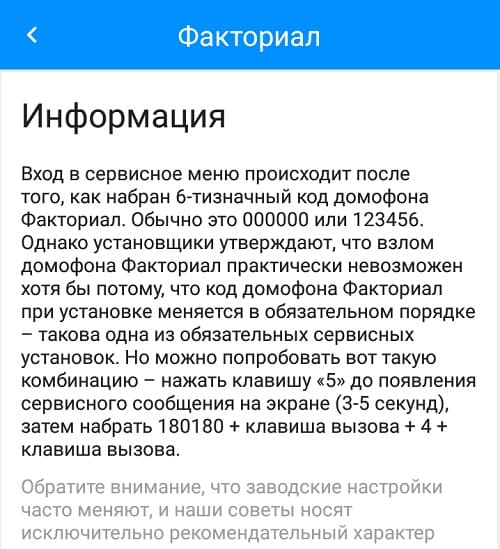
Как нарисовать граф на 1С Промо

Описывается реализация на языке запросов 1С метода расположения вершин графа на плоскости, основанного на использовании электромеханической аналогии. При этом вершины графа представляются одноименными электрическими зарядами, дуги — пружинками. Силы взаимодействия вершин в этой системе переводят их из случайного начального в нужное конечное положение. Приведена обработка рисования графов «ГрафОграф», реализующая данный подход, показывающая также динамику процесса. Граф можно задать списком ребер вручную, выбрать из нескольких предопределенных примеров или сформировать по данным информационной базы.

1 стартмани

Приложения

Хотя факториальная функция уходит корнями в комбинаторику , формулы, включающие факториалы, встречаются во многих областях математики.

Есть n ! различные способы упорядочивания n различных объектов в последовательность, перестановки этих объектов.
Часто факториалы появляются в знаменателе формулы, чтобы учесть тот факт, что порядок следует игнорировать. Классический пример — подсчет k — комбинаций (подмножеств из k элементов) из набора с n элементами. Такую комбинацию можно получить, выбрав k -перестановку: последовательно выбирая и удаляя один элемент набора k раз, всего

(п-)(п-1)(п-2)⋯(п-(k-1))знак равноп!(п-k)!знак равнопk_{\ Displaystyle (п-0) (п-1) (п-2) \ cdots \ влево (п- (к-1) \ вправо) = {\ гидроразрыва {п!} {(пк)!}} = п ^ {\ underline {k}}}

возможности. Это, однако, производит k -комбинации в определенном порядке, который нужно игнорировать; так как каждая k -комбинация получается за k ! разными способами правильное количество k- комбинаций

п(п-1)(п-2)⋯(п-k+1)k(k-1)(k-2)⋯1знак равнопk_k!знак равноп!(п-k)!k!знак равно(пk).{\ Displaystyle {\ гидроразрыва {п (п-1) (п-2) \ cdots (п-к + 1)} {к (к-1) (к-2) \ cdots 1}} = {\ гидроразрыва { n ^ {\ underline {k}}} {k!}} = {\ frac {n!} {(nk)! k!}} = {\ binom {n} {k}}.}.}

Это число известно как биномиальный коэффициент , потому что это также коэффициент при x k в (1 + x ) n . Этот термин часто называют падающим факториалом (произносится как « n к падающему k »).пk_{\ displaystyle n ^ {\ underline {k}}}

Факториалы возникают в алгебре по разным причинам, например, через уже упомянутые коэффициенты биномиальной формулы или через усреднение по перестановкам для симметризации определенных операций.
Факториалы также встречаются в исчислении ; например, они встречаются в знаменателях терминов формулы Тейлора , где они используются в качестве компенсации терминов в связи с п — й производной от й п , эквивалентным п ! .
Факториалы также широко используются в теории вероятностей и теории чисел ( ).
Факториалы могут быть полезны для облегчения манипуляции выражениями. Например, количество k -перестановок n можно записать как

пk_знак равноп!(п-k)!;{\ displaystyle n ^ {\ underline {k}} = {\ frac {n!} {(nk)!}} \ ,;}

хотя это неэффективно как средство для вычисления этого числа, оно может служить для доказательства свойства симметрии биномиальных коэффициентов:

(пk)знак равнопk_k!знак равноп!(п-k)!k!знак равнопп-k_(п-k)!знак равно(пп-k).{\ displaystyle {\ binom {n} {k}} = {\ frac {n ^ {\ underline {k}}} {k!}} = {\ frac {n!} {(nk)! k!}} = {\ frac {n ^ {\ underline {nk}}} {(nk)!}} = {\ binom {n} {nk}} \ ,.}

Факториальную функцию можно показать, используя правило мощности , как

п!знак равноDпИкспзнак равноdпdИкспИксп{\ displaystyle n! = D ^ {n} \, x ^ {n} = {\ frac {d ^ {n}} {dx ^ {n}}} \, x ^ {n}}

где D п х п является для п — й производной по й п .

Завершить шаблон

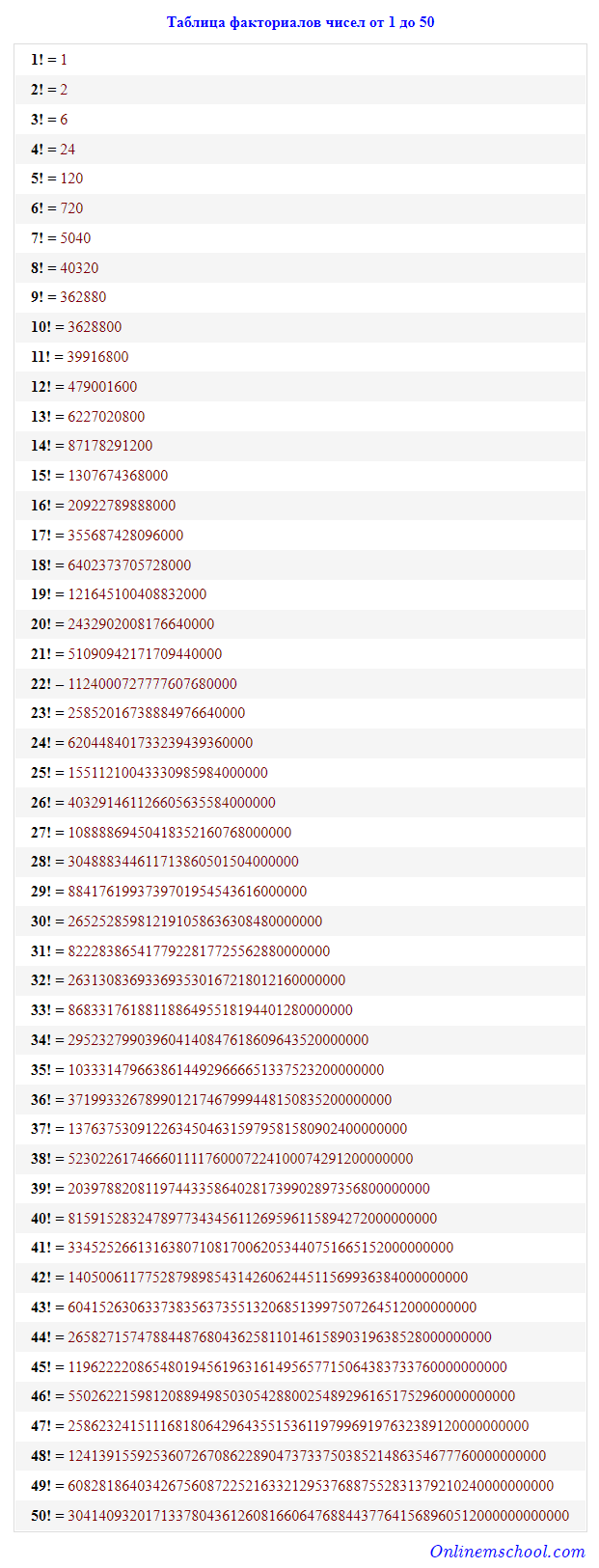
1! = 1 * 1 = 1

2! = 1 * 2 = 2

3! = 1 * 2 * 3 = 6

4! = 1 * 2 * 3 * 4 = 24

Если, (n-1)! = 1 * 2 * 3 * 4

(П-3) * (п-2) * (N-1)

Тогда, логически, n! = 1 * 2 * 3 * 4

(П-3) * (п-2) * (п-1) * п

Или, n! = n * (n-1)! — (i)

Если вы внимательно посмотрите на эти тропы, картина покажет себя. Давайте завершим его, пока он не сумеет получить законные результаты:

4! / 4 = 3!

3! / 3 = 2!

2! / 2 = 1!

1! / 1 = 0!

Или, 0! = 1

Можно прийти к такому результату, просто подключив 1 для «n» в (i), чтобы получить:

1! = 1 * (1-1)!

1 = 1 * 0!

Или, 0! = 1

Однако это объяснение ничего не говорит о том, почему факториалы отрицательных чисел не могут существовать. Давайте снова обратимся к нашему шаблону, чтобы узнать, почему.

2! / 2 = 1!

1! / 1 = 0!

0! / 0 =

Я бы согласился, что эти методы немного подозрительны; они кажутся лукавыми, неявными способами определения факториала нуля. Это похоже на споры в пользу соломы. Однако можно найти объяснение в поле, все его существование зависит от вычисления факториалов — комбинаторики.

Обобщения

Двойной факториал

Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,

По определению полагают .

Последовательность значений n!! начинается так:

1, 1, 2, 3, 8, 15, 48, 105, 384, 945, … (последовательность A006882 в OEIS)

Кратный факториал

m-кратный факториал числа n обозначается и определяется следующим образом:

Пусть число n представимо в виде , где , . Тогда

Двойной факториал является частным случаем m-кратного факториала для m = 2.

Убывающий факториал

Убывающим факториалом (или неполным факториалом) называется выражение

Убывающий факториал даёт число размещений из n по k.

Возрастающим факториалом называется выражение

Праймориал или примориал

Праймориал или примориал (англ. primorial) числа n обозначается n# и определяется как произведение простых чисел, не превышающих n. Например,

Последовательность праймориалов (включая ) начинается так:

, , , , , , 30030, 510510, 9699690, … (последовательность A002110 в OEIS)

Суперфакториалы

Основная статья: Большие числа

Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых факториалов. Согласно этому определению суперфакториал четырёх равен (поскольку устоявшегося обозначения нет, используется функциональное)

В общем

Последовательность суперфакториалов чисел n⩾0 начинается так:

1, 1, 2, 12, 288, 34560, 24883200, … (последовательность A000178 в OEIS)

Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Super-duper-factorial), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел n⩾0 начинается так:

1, 1, 2, 24, 6912, 238878720, 5944066965504000, … (последовательность A055462 в OEIS)

Продолжая рекуррентно, можно определить факториал кратного уровня, где m-уровневый факториал числа n как произведение первых n (m-1)-уровневых факториалов, то есть

где для и .

Субфакториал

Основная статья: Субфакториал

Субфакториал определяется как количество беспорядков порядка , то есть перестановок -элементного множества без неподвижных точек.

История

Факториальные выражения появились ещё в ранних исследованиях по комбинаторике, хотя компактное обозначение n!{\displaystyle n!} предложил французский математик Кристиан Крамп только в 1808 году. Важным этапом стало открытие формулы Стирлинга, которую Джеймс Стирлинг опубликовал в своём трактате «Дифференциальный метод» (лат. Methodus differentialis, 1730 год). Немного ранее почти такую же формулу опубликовал друг Стирлинга Абрахам де Муавр, но в менее завершённом виде (вместо коэффициента 2π{\displaystyle {\sqrt {2\pi }}} была неопределённая константа).

Стирлинг подробно исследовал свойства факториала, вплоть до выяснения вопроса о том, нельзя ли распространить это понятие на произвольные вещественные числа. Он описал несколько возможных путей к реализации этой идеи и высказал мнение, что:

(12)!=π2{\displaystyle \left({1 \over 2}\right)!={\frac {\sqrt {\pi }}{2}}}

Стирлинг не знал, что годом ранее решение проблемы уже нашёл Леонард Эйлер. В письме к Кристиану Гольдбаху Эйлер описал требуемое обобщение:

x!=limm→∞mxm!(x+1)(x+2)…(x+m){\displaystyle x!=\lim _{m\to \infty }{\frac {m^{x}m!}{(x+1)(x+2)\dots (x+m)}}}

Развивая эту идею, Эйлер в следующем, 1730 году ввёл понятие гамма-функции в виде классического интеграла. Эти результаты он опубликовал в журнале Санкт-Петербургской Академии наук в 1729—1730 годах.

Описание формата внутреннего представления данных 1С в контексте обмена данными

Фирма 1С не рекомендует использовать внутреннее представление данных для любых целей, которые отличны от обмена с 1С:Предприятием 7.7. Но сама возможность заглянуть на «внутреннюю кухню» платформы с помощью функций ЗначениеВСтрокуВнутр(), ЗначениеВФайл(), ЗначениеИзСтрокиВнутр() и ЗначениеИзФайла(), дала возможность сообществу программистов 1С разработать новые приемы разработки и анализа.

Так, именно на использовании внутреннего представления был построен алгоритм «быстрого массива», который позволяет практически мгновенно создать массив в памяти на основании строки с разделителями. С помощью разбора внутреннего представления можно «на лету» программным кодом выполнить анализ обычной формы и даже сделать редактор графической схемы. Во внутреннем формате сохраняют свои данные между сеансами различные популярные внешние обработки. А еще это возможность сделать быстрый обмен с внешними системами.

1 стартмани

Вычисление

Если эффективность не важна, вычисление факториалов тривиально с алгоритмической точки зрения: последовательное умножение переменной, инициализированной до 1, на целые числа до n (если есть) вычислит n ! при условии, что результат подходит для переменной. В функциональных языках рекурсивное определение часто реализуется непосредственно для иллюстрации рекурсивных функций.

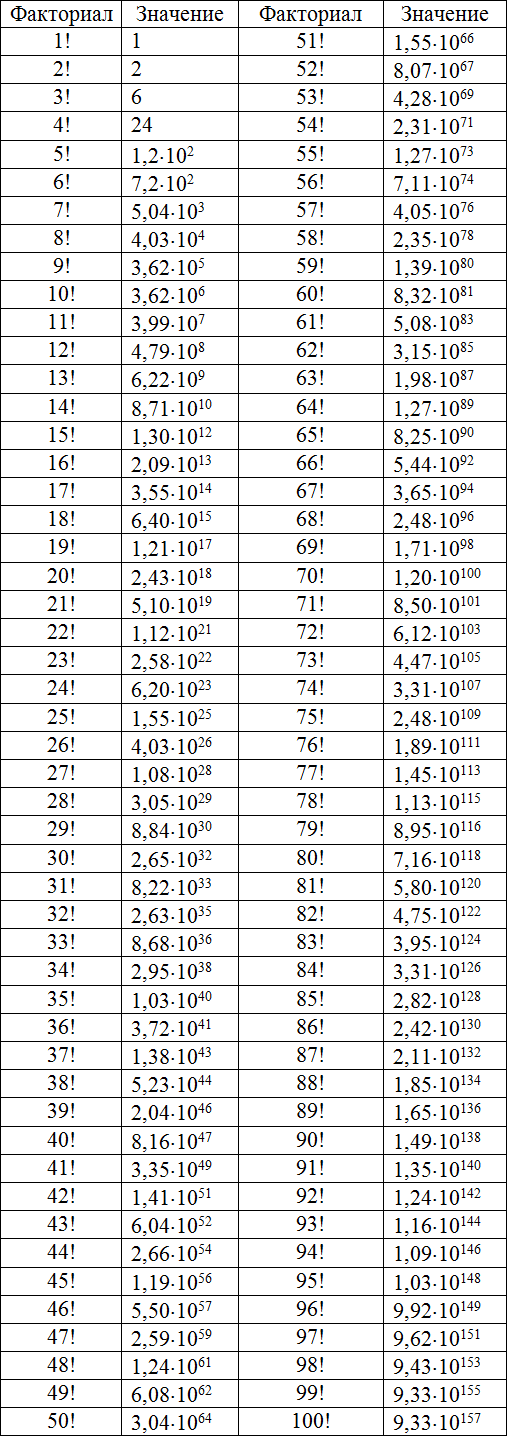
Основная практическая трудность при вычислении факториалов — это размер результата. Чтобы гарантировать, что точный результат будет соответствовать всем допустимым значениям даже самого маленького обычно используемого целого типа (8-битные целые числа со знаком), потребуется более 700 бит, поэтому никакая разумная спецификация факториальной функции с использованием типов фиксированного размера не может избежать вопросов переполнения. Ценности 12! и 20! являются наибольшими факториалами, которые могут быть сохранены соответственно в 32-битных и 64-битных целых числах, обычно используемых в персональных компьютерах , однако многие языки поддерживают целочисленные типы переменной длины, способные вычислять очень большие значения. Представление приближенного результата с плавающей запятой позволяет пойти немного дальше, но это также остается весьма ограниченным возможным переполнением. Большинство калькуляторов используют научную нотацию с двухзначным десятичным показателем, и тогда наибольший подходящий факториал равен 69 !, потому что 69! <10 100 <70! . Другие реализации (например, компьютерное программное обеспечение, например программы электронных таблиц) часто могут обрабатывать большие значения.

Большинство программных приложений вычисляют небольшие факториалы путем прямого умножения или поиска в таблице. Большие факториальные значения могут быть аппроксимированы с помощью формулы Стирлинга . Wolfram Alpha может вычислить точные результаты для функции потолка и функции пола применительно к двоичной , натурального и десятичного логарифма от п ! для значений n до249 999 и до20 000 000 ! для целых чисел.

Если требуются точные значения больших факториалов, их можно вычислить с помощью арифметики произвольной точности . Вместо того, чтобы выполнять последовательные умножения ((1 × 2) × 3) × 4 … , программа может разделить последовательность на две части, продукты которых имеют примерно одинаковый размер, и умножить их, используя метод « разделяй и властвуй». . Часто это более эффективно.

Асимптотически наилучшая эффективность получается при вычислении n ! от его простой факторизации. Как задокументировал Питер Борвейн , разложение на простые множители позволяет n ! вычисляться за время O ( n (log n log log n ) 2 ) , при условии, что используется алгоритм быстрого умножения (например, алгоритм Шёнхаге – Штрассена ). Питер Лушни представляет исходный код и тесты для нескольких эффективных факторных алгоритмов с использованием или без использования простого сита .

Свойства

Комбинаторная интерпретация

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Комбинаторная интерпретация факториала подтверждает целесообразность соглашения !=1{\displaystyle 0!=1}. Так, формула для числа размещений из n{\displaystyle n} элементов по m{\displaystyle m}

Anm=n!(n−m)!{\displaystyle A_{n}^{m}={\frac {n!}{(n-m)!}}}

при n=m{\displaystyle n=m} обращается в формулу для числа перестановок из n{\displaystyle n} элементов (порядка n{\displaystyle n}), которое равно n!{\displaystyle n!}.

Связь с гамма-функцией

Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.

Факториал связан с гамма-функцией от целочисленного аргумента соотношением

n!=Γ(n+1){\displaystyle n!=\Gamma (n+1)}.

Это же выражение используют для обобщения понятия факториала на множество вещественных чисел. Используя аналитическое продолжение гамма-функции, область определения факториала также расширяют на всю комплексную плоскость, исключая особые точки при n=−1,−2,−3…{\displaystyle n=-1,-2,-3\ldots }.

Непосредственным обобщением факториала на множества вещественных и комплексных чисел служит пи-функция Π(z)=Γ(z+1){\displaystyle \Pi (z)=\Gamma (z+1)}, которая при Re(z)>−1{\displaystyle \mathrm {Re} (z)>-1} может быть определена как

Π(z)=∫∞tze−tdt{\displaystyle \Pi (z)=\int _{0}^{\infty }t^{z}e^{-t}\,\mathrm {d} t} (интегральное определение).

Пи-функция натурального числа или нуля совпадает с его факториалом: Π(n)=n!{\displaystyle \Pi (n)=n!}. Как и факториал, пи-функция удовлетворяет рекуррентному соотношению Π(z)=zΠ(z−1){\displaystyle \Pi (z)=z\Pi (z-1)}.

Формула Стирлинга

Основная статья: Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

n!=2πn(ne)n(1+112n+1288n2−13951840n3−5712488320n4+163879209018880n5+524681975246796800n6+O(n−7)),{\displaystyle n!={\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\left(1+{\frac {1}{12n}}+{\frac {1}{288n^{2}}}-{\frac {139}{51840n^{3}}}-{\frac {571}{2488320n^{4}}}+{\frac {163879}{209018880n^{5}}}+{\frac {5246819}{75246796800n^{6}}}+O\left(n^{-7}\right)\right),}

см. O-большое.

Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:

n!≈2πn(ne)n.{\displaystyle n!\approx {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}.}

При этом можно утверждать, что

2πn(ne)ne1(12n+1)<n!<2πn(ne)ne1(12n).{\displaystyle {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}e^{1/(12n+1)}<n!<{\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}e^{1/(12n)}.}

Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Например, с помощью формулы Стирлинга легко подсчитать, что

100! ≈ 9,33×10157;
1000! ≈ 4,02×102567;
10 000! ≈ 2,85×1035 659.

Разложение на простые числа

Каждое простое число p входит в разложение n! на простые множители в степени

⌊np⌋+⌊np2⌋+⌊np3⌋+….{\displaystyle \left\lfloor {\frac {n}{p}}\right\rfloor +\left\lfloor {\frac {n}{p^{2}}}\right\rfloor +\left\lfloor {\frac {n}{p^{3}}}\right\rfloor +\ldots .}

Таким образом,

n!=∏pp⌊np⌋+⌊np2⌋+…,{\displaystyle n!=\prod _{p}p^{\lfloor {\frac {n}{p}}\rfloor +\lfloor {\frac {n}{p^{2}}}\rfloor +\ldots },}

где произведение берётся по всем простым числам. Можно заметить, что для всякого простого p большего n соответствующий множитель в произведении равен 1, следовательно произведение можно брать лишь по простым p, не превосходящим n.

Связь с производной от степенной функции

Для целого неотрицательного числа n:

(xn)(n)=n!{\displaystyle \left(x^{n}\right)^{(n)}=n!}

Например:

(x5)(5)=(5⋅x4)(4)=(5⋅4⋅x3)‴=(5⋅4⋅3⋅x2)″=(5⋅4⋅3⋅2⋅x)′=5⋅4⋅3⋅2⋅1=5!{\displaystyle \left(x^{5}\right)^{(5)}=\left(5\cdot x^{4}\right)^{(4)}=\left(5\cdot 4\cdot x^{3}\right)»’=\left(5\cdot 4\cdot 3\cdot x^{2}\right)»=\left(5\cdot 4\cdot 3\cdot 2\cdot x\right)’={5\cdot 4\cdot 3\cdot 2\cdot 1}=5!}

Другие свойства

Для натурального числа n:

n!2⩾nn⩾n!⩾n{\displaystyle n!^{2}\geqslant n^{n}\geqslant n!\geqslant n}

Для любого n>1:

n!{\displaystyle n!} не является квадратом целого числа.

Бесплатный онлайн калькулятор факториалов

Наш бесплатный решатель позволяет расчитать факториалы онлайн любой сложности за считанные секунды. Все,
что вам необходимо
сделать — это просто ввести свои данные в калькуляторе. Так же вы можете и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то
вы
можете задать их в нашей группе Вконтакте.

Запрос напоминает, почему число, поднятое до нулевой мощности, равно единице, запрос, который я разрешил в более ранней статье. Кроме того, позвольте мне заверить, что я ранее заверил, объясняя этот очевидный, бесстыдно принятый, но необъяснимый факт — отношение не является произвольным.

Существует три способа определить, почему факторный нуль равен единице.