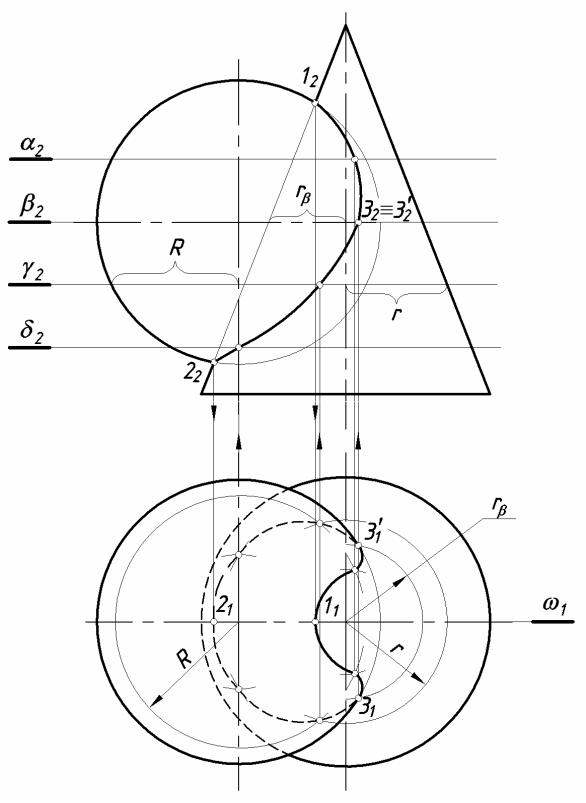
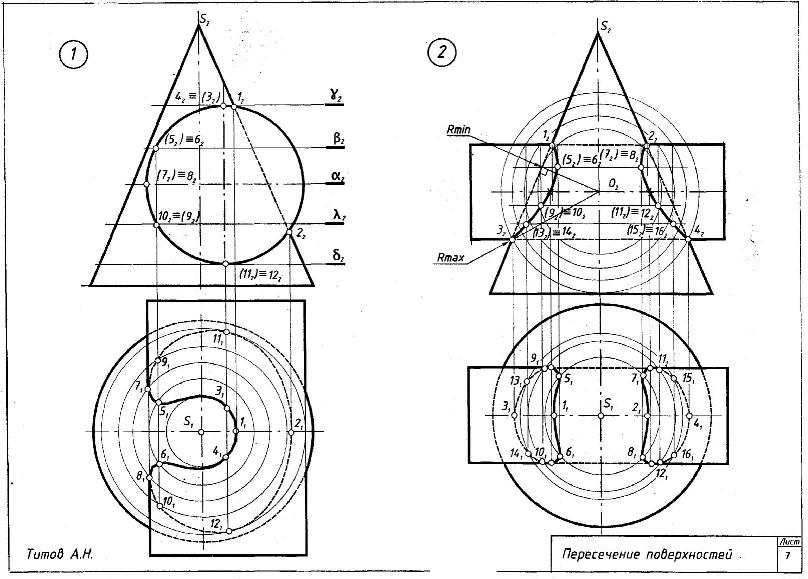
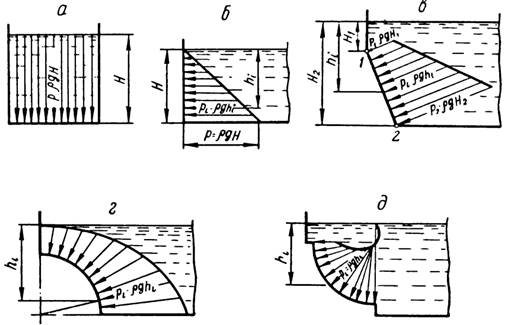
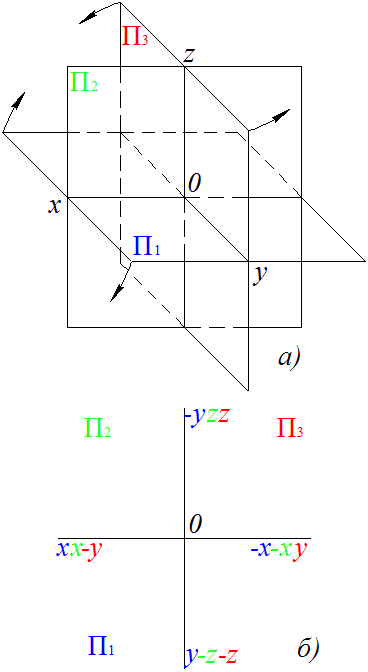Эпюр

Построение эпюры нормальных напряжений

Переходим к эпюре нормальных напряжений. В отличие от продольных сил, нормальные напряжения зависят от формы бурса, а если точнее, то от площади его поперечных сечений и вычисляются они, по следующей формуле:

Для того, чтобы построить эпюру нормальных напряжений, нужно рассчитать ее для любого сечения, каждого участка. В отличие, от продольной силы, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашего подопытного бруса, нужно наметить три участка и вычислить напряжение, соответственно, 3 раза:

Зададим брусу на первом участке (I) площадь поперечного сечения A₁=2 см2, а вторая ступень бруса, допустим, будет иметь площадь A₂=4 см2 (II, III участки). В вашей домашней задаче, эти величины будут даны по условию. Также в задачах, часто, просят определить эти площади из условия прочности, с учетом допустимого напряжения, обязательно сделаю статью про это.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

Суть метода

Брус рассекается на две части и рассматривается только одна его часть, а воздействие на нее другой части заменяется соответствующими внутренними усилиями, которые определяются из условия равновесия.

Рассмотрим его на примере прямого бруса, к которому приложена произвольная плоская система нагрузок. Отметим, что указанная система нагрузок удерживает брус в неподвижном (статичном) положении.

Обозначим характерные точки бруса:

Эти точки одновременно являются границами силовых участков бруса, т.е. данный брус имеет 5 силовых участков.

Для того чтобы определить внутренние усилия например на участке DK в любом месте участка проведем сечение которое условно делит брус на две части, в данном случае левую и правую:

Зная, что весь брус изначально статичен, можно утверждать, что так же будет статичен любой его фрагмент, включая обе показанные части.

Для определения внутренних усилий можно выбрать любую из них, при этом результаты расчетов будут одинаковы. Поэтому для упрощения вычислений принято выбирать ту часть, к которой приложено меньше нагрузок.

В данном случае к левой части приложено 4 усилия, а к правой всего два.

Здесь выбор правой части бруса снижает вероятность ошибки при расчетах.

Выбрав оптимальную часть бруса, обозначим расстояние от ближайшей границы силового участка до рассматриваемого сечения переменной z.

На данном участке сечение может занимать любое положение между точками K (где z=0) и D (где z равно длине участка DK), включая сами эти точки.

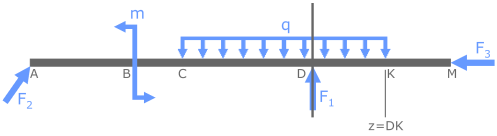
Это записывается как 0≤z≤DK.

Затем для каждого внутреннего силового фактора записываются выражения в виде суммы соответствующих внешних нагрузок приложенных к рассматриваемой части бруса.

Далее рассчитываются их значения на границах силовых участков при z=0 и z=DK.

В случаях, когда переменная z в выражениях имеет степень 2 или выше (т.е. эпюра будет иметь вид параболы) можно рассчитать величину внутренних сил для промежуточных положений сечения, например при z=DK/2.

Указанные действия необходимо проделать по каждому силовому участку.
По полученным данным строятся необходимые эпюры.

Порядок построения эпюр методом сечений:

Определяются опорные реакции,
Определяется количество силовых участков бруса,
В пределах каждого участка брус делится на две части поперечным сечением,
Выбирается часть, к которой приложено меньше нагрузок,
Записываются необходимые выражения для внутренних силовых факторов,
Рассчитываются значения для характерных положений сечения,
Строятся эпюры.

Основные деформации >Примеры решения задач >

История

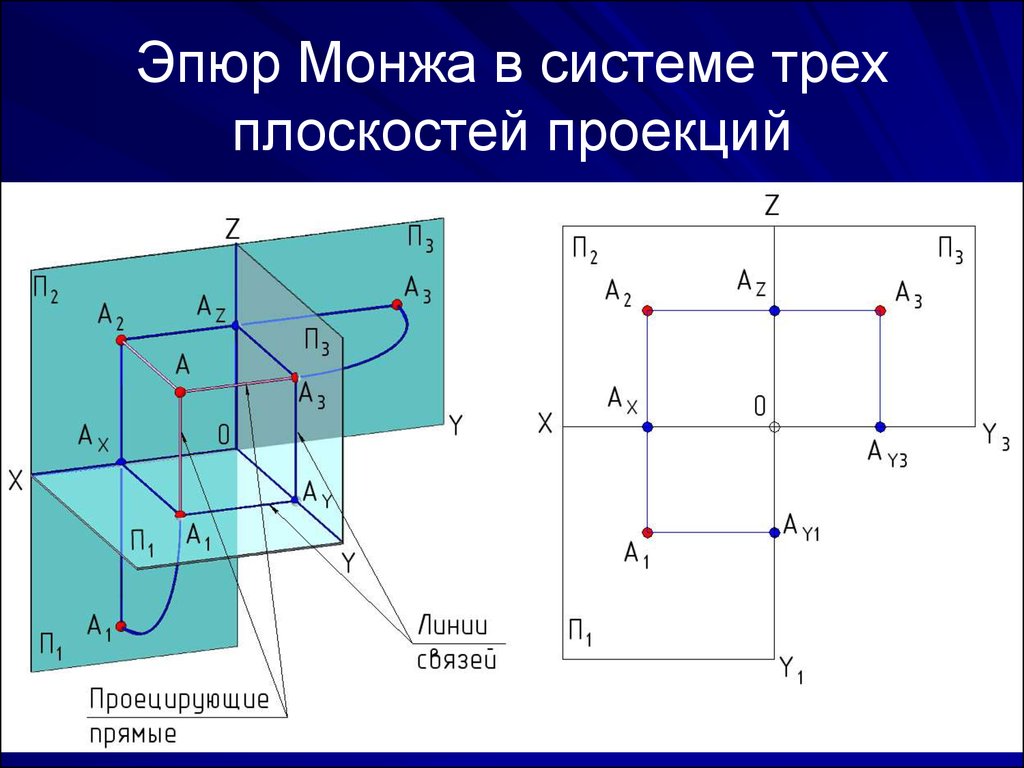
Сведения и приемы построений, обусловливаемые потребностью в плоских изображениях пространственных форм, накапливались постепенно еще с древних времен. В течение продолжительного периода плоские изображения выполнялись преимущественно как изображения наглядные. С развитием техники первостепенное значение приобрел вопрос о применении метода, обеспечивающего точность и удобоизмеримость изображений, то есть возможность точно установить место каждой точки изображения относительно других точек или плоскостей и путём простых приемов определить размеры отрезков линий и фигур.

Будучи одним из министров в революционном правительстве Франции, Гаспар Монж много сделал для её защиты от иностранной интервенции и для победы революционных войск. Начав с задачи точной резки камней по заданным эскизам применительно к архитектуре и фортификации, Монж пришёл к созданию методов, обобщённых им впоследствии в новой науке — начертательной геометрии, творцом которой он по праву считается. Учитывая возможность применения методов начертательной геометрии в военных целях при строительстве укреплений, руководство Мезьерской школы не допускало открытой публикации вплоть до 1799 года (стенографическая запись лекций была сделана в 1795 году).

Сопромат — наука о прочности

Сопротивление материалов — раздел технической механики, в котором изучаются экспериментальные и теоретические основы и методы расчета наиболее распространенных элементов различных конструкций, находящихся под воздействием внешних нагрузок, на прочность, жесткость и устойчивость, с учетом требований надежности, экономичности, технологичности изготовления, удобства транспортировки и монтажа, а также безопасности при эксплуатации.

Короткое видео о том что такое сопромат и зачем он нужен:

Сопротивление материалов является одной из фундаментальных дисциплин общеинженерной подготовки специалистов в сфере высшего технического образования.

17.Изгибающий момент. Правила (порядок) построения эпюры изгибающих моментов.

Изгибающий
момент—
внутреннее
усилие возникающее от действия внешней
нагрузки( изгиба , внецентренного сжатия
–растяжения).

Порядок
построения эпюры изгибающих моментов:

1.Определение
опорных реакций данной конструкции.

2.Определение
участков данной конструкции ,в пределах
которых изгибающий момент будет
изменяться по одному и тому же закону.

3.Произвести
сечение данной конструкции в окрестности
точки , которая разделяет участки.

4.Отбросить
одну из частей конструкции, разделённой
пополам.

5.Найти
момент ,который уравновесит действие
на одну из оставшихся частей конструкции
всех внешних нагрузок и реакций связи.

6.Нанести
значение этого момента, с учётом знака
и выбранного масштаба, на эпюру.

Вопрос
№ 18.Поперечная сила. Построение эпюры
поперечных сил, используя эпюру изгибающих
моментов.

Поперечная
сила Q
–внутреннее усилие возникающее в
стержне под воздействием внешней
нагрузки( изгиб, поперечная нагрузка).
Поперечная сила направлена перпендикулярно
оси стержня.

Эпюра
поперечных сил Q
строится исходя из следующей
дифференциальной зависимости:
,т.е.
Первая
производная от изгибающего момента по
продольной координате равна поперечной
силе.

Знак
поперечной силы определяется исходя
из следующего положения:

Если
нейтральная ось конструкции на эпюре
моментов поворачивается к оси эпюры по
часовой стрелке, то эпюра поперечных
сил имеет знак плюс, если против- минус.

В
зависимости от эпюры M
эпюра Q
может принимать тот или иной вид:

1.если эпюра
моментов имеет вид прямоугольника , то
эпюра поперечных сил равна нулю.

2.Если эпюра
моментов представляет собой треугольник
, то эпюра поперечных сил имеет вид
прямоугольника.

3.Если эпюра
моментов имеет вид квадратной параболы
, то эпюра поперечных сил имеет
треугольника и строится по следующему
принципу

Вопрос
№19 . Продольная сила. Метод построения
эпюры продольных сил используя эпюру
поперечных сил. Правило знаков.

Полольная
сила N- внутреннее усилие
возникающее вследствие центрального
и внецентренного растяжения-сжатия.
Продольная сила направлена вдоль оси
стержня.

Для того
что бы построить эпюру продольных усилий
нужно:

1.Вырезать
узел данной конструкции. Если мы имеем
дело с одномерной конструкцией , то
сделать сечение на интересующем нас
участке этой конструкции.

2.Снять с
эпюры Q значения усилий
действующих в непосредственной близости
от вырезанного узла.

3.Дать
направление векторам поперечных сил,
исходя из того какой знак имеет данное
поперечное усилие на эпюре Q
по следующим правилам: если поперечная
сила имеет на эпюре Q знак
плюс , то её нужно направить так , что бы
она вращала данный узел по часовой
стрелке, если поперечная сила имеет
знак минус –против часовой стрелки.
Если внешняя сила проложена к узлу , то
её нужно оставить и рассматривать узел
вместе с ней.

4.Уравновесить
узел продольными усилиями N.

5.Правило
знаков для N:если продольная
сила направлена к сечению , то она имеет
знак минус ( работает на сжатие).если
продольная сила направлена от сечения
, она имеет знак плюс ( работает на
растяжение).

Вопрос №
20.Правилаприменяемые для проверки
правильности построения эпюр внутренних
усилий M,Q,N.

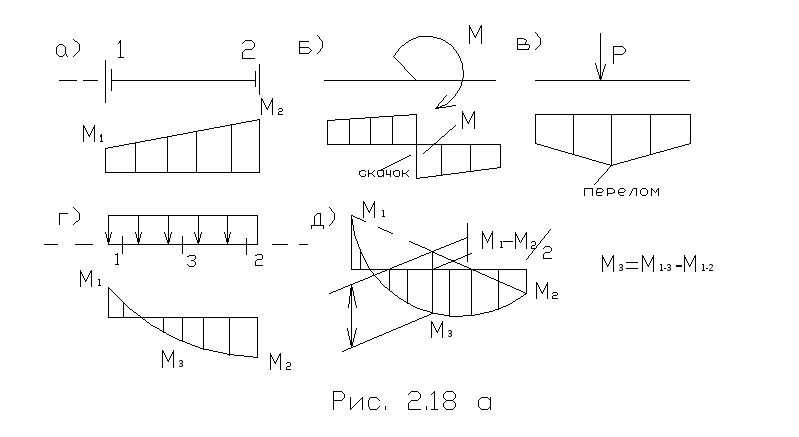
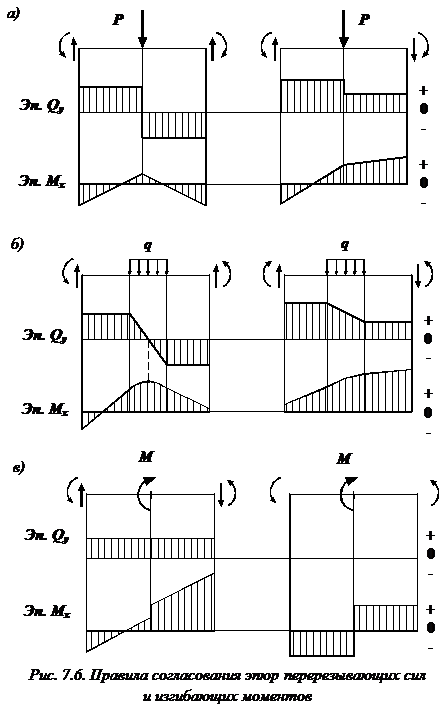
1.
В сечении, где приложена сосредоточенная
сила F,
на
эпюре Q
будет
скачок, равный значению этой силы и
направленный в ту же сторону (при
построении эпюры слева направо), а эпюра
М будет иметь перелом, направ-
ленный
в сторону действия силы F.

В сечении, где приложен сосредоточенный
изгибающий момент на эпюре М, будет
скачок, равный значению момента М; на
эпюре Q
изменений
не будет. При этом направление скачка
будет вниз (при построении
эпюры слева
направо), если сосредоточенный момент
действует по ходу часовой стрелки, и
вверх, если против хода часовой стрелки.

3.Если
на
участке, где имеется равномерно
распределенная нагрузка, поперечная
сила в одном из сечений равна нулю
(Q=M’=0),
то изгибающий момент в этом сечении
принимает экстремальное значение
М_экстр
— максимум или минимум (здесь касательная
к
эпюре М горизонтальна).

4.Для
проверки правильности построения эпюры
М можно использовать метод вырезания
узлов. При этом момент приложенный в
узле нужно при вырезании узла оставлять.

Правильность
построения эпюр Q
и M
можно проверить, дублируя метод вырезания
узлов методом сечений и наоборот.

Верещагин и его метод, правило или способ

А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть любой. Кроме того, ордината берется прямолинейной эпюры

Когда эпюры обе прямолинейны, то тут совсем не важно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:

${ V={ M }_{ F } }\cdot \overline { M } ={ \omega }_{ C }\cdot { \overline { M } }_{ C } $

Проиллюстрировано перемножение эпюр по Верещагину: C — центр тяжести первой эпюры, ωс — площадь первой эпюры, Mc — ордината второй эпюры под центром тяжести первой.

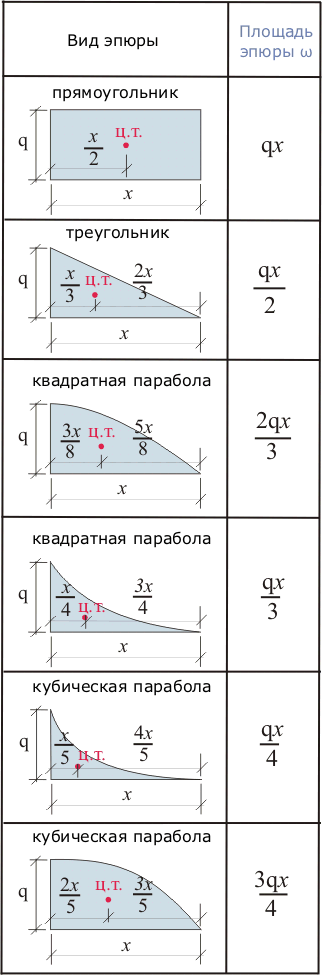
Площадь и центр тяжести эпюр

При использовании метода Верещагина, берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.

Любую эпюру можно расслоить всего на три фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.

Поэтому именно с этими фигурами будем дальше работать. Напомню, как вычислить их площадь и где у них находится центр тяжести. Все формулы и размеры оформил в виде таблицы:

Объект изучения

В сопромате главным объектом для расчета является брус, нагруженный системой внешних усилий (сил, моментов и распределенных нагрузок).

Для него могут проводится следующие виды расчетов:

на прочность;
на жесткость;
на устойчивость.

Расчет на прочность является основным, т.к. абсолютно все конструкции должны быть прочными.

Различают три вида задачи при расчетах на прочность:

Проверка на прочность (проверочный расчет);
Подбор размеров сечения бруса (проектировочный расчет);
Определение грузоподъемности.

При расчетах на жесткость определяются деформации бруса и перемещение его сечений, на основании чего делается заключение о жесткости бруса. При невыполнении условия жесткости определяются необходимые размеры сечения.

Линейные перемещения

Отметим в произвольном месте балки точку K и приложим к свободному концу консоли сосредоточенную силу F.
Под действием этой силы балка изогнется, и точка K переместится в новое положение K’.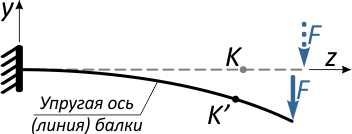
Очевидно, что перемещение точки K произойдет, не строго вертикально, поэтому разложим его на две составляющие:
вертикальное перемещение по оси y, называемое прогибом балки в т. K (y_K)
и горизонтальное (осевое) смещение точки вдоль горизонтальной оси — z_K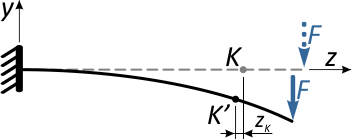
Практические расчеты показывают, что осевые смещения как правило, несоизмеримо меньше вертикальных перемещений (например, в данном случае z_KK), поэтому ими пренебрегают, ограничиваясь вычислением прогибов.

Линейные перемещения (прогибы балки) измеряются в метрах или кратных единицах измерения (миллиметрах и сантиметрах).

Прогибы, при которых сечение в результате деформации балки перемещается вверх принимаются положительными.

Именно по величине прогибов определяется жесткость балки.

Построение эпюры перемещений

Самое время перейти к последней эпюре, которая называется эпюрой осевых перемещений поперечных сечений. Для краткости, ее еще называют просто эпюрой перемещений. Для расчета данного графика, пользуются следующей формулой:

Эта формула, является следствием закона Гука. Также ее можно записать как:

Сейчас покажу как ею пользоваться. Все характерные сечения бруса назовем буквами английского алфавита, чтобы потом в решении, было удобно ссылаться на них:

Традиционно расчет перемещений начинают с жестко защемленного торца. Так как сечение в заделке, не имеет возможности перемещаться, то и в решение записываем, что перемещение этого сечения равно нулю:

Далее, для построения эпюры нужно вычислить перемещения в характерных сечениях, которые находятся на границах участков (B, C и D). Этого будет достаточно, так как в пределах участков, эпюра будет меняться по линейному закону. Исключениями могут быть участки, на которых действует распределенная нагрузка, но это тема отдельной статьи.

Приступаем к расчету перемещения сечения B. По формуле, оно будет равно площади эпюры σ, на третьем участке, деленной на модуль упругости — E. При этом, обязательно, учитываем знак эпюры:

Для других сечений, перемещения будут вычисляться аналогичным образом:

По полученным значениям, откладываем эпюру перемещений:

Вот так, достаточно просто можно построить эпюры для бруса, работающего на растяжение (сжатие). В рамках статьи, была рассмотрена достаточно простая расчетная схема, если Вы хотите развить свои навыки по построению эпюр, то приглашаю Вас на страничку про различные эпюры, где можно найти примеры расчета более сложных брусьев с распределенными нагрузками, где о каждой эпюре подготовлена отдельная статья.

Расчет и построение эпюр

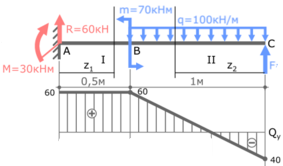
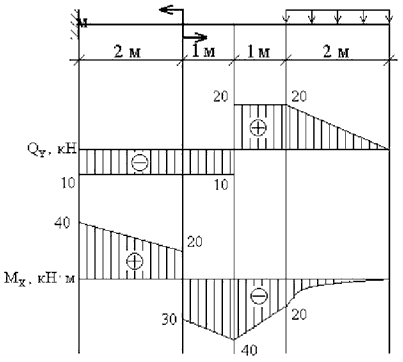
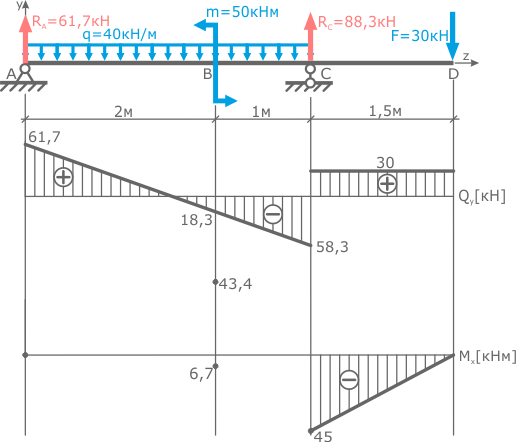
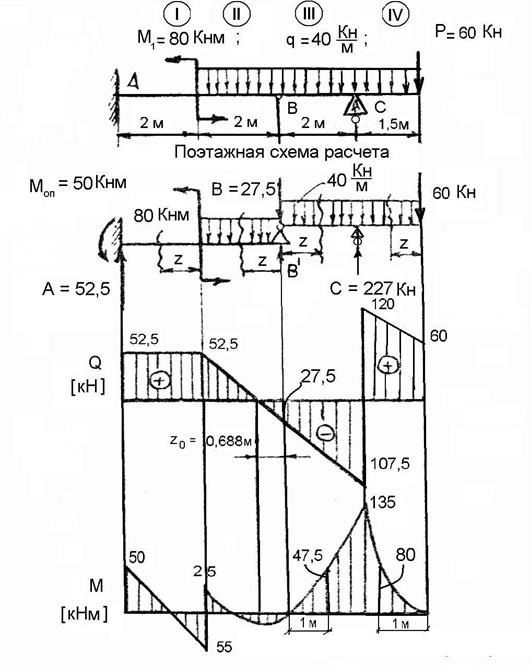
Для расчета эпюр сначала нужно наметить участки, на которых эпюра будет либо постоянна, либо меняться по одному закону. Опознать эти участки достаточно просто. Границами участков служат те места, где прикладываются нагрузки (сосредоточенные силы и моменты, в том числе реакции опор). Если на балку действует распределенная нагрузка, то границы – это ее начало и конец. В нашем случае, как видите, 2 участка, каждый по 2 метра:

Рассматриваем произвольное сечение первого участка, которое обзовем буквой – С. Оно будет находится на расстоянии z1 от левого торца балки. И относительного него будем записывать законы, по которым меняются поперечные силы и изгибающие моменты на этом участке:

Записываем уравнение для поперечной силы

Поперечная сила будет равняться сумме всех сосредоточенных сил, находящихся слева от сечения (или справа). Мы будем подсчитывать все, что находится слева, т.к. там меньше нагрузки. В уравнении поперечной силы, все внешние нагрузки нужно учитывать с учетом правила знаков: если сила, относительно рассматриваемого сечения, поворачивает ПО часовой стрелке, то в уравнение она пойдет с ПЛЮСОМ (и наоборот).

В рассматриваемом примере, реакция RA поворачивает ПО часовой стрелке, и уравнение получится такое:

Причем, как видно, эта зависимость справедлива для любого сечения на первом участке, тем самым поперечная сила в пределах этого участка постоянна и равна – 5 кН. Откладываем это значение на графике:

Эпюры заштриховываются перпендикулярно нулевой линии и на каждом участке проставляются знаки поперечной силы.

Записываем уравнение для изгибающего момента

Что касается изгибающего момента, то тут в уравнении нужно учесть сумму моментов, находящихся по одну сторону от сечения. Реакция RA, относительно сечения С создает момент RA·z1. Напомню, что момент – это сила, умноженная на плечо. Где плечо – это расстояние от силы до центра момента (в этом случае, центр – это рассматриваемое сечение). В уравнении моментов, все моменты нужно учитывать с учетом правила знаков: если момент силы, стремится растянуть нижние волокна, то в уравнении будем записывать его со знаком «+». И наоборот.

Придерживаясь этого правила, будем откладывать эпюры изгибающих моментов со стороны РАСТЯНУТЫХ волокон. Что практикуется у инженеров-строителей. У механиков, другие правила, они рисуют эти эпюры со стороны сжатых волокон. Кстати, что такое растянутое и сжатое волокно? Покажу на нашем же примере:

Как видно, сила RA, при повороте, стремится растянуть нижние волокна, поэтому в уравнение будем записывать момент этой силы со знаком плюс:

Анализируя это уравнение, видим, что изгибающий момент будет меняться по линейному закону и зависеть от координаты z1. И чтобы рассчитать и построить эпюру на этом участке достаточно подставить в уравнение координаты начала участка z1=0 и конца z1=2 м. После чего отложить эти точки на графике и соединить прямой линией:

Эпюры для второго участка балки

С учетом всех вышеописанных рекомендаций, я думаю Вы сами теперь сможете построить эпюры для второго участка. Подробно комментировать уже не буду, приведу сразу решение и окончательные эпюры для этой балки:

Сегодня мы рассмотрели урок по построению эпюр для простой балки. Однако, много нюансов по расчету и построению я не рассказал, т.к. все это уместить в одном уроке, довольно сложно и не всем это нужно, статья ведь для чайников! Если Вы хотите прокачать свой знания, в этих вопросах, обязательно прочитайте эти материалы о эпюрах. Здесь можно найти подробные статьи о поперечной силе, о изгибающем моменте. Где я рассказывал о 3-х методиках расчета, причем один из них, даже проще, чем мы рассматривали в данной статье. С помощью которого можно устно рисовать эти эпюры. Также там можно посмотреть, как учитывать моменты и распределенные нагрузки при расчете эпюр и какие особенности есть по построению при действии данных видов нагрузок.

Процесс построения эпюр

Процесс построения эпюры стандартизирован и осуществляется по определенным правилам. Это сделано для общего понимания графиков всеми участниками производственного процесса.

Сначала строится нулевая линия. С левой стороны от линии пишется символическое название эпюры: $N$ — продольные силы, $Q$ — поперечные силы, $Mиз$ — изгибающие моменты, $T$ или $Mкр$ — вращающие момент, $σ$ и $τ$ — нормальное и касательное напряжения. Название сопровождается единицей измерения в соответствии с параметром (наименованием эпюры), например, $МПа$ — мегапаскаль.

Затем определяются границы силовых участков, то есть таких участков, где силовой фактор (деформация) остается постоянным или изменяется в рамках одной закономерности. Зачастую, границы силовых участков представляют собой сечения с приложенной внешней нагрузкой. Обозначение границ на эпюре реализуется в виде тонких вертикальных линий.

Замечание 1

Если брус обладает сложной объемной формой, то границы определяют аналитически.

Далее эпюра масштабируется. Масштаб выбирается в соответствии с предварительным просчетом отображаемого фактора по всем контрольным сечениям (КС) бруса.

После выбора масштаба и построения внешнего контура эпюры КС присваиваются значения фактора без указания знака (“$+$” и “$–$”). Факторы с положительными значениями чертятся над нулевой линией, а с отрицательными под.

В области с положительными значениями на самом широком участке пишется знак “$+$” и обводится кружком, а с отрицательными выполняется также операция, но указывается знак “$–$”. Можно поставить знаки справа и слева от “$0$”, при этом кружками они обводится не будут.

Упрощенный способ построения эпюры

Итак, продолжим изучать технологии построения эпюры поперечных сил. В этом методе будем учится рассчитывать эту эпюру без вынесения отдельных участков балки и без записи уравнений равновесия. Будем выводить сразу следствия из этих уравнений. Также как, в первом случае, балку нужно разбить на 2 участка.

Первый участок

Запишем закон изменения поперечной силы на первом участке. Для этого отметим сечение С, отстающее от правого торца балки на величину z₁. Поперечная сила в этом сечении будет равна сумме проекций всех сил на вертикальную ось, находящихся справа (или слева) от сечения. Мы ведем расчет этого участка справа-налево, так как в данном случае справа нагрузки меньше.

Для того чтобы правильно записать уравнение поперечных сил для любого участка, нужно придерживаться следующих правил:

Если нагрузка относительно рассматриваемого сечения стремится повернуть ПО часовой стрелки, то в уравнении она учитывается со знаком «+»;
Если нагрузка относительно рассматриваемого сечения стремится повернуть ПРОТИВ часовой стрелки, то в уравнении она учитывается со знаком «-».

Продемонстрирую вышеописанные правила на нашем примере. Относительно сечения С, сила R_B, находящаяся справа от сечения, стремится повернуть против часовой стрелки, поэтому в уравнение она пойдет со знаком «-»:

Как видно из уравнения, поперечная сила, на первом участке, не зависет от координаты z₁, поэтому во всех сечениях она одинаковая.

Кстати, помните я писал, что нагрузку можно учитывать, как справа, так и слева? Так вот, давайте запишем уравнение, просуммировав нагрузку, находящуюся слева от сечения С и посмотрим результат.

Реакция R_A, относительно сечения С, стремится повернуть ПО часовой стрелке, в уравнение пойдет с плюсом:

Нагрузку q, сворачиваем до сосредоточенной силы, как в подробном способе. Она стремится повернутся ПРОТИВ часовой стрелке, в уравнение пойдет со знаком «минус»:

Подставляя численные значения нагрузки, получим следующий результат:

Теперь перейдем ко второму участку.