Энтальпия

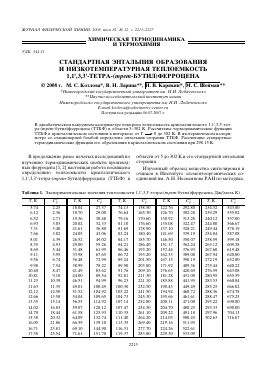
Инвариантная энтальпия в релятивистской термодинамике

При построении релятивистской термодинамики (с учётом специальной теории относительности) обычно наиболее удобным подходом является использование так называемой инвариантной энтальпии — для системы, находящейся в некотором сосуде.

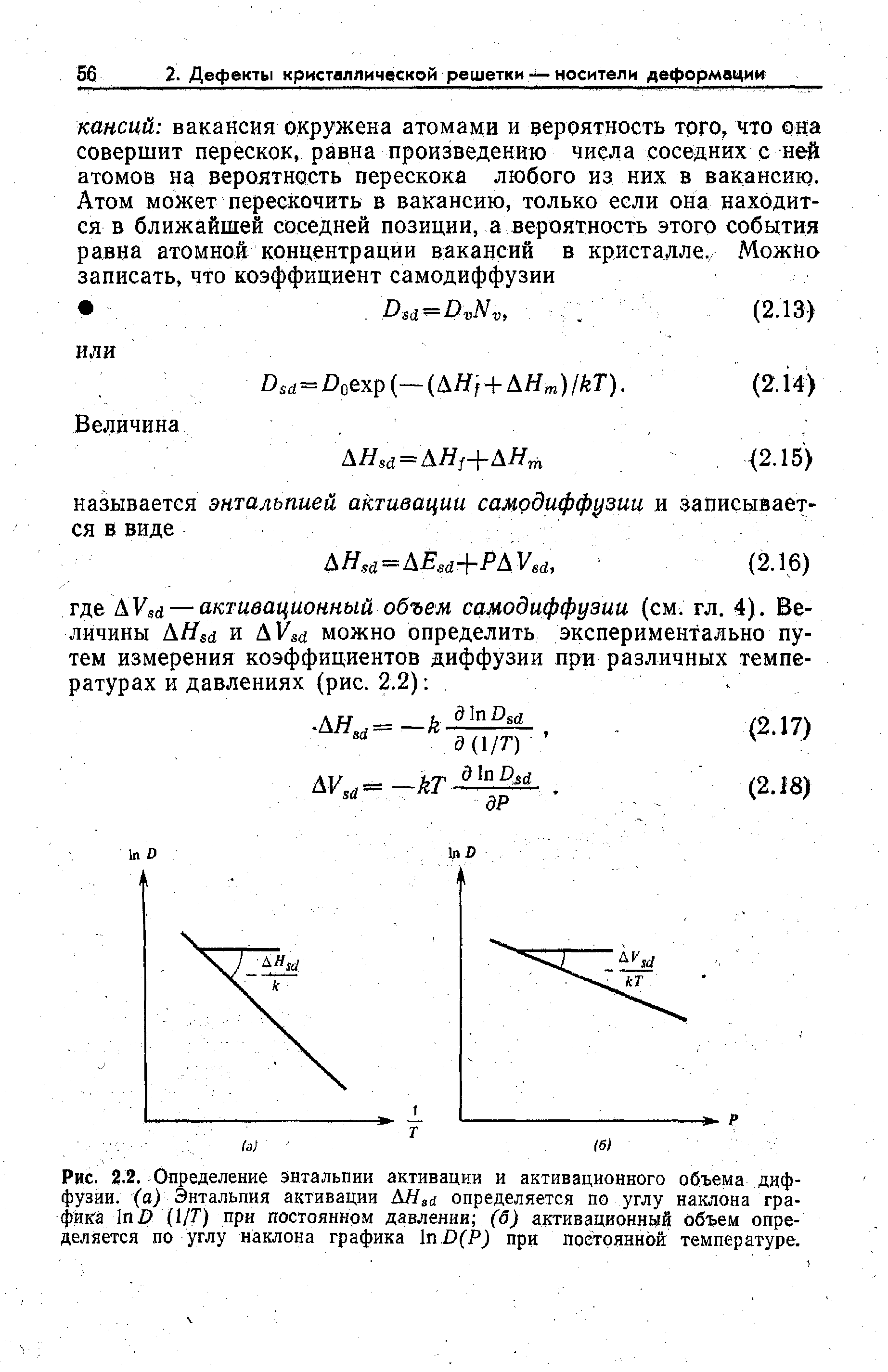
При этом подходе температура T{\displaystyle T} определяется как лоренц-инвариант. Энтропия S{\displaystyle S} — также инвариант. Поскольку стенки влияют на систему, наиболее естественной независимой переменной является давление p{\displaystyle p}, в связи с чем в качестве термодинамического потенциала удобно брать именно энтальпию.

Для такой системы «обычная» энтальпия и импульс системы g→{\displaystyle {\vec {g}}} образуют 4-вектор, и за определение инвариантной энтальпии, одинаковой во всех системах отсчёта, берётся инвариантная функция этого 4-вектора:

H=(U+pV)2−c2g→2.{\displaystyle H={\sqrt {\left(U+p\,V\right)^{2}-c^{2}{\vec {g}}^{2}}}.}

Основное уравнение релятивистской термодинамики записывается через дифференциал инвариантной энтальпии следующим образом:

dH=TdS+V1−v2c2dp+μdN.{\displaystyle dH=T\,dS+{\frac {V}{\sqrt {1-v^{2}/c^{2}}}}\,dp+\mu \,dN.}

Пользуясь этим уравнением, можно решить любой вопрос термодинамики движущихся систем, если известна функция H(S,p,N){\displaystyle H(S,p,N)}.

Примеры

**Неорганические соединения (при 25 °C)***стандартная энтальпия образования*
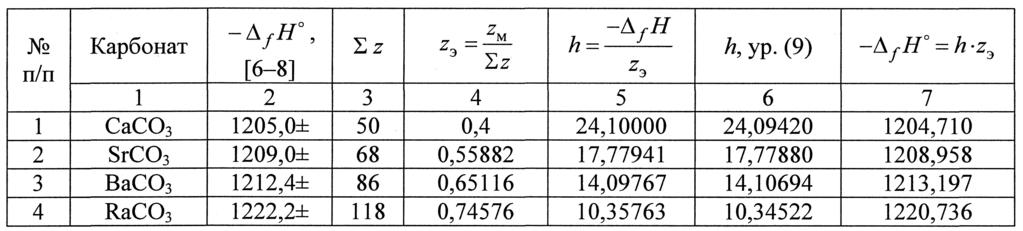
Хим соединение	Фаза (вещества)	Химическая формула	Δ H_f кДж/моль
Аммиак	сольватированный	NH₃ (NH₄OH)	−80.8
Аммиак	газообразный	NH₃	−46.1
Карбонат натрия	твёрдый	Na₂CO₃	−1131
Хлорид натрия (соль)	сольватированный	NaCl	−407
Хлорид натрия (соль)	твёрдый	NaCl	−411.12
Хлорид натрия (соль)	жидкий	NaCl	−385.92
Хлорид натрия (соль)	газообразный	NaCl	−181.42
Гидроксид натрия	сольватированный	NaOH	−469.6
Гидроксид натрия	твёрдый	NaOH	−426.7
Нитрат натрия	сольватированный	NaNO₃	−446.2
Нитрат натрия	твёрдый	NaNO₃	−424.8
Диоксид серы	газообразный	SO₂	−297
Серная кислота	жидкий	H₂SO₄	−814
Диоксид кремния	твёрдый	SiO₂	−911
Диоксид азота	газообразный	NO₂	+33
Монооксид азота	газообразный	NO	+90
Вода	жидкий	H₂O	−286
Вода	газообразный	H₂O	−241.8
Диоксид углерода	газообразный	CO₂	−393.5
Водород	газообразный	H₂
Фтор	газообразный	F₂
Хлор	газообразный	Cl₂
Бром	жидкий	Br₂
Бром	газообразный	Br₂	30.73

Самопроизвольное протекание процесса

В термодинамической системе самопроизвольно протекает процесс в том случае, когда происходит уменьшение свободной энергии взаимодействующей системы. В качестве условия достижения термодинамического равновесия рассматривается минимальная величина термодинамического потенциала.

Только при условии сохранения во времени постоянных внешних условий, можно вести речь о неизменности взаимодействия.

Один из разделов термодинамики изучает именно равновесные состояния, в которых энтальпия — это величина, рассчитываемая для каждого отдельного процесса.

Химические процессы являются обратимыми в тех случаях, когда они протекают сразу в двух взаимно реверсных направлениях: обратном и прямом. Если в закрытой системе наблюдается обратный процесс, в таком случае через определенный временной промежуток система достигнет равновесного состояния. Оно характеризуется прекращением изменения концентрации всех веществ во времени. Такое состояние не означает полного прекращения реакции между исходными веществами, поскольку равновесие является динамическим процессом.

Энтальпия — это физическая величина, которую можно вычислить для разных химических веществ. Количественной характеристикой равновесного процесса является константа равновесия, выражаемая через парциальные давления, равновесные концентрации, мольные доли взаимодействующих веществ.

Для любого обратимого процесса можно вычислить константу равновесия. Она зависит от температуры, а также от природы взаимодействующих компонентов.

Рассмотрим пример возникновения в системе состояния равновесия. В начальный момент времени в системе есть только исходные вещества А и В. Скорость прямой реакции имеет максимальную величину, а обратный процесс не протекает. По мере снижения концентрации исходных компонентов наблюдается увеличение скорости обратного процесса.

Учитывая, что энтальпия — это физическая величина, которую можно рассчитать для реагирующих веществ, а также для продуктов процесса, можно сделать определенные выводы.

Спустя определенный временной промежуток, скорость прямого процесса равна скорости обратного взаимодействия. Константа равновесия представляет собой отношение констант скорости прямого и обратного процесса. Физический смысл этой величины показывает, во сколько раз скорость прямого процесса превышает величину обратного взаимодействия при определенной концентрации и температуре.

Ключевые концепции для расчета энтальпии

Когда реакция меняется на противоположную, величина Δ H остается прежней, но меняется знак.
Когда сбалансированное уравнение реакции умножается на целое число, соответствующее значение Δ H также должно быть умножено на это целое число.
Изменение энтальпии реакции можно рассчитать на основании энтальпий образования реагентов и продуктов.
Элементы в их стандартных состояниях не вносят вклад в расчет энтальпии реакции, поскольку энтальпия элемента в его стандартном состоянии равна нулю. Аллотропы элемента, отличного от стандартного состояния, обычно имеют ненулевые стандартные энтальпии образования.

Определение

Энтальпия H термодинамической системы определяется как сумма ее внутренней энергии U и работы, необходимой для достижения ее давления и объема:

H = U + pV ,

где p — давление , V — объем системы.

Энтальпия — обширное свойство ; он пропорционален размеру системы (для однородных систем). В интенсивных свойств , то удельная энтальпия ч =ЧАСмотносится к единице массы m системы, а молярная энтальпия H _m равнаЧАСп, где n — количество молей . Для неоднородных систем энтальпия — это сумма энтальпий составляющих подсистем:

ЧАСзнак равно∑kЧАСk,{\ displaystyle H = \ sum _ {k} H_ {k},}

где

H — полная энтальпия всех подсистем,

k относится к различным подсистемам,

H _k относится к энтальпии каждой подсистемы.

Замкнутая система может находиться в термодинамическом равновесии в статическом гравитационном поле , так что ее давление p непрерывно изменяется с высотой , в то время как из-за требования равновесия ее температура T инвариантна с высотой. (Соответственно, плотность гравитационной потенциальной энергии системы также изменяется с высотой.) Тогда суммирование энтальпий становится интегралом :

ЧАСзнак равно∫(ρчас)dV,{\ Displaystyle H = \ int (\ rho h) \, dV,}

где

ρ (« ро ») — плотность (масса на единицу объема),

h — удельная энтальпия (энтальпия на единицу массы),

( ρh ) представляет собой плотность энтальпии (энтальпия на единицу объема),

dV обозначает бесконечно малый элемент объема внутри системы, например, объем бесконечно тонкого горизонтального слоя,

поэтому интеграл представляет собой сумму энтальпий всех элементов объема.

Энтальпия замкнутой однородной системы — это ее H ( S , p ) , с переменными естественного состояния, ее энтропия S [ p ] и ее давление p . Дифференциальное соотношение для него можно вывести следующим образом. Начнем с первого закона термодинамики для замкнутых систем для бесконечно малого процесса:

dUзнак равноδQ-δW,{\ displaystyle dU = \ delta Q- \ delta W,}

где

Δ Q — небольшое количество тепла, добавляемого к системе,

Δ W небольшой объем работы, выполняемой системой.

В однородной системе, в которой рассматриваются только обратимые или квазистатические процессы, второй закон термодинамики дает Δ Q = T dS , где T — абсолютная температура, а dS — бесконечно малое изменение энтропии S системы. Кроме того, если выполняется только работа pV , Δ W = p dV . В следствии,

dUзнак равноТdS-пdV.{\ displaystyle dU = T \, dS-p \, dV.}

Добавление d ( pV ) к обеим сторонам этого выражения дает

dU+d(пV)знак равноТdS-пdV+d(пV),{\ Displaystyle dU + d (pV) = T \, dS-p \, dV + d (pV),}

или

d(U+пV)знак равноТdS+Vdп.{\ Displaystyle d (U + pV) = T \, dS + V \, dp.}

Так

dЧАС(S,п)знак равноТdS+Vdп.{\ Displaystyle dH (S, p) = T \, dS + V \, dp.}

Органические соединения

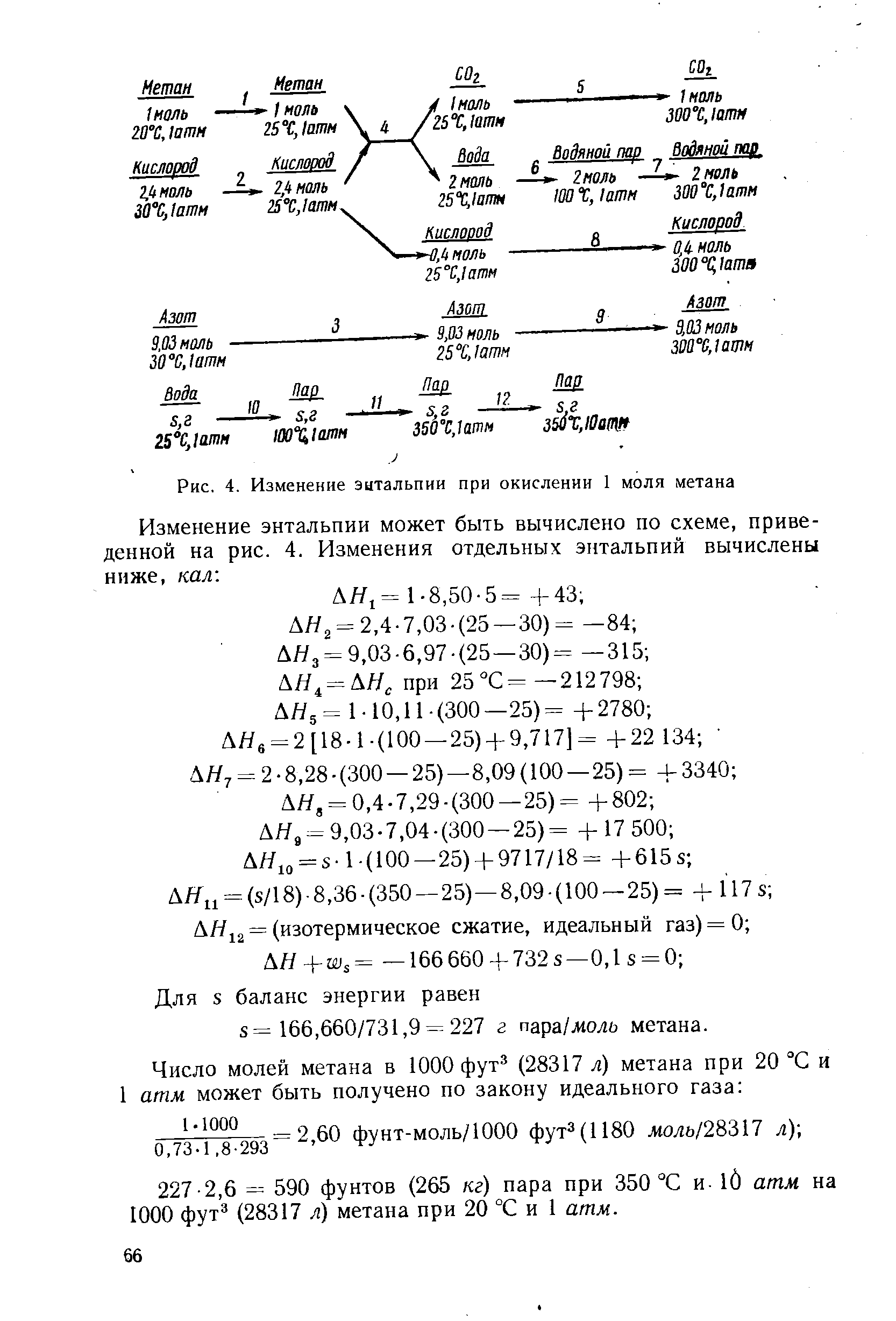
Реакции образования большинства органических соединений являются гипотетическими. Например, углерод и водород не будут напрямую реагировать с образованием метана (CH ₄ ), поэтому стандартную энтальпию образования нельзя измерить напрямую. Однако стандартную энтальпию сгорания легко измерить с помощью . Затем определяется стандартная энтальпия образования с использованием закона Гесса . Сжигание метана (CH ₄ + 2 O ₂ → CO ₂ + 2 H ₂ O) эквивалентно сумме гипотетического разложения на элементы с последующим сгоранием элементов с образованием диоксида углерода и воды:

СН ₄ → С + 2 Н ₂

С + О ₂ → СО ₂

2 Н ₂ + О ₂ → 2 Н ₂ О

Применяя закон Гесса,

Δ _{гребешок}H ⦵ (CH ₄ ) = [Δ _fH ⦵ (CO ₂ ) + 2 Δ _fH ⦵ (H ₂ O)] — Δ _fH ⦵ (CH ₄ ).

Решая эталон энтальпии образования,

Δ _fH ⦵ (CH ₄ ) = [Δ _fH ⦵ (CO ₂ ) + 2 Δ _fH ⦵ (H ₂ O)] — Δ _combH ⦵ (CH ₄ ).

Значение Δ _fH ⦵ (CH ₄ ) определено как -74,8 кДж / моль. Отрицательный знак показывает, что реакция, если бы она продолжалась, была бы экзотермической ; то есть метан энтальпически более стабилен, чем газообразный водород и углерод.

С помощью метода групповой аддитивности теплоты образования можно прогнозировать теплоту образования простых недеформированных органических соединений .

Теплота реакции

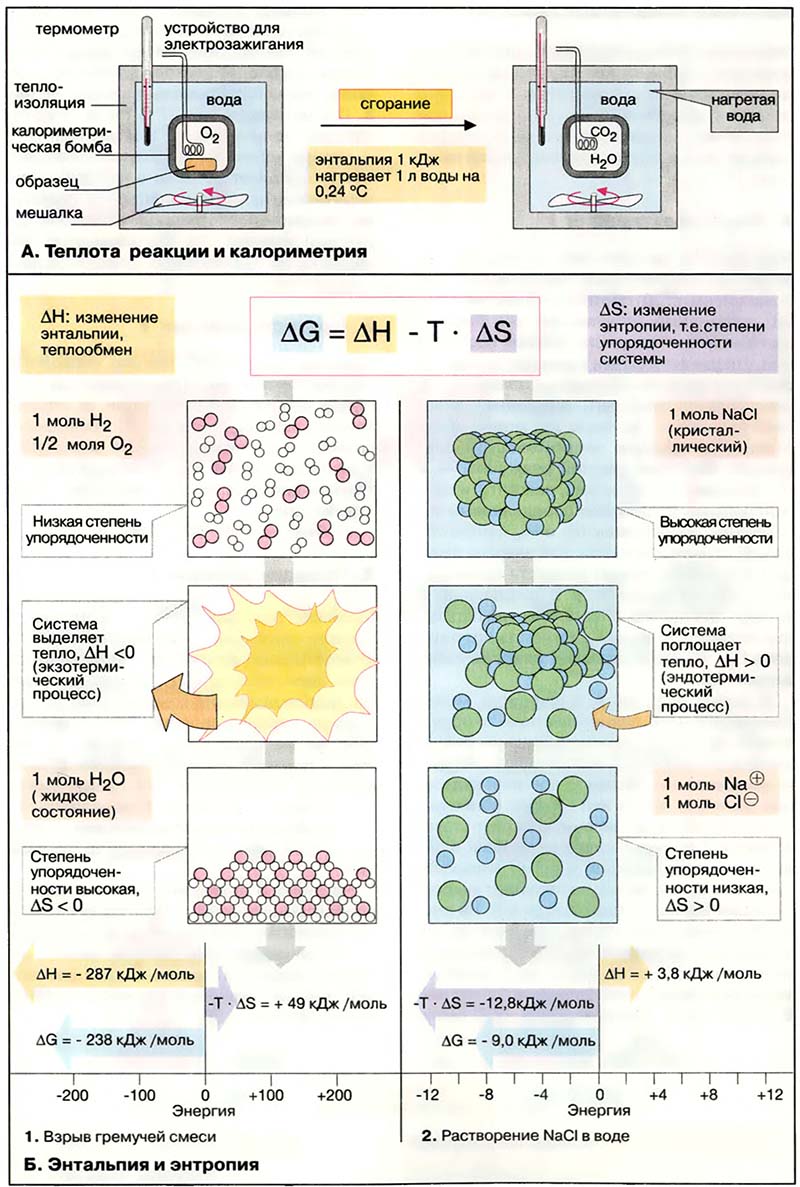
Представление о законе сохранения энергии можно получить на примере разложения пероксида водорода, H₂O₂. Когда водный раствор H₂O₂ реагирует с образованием газообразного кислорода и жидкой воды, происходит заметное выделение тепла: разложение 1 моля H₂O₂ при 25°С (комнатная температура) сопровождается выделением 94,7 кДж (94700 Дж) тепла.

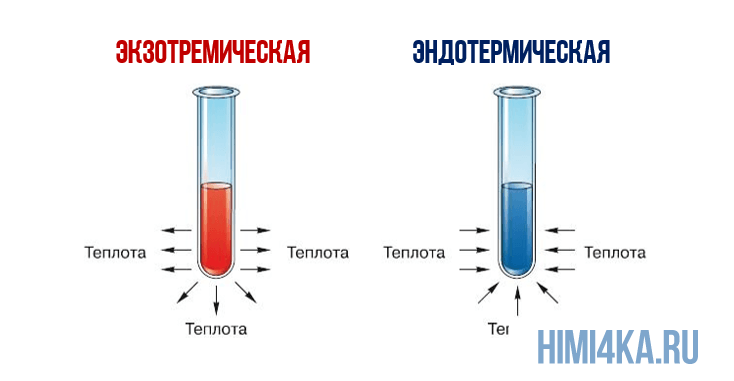
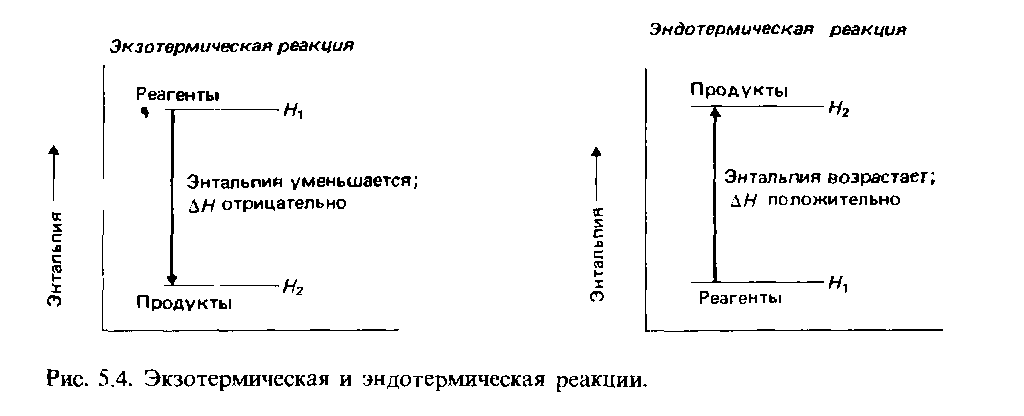
Теплоту химической реакции, проводимой при постоянном давлении, принято называть изменением энтальпии реагирующей системы, ΔH (читается «дельта-аш»). Если в процессе реакции выделяется теплота, то энтальпия реагирующей системы убывает и ΔH отрицательно, а сами реакции называются экзотермическими. Напротив, эндотермические реакции протекают с поглощением теплоты и сопровождаются возрастанием энтальпии реакционной смеси. Для реакции разложения пероксида водорода можно записать:

H2O2(водн.) → H2O(ж.) + ½O2(г.) ΔH = -94,7 кДж (1)

Это количество теплоты, которое выделяется при разложении 1 моля пероксида водорода на 1 моль воды и 1/2 моля газообразного кислорода, т.е. в расчете на 1 моль реагента. Если удвоить все коэффициенты в уравнении реакции, то придется удвоить и теплоту реакции, поскольку она будет относиться теперь к вдвое большему количеству реагента:

2H2O2(водн.) → 2H2O(ж.) + O2(г.) ΔH = -189,4 кДж (2)

Физическое состояние реагентов и продуктов также оказывает влияние на теплоту реакции (изменение энтальпии). Если H₂O₂ заставить разлагаться на газообразный кислород и водяной пар, а не жидкую воду, часть молярной теплоты разложения H₂O₂ (94,7 кДж) затратится на испарение H₂O, которое описывается уравнением:

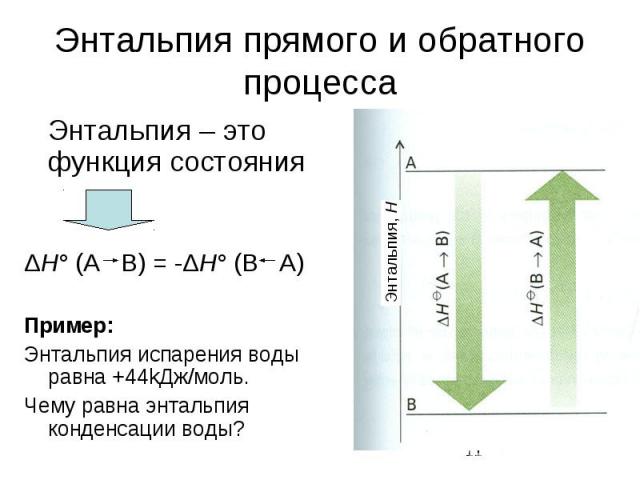
H2O(водн.) → H2O(г.) ΔH = +44,0 кДж (3)

и поэтому при таком разложении пероксида водорода будет выделяться меньше теплоты:

H2O2(водн.) → H2O(г.) + ½O2(г.) ΔH = -50,7 кДж (4)

Здесь мы молчаливо воспользовались очень важным предположением, что теплоты реакций аддитивны. Уравнение (1) в сумме с уравнением (3) дает уравнение (4), и поэтому мы предположили, что теплота третьей из этих реакций должна быть равна сумме первых двух:

ΔH = -94,7 кДж + 44,0 кДж = -50,7 кДж (5)

Физическая интерпретация

U термин может быть интерпретирован как энергия , необходимой для создания системы, и р срок в качестве работы , которые потребовались бы , чтобы «освободить место» для системы , если давление окружающей среды оставались постоянная. Когда система, например, n моль газа объема V при давлении p и температуре T , создается или приводится в текущее состояние от абсолютного нуля , необходимо подвести энергию, равную ее внутренней энергии U плюс pV , где pV равно работа сделана в продвижении против окружающей среды (атмосферного) давления.

В фундаментальной физике и статистической механике может быть более интересно изучить внутренние свойства системы, и поэтому используется внутренняя энергия. В базовой химии эксперименты часто проводятся при постоянном атмосферном давлении , а работа давления и объема представляет собой обмен энергией с атмосферой, к которому нельзя получить доступ или который нельзя контролировать, так что Δ H — это выражение, выбранное для теплоты реакции .

Для теплового двигателя изменение его внутренней энергии — это разница между подводимым теплом и совершаемой рабочим телом, а изменение его энтальпии — это разница между подводимым теплом и работой, выполняемой двигателем:

dЧАСзнак равноδQ-δW{\ Displaystyle dH = \ дельта Q- \ дельта W}

где работа W, выполненная двигателем, равна:

Wзнак равно-∮⁡пdV{\ Displaystyle W = — \ oint pdV}

Примечания

↑ , с. 450.
↑ , с. 16.
↑ , с. 522—523.
, с. 290.
, с. 21.
, с. 17, 63.
, с. 311.
, с. 174.
, с. 6.
Состояние простой термодинамической системы (газы и изотропные жидкости в ситуации, когда поверхностными эффектами и наличием внешних силовых полей можно пренебречь) полностью задано её объёмом, давлением в системе и массами составляющих систему веществ.
, с. 143.
, с. 103.
Бесконечно малым (элементарным, инфинитезимальным) называют процесс, для которого разница между начальным и конечным состояниями системы бесконечно мала.
Под теплотой здесь подразумевается изменение энергии системы в результате теплопередачи через граничную поверхность (см. Теплота).
, с. 8.
, с. 114.
, с. 54.
, p. 14.
, с. 31.
, p. 36.
, с. 257.
, с. 125.
, с. 11.
↑ , с. 87.
↑ , с. 10.
, с. 127.
, с. 128.
То, что конечное состояние может оказаться недостижимым в действительности, применительно к данному рассмотрению не имеет значения.
, с. 130.
, с. 24.
, с. 17.
, с. 131.
, с. 102.
, с. 23.
, с. 245.
, с. 18.
До 1982 года ИЮПАК принимал в качестве стандартного давления 1 атм = 101325 Па; это следует учитывать при использовании данных из литературы, изданной ранее.
↑ , с. 563.
Курс физической химии // Под ред. Я. И. Герасимова. М.-Л.: Химия, 1964. — Т. 1. — С. 55.
Жуховицкий А. А., Шварцман Л. А. Физическая химия. — М.: Металлургия, 1976. — 544 с.
Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим.-технол. спец. вузов / Под ред. А. Г. Стромберга. — 2-е изд. — М.: Высш. шк., 1988. — 496 с.
Пригожин И., Дефэй Р. Химическая термодинамика = Chemical Thermodynamics / Перевод с англ. под ред. В. А. Михайлова. — Новосибирск: Наука, 1966. — 502 с.

Энтальпия

Энтальпи́я, также тепловаяфункция и теплосодержание —термодинамический потенциал,характеризующий состояние системы втермодинамическом равновесии при выборев качестве независимых переменныхдавления, энтропии и числа частиц.

Проще говоря, энтальпия —это та энергия, которая доступна дляпреобразования в теплоту при определенныхтемпературе и давлении.

Определением этой величиныслужит тождество: H=U+PV

Размерность энтальпии-Дж/моль.

В химии чащевсего рассматривают изобарическиепроцессы (P =const), и тепловой эффект в этом случаеназывают изменением энтальпии системыили энтальпиейпроцесса:

В термодинамическойсистеме выделяющуюся теплоту химическогопроцесса условились считать отрицательной(экзотермический процесс, ΔH 0.

Энтропия

Основноесодержание второго начала термодинамикизаключается в постулировании существованияфункции, называемой энтропией S,которая для обратимых процессовопределяется по уравнению

адля самопроизвольных

Изменениеэнтропии реакции можно рассчитать поформуле

Зависимостьизменения энтропии от температурывыражается законом Кирхгофа:

Дляизолированной системы изменение энтропии– критерий возможности самопроизвольногопротекания процесса. Если ,то процесс возможен; если,то в прямом направлении процессневозможен; если,то в системе равновесие.

Термодинамические потенциалы. Свободная энергия Гиббса и Гельмгольца

Дл яхарактеристики процессов, протекающихв закрытых системах, введем новыетермодинамические функции состояния:изобарно-изотермический потенциал(свободная энергия Гиббса G)и изохорно-изотермический потенциал(свободная энергия Гельмгольца F).

Для закрытойсистемы, в которой осуществляетсяравновесный процесс при постоянныхтемпературе и объеме, выразим работуданного процесса. Которую обозначимАmax(посколько работа процесса, проводимогоравновесно, максимальна):

Amax=T∆S-∆U

Введем функциюF=U-TS-изохорно-изотермическийпотенциал, определяющий направление ипредел самопроизвольного протеканияпроцесса в закрытой системе, находящейсяв изохорно-изотермических условиях иполучим:

∆F=∆U-T∆S

Изменениеэнергии Гельмгольца определяется тольконачальным и конечным состоянием системыи не зависит от характера процесса,поскольку оно определяется двумяфункциями состояния: U и S. Напомним, чтоот способа проведения процесса припереходе системы из начального в конечноесостояние может зависеть величинаполученной или затраченной работы, ноне изменение функции.

Закрытуюсистему, находящуюся в изобарно-изотермических условиях, характеризуетизобарно-изотермический потенциал G:

G=U+PV-TS=H-TS

∆G=∆H-T∆S

ДифференциалэнергииГиббса для системы с постоянным числомчастиц, выраженный в собственныхпеременных — черездавлениеpитемпературуT:

Для системы с переменным числом частицэтот дифференциал записывается так:

Здесь —химическийпотенциал, который можно определитькак энергию, которую необходимо затратить,чтобы добавить в систему ещё однучастицу.

Анализ уравнения ∆G=∆H-T∆Sпозволяет установить, какой изфакторов, составляющих энергию Гиббса,ответственен за направление протеканияхимической реакции, энтальпийный (ΔH)или энтропийный (ΔS · T).

Если ΔH 0, то всегда ΔG

Если ΔH > 0 и ΔS 0, иреакция с поглощением теплоты иуменьшением энтропии невозможна ни прикаких условиях.

В остальных случаях (ΔH 0, ΔS > 0) знак ΔG зависит от соотношенияΔH и TΔS.

Поэтому большинствореакций, протекающих при комнатнойтемпературе, экзотермичны. Чем вышетемпература, тем больше TΔS, и дажеэндотермические реакции становятсяосуществляемыми.

Под стандартной энергией Гиббсаобразования ΔG°, понимают изменениеэнергии Гиббса при реакции образования1 моль вещества, находящегося в стандартномсостоянии. Это определение подразумевает,что стандартная энергия Гиббса образованияпростого вещества, устойчивого встандартных условиях, равна нулю.

Изменение энергии Гиббса не зависит отпути процесса, следовательно можнополучать разные неизвестные значенияэнергий Гиббса образования из уравнений,в которых с одной стороны записаннысуммы энергий продуктов реакции, а сдругой – суммы энергий исходных веществ.

При пользовании значениями стандартнойэнергии Гиббса критерием принципиальнойвозможности процесса в нестандартныхусловиях принимается условие ΔG° 0. В то же время, еслистандартная энергия Гиббса равна нулю,это не означает, что в реальных условиях(отличных от стандартных) система будетв равновесии.

Условиясамопроизвольного протекания процессовв закрытый системах :

∆G

Отношение к теплу

Чтобы обсудить связь между увеличением энтальпии и подводом тепла, мы вернемся к первому закону для замкнутых систем с физическим соглашением о знаках: dU = δQ — δW , где тепло δQ передается за счет теплопроводности, излучения и джоулева нагрева. . Применим его к частному случаю с постоянным давлением на поверхность. В этом случае рабочий член можно разделить на два вклада, так называемую работу pV , определяемую как p dV (где p — давление на поверхности, dV — увеличение объема системы), и так называемая работа pV. — так называемая изохорная механическая работа δW ‘ , такая как перемешивание валом с лопастями или внешним магнитным полем, действующим на внутренний ротор. Случаи дальнодействующего электромагнитного взаимодействия требуют дополнительных переменных состояния в своей формулировке и здесь не рассматриваются. Итак, мы пишем δW = p dV + δW ′ . В этом случае первый закон гласит:

dUзнак равноδQ-пdV-δW′.{\ displaystyle dU = \ delta Qp \, dV- \ delta W ‘.}

Сейчас,

dЧАСзнак равноdU+d(пV).{\ displaystyle dH = dU + d (pV).}

Так

dЧАСзнак равноδQ+Vdп+пdV-пdV-δW′{\ Displaystyle dH = \ дельта Q + V \, dp + p \, dV-p \, dV- \ delta W ‘}

знак равноδQ+Vdп-δW′.{\ Displaystyle \, \, = \ дельта Q + V \, dp- \ delta W ‘.}

Согласно физическому соглашению о знаках , δW ‘ <0 , потому что работа изохорного вала, выполняемая внешним устройством в системе, добавляет системе энергии и может рассматриваться как виртуальное добавление тепла. Единственная термодинамическая механическая работа, совершаемая системой, — это работа расширения p dV .

Система находится под постоянным давлением ( dp = 0 ). Следовательно, увеличение энтальпии системы равно добавленному теплу и виртуальному теплу:

dЧАСзнак равноδQ-δW′.{\ displaystyle dH = \ delta Q- \ delta W ‘.}

Вот почему в 19 веке использовался устаревший термин .

Понятие энтропии

В переводе с греческого слово «энтропия» означает превращение.

Рассмотрим элементарный термодинамический процесс, в ходе которого 1 кг газа обменивается с внешней средой пренебрежительно малым количеством теплоты dq, при этом его температура Т остается неизменной.
На основании первого закона термодинамики можно записать:

dq = du + pdv.

Если разделить обе части этого уравнения на температуру Т, получим:

dq/T = du/T + pdv/T.

Обозначим соотношение dq/T = ds.Энтропия s – это величина, изменение которой ds в элементарном термодинамическом процессе равно отношению элементарного количества теплоты dq к постоянной температуре Т.
Изменение энтропии тела, а не ее абсолютное значение в каких-либо состояниях характеризует количество теплоты, участвующей в термодинамическом процессе. При этом изменение энтропии зависит от параметров газа в начальном и конечном состояниях и не зависит от процесса, по которому изменяется это состояние.
Поэтому энтропию можно рассматривать, как параметр состояния рабочего тела.

Этот параметр не имеет физического смысла и введен формально на основании математических построений для облегчения решения многих теплотехнических задач применительно к идеальному газу.

Энтропия — это мера экстенсивности термодинамической системы в случае, когда переменным параметром является температура.
Проще говоря, энтропия — это мера вероятности протекания в какой-либо изолированной термодинамической системе (с конкретными параметрами) самопроизвольного процесса, при котором все элементы системы (например, молекулы вещества) примут в результате процесса равновесное энергетическое состояние, т. е. система станет энергетически устойчивой. После этого станет невозможен никакой дальнейший термодинамический процесс.

Если еще проще — энтропия характеризует разницу энергии отдельных частей (элементов) изолированной термодинамической системы при приращении температуры. Чем существеннее эта разница, тем большей энтропией обладает система, т. е. вероятность самопроизвольных процессов для установления равновесия между элементами системы (молекулами) выше. Если учесть, что весь окружающий нас физический мир стремится к состоянию максимального энергетического покоя (равновесия), то энтропия характеризует неравновесное состояние термодинамической системы, т. е. выражает степень ее стремления к термодинамическому покою.

Произведение энтропии на изменение температуры системы характеризует изменение энергии системы. При этом даже если энергия системы будет изменяться, энтропия этой системы может оставаться неизменной. Очевидно, что при изотермических процессах (температура системы неизменна) составляющая энергии системы в которую входит энтропия равна нулю.
В общем случае изменение энергии термодинамической системы не является обязательным условием изменения энтропии этой системы.

***

Скачать теоретические вопросы к экзаменационным билетам
по учебной дисциплине «Основы гидравлики и теплотехники» (в формате Word, размер файла 68 кБ)

Скачать рабочую программу
по учебной дисциплине «Основы гидравлики и теплотехники» (в формате Word):

для специальности СПО «Механизация сельского хозяйства»
для специальности СПО «Техническое обслуживание и ремонт автомобильного транспорта»

Скачать календарно-тематический план
по учебной дисциплине «Основы гидравлики и теплотехники» (в формате Word):

для специальности СПО «Механизация сельского хозяйства»
для специальности СПО «Техническое обслуживание и ремонт автомобильного транспорта»

Учебные дисциплины

Инженерная графика
МДК.01.01. «Устройство автомобилей»
Карта раздела
Общее устройство автомобиля
Автомобильный двигатель
Трансмиссия автомобиля
Рулевое управление
Тормозная система
Подвеска
Колеса
Кузов
Электрооборудование автомобиля
Основы теории автомобиля
Основы технической диагностики
Основы гидравлики и теплотехники
Метрология и стандартизация
Сельскохозяйственные машины
Основы агрономии
Перевозка опасных грузов
Материаловедение
Менеджмент
Техническая механика
Советы дипломнику

Олимпиады и тесты

«Инженерная графика»
«Техническая механика»
«Двигатель и его системы»
«Шасси автомобиля»
«Электрооборудование автомобиля»

Единица измерения теплоты

Так как это курс химии, а не физики, то совсем мельком напомню, что теплота и работа являются хоть и различными, но формами энергии, поэтому измеряются в одинаковых единицах (в Дж). Если вы совершаете работу над каким-либо телом или совокупностью тел, можно повысить энергию этой системы или нагреть ее в зависимости от того, каким образом совершается работа. К примеру, когда мы поднимает какой-либо предмет, работа превращается в потенциальную энергию, а если потереть этот предмет, то работа (трение) переходит в теплоту. И наоборот, при падении тяжелого предмета энергия превращается в теплоту, а при работе двигателя внутреннего сгорания выделяемая в нем теплота переходит в работу. Химиков, в отличии от физиков, занимает не работа, а теплота, которая может поглощаться и выделяться при протекании химической реакции.

Единицей измерения теплоты служит — Джоуль (Дж). 1 Джоуль можно определить как количество теплоты, необходимое для повышения температуры 1 г чистой воды на 1/4 градуса. В повседневной жизни 1 джоуль энергии требуется для поднятия небольшого яблока (102 г) строго вертикально на высоту один метр.

Про энтальпию на простом языке

При работе с какими-либо расчётами, вычислениями и выполнении прогноза разнообразных явлений, связанных с теплотехникой, каждый сталкивается с понятием энтальпия. Но для людей, специальность которых не касается теплоэнергетики или которые лишь поверхностно сталкиваются с подобными терминами, слово «энтальпия» будет наводить страх и ужас. Итак, давайте разберёмся, действительно ли всё так страшно и непонятно?

Если попытаться сказать совсем просто, под термином энтальпия понимается энергия, которая доступна для преобразования в теплоту при некотором постоянном давлении. Понятие энтальпия в переводе с греческого значит «нагреваю». То есть формулу, содержащую элементарную сумму внутренней энергии и произведенную работу, называют энтальпией. Эта величина обозначается буквой i.

Если записать вышесказанное физическими величинами, преобразовать и вывести формулу, то получится i = u + pv (где u – внутренняя энергия; p, u – давление и удельный объем рабочего тела в том же состоянии, для которого взято значение внутренней энергии). Энтальпия — аддитивная функция, т. е. энтальпия всей системы равна сумме всех составляющих её частей.

Термин «энтальпия» сложен и многогранен.

Но если постараться в нём разобраться, то всё пойдёт очень просто и понятно.

Во-первых, чтобы понять, что же такое энтальпия, стоит узнать общее определение, что мы и сделали.
Во-вторых, стоит найти мпеханизм появления этой физической единицы, понять, откуда она взялась.
В-третьих, нужно найти связь с другими физическими единицами, которые неразрывно с ними взаимосвязаны.
И, наконец, в-четвёртых, нужно посмотреть примеры и формулу.

Ну, что же, механизм работы понятен. Вам лишь нужно внимательно читать и вникать. С термином «Энтальпии» мы уже разобрались, также привели и его формулу. Но тут же возникает ещё один вопрос: откуда взялась эта формула и почему энтропия связана, к примеру, с внутренней энергией и давлением?

Суть и смысл

Для того, чтобы попытаться выяснить физический смысл понятия «энтальпия» нужно знать первый закон термодинамики:

энергия не исчезает в никуда и не возникает из ничего, а лишь переходит из одного вида в другой в одинаковых количествах. Таким примером может служить переход теплоты (тепловой энергии) в механическую энергию, и наоборот.

Уравнение первого закона термодинамики нам нужно преобразить в вид dq = du + pdv = du + pdv + vdp – vdp = d(u + pv) – vdp. Отсюда мы видим выражение (u + pv). Именно это выражение и называется энтальпией (полная формула приводилась выше).

Энтальпия также является величиной состояния, потому что составляющие u (напряжение) и p (давление), v (удельный объём) имеют для каждой величины определенные значения. Зная это, первый закон термодинамики возможно переписать в виде: dq = di – vdp.

В технической термодинамике используются значения энтальпии, которые высчитываются от условно принятого нуля. Все абсолютные значения этих величин весьма трудно определить, так как для этого необходимо учесть все составляющие внутренней энергии вещества при изменении его состояния от О к К.

Формулу и значения энтальпии привёл в 1909 г. учёный Г.Камерлинг-Оннесом.

В выражении i — удельная энтальпия, для всей массы тела полная энтальпия обозначается буквой I, по всемирной системе единиц энтальпия измеряется в Джоулях на килограмм и рассчитывается как:

i=mi=U+pv.

Функции

Энтальпия («Э») является одной из вспомогательных функций, благодаря использованию которой можно значительно упростить термодинамический расчёт. Так например, огромное количество процессов подвода теплоты в теплоэнергетике (в паровых котлах или камере сгорания газовых турбин и реактивных двигателей, а также в теплообменных аппаратах) осуществляют при постоянном давлении. По этой причине в таблицах термодинамических свойств обычно приводят значения энтальпии.

Условие сохранения энтальпии лежит, в частности, в основе теории Джоуля — Томсона

Или эффекта, нашедшего важное практическое применение при сжижении газов. Таким образом, энтальпия есть полная энергия расширенной системы, представляющая сумму внутренней энергии и внешней – потенциальной энергии давления

Как любой параметр состояния, энтальпия может быть определена любой парой независимых параметров состояния.

Также, исходя из приведённых выше формул, можно сказать: «Э» химической реакции равна сумме энтальпий сгорания исходных веществ за вычетом суммы энтальпий сгорания продуктов реакции.
В общем случае изменение энергии термодинамической системы не является необходимым условием для изменения энтропии этой системы.