Примеры решения задач
Пример 1
Задача
Задан эллипс уравнением
и точки
. Необходимо:
- убедиться, что точки
и
лежат на эллипсе; - найти полуоси эллипса и координаты его фокусов;
- найти расстояние от точки
к фокусам; - убедиться, что сумма этих расстояний равна длине большой оси;
- найти эксентриситет эллипса.
Решение
1. Подставим координаты
точки
в левую часть уравнения эллипса:
– точка
лежит на эллипсе. Аналогично для
:
точка
лежит на эллипсе.
2. С канонического
и данного уравнения
эллипса выходит:
Из равенства
получается:
– полуфокусное расстояние. Координаты фокусов
и
.
3. Найдём фокальные радиусы точки
4. Найдём сумму
, что отвечает определению эллипса.
5. Эксцентриситет находится по формуле
.
Пример 2
Задача
Найти оси, вершины и фокусы эллипса
Решение
Сведём обычное уравнение к каноническому:
,
. Вершины эллипса в точках
,
,
,
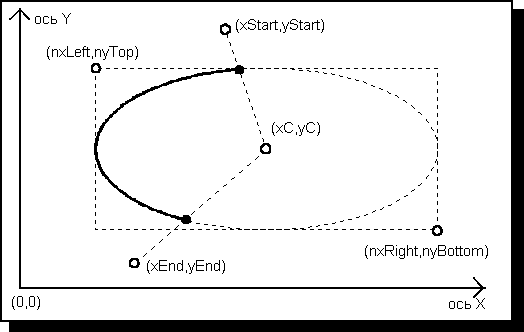
. Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае
больше, чем
, то эллипс, который вытянут вдоль оси
, находим полуфокусное расстояние
.
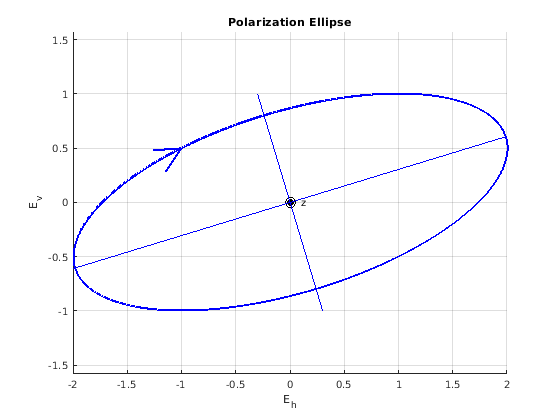
Фокусы в точках
и
. (см. рис. 3)
Рис. 4
Пример 3
Найти оси, вершины и фокусы эллипса
или
. Построить эллипс.
Сравнивая последнее уравнение с уравнением (2), у нас получается:
,
. Откуда находим оси эллипса:
,
и координаты вершин:
,
,
,
. Дальше из формулы:
. Значит, фокусами эллипса есть точки:
и
. Для построения эллипса отложим на осях
и
вершины
соответственно соединим их плавной линией, (см. задачу 1).
Замечание! Если в каноническом уравнении
большей полуосью будет
, тогда фокусы эллипса будут расположены на оси
и тогда
.
Эллипсис
Функции, использующие эллипсис, выглядят следующим образом:
— это один или несколько обычных параметров функции
Обратите внимание, функции, которые используют эллипсис, должны иметь по крайней мере один параметр, который не является эллипсисом
Эллипсис (англ. «ellipsis»), который представлен в виде многоточия в языке C++, всегда должен быть последним параметром в функции. О нем можно думать, как о массиве, который содержит любые другие параметры, кроме тех, которые указаны в .
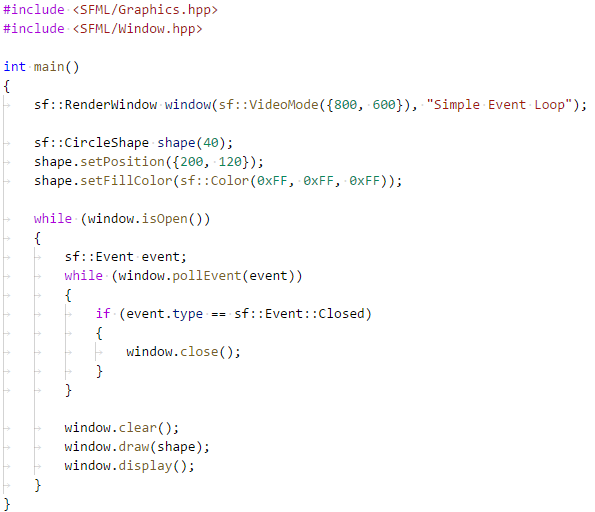
Рассмотрим пример с использованием эллипсиса. Предположим, что нам нужно написать функцию, которая вычисляет среднее арифметическое переданных аргументов:
#include <iostream>
#include <cstdarg> // требуется для использования эллипсиса
// Эллипсис должен быть последним параметром.
// Переменная count — это количество переданных аргументов
double findAverage(int count, …)
{
double sum = 0;
// Мы получаем доступ к эллипсису через va_list, поэтому объявляем переменную этого типа
va_list list;
// Инициализируем va_list, используя va_start. Первый параметр — это список, который нужно инициализировать.
// Второй параметр — это последний параметр, который не является эллипсисом
va_start(list, count);
// Перебираем каждый из аргументов эллипсиса
for (int arg=0; arg < count; ++arg)
// Используем va_arg для получения параметров из эллипсиса.
// Первый параметр — это va_list, который мы используем.
// Второй параметр — это ожидаемый тип параметров
sum += va_arg(list, int);
// Выполняем очистку va_list, когда уже сделали всё необходимое
va_end(list);
return sum / count;
}
int main()
{
std::cout << findAverage(4, 1, 2, 3, 4) << ‘\n’;
std::cout << findAverage(5, 1, 2, 3, 4, 5) << ‘\n’;
}
|
1 |
#include <iostream> // Эллипсис должен быть последним параметром. doublefindAverage(intcount,…) { doublesum=; // Мы получаем доступ к эллипсису через va_list, поэтому объявляем переменную этого типа va_list list; // Инициализируем va_list, используя va_start. Первый параметр — это список, который нужно инициализировать. // Второй параметр — это последний параметр, который не является эллипсисом va_start(list,count); // Перебираем каждый из аргументов эллипсиса for(intarg=;arg<count;++arg) // Используем va_arg для получения параметров из эллипсиса. // Первый параметр — это va_list, который мы используем. // Второй параметр — это ожидаемый тип параметров sum+=va_arg(list,int); // Выполняем очистку va_list, когда уже сделали всё необходимое va_end(list); returnsumcount; } intmain() { std::cout<<findAverage(4,1,2,3,4)<<‘\n’; std::cout<<findAverage(5,1,2,3,4,5)<<‘\n’; } |
Результат выполнения программы:
Как вы можете видеть, функция findAverage() принимает переменную , которая указывает на количество передаваемых аргументов. Рассмотрим другие компоненты этого примера.
Во-первых, мы должны подключить заголовочный файл cstdarg. Этот заголовок определяет , и — макросы, необходимые для доступа к параметрам, которые являются частью эллипсиса.
Затем мы объявляем функцию, которая использует эллипсис. Помните, что должен быть представлен одним или несколькими фиксированными параметрами. Здесь мы передаем одно целочисленное значение, которое сообщает функции, сколько будет параметров.
Обратите внимание, в эллипсисе нет никаких имен переменных! Вместо этого мы получаем доступ к значениям через специальный тип —. О можно думать, как об указателе, который указывает на массив с эллипсисом
Сначала мы объявляем переменную , которую называем просто для удобства использования.
Затем нам нужно, чтобы указывал на параметры эллипсиса. Делается это с помощью , который имеет два параметра: и имя последнего параметра, который не является эллипсисом. После того, как был вызван, указывает на первый параметр из списка передаваемых аргументов.
Чтобы получить значение параметра, на который указывает , нужно использовать , который также имеет два параметра: и тип данных параметра, к которому мы пытаемся получить доступ
Обратите внимание, с помощью мы также переходим к следующему параметру !. Наконец, когда мы уже всё сделали, нужно выполнить очистку: с параметром
Наконец, когда мы уже всё сделали, нужно выполнить очистку: с параметром .
Рекомендации по безопасному использованию эллипсиса
Во-первых, если это возможно, не используйте эллипсис вообще! Часто доступны другие разумные решения, даже если они требуют немного больше работы и времени. Например, в функции findAverage() в вышеприведенной программе мы могли бы передать динамически выделенный массив целых чисел, вместо использования эллипсиса. Это бы обеспечило проверку типов (гарантируя, что caller не попытается сделать что-то бессмысленное), сохраняя при этом возможность передавать переменную-длину, которая бы указывала на количество всех передаваемых значений.
Во-вторых, если вы используете эллипсис, не смешивайте разные типы аргументов в пределах вашего эллипсиса, если это возможно. Это уменьшит вероятность того, что caller случайно передаст данные не того типа, а произведет результат-мусор.
В-третьих, использование параметра или строки-декодера в качестве обычно безопаснее, чем использование контрольного значения. Это гарантирует, что цикл эллипсиса будет завершен после четко определенного количества итераций.
Основные свойства эллипса
Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.
1. Угол между касательной к эллипсу и фокальным радиусом
2. Уравнение касательной к эллипсу в точке
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).
4. Эволюта эллипсa – это астероида, которая растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами
Эллипсис в музыке
Как уже было отмечено выше, этот термин употребляется как в лингвистике, так и в музыке. В обоих случаях эллипсис — это приблизительно одинаковое по смыслу понятие. И если в литературоведении оно означает опущение того или иного слова, словосочетания или же предложения с целью усиления эффекта от сказанного, то в музыке этим термином обозначают замену ожидаемого аккорда на какой-либо другой, который не есть функциональное следствие первого аккорда. Кроме этого определения можно дать и другое. Согласно нему эллиптический оборот, который бывает в музыке либо внутритональным, либо модульным, можно также охарактеризовать как пропуск одного из звеньев гармонии или ожидаемого аккорда.

Как уже было отмечено, эллипсисы в гармонии бывают внутритональными и модулирующими. Что это означает? Рассмотрим каждый отдельно.
- Внутритональный эллипсис образован из аккордов, которые своей последовательностью противоречат логике этого вида лада.
- Модулирующий же эллипсис иначе называется мелодико-гармонической модуляцией. Она происходит как следствие столкновения нескольких неустойчивых аккордов. Зачастую они являются диссонирующими и находятся в разных тональностях, но соединены плавно текущим голосоведением, которое, тем не менее, не имеет явных функциональных связей.
Условно выделяют четыре вида столкновения этих диссонирующих аккордов (те, кто знаком с музыкальной грамотой, поймут, о чем идет речь):
- S-S (они встречаются у Ференца Листа, например, в произведении “Радость и горе”).
- D-D (этим приемом любил пользоваться “великий глухой” — Л. В. Бетховен, например, в своем произведении «Соната № 2»).
- S-D.
- D-S (Э. Григ – произведение “Свежа ты как весна”).
Кстати, эллиптическая модуляция, как правило, бывает внезапной, поскольку в ней вступают во взаимодействие неродственные тональности. Кроме эклиптической, в музыке существуют и другие виды модуляции, и они характерны для развивающихся частей музыкальных форм.
Предварительные комментарии
Варианты эллипсиса долго формировали центральный explicandum для лингвистической теории, так как эллиптические явления, кажется, в состоянии пролить свет на основные вопросы означающей форму корреспонденции: в частности обычные механизмы схватывания значения от формы, кажется, обойдены или вытеснены в интерпретации эллиптических структур, в которых там означает без формы. В порождающей лингвистике термин эллипсис был применен к диапазону явлений, в которых воспринятая интерпретация более полная, чем это, которое ожидалось бы базируемое исключительно на присутствии лингвистических форм.
Одна черта, которую много типов и случаев эллипсиса имеют вместе, — то, что появление эллипсиса дополнительное. Возникновение VP-эллипсиса, например, часто дополнительное, например, Он поможет, и она (поможет), также. Игнорируется ли помощь глагола в этом предложении, до спикера и к коммуникативным аспектам ситуативного контекста, в котором произнесено предложение. Эти возможности — ясный признак эллипсиса. В других случаях, однако, эллипсис, кажется, обязателен, например со случаями сравнительного удаления, например, *, Больше девочек было там сегодня, чем девочки были там вчера. Второе возникновение девочек должно быть опущено в этом предложении (Больше девочек было там сегодня, чем были там вчера). Обязательное возникновение эллипсиса усложняет анализ, так как можно утверждать, что обязательные случаи не действительно случаи эллипсиса вообще, а скорее пустой указатель для проформы включен. Эти аспекты теории должны быть учтены, считая различные типы и случаи эллипсиса перечисленными ниже.
10.8. Эллипс и его свойства window.top.document.title = «10.8. Эллипс и его свойства»;
В § 7 было получено уравнение фигуры, которую мы назвали эллипсом:
В соответствии с формулами преобразования координат выразим старые координаты через новые по формулам:
канонической
k < 1a > b > 0x’ (y’)x (y)
каноническим уравнением эллипса
Рассмотрим свойства эллипса.
Свойство 10.1.
Эллипс пересекает каждую из осей координат в двух точках.
Точки A, B, C и D называются вершинами эллипса. Отрезок AC называется большой осью эллипса, отрезок BD – малой осью. Числа a и b называют полуосями эллипса. Точки и где называются фокусами эллипса.
Пусть M (x; y) – произвольная точка эллипса. Найдем расстояния от точки M до фокусов эллипса.
(x; y)M
Величину называют эксцентриситетом эллипса. Очевидно, для эллипса ε < 1. Поскольку то отсюда следует, что a – εx > 0. Поэтому
Свойство 10.2.
Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси.
Свойство 10.3.
Эллипс имеет две взаимно перпендикулярные оси симметрии.
Свойство 10.4.
Эллипс имеет центр симметрии.
Центр симметрии эллипса называется центром эллипса.
Свойство 10.5.
Эллипс может быть получен сжатием окружности.
В качестве характеристики формы эллипса удобнее пользоваться эксцентриситетом. Так как
При малых значениях эксцентриситета эллипс мало отличается от окружности. При ε = 0 эллипс превращается в окружность.
В § 7 мы определили эллипс как множество точек, отношение расстояний от которых до данной точки A и данной прямой l есть величина постоянная и равная числу k.
Рассмотрим, какие координаты имеет точка A и какое уравнение – прямая l в канонической системе координат. Для начала отметим, что в силу введенных ранее обозначений
Al
Координаты точки при переходе в новую систему будут равны:
A
Уравнение прямой в исходной системе координат имело вид После замены системы координат получим новое уравнение прямой l
ε < 1
Прямая x = –d называется директрисой, соответствующей фокусу F1(-c; 0). Наряду с этой директрисой вводят прямую x = d, которая является директрисой, соответствующей фокусу F2(c; 0).
С учетом свойств симметрии эллипса, свойство, с помощью которого мы определили эллипс, в новых терминах можно сформулировать следующим образом: отношение расстояния от любой точки эллипса до одного из его фокусов к расстоянию от этой точки до соответствующей ему директрисы есть величина постоянная и равная эксцентриситету. Вид эллипса в канонической системе координат и его директрисы приведены на рис. 10.8.1.
| Рисунок 10.8.1 |
Эллиптичность
Понятие, которое непосредственно связано с этим термином, называется “эллиптичностью”. Это очень интересный стилистический прием. В его основе лежит эллипсис. Это синтаксическая фигура (об этом уже говорилось выше), которая выражается в пропуске слов и словосочетаний в предложении, и даже предложений в тексте. В разговорной речи пропуски происходят из-за того, что собеседникам известны подробности той темы, вокруг которой ведется диалог, или же стали известны в ходе разговора, из предыдущих реплик. Иногда наряду с пропусками слов в речи, то есть “проглатыванием” слов, собеседники в беседе пользуются жестами, многозначительными взглядами, пожатием плеч и т. д. Этот прием также используется в театре. Здесь умышленно умалчиваются целые фразы, и зрителю необходимо подключить свою смекалку, чтобы понять то, что скрывается за молчанием актеров.

Теоретические проблемы
Теоретические счета борьбы эллипсиса. Одна причина, почему они борются, состоит в том, что игнорируемый материал многих случаев эллипсиса (например, подподготовленный материал выше) часто не готовятся как элемент, элемент, являющийся основной единицей синтаксического анализа, связанного с грамматиками структуры фразы. То, что это означает, — то, что формальные счета эллипсиса должны искать некоторый способ составлять факт, что многие механизмы эллипсиса, перечисленные выше, могут игнорировать словосочетания, которые не готовятся как никакая распознаваемая единица (структура фразы) синтаксис.
Один широко распространенный подход к проблеме должен принять движение (или некоторое понятие, сродни движению). То, что происходит, — то, что остатки перемещены из большего избирателя сначала так, чтобы больший избиратель мог тогда игнорироваться полностью. Принимая движение сначала и второй эллипсис, теория синтаксиса может сохраняться, который продолжает основываться на элементе как на основной единице синтаксического анализа.
Другой, более свежий подход заявляет, что проблемы, поставленные эллипсисом, чтобы выразить теории структуры синтаксиса, должны точно к компоненту структуры фразы грамматики. Другими словами, трудности, стоящие перед теориями структуры фразы, должны теоретическая предпосылка что синтаксическая структура быть проанализированными с точки зрения элементов, связанных с грамматиками избирательного округа (= грамматики структуры фразы). Если теория отступает от структур фразы и признает структуры зависимости грамматик зависимости вместо этого, способность признать различный вид синтаксической единицы, поскольку фундаментальный открывает дверь в намного большее количество скупой теории эллипсиса. Эта единица — цепь. Предположение — то, теперь, когда механизмы эллипсиса игнорируют catenae, посредством чего многие из этих catenae не квалифицируют элементы. Этим способом потребность установить движение, чтобы «исправить» большую часть данных об эллипсисе исчезает.
Эллиптичность
Понятие, которое непосредственно связано с этим термином, называется “эллиптичностью”. Это очень интересный стилистический прием. В его основе лежит эллипсис. Это синтаксическая фигура (об этом уже говорилось выше), которая выражается в пропуске слов и словосочетаний в предложении, и даже предложений в тексте. В разговорной речи пропуски происходят из-за того, что собеседникам известны подробности той темы, вокруг которой ведется диалог, или же стали известны в ходе разговора, из предыдущих реплик. Иногда наряду с пропусками слов в речи, то есть “проглатыванием” слов, собеседники в беседе пользуются жестами, многозначительными взглядами, пожатием плеч и т. д. Этот прием также используется в театре. Здесь умышленно умалчиваются целые фразы, и зрителю необходимо подключить свою смекалку, чтобы понять то, что скрывается за молчанием актеров.

Примечания
- Ágel, V., Людвиг Айхингер, Ханс — Вернер Эромс, Питер Хеллвиг, Ганс Херингер и Хенниг Лобин (редакторы). 2003/6. Зависимость и Валентность: международное руководство современного исследования. Берлин: Уолтер де Грюите.
- Джонсон, Кайл 2001. Что эллипсис VP может сделать, и что он не может, но не почему. В руководстве современной синтаксической теории, редактора Марка Бэлтина и Криса Коллинза, 439–479. Оксфорд: Издатели Блэквелла.
- Lappin, Шалом 1996. Интерпретация эллипсиса. В руководстве современной семантической теории, редактор Шалом Lappin. Оксфорд: Блэквелл.
- Lobeck, Энн. 1995. Эллипсис: Функциональные головы, лицензирование и идентификация. Нью-Йорк: Издательство Оксфордского университета.
- Lobeck, Энн. 2006. Эллипсис в РАЗНОСТИ ПОТЕНЦИАЛОВ. В Компаньоне Блэквелла к Синтаксису, редакторе Мартином Эверэертом и др., изданием 2, стр 145-173. Оксфорд: Блэквелл.
- Продавец, Джейсон. 2001. Синтаксис тишины: Шлюзование, острова и теория эллипсиса. Оксфорд: Издательство Оксфордского университета.
- Осборн, Тимоти и Томас Грос 2012. Строительство — catenae: Строительная Грамматика встречает Грамматику Зависимости. Когнитивная лингвистика 23, 1: 163-214.
- Перекос, Иван 1976. Удаление и логическая форма. Докторская Диссертация, Массачусетский технологический институт, Кембридж, Массачусетс.