Экстремум

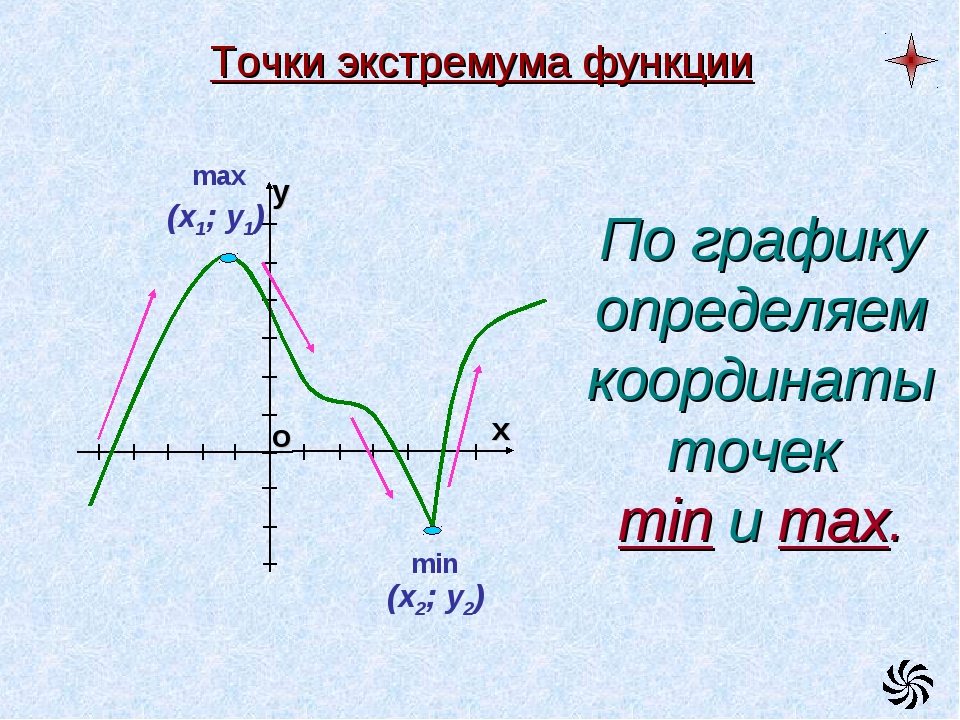
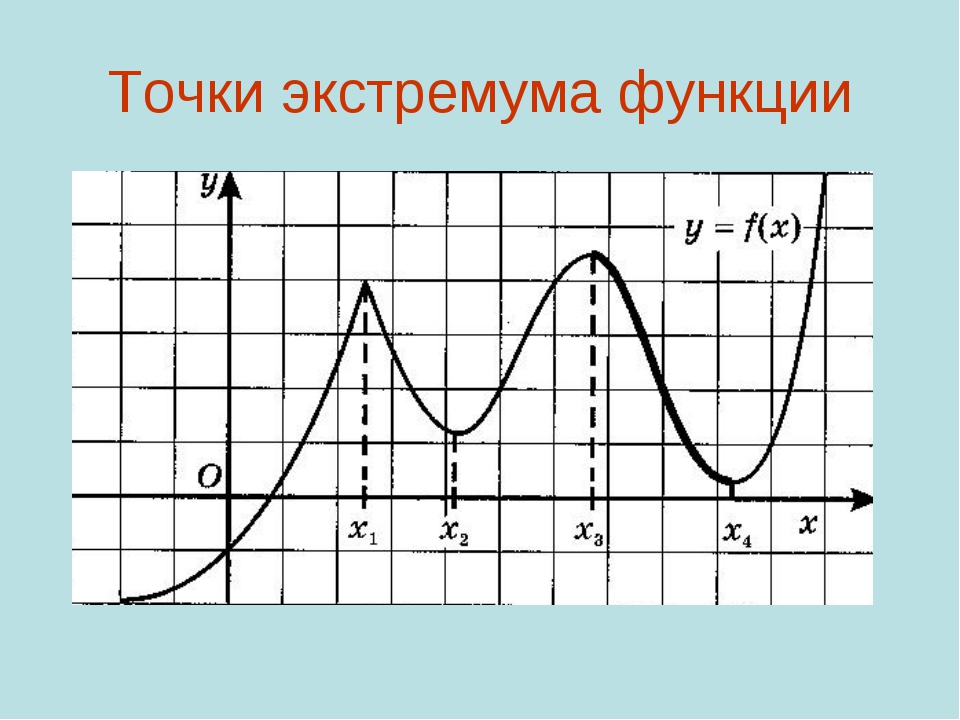
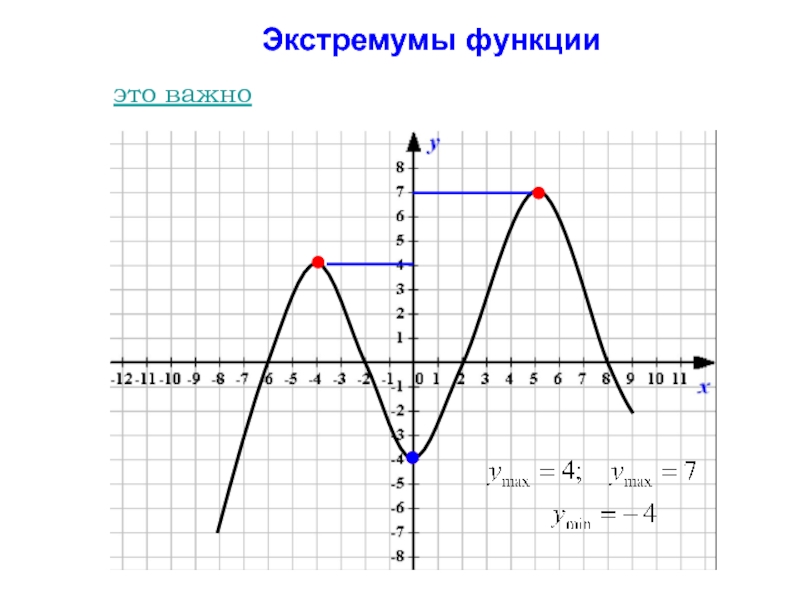
Постановка классической задачи на условный экстремум

Пусть G⊂Rn{\displaystyle {G\subset \mathbb {R} ^{n}}} — открытое множество, и на нём заданы функции  yi=fi(x→),i=1,2,…,m.{\displaystyle y_{i}=f_{i}({\vec {x}}),\;i=1,2,\dots ,m.}  Пусть E={x→∈Gfi(x→)=∀i=1,2,…,m}.{\displaystyle E=\lbrace \,{\vec {x}}\in G:\,f_{i}({\vec {x}})=0\;\;\forall \,i=1,2,\dots ,m\,\rbrace .}

Уравнения

(∗)fi(x→)={\displaystyle (*)\qquad f_{i}({\vec {x}})=0}

называют уравнениями связей (терминология заимствована из механики).

Пусть на G{\displaystyle G} определена также функция y=f(x→).{\displaystyle y=f_{0}({\vec {x}}).}  Точка x→∈E{\displaystyle {\vec {x}}_{0}\in E} называется точкой условного экстремума данной функции относительно уравнений связей (∗),{\displaystyle (*),} если она является точкой обычного (безусловного) экстремума функции f{\displaystyle f_{0}} на множестве E{\displaystyle E}  (модификация определения экстремума сводится к тому, что в нём вместо окрестностей в G{\displaystyle G}, то есть UG(x→){\displaystyle U_{G}({\vec {x}}_{0})}, рассматриваются окрестности в E{\displaystyle E}, то есть UE(x→)=UG(x→)⋂E{\displaystyle U_{E}({\vec {x}}_{0})=U_{G}({\vec {x}}_{0})\bigcap E}).

Определение экстремума

Нам часто задают вопросы:

• что такое экстремум?
• как найти минимум функции?
• как найти максимум функции?
• как найти экстремум функции?
• как найти точки экстремума?

В данной статье мы ответим на эти вопросы.

Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x₁< x₂ выполняется неравенство(f(x₁) < f (x₂) (f(x₁) >f(x₂)).

Если дифференцируемая функция y = f(x) на отрезке возрастает (убывает), то ее производная на этом отрезке f ‘(x) > 0 , (f ‘ (x) < 0).

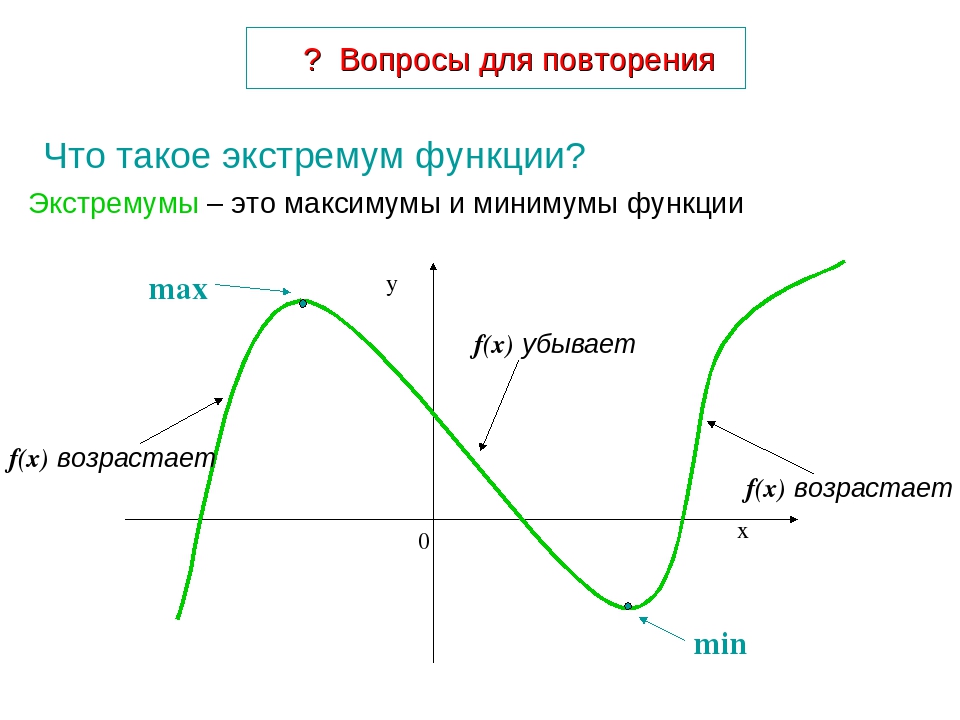
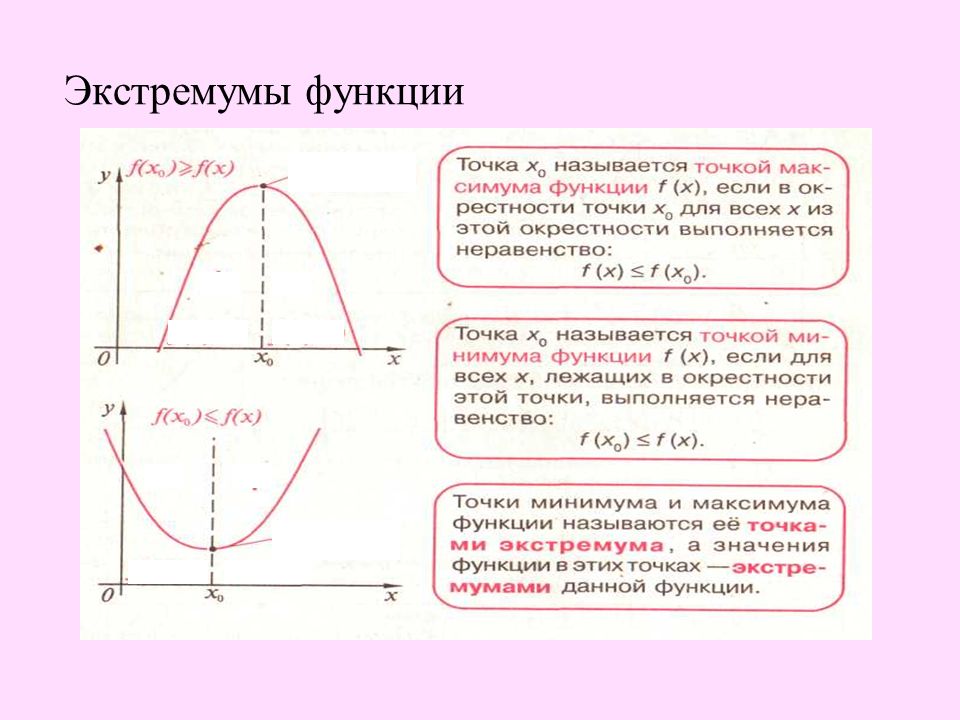
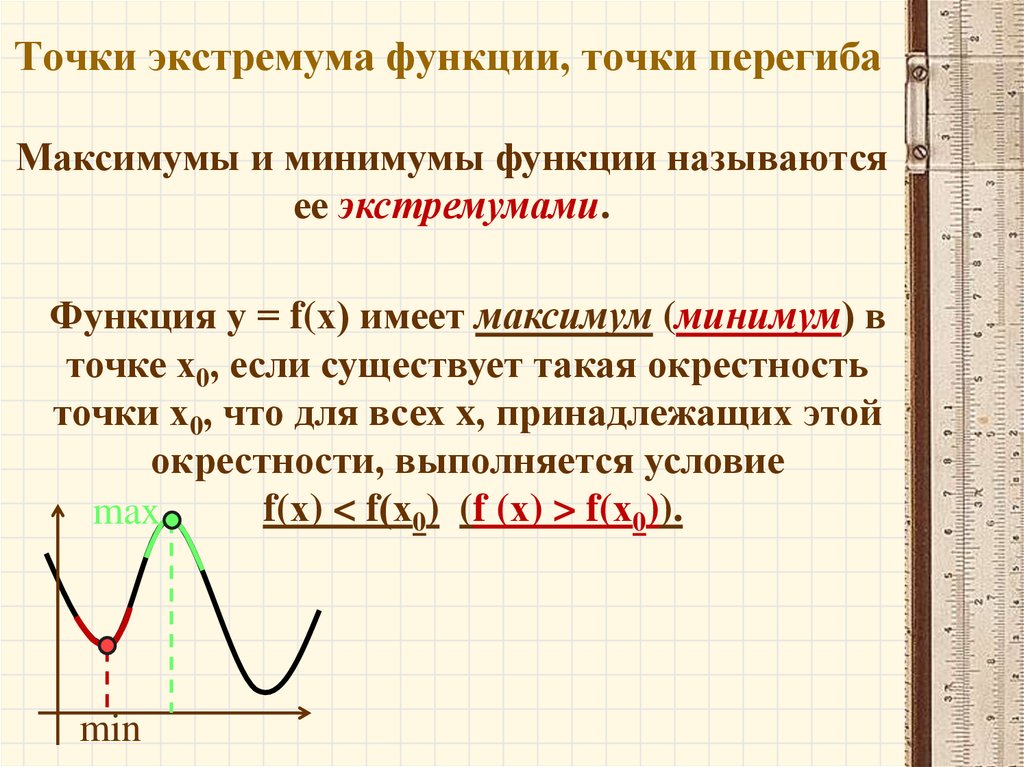
Точка x_оназывается точкой локального максимума (минимума) функции f(x), если существует окрестность x_о, для всех точек которой верно неравенство f(x) ≤ f(x_о), (f(x) ≥f(x_о)).

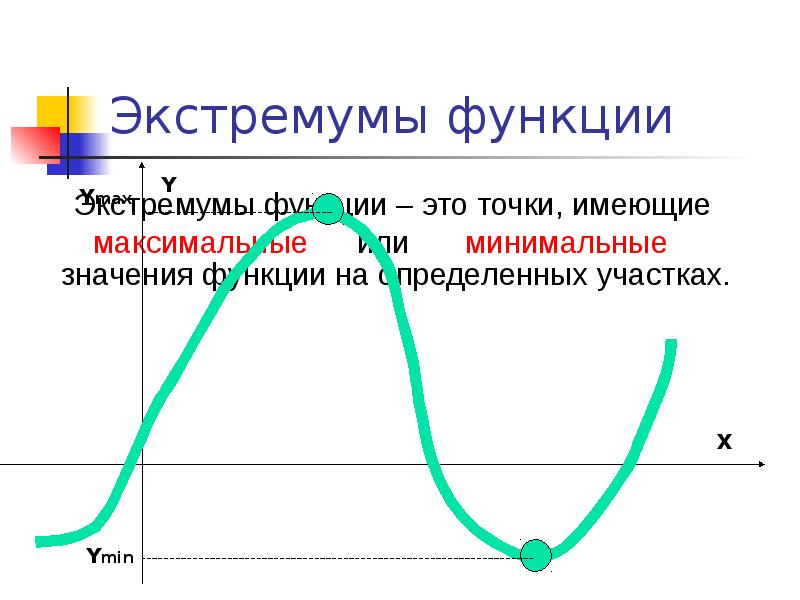
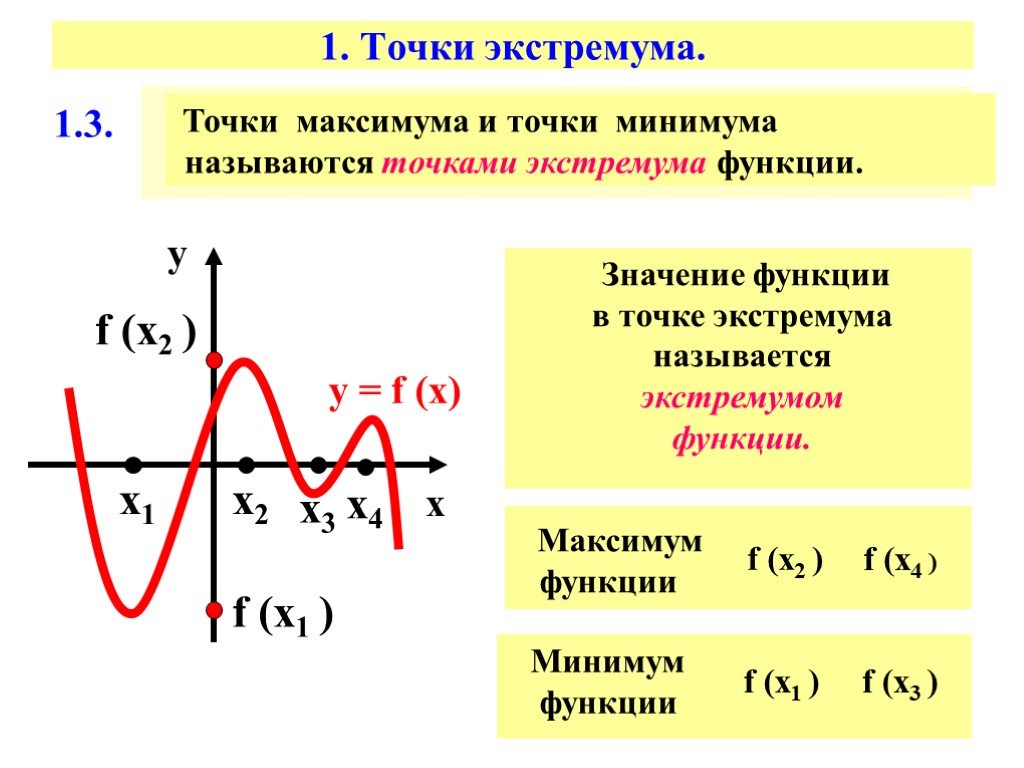
Точки максимума и минимума называются точками экстремума, значения функции в них — ее экстремумами.

Задача Лагранжа

Данная задача относится к вариационному исчислению и является одним из возможных обобщений классической задачи на условный экстремум. В задаче Лагранжа требуется найти непрерывно дифференцируемую функцию x→=x→(t),{\displaystyle {\vec {x}}={\vec {x}}(t),}  заданную на отрезке t,t1{\displaystyle }  и доставляющую экстремум (максимум или минимум) функционалу

J=∫tt1F(t,x→(t),x→˙(t))dt{\displaystyle J\;=\;\int \limits _{t_{0}}^{t_{1}}F\,(t,{\vec {x}}(t),{\dot {\vec {x}}}(t))\,\,{\rm {d}}t}

(точкой обозначена операция дифференцирования по t{\displaystyle t})  при фиксированных граничных условиях  x→(t)=x→,{\displaystyle {\vec {x}}(t_{0})={\vec {x}}_{0},}  x→(t1)=x→1{\displaystyle {\vec {x}}(t_{1})={\vec {x}}_{1}}  и выполнении уравнений связей

fi(t,x→(t),x→˙(t))=,{\displaystyle f_{i}\,(t,{\vec {x}}(t),{\dot {\vec {x}}}(t))\,=\,0\,,}

где i=1,2,…,m{\displaystyle i=1,2,\dots ,m} .

В данной задаче также применим метод множителей Лагранжа. Предполагая уравнения связей независимыми, вводят в рассмотрение m{\displaystyle m} неизвестных функций λ1(t),…,λm(t){\displaystyle \lambda _{1}(t),\dots ,\lambda _{m}(t)}  и сводят исходную задачу к задаче безусловной оптимизации, заменяя подынтегральную функцию функцией

Φ=F(t,x→(t),x→˙(t))+∑i=1mλi(t)fi(t,x→(t),x→˙(t));{\displaystyle \Phi \,=\,F\,(t,{\vec {x}}(t),{\dot {\vec {x}}}(t))\,+\,\sum _{i=1}^{m}\lambda _{i}(t)\,f_{i}\,(t,{\vec {x}}(t),{\dot {\vec {x}}}(t))\,;}

в качестве аналога равенств (∗∗){\displaystyle (**)} (т. e. в роли необходимых условий экстремума) теперь выступают уравнения Эйлера — Лагранжа, имеющие в рассматриваемом случае вид

ddt∂Φ∂x˙k−∂Φ∂xk=,{\displaystyle {\frac {\rm {d}}{{\rm {d}}t}}{\frac {\partial \Phi }{\partial {\dot {x}}_{k}}}-{\frac {\partial \Phi }{\partial x_{k}}}\,=\,0\,,}

где k=1,2,…,n.{\displaystyle k=1,2,\dots ,n.}  Из этих n{\displaystyle n} обыкновенных дифференциальных уравнений, дополненных уравнениями связей, находят (с учётом имеющихся граничных условий) n+m{\displaystyle n+m} неизвестных функций x1(t),…,xn(t),λ1(t),…,λm(t){\displaystyle x_{1}(t),\dots ,x_{n}(t),\lambda _{1}(t),\dots ,\lambda _{m}(t)} .

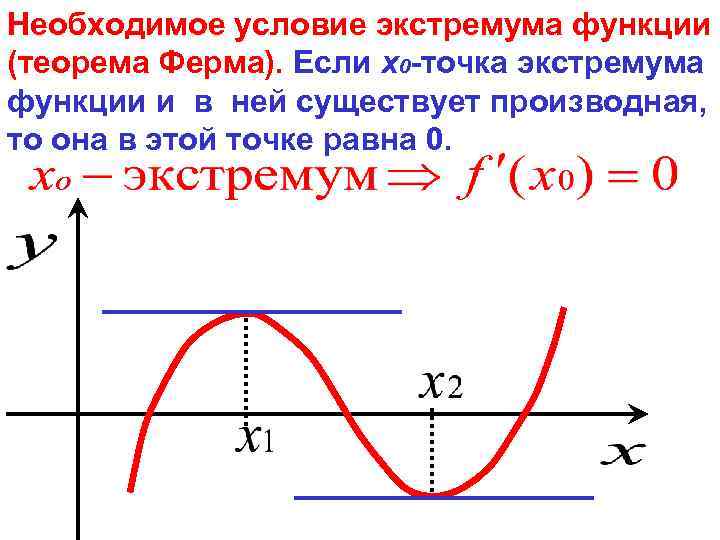
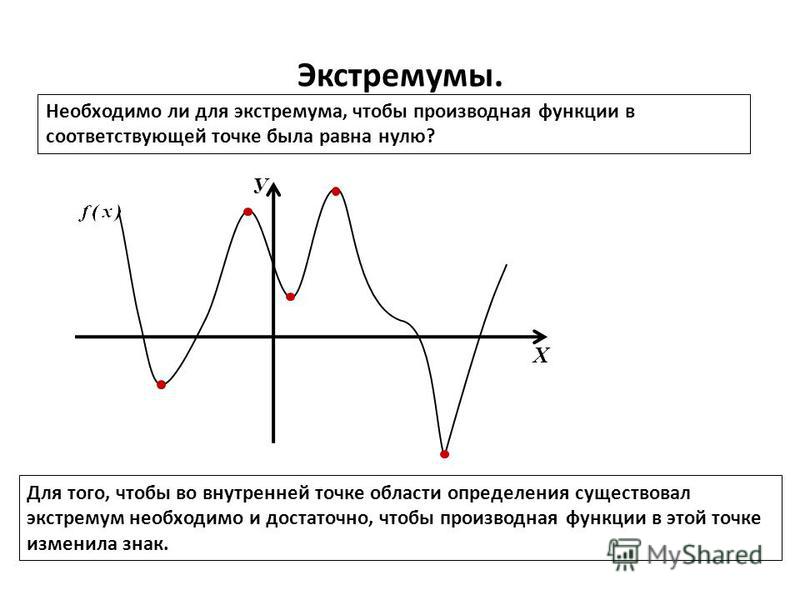
Необходимое условие экстремума функции

Для того чтобы существовал экстремум, важно, чтобы были как точки минимума, так и точки максимума. В случае если это правило соблюдено лишь частично, то условие существование экстремума нарушается

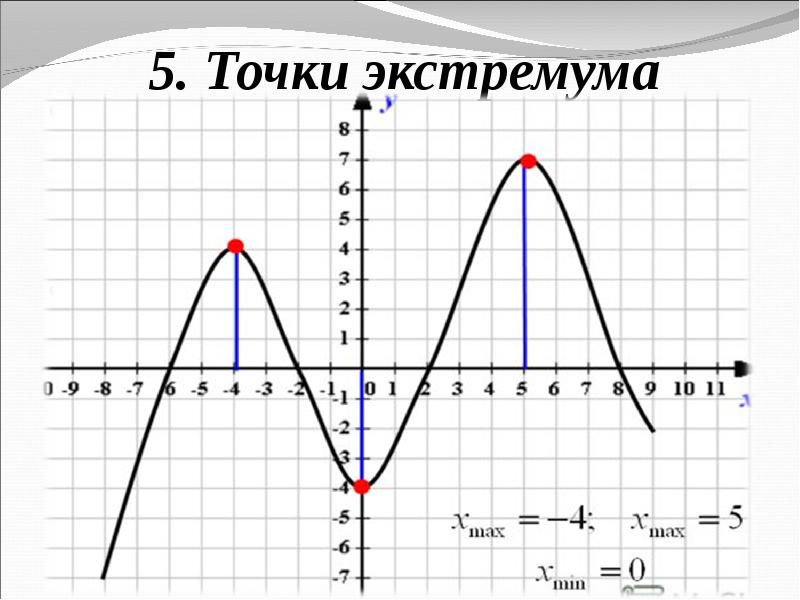
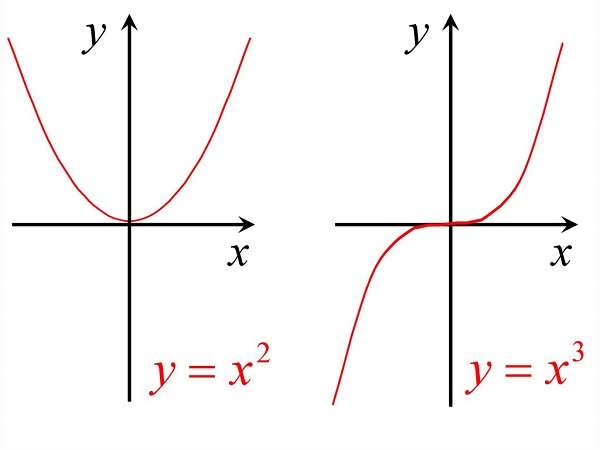Точки минимума и максимума

Каждая функция в любом положении должна быть продифференцирована с целью выявления ее новых значений

Важно понимать, что случай обращения точки в ноль не является основным принципом нахождения дифференцируемой точки

Острый экстремум, также как и минимум функции – это крайне важный аспект решения математической задачи с использованием экстремальных значений

Для того чтобы лучше понимать данную составляющую, важно обратиться к табличным значениям по заданию функционала

Полное исследование значения Построение графика значения 1.      Определение точек возрастания и убывания значений. 2.      Нахождение точек разрыва, экстремума и пересечение с координатными осями. 3.      Процесс определения изменений положения на графике. 4.      Определение показателя и направления выпуклости и выгнутости с учетом наличия асимптот. 5.      Создание сводной таблицы исследования с точки зрения определения ее координат. 6.      Нахождение промежутков возрастания и убывания крайних и острых точек. 7.      Определение выпуклости и вогнутости кривой. 8.      Построение графика с учетом исследования позволяет найти минимум либо максимум. Основным элементом при необходимости работы с экстремумами является точное построение его графика

Школьные учителя не часто уделяют столь важному аспекту максимум внимания, что является грубейшим нарушением учебного процесса. Построение графика происходит только по итогам исследования функциональных данных, определения острых экстремумов, а также точек на графике

Острые экстремумы производной функции отображаются на графике точных значений, с использованием стандартной процедуры определения асимптот. Точки максимума и минимума функции сопровождаются более сложными построениями графика. Это обусловлено более глубокой необходимостью прорабатывать проблему острого экстремума. Необходимо также находить производную сложной и простой функции, так как это одно из самых главных понятий проблематики экстремума.

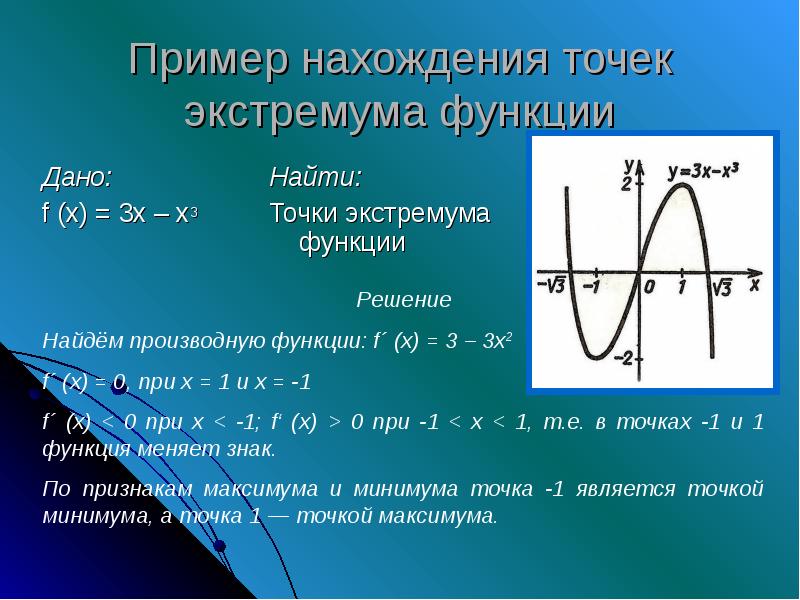
Экстремальное значение функции

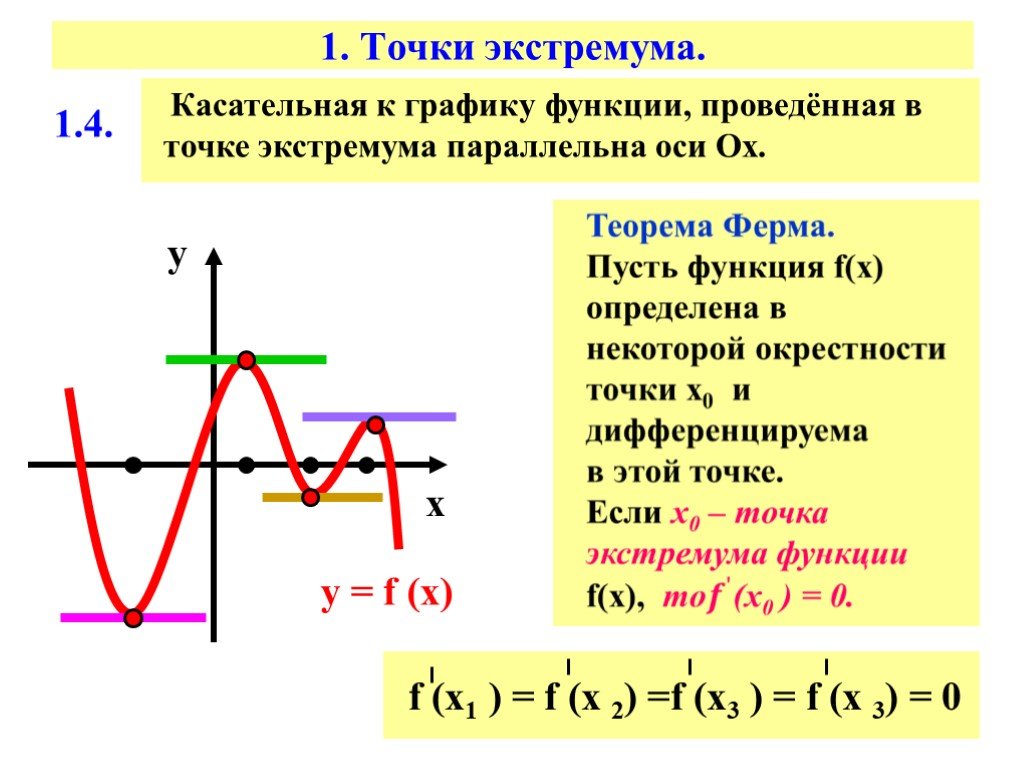
Для определения такого понятия прибегают к использованию теоремы Ферма. Она является важнейшей в ходе изучения крайних точек и дает четкое представление об их существовании в том или ином их виде

Для обеспечения экстремальности важно создать определенные условия для убывания либо возрастания на графике

Для точного ответить на вопрос «как найти точку максимума», необходимо следовать таким положениям:

1. Нахождение точной области определения на графике.
2. Поиск производной функции и точки экстремума.
3. Решать стандартные неравенства на область нахождения аргумента.
4. Уметь доказывать, в каких функциях точка на графике определена и непрерывна.

Экстремальное значение функции Внимание! Поиск критической точки функции возможен только в случае существования производной не менее второго порядка, что обеспечивается высокой долей наличия точки экстремума

Задачи на нахождения экстремума функции

Пример 2. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, четвертой стороной примыкала к стене. Для этого имеется a погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?

Решение. Обозначим стороны площадки через x и y. Площадь площадки равна S = xy. Пусть y — это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2x +y =a. Поэтому y = a — 2x и S =x(a — 2x), где
0 ≤x ≤a/2 (длина и ширина площадки не могут быть отрицательными).
S ‘ = a — 4x, a — 4x = 0 при x = a/4, откуда
y = a — 2×a/4 = a/2. Поскольку x = a/4 — единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При x < a/4, S ‘ > 0, a при x > a/4, S ‘< 0, значит, в точке x = a/4 функция S имеет максимум. Значение функции S(a/4) = a/4(a — a/2) = a2 /8 (кв. ед). Поскольку S непрерывна на [0,a/2] и ее значения на концах S(0) и S(a/2) равны нулю, то найденное значение будет наибольшим значением функции. Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является y = 2x.

Пример 3. Требуется изготовить закрытый цилиндрический бак вместимостью V=16p ≈ 50 м3. Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?

Решение. Площадь полной поверхности цилиндра равна S = 2pR(R+Н). Мы знаем объем цилиндра V = pR2Н Þ Н = V/pR2 =16p/pR2 = 16/R2. Значит, S(R) = 2p(R2+16/R). Находим производную этой функции:
S ‘ (R) = 2p(2R- 16/R2) = 4p (R- 8/R2). S ‘(R) = 0 при R3 = 8, следовательно,
R = 2, Н = 16/4 = 4.

Пример 4. Найти экстремумы функцииf(x) = 2×3 — 15×2+ 36x — 14.

Решение. Так как f ‘(x) = 6×2 — 30x +36 = 6(x -2)(x — 3), то критические точки функции x₁ = 2 и x₂ = 3. Экстремумы могут быть только в них. Так как при переходе через x₁ = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через x₂ = 3 производная меняет знак минус на плюс, поэтому в точке x₂ = 3 у функции минимум. Вычислив значения функции при
x₁ = 2 и x₂ = 3, найдем экстремумы функции: максимумf(2) = 14 и минимумf(3) = 13.

Пример 5. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, четвертой стороной примыкала к стене. Для этого имеется c погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?

Решение. Обозначим стороны площадки через x и y. Площадь площадки равна S = xy. Пусть y — это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2x +y =c. Поэтому y = c — 2x и S = x(c — 2x), где
0 ≤x ≤c/2 (длина и ширина площадки не могут быть отрицательными). S ‘ = c — 4x, c — 4x = 0 при x = c/4, откуда
y = c — 2c/4 = c/2. Поскольку x = c/4 — единственная критическая точка, проверим, меняется ли знак производной при переходе через неё. Приx < c/4, S ‘ > 0, при x >c/4 S ‘< 0, значит, при x=c/4 функция S имеет максимум. Значение функции S(c/4) = c/4(c — c/2) = c2 /8 (кв. ед). Поскольку S непрерывна на [0,c/2] и ее значения на концах S(0) и S(c/2) равны нулю, то найденное значение будет наибольшим значением функции. Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является y = 2x.

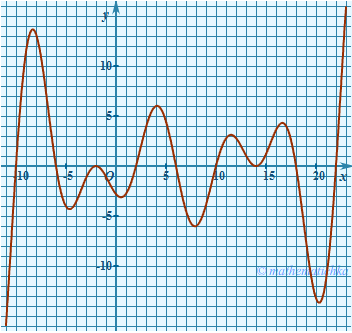
Точки экстремума

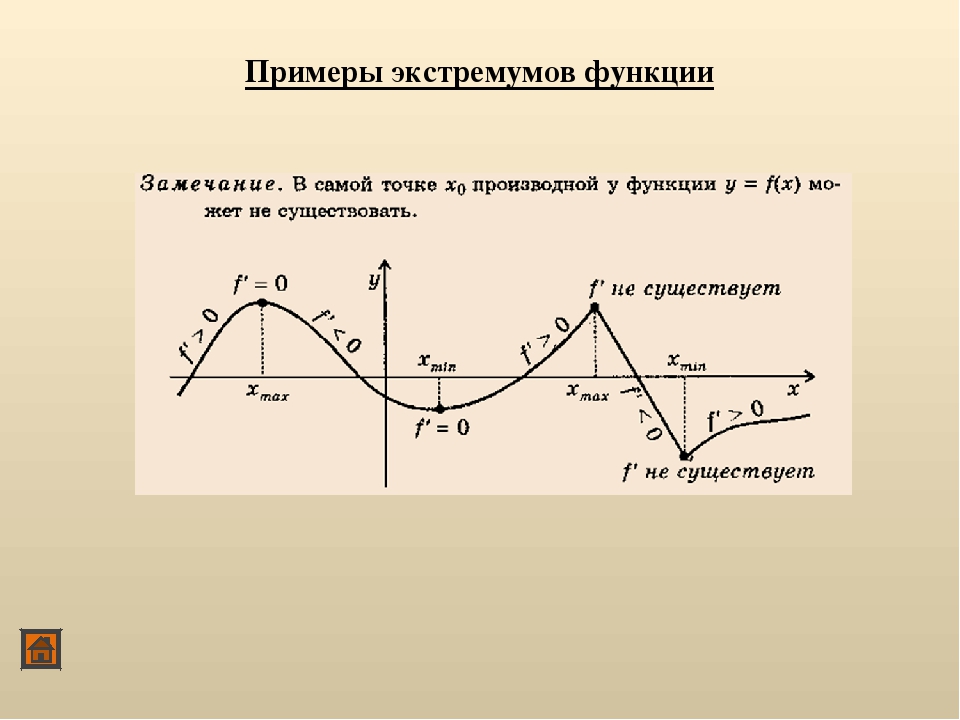
Необходимые условия экстремума. Если x_о является точкой экстремума функции f(x), то либо f ‘(x_о) = 0, либо f (x_о) не существует. Такие точки называют критическими, причем сама функция в них определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x_о — критическая точка. Если f ‘ (x) при переходе через x_о меняет знак плюс на минус, то в точке x_о функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в x_о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную
f ‘ (x) в окрестности x_ои вторую производную f»(x) в самой точке x_о. Если f ‘ (x_о) = 0, f»(x)>0, (f»(x)<0), то x_оявляется точкой локального минимума (максимума) функции f(x). Если же f»(x)=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке функция y =f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка .

Пример 1. Найти экстремумы функции f(x) = 2×3 — 15×2+ 36x — 14.

Решение. График функции f(x)

Так как f ‘(x) = 6×2 — 30x +36 = 6(x -2)(x — 3), то критические точки функции x₁ = 2 и x₂ = 3. Экстремумы могут быть только в этих точках. Так как при переходе через x₁ = 2 производная меняет знак плюс на минус, то в ней функция имеет максимум. При переходе через точку x₂ = 3 производная меняет знак минус на плюс, поэтому в x₂ = 3 у функции минимум. Вычислив значения функции в
x₁ = 2 и x₂ = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.

Достаточные условия существования локальных экстремумов

Пусть функция f∈C(x0){\displaystyle f\in C(x_{0})} непрерывна в x0∈M0,{\displaystyle x_{0}\in M^{0},} и существуют конечные или бесконечные односторонние производные f+′(x0),f−′(x0){\displaystyle f’_{+}(x_{0}),f’_{-}(x_{0})}. Тогда при условии

f+′(x)<,f−′(x)>{\displaystyle f’_{+}(x_{0})<0,\;f’_{-}(x_{0})>0}

x{\displaystyle x_{0}} является точкой строгого локального максимума. А если

f+′(x)>,f−′(x)<,{\displaystyle f’_{+}(x_{0})>0,\;f’_{-}(x_{0})<0,}

то x{\displaystyle x_{0}} является точкой строгого локального минимума.

Заметим, что при этом функция не дифференцируема в точке x{\displaystyle x_{0}}.

Пусть функция f{\displaystyle f} непрерывна и дважды дифференцируема в точке x0{\displaystyle x_{0}}. Тогда при условии

f′(x)={\displaystyle f'(x_{0})=0} и f″(x)<{\displaystyle f»(x_{0})<0}

x{\displaystyle x_{0}} является точкой локального максимума. А если

f′(x)={\displaystyle f'(x_{0})=0} и f″(x)>{\displaystyle f»(x_{0})>0}

то x{\displaystyle x_{0}} является точкой локального минимума.

Пусть функция f{\displaystyle f} дифференцируема n{\displaystyle n} раз в точке x0{\displaystyle x_{0}} и f′(x0)=f″(x0)=⋯=f(n−1)(x0)=0{\displaystyle f'(x_{0})=f»(x_{0})=\dots =f^{(n-1)}(x_{0})=0}, а f(n)(x0)≠0{\displaystyle f^{(n)}(x_{0})\neq 0}.

Если n{\displaystyle n} чётно и f(n)(x)<{\displaystyle f^{(n)}(x_{0})<0}, то x{\displaystyle x_{0}} — точка локального максимума.
Если n{\displaystyle n} чётно и f(n)(x)>{\displaystyle f^{(n)}(x_{0})>0}, то x{\displaystyle x_{0}} — точка локального минимума.
Если n{\displaystyle n} нечётно, то экстремума нет.

Что такое экстремум?

В школьном курсе дается множество определений понятия «экстремум». Данная статья призвана дать самое глубокое и четкое представление о термине для несведущих в вопросе лиц. Итак, под термином понимают, насколько функциональный промежуток приобретает минимальное либо максимальное значение на том или ином множестве.

Экстремум – это и минимальное значение функции, и максимальное одновременно. Различают точку минимума и точку максимума, то есть крайние значения аргумента на графике. Основные науки, в которых используют данный концепт:

• экономика,
• статистика,
• биология,
• машинное управление,
• эконометрика.

Точки экстремума играют важную роль в определении последовательности заданной функции. Система координат на графике в лучшем виде показывает изменение экстремального положения в зависимости от изменения функциональности.