Дробь охотничья: виды, размеры, классификация. изготовление дроби в домашних условиях

История и этимология термина

Русский термин дробь, как и его аналоги в других языках, происходит от лат. fractura, который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять. Фундамент теории обыкновенных дробей заложили греческие и индийские математики. Через арабов термин, в переводе на латинский, перешёл в Европу, он упоминается уже у Фибоначчи (1202 год). Слова числитель и знаменатель ввёл в оборот греческий математик Максим Плануд.

Дроби вычислялись ещё в Древнем Египте. До наших дней сохранились математические источники о египетских дробях: Математический папирус Ринда (ок. 1650 год до н. э.), Египетский математический кожаный свиток (XVII век до н. э.), Московский математический папирус (ок. 1850 год до н.э.), Деревянная табличка из Ахмима (англ.) (ок. 1950 год до н.э.).

В Китае обыкновенные дроби встречаются в труде «Математика в девяти книгах» (X-II в до н. э.), отредактированной во II в до н. э. финансовым чиновником Чжан Цаном . Десятичные дроби впервые встречаются в Китае примерно с III века н. э. при вычислениях на счётной доске (суаньпань). В письменных источниках десятичные дроби ещё некоторое время изображали в традиционном (не позиционном) формате, но постепенно позиционная система вытеснила традиционную. Персидский математик и астроном Джамшид Гияс-ад-дин ал-Каши (1380—1429) в трактате «Ключ арифметики» (1427 г.) объявил себя изобретателем десятичных дробей, хотя они встречались в трудах Ал-Уклидиси, жившего на пять веков раньше.

Поначалу европейские математики оперировали только с обыкновенными дробями, а в астрономии — с шестидесятеричными. Современное обозначение обыкновенных дробей происходит из — вначале его позаимствовали арабы, а затем, в XII-XVI веках, — европейцы. Вначале в дробях не использовалась дробная черта: числа 14,215{\displaystyle {\tfrac {1}{4}},2{\tfrac {1}{5}}} записывались таким способом: 14,2I5.{\displaystyle {\begin{smallmatrix}1\\4\end{smallmatrix}},{\begin{smallmatrix}2\\\mathrm {I} \\5\end{smallmatrix}}.} Использование черты дроби стало постоянным лишь около 300 лет назад. В Европе первым учёным, который использовал и распространял индийскую систему счёта (известную как «арабские цифры»), в том числе способ записи дробей, стал итальянский купец, путешественник, сын городского писаря — Фибоначчи (Леонардо Пизанский). Полноценная теория обыкновенных дробей и действий с ними сложилась в XVI веке (Тарталья, Клавиус).

В Европе первые десятичные дроби ввёл Иммануил Бонфис около 1350 года, но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585). Стевин записывал десятичные дроби сложными способами: например, число 42,53 записывалось как 42 51 32{\displaystyle {\overset {\underset {0}{}}{4}}2~{\overset {\underset {1}{}}{5}}~{\overset {\underset {2}{}}{3}}} или 42 ⓪ 5 ① 3 ②, где в круге или над строкой означал целую часть, 1 — десятые, 2 — сотые, и так далее. Запятую для отделения целой части стали использовать с XVII века.

На Руси дроби называли долями. В первых российских учебниках математики — в XVII веке — дроби назывались ломаными числами. Термин дробь, как аналог латинского fractura, используется в «Арифметике» Магницкого (1703) как для обыкновенных, так и для десятичных дробей.

Виды дробей

Обыкновенные дроби

Наглядное представление дроби 34{\displaystyle 3 \over 4}

Обыкновенная (или простая) дробь — запись рационального числа в виде ±mn{\displaystyle \pm {\frac {m}{n}}} или ±mn,{\displaystyle \pm m/n,} где n≠{\displaystyle n\neq 0.} Горизонтальная или косая черта обозначает знак деления, в результате чего получается частное. Делимое называется числителем дроби, а делитель — знаменателем.

Обозначения обыкновенных дробей

Есть несколько видов записи обыкновенных дробей в печатном виде:

½
1/2 или 12{\displaystyle {}^{1}/{}_{2}} (наклонная черта называется «солидус»)
выключная формула: 12{\displaystyle {\frac {1}{2}}} (горизонтальная черта называется Винкулум (англ.)русск.)
строчная формула: 12{\displaystyle {\tfrac {1}{2}}}

Правильные и неправильные дроби

Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Дробь, не являющаяся правильной, называется неправильной, и представляет рациональное число, по модулю большее или равное единице.

Например, дроби 35{\displaystyle {\frac {3}{5}}}, 78{\displaystyle {\frac {7}{8}}} и 12{\displaystyle {\frac {1}{2}}} — правильные дроби, в то время как 83{\displaystyle {\frac {8}{3}}}, 95{\displaystyle {\frac {9}{5}}}, 21{\displaystyle {\frac {2}{1}}} и 11{\displaystyle {\frac {1}{1}}} — неправильные дроби. Всякое отличное от нуля целое число можно представить в виде неправильной обыкновенной дроби со знаменателем 1.

Смешанные дроби

Дробь, записанная в виде целого числа и правильной дроби, называется смешанной дробью и понимается как сумма этого числа и дроби. Любое рациональное число можно записать в виде смешанной дроби. В противоположность смешанной дроби, дробь, содержащая лишь числитель и знаменатель, называется простой.

Например, 237=2+37=147+37=177{\displaystyle 2{\frac {3}{7}}=2+{\frac {3}{7}}={\frac {14}{7}}+{\frac {3}{7}}={\frac {17}{7}}}. В строгой математической литературе такую запись предпочитают не использовать из-за схожести обозначения смешанной дроби с обозначением произведения целого числа на дробь, а также из-за более громоздкой записи и менее удобных вычислений.

Составные дроби

Многоэтажной, или составной, дробью называется выражение, содержащее несколько горизонтальных (или реже — наклонных) черт:

1213{\displaystyle {\frac {1}{2}}/{\frac {1}{3}}} или 1213{\displaystyle {\frac {1/2}{1/3}}} или 123426{\displaystyle {\frac {12{\frac {3}{4}}}{26}}}

Десятичные дроби

Десятичной дробью называют позиционную запись дроби. Она выглядит следующим образом:

±a1a2…an,b1b2…{\displaystyle \pm a_{1}a_{2}\dots a_{n}{,}b_{1}b_{2}\dots }

Пример: 3,1415926{\displaystyle 3{,}1415926}.

Часть записи, которая стоит до позиционной запятой, является целой частью числа (дроби), а стоящая после запятой — дробной частью. Всякую обыкновенную дробь можно преобразовать в десятичную, которая в этом случае либо имеет конечное число знаков после запятой, либо является периодической дробью.

Вообще говоря, для позиционной записи числа́ можно использовать не только десятичную систему счисления, но и другие (в том числе и специфические, такие, как фибоначчиева).

Примечания

.
(англ.). British Museum. Дата обращения 13 января 2019.
Clagett, Marshall. Ancient Egyptian Science: A Source Book. — Philadelphia: American Philosophical Society, 1999. — Т. 3: Ancient Egyptian Mathematics. Memoirs of the American Philosophical Society 232. — С. 17—18, 25, 37—38, 255—257.
William K. Simpson. An Additional Fragment from the «Hatnub» Stela // Journal of Near Eastern Studies. — 1961. — Январь (т. 20, № 1). — С. 25—30.
Jean-Claude Martzloff. A History of Chinese Mathematics. Springer. 1997. ISBN 3-540-33782-2.
Berggren, J. Lennart. Mathematics in Medieval Islam // The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook (англ.). — Princeton University Press, 2007. — P. 518. — ISBN 978-0-691-11485-9.
↑ Математика: Учеб. для 5 кл. средн. шк. / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 4-е изд. — Чебоксары : Чув. кн. изд-во, 1997. — 320 с.: ил. — С. 202—203, 230.

Возможные действия

Все основные виды вычислений доступны при счете долей, как и с целыми цифрами: сложение, вычитание и прочие. Рассмотрим каждое действие по отдельности с примерами:

Сложение и вычитание

Складывать доли можно двумя путями, в зависимости от их делителя. Они бывают одинаковыми и разными. Рассмотрим пример складывания долей с одинаковыми делителями.

Для решения + необходимо по отдельности сложить делимое долей, а делитель не трогать: 1+1. Результатом станет цифра , но поскольку она неправильная, то ее можно преобразовать в смешанную, разделив делимое на делитель: 2:2= 1. Неправильную долю всегда (!) следует приводить к правильной и несокращаемой, т. е. если ее делимое и делитель можно поделить на одинаковый множитель – это следует сделать в обязательно порядке.

В случае сложения долей с различными делителями, их необходимо изначально привести к одинаковому. Например, для решения : необходимо:

Найти наименьшее общее кратное (НОК) для делителей. Здесь у делителей 2 и 3 меньшее кратное – 6.
НОК делят вначале на первый делитель, а затем на второй: 6:3=2 и 6:3=2. В данном случае полученные 2 и 3 – это первый и второй дополнительные множители.
Каждое слагаемое первоначального примера умножить на найденные множители: + = + .
Далее складываем доли: .
Преобразуем: 1.

Вычитание осуществляется точно так же: в случае с одинаковыми делителями их не трогаем, а числители последовательно вычитаем: = = . Если же знаменатели различные, то следует поступить, как и при сложении: найти НОК, множители, умножить доли, а затем вычесть уже доли с одинаковыми делителями.

Сложение дробей

Умножение и деление

При умножении необходимо последовательно перемножить их верх и низ между собой: = поскольку есть возможность сокращения на 6. В случае деления все несколько сложнее.

Для деления следует:

Умножить первый множитель на долю, обратную второй, т. е. ,
Далее действует правило умножения: = = , поскольку первоначальный результат можно сократить на 2.

Важно! Деление всегда можно заменить умножением, но только при соблюдении условия замены делителя на обратное ему число. Перевод смешанного числа в неправильную дробь

Перевод смешанного числа в неправильную дробь

Выделение целой части из неправильной дроби

Чтобы правильно решать подобные примеры, следует запомнить главное свойство и правила сокращения

Что касается операций, то важно знать, как правильно складывать и умножать при одинаковых и разных знаменателях, поскольку делятся и вычитаются они по одинаковому принципу

Виды дробей: обыкновенные и десятичные

Все математические дроби делятся на два больших разряда: обыкновенные и десятичные

Об особенностях первого из них было рассказано в предыдущем пункте, так что теперь стоит уделить внимание второму

Десятичной называют позиционную запись дроби числа, которая фиксируется на письме через запятую, без черточки или слеша. Например: 0,75, 0,5.

Фактически десятичная дробь идентична обыкновенной, однако, в ее знаменателе всегда единица с последующими нулями – отсюда произошло и ее название.

Число, предшествующее запятой, – это целая часть, а все находящееся после — дробная. Любую простую дробь можно перевести в десятичную. Так, указанные в предыдущем примере десятичные дроби можно записать как обычные: ¾ и ½.

Стоит отметить, что и десятичные, и обыкновенные дроби могут быть как положительными, так и отрицательными. Если перед ними стоит знак «-«, данная дробь отрицательная, если «+» — то положительная.

Значение дроби и основное свойство дроби

Дробь является всего лишь записью числа. Одному и тому же числу могут соответствовать разные дроби, как обыкновенные, так и десятичные.

Если умножить числитель и знаменатель дроби на одинаковую величину:

PR=C⋅PC⋅R{\displaystyle {\frac {P}{R}}={\frac {C\cdot P}{C\cdot R}}}

то значение дроби останется прежним, хотя дроби — разные.
Например:

34=912=1216{\displaystyle {\frac {3}{4}}={\frac {9}{12}}={\frac {12}{16}}}

И обратно, если числитель и знаменатель заданной дроби имеют общий делитель, то обе части можно разделить на него; такая операция называется сокращением дроби. Пример:

1216=124164=34{\displaystyle {\frac {12}{16}}={\frac {12:4}{16:4}}={\frac {3}{4}}} — здесь числитель и знаменатель дроби сократили на общий делитель 4.

Несократимой называется дробь, числитель и знаменатель которой взаимно просты, то есть не имеют общих делителей, кроме ±1.{\displaystyle \pm 1.}

Для десятичной дроби запись почти всегда однозначна, однако имеются исключения. Пример:

,999…=1{\displaystyle 0,\!999…=1} — две разные дроби соответствуют одному числу.

Действия с дробями

Разберем в отдельности каждое действие с дробями, которое можно выполнить по тому или иному алгоритму:

Сложение и вычитание дробей. Для того, чтобы сложить или вычесть дроби, нужно привести их к общему знаменателю. Для этого числитель и знаменатель каждой дроби домножают на какое-то число так, чтобы получившиеся знаменатели совпали. После этого числители складываются или вычитаются, а знаменатель остается прежним.
Умножение дробей.

При умножении дробей числитель умножается на числитель, а знаменатель на знаменатель.
Деление дробей. При делении дробь-делитель переворачивается, то есть числитель становится знаменателем, а знаменатель числителем. После этого делимое умножают на перевернутый делитель.
Для возведения в степень дроби, отдельно в степень возводят числитель и отдельно знаменатель.

Что мы узнали?

Мы узнали, что такое дробь. Перечислили основные виды дробей, рассматриваемые в математике 5 класса. Сказали, к какому подмножеству чисел относится дробь. Выделили основные действия, выполняемые с дробями, и кратко описали алгоритмы этих действий.

Значение дроби и основное свойство дроби

Если умножить числитель и знаменатель дроби на одинаковую величину:

PR=C⋅PC⋅R{\displaystyle {\frac {P}{R}}={\frac {C\cdot P}{C\cdot R}}}

то значение дроби останется прежним, хотя дроби — разные.
Например:

34=912=1216{\displaystyle {\frac {3}{4}}={\frac {9}{12}}={\frac {12}{16}}}

И обратно, если числитель и знаменатель заданной дроби имеют общий делитель, то обе части можно разделить на него; такая операция называется сокращением дроби. Пример:

1216=124164=34{\displaystyle {\frac {12}{16}}={\frac {12:4}{16:4}}={\frac {3}{4}}} — здесь числитель и знаменатель дроби сократили на общий делитель 4{\displaystyle 4}.

Несократимой называется дробь, числитель и знаменатель которой взаимно просты, то есть не имеют общих делителей, кроме ±1.{\displaystyle \pm 1.}

Для десятичной дроби запись почти всегда однозначна, однако имеются исключения. Пример:

,999…=1{\displaystyle 0,\!999…=1} — две разные дроби соответствуют одному числу.

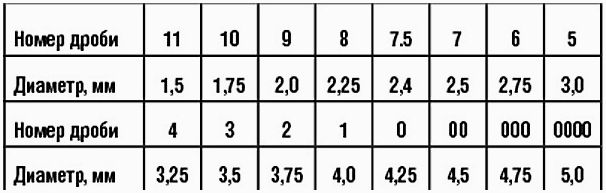
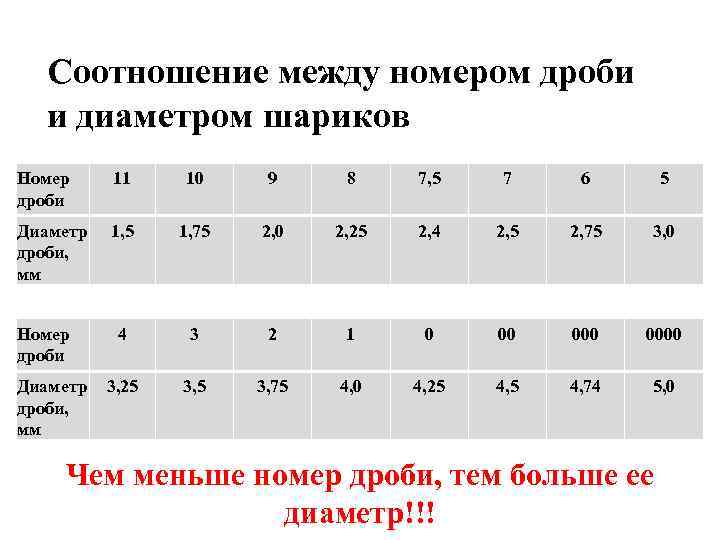
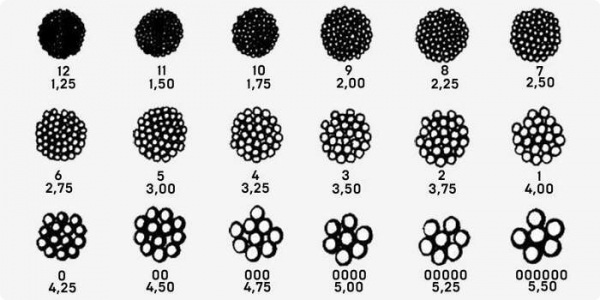
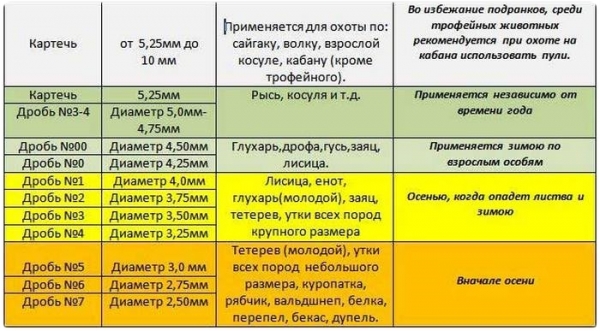
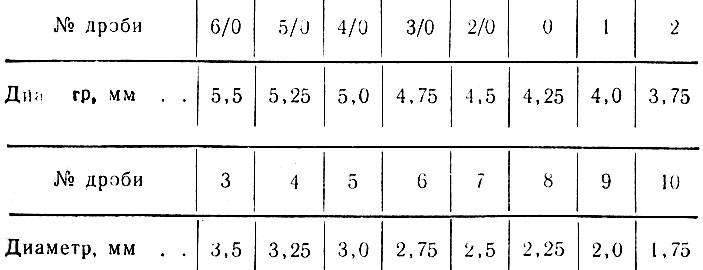
Какую дробь для какой дичи использовать

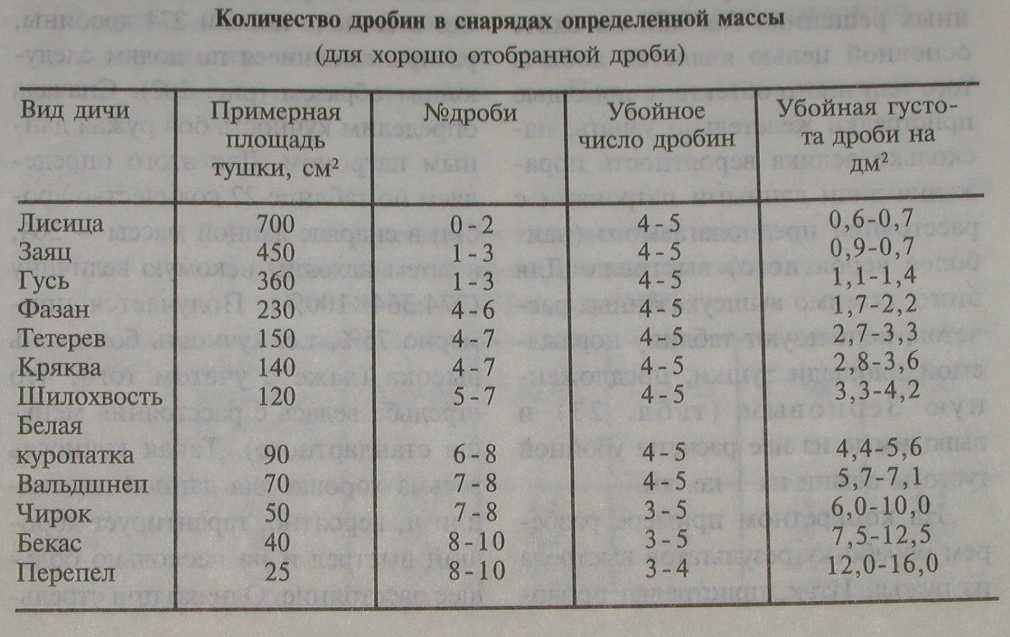
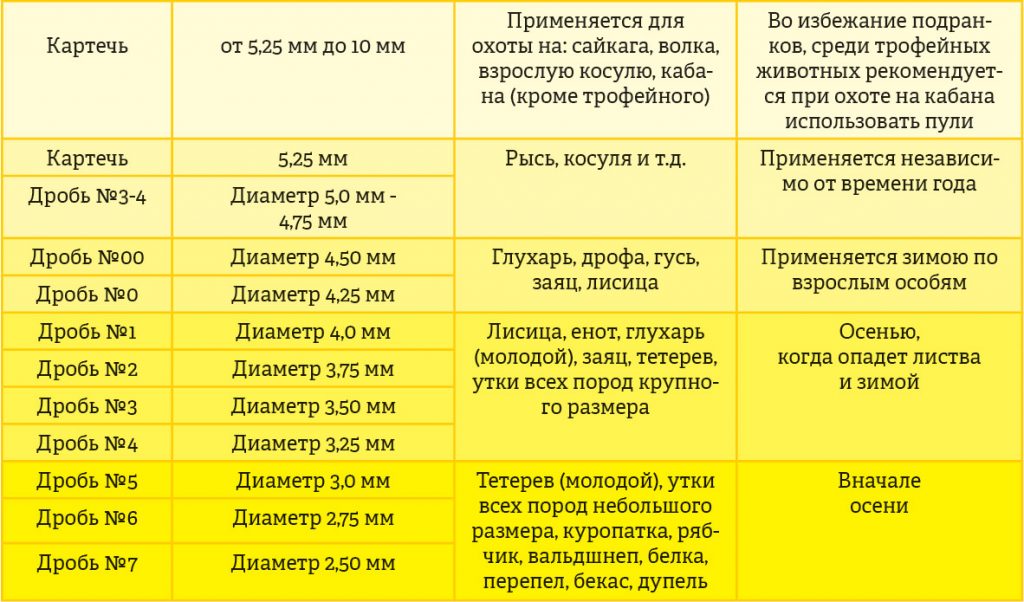
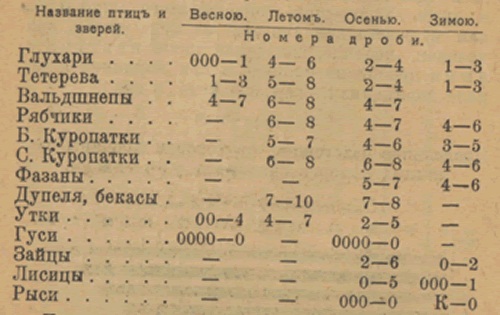
Многие охотники спрашивают, кого (гуся, тетерева, фазана, зайца, глухаря) нужно бить и какими именно снарядами? О том, кого и чем надо бить, смотрите ниже:

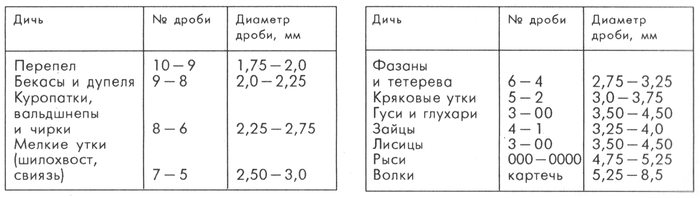
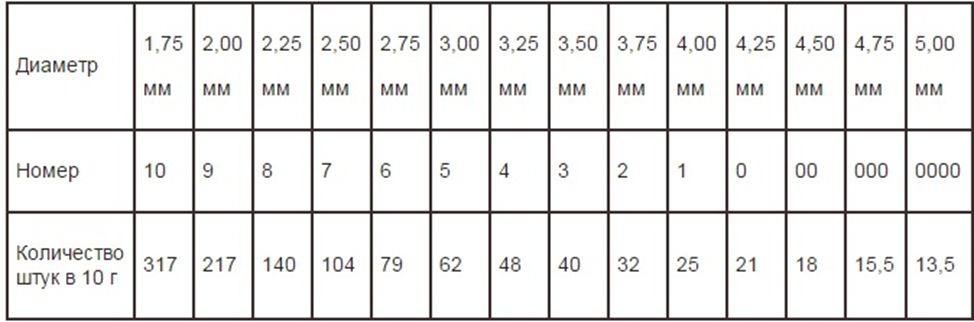
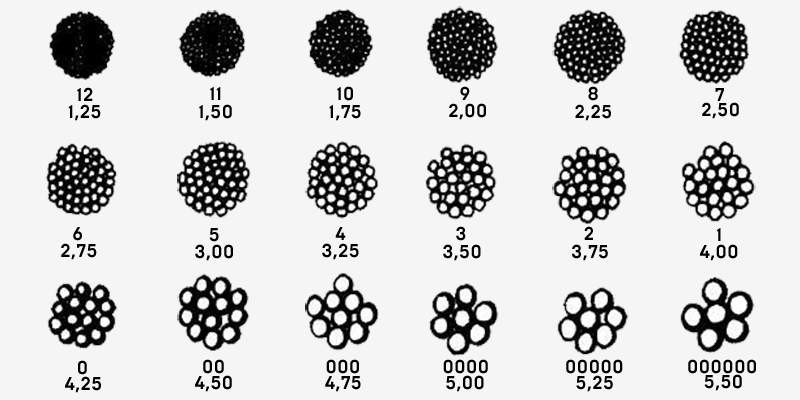
Перепелов, бекасов, дупелей и прочих мелких куликов рекомендуется бить 8, 9 и 10 номерами.
Куропаток, чириков, вальдшнепов, рябчиков возьмет уже 6 или 7 номер.
Тетеревов, уток, диких голубей и фазанов поможет добыть 5 и 6 номер.
Уток, зайцев, глухарей, гусей стреляют 2, 1, 0 номером.
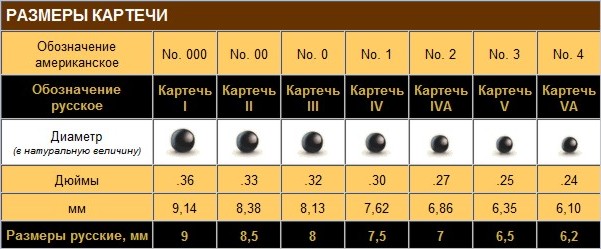
Лисица, волк, косуля – 00, 000, 0000 номер.

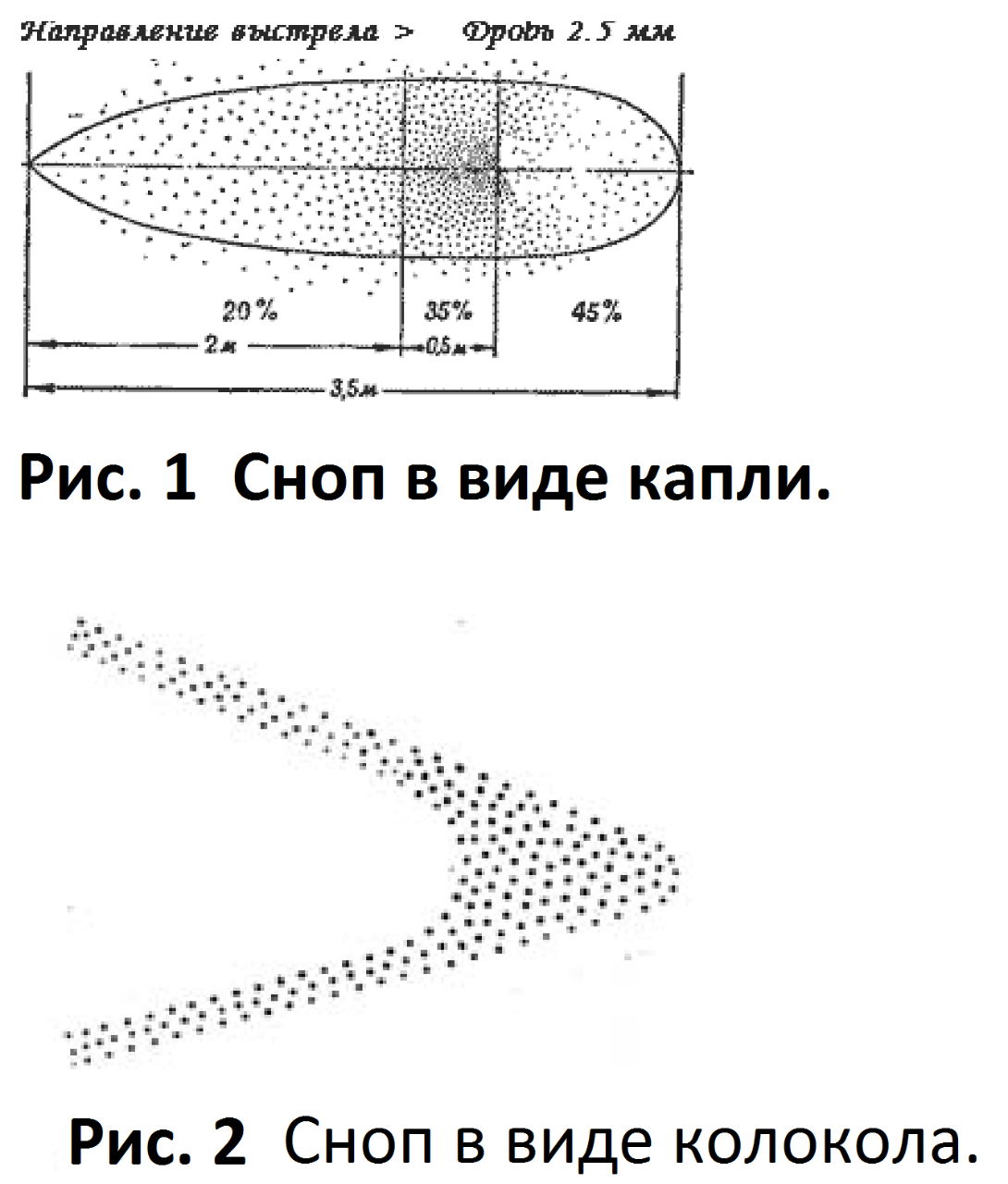
При определении необходимого номера дроби помните, что в дичь должны попасть около 4-5 дробинок, поэтому, при стрельбе по мелким целям (гусь, утка, заяц, фазан, глухарь) картечью в лучшем случае попадет 1-2 дробинки, а значит, вы оставите подранка. С другой стороны, если дробовая осыпь будет все-таки удовлетворительной, то дичь (утка, глухарь, тетерев, фазан, заяц) будет просто разорвана и потеряет всю свою ценность.

С другой стороны, стреляя слишком мелкими снарядами, вы не пробьете оперение тетерева или гуся, а также шкуру косули, поэтому стрелять вы будете впустую.

Крайне не рекомендуется делать смесь из нескольких номеров при стрельбе, поскольку при этом заметно падает кучность и дальность боя.

Как сделать точность боя выше с охотничьей дробью?

Лучший результат при стрельбе показывает согласованная дробь. Делается это в домашних условиях: насыпьте дробь в гильзу и как следует утрясите, причем так, чтобы она лежала ровным слоем. Сразу же закройте ее прокладкой, чтобы она не пересыпалась. Если сделать ровный слой не получается, попробуйте использовать диаметр на один больше или меньше. Так вы точно попадете в тетерева, гуся, зайца, фазана.
Еще один способ для поднятия кучности своими руками: пересыпьте боеприпасы крахмалом, тальком и т.п. На пыж насыпается половина зарядной дроби, пересыпается и утрясается, после этого засыпается другая половина и процесс повторяется. Сверху кладется пыж, и патрон готов.