Виды дифференциальных уравнений, примеры, методы решения

Примеры.

Следующие примеры позволяют лучше понять, как различные задачи формулируются на языке дифференциальных уравнений.

1) Закон распада некоторых радиоактивных веществ состоит в том, что скорость распада пропорциональна наличному количеству этого вещества. Если x – количество вещества в некоторый момент времени t, то этот закон можно записать так:

где dx/dt – скорость распада, а k – некоторая положительная постоянная, характеризующая данное вещество. (Знак «минус» в правой части указывает на то, что x убывает со временем; знак «плюс», подразумеваемый всегда, когда знак явно не указан, означал бы, что x возрастает со временем.)

2) Емкость первоначально содержит 10 кг соли, растворенной в 100 м3 воды. Если чистая вода вливается в емкость со скоростью 1 м3 в минуту и равномерно перемешивается с раствором, а образовавшийся раствор вытекает из емкости с такой же скоростью, то сколько соли окажется в емкости в любой последующий момент времени? Если x – количество соли (в кг) в емкости в момент времени t, то в любой момент времени t в 1 м3 раствора в емкости содержится x/100 кг соли; поэтому количество соли убывает со скоростью x/100 кг/мин, или

3) Пусть на тело массы m, подвешенное к концу пружины, действует возвращающая сила, пропорциональная величине растяжения пружины. Пусть x – величина отклонения тела от положения равновесия. Тогда по второму закону Ньютона, который утверждает, что ускорение (вторая производная от x по времени, обозначаемая d 2x/dt 2) пропорционально силе:

Правая часть стоит со знаком минус потому, что возвращающая сила уменьшает растяжение пружины.

4) Закон охлаждения тел утверждает, что количество тепла в теле убывает пропорционально разности температур тела и окружающей среды. Если чашка кофе, разогретого до температуры 90° С находится в помещении, температура в котором равна 20° С, то

где T – температура кофе в момент времени t.

5) Министр иностранных дел государства Блефуску утверждает, что принятая Лиллипутией программа вооружений вынуждает его страну увеличить военные расходы на сколько это только возможно. С аналогичными заявлениями выступает и министр иностранных дел Лиллипутии. Возникающую в результате ситуацию (в простейшей интерпретации) можно точно описать двумя дифференциальными уравнениями. Пусть x и y – расходы на вооружение Лиллипутии и Блефуску. Предполагая, что Лиллипутия увеличивает свои расходы на вооружение со скоростью, пропорциональной скорости увеличения расходов на вооружение Блефуску, и наоборот, получаем:

где члены -ax и -by описывают военные расходы каждой из стран, k и l – положительные постоянные. (Эту задачу впервые таким образом сформулировал в 1939 Л.Ричардсон.)

После того, как задача записана на языке дифференциальных уравнений, следует попытаться их решить, т.е. найти величины, скорости изменения которых входят в уравнения. Иногда решения находятся в виде явных формул, но чаще их удается представить лишь в приближенном виде или же получить о них качественную информацию. Часто бывает трудно установить, существует ли решение вообще, не говоря уже о том, чтобы найти его. Важный раздел теории дифференциальных уравнений составляют так называемые «теоремы существования», в которых доказывается наличие решения у того или иного типа дифференциальных уравнений.

Первоначальная математическая формулировка физической задачи обычно содержит упрощающие предположения; критерием их разумности может служить степень согласованности математического решения с имеющимися наблюдениями.

Простейшие дифференциальные уравнения первого порядка

Простейшие дифференциальные уравнения первого порядка — класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные уравнения первого порядка и линейные уравнения первого порядка. Все эти уравнения можно проинтегрировать в конечном виде.

Отправной точкой изложения будет служить дифференциальное уравнение первого порядка, записанное в т. н. симметричной форме:

P(t,x)dt+Q(t,x)dx=(1),{\displaystyle {\begin{matrix}P(t,x)dt+Q(t,x)dx=0\end{matrix}}\qquad (1),}

где функции P(t,x){\displaystyle P(t,x)} и Q(t,x){\displaystyle Q(t,x)} определены и непрерывны в некоторой области Ω⊆Rt,x2{\displaystyle \Omega \subseteq \mathbb {R} _{t,x}^{2}}.

Дифференциальные уравнения первого порядка.

Простейшие дифференциальные уравнения первого порядка вида .

Запишем несколько примеров таких ДУ .

Дифференциальные уравнения можно разрешить относительно производной, произведя деление обеих частей равенства на f(x). В этом случае приходим к уравнению , которое будет эквивалентно исходному при f(x) ≠ . Примерами таких ОДУ являются .

Если существуют значения аргумента x, при которых функции f(x) и g(x) одновременно обращаются в ноль, то появляются дополнительные решения. Дополнительными решениями уравнения при данных x являются любые функции, определенные для этих значений аргумента. В качестве примеров таких дифференциальных уравнений можно привести .

В статье простейшие дифференциальные уравнения первого порядка. Вы можете ознакомиться с подробной теорией и посмотреть примеры решения таких ОДУ.
Дифференциальные уравнения с разделяющимися переменными вида или .

Дифференциальные уравнения называют уравнениями с разделенными переменными.

Название этого вида дифференциальных уравнений достаточно показательно: выражения, содержащие переменные x и y, разделены знаком равенства, то есть, находятся по разные стороны от него.

Общее решение дифференциальных уравнений с разделенными переменными можно найти, проинтегрировав обе части равенства: ∫ f(y)dy = ∫ f(x)dx.

В качестве примеров ОДУ с разделенными переменными приведем .

Дифференциальные уравнения с разделяющимися переменными приводятся к ОДУ с разделенными переменными делением обеих частей уравнения на произведение f₂(y) ⋅ g₁(x). То есть, получим . Такое преобразование будет эквивалентным, если одновременно f₂(y) ≠ 0 и g₁(x) ≠ 0. Иначе могут потеряться некоторые решения.

Примерами ОДУ с разделяющимися переменными являются .

Некоторые дифференциальные уравнения можно свести к уравнениям с разделяющимися переменными с помощью замены переменных.

Дифференциальные уравнения приводятся к ОДУ с разделяющимися переменными подстановкой z = ax+by. К примеру, уравнение с помощью подстановки z = 2x+3y приобретает вид .

ОДУ или преобразуются к уравнениям с разделяющимися переменными с помощью замен или . Например, дифференциальное уравнение после замены принимает вид .

Некоторые дифференциальные уравнения следует немного преобразовать, чтобы можно провести замену. К примеру, достаточно разделить на x2 или y2 числитель и знаменатель правой части дифференциального уравнения , чтобы оно соответствовало случаям или соответственно.

Дифференциальные уравнения преобразуются к только что рассмотренным ОДУ или , если ввести новые переменные , где — решение системы линейных уравнений и провести некоторые преобразования.

Например, дифференциальное уравнение после введения новых переменных преобразуется к виду . Проводим деление на u числителя и знаменателя правой части полученного уравнения и принимаем . В результате приходим к уравнению с разделяющимися переменными .

В разделе дифференциальные уравнения с разделяющимися переменными подробно разобрана теория и приведены подробные решения аналогичных примеров.
Линейные неоднородные дифференциальные уравнения первого порядка .

В качестве примеров линейных неоднородных дифференциальных уравнений первого порядка можно привести .

Для решения ЛНДУ используют метод вариации произвольной постоянной. Также существует метод, основанный на представлении искомой функции y в виде произведения: y(x) = u(x)v(x).

В статье линейные неоднородные дифференциальные уравнения первого порядка подробно изложены методы интегрирования таких ЛНДУ и приведены подробные решения примеров и задач.
Дифференциальное уравнение Бернулли .

Примерами дифференциальных уравнений Бернулли являются, например, .

Дифференциальное уравнение Бернулли сводится к линейному дифференциальному уравнению первого порядка подстановкой .

Можно также пользоваться методом, основанным на представлении функции y как y(x) = u(x)v(x).

В разделе дифференциальное уравнение Бернулли подробно расписаны методы нахождения решений и разобраны решения примеров и задач.
Уравнения в полных дифференциалах .

Если для любых значений x и y выполняется , то этого условия необходимо и достаточно, чтобы выражение P(x, y)dx+Q(x, y)dy представляло собой полный дифференциал некоторой функции U(x, y) = 0, то есть, dU(x, y) = P(x, y)dx + Q(x, y)dy. Таким образом, задача сводится к восстановлению функции U(x, y) = 0 по ее полному дифференциалу.

К примеру, левая часть дифференциального уравнения представляет собой полный дифференциал функции .

Подробное описание теории и решение примеров изложены в разделе уравнения в полных дифференциалах.

Метод Эйлера

Задано уравнение

dY/dx = f(x,Y). (4)

Начальные условия : при x = x Y(x) = Y, x > x

Значения функции в узлах x, x₁, . . . , x_n заменим сеточной функцией y, y₁, . . . , y_n. Для простоты примем постоянным шаг h = Dx_i = x_i₊₁ — x_i = const. Заменим производную конечно-разностным отношением :

(y_i — y_i-1)/h =f(x_i-1, y_i-1)

Отсюда

y_i = y_i-1 + h f(x_i-1, y_i-1). (5)

Зная значение функции в начальной точке y, последовательно можно найти значения функции во всех точках сетки. Метод явный одношаговый. Рассмотрим его геометрическую интерпретацию (рис.8.2).

Точку b(x₁,y₁) получим, проведя касательную к кривой, проходящей через начальную точку, до пересечения касательной со следующей интегральной кривой. Далее, проведя касательную в точке b до пересечения со следующей кривой, получим точку c(x₂,y₂) и т.д.

Точным решением уравнения является интегральная кривая, которая проходит через точку a (x, y). Значит, вместо кривой, проходящей через точку a(x,y), получили ломаную abc.

Оценим погрешность метода. Формулу (5) можно рассматривать как полученную разложением функции Y в ряд Тейлора:

Y(x_i+Δx_i) = Y(x_i) + Y’(x_i)Δx_i +O(Δx_i2).

Заменяя значения Y в узлах на значения сеточной функции y и учитывая в соответствии с (1):

Y’(x_i) = f(x_i, y_i),

получим:

y_i = y_i-1 + h f(x_i-1, y_i-1) + O(h2).

На каждом шаге погрешность имеет порядок O(h2). При нахождении решения в точке x_n, отстоящей от x на расстояние L, погрешность суммируется. Суммарная (глобальная) погрешность на n-ном шаге равна nO(h2). Так как h = L/n, то

nO(h2) = LO(h2)/h = O(h).

Метод Эйлера имеет первый порядок точности. Он используется сравнительно редко.

Алгоритм метода Эйлера

x, x_k — концы интервала; h — шаг интегрирования;

y = y(x)- начальное условие;

f(x,y) — правая часть уравнения

Ввод h, x, x_k , y

x=x; y=y

Начало цикла

y = y + hf(x,y)

x = x+h

Печать x, y

Конец цикла, по условию x > x_k

Рассмотрим в качестве примера систему трех уравнений:

y₁’ = f₁(x, y₁, y₂, y₃)

y₂’ = f₂(x, y₁, y₂, y₃)

y₃’ = f₃(x, y₁, y₂, y₃).

Начальные условия: при x = x y₁ = y₁₀; y₂ = y₂₀, y₃ = y₃₀.

Для решения системы дифференциальных уравнений формула (5) запишется в виде:

y_j,i = y_j,i-1 + hf_j(x_i-1, y_1,i-1, y_2,i-1, . . . , y_n,i-1),

где j — номер неизвестного j = 1,2,. . .n; i – номер точки.

Алгоритм метода Эйлера для системы уравнений

x, x_k — концы интервала; h — шаг интегрирования;

Начальные условия: при x = x y₁ = y₀₁; y₂ = y₀₂, y₃ = y₀₃

Ввод h, x, x_k_, y₀₁, y₀₂, y₀₃

x=x; y₁ =y₀₁, y₂ = y₀₂, y₃ = y₀₃

Начало цикла

y₁ = y₁ + hf₁(x, y₁, y₂, y₃)

y₂ = y₂ + hf₂(x, y₁, y₂, y₃)

y₃ = y₃ +hf₃(x, y₁, y₂, y₃)

x = x+h

Печать x, y₁, y₂, y₃

Конец цикла, по условию x > x_k

Решение дифференциальных уравнений

Производные от элементарных функций выражаются через элементарные функции. Интегралы от элементарных функций часто не выражаются через элементарные функции. С дифференциальными уравнениями дело обстоит еще хуже. В результате решения можно получить следующее.

Явную зависимость функции от переменной.

Решение дифференциального уравнения

– это функция , которая определена, раз дифференцируема, и удовлетворяет исходному уравнению: .
Неявную зависимость в виде уравнения типа или системы уравнений.

Интеграл дифференциального уравнения

– это решение дифференциального уравнения, которое имеет неявный вид.
Зависимость, выраженную через элементарные функции и интегралы от них.

Решение дифференциального уравнения в квадратурах

– это решение ДУ, выраженное в виде комбинации элементарных функций и интегралов от них.
Решение может не выражается через элементарные функции.

Интегрирование дифференциального уравнения: Процесс решения ДУ называется интегрированием дифференциального уравнения.

Поскольку решение дифференциальных уравнений сводится к вычислению интегралов, то в состав решения входит набор постоянных . Количество постоянных равно порядку уравнения.

Общее решение дифференциального уравнения: – это множество всех, без исключений, решений дифференциального уравнения. Общее решение ДУ — го порядка часто записывают в виде функции, зависящей от независимой переменной , и от произвольных постоянных (1) .
Частное решение дифференциального уравнения: – это одно из решений ДУ. Если общее решение имеет вид (1), то в частном решении постоянные имеют заданные значения.
Общий интеграл дифференциального уравнения: – это общее решение, которое имеет неявный вид .
Частный интеграл дифференциального уравнения: – это общий интеграл при заданных значениях постоянных .

Также, под интегралом дифференциального уравнения понимают решение, записанное в виде. Дифференциальное уравнение первого порядка имеет один интеграл. Уравнение n — го порядка имеет n интегралов:;;;.

Использованная литература: В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015. Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Литература

Учебники

Арнольд В. И. Обыкновенные дифференциальные уравнения, — Любое издание.
Арнольд В. И. Дополнительные главы теории обыкновенных дифференциальных уравнений, — Любое

издание.

Арнольд В. И. Геометрические методы в теории обыкновенных дифференциальных уравнений, — Любое издание.
Арнольд В. И., Ильяшенко Ю. С. Обыкновенные дифференциальные уравнения, — Итоги науки и техн. Сер. Совр. пробл. мат. Фундам. направ., 1985, том 1.
Петровский И. Г. Лекции по теории обыкновенных дифференциальных уравнений, — Любое издание.
Понтрягин Л. С. Обыкновенные дифференциальные уравнения, — Любое издание.
Степанов В. В. Курс дифференциальных уравнений, — Любое издание.
Трикоми Ф. Дифференциальные уравнения, — Любое издание.
Филиппов А. Ф. Введение в теорию дифференциальных уравнений, — Любое издание.
Филипс Г. Дифференциальные уравнения, — Любое издание.
Хартман Ф. Обыкновенные дифференциальные уравнения, — Любое издание.
Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление, — Любое издание.

Справочники

Камке Э. Справочник по обыкновенным дифференциальным уравнениям, — Любое издание.
Зайцев В. Ф., Полянин А. Д. Справочник по обыкновенным дифференциальным уравнениям, — Любое издание.

Линейные неоднородные системы дифференциальных уравнений

Практически то же самое, только решение будет несколько длиннее.

Неоднородная система дифференциальных уравнений, которая в большинстве случаев может встретиться вам в задачах, имеет следующий вид:

По сравнению с однородной системой в каждом уравнении дополнительно добавляется некоторая функция, зависящая от «тэ». Функции могут быть константами (причем, по крайне мере одна из них не равна нулю), экспонентами, синусами, косинусами и т.д.

Пример 3

Найти частное решение системы линейных ДУ, соответствующее заданным начальным условиям

Решение: Дана линейная неоднородная система дифференциальных уравнений, в качестве «добавок» выступают константы. Используем метод исключения, при этом сам алгоритм решения полностью сохраняется. Для разнообразия я начну как раз с первого уравнения.

1) Из первого уравнения системы выражаем:

Это важная штуковина, поэтому я её снова замаркирую звёздочкой. Скобки лучше не раскрывать, зачем лишние дроби?

И еще раз заметьте, что из первого уравнения выражается именно «игрек» – через два «икса» и константу.

2) Дифференцируем по обе части:

Константа (тройка) исчезла, ввиду того, что производная константы равна нулю.

3) Подставим и во второе уравнение системы :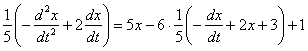

Сразу после подстановки целесообразно избавиться от дробей, для этого каждую часть уравнения умножаем на 5:

Теперь проводим упрощения:

В результате получено линейное неоднородное уравнение второго порядка с постоянными коэффициентами. Вот, по сути, и всё отличие от решения однородной системы уравнений, разобранного в предыдущем параграфе.

Примечание: Тем не менее, в неоднородной системе иногда может получиться и однородное уравнение.

Найдем общее решение соответствующего однородного уравнения:

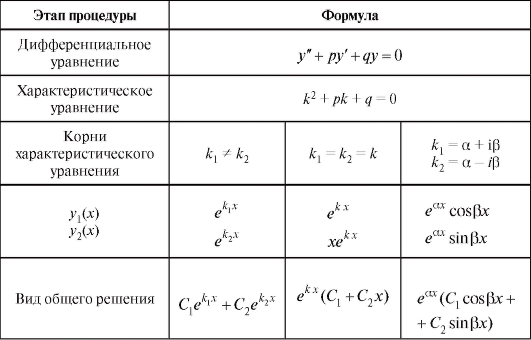
Составим и решим характеристическое уравнение: – получены сопряженные комплексные корни, поэтому:.

Корни характеристического уравнения опять получились «хорошими», значит, мы на верном пути.

Частное решение неоднородного уравнения ищем в виде .
Найдем первую и вторую производную:

Подставим в левую часть неоднородного уравнения:

Таким образом:

Следует отметить, что частное решение легко подбирается устно, и вполне допустимо вместо длинных выкладок написать: «Очевидно, что частное решение неоднородного уравнения: ».

В результате:

4) Ищем функцию . Сначала находим производную от уже найденной функции :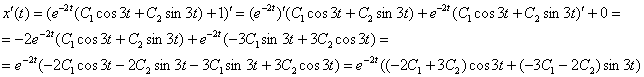
Не особо приятно, но подобные производные в диффурах приходится находить часто.

Шторм в самом разгаре, и сейчас будет девятый вал. Привяжите себя канатом к палубе.

Подставим
и в уравнение (*):

6) Найдем частное решение, соответствующее начальным условиям :

Окончательно, частное решение:

Вот видите, какая история со счастливым концом, теперь можно безбоязненно плавать на шлюпках по безмятежному морю под ласковым солнцем.

Ответ: частное решение:

Кстати, если начать решать эту систему со второго уравнения, то вычисления получатся заметно проще (можете попробовать), но многие посетители сайта просили разбирать и более трудные вещи. Как тут откажешь? =) Пусть будут и более серьезные примеры.

Пример проще для самостоятельного решения:

Пример 4

Найти частное решение линейной неоднородной системы дифференциальных уравнений, соответствующее заданным начальным условиям

Данная задача решена мной по образцу Примера №1, то есть, из второго уравнения выражен «икс». Решение и ответ в конце урока.

В рассмотренных примерах я не случайно использовал различные обозначения, применял разные пути решения. Так, например, производные в одном и том же задании записывались тремя способами: . В высшей математике не нужно бояться всяких закорючек, главное, понимать алгоритм решения.

Терминология и классификация

Порядок дифференциального уравнения — наивысший , входящих в него интегралов.

Если дифференциальное уравнение является многочленом относительно старшей производной, то степень этого многочлена называется степенью дифференциального уравнения. Так, например, уравнение (y″)4+y′+y6+x7={\displaystyle (y»)^{4}+y’+y^{6}+x^{7}=0} является уравнением второго порядка, четвёртой степени.

Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные y′(x),y″(x),…,y(n)(x){\displaystyle y'(x),y»(x),…,y^{(n)}(x)} до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции y(x){\displaystyle y(x)} удается привести к квадратуре, (т. е. к виду y=∫f(x) dx{\displaystyle y=\int f(x)\ dx}, где f(x){\displaystyle f(x)} — элементарная функция) независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет.

Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.

В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные

В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных.. Важнейшим вопросом для дифференциальных уравнений является существование и единственность их решения

Разрешение этого вопроса дают теоремы существования и единственности, указывающие необходимые и достаточные для этого условия. Для обыкновенных дифференциальных уравнений такие условия были сформулированы Липшицем (1864). Для уравнений в частных производных соответствующая теорема была доказана С. В. Ковалевской (1874).

Важнейшим вопросом для дифференциальных уравнений является существование и единственность их решения. Разрешение этого вопроса дают теоремы существования и единственности, указывающие необходимые и достаточные для этого условия. Для обыкновенных дифференциальных уравнений такие условия были сформулированы Липшицем (1864). Для уравнений в частных производных соответствующая теорема была доказана С. В. Ковалевской (1874).

Решения дифференциальных уравнений подразделяются на общие и частные решения. Общие решения включают в себя неопределенные постоянные, а для уравнений в частных производных — произвольные функции от независимых переменных, которые могут быть уточнены из дополнительных условий интегрирования (начальных условий для обыкновенных дифференциальных уравнений, начальных и граничных условий для уравнений в частных производных). После определения вида указанных постоянных и неопределенных функций решения становятся частными.

Поиск решений обыкновенных дифференциальных уравнений привёл к установлению класса специальных функций — часто встречающихся в приложениях функций, не выражающихся через известные элементарные функции. Их свойства были подробно изучены, составлены таблицы значений, определены взаимные связи и т. д.

Развитие теории дифференциальных уравнений позволило в ряде случаев отказаться от требования непрерывности исследуемых функций и ввести обобщённые решения дифференциальных уравнений.

Решение уравнений математической физики

Существует два вида методов решения данного типа уравнений:

аналитический, при котором результат выводится различными математическими преобразованиями;
численный, при котором полученный результат соответствует действительному с заданной точностью, но который требует много рутинных вычислений и поэтому выполним только при помощи вычислительной техники (ЭВМ).

Аналитическое решение

Аналитические решения уравнений математической физики можно получить различными способами. Например:

Используя функцию Грина;
Используя метод разделения переменных Фурье;
С помощью теории потенциала;
Используя формулу Кирхгофа.

Эти методы разработаны для различных типов уравнений и в некоторых простых случаях позволяют получить решение в виде некоторой формулы или сходящегося ряда, например для уравнения колебаний струны:

Δu=a2∂2u∂t2{\displaystyle \Delta u=a^{2}{\frac {\partial ^{2}u}{\partial t^{2}}}}

u(x,t)|x==u(x,t)|x=L={\displaystyle u(x,t){\big |}_{x=0}=u(x,t){\big |}_{x=L}=0}

u(x,t)|t==f(x), ∂u∂t(x,t)|t==g(x){\displaystyle u(x,t){\big |}_{t=0}=f(x),\ {\dfrac {\partial u}{\partial t}}(x,t){\big |}_{t=0}=g(x)}

аналитическое решение с помощью метода Фурье имеет вид:

u(x,t)=∑n=∞Ancos⁡(aπnLt)+Bnsin⁡(aπnLt)sin⁡(πnxL){\displaystyle u(x,t)\,=\sum \limits _{n=0}^{\infty }\left\sin \left({\dfrac {\pi nx}{L}}\right)}

An=2L∫Lf(x)sin⁡(πnxL)dx,Bn=2nπa∫Lg(x)sin⁡(πnxL)dx{\displaystyle A_{n}={\dfrac {2}{L}}\int \limits _{0}^{L}f(x)\sin \left({\dfrac {\pi nx}{L}}\right)dx,\quad B_{n}={\dfrac {2}{n\pi a}}\int \limits _{0}^{L}g(x)\sin \left({\dfrac {\pi nx}{L}}\right)dx}

Численное решение

Нахождение пятой точки по четырём известным

Поскольку нахождение аналитического решения даже простого уравнения в сложной области не всегда возможно, то было разработано множество методов решения уравнений математической физики. Некоторые из них основываются на аппроксимации дифференциального оператора некоторыми выражениями, другие сводят задачу к проекционной или вариационной и решают её, некоторые из часто используемых численных методов:

Метод конечных разностей;
Метод конечных элементов;
Метод конечных объёмов.

У каждого из методов свои особенности и свои классы решаемых задач.
Например решение методом конечных разностей уравнения колебаний может быть получено с использованием следующей разностной схемы:

uij+1=τ2a2h2(ui+1j−2uij+ui−1j)+2uij−uij−1{\displaystyle u_{i}^{j+1}={\tau ^{2}a^{2} \over h^{2}}\left(u_{i+1}^{j}-2u_{i}^{j}+u_{i-1}^{j}\right)+2u_{i}^{j}-u_{i}^{j-1}},

где τ{\displaystyle \tau } — шаг по времени, h{\displaystyle h} — шаг по пространству.