Диаграммы. какую и для чего выбирать. советы по использованию

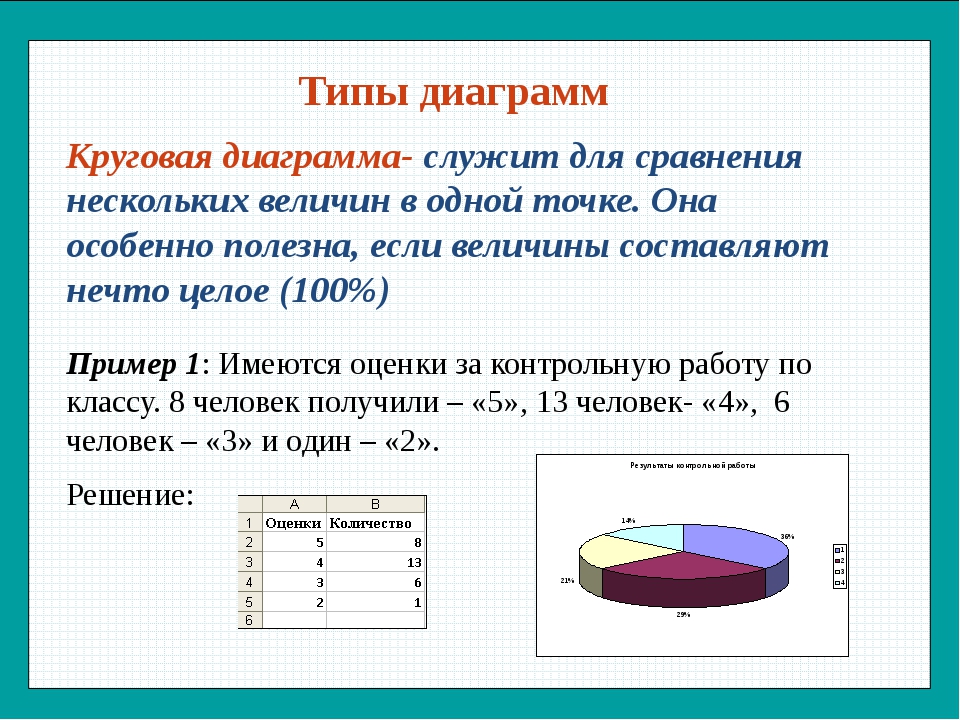
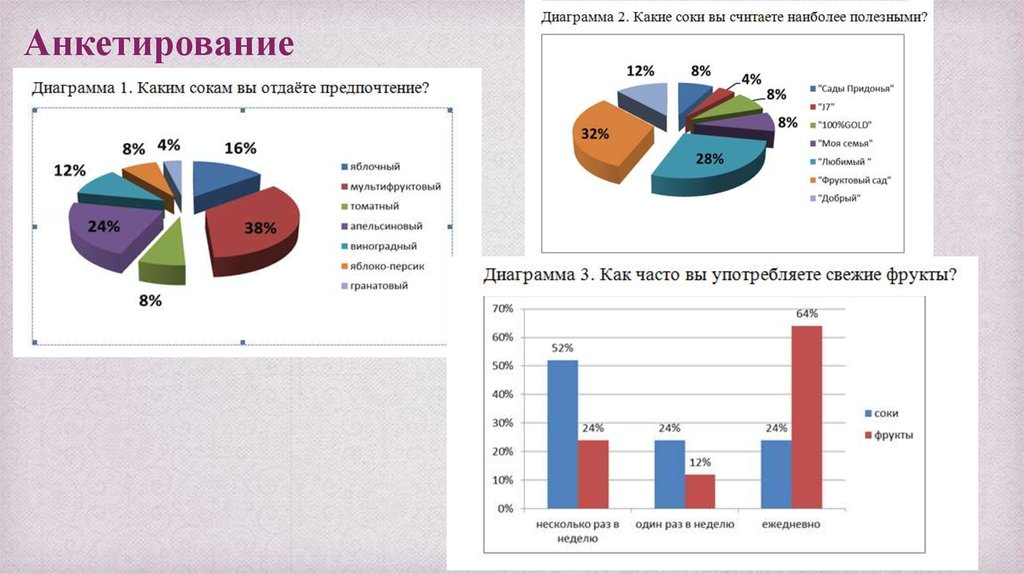
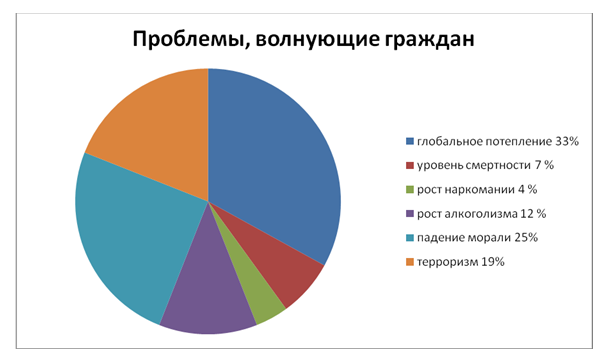
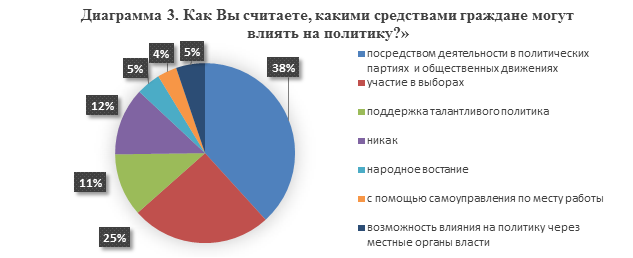
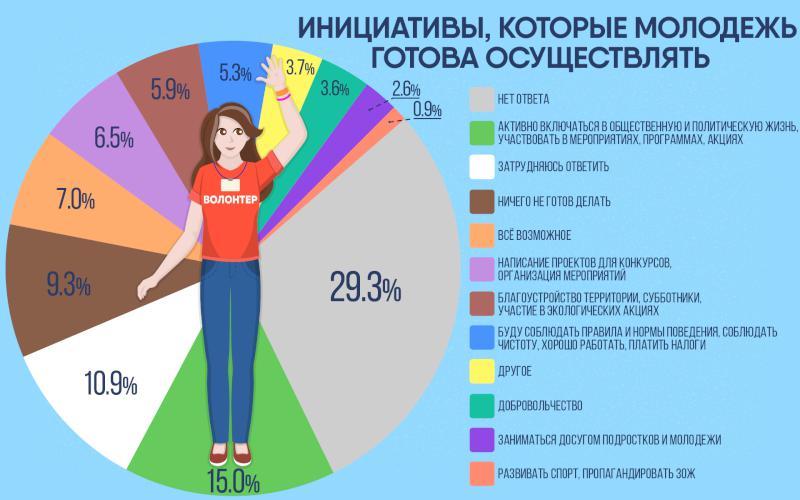
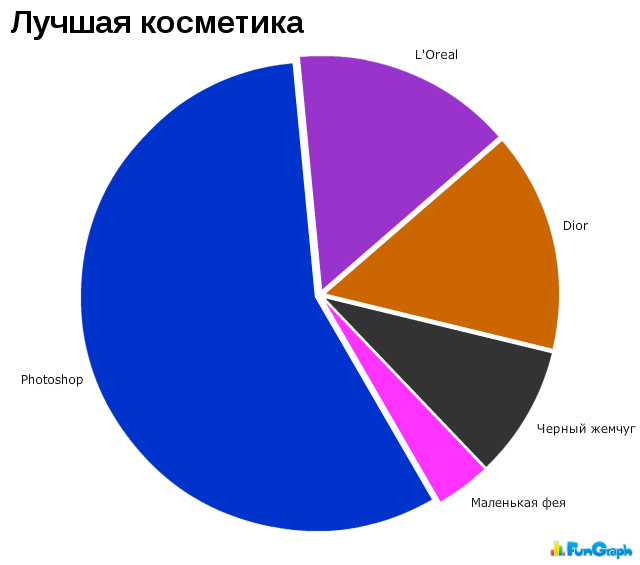
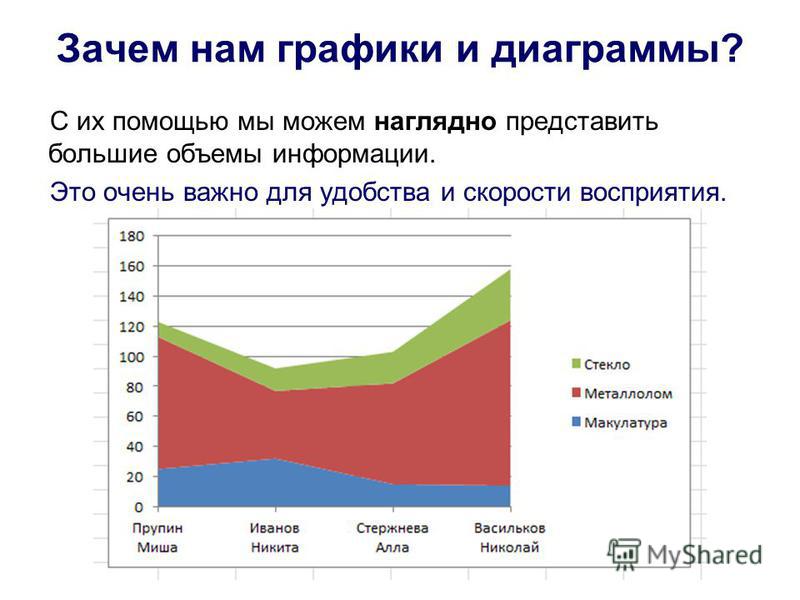
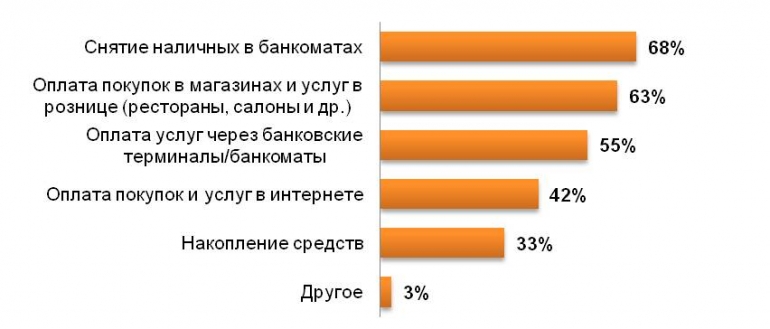
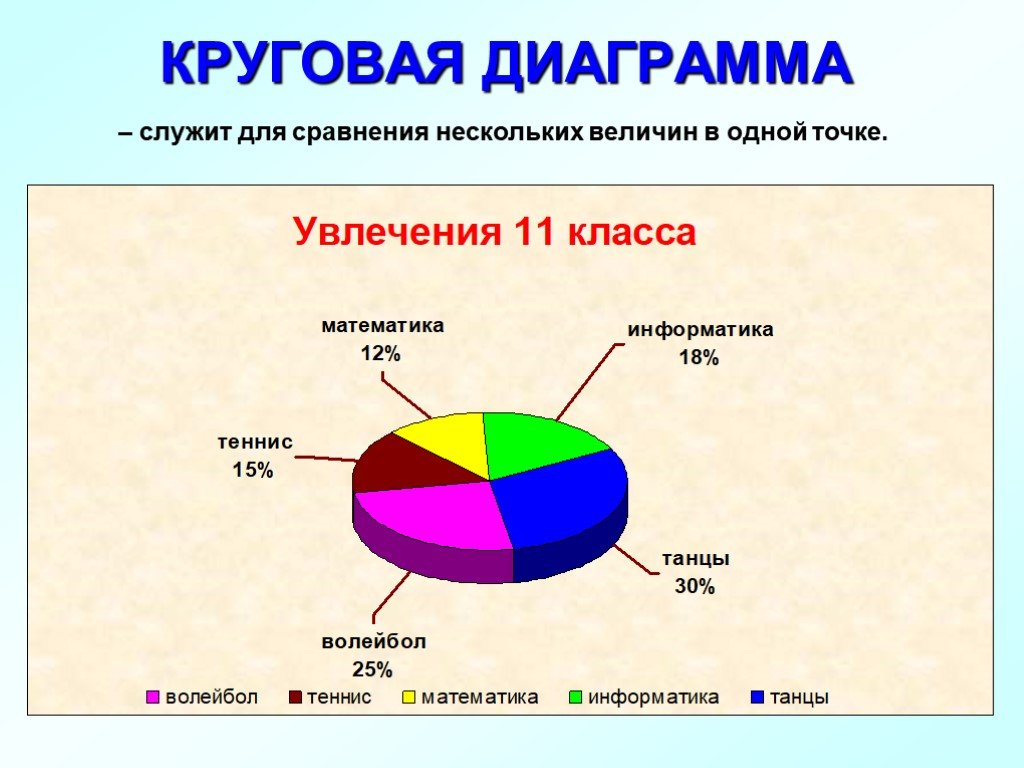
Диаграмма Парето

Это график, созданный экономистом Вильфредо Парето, который используется для поиска и упорядочения основных случаев потерь или проблем в компании.

Диаграмма основана на принципе Парето 80/20. Согласно этому принципу, 80% полученных результатов вызваны только 20% причин. Это означает, что небольшое количество проблем может привести к значительным убыткам для компании, в то время как многие мелкие проблемы могут иметь меньше последствий.

Как использовать диаграмму Парето

Первый шаг — определить проблему или потерю, которую вы хотите исследовать и решить. Затем необходимо организовать таблицу, в которую будут помещены данные о выбранной проблеме, с указанием количества записей ее возникновения. Например: проблема 1 случалась 15 раз, проблема 2 возникала 12 раз и так далее.

После записи этих данных вам необходимо выбрать, какие аспекты проблемы будут проанализированы. Эти данные также должны быть упорядочены по количеству вхождений, в порядке наибольшего вхождения в наименьшее

После того, как все числа введены, вы должны рассчитать, как часто происходит каждая ситуация. Именно эти данные должны быть использованы для построения диаграммы.

Узнайте больше о значении диаграммы Парето.

Гистограмма (Bar Histograms)

Источник Testent

Ещё один график из школьных учебников. Гистограммы используют для представления числовых данных одной категории и их изменения с течением времени. Пример — изменение численности населения страны за конкретный период.

Как и столбчатые диаграммы, гистограммы состоят из столбцов. Поэтому эти два вида графиков часто путают. Давайте разбираться.

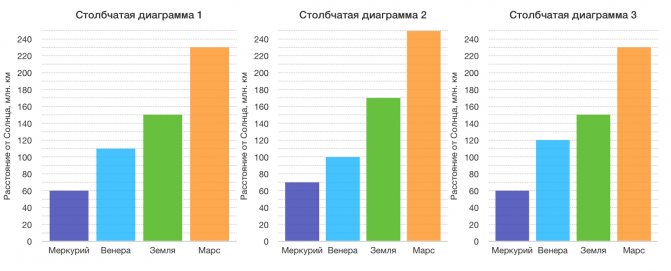
Столбчатая диаграмма

Гистограмма

Столбчатая диаграммаГистограмма

Есть расстояние между столбцами
Нет расстояния между столбцами

Применяются для сравнения категориальных данных
Применяются для выявления зависимости качественных данных

Если переставить местами столбцы, логика не нарушится. Венера и Земля — две категории, которые друг от друга не зависят.
Если в гистограмме наблюдаемых температур переставить местами столбцы, нарушится логика, так как рассматривается одна величина (температура), а не разные категории

Диаграмма Венна

Диаграмма Венна, также называемая Диаграммой множеств или логической диаграммой, была создана математиком Джоном Венном и широко используется в математике и статистике.

Это форма организации, которая использует числовые наборы, в которых данные группируются с использованием геометрических фигур, особенно кружков, которые соединяют наборы чисел или информации

Эта форма организации с геометрическими фигурами облегчает визуализацию и интерпретацию данных.

Диаграмма Венна помогает вам легко увидеть, какие данные присутствуют в одной ситуации и какие данные являются частью более чем одной ситуации за раз.

Также легко визуализировать, какое объединение (U) данных и какое пересечение (∩), то есть данные, общие для всех множеств. Смотрите пример:

Преимущества диаграмм

Преимущество диаграмм перед другими типами наглядной статистической информации заключается в том, что они позволяют быстро произвести логический вывод из большого количества полученных данных. Результаты расчётов, выполненных с помощью систем статистических вычислений, заносятся в таблицы. Они являются основой для последующего анализа или для подготовки статистического отчёта.

Сами по себе цифры в этих таблицах не являются достаточно наглядными, а если их много, они не производят достаточного впечатления. Кроме того, графическое изображение позволяет осуществить контроль достоверности полученных данных, так как на графике достаточно ярко проявляются возможные неточности, которые могут быть связаны с ошибками на каком-либо этапе проведения исследования. В основном все статистические пакеты позволяют графически предоставить полученную числовую информацию в виде различных диаграмм, а затем, если это необходимо, перенести их в текстовый редактор для сборки окончательного варианта статистического отчёта.

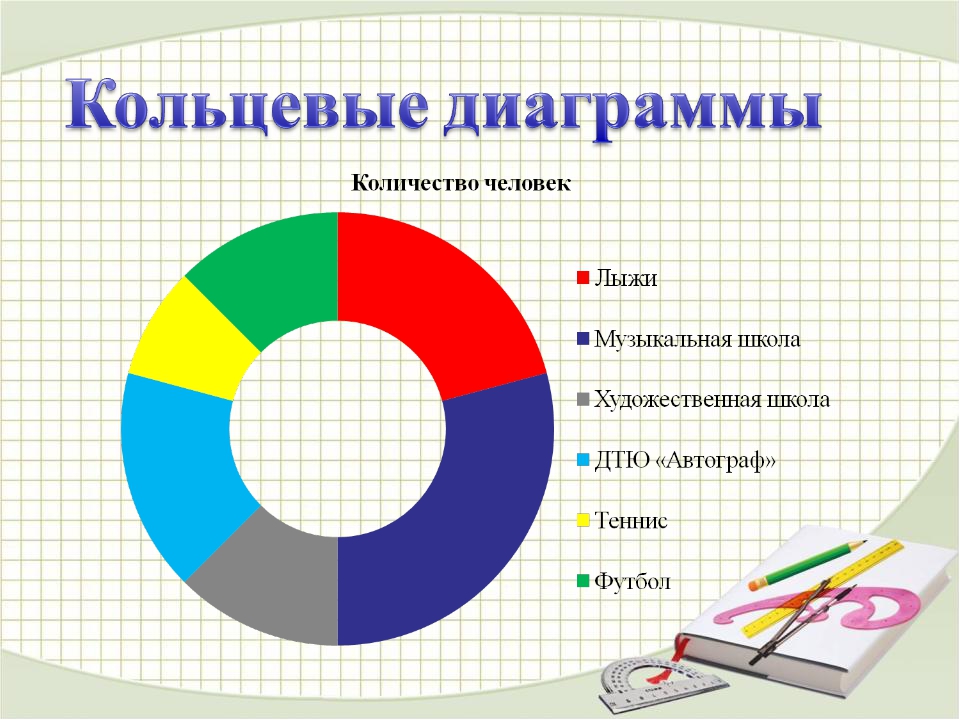
Интерактивная кольцевая диаграмма (Donut Transitions)

Источник GIPHY

Это та же кольцевая диаграмма, только анимированная. Интерактивная кольцевая диаграмма — один из лучших способов для выявления закономерностей между несколькими параметрами. Эффективна для представления части целого и анализа зависимости величин. При изменении анализируемых параметров изменяются и пропорции диаграммы. Пригодится тем, кто следит за динамикой изменения — например, изменения стоимости акций в результате каких-либо действий компании.

p.p1 {margin: 0.0px 0.0px 0.0px 0.0px; font: 12.0px ‘Helvetica Neue’; color: #454545}

Читать ещё: «Инфографика для СМИ»

Это одни из наиболее эффективных способов визуализации данных. Какие-то из них более привычны, о других пока мало кто знает. Новые виды графиков и диаграмм появляются вместе с новыми видами данных, что происходит непрерывно. Это значит, что скоро появятся более продвинутые способы визуализации.

Мнение автора и редакции может не совпадать. Хотите написать колонку для «Нетологии»? Читайте наши условия публикации.

Диаграмма Исикавы

Эта диаграмма, также называемая Диаграмма причин и следствий, Диаграмма Рыбьих костей или Диаграмма 6M, была создана Каору Исикавой.

Основная полезность заключается в том, чтобы быть инструментом для улучшения контроля качества путем выявления наиболее важных аспектов проблемы, чтобы решить ее и предотвратить ее повторение.

Диаграмма Исикавы используется компаниями и рабочими группами для проведения оценок и контроля качества их административных процессов и их работы.

Диаграмма помогает определить возможные причины проблем, которые можно классифицировать на шесть различных типов, называемых 6M: метод работы, сырье, рабочая сила, машины, измерения и окружающая среда.

Как использовать диаграмму Исикавы

Чтобы использовать диаграмму, вам нужно определить проблему, которую нужно решить, и собрать информацию о ней. Рабочая группа, задействованная в этой области, должна встретиться и использовать собранную информацию для сборки схемы 6M.

Диаграмма должна содержать: название, анализируемую проблему, центральную ось, которая указывает на желаемое решение, факторы, которые влияют, и возможные причины, связанные с проблемой.

Смотрите значение диаграммы Исикавы.

Диаграмма Нолана

Эта диаграмма, созданная политологом Дэвидом Ноланом, призвана помочь определить, какие политические взгляды преобладают в мышлении человека.

Нолан разработал диаграмму с учетом наиболее известных течений политической мысли. Он установил разделение на пять направлений: правое, левое, либеральное, тоталитарное и центральное.

Для использования диаграммы вам необходимо ответить на анкету, которая в настоящее время имеет разные версии. Из ответов на вопросник можно узнать, с каким течением политической мысли больше отождествляется.

Согласно Нолану, возможные результаты следующие:

правильная тенденция (предпочитает, чтобы в экономику не вмешивалось, и принимает некоторые моральные ограничения);
(предпочитая вмешательство в экономику и не соглашаясь с вмешательством в моральные ценности);
к центру (положение большего баланса между свободами и наложенными ограничениями);
либеральная тенденция (отождествление со свободой в экономических и моральных вопросах);
государственническая тенденция (поддерживает некоторые ограничения по экономическим и моральным вопросам).

Узнайте больше о диаграмме Нолана.

Зачем нужна нотация DFD?

Из чего состоит информационная система?
Что нужно, чтобы обработать информацию?

Процесс (англ. Process), т.е. функция или последовательность действий, которые нужно предпринять, чтобы данные были обработаны. Это может быть создание заказа, регистрация клиента и т.д. В названиях процессов принято использовать глаголы, т.е. «Создать клиента» (а не «создание клиента») или «обработать заказ» (а не «проведение заказа»). Здесь нет строгой системы требований, как, например, в IDEF0 или BPMN, где нотации имеют жестко определенный синтаксис, так как они могут быть исполняемыми. Но все же определенных правил стоит придерживаться, чтобы не вносить путаницу при чтении DFD другими людьми.
Внешние сущности (англ. External Entity). Это любые объекты, которые не входят в саму систему, но являются для нее источником информации либо получателями какой-либо информации из системы после обработки данных. Это может быть человек, внешняя система, какие-либо носители информации и хранилища данных.
Хранилище данных (англ. Data store). Внутреннее хранилище данных для процессов в системе. Поступившие данные перед обработкой и результат после обработки, а также промежуточные значения должны где-то храниться. Это и есть базы данных, таблицы или любой другой вариант организации и хранения данных. Здесь будут храниться данные о клиентах, заявки клиентов, расходные накладные и любые другие данные, которые поступили в систему или являются результатом обработки процессов.
Поток данных (англ. Data flow). В нотации отображается в виде стрелок, которые показывают, какая информация входит, а какая исходит из того или иного блока на диаграмме.

Линус Полинг диаграмма

Эта диаграмма, созданная ученым Линусом Полингом, также известна как Электронная Диаграмма Распределения или Принцип Ауфбау.

Он используется в химии для исследований, связанных с атомами. Этот метод исследования помогает понять свойства и характеристики атомов, их электронов и ионов, исходя из их энергетических подуровней.

Диаграмма считается одним из лучших объяснений того, как ионы и электроны распределяются по слоям атомов. С его помощью можно узнать, например, сколько слоев заполнено каждым из элементов атома.

Линус Полинг создал диаграмму из порядка распределения химических элементов в периодической таблице, которые организованы по количеству атомов, от самых маленьких до самых больших. Для этого он рассмотрел семь слоев атомов, которые представлены буквами K, L, M, N, O, P, Q. См. Ниже:

Смотрите более подробную информацию на диаграмме Линуса Полинга.

Ботанические диаграммы

См. также: Формула цветка

Диаграмма цветка. 1 — ось соцветия, 2 — прицветник, 3 — чашелистик, 4 — лепесток, 5 — тычинка, 6 — гинецей, 7 — кроющий лист.

Диаграмма цветка — схематическая проекция цветка на плоскость, перпендикулярную его оси и проходящую через кроющий лист и ось соцветия или побега, на котором сидит цветок. Она отражает число, относительные размеры и взаимное расположение частей цветка.

Построение диаграммы производится на основании поперечных разрезов бутона, так как при распускании цветка некоторые части могут опадать (например, чашелистики у маковых или околоцветник у винограда). Диаграмма ориентируется так, чтобы ось соцветия находилась вверху, а кроющий лист — внизу.

Обозначения на диаграмме цветка:

Ось соцветия — точка (если цветок верхушечный, ось соцветия не изображается);
Кроющий лист, прицветники и чашелистики — скобки с килем (фигурные скобки) различного размера;
Лепестки — круглые скобки;
Тычинки — почковидные фигуры, показывающие поперечный срез через пыльник (при большом числе тычинок возможно упрощенное изображение в виде затушёванного эллипса);
Пестик — круги или овалы, отражающие поперечный разрез завязи; внутри завязи показывают семязачатки маленькими кружками на соответствующих частях плодолистиков.
В случае срастания между собой частей цветка их значки на диаграмме соединяют линиями.
Также могут быть показаны дополнительные элементы цветка, например, нектарники или диски.

В диаграмме цветка могут быть изображены либо только те части, которые видны на разрезе (эмпирическая диаграмма цветка), либо также (пунктиром) недоразвитые и исчезнувшие в процессе эволюции части (теоретическая диаграмма цветка, составляемая на основании изучения нескольких эмпирических диаграмм).

Диаграмма побега отражает схему поперечного разреза через вегетативную почку.

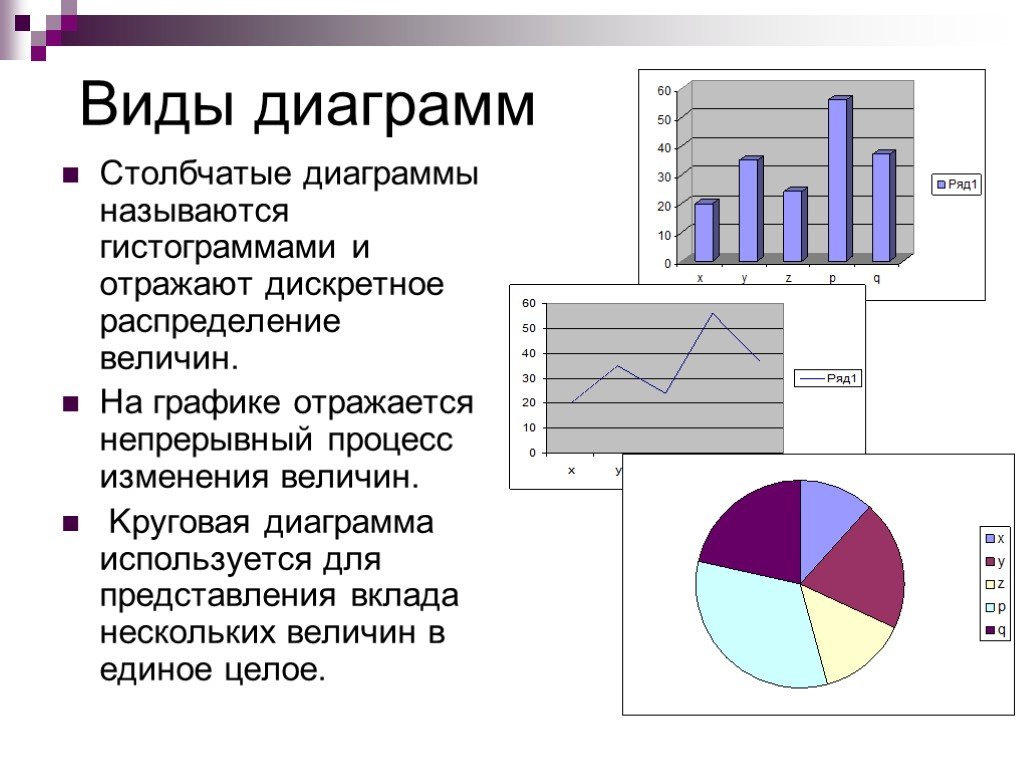
Столбчатая диаграмма (Column Chart)

Столбчатая диаграмма самая популярная

Она лучше всего подходит для сравнения значений, когда важно дать возможность сравнить каждое значение с каждым

Советы для столбчатой диаграммы

Не сравнивайте не более 7 значений.
Если вы показываете изменения во времени, всегда указывайте типа периода на горизонтальной оси и значение периода. (Например, к какому году или месяцу относится конкретное значение).
Начало точки отсчета для значений всегда начинается с нуля.
Не используйте обводку для столбцов.
Использовать столбчатую диаграмму для отображения тенденции изменения значения во времени можно, если значений не больше 20 и каждая точка имеет четкое, видимое значение.

Анимированные диаграммы

В некоторых случаях стандартных свойств обычных неподвижных диаграмм и графиков бывает недостаточно. С целью повышения информативности, возникла идея: к обычным свойствам статичных диаграмм (формам, цветам, способам отображения и тематики) добавить свойство подвижности и изменения с течением времени. То есть представить диаграммы в виде определённых анимаций.

Группой исследователей из Массачусетского технологического института был найден способ отображения информации с помощью анимированных диаграмм. Разработанные ими диаграммы представляют собой анимированные интерактивные графики, работающие в режиме реального времени. В качестве примера разработки были взяты данные о поведении и действиях пользователей одного из сетевых ресурсов.

Под руководством Френсиса Лама (Francis Lam) исследователи создали два интерфейса анимированных диаграмм Seascape и Volcano. Характер изменений изображения на диаграммах свидетельствует о социальной активности пользователей ресурса. Например, размер квадратиков указывает на объём темы — чем больше площадь квадратика, тем больше объём обсуждаемой темы. Эти квадратики находятся в постоянном движении, представляющем собой, похожие на гармонические, колебания в плоскости диаграммы, смещающиеся линейно в какую-либо из сторон. По скорости движения можно судить об активности темы, а амплитуда колебаний показывает разницу во времени появления новых сообщений. В любой момент, наведя курсор в плоскость диаграммы, её можно остановить, выбрать интересующий квадратик и открыть тему, которой он соответствует. Открывающаяся в этом же окне тема, также представляет собой анимацию из кружочков, движущихся в разные стороны в пределах окна по типу Броуновского движения. Кружочки символизируют действия отдельных пользователей, и скорость их движения напрямую зависит от активности этих пользователей.

Seascape и Volcano отличаются друг от друга цветовой гаммой и количеством визуализированных данных. У Volcano, в отличие от Seascape отсутствуют волнообразные колебания.

По словам разработчиков, построение графиков с помощью анимированных диаграмм, должно позволить человеку быстрее воспринимать информацию с них путём привлечения внимания пользователя диаграммой и быстрой передачей данных в мозг. В данный момент ещё не приняты какие-либо требования или стандарты к генерации анимированных диаграмм.

История возникновения диаграмм

График функции f(x)=x3 {\displaystyle f(x)={x^{3}}\!\ }

Во всех диаграммах используется функциональная зависимость как минимум двух типов данных. Соответственно, первыми диаграммами были обыкновенные графики функций, в которых допустимые значения аргумента соответствуют значениям функций.

Идеи функциональной зависимости использовались в древности. Она обнаруживается уже в первых математически выраженных соотношениях между величинами, а также в первых правилах действий над числами, в первых формулах для нахождения площади и объёма геометрических фигур. Вавилонские учёные, таким образом, несознательно установили, что площадь круга является функцией от его радиуса 4—5 тыс. лет назад. Астрономические таблицы вавилонян, древних греков и индийцев — яркий пример табличного задания функции, а таблицы, соответственно, являются хранилищем данных для диаграмм.

В XVII веке французские учёные Франсуа Виет и Рене Декарт заложили основы понятия функции и разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Также геометрические работы Декарта и Пьера Ферма проявили отчётливое представление переменной величины и прямоугольной системы координат — вспомогательных элементов всех современных диаграмм.

Первые статистические графики начал строить английский экономист У. Плейфер в работе «Коммерческий и политический атлас» 1786 года. Это произведение послужило толчком для развития графических методов в общественных науках.

Пространственные (трёхмерные) диаграммы

Трёхмерные диаграммы бывают двух видов.

«Отрёхмеренные» линейные, секторные и прочие. Имеют «солидный» вид, из-за этого часто используются в телевидении и бизнесе, однако тенденциозно показывают информацию: из-за незначащих поверхностей (боковой поверхности цилиндра в секторной, торца в столбцовой) и искажений трёхмерности закрашенная площадь не соответствует отображаемой величине. В частности, на втором рисунке искажения трёхмерности приводят к тому, что 22 % с виду почти того же размера, что и 35 %, а на третьем — 22 % почти вдвое меньше.
Особые диаграммы, не имеющие двухмерных аналогов: трёхмерная точечная диаграмма, столбцовая с матрицей столбцов и прочие. Многие из таких диаграмм бесполезны на бумаге или телевидении — когда пользователь не способен покрутить изображение мышью.

Линейная диаграмма (Line Charts)

Впервые с линейной диаграммой мы знакомимся с в школе, когда чертим график функции в системе координат. Линейная диаграмма отлично подходит , если —

набор ваших данных непрерывен;
количество значений больше 20;
вы хотите показать тренд изменений значений.

В этом типе диаграмм возможность сравнивать значения уходит на второй план, но все еще остается возможной, с помощью маркеров на графике, которые ставятся через одинаковые промежутки.

Советы для линейной диаграммы

Линейные диаграммы хорошо подходят, чтобы показать непрерывные данные, разбитые на равные по размеру интервалы.
Начинайте ось значений всегда с нуля. Если у вас появилась крутая идея начать не с нуля, скорее всего вы не правы.
Время в линейной диаграмме всегда идет слева направо.
Не пропускайте значения в интервалах данных, если они равны нулю или выбиваются из общих значениях. Например, определенные дни с нулевыми значениями, если во все остальные дни значения не нулевые.
Если вам нужно подчеркнуть тренд, удалите все подписи к значениям диаграммы.
Для подписей интервалов на диаграмме используйте наклон в 45 градусов слева направо.

Определение слова «График» по БСЭ:

График — геометрическое изображение функциональной зависимости при помощи линии на плоскости. Например, на рис. 1 изображен Г. изменения атмосферного давления со временем. Г. применяют как для наглядного изображения функциональных зависимостей и придания наглядности их исследованию, так и для быстрого фактического нахождения значений функций по значениям аргументов. Виды Г. очень разнообразны и зависят от того, какая система координат на плоскости положена в их основу. Если система координат выбрана, то Г. функции &fnof.(x) есть не что иное, как множество (или, как иначе говорят, «геометрическое место»)тех точек плоскости, координаты которых удовлетворяют уравнению y = &fnof.(x). В большинстве случаев Г. строят в декартовых прямоугольных координатах. На рис. 2 изображен Г. функции у = хІ — парабола, а на рис. 3 — Г. функции 7/0702697.tif представляющий полуокружность, начинающуюся в точке с координатами (-1, 0) и кончающуюся в точке с координатами (+1, 0).В прямоугольной системе координат масштабы по осям одинаковы. на практике от этого неудобного ограничения отказываются, выбирая разные масштабы по осям координат так, чтобы наилучшим образом использовать площадь листа бумаги, отводимую для Г. Употребляются также Г., основанные на других системах координат, например полярной. последняя особенно удобна для изображения функций углового аргумента (на рис. 4 даны построенные в полярной системе координат Г. распределения силы света, испускаемого по различным направлениям тремя типами дуговых фонарей). Иногда для упрощения вида Г. целесообразно принимать за координаты точки те или иные функции от переменных x и y. (О возникающем отсюда особом способе графического изображения функций см. ст. Номография.) Например, если значениям аргумента и функции — значениям (x, у) — ставить в соответствие точку с декартовыми координатами (lgx, lgy), то Г. функции у = хn при любом показателе n оказываются прямолинейными (рис. 5). Для быстрого вычерчивания подобных Г. служит полулогарифмическая и Логарифмическая бумага.Если Г. является прямой линией или дугой окружности, то его можно строить с помощью линейки или циркуля по двум, соответственно трём точкам. В остальных случаях для вычерчивания Г. приходится наносить на бумагу достаточно большое число принадлежащих ему точек, а затем проводить через эти точки линию Г. «на глаз».Эта операция, всегда несколько произвольная, во всяком случае имеет смысл лишь в предположении непрерывности функции. Если функция не только непрерывная, но и достаточно «гладкая» (т. е. её производные первых двух-трёх порядков меняются с изменением аргумента не слишком быстро), то при некотором навыке проведение Г. по точкам делается очень точно. Нанеся на один чертёж Г. функций y =&phi.₁(x) и y = &phi.₂(x), по точкам их пересечения можно определить корни уравнения &phi.₁(x) = &phi.₂(x) (см. рис. 3 в ст. Графические вычисления).Существует большое число самопишущих приборов, автоматически наносящих на бумагу Г. наблюдаемой функциональной зависимости, минуя её аналитическое выражение (например, Барограф, строящий Г. давления атмосферы в функции времени). Часто для графического изображения зависимости между величинами пользуются Диаграммами. В экономике и организации производства распространение получили контрольные и плановые Г. (см. Графические методы в управлении производством) и организационные Г., изображающие организационные связи и зависимости (например, схема управления предприятием). Во многих вопросах целесообразно одновременно рассматривать Г. нескольких различных функций, изображая их на одном и том же чертеже. Типичным примером таких Г. являются графики движения на транспорте.Рис. 1. График изменения атмосферного давления (в мм рт. ст.) за время от 24 апреля до 5 мая.Рис. 2. График функции у = хІ (парабола).Рис. 3. График функции 7/0702701.tif (полуокружность).Рис. 4. График в полярных координатах. Диаграмма направленности силы света трёх типов дуговых фонарей.Рис. 5. Графики функции у = xn при n = Ѕ, 1, 2. По осям координат отложены lgx и lgy.Графическое решение уравнения &phi.₁(x) = &phi.₂(x).

Пузырьковая диаграмма (Bubbles Chart)

Пузырьковая диаграмма — это диаграмма рассеяния к которой добавляет еще одно измерение. Это позволяет сравнивать значения между собой. Если пузырьки очень похожи по размеру, используйте метки.

Фактически мы могли бы добавить четвертую переменную путем цветокоррекции этих пузырьков или отображения их в виде круговых диаграмм, но это плохая идея и делать так не надо.

Хорошим примером пузырьковой диаграммы будет график, показывающий маркетинговые расходы по сравнению с прибылью. Стандартный график рассеяния может показать положительную корреляцию маркетинговых затрат и прибыли. Пузырьковая диаграмма покажет, что увеличение маркетинговых издержек съедает получаемую прибыль.

История возникновения диаграмм

График функции f(x)=x3 {\displaystyle f(x)={x^{3}}\!\ }

Анимированные диаграммы

Диаграмма дисперсии

Эта диаграмма используется для демонстрации значений набора данных и подтверждения связи, существующей между ними.

Она также называется диаграммой корреляции, поскольку размещение данных в диаграмме позволяет легко увидеть взаимосвязь между значениями или элементами.

Полученные значения отображаются на графике с координатами, организованными по горизонтальной оси и вертикальной оси. Точки, в которых соединяются данные, затем отмечаются.

Диаграмма используется как качественный инструмент для оценки отношений влияния или причины и следствия между элементами.

Например, связь между расходами и доходами, между показателями качества жизни и ожидаемой продолжительности жизни, а также связь между весом / ростом, ожидаемым для возраста.

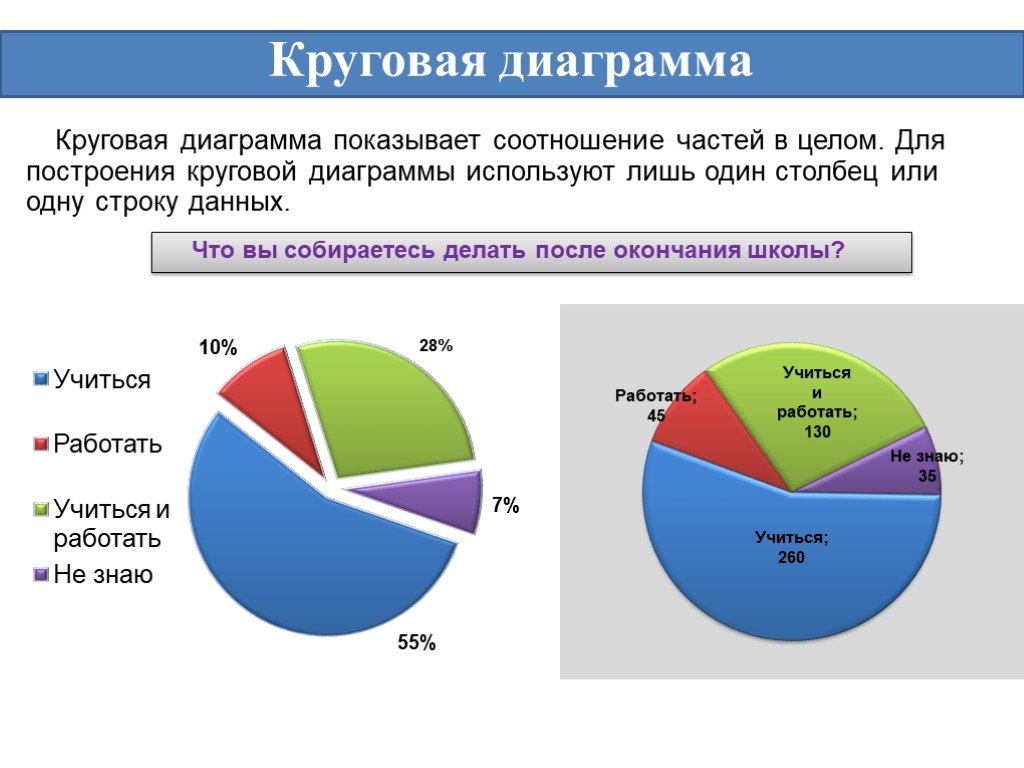
Что такое диаграмма:

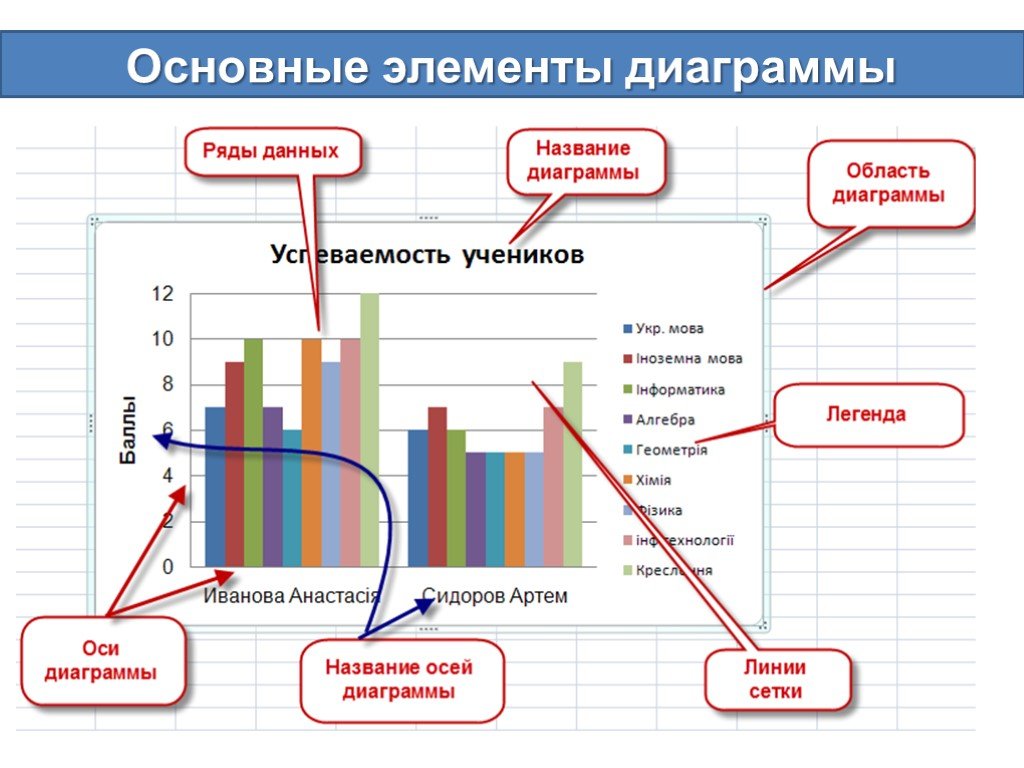
Диаграмма — это графическое представление, используемое для демонстрации упрощенной схемы или краткого описания предмета.

Обычно он состоит из ключевых слов или концепций, связанных линиями и стрелками, которые определяют обоснование, которому необходимо следовать, чтобы понять тему.

Слово происходит от латинского терминаgramma.atis . Они могут быть синонимами: графика, рисунок, схема, рисунок и эскиз.

Диаграммы часто используются в качестве учебного пособия, поскольку известно, что усвоение содержимого происходит легче с помощью схем и графических представлений. Это может также использоваться, чтобы продемонстрировать организационный поток компании.

Диаграмма — это имя, данное схеме, используемой в качестве основы для организации сценариев в фильмах или телевизионных программах.

Диаграмма, используемая в качестве глагола, имеет смысл организации и распространения графических элементов, используемых в публикации, таких как газеты, книги, плакаты и веб-сайты.