Деление (математика)

Способы деления

Имея два числа 12 и 4, мы можем разделить 12 на 4 различными способами.

С помощью сложения мы можем определить, сколько раз нужно взять 4 слагаемым для того, чтобы получить в сумме 12. Так, взяв 4 слагаемым 3 раза, находим в сумме:

4 + 4 + 4 = 12,

следовательно, 4 содержится в 12 три раза.
С помощью вычитания определяем, сколько раз можно из большего числа 12 вычесть меньшее 4. При этом мы вычитаем делитель до тех пор, пока это возможно. Так, вычитая последовательно из 12 по 4, имеем:

12 — 4 = 8
8 — 4 = 4
4 — 4 = 0

Отсюда находим, что можно вычесть 4 из 12 ровно три раза.

Деление есть сокращенное вычитание равных вычитаемых.
Наконец, посредством умножения, мы можем определить, на какое число нужно помножить 4, чтобы получить 12. Умножая последовательно 4 на 1, 2, 3, находим, что для того, чтобы получить 12, нужно 4 помножить на 3.

Деление на ноль

По определению числовых множеств N,Z,Q,R,C{\displaystyle \mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} } деление на число 0 не определено. Частное от деления какого-либо числа, отличного от нуля, на нуль не существует, так как в этом случае никакое число не может удовлетворять определению частного. Для определения данной ситуации полагают, что результат этой операции считается «бесконечно большим» или «равным бесконечности» (положительной или отрицательной, в зависимости от знака операндов). С геометрической точки зрения выполняется аффинное расширение числовой прямой. То есть привычная последовательность вещественных чисел «сжимается» так, чтобы можно было оперировать границами этой последовательности. В качестве границ (условных) введены две абстрактные бесконечно большие величины +∞,−∞{\displaystyle +\infty ,-\infty }. С точки зрения общей топологии выполняется двухточечная компактификация числовой прямой путем добавления двух идеализированных точек (бесконечностей с противоположным знаком). Пишут:

Топологическая картинка проективного расширения числовой прямой и точки 0/0

a=±∞{\displaystyle a:0=\pm \infty }, где a≠{\displaystyle a\neq 0.}

Если произвести проективное расширение множества вещественных чисел введением идеализированной точки ∞ {\displaystyle \infty ~},которая соединяет оба конца вещественной прямой, тогда с точки зрения общей топологии будет выполнена числовой прямой путем добавления бесконечности без знака. Дополним полученное множество чисел новым элементом ⊥={\displaystyle \perp =0/0}, в результате получится R⊥∞=R∪{∞,⊥}{\displaystyle \mathbb {R} _{\perp }^{\infty }=\mathbb {R} \cup \{\infty ,\perp \}}, на данной основе строится алгебраическая структура W=⟨R⊥∞,,1,+,⋅,⟩ {\displaystyle {\mathfrak {W}}=\langle \mathbb {R} _{\perp }^{\infty },0,1,+,\cdot ,/\rangle ~}называемая «» (Wheel). Термин был взят из-за схожести с топологической картинкой проективного расширения числовой прямой и точки 0/0. Внесенные изменения превращают эту алгебраическую систему в моноид как по операции сложения (с нулем в качестве нейтрального элемента), так и по операции умножения (с единицей в качестве нейтрального элемента). Это тип алгебры, где деление всегда определено. В частности, деление на ноль имеет смысл.

Существуют и другие алгебраические системы с делением на ноль. Например, «общие луга» (common meadows). Они чуть проще, так как не расширяют пространство, вводя новые элементы. Цель достигается как в колесах, трансформацией операций сложения и умножения, а также отказом от бинарного деления.

Деление многозначного числа на многозначное

При делении многозначного числа на многозначное поступаем точно так же, как поступали при делении многозначного числа на однозначное.

Разделяя число 37207 на 47, мы прежде всего определяем, из скольких цифр состоит частное. Частное меньше 1000 и больше 100, ибо 37207 меньше 47000 (47 × 1000) и больше 4700 (47 × 100), следовательно, частное состоит из сотен, десятков и единиц. Начиная с сотен, мы определяем каждую цифру частного отдельно:

Определяем сотни частного:

Делимое 37207 имеет 372 сотни. Десятки и единицы делимого не имеют влияния на цифру сотен частного. В частном может быть только 7 сотен, ибо 47 содержится в 372 семь раз; пишем в частном 700.

Умножая делитель на частное и вычитая из делимого, получаем первый остаток 4307.
Определяем десятки частного:

Остаток 4307 содержит 430 десятков. Единицы не имеют влияния на цифру десятков частного. Делитель 47 содержится в 430 девять раз; пишем в частном 90.

Умножая 90 на частное 47 и вычитая произведение 4330, получаем в остатке 77.
Определяем единицы частного:

47 содержится в 77 один раз. Пишем в частном 1 и, вычитая из 77 произведение единицы на делитель, получаем в остатке 30.

Итак, после деления имеем в целом частном 791 и в остатке 30.

Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, ход вычисления изобразится письменно:

словесно:

Отделяем в делимом от левой руки к правой столько цифр, чтобы делитель мог содержаться в отделенной части делимого. В данном случае отделяем 3 цифры, 47 содержится в 372 семь раз; умножаем делитель 47 на 7, цифру частного, и, вычитая произведение 47 × 7 = 329 из 372, получаем в остатке 43.
К остатку 43 сносим 0, следующую цифру делимого; 47 содержится в 430 девять раз, пишем в частном 9. Умножая 47 на 9 и вычитая произведение 423 из 430, получаем остаток 7.
Сносим к остатку следующую цифру частного 7; 47 содержится в 77 один раз. Пишем единицу в частном.

Умножая ею делитель и вычитая 47 из 77, получаем в остатке 30 и в целом частно 791.

Пример. Разделить 671064 на 335. Деление изобразится письменно:

словесно:

Отделяем 671 в делимом; 335 содержится в 671 два раза, пишем в частном 2. Умножая 335 на 2 и вычитая произведение 670, получим в остатке 1.
Сносим 0, следующую цифру делимого; 335 не содержится в 10, — пишем для второй цифры частного 0.
Сносим 6, следующую цифру делимого; 335 не содержится в 106, — пишем для третьей цифры частного 0.
Сносим следующую цифру делимого 4; 335 содержится в 1064 три раза, — пишем в частном 3. Умножая делитель на 3 и вычитая произведение, получим в остатке 59 и в целом частном 2003.

Из предложенных примеров выводим следующее правило:

Чтобы разделить многозначное число на однозначное или многозначное, нужно отделить в делимом от левой руки к правой столько цифр, сколько их находится в делителе. Если делитель не содержится, отделяют в делимом одной цифрой больше. Разделив отделенное число на делитель, получают первую цифру частного, умножают ей делитель и полученное произведение вычитают из отделенной части делимого.
К остатку сносят следующую цифру делимого и снова задаются.
Если при этом получается число меньше делителя, пишут в частном нуль, сносят следующую цифру и снова задаются.
Получив новую цифру частного, поступают с нею так же, как и с первой цифрой.
Деление продолжают до тех пор, пока не снесут всех цифр делимого и не получат таким образом всех цифр частного.

Всякий раз, когда приходится делить, нужно задаваться в частном такою цифрой, чтобы остаток был меньше делителя

Чтобы легче найти такую цифру частного, при делении многозначного числа на многозначное обращают внимание на одну или две старшие цифры делителя и задаются только ими в соответствующей части делимого. При этом в делимом и в делителе отделяют от правой руки к левой одинаковое число цифр

Так, определяя, сколько раз содержится 6373 в 27302, мы задаемся четырьмя, ибо 6 в 27 содержится 4 раза.

Полученная при этом цифра частного будет или равна или больше действительной. В последнем случае ее нужно уменьшить.

Иногда при делении не подписывают произведение цифры частного на делитель, а, подразумевая его в уме, подписывают один остаток. Сокращая таким образом деление, изображают его письменно:

словесно:

8 в 43 содержится 5 раз; 5-ю 8 — сорок. Вычитая 40 из 43, получаем в остатке 3.
Сносим 2; 8 в 32 содержится 4 раза; 4-жды 8 составляет 32. Вычитая 32, получим в остатке нуль.
Сносим 8; 8 в 8-ми содержится 1 раз, 1-жды 8 составляет 8. Вычитая 8, получаем в остатке нуль и в частном 541.

Свойства

Операция деления на числовых множествах N,Z,Q,R,C{\displaystyle \mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} } имеет следующие основные свойства:

Деление не перестановочно (не коммутативно) — от перемены мест аргументов частное изменяется:

ab≠ba;{\displaystyle a:b\neq b:a;}

Деление не ассоциативно — при последовательном выполнении деления трёх или более чисел последовательность выполнения операций имеет значение, результат изменится:

(ab)c≠a(bc);{\displaystyle (a:b):c\neq a:(b:c);}

Деление дистрибутивно справа, это — свойство согласованности двух бинарных операций, определённых на одном и том же множестве, также известно, как распределительный закон :

Дистрибутивность: (a+b)x=(ax)+(bx), x≠;{\displaystyle (a+b):x=(a:x)+(b:x),~x\neq 0;}

Относительно деления в множестве A{\displaystyle A} существует единственный нейтральный элемент справа (число 1{\displaystyle 1}), деление на единицу (или нейтральный элемент) даёт число, равное исходному:

Нейтральный элемент справа: x1=x;{\displaystyle x:1=x;}

Относительно деления в множестве A{\displaystyle A} существует единственный обратный элемент, получаемый делением единицы на число, что даёт число, обратное исходному:

Обратный элемент: 1x=1x=x−1, x≠;{\displaystyle 1:x={\frac {1}{x}}=x^{-1},~x\neq 0;}

Относительно деления в множестве A{\displaystyle A} существует единственный нулевой элемент слева — число 0{\displaystyle 0}, делённое на любое число, даёт нуль:

Нулевой элемент слева: x=,∃∈A, x≠;{\displaystyle 0:x=0,\quad \exists 0\in A,~x\neq 0;}

По правилам обычной арифметики деление на ноль 0{\displaystyle 0} (нулевой элемент) не определено;

Деление на ноль: x=∞,∃∈A, x≠;{\displaystyle x:0=\infty ,\quad \exists 0\in A,~x\neq 0;}

Деление на противоположный элемент даёт минус единицу:

x(−x)=−1,∃!−x∈A, x≠{\displaystyle x:(-x)=-1,\quad \exists !-x\in A,~x\neq 0.}.

Результат деления не всегда является определённым для множеств натуральных чисел N{\displaystyle \mathbb {N} } и целых чисел Z{\displaystyle \mathbb {Z} }, чтобы получить натуральное или целое число в результате деления, делимое должно быть кратно делителю. Невозможно в рамках этих чисел получить дробный результат. В этом случае говорится о делении с остатком. То есть деление на этих множествах есть частичная бинарная операция.

Операция деления, определённая на множествах (в полях) рациональных Q{\displaystyle \mathbb {Q} }, вещественных R{\displaystyle \mathbb {R} } и комплексных чисел C{\displaystyle \mathbb {C} }, даёт число (частное), принадлежащее этому же множеству, следовательно, множества Q−,R−,C−{\displaystyle \mathbb {Q_{-0}} ,\mathbb {R_{-0}} ,\mathbb {C_{-0}} } замкнуты относительно операции деления (в точке 0 имеется разрыв второго рода — следовательно кольца рациональных, вещественных и комплексных чисел разомкнуты относительно операции деления).

В математических выражениях операция деления имеет более высокий приоритет по отношению к операциям сложения и вычитания, то есть она выполняется перед ними.

Различные случаи при делении

При делении целых чисел бывают два случая:

Разделяя 12 на 4, мы находим в частном 3. Делитель 4 содержится ровно 3 раза в делимом 12. Вычитая последовательно из 12 по 4, мы могли вычесть число 4 ровно три раза и не получили никакого остатка. В этом случае говорят, что деление совершилось нацело или без остатка. Умножив частное 3 на делитель 4, получаем делимое 12.
Разделяя 26 на 8, мы при последовательном вычитании получаем:

26 — 8 = 18
18 — 8 = 10
10 — 8 = 2

Далее нельзя продолжать вычитания, потому что из 2 нельзя вычесть делитель 8. Число 2 называют остатком.

Остаток всегда меньше делителя. В этом случае говорят, что деление не совершается нацело или деление совершается с остатком.

Разделяя 26 на 8, мы могли вычесть делитель 8 три раза, и у нас получился остаток 2. Число 3 мы будем называть целым частным. Целое частное есть не полное частное, ибо оно не выражает вполне, сколько раз меньшее число содержится в большем. Число 8 не содержится в 26 ровно 3 раза. В этом случае говорят: число 8 содержится в 26 три раза и еще получается остаток. Умножив делитель 8 на целое частное 3, мы не получим делимого 26, а число 24 — меньшее делимого. Чтобы получить делимое, нужно к этому произведению прибавить еще остаток 2.

Целое частное иногда называют просто частным.

Итак, при делении мы имеем два случая:

Деление нацело или без остатка. Когда делитель содержится в делимом ровное число раз, тогда деление совершается нацело или без остатка. Частное выражает, сколько раз делитель содержится в делимом. Делимое равно делителю, умноженному на частное. В этом случае деление есть действие в котором по данному произведению и одному из производителей находится другой производитель.

Если дается произведение и множимое, отыскивают множитель, то есть число равных слагаемых; если дается произведение и множитель, отыскивают множимое, то есть величину равных слагаемых.
Деление с остатком. Когда делитель не содержится в делимом ровное число раз, тогда деление не совершается нацело, или деление совершается с остатком. Остаток всегда меньше делителя и делимое равно произведению делителя на целое частное, сложенное с остатком.

При делении целых чисел делимое всегда уменьшается во столько раз, сколько в делителе единиц, поэтому деление есть действие, обратное умножению.

Свойства

Деление антикоммутативно — от перемены мест аргументов частное изменяется:

Антикоммутативность: ab≠ba;{\displaystyle a:b\neq b:a;}

Деление антиассоциативно — при последовательном выполнении деления трёх или более чисел последовательность выполнения операций имеет значение, результат изменится:

Антиассоциативность: (ab)c≠a(bc);{\displaystyle (a:b):c\neq a:(b:c);}

Деление дистрибутивно справа, это — свойство согласованности двух бинарных операций, определённых на одном и том же множестве, так-же известно, как распределительный закон :

Дистрибутивность: (a+b)x=(ax)+(bx), x≠;{\displaystyle (a+b):x=(a:x)+(b:x),~x\neq 0;}

Нейтральный элемент справа: x1=x;{\displaystyle x:1=x;}

Относительно деления в множестве A{\displaystyle A} существует единственный обратный элемент, получаемый делением единицы на число, что даёт число обратное исходному:

Обратный элемент: 1x=1x=x−1, x≠;{\displaystyle 1:x={\frac {1}{x}}=x^{-1},~x\neq 0;}

Относительно деления в множестве A{\displaystyle A} существует единственный нулевой элемент слева, число 0{\displaystyle 0} делённое на любое число даёт нуль:

Нулевой элемент слева: x=,∃∈A, x≠;{\displaystyle 0:x=0,\quad \exists 0\in A,~x\neq 0;}

По правилам обычной арифметики деление на ноль 0{\displaystyle 0} (нулевой элемент) не определено;

Деление на ноль: x=∞,∃∈A, x≠;{\displaystyle x:0=\infty ,\quad \exists 0\in A,~x\neq 0;}

Деление на противоположный элемент даёт минус единицу:

x(−x)=−1,∃!−x∈A, x≠{\displaystyle x:(-x)=-1,\quad \exists !-x\in A,~x\neq 0.}.

Операция деления определённая на множествах (в полях) рациональных Q{\displaystyle \mathbb {Q} }, вещественных R{\displaystyle \mathbb {R} } и комплексных чисел C{\displaystyle \mathbb {C} } даёт число (частное) принадлежащее этому-же множеству, следовательно множества Q−,R−,C−{\displaystyle \mathbb {Q_{-0}} ,\mathbb {R_{-0}} ,\mathbb {C_{-0}} } замкнуты относительно операции деления (в точке 0 имеется разрыв второго рода — следовательно кольца рациональных, вещественных и комплексных чисел разомкнуты относительно операции деления).

Деление в алгебре

В отличие от простейших арифметических случаев на произвольных множествах и структурах деление может быть не только не определено, но и обладать множественностью результата.

Обычно в алгебре деление вводится через понятие единичного и обратного элементов. Если единичный элемент вводится однозначным образом (обычно аксиоматически или по определению), то обратный элемент часто может быть как левым (x−1∗x=e{\displaystyle x^{-1}*x=e}), так и правым (x∗x−1=e{\displaystyle x*x^{-1}=e}). Эти два обратных элемента могут по отдельности существовать или не существовать, равняться или не равняться друг другу.

К примеру, отношение матриц определяется через обратную матрицу, при этом даже для квадратных матриц может быть:

B−1⋅A≠A⋅B−1{\displaystyle B^{-1}\cdot A\neq A\cdot B^{-1}}.

Отношение тензоров в общем случае не определено.

Умножение и деление

Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение. В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.

Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.

Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление в алгебре

B−1⋅A≠A⋅B−1{\displaystyle B^{-1}\cdot A\neq A\cdot B^{-1}}.

Отношение тензоров в общем случае не определено.

Правило встречается в следующих упражнениях:

2 класс

Страница 59. Вариант 2. № 1,
Моро, Волкова, Проверочные работы

Страница 66. Вариант 1. Тест 2,
Моро, Волкова, Проверочные работы

Страница 67. Вариант 2. Тест 2,
Моро, Волкова, Проверочные работы

Страница 59,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 60,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 62,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 73,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 103,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

3 класс

Страница 29,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 48,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 71,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 12. Вариант 1. Тест,
Моро, Волкова, Проверочные работы

Страница 18. Вариант 1. № 4,
Моро, Волкова, Проверочные работы

Страница 32. Вариант 1. № 2,
Моро, Волкова, Проверочные работы

Страница 43. Вариант 2. Тест 1,
Моро, Волкова, Проверочные работы

Страница 16,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 46,
Моро, Волкова, Рабочая тетрадь, 2 часть

4 класс

Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 90,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 6,
Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 26,
Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 48,
Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 47,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 82,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

5 класс

Задание 441,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 673,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 818,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Упражнение 36,
Мерзляк, Полонский, Якир, Учебник

Упражнение 1,
Мерзляк, Полонский, Якир, Учебник

Упражнение 520,
Мерзляк, Полонский, Якир, Учебник

Упражнение 656,
Мерзляк, Полонский, Якир, Учебник

Упражнение 657,
Мерзляк, Полонский, Якир, Учебник

Упражнение 673,
Мерзляк, Полонский, Якир, Учебник

Упражнение 1050,
Мерзляк, Полонский, Якир, Учебник

Деление физических величин

Единица измерения физической величины имеет определённое наименование (размерность): для длины (L) — метр (м), для времени (T) — секунда (с), для массы (M) — грамм (г) и так далее. Поэтому, результат измерения той или иной величины представляет собой не просто число, а число с наименованием. Наименование представляет собой самостоятельный объект, который равноправно участвует в операции деления. При производстве операции деления над физическими величинами, делятся как сами числовые составляющие, так и их наименования.

Помимо размерных физических величин существуют безразмерные (количественные) величины, которые формально являются элементами числовой оси, то есть числами, не имеющие привязки к определённым физическим явлениям (измеряются «штуками», «разами» и тому подобное). При делении чисел представляющих собой физические величины на безразмерную величину, делимое число изменяется по величине и сохраняет единицу измерения. Например если взять 15 гвоздей и разложить в 3 коробки, то в результате деления получим 5 гвоздей в каждой коробке:

15 гв3=5 гв.{\displaystyle 15~{\text{гв}}:3=5~{\text{гв}}.}

Деление разнородных физических величин надо рассматривать как нахождение новой физической величины, принципиально отличающейся от величин, которые мы делим. Если физически возможно создание такого частного, например, при нахождении работы, скорости или других величин, то эта величина образует множество, отличное от начальных. В этом случае композиции этих величин присваивается новое обозначение (новый термин), например: плотность, ускорение, мощность и прочее.

Например, если разделить длину L=8 м {\displaystyle L=8~{\text{м}}~}на время T=2 с, {\displaystyle T=2~{\text{с}},~}соответствующие одному физическому процессу, то получится именованное число (физическая величина) соответствующее этому же физическому процессу, которая называется «скорость» и измеряется в «метрах в секунду»: V=4 м/с.{\displaystyle V=4~{\text{м/с}}.}

V=LT=8 м2 с=4 (м : с)=4 м/с.{\displaystyle V=L:T=8~{\text{м}}:2~{\text{с}}=4~~{\text{(м : с)}}=4~{\text{м/с}}.}

При описании математическими средствами физических процессов немаловажную роль играет понятие однородности, которое означает например, что «1 кг муки» и «1 кг меди» принадлежат разным множествам {мука} и {медь} соответственно и не могут быть непосредственно разделены. Также понятие однородности предполагает, что делимые величины принадлежат одному физическому процессу. Недопустимо делить, например скорость лошади на время собаки.

Выполнение деления

Пример пошагового деления числа 8 на число 4 на числовой прямой.

Деление является гипероператором вычитания и сводится к последовательному вычитанию. :

ab=hyper-2⁡(a,b)=hyper⁡(a,−2,b)=a(−2)b=c.{\displaystyle a:b=\operatorname {hyper-2} (a,b)=\operatorname {hyper} (a,-2,b)=a^{(-2)}b=c.}

a(−2)b=ab=a−b−b−⋯−b⏟c.{\displaystyle a{^{(-2)}}b=a:b=a\underbrace {-b-b-\dots -b} _{c}.}

где: −b−b−⋯−b{\displaystyle -b-b-\dots -b} — последовательность операций вычитания, выполненная c{\displaystyle c} раз.

При практическом решении задачи деления двух чисел необходимо свести её к последовательности более простых операций: вычитание, сравнение, перенос и др. Для этого разработаны различные методы деления, например для чисел, дробей, векторов и др. В русскоязычных учебниках математики в настоящее время используется алгоритм деления столбиком. При этом следует рассматривать деление как процедуру (в отличие от операции).

Схема, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком:

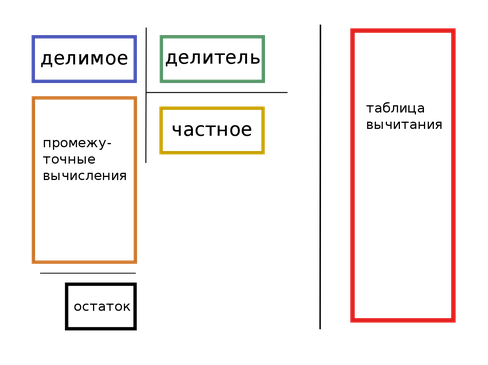Деление столбиком

Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места.

Примерный алгоритм процедуры деления натуральных чисел столбиком

Как видим, процедура достаточно сложная, состоит из относительно большого числа шагов и при делении больших чисел может занять продолжительное время. Данная процедура применима к делению натуральных и целых (с учётом знака) чисел. Для других чисел используются более сложные алгоритмы.

Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно пользоваться таблицей вычитания соответствующей данному основанию P{\displaystyle P} системы счисления.

Пример деления натуральных чисел в двоичной, десятичной и шестнадцатеричной системах счисления:

     110010│101   │    0 — 0           50800│25    │    0 — 0           CD530│A8     │    0 — 0
     101   │1010  │ -101 — 1           50   │2032  │  -25 — 1           A8   │138E   │  -A8 — 1
       10                               08         │  -50 — 2           255          │ -150 — 2
                                                │  -75 — 3           1F8          │ -1F8 — 3
       101                               80        │ -100 — 4            5D3         │ -2A0 — 4
       101                               75        │  ... — ...          540         │ -348 — 5
         00                               50                              930        │ -3F0 — 6
                                         50                              930        │ -498 — 7
          0.                               0.                               0.       │ -540 — 8
                                                                                     │ -5E8 — 9
                                                                                     │ -690 — A
                                                                                     │ -738 — B
                                                                                     │ -7E0 — C
                                                                                     │ -888 — D
                                                                                     │ -930 — E

Формы записи и терминология

Символы деления в математике

Деление записывается с использованием одного из «знаков деления» — «÷, , , −{\displaystyle \div ,~/,~:,~-}» между аргументами, такая форма записи называется инфиксной нотацией. В данном контексте знак деления является бинарным оператором. Знак деления не имеет специального названия, как например знак сложения, который называется «плюс».

Самый старый из используемых символов видимо — косая черта (/). Впервые его использовал английский математик Уильям Отред в своём труде «Clavis Mathematicae» 1631 г.
Немецкий математик Лейбниц предпочитал знак в виде двоеточия (:) Этот символ он использовал в своём труде Acta eruditorum 1684 г. До Лейбница этот знак был использован англичанином Джонсоном в 1633 году в своей книге, но как знак дроби, а не деления в узком смысле.
Йоханн Ран ввёл знак обелюс (÷) в качестве знака деления, она появилась в его книге «Teutsche Algebra» 1659 г. Знак Рана часто называют «английским знаком деления».

В русскоязычных учебниках математики в основном используется знак в виде двоеточия (:). Косая черта (/) используется в компьютерной нотации. Результат записывается с использованием знака равенства «={\displaystyle =}», например:

ab=c{\displaystyle a:b=c} ;

63=2{\displaystyle 6:3=2} («шесть разделить на три равно два») ;

655=13{\displaystyle 65:5=13} («шестьдесят пять разделить на пять равно тринадцать») .

В математических выражениях часто в качестве знака деления используется дробная черта. На письме знак деления очень похож на другие письменные символы. Следует внимательнее разбирать выражение, чтобы не возникло ошибочной идентификации символа.