Действительные числа, определение, примеры

Пополнение рациональных чисел

Вещественные числа могут быть построены как пополнение множества рациональных чисел по отношению к обычной метрике . Рассмотрим семейство фундаментальных последовательностей рациональных чисел Назовём две последовательности и эквивалентными, если существует предел

Введённое таким образом отношение является отношением эквивалентности и следовательно разбивает рассматриваемое семейство на непересекающиеся классы эквивалентности. Отождествляя рациональное число с фундаментальной последовательностью , можно считать, что полученное фактор-множество содержит рациональные числа. Зададим на фактор-множестве бинарные операции и порядок следующим образом:

Непосредственно проверяется, что это построение корректно и полученная таким образом четвёрка является полным упорядоченным полем. В силу изоморфизма полных упорядоченных полей эту структуру можно называть полем действительных чисел и более того считать, что

Какие числа называются действительными?

Рубрики Алгебра

__Большие и маленькие, длинные и короткие, целые и дробные, рациональные и не очень — все они составляют одно огромное множество — множество действительных чисел. и 100, два и корень из двух, 1.618, 3.14, -12 и даже +100500 – все это действительные числа.

__Давайте же строго научно определим, какие числа называются действительными, а также попытаемся ответить на следующие часто встречающиеся вопросы:

является ли ноль действительным числом?

что такое целая часть действительного числа?

какими свойствами обладает модуль действительного числа?

__На самом деле эти вопросы не такие уж сложные, как может показаться на первый взгляд. Для начала определимся с самим понятием действительного числа.

Определение действительного числа

Определение1:  Действительное число (также его часто называют вещественным ) — это любое положительное число, отрицательное число или нуль.

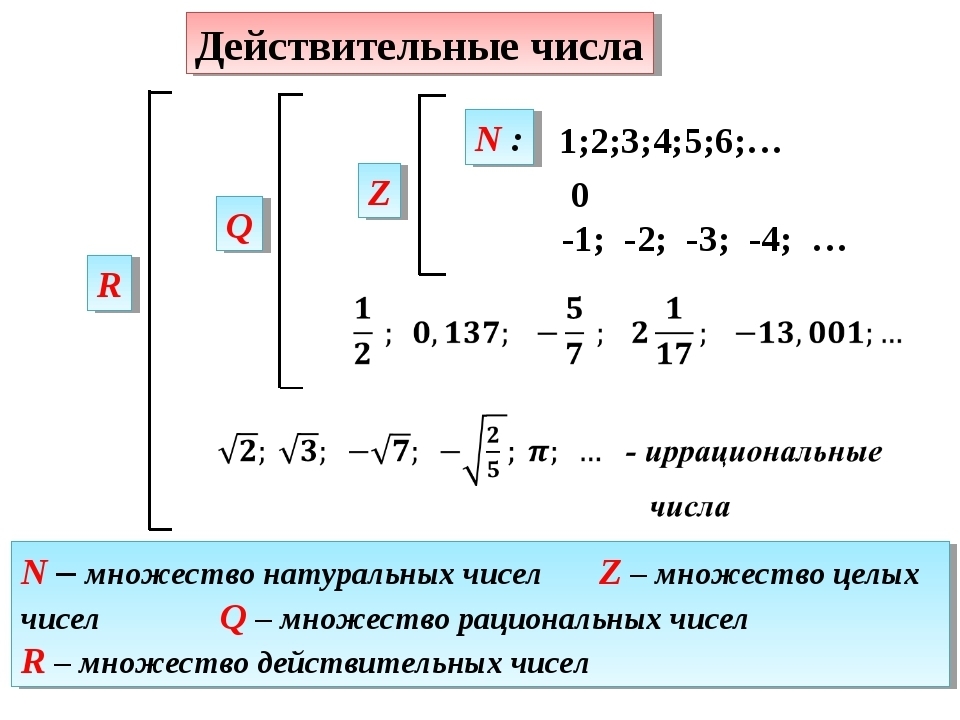
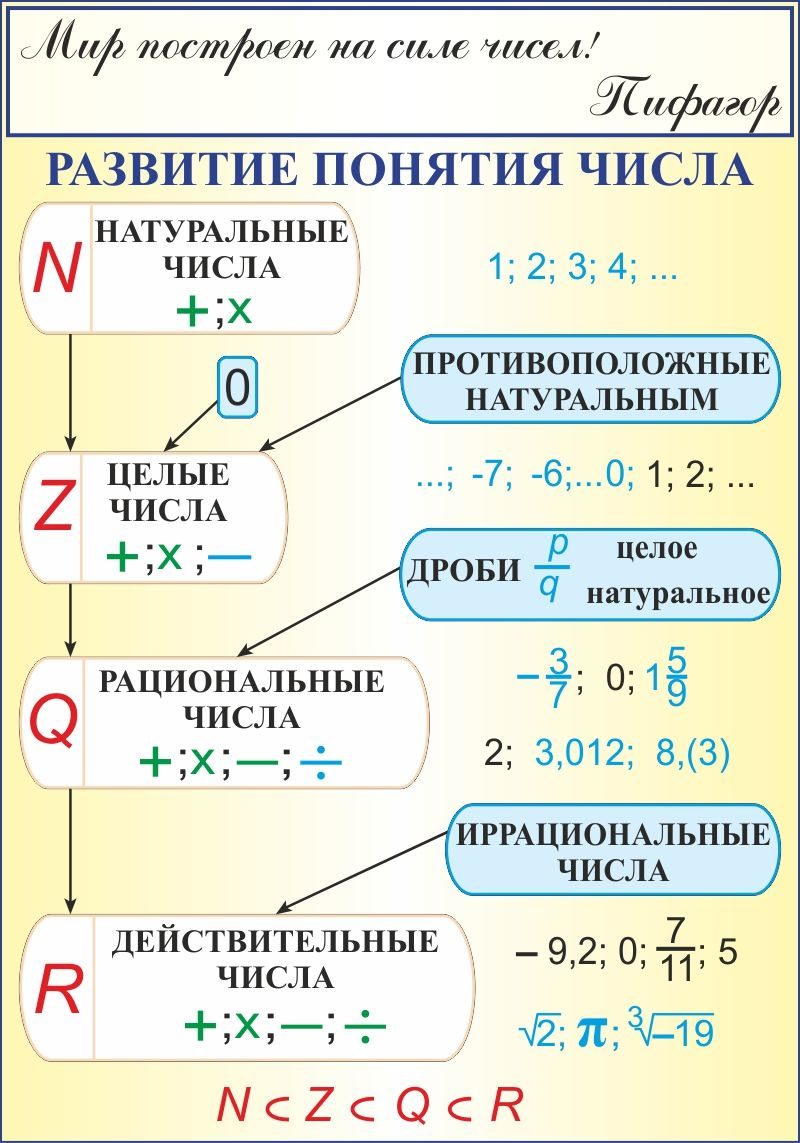
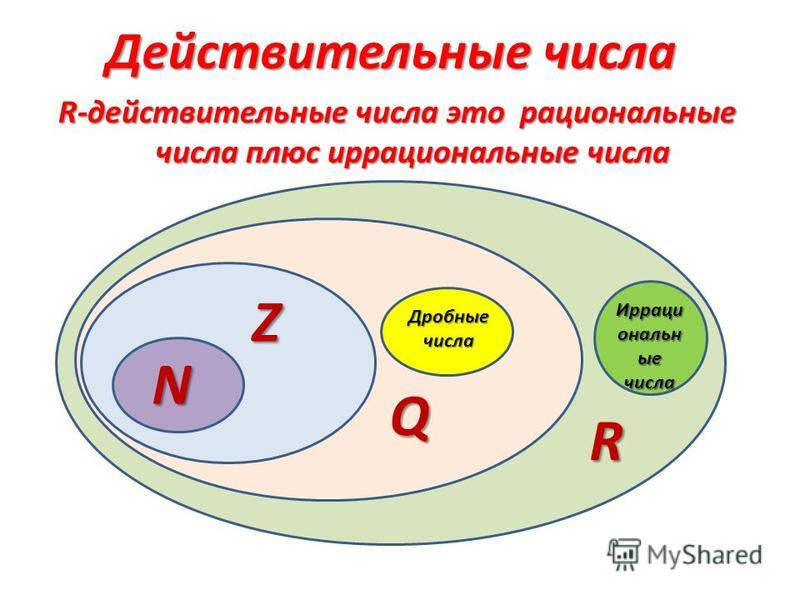
Определение2: Множеством действительных чисел называют объединение множеств рациональных и иррациональных чисел.

 Строго Научное Определение:

Положительным действительным (вещественным) числом «α» называют бесконечную десятичную дробь N, n₁ n₂… n_k,… не оканчивающуюся последовательностью девяток.

Отрицательным действительным числом (вещественным) называют бесконечную десятичную дробь вида «α» = — N, n₁ n₂… n_k. . . не оканчивающуюся последовательностью девяток.

__Добавив к отрицательным и положительным действительным числам число 0 получим полное множество действительных чисел

Обратите внимание на нюанс, указанный в Строго Научном Определении. Все дело в том, что любую конечную десятичную дробь N, n1 n2… nk можно записать в виде бесконечной десятичной дроби N, n1 n2… nk 000…0… оканчивающейся «хвостом» из нулей

Например:

 1,1=1,1000…000….

При этом дроби 1,1 соответствует последовательность пар десятичных приближений :

(1,1; 1,2) , (1,10; 1,11) , (1,100; 1,101) и т. д. Заметьте, все приближения по недостатку для этой дроби одинаковы 1,1=1,10=1,100=…

Рассмотрим теперь бесконечную десятичную дробь 1,09999…. Для неё последовательность пар десятичных приближений имеет вид (1,09; 1,10), (1,099; 1,100) и т. д.

В этом случае совпадают все десятичные приближения по избытку: 1,10=1,100=…

__Обратите внимание, приближения по недостатку для первой дроби совпадают с приближениями по избытку для дроби второй. Таким образом обе дроби геометрически выражают одну и ту же длину

Именно поэтому, (для того чтобы не обозначать одно и то же число двумя способами ) условились не использовать бесконечных десятичных дробей, оканчивающихся бесконечной последовательностью девяток. Такие дроби всегда можно заменить конечной десятичной дробью, поставив вместо девяток нули и увеличив на 1 цифру, стоящую перед ними. Например :

 4,4749999…99..=4,475000…0..

 99,999999999…=100,00000000…

 Еще один нюанс: последовательность из девяток должна быть именно бесконечной,

 99,999 ≠ 100.

Давайте подведем итог.

Действительным ( иногда его называют вещественным) числом называется любое целое число, а также все конечные и бесконечные дроби.

Дроби, оканчивающиеся бесконечной последовательностью девяток для удобства использования округляют в большую сторону.

Различают положительные действительные числа, отрицательные действительные числа и ноль.

Множество действительных чисел разделяется на множества рациональных и иррациональных чисел.

__Надеюсь вы разобрались с понятием действительного числа и со всеми теми особенностями, которые присущи таким числам. Если же вам по прежнему что-то непонятно — добро пожаловать в Вопрос-Ответник.

Множества чисел

Зачем вообще нужно определение разных множеств чисел? Ведь было бы куда проще просто взять число и начать выполнять какие-либо действия. Но все не так просто.

Вы наверняка уже сталкивались со сложностью вычисления дробей? Сложение, умножение, деление и вычитания – все действия с дробями отличаются от действий с привычными нам натуральными числами, ведь они относятся другому подмножеству.

То же касается, к примеру, отрицательных чисел. Складывать их с положительными можно, но только по отдельным правилам. Поэтому в вопросе множеств чисел нужно разбираться с самого начала.

Все существующие числа можно разделить на действительные и комплексные. Комплексные числа в школьном курсе не изучаются. В этом подмножестве можно извлечь корень из -1, это единственное, что в 6 классе нужно знать о комплексных числах. А знать это нужно, чтобы понимать: если у уравнения нет решений, то, скорее всего, его нет только среди действительных чисел. А вот среди комплексных это решение может и найтись.

Действительным числами зовутся любые:

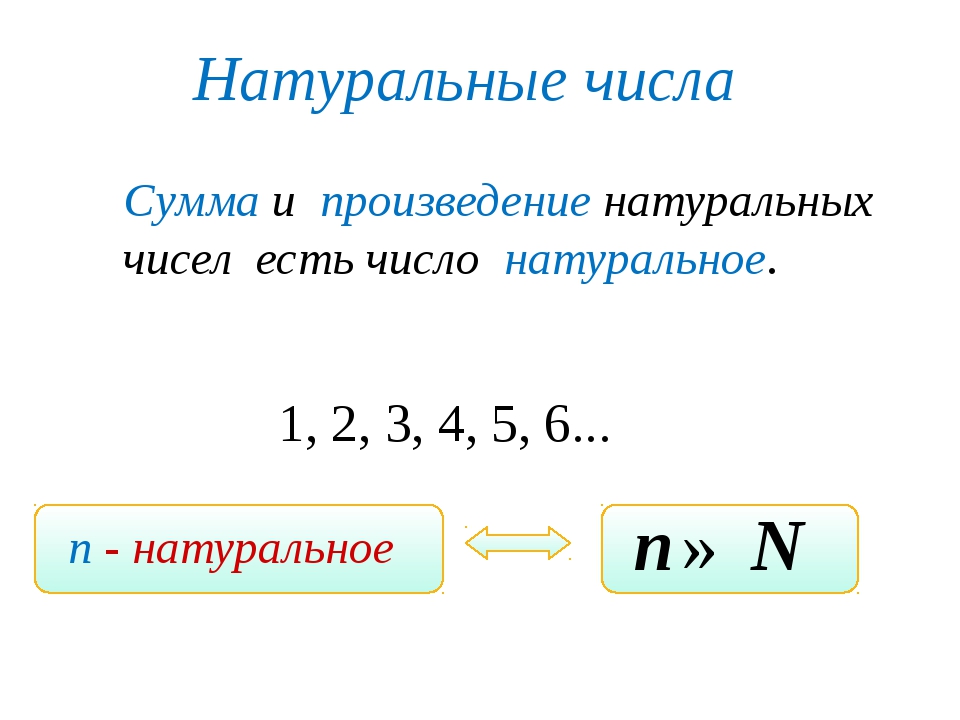
• Положительные числа: целые и дробные.
• Отрицательные числа: целые и дробные.
• Число ноль.

Это именно те числа, которые мы используем для наиболее распространенных математических действий. Примеры действительных чисел: 5; 5,13; $\sqrt{13}$.

Иррациональные числа так же входят в сообщество действительных чисел.

[править] Обобщения

В алгебре и анализе вводятся комплексные числа — числа, представляющих собой сумму вещественного и мнимого числа (вещественное число, умноженное на абстрактную величину «корень из −1», обозначаемую буквой i). В рамках нестандартного анализа к вещественным числам добавляют бесконечно малые и бесконечно большие числа разных порядков. Рассматривается также алгебра кватернионов и др. обобщения.

Рациональные числа можно расширить не только до поля вещественных чисел, но и до поля p-адических чисел, если использовать другую метрику, связанную с делимостью на заданное простое число p (у «маленьких чисел» числитель дроби в несократимом представлении делится на «большую» степень простого числа p) и рассмотреть пополнение рациональных чисел по этой метрике. На базе p-адических чисел удается построить аналоги многих конструкций из математического анализа, созданных для вещественных чисел.

[править] Аксиоматическое определение

Вещественные числа можно определить аксиоматически. Записанные в сокращенном виде аксиомы вещественных чисел выглядят так.

Пусть на множестве X заданы две бинарные операции — сложение (+) и умножение (·), а также задано отношение порядка . Четвёрка (X,+,\cdot,\le) называется полным упорядоченным полем, если

1. (X,+,\cdot) представляет собой алгебраическое поле;
2. (X,\le) является полностью упорядоченным множество с отношением порядка, то есть
   • порядок устойчив относительно сложения:

     \forall x,y,z\in X \quad \bigl( x \le y \bigr) \Rightarrow \bigl( x+z \le y+z \bigr)

   • порядок устойчив относительно умножения:

     \forall x,y\in X \quad \bigl(0 \le x\bigr) \wedge \bigl( 0 \le y \bigr) \Rightarrow \bigl( 0 \le x \cdot y \bigr).

3. упорядоченное множество (X,\le) удовлетворяет принципу полноты, у которого есть три эквивалентные формулировки:
   1. если A и B непустые подмножества действительных чисел и для любых a из A и b из B выполняется неравенство a < b, то существует такое действительное число c, что для любых a из A и b из B a ≤ с ≤ b.
   2. любая последовательность вложенных отрезков (то есть любой отрезок последовательности содержит отрезки с большими номерами) имеет общую точку (Принцип полноты Кантора).
   3. любое непустое ограниченное сверху множество действительных чисел имеет точную верхнюю грань (принцип полноты Вейерштрасса, его также можно сформулировать в виде, что любое непустое ограниченное снизу множество вещественных чисел имеет точную нижнюю грань).

Доказывается, что эти аксиомы определяют единственный с точностью до изоморфизма объект (сами числа, как уже сказано выше, можно представлять в виде бесконечных десятичных дробей).

Из этих аксиом выводятся остальные свойства вещественных чисел.