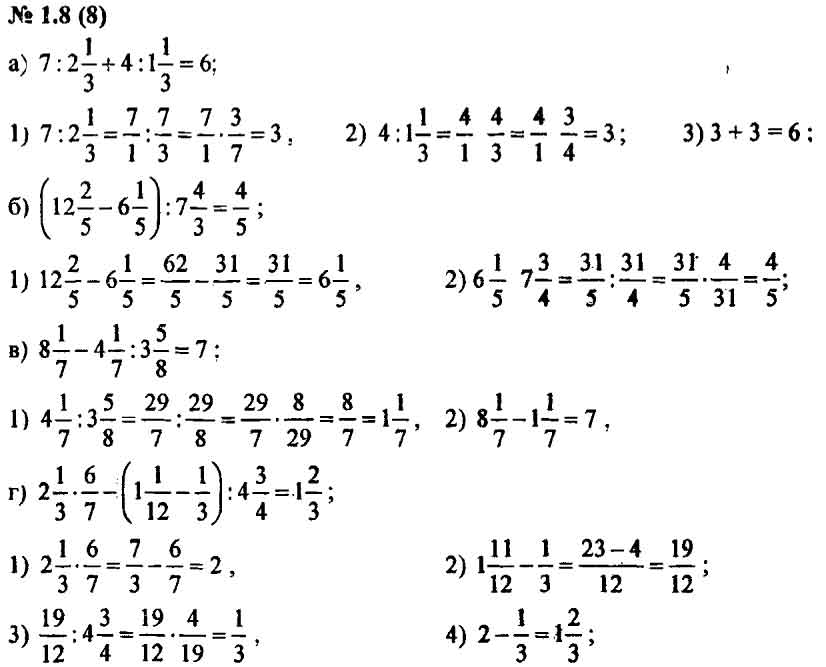Числовые и алгебраические выражения

Исключение из правил

Алгебра — дисциплина, в которой следует учитывать оптимизацию вычислений, поскольку это сказывается на времени выполнения поставленной задачи. Приоритета операций следует придерживаться, но существует сокращение или упрощение. Это значит, что перед выполнением математических преобразований, необходимо сократить одинаковые компоненты тождества.

Однако для лучшей иллюстрации применения методики необходимо решить пример: / . Сразу раскрывать скобки необязательно, поскольку это приведет к увеличению объемов расчетов. Выполнять вычисления лучше по такому алгоритму:

1. Выполнить анализ тождества: в числителе и знаменателе видны равные выражения, которые нужно привести к общему виду, используя формулы сокращенного умножения.
2. Записать выражение «(u 2 -2u+1)», используя правила сокращенного умножения: (u 2 -1).
3. Вынести общий множитель в числителе и знаменателе: / = / .
4. Сократить дробь на (u-1)^2: / .
5. Привести подобные слагаемые, раскрыв скобки: / = / .

Однако этот подход занял бы намного больше времени, а также привел к возможным ошибкам. Исходя из этого можно сформулировать главный принцип не только алгебры, но и других дисциплин с физико-математическим уклоном. Суть его состоит в следующем: любое выражение перед нахождением окончательного результата следует привести к простому виду.

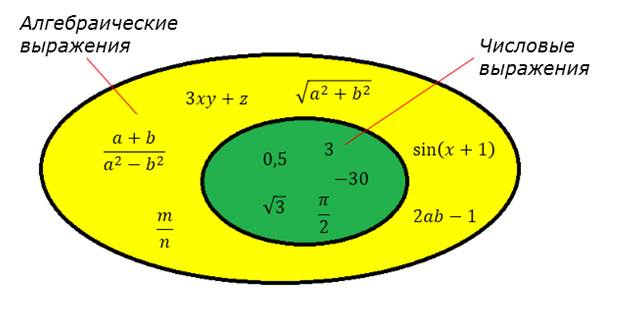
Алгебраические выражения

Примеры алгебраических выражений

Рассмотрим какое-нибудь , например:

\(\footnotesize \textcolor{#ed5fa6}{a}(\textcolor{#ed5fa6}{a}+1).\)

При

\(\footnotesize \textcolor{#ed5fa6}{a}=\textcolor{#3eb489}{2}\)

его значение равно

\(\footnotesize 6,\)

так как

\(\footnotesize \textcolor{#3eb489}{2}\cdot (\textcolor{#3eb489}{2}+1)=6.\)

При

\(\footnotesize a=8\)

значение этого выражения равно

\(\footnotesize 72,\)

при

\(\footnotesize a=-1\)

— нулю, при

\(\footnotesize a=0\)

тоже нулю.

Если значения переменной

\(\footnotesize a\)

образуют множество

\(\footnotesize A=\begin{Bmatrix} 2; 8; -1; 0 \end{Bmatrix},\)

то значения выражения

\(\footnotesize a(a+1)\)

составят множество

\(\footnotesize B=\begin{Bmatrix} 6; 72; 0 \end{Bmatrix}.\)

Если множество значений переменной, входящей в выражение, не указано, то считается, что переменная принимает все те значения, при которых выражение имеет смысл. Например, если ничего не сказано о множестве значений переменной

\(\footnotesize p\)

в выражении

\(\footnotesize \frac{p}{2p-6},\)

то имеется в виду, что переменная

\(\footnotesize p\)

принимает любые числовые значения, кроме

\(\footnotesize 3.\)

Значение выражения

\(\footnotesize (x-2y)^2\)

зависит от значений переменных

\(\footnotesize x\)

и

\(\footnotesize y.\)

Пусть переменная

\(\footnotesize x\)

принимает значения из множества

\(\footnotesize X=\begin{Bmatrix} 1; 5 \end{Bmatrix}\)

, а переменная

\(\footnotesize y\)

— из множества

\(\footnotesize Y=\begin{Bmatrix} 1; 2; 5 \end{Bmatrix}\)

\(
(x-2y)^2 = \begin{cases}
81 \leftarrow\textcolor{gray}{если \ x=1, y=5,}\\
9 \leftarrow\textcolor{gray}{если \ x=5, y=1;}
\end{cases}
\)

Каждой паре значений переменных

\(\footnotesize x\)

и

\(\footnotesize y\)

соответствует определенное значение выражения

\(\footnotesize (x-2y)^2\)

причем единственное. Составим всевозможные пары значений

\(\footnotesize x\)

и

\(\footnotesize y\)

и для каждой из них найдем соответствующее значение выражения:

\	\	\
\	\	\
\	\	\
\	\	\
\	\	\
\	\	\
\	\	\

Значения выражения

\(\footnotesize (x-2y)^2\)

образуют множество

\(\footnotesize \begin{Bmatrix} 1; 9; 81; 25 \end{Bmatrix}.\)

Если в выражении с двумя переменными множества их значений не указаны, то считают, что переменные принимают любые значения, при которых данное выражение имеет смысл.

Например, если ничего не сказано о множествах значений переменных

\(\small \textcolor{#3eb489}{x}\)

и

\(\small \textcolor{#ed5fa6}{y}\)

в выражении

\( \frac{5}{\textcolor{#3eb489}{x}-\textcolor{#ed5fa6}{y}},\)

то считается, что переменные

\(\small \textcolor{#3eb489}{x}\)

и

\(\small \textcolor{#ed5fa6}{y}\)

принимают любые не равные между собой значения.

Приоритет операций

Чтобы вычислить значение какого-либо выражения, нужно разобраться в приоритете. Он задается скобками, т. е. выполняются первые действия, находящиеся в них. Если тождество содержит много групп, отделенных скобками, рекомендуется выполнять операции слева направо (последовательно).

Умножение и деление имеют высший приоритет по сравнению с другими операциями. Однако существуют и другие более сложные расчеты, которые следует выполнять в первую очередь. К ним относятся следующие:

1. Возведение в степень.
2. Вычисление выражения под знаком радикала (корня).
3. Нахождение логарифма.
4. Расчет факториала.
5. Получение результата при решении тригонометрических функций.
6. Нахождение производной или дифференциала.

Знак скобки обладает наивысшим приоритетом. Чтобы понять механизм последнего, следует разобрать следующий пример: 2*(2*(3−1)+2−2*5+7−7*2). В этом случае следует составить план решения выражения (нумерация пунктов соответствует порядку выполнения вычислений):

1. (3−1) = 2.
2. 2*(3−1) = 2*2 = 4.
3. 2*5 = 10.
4. 2−10 = -8.
5. 7*2 = 14.
6. 7−14 = -7.
7. 4−8−7 = 4−15 = -11.
8. 2*(-11) = -22.

Ответ, полученный при решении числового выражения для алгебры 7 класса, эквивалентен значению -22. Если приоритет не учитывать, получится такой ход решения выражения:

1. (3−1) = 2.
2. 2*(3−1) = 4.
3. 2*(3−1) + 2 = 6.
4. 6−2 = 4.
5. 4*5 = 20.
6. 20+7 = 27.
7. 27−7 = 20.
8. 20*2 = 40.
9. 40*2 = 80.

В результате при неверных расчетах получается значение, равное 80. При этом значения в первом и втором случаях сильно отличаются. Этот пример доказывает, что знание приоритета арифметической операции сильно влияет на результаты вычислений. Иногда для удобства можно отступить от правил.

Общие сведения

В алгебре существует 2 типа выражений: числовой и алгебраический. Многие их путают, поскольку не знают смыслового значения. Определение для первого типа: числовое — вид тождества, которое состоит из чисел, скобок и знаков арифметических операций.

Иными словами, числовое выражение представляет собой совокупность чисел и знаков арифметических операций, имеющую логическое завершение. Алгебраическое — тождество, содержащее не только все компоненты числового, но и неизвестные (переменные) величины. Например, 25-(25-m)+2 (3−2m).

Например, тождество «25-(25 / 5)*2» является числовым выражением, а «25-*2+*3» — просто набор математических символов. Последний нельзя называть числовым или алгебраическим.

Операция сложения обозначается знаком «+», вычитания — «-«, умножения (произведения) — «*», деления — «/» или «:». В первом случае основными компонентами выражения являются 2 слагаемых и результат — сумма. Следует отметить, что слагаемых может быть любое количество.

Произведение состоит также из нескольких компонентов: множимое, множитель и произведение. Первый элемент — число, которое следует умножить. Второй — на какое значение умножается. Результат называется произведением. Однако для простоты используется сокращенное название элементов — множители. Это обусловлено ассоциативным свойством умножения: от перестановки коэффициентов его величина не изменится. Существует следующие типы записей:

1. Полная: 25*(25-n)+2*(3−2*n)-2*(7*n+2*n).
2. Сокращенная: 25 (25-n)+2 (3−2n)-2 (7n+2n).

Операция деления состоит из следующих компонентов: делимого, делителя и частного. Первый элемент — число, которое следует разделить на делитель. При этом результат бывает целым и дробным. Последний записывается в виде десятичной (целая часть отделяется от дробной запятой) или обыкновенной дроби, состоящей из числителя (расположен вверху) и знаменателя (внизу).

Что такое выражение в математике?

Выражение в математике — это очень широкое понятие. Практически всё то, с чем мы имеем дело в математике — это набор математических выражений. Любые примеры, формулы, дроби, уравнения и так далее — это всё состоит из математических выражений.

3+2 — это математическое выражение. с2- d2 — это тоже математическое выражение. И здоровущая дробь, и даже одно число — это всё математические выражения. Уравнение, например, вот такое:

5х + 2 = 12

состоит из двух математических выражений, соединённых знаком равенства. Одно выражение — слева, другое — справа.

В общем виде термин «математическое выражение» применяется, чаще всего, чтобы не мычать. Спросят вас, что такое обыкновенная дробь, например? И как ответить?!

Первый вариант ответа: «Это… м-м-м-м… такая штука… в которой… А можно я лучше напишу дробь? Вам какую?»

Второй вариант ответа: «Обыкновенная дробь — это (бодро и радостно!) математическое выражение, которое состоит из числителя и знаменателя!»

Второй вариант как-то посолидней будет, правда?)

Вот в этих целях фраза «математическое выражение» очень хороша. И правильно, и солидно. Но для практического применения надо хорошо разбираться в конкретных видах выражений в математике.

Конкретный вид- это другое дело. Это совсем другое дело! У каждого вида математических выражений есть свой набор правил и приёмов, который необходимо использовать при решении. Для работы с дробями — один набор. Для работы с тригонометрическими выражениями — второй. Для работы с логарифмами — третий. И так далее. Где-то эти правила совпадают, где-то — резко отличаются. Но не пугайтесь этих страшных слов. Логарифмы, тригонометрию и прочие загадочные вещи мы будем осваивать в соответствующих разделах.

Здесь мы освоим (или — повторим, кому как…) два основных вида математических выражений. Числовые выражения и алгебраические выражения.

Универсальный алгоритм

Математики разработали специальный алгоритм, облегчающий вычисления на начальном этапе обучения. Кроме того, его можно применять и при сложных расчетах. Суть его заключается в разбиении сложного выражения на модули (части). Это понятие впервые было введено древнегреческим ученым Пифагором.

Для примера следует разобрать выражение, состоящее из всех арифметических операций: / . Чтобы его решить, необходимо руководствоваться следующим универсальным алгоритмом:

1. Ввести обозначения: К = 2s (2-s), L = (s-1)^2, М = s 2 , N = 3, О = (1-s)(1+s) и Р = 3s 2 .
2. Записать полученное выражение: (K +L+M) / (N*O+P).
3. Вычислить значение K, раскрыв скобки: 2s (2-s) = 4s-2s 2 .
4. Найти L: s 2 -2s + 1.
5. Записать числитель обыкновенной дроби, а затем осуществить сложение подобных компонентов: К+L+М = 4s-2s 2 +s 2 -2s+1+s 2 = 4s-2s+1 = 2s+1.
6. Вычислить О, используя формулу: (1-s)(1+s) = 1-s 2 .
7. Записать произведение компонентов (N*О: N*О = 3 (1-s 2 ) = 3−3s 2 .
8. Конечная запись знаменателя: N*O+P = 3−3s 2 +3s 2 = 3.
9. Результат вычисления: (K+L+M) / (P+N*O) = (2s+1) / 3.

Вычисление выражения позволяет сформулировать основное правило: при решении сложного тождества нужно разбить его на простые элементы. Этот принцип позволяет решать задачи, связанные с такими направлениями: бизнес, программирование, научные исследования и т. д.

Преобразование выражений. Тождественные преобразования.

Мы познакомились с числовыми и алгебраическими выражениями. Поняли, что означает фраза «выражение не имеет смысла». Теперь надо разобраться, что такое преобразование выражений. Ответ прост, до безобразия.) Это любое действие с выражением. И всё. Вы эти преобразования делали с первого класса.

Возьмём крутое числовое выражение 3+5. Как его можно преобразовать? Да очень просто! Посчитать:

3+5 = 8

Вот этот расчёт и будет преобразованием выражения. Можно записать то же самое выражение по-другому:

3+5 = 5+3

Тут мы вообще ничего не считали. Просто записали выражение в другом виде. Это тоже будет преобразованием выражения. Можно записать вот так:

3+5 = 10-2

И это тоже — преобразование выражения. Таких преобразований можно понаделать сколько хочешь.

Уловили?

Любое действие над выражением, любая запись его в другом виде называется преобразованием выражения. И все дела. Всё очень просто

Но есть здесь одно очень важное правило. Настолько важное, что его смело можно назвать главным правилом всей математики

Нарушение этого правила неизбежно приводит к ошибкам. Вникаем?)

Предположим, мы преобразовали наше выражение как попало, вот так:

3+5 = 2+1

Преобразование? Конечно. Мы же записали выражение в другом виде, что здесь не так?

Всё не так.) Дело в том, что преобразования «как попало» математику не интересуют вообще.) Вся математика построена на преобразованиях, в которых меняется внешний вид, но суть выражения не меняется. Три плюс пять можно записать в каком угодно виде, но это должно быть восемь.

Преобразования, не меняющие сути выражения называются тождественными.

Именно тождественные преобразования и позволяют нам, шаг за шагом, превращать сложный пример в простое выражение, сохраняя суть примера. Если в цепочке преобразований мы ошибёмся, сделаем НЕ тождественное преобразование, дальше мы будем решать уже другой пример. С другими ответами, которые не имеют отношения к правильным.)

Вот оно и главное правило решения любых заданий: соблюдение тождественности преобразований.

Пример с числовыми выражением 3+5 я привёл для наглядности. В алгебраических выражениях тождественные преобразования даются формулами и правилами. Скажем, в алгебре есть формула:

a(b+c) = ab + ac

Значит, мы в любом примере можем вместо выражения a(b+c) смело написать выражение ab + ac. И наоборот. Это тождественное преобразование. Математика предоставляет нам выбор из этих двух выражений. А уж какое из них писать — от конкретного примера зависит.

Как вы, наверняка, догадались, эту цепочку можно продолжать до бесконечности…) Очень важное свойство. Именно оно позволяет превращать всякие монстры-примеры в белые и пушистые.). Формул, задающих тождественные преобразования, — много

Но самых главных — вполне разумное количество. Одно из базовых преобразований — разложение на множители. Оно используется во всей математике — от элементарной до высшей. С него и начнём. В следующем уроке.)

Формул, задающих тождественные преобразования, — много. Но самых главных — вполне разумное количество. Одно из базовых преобразований — разложение на множители. Оно используется во всей математике — от элементарной до высшей. С него и начнём. В следующем уроке.)

Следующая страница: Разложение на множители. Примеры.

Значение буквенного выражения и выражения с переменными

Помимо числовых выражений изучают буквенные выражения, то есть выражения, в записи которых вместе с числами присутствует одна или несколько букв. Буквы в буквенном выражении могут обозначать различные числа, и если буквы заменить этими числами, то буквенное выражение станет числовым.

Определение.

Числа, которыми заменяют буквы в буквенном выражении, называют значениями этих букв, а значение полученного при этом числового выражения называют значением буквенного выражения при данных значениях букв.

Итак, для буквенных выражений говорят не просто о значении буквенного выражения, а о значении буквенного выражения при данных (заданных, указанных и т.п.) значениях букв.

Приведем пример. Возьмем буквенное выражение 2·a+b. Пусть заданы значения букв a и b, например, a=1 и b=6. Заменив буквы в исходном выражении их значениями, получим числовое выражение вида 2·1+6, его значение равно 8. Таким образом, число 8 есть значение буквенного выражения 2·a+b при заданных значениях букв a=1 и b=6. Если бы были даны другие значения букв, то мы бы получили значение буквенного выражения для этих значений букв. Например, при a=5 и b=1 имеем значение 2·5+1=11.

В старших классах при изучении алгебры буквам в буквенных выражениях позволяют принимать различные значения, такие буквы называют переменными, а буквенные выражения – выражениями с переменными. Для этих выражений вводится понятие значения выражения с переменными при выбранных значениях переменных. Разберемся, что это такое.

Определение.

Значением выражения с переменными при выбранных значениях переменных называется значение числового выражения, которое получается после подстановки выбранных значений переменных в исходное выражение.

Поясним озвученное определение на примере. Рассмотрим выражение с переменными x и y вида 3·x·y+y. Возьмем x=2 и y=4, подставим эти значения переменных в исходное выражение, получаем числовое выражение 3·2·4+4. Вычислим значение этого выражения: 3·2·4+4=24+4=28. Найденное значение 28 является значением исходного выражения с переменными 3·x·y+y при выбранных значениях переменных x=2 и y=4.

Если выбрать другие значения переменных, например, x=5 и y=0, то этим выбранным значениям переменных будет соответствовать значение выражения с переменными, равное 3·5·0+0=0.

Можно отметить, что иногда для различных выбранных значений переменных могут получаться равные значения выражения. К примеру, для x=9 и y=1 значение выражения 3·x·y+y равно 28 (так как 3·9·1+1=27+1=28), а выше мы показали, что такое же значение это выражение с переменными имеет при x=2 и y=4.

Значения переменных можно выбирать из соответствующих им областей допустимых значений. В противном случае при подстановке в исходное выражение значений этих переменных получится числовое выражение, не имеющее смысла. К примеру, если выбрать x=0, и подставить это значение в выражение 1/x, то получится числовое выражение 1/0, которое не имеет смысла, так как деление на нуль не определено.

Остается лишь добавить, что существуют выражения с переменными, значения которых не зависят от значений входящих в них переменных. Например, значение выражения с переменной x вида 2+x−x не зависит от значения этой переменной, оно равно 2 при любом выбранном значении переменной x из области ее допустимых значений, которая в данном случае является множеством всех действительных чисел.

Список литературы.

• Математика: учеб. для 5 кл. общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 21-е изд., стер. — М.: Мнемозина, 2007. — 280 с.: ил. ISBN 5-346-00699-0.
• Алгебра: учеб. для 7 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
• Алгебра: учеб. для 8 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.

Как решать алгебраические выражения?

Для вычисления значений нужно делать преобразование алгебраических выражений. А для этого вам еще нужно учесть несколько правил.

Во-первых: областью определения алгебраических выражений являются все возможные значения переменной, при которых это выражение может иметь смысл. Что подразумевается? Например, нельзя подставлять такое значение переменной, при котором пришлось бы делить на нуль. В выражении1/(х – 2)из области определения надо исключить 2.

Во-вторых, запомните, как упрощать выражения: раскладывать на множители, выносить за скобки одинаковые переменные и т.п. Например: если поменять местами слагаемые, сумма от этого не изменится (у + х = х +у). Аналогично и произведение не изменится, если поменять местами множители (х*у = у*х).

А вообще для упрощения алгебраических выражений отлично служат формулы сокращенного умножения. Тем, кто их еще не выучил, обязательно надо это сделать – все равно пригодятся не раз:

• находим разность переменных, возведенных в квадрат: х2 – у2 = (х – у)(х + у);

• находим сумму, возведенную в квадрат: (х + у)2 = х2 + 2ху + у2;

• вычисляем разность, возведенную в квадрат: (х – у)2 = х2 – 2ху + у2;

• возводим сумму в куб: (х + у)3 = х3 + 3х2у + 3ху2 + у3 или (х + у)3 = х3 + у3 + 3ху(х + у);

• возводим в куб разность: (х – у)3 = х3 – 3х2у + 3ху2 – у3 или (х – у)3 = х3 – у3 – 3ху(х – у);

• находим сумму переменных, возведенных в куб: х3 + у3 = (х +у)(х2 – ху + у2);

• вычисляем разность переменных, возведенных в куб: х3 – у3 = (х – у)(х2 + ху + у2);

• используем корни: ха2 + уа + z = х(а – а₁)(а – а₂), а₁ и а₂ – это корни выражения ха2 + уа + z.

Еще вам стоит иметь представление о видах алгебраических выражений. Они бывают:

рациональные, и те в свою очередь подразделяются на:

• целые(в них нет деления на переменные, нет извлечения корней из переменных и нет возведения в дробную степень): 3a3b + 4a2b * (a – b).Область определения – все возможные значения переменных;

• дробные(кроме остальных математических операций, вроде сложения, вычитания, умножения, в этих выражениях делят на переменную и возводят в степень (с натуральным показателем): (2/b – 3/a + с/4)2. Область определения – все значения переменных, при которых выражение не равно нулю;

иррациональные– чтобы алгебраическое выражение считалось таковым, в нем должно присутствовать возведение переменных в степень с дробным показателем и/или извлечение корней из переменных: √а + b3/4. Область определения – все значения переменных, исключая те, при которых выражение под корнем четной степени или под дробной степенью становится отрицательным числом.

Тождественные преобразования алгебраических выражений – еще один полезный прием для их решения.Тождество – такое выражение, которое будет верным при любых входящих в область определения переменных, которые в него подставят.

Выражение, которое зависит от некоторых переменных, может быть тождественно равно другому выражению, если то зависит от тех же переменных и если значения обоих выражений равны, какие бы значения переменных не были выбраны. Другими словами, если выражение можно выразить двумя разными способами (выражениями), значения которых одинаковые, эти выражения тождественно равны. Например: у + у = 2у, или х7 = х4*х3, или x +y +z = z + x +y.

При выполнении заданий с алгебраическими выражениями тождественное преобразование служит для того, чтобы одно выражение можно было заменить на другое, тождественное ему. К примеру, заменить х9 на произведение х5*х4.

Выражения с переменными

Если в буквенном выражении буква обозначает величину, которая принимает не какое-то одно конкретное значение, а может принимать различные значения, то эту букву называют переменной и выражение называют выражением с переменной.

Определение.

Выражение с переменными – это буквенное выражение, в котором буквы (все или некоторые) обозначают величины, принимающие различные значения.

Например, пусть в выражении x2−1 буква x может принимать любые натуральные значения из интервала от до 10, тогда x – есть переменная, а выражение x2−1 есть выражение с переменной x.

Стоит отметить, что переменных в выражении может быть несколько. К примеру, если считать x и y переменными, то выражение является выражением с двумя переменными x и y.

Вообще, переход от понятия буквенного выражения к выражению с переменными происходит в 7 классе, когда начинают изучать алгебру. До этого момента буквенные выражения моделировали какие-то конкретные задачи. В алгебре же начинают смотреть на выражение более общо, без привязки к конкретной задаче, с пониманием того, что данное выражение подходит под огромное число задач.

В заключение этого пункта обратим внимание еще на один момент: по внешнему виду буквенного выражения невозможно узнать, являются ли входящие в него буквы переменными или нет. Поэтому ничто нам не мешает считать эти буквы переменными

При этом разница между терминами «буквенное выражение» и «выражение с переменными» исчезает.

Список литературы.

• Математика. 2 кл. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / — 3-е изд. — М.: Просведение, 2012. — 96 с.: ил. — (Школа России). — ISBN 978-5-09-028297-0.
• Математика: учеб. для 5 кл. общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 21-е изд., стер. — М.: Мнемозина, 2007. — 280 с.: ил. ISBN 5-346-00699-0.
• Алгебра: учеб. для 7 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
• Алгебра: учеб. для 8 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.

Числовые выражения – что это?

Знакомство с числовыми выражениями начинается чуть ли не с самых первых уроков математики. Но свое имя – числовые выражения – они официально приобретают немного позже. Например, если следовать курсу М. И. Моро, то это происходит на страницах учебника математики для 2 классов. Там представление о числовых выражениях дается так: 3+5, 12+1−6, 18−(4+6), 1+1+1+1+1 и т.п. – это все числовые выражения, а если в выражении выполнить указанные действия, то найдем значение выражения.

Можно сделать вывод, что на этом этапе изучения математики числовыми выражениями называют имеющие математический смысл записи, составленные из чисел, скобок и знаков сложения и вычитания.

Чуть позже, после знакомства с умножением и делением, записи числовых выражений начинают содержать знаки «·» и «:». Приведем несколько примеров: 6·4, (2+5)·2, 6:2, (9·3):3 и т.п.

Дальше числа увеличиваются, а числовые выражения становятся более разнообразными: 212·5−12·2, (515−225)·3−916:4·7 и так далее.

А в старших классах разнообразие записей числовых выражений разрастается как снежный ком, катящийся с горы. В них появляются обыкновенные и десятичные дроби, смешанные числа и отрицательные числа, степени, корни, логарифмы, синусы, косинусы и так далее.

Обобщим всю информацию в определение числового выражения:

Определение.

Числовое выражение — это комбинация чисел, знаков арифметических действий, дробных черт, знаков корня (радикалов), логарифмов, обозначений тригонометрических, обратных тригонометрических и других функций, а также скобок и других специальных математических символов, составленная в соответствии с принятыми в математике правилами.

Разъясним все составные части озвученного определения.

В числовых выражениях могут участвовать абсолютно любые числа: от натуральных до действительных, и даже комплексных. То есть, в числовых выражениях можно встретить

• натуральные числа 5, 172, 4,
• целые числа −17, , 63,
• рациональные числа в виде
  • обыкновенных дробей 1/2, ,
  • смешанных чисел ,
  • непериодических и периодических десятичных дробей 7,22 и −8,17(53),
• иррациональные числа ,
• а также комплексные числа с мнимой единицей .

Со знаками арифметических действий все понятно – это знаки сложения, вычитания, умножения и деления, имеющие соответственно вид «+», «−» , «·» и «:». В числовых выражениях может присутствовать один из этих знаков, некоторые из них или все сразу, и причем по нескольку раз. Вот примеры числовых выражений с ними: 3+6, 2,2+3,3+4,4+5,5, 41−2·4:2−5+12·3·2:2:3:12−1/12.

Что касается скобок, то имеют место как числовые выражения, в которых есть скобки, так и выражения без них. Если в числовом выражении есть скобки, то они в основном

• указывают порядок выполнения действий, например, 2·(2,3−1/5) или (1+2·(2−(5−4)))·(3−1,7);
• содержат отрицательное число, например, 5·(−2)+14:(−7) или ;
• отделяют аргумент функции, например, log₂(3+15·4+1) или sin(π/2−π/6)+cos(π/4);
• отделяют основание степени, например, (2−1,3)2.

А иногда скобки в числовых выражениях имеют какое-нибудь определенное отдельно указанное специальное предназначение. К примеру, можно встретить квадратные скобки, обозначающие целую часть числа, так числовое выражение +2 обозначает, что к целой части числа 1,75 прибавляется число 2.

Из определения числового выражения также видно, что в выражении могут присутствовать степени, корни , логарифмы log, ln, lg, обозначения sin, cos, tg, ctg или arcsin, arccos, arctg, arcctg и т.п. Вот примеры числовых выражений с ними: tgπ, arcsin1+arccos1−π/2 и .

Деление в числовых выражениях может быть обозначено с помощью . В этом случае имеют место числовые выражения с дробями. Приведем примеры таких выражений: 1/(1+2), 5+(2·3+1)/(7−2,2)+3 и .

В качестве специальных математических символов и обозначений, которые можно встретить в числовых выражениях, приведем . Для примера покажем числовое выражение с модулем .

Пример задачи

Для того, чтобы лучше понять тему, рассмотрим пример решения задачи. Как решить задачу числовым выражением?

Дано: две машины выезжают из одного пункта в другой. Они поедут по разным дорогам. Одной машине предстоит проехать 35 км., а другой – 42 км. Первая машина едет со скоростью 70 км/ч, а вторая – 84 км/ч Окажутся ли они в конечном пункте в одно и то же время?

Решение: нужно составить два числовых выражения, чтобы найти время в пути у каждой машины. Если они окажутся одинаковыми, значит, машины придут в конечный пункт одновременно. Для того, чтобы найти время, нужно расстояние разделить на скорость. 35 км:70 км/ч=0,5 ч. 42 км:84 км/ч=0,5 ч.

Итак, обе машины приехали в конечный пункт через полчаса.

Как читать математические выражения

Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:

• \(2+3\) – сумма чисел 2 и 3
• \(5\cdot 4\) – произведение чисел 5 и 4
• \(24\div 6\) – частное чисел 24 и 6
• \(35-5\) – разность чисел 35 и 5

Более сложные выражения, называют по последнему выполняемому действию:

• \((a+b)-c\) – разность суммы чисел a и b и числа c
• \((a+b)\cdot (a-b)\) – произведение суммы чисел a и b и разности чисел a и b
• \(a\div (c\cdot d)\) – частное числа a и произведения чисел c и d

Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:

• Сумма первых пяти натуральных чисел – \(1+2+3+4+5\)
• Произведение всех однозначных чисел – \(1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7\cdot 8\cdot 9\)
• Сумма всех двузначных чётных чисел – \(10+12+14+…+94+96+98\)

Алгоритм чтения математических выражений

Чтобы прочитать математическое выражение, нужно:

1. Определить порядок действий в выражении
2. Прочитать, начиная с последнего действия

При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.

Например:

• \(35\cdot (28-12)\) – Произведение числа 35 и разности чисел 28 и 12
• \(35\cdot (28-12)+64\) – Сумма произведения числа 35 с разностью чисел 28 и 12, и числа 64.
• \(35\cdot (28-12)+64–32\div 16\) – Разность суммы произведения числа 35 и разности чисел 28 и 12 с числом 64, и частного чисел 32 и 16

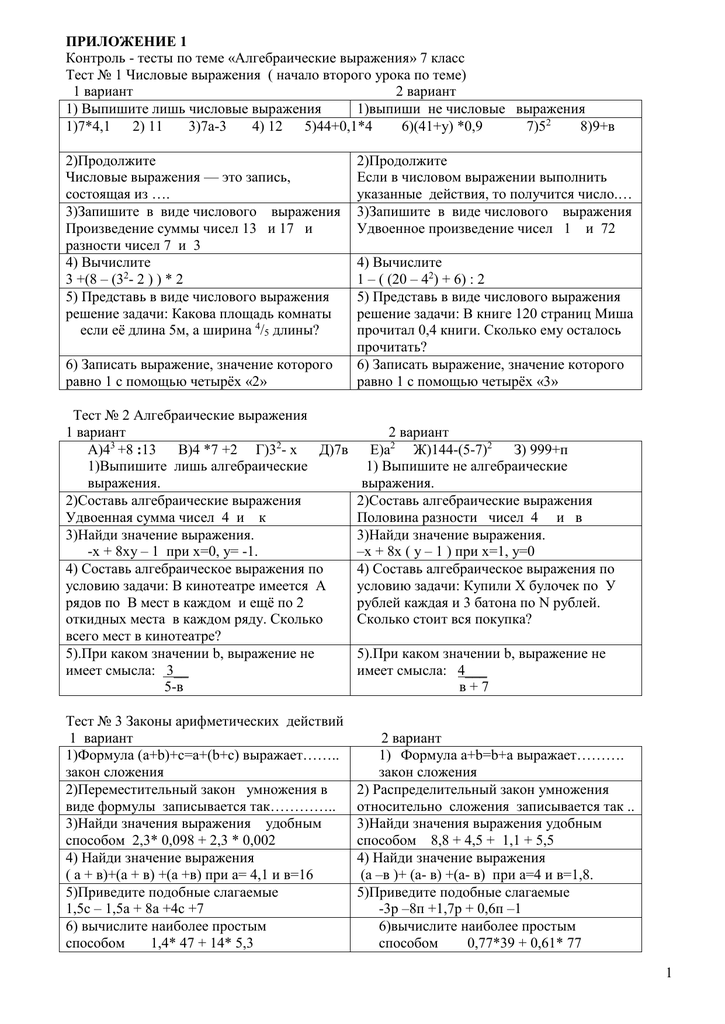
Правило встречается в следующих упражнениях:

2 класс

Страница 46,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 52,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 53,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 36. Вариант 1. № 5,
Моро, Волкова, Проверочные работы

Страница 45. Вариант 2. № 2,
Моро, Волкова, Проверочные работы

Страница 49. Вариант 2. № 4,
Моро, Волкова, Проверочные работы

Страница 56,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 104,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 50,
Моро, Волкова, Рабочая тетрадь, часть 2

3 класс

Страница 41,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 48,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 64,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 71,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 10. Вариант 1. № 1,
Моро, Волкова, Проверочные работы

Страница 7,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 61,
Моро, Волкова, Рабочая тетрадь, часть 2

4 класс

Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 58,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 56,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 58,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 14,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 36,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 63,
Моро, Волкова, Рабочая тетрадь, часть 2

5 класс

Задание 1012,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1406,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1440,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1723,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1836,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Упражнение 292,
Мерзляк, Полонский, Якир, Учебник

Упражнение 317,
Мерзляк, Полонский, Якир, Учебник

Упражнение 434,
Мерзляк, Полонский, Якир, Учебник

Упражнение 544,
Мерзляк, Полонский, Якир, Учебник

Упражнение 929,
Мерзляк, Полонский, Якир, Учебник

6 класс

Задание 473,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 481,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 551,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 569,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 583,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 597,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 698,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 699,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 704,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 705,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник