Математика — это просто!
- ОКРУЖНОСТЬ и КРУГ
-
· Что такое окружность
· Что такое круг
· Касательная к окружности
· Вписанная окружность
· Описанная окружность - ПЛОСКИЕ ФИГУРЫ
-
· Отрезок, луч, прямая
· Угол
· Разновидности углов
· Признаки параллельности - МНОГОУГОЛЬНИКИ
-
· Виды треугольников
· Биссектриса и высота
· Признаки равенства треугольников
· Равнобедренные треугольники
· Площадь треугольника
· Теорема Пифагора
· Теорема синусов
· Теорема косинусов
· Подобные треугольники
· Параллелограмм
· Ромб, квадрат
· Трапеция - ВЕКТОРЫ
-
· Что такое вектор
· Сложение и вычитание векторов
· Умножение вектора на число
· Координаторы вектора
· Угол между векторами
· Скалярное произведение векторов - НАТУРАЛЬНЫЕ ЧИСЛА
- ДРОБИ
- УРАВНЕНИЯ и ТОЖДЕСТВА
- ОДНОЧЛЕНЫ и МНОГОЧЛЕНЫ
- ФУНКЦИИ
- ТРИГОНОМЕТРИЯ
- ВЫСШАЯ МАТЕМАТИКА
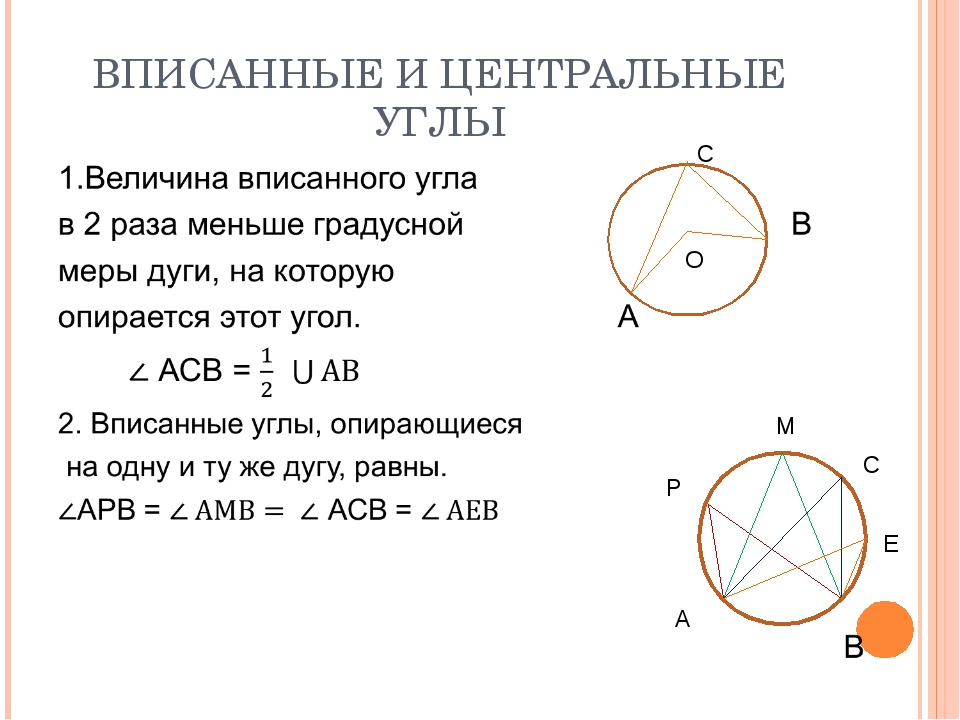
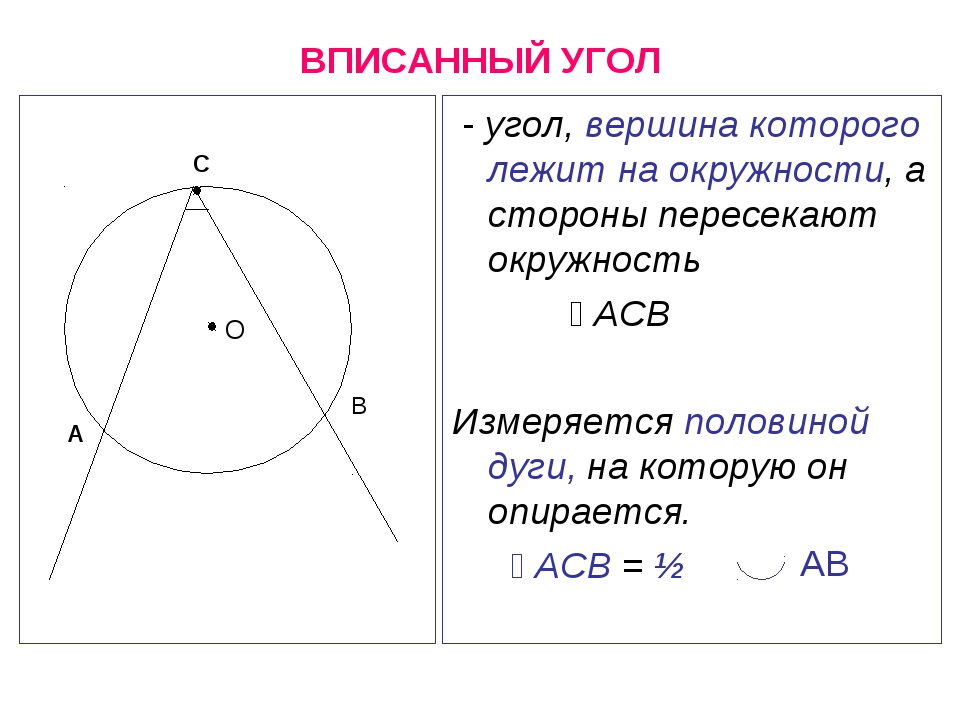
Теоремы об углах, образованных хордами, касательными и секущими
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися |
Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. |
||
| Угол, образованный , которые пересекаются вне круга |  |
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
|
| Угол, образованный и , проходящей через точку касания |
Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами |
||
| Угол, образованный и | 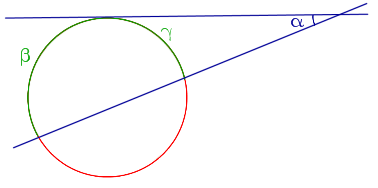 |
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
|
| Угол, образованный двумя к окружности |  |
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный пересекающимися |
| Формула: |
|
Теорема Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. |
| Угол, образованный, которые пересекаются вне круга |
| Формула: |
|
Теорема Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный и, проходящей через точку касания |
| Формула: |
|
Теорема Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами |
| Угол, образованный и и |
| Формула: |
|
Теорема Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя к окружности |
| Формулы: |
|
Теорема Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами |
Доказательства теорем об углах, связанных с окружностью
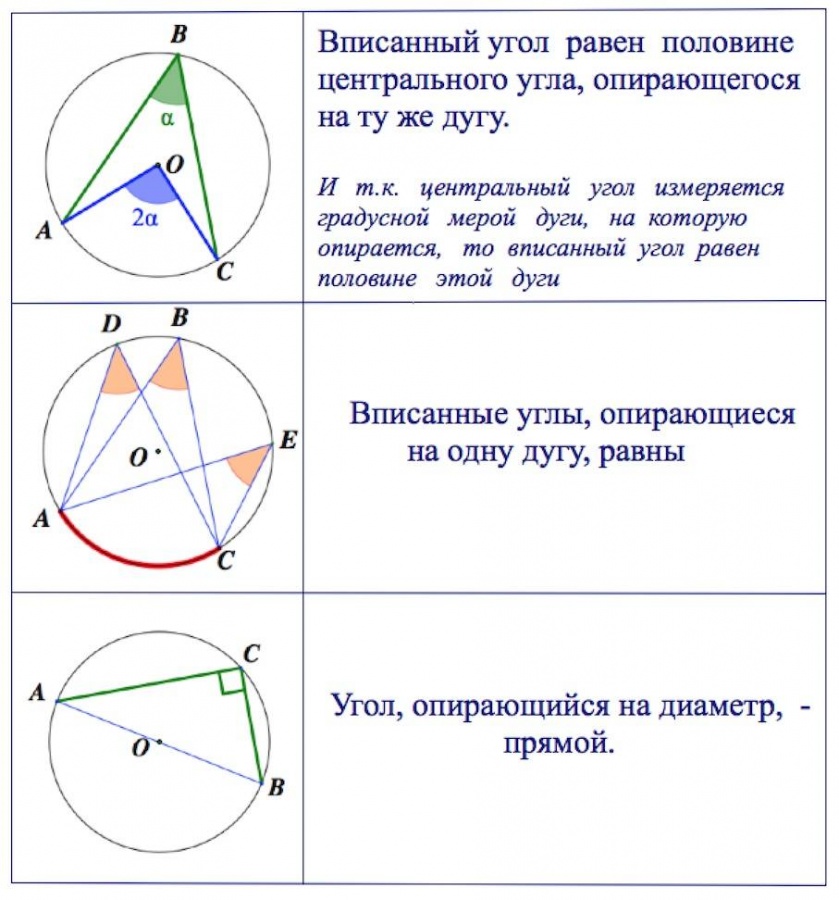
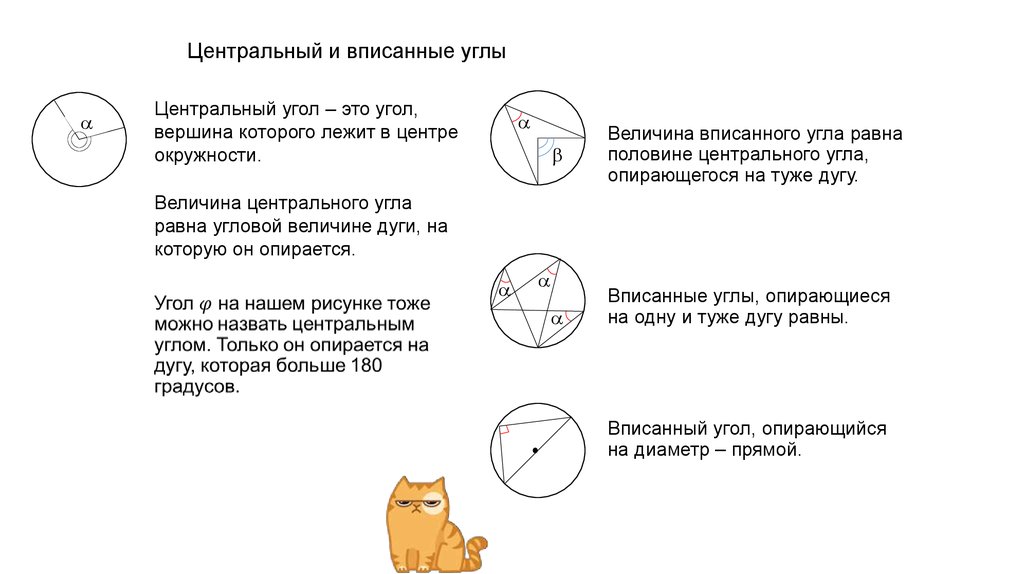
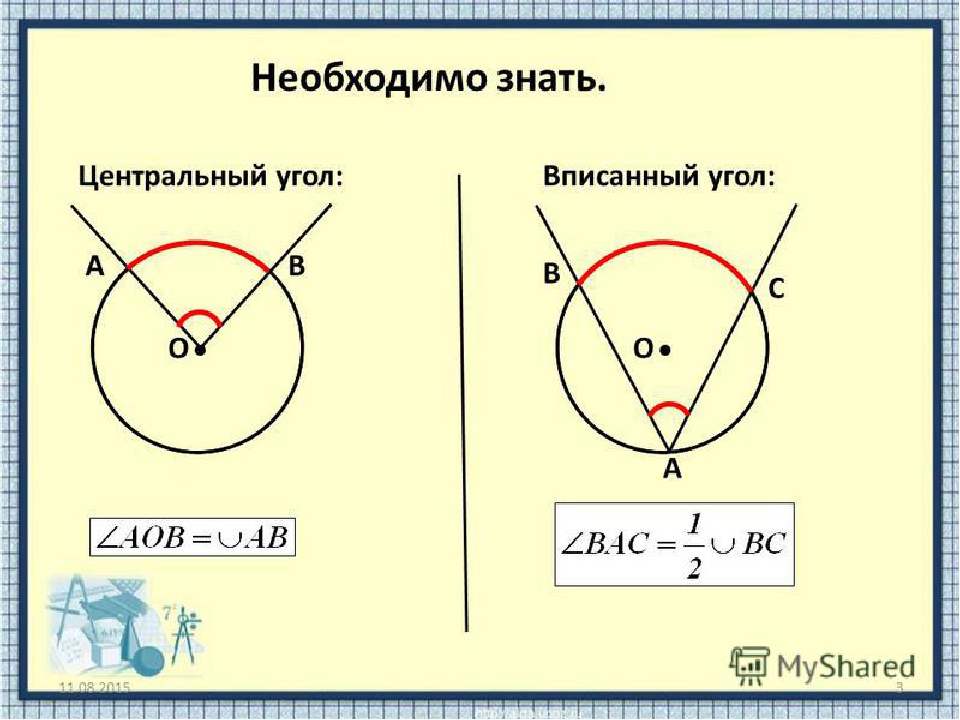
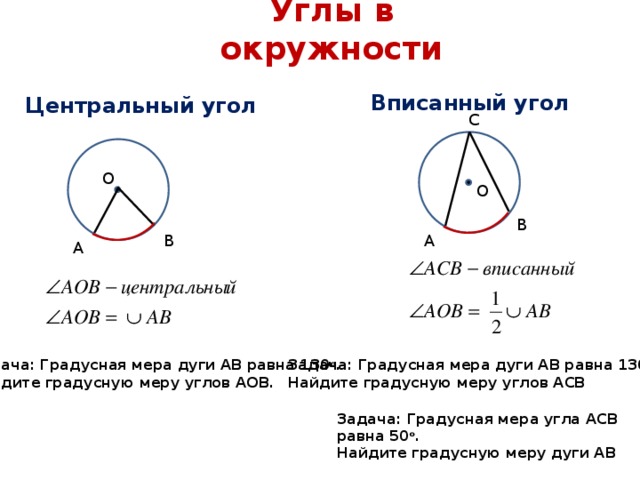
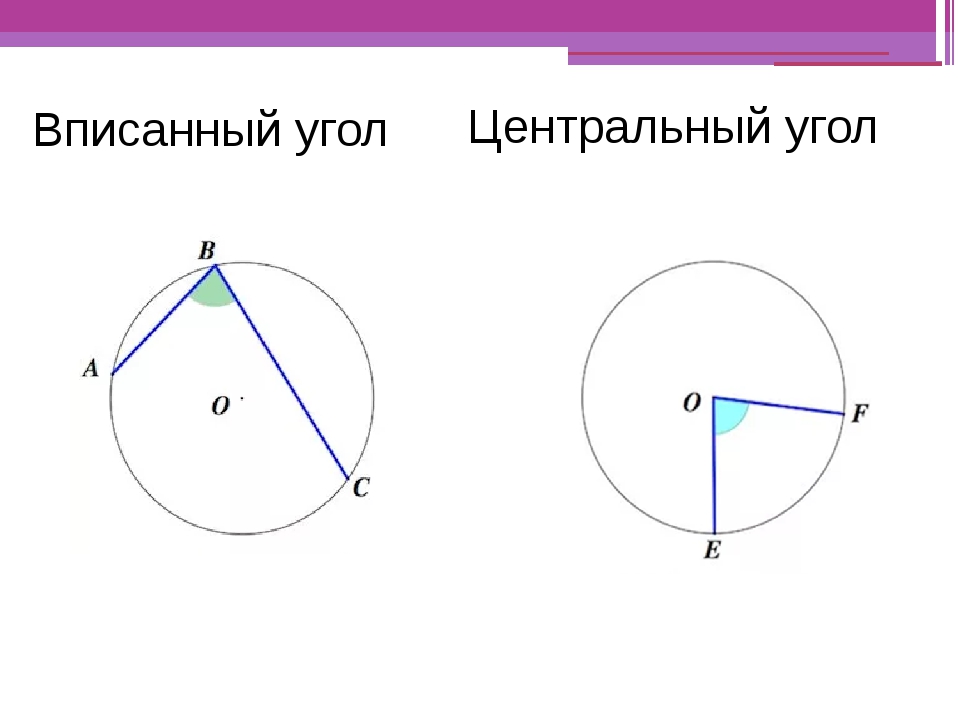
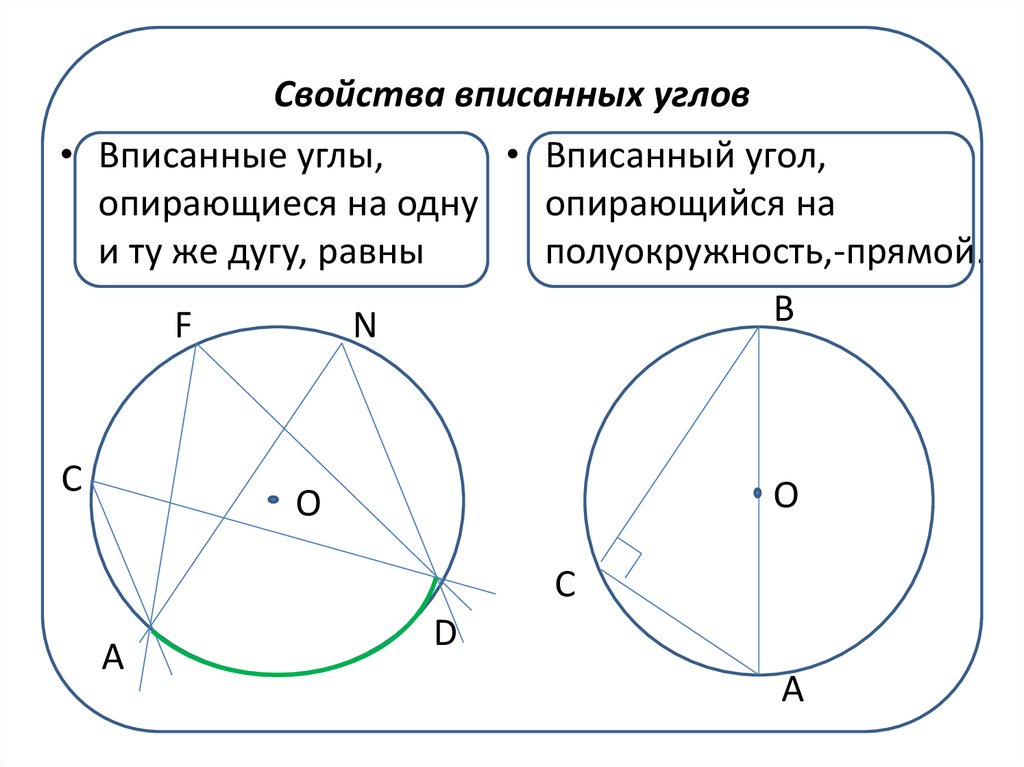
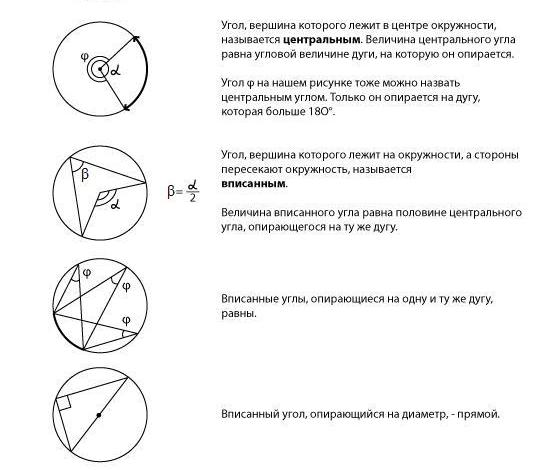
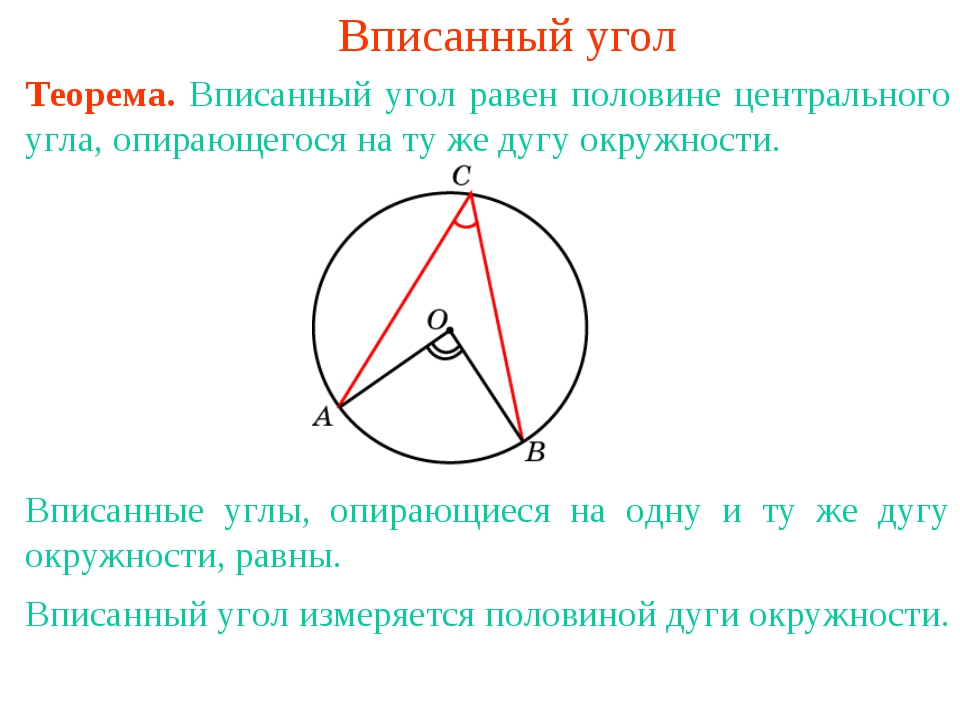
Теорема 1. Величина равна половине величины , опирающегося на ту же дугу.
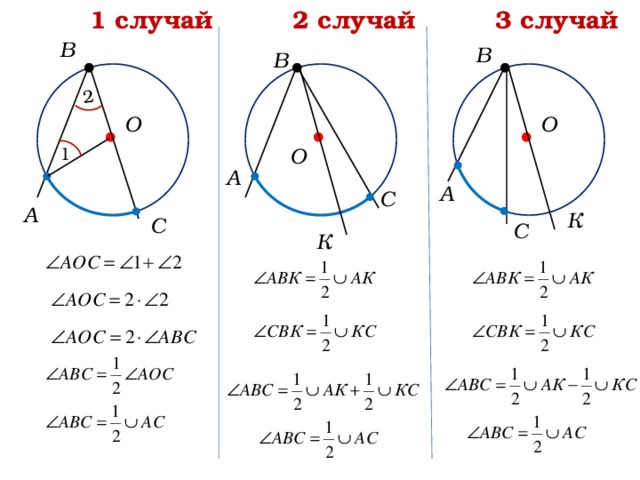
Доказательство. Рассмотрим сначала вписанный угол ABC, сторона BC которого является, и центральный угол AOC (рис. 5).
Рис. 5
Так как отрезки AO и BO являются, то треугольник AOB – равнобедренный, и угол ABO равен углу OAB. Поскольку угол AOC является AOB, то справедливы равенства
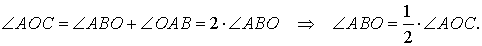
Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.
Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).
Рис. 6
В этом случае справедливы равенства

и теорема 1 в этом случае доказана.
Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).
Рис. 7
В этом случае справедливы равенства
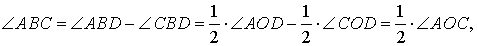
что и завершает доказательство теоремы 1.
Теорема 2. Величина угла, образованного пересекающимися, равна половине суммы величин дуг, заключённых между его сторонами.
Доказательство. Рассмотрим рисунок 8.
Рис. 8
Нас интересует величина угла AED, образованного пересекающимися в точке E хордами AB и CD. Поскольку угол AED – BED, а углы CDB и ABD являются , то справедливы равенства

что и требовалось доказать.
Теорема 3. Величина угла, образованного, пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство. Рассмотрим рисунок 9.
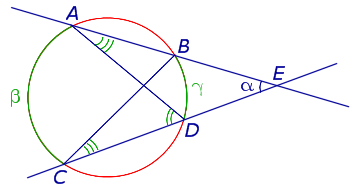
Рис. 9
Нас интересует величина угла BED, образованного пересекающимися в точке E секущими AB и CD. Поскольку угол ADC – ADE, а углы ADC , DCB и DAB являются , то справедливы равенства
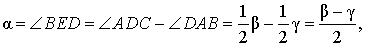
что и требовалось доказать.
Теорема 4. Величина угла, образованного и и , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.
Доказательство. Рассмотрим рисунок 10.

Рис. 10
Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD –, проходящий через точку касания, а угол ACD – , опирающийся на диаметр, . Поэтому справедливы равенства
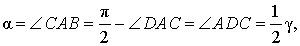
что и требовалось доказать
Теорема 5. Величина угла, образованного, равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство. Рассмотрим рисунок 11.

Рис. 11
Нас интересует величина угла BED, образованного касательной AB и секущей CD. Заметим, что угол BDC – DBE, а углы BDC и BCD являются . Кроме того, углы DBE и DCB, в силу , равны. Поэтому справедливы равенства
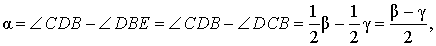
что и требовалось доказать.
Теорема 6.Величина угла, образованного двумя, равна половине разности величин дуг, заключённых между его сторонами.
Доказательство. Рассмотрим рисунок 12.

Рис. 12
Нас интересует величина угла BED, образованного касательными AB и CD. Заметим, что . Поэтому справедливо равенство
α = π – γ .
Далее получаем
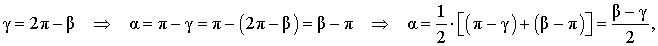
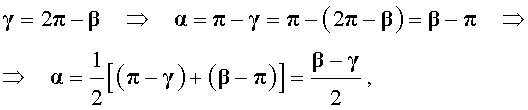
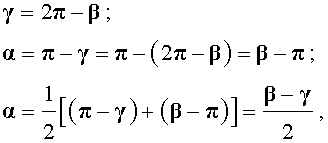
что и требовалось доказать.