Создание ускорения. Динамика точки
Первый закон Ньютона постулирует существование инерциальных систем отсчёта. В этих системах отсчёта равномерное прямолинейное движение имеет место в том случае, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом, постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчёта всегда является некоторое внешнее силовое воздействие.
Классическая механика
Второй закон Ньютона применительно к нерелятивистскому движению (то есть к движению со скоростями, много меньшими скорости света) утверждает, что ускорение материальной точки всегда пропорционально приложенной к ней и порождающей ускорение силе, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется инертной массой материальной точки):
- ma→=F→.{\displaystyle m{\vec {a}}={\vec {F}}.}
Если известны масса материальной точки и (как функция времени) сила, действующая на неё, то из второго закона Ньютона известно и её ускорение: a→=F→m.{\displaystyle {\vec {a}}={\vec {F}}/m.} При постоянстве силы ускорение также будет постоянным. Скорость и координаты точки в любой момент времени можно получить, проинтегрировав ускорение по формулам из раздела о кинематике точки при заданных начальных скорости и координатах.
Релятивистская механика
В релятивистской физике второй закон Ньютона записывается в форме
- mddtv→1−v2c2=F→{\displaystyle m{\frac {d}{dt}}{\frac {\vec {v}}{\sqrt {1-v^{2}/c^{2}}}}={\vec {F}}}
что делает нахождение ускорения более сложной задачей, чем в классическом случае. В частности, длительное движение с постоянным ускорением принципиально невозможно (иначе скорость точки в конце концов превысит скорость света), а неизменность силы не означает неизменности ускорения: оно будет стремиться к нулю при нарастании скорости. Тем не менее, если зависимость a→(t){\displaystyle {\vec {a}}(t)} всё же найдена, расчёт v→(t){\displaystyle {\vec {v}}(t)} и r→(t){\displaystyle {\vec {r}}(t)} осуществим по тем же формулам, что и в нерелятивистском пределе.
Измерения ускорений
Используемые единицы
- метр на секунду в квадрате (метр в секунду за секунду), м/с², производная единица системы СИ;
- сантиметр на секунду в квадрате (сантиметр в секунду за секунду), см/с², производная единица системы СГС, имеет также собственное наименование гал, или галилео (применяется преимущественно в гравиметрии);
- g (произносится «же»), стандартное ускорение свободного падения на поверхности Земли, равное по определению 9,80665 м/с². В технических расчётах, не требующих точности выше 2 %, часто используется приближение g ≈ 10 м/с².
| м/с2 | фут/с2 | g | см/с2 | |
|---|---|---|---|---|
| 1 м/с2 = | 1 | 3,28084 | 0,101972 | 100 |
| 1 фут/с2 = | 0,304800 | 1 | 0,0310810 | 30,4800 |
| 1 g = | 9,80665 | 32,1740 | 1 | 980,665 |
| 1 см/с2 = | 0,01 | 0,0328084 | 0,00101972 | 1 |
Технические средства
Приборы для измерения ускорения называются акселерометрами. Они не «детектируют» ускорение непосредственно, а измеряют силу реакции (укр.)русск. опоры, возникающую при ускоренном движении. Поскольку аналогичные силы сопротивления возникают в поле тяготения, с помощью акселерометров можно измерять также гравитацию.
Акселерографы — приборы, измеряющие и автоматически записывающие (в виде графиков) значения ускорения поступательного и вращательного движения.
Значения ускорения в некоторых случаях
Значения ускорений различных движений:
| Вид движения | Ускорение, м/с2 |
|---|---|
| Центростремительное ускорение Солнечной системы при орбитальном движении в Галактике | 2,2·10−10 |
| Центростремительное ускорение Земли при орбитальном движении вокруг Солнца | 0,0060 |
| Центростремительное ускорение Луны при орбитальном движении вокруг Земли | 0,0027 |
| Пассажирский лифт | 0,9—1,6 |
| Поезд метро | 1 |
| Автомобиль «Жигули» | 1,5 |
| Бегун на коротких дистанциях | 1,5 |
| Велосипедист | 1,7 |
| Конькобежец | 1,9 |
| Мотоцикл | 3—6 |
| Аварийное торможение автомобиля | 4—6 |
| Усэйн Болт, максимальное ускорение | 8 |
| Гоночный автомобиль | 8—9 |
| Торможение при открытии парашюта | 30 (3 g) |
| Запуск и торможение космического корабля | 40—60 (4—6 g) |
| Манёвр реактивного самолёта | до 100 (до 10 g) |
| Свая после удара копром | 300 (30 g) |
| Поршень двигателя внутреннего сгорания | 3×103 |
| Пуля в стволе винтовки | 2,5×105 |
| Микрочастицы в ускорителе | (2—50)×1014 |
| Электроны между катодом и анодом трубки цветного телевизора (20 кВ, 0,5 м) | ≈7×1015 |
| Электроны при соударении с люминофором трубки цветного телевизора (20 кВ) | ≈1022 |
| Альфа-частицы в атомном ядре | ≈1027 |
Примечание: здесь g ≈ 10 м/с2.
Понятие «обобщённое ускорение»
Если динамика механической системы описывается не в декартовых, а в обобщённых координатах qi{\displaystyle q_{i}} (например, в гамильтоновой или в лагранжевой формулировках механики), то можно ввести обобщённые ускорения qi¨{\displaystyle {\ddot {q_{i}}}} — первые производные по времени обобщённых скоростей qi˙{\displaystyle {\dot {q_{i}}}} или вторые производные по времени обобщённых координат; например, если в качестве одной из обобщённых координат выбран угол, то обобщённым ускорением будет соответствующее угловое ускорение. Размерность обобщённых ускорений в общем случае не равна LT−2.
Суд в США обязал Сноудена отказаться от миллионов, полученных за книгу об американской разведке
Страна.ua
вчера в 20:26
Понятие «обобщённое ускорение»
Если динамика механической системы описывается не в декартовых, а в обобщённых координатах qi{\displaystyle q_{i}} (например, в гамильтоновой или в лагранжевой формулировках механики), то можно ввести обобщённые ускорения qi¨{\displaystyle {\ddot {q_{i}}}} — первые производные по времени обобщённых скоростей qi˙{\displaystyle {\dot {q_{i}}}} или вторые производные по времени обобщённых координат; например, если в качестве одной из обобщённых координат выбран угол, то обобщённым ускорением будет соответствующее угловое ускорение. Размерность обобщённых ускорений в общем случае не равна LT−2.
Ускорения в кинематике твёрдого тела
Связь ускорений двух точек абсолютно твёрдого тела A и B можно получить из формулы Эйлера для скоростей этих точек:
- v→B=v→A+ω→×AB→,{\displaystyle {\vec {v}}_{B}={\vec {v}}_{A}+\left,}
где ω→{\displaystyle {\vec {\omega }}} — вектор угловой скорости тела. Продифференцировав её по времени, получаем формулу Ривальса (Marc-Joseph-Émilien Rivals, 1833–1889):
- a→B=a→A+ω→×ω→×AB→+ε→×AB→,{\displaystyle {\vec {a}}_{B}={\vec {a}}_{A}+\left\right]+\left,}
где ε→{\displaystyle {\vec {\varepsilon }}} — вектор углового ускорения тела.
Второе слагаемое называется осестремительным ускорением, а третье — вращательным ускорением.
Полезные свойства улитки
Ускорение в теории относительности
В теории относительности движение тела с переменной скоростью вдоль мировой линии в 4-мерном пространстве-времени характеризуется определённой величиной, аналогичной ускорению. В отличие от обычного (трёхмерного) вектора ускорения, 4-вектор ускорения (называемый 4-ускорением) ai является второй производной от 4-вектора координат xi не по времени, а по пространственно-временному интервалу τ (или, что то же самое, по собственному времени) вдоль мировой линии тела:
- ai=d2xidτ2=duidτ.{\displaystyle a^{i}={\frac {d^{2}x^{i}}{d\tau ^{2}}}={\frac {du^{i}}{d\tau }}.}
В любой точке мировой линии 4-вектор ускорения всегда ортогонален к 4-скорости:
- uiai=.{\displaystyle u_{i}a^{i}=0\,.}
Это означает, в частности, что 4-скорости меняются не по модулю, а лишь по направлению: независимо от направления в пространстве-времени 4-скорость любого тела равна по модулю скорости света. Геометрически, 4-ускорение совпадает с кривизной мировой линии и является аналогом нормального ускорения в классической кинематике.
В классической механике значение ускорения не изменяется при переходе от одной инерциальной системы отсчета к другой, то есть ускорение инвариантно относительно преобразований Галилея. В релятивистской механике 4-ускорение является 4-вектором, то есть при преобразованиях Лоренца изменяется аналогично пространственно-временным координатам.
«Обычный» трёхмерный вектор ускорения w→{\displaystyle {\vec {w}}} (то же, что a→(t){\displaystyle {\vec {a}}(t)} в предыдущих разделах, обозначение заменено во избежание путаницы с 4-ускорением), определяемый как производная «обычной» трёхмерной скорости v→{\displaystyle {\vec {v}}} по координатному времени w→=dv→dt{\displaystyle {\vec {w}}=d{\vec {v}}/dt}, применяется и в рамках релятивистской кинематики, но инвариантом преобразований Лоренца не является. В мгновенно сопутствующей инерциальной системе отсчёта 4-ускорение — это a=(,w→).{\displaystyle a=(0,{\vec {w}}).} При действии постоянной силы ускорение точки w→{\displaystyle {\vec {w}}} уменьшается с ростом скорости, однако 4-ускорение остаётся неизменным (такой случай именуют релятивистски равноускоренным движением, хотя «обычное» ускорение при этом не постоянно).
Что такое ускоренное движение
Ускоренное движение — что это такое? Хороший вопрос. Давайте разберем это понятие по словам.
«Движение» — значит, что-то двигается. Ага, значит тело перемещается, значит у него есть какая-то скорость.
«Ускоренное» — значит «убыстренное», с возрастающей скоростью, когда тело двигается все быстрее и быстрее. Ага, значит скорость не постоянная. Она меняется. Тело двигается все быстрее, быстрее и быстрее… То есть скорость все время увеличивается.
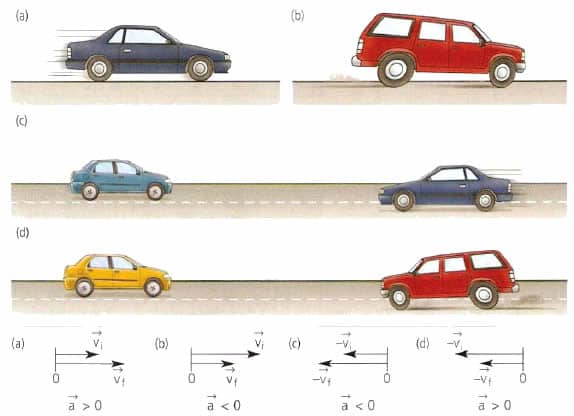
Это может прозвучать странно, но случай, когда скорость уменьшается и уменьшается, а тело двигается все медленнее, медленнее и медленнее, — это тоже «ускоренное» движение. В это трудно поверить (и это трудно понять) прямо сейчас, но позже вам станет понятнее. Иногда такое движение с уменьшением скорости называют равнозамедленным движением.
Чтобы быть конкретнее, посмотрим на пример: мальчик на велосипеде разгоняется из состояния покоя. Сначала у него скорость 555 км/ч, потом 1101 км/ч, потом 151515 км/ч, 2202 км/ч, 252525 км/ч, 3303 км/ч и т.д. — насколько у него хватит сил.
Точно так же, как мальчик разгоняется на велосипеде, кто-то, например девочка на самокате, может тормозить, останавливаться, двигаться все медленнее, медленнее и медленнее. В конце — остановиться. Сначала у нее может быть скорость 1101 км/ч, потом 555 км/ч, а потом км/ч. То есть скорость все время уменьшается на 555 км/ч.
Следуя этой логике, через мгновение после скорости в км/ч скорость должна вновь уменьшиться на 555 км/ч, и тогда скорость будет равна −5-5−5 км/ч, а потом еще уменьшиться на 555 км/ч и стать уже −1-10−1 км/ч, а потом и −15-15−15 км/ч и т.д. Ведь уменьшение скорости должно происходить и дальше. Кому-то отрицательная скорость может показаться странной. Тем, кому она кажется странной, хочу напомнить, что когда мы говорим о скорости не как о векторе (не как о «стрелочке»), то чаще всего мы имеем в виду проекцию скорости на некоторую ось. Если направление вектора совпадает с направлением этой оси, то проекция получается положительной. Если скорость противоположна направлению оси — то проекция получается отрицательной. Тем, кому приведенные объяснения кажутся непонятными, мы рекомендуем прочитать темы «Два вида физических величин: скалярные величины и векторные величины» и «Проектирование векторов на оси». В этих темах подробно рассказывается о том, как вектора проецируются на оси координат.
Вернемся к примеру с девочкой. Мы видим, что ее скорость начинает возрастать в отрицательном направлении. То есть наше замедленное движение девочки на самокате переходит в ускоренное движение (когда скорость набирается), но уже в противоположную сторону. Именно поэтому замедленное движение — это вариант ускоренного движения. Поэтому между ускоренным и замедленным движениями (как правило) не делают различий и называют их просто ускоренным движением.
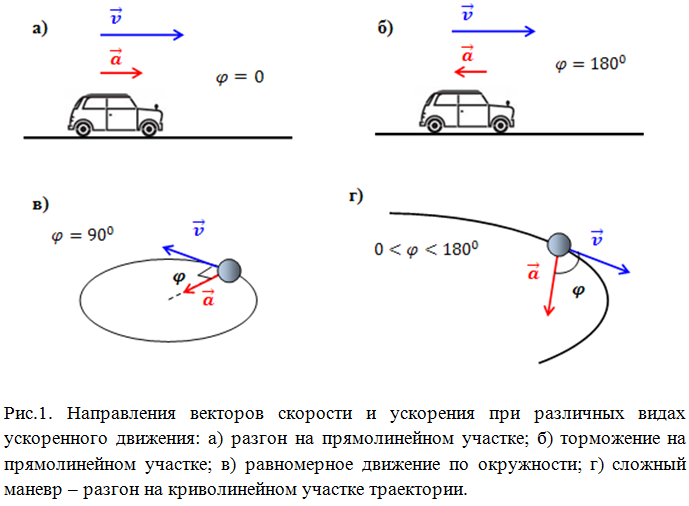
В итоге мы пришли к тому, что ускоренное движение — это движение, при котором меняется скорость. Но мы помним, что скорость — это векторная величина. А любой вектор характеризуется двумя величинами: длиной и направлением. Так вот, оказывается, что тело движется с ускорением в случае, если меняется скорость по величине (тело убыстряет свое движение) или же тело меняет направление скорости (тело поворачивает). Первый случай (с изменением величины — или, как говорят, модуля) мы рассмотрим сейчас в теме «Равноускоренное движение», а второй случай — с поворотом — в теме «Движение по окружности», когда тело поворачивает, а значит — изменяет направление скорости.
Виды ускорений
Что такое ускорение в формулах. Вид ускорения зависит от вектора движения тела. В физике это может быть движение по прямой, по кривой линии и по окружности.
- Если предмет движется по прямой линии, движение будет равноускоренным, и на него начнут действовать линейные ускорения. Формула для его вычисления (смотри формулу 1 на рис): a=dv/dt
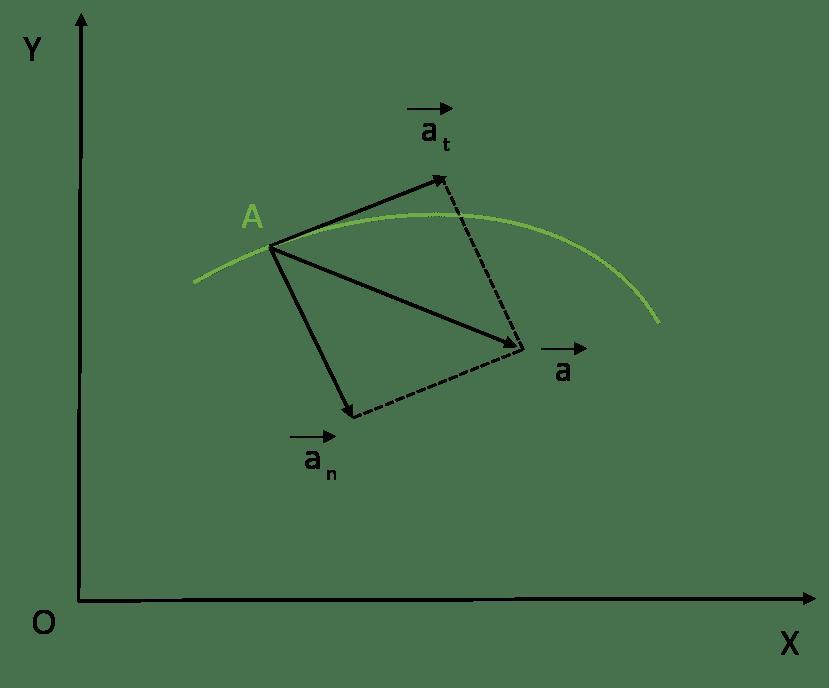
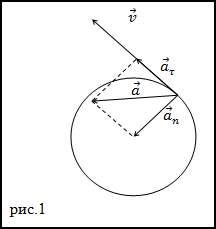
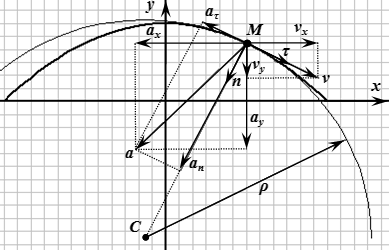
- В случае, если речь идет о движении тела по окружности, то ускорение будет состоять из двух частей (a=aт+an): тангенциального и нормального ускорения. Оба они характеризуются скоростью движения предмета. Тангенциальное — изменением скорости по модулю. Его направление идет по касательной к траектории. Такое ускорение вычисляется по формуле (см. формулу 2 на рис): at=d|v|/dt
- Если же скорость движения предмета по окружности постоянна, ускорение называется центростремительным или нормальным. Вектор такого ускорения постоянно направлен к центру окружности, а значение модуля равно (смотри формулу 3 на рис): |a(вектор)|=w2r=V2/r
- Когда скорость тела по окружности разная, возникает угловое ускорение. Оно показывает, как изменилась угловая скорость за единицу времени и равно (см. формулу 4 на рис.):E(вектор)=dw(вектор)/dt
- В физике также рассматриваются варианты, когда тело движется по окружности, но при этом приближается или удаляется от центра. В этом случае на предмет действуют ускорения Кориолиса.Когда тело движется по кривой линии, вектор его ускорения будет вычисляться по формуле (см. формулу 5 на рис): a (вектор)=aTT+ann(вектор)+abb(вектор)=dv/dtT+v2/Rn(вектор)+abb(вектор),в которой:
- v — скорость
- T (вектор) — единичный касательный к траектории вектор, идущий вдоль скорости (касательный орт)
- n (вектор) — орт главной нормали относительно траектории, который определяется как единичный вектор в направлении dT (вектор)/dl
- b (вектор) — орт бинормали относительно траектории
- R — радиус кривизны траектории
При этом бинормальное ускорение abb(вектор) всегда равно нулю. Поэтому конечная формула выглядит так (см. формулу 6 на рис): a (вектор)=aTT+ann(вектор)+abb(вектор)=dv/dtT+v2/Rn(вектор)
Создание ускорения. Динамика точки
Первый закон Ньютона постулирует существование инерциальных систем отсчёта. В этих системах отсчёта равномерное прямолинейное движение имеет место в том случае, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом, постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчёта всегда является некоторое внешнее силовое воздействие.
Классическая механика
Второй закон Ньютона применительно к нерелятивистскому движению (то есть к движению со скоростями, много меньшими скорости света) утверждает, что ускорение материальной точки всегда пропорционально приложенной к ней и порождающей ускорение силе, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется инертной массой материальной точки):
- ma→=F→.{\displaystyle m{\vec {a}}={\vec {F}}.}
Если известны масса материальной точки и (как функция времени) сила, действующая на неё, то из второго закона Ньютона известно и её ускорение: a→=F→m.{\displaystyle {\vec {a}}={\vec {F}}/m.} При постоянстве силы ускорение также будет постоянным. Скорость и координаты точки в любой момент времени можно получить, проинтегрировав ускорение по формулам из раздела о кинематике точки при заданных начальных скорости и координатах.
Релятивистская механика
В релятивистской физике второй закон Ньютона записывается в форме
- mddtv→1−v2c2=F→{\displaystyle m{\frac {d}{dt}}{\frac {\vec {v}}{\sqrt {1-v^{2}/c^{2}}}}={\vec {F}}}
что делает нахождение ускорения более сложной задачей, чем в классическом случае. В частности, длительное движение с постоянным ускорением принципиально невозможно (иначе скорость точки в конце концов превысит скорость света), а неизменность силы не означает неизменности ускорения: оно будет стремиться к нулю при нарастании скорости. Тем не менее, если зависимость a→(t){\displaystyle {\vec {a}}(t)} всё же найдена, расчёт v→(t){\displaystyle {\vec {v}}(t)} и r→(t){\displaystyle {\vec {r}}(t)} осуществим по тем же формулам, что и в нерелятивистском пределе.
Ускорения в кинематике твёрдого тела
Связь ускорений двух точек абсолютно твёрдого тела A и B можно получить из формулы Эйлера для скоростей этих точек:
- v→B=v→A+ω→×AB→,{\displaystyle {\vec {v}}_{B}={\vec {v}}_{A}+\left,}
где ω→{\displaystyle {\vec {\omega }}} — вектор угловой скорости тела. Продифференцировав её по времени, получаем формулу Ривальса (Marc-Joseph-Émilien Rivals, 1833–1889):
- a→B=a→A+ω→×ω→×AB→+ε→×AB→,{\displaystyle {\vec {a}}_{B}={\vec {a}}_{A}+\left\right]+\left,}
где ε→{\displaystyle {\vec {\varepsilon }}} — вектор углового ускорения тела.
Второе слагаемое называется осестремительным ускорением, а третье — вращательным ускорением.
Ускорение и путь
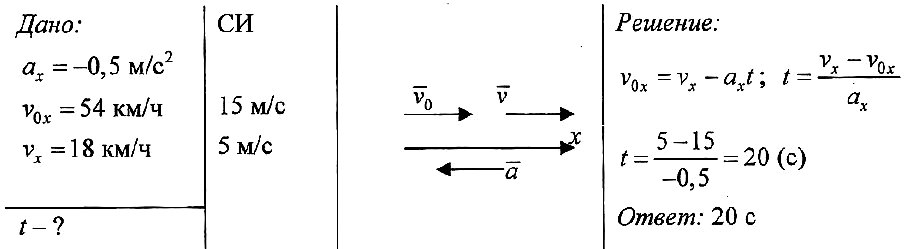
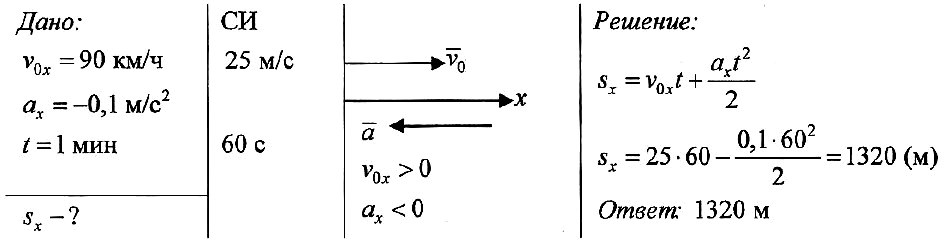
При решении задач на равноускоренное перемещение часто требуется найти ускорение, зная пройденный путь. Покажем, какие формулы для этого следует применять.
Путь рассчитать несложно при равноускоренном движении по прямой. Для этого следует взять интеграл по времени от уравнения v(t). Выполнив это математическое действие, получим три рабочие формулы:
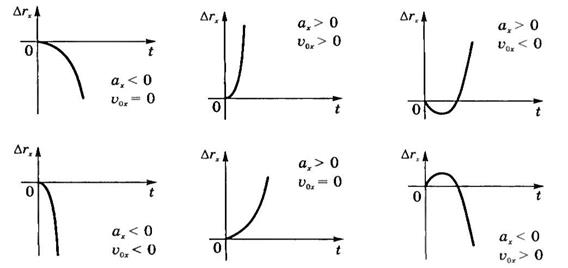
Первое выражение описывает ускоренное перемещение тела из состояния покоя, второе — ускоренное перемещение с наличием начальной скорости, третье — торможение. Графики всех трех функций S(t) являются параболами.
Как выразить ускорение из формул равноускоренного движения для пути? Для этого необходимо изолировать множитель a*t2 в одной части равенства, а затем все равенство поделить на квадрат времени. Из формул выше получаем:
Первое уравнение используется для экспериментального определения ускорения свободного падения g, когда тяжелые тела сбрасывают вниз с некоторой высоты. Подобные эксперименты проводил еще Галилей в конце XVI века. В настоящее время для определения ускорения g в исследуемой местности используют абсолютные гравиметры, принцип работы которых также основан на свободном падении.

Два последних уравнения отличаются друг от друга лишь знаком ускорения. При торможении ускорение считают отрицательным.
Все три выражения приводят к одной и той же единице измерения величины a — м/с2.
Ускорение в теории относительности
В теории относительности движение тела с переменной скоростью вдоль мировой линии в 4-мерном пространстве-времени характеризуется определённой величиной, аналогичной ускорению. В отличие от обычного (трёхмерного) вектора ускорения, 4-вектор ускорения (называемый 4-ускорением) ai является второй производной от 4-вектора координат xi не по времени, а по пространственно-временному интервалу τ (или, что то же самое, по собственному времени) вдоль мировой линии тела:
- ai=d2xidτ2=duidτ.{\displaystyle a^{i}={\frac {d^{2}x^{i}}{d\tau ^{2}}}={\frac {du^{i}}{d\tau }}.}
В любой точке мировой линии 4-вектор ускорения всегда ортогонален к 4-скорости:
- uiai=.{\displaystyle u_{i}a^{i}=0\,.}
Это означает, в частности, что 4-скорости меняются не по модулю, а лишь по направлению: независимо от направления в пространстве-времени 4-скорость любого тела равна по модулю скорости света. Геометрически, 4-ускорение совпадает с кривизной мировой линии и является аналогом нормального ускорения в классической кинематике.
В классической механике значение ускорения не изменяется при переходе от одной инерциальной системы отсчета к другой, то есть ускорение инвариантно относительно преобразований Галилея. В релятивистской механике 4-ускорение является 4-вектором, то есть при преобразованиях Лоренца изменяется аналогично пространственно-временным координатам.
«Обычный» трёхмерный вектор ускорения w→{\displaystyle {\vec {w}}} (то же, что a→(t){\displaystyle {\vec {a}}(t)} в предыдущих разделах, обозначение заменено во избежание путаницы с 4-ускорением), определяемый как производная «обычной» трёхмерной скорости v→{\displaystyle {\vec {v}}} по координатному времени w→=dv→dt{\displaystyle {\vec {w}}=d{\vec {v}}/dt}, применяется и в рамках релятивистской кинематики, но инвариантом преобразований Лоренца не является. В мгновенно сопутствующей инерциальной системе отсчёта 4-ускорение — это a=(,w→).{\displaystyle a=(0,{\vec {w}}).} При действии постоянной силы ускорение точки w→{\displaystyle {\vec {w}}} уменьшается с ростом скорости, однако 4-ускорение остаётся неизменным (такой случай именуют релятивистски равноускоренным движением, хотя «обычное» ускорение при этом не постоянно).
Ареал обитания
Основные понятия и законы кинематики
кинематикойМеханическим движениемСистемой отсчётаТелом отсчётаМатериальной точкойТраекториейпрямолинейноекриволинейное
Путь — это длина траектории, которую описывает материальная точка за данный промежуток времени. Это скалярная величина.Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).
Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение — это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось)
А путь — это, наборот, скалярная величина, отражающая длину пройденной траектории.
Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещенияСкоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:
Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:
Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину
Ускорением
Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x + Vxt, где x — начальная координата тела, Vx — скорость движения.Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с2, не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.
Скорость при свободном падении рассчитывается по формуле:
Перемещение по вертикали рассчитывается по формуле:
Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости
ω:
Угловая скорость связана с линейной скоростью соотношением где r — радиус окружности.
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду — частота обращения — ν
Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением, оно направлено по радиусу к центру окружности: