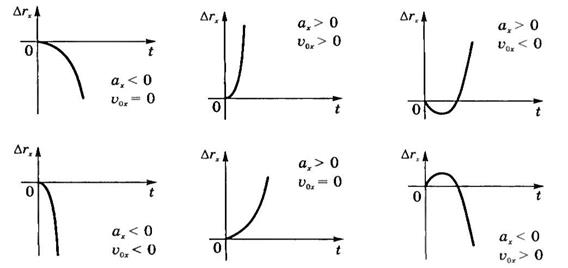
Индивидуализация
Наиболее адекватным ответом на новые проблемы в организации образования стала индивидуализация — опора на личные особенности и пристрастия ученика. Для этого учитель и ученик должны оказаться созвучны, взаимоинтересны и полезны. Вариантов может быть много. Для тьютора это акцент исключительно на формирование личного позыва ребенка (тьюторанта) — он сам является источником образовательной программы. На западе это часто называют персонализацией. Но есть и более технологичный вариант, когда можно выбрать из набора — это более традиционный вариант индивидуализации, в противовес строго персональному (заказному) подходу. Во втором варианте всегда есть образовательная программа в традиционном смысле, но набор учебных курсов у каждого получается свой — все траектории разные. В первом варианте образовательная программа может быть как традиционная, так и в специфическом понимании тьюторов. А траектория тоже индивидуальная.
Итак, 3 варианта формирования образовательной программы в разных смыслах, но во всех формируется индивидуальная образовательная траектория.
Если предположить, что с учетом стремительного расширения способов и каналов обучения каждый ученик окажется перед широчайшим разнообразием выбора, то проблемой станет акт выбора. Что услуги консультантов будут остро востребованы и что искусственный интеллект будет с живыми консультантами успешно конкурировать, уже понятно. Интересно, что будет первично, программа (маршрут) или траектория?
Берусь утверждать, что в условиях быстрых изменений и широкого выбора, каждый следующий образовательный выбор будет в значительной мере ситуативен и спонтанен. Могу предположить манипулятивные управляющие действия на молодежь, но этот вариант рассматривать не хочу — это социальные риски. В открытой среде на выбор смогут влиять значимые субъекты. В профессии останутся только значимые для ребенка люди, имеющие вес своими эмоциональными, социальными, профессиональными компетенциями. Именно они смогут выстраивать ситуации, в которых дети с удовольствием будут что-то осваивать. Именно они смогут через серию успехов и формирования уверенной компетенции подвести их к целевому поведению, в котором требуется построение маршрутов и программ, а не только сиюминутных образовательных продвижений.
Учитывая, что и для старшего поколения, воспитанного в проектной логике, она не стала определяющей для всех, надеяться на всеобщий охват программным (проектным) мышлением не приходится. Но он не всем нужен, как выясняется по жизни, несмотря на постоянное давление, создаваемое рекламой про лидерство и организованность.
Описание траектории
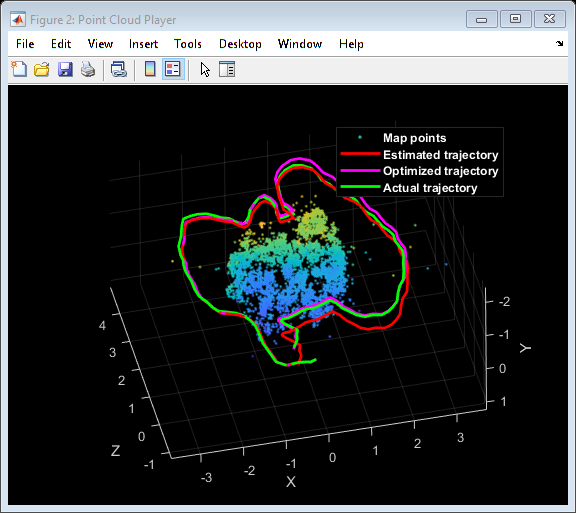
Рис. 2. Прямолинейное равномерно ускоряющееся движение в одной инерциальной системе в общем случае будет параболическим в другой равномерно двигающейся инерциальной системе отсчёта.
Принято описывать траекторию материальной точки в наперёд заданной системе координат при помощи радиус-вектора, направление, длина и начальная точка которого зависят от времени. При этом кривая, описываемая концом радиус-вектора в пространстве может быть представлена в виде сопряжённых дуг различной кривизны, находящихся в общем случае в пересекающихся плоскостях. При этом кривизна каждой дуги определяется её радиусом кривизны, направленном к дуге из мгновенного центра поворота, находящегося в той же плоскости, что и сама дуга. При том прямая линия рассматривается как предельный случай кривой, радиус кривизны которой может считаться равным бесконечности. И потому траектория в общем случае может быть представлена как совокупность сопряжённых дуг.
Существенно, что форма траектории зависит от системы отсчёта, избранной для описания движения материальной точки. Так, прямолинейное равномерно ускоряющееся движение в одной инерциальной системе в общем случае будет параболическим в другой равномерно двигающейся инерциальной системе отсчёта.
Участок траектории материальной точки в физике обычно называют путём и обычно обозначают символом S — от итал. spostamento (перемещение).
Полемика по терминам
Оттолкнусь от позиции Татьяны Ковалевой, как я ее понял.
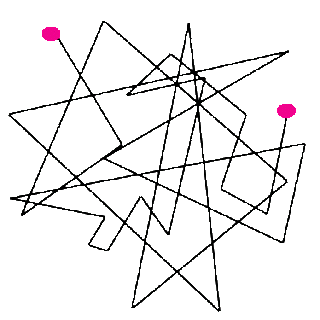
Траектория — путь пройденный пассивным телом, а тьюторы ставят перед собой задачу активного самоопределения ребенка (тьюторанта), поэтому они исключают траекторию из своего вокабуляра. Они выводят ребенка на построение индивидуальной образовательной программы. Для этого они вместе с ребенком строят его личную (индивидуальную) ресурсную карту (топику, векторность, масштаб), а программой называют выбор очередного образовательного (развивающего) шага. В их логике у программы нет конечной точки, ибо человек постоянно развивается: «Программа — это личная свертка ресурсной карты в данный момент». На вопрос о том, что такое определение термина «программа» заметно отличается от общепринятого, было дано подтверждение: да, они этот термин трактуют по своему, опираясь на позицию философа и культуролога Вадима Марковича Розина.
Похожее отношение к траектории у Анатолия Сторожева: «Образовательная траектория — это когда меня запулили и я лечу по инерции мышления. Образовательный маршрут — это когда я его прохожу, это мой жизненный Путь, я строил его карту, я могу изменить свои планы, посидеть и осмотреться, принять новые решения».
Четкий доклад Ковалевой позволяет опереться на ее тезисы и обозначить свои. Прежде всего, она сразу обозначила свою позицию как тьютора. Это облегчает мои рассуждения, потому что позиций может быть много, и моя — не тьюторская. Моя позиция — конструктора новой системы образования, в которой тьютор является одной из важных ролей, но далеко не единственной
Мне важно понять ролевой ассортимент системы и модель отношений между ролями, чтобы вся совокупность максимально отвечала целям всех участников:
- траектория — кинетический термин, имеющий весьма четкую коннотацию в физике: след движения тела. Никаких указаний на его активность или пассивность нет. В задачах часто фигурируют управляемые объекты;
- маршрут — логистический термин: предполагаемый вариант движения. В идеале траектория должна совпасть с маршрутом, но это редко случается. Кроме того, маршрут не всегда прорабатывается настолько четко, чтобы траектория могла с ним совпасть: маршрут может содержать только контрольные точки с предполагаемым диапазоном времени;
- программа в традиционном понимании — план действий с описанием ожидаемых результатов и используемых ресурсов. Маршрут может быть частным случаем программы.
Если мы накладываем эти понятия на образовательные задачи, то траектория — это ретроспектива движения по образовательной среде, а программа и маршрут — перспектива этого движения. Причем, чтобы понятия имели разное содержание, имеет смысл считать программу подробно прописанным планом действий, а маршрут— в виде контрольных точек, оставляя свободу реализации движения между ними.
При такой трактовке, как мне кажется, тьюторы не могут игнорировать образовательную траекторию, ибо «здесь и сейчас» любого человека определяется накопленным багажом, отталкиваясь от которого можно строить планы (программы, маршруты). В такой логике, на первый взгляд, невозможно строить образовательную траекторию — только планы. И второе замечание — планы могут быть любыми, а траектория исключительно индивидуальная, ибо у каждого она своя, уже пройденная.
Следует обратить внимание, что подобное заимствование терминов из другой сферы происходит только тогда, когда появляются новые смыслы, для которых нет адекватных терминов. Тогда по ассоциации из другой области берется термин, который аналогичен неопределенному новому смыслу
Но дальше происходит расширение ассоциаций — экспансия слова из другой сферы в гораздо большем объеме. Например, траектория начинает трактоваться не только как след от движения, но и как возможность прогноза этого движения на основании расчетов, хотя в нашем случае такая ассоциация становится предельно неопределенной, в отличие от понятных задач баллистики. Или накладываются непонятные дополнительные ограничения типа пассивности объекта — так воспринимается термин специалистом в другой сфере знаний. Поэтому нужно либо строже договариваться о введении новых понятий, либо игнорировать их произвольное употребление и каждый раз уточнять, кто какой смысл в него вкладывает.
Примечания
- Понятие траектории достаточно наглядно может быть проиллюстрировано трассой бобслея. (Если по условиям задачи можно пренебречь её шириной). И именно трассой, а не самим бобом.
- Так улица, в начале которой висит знак «кирпич» останется в принципе траекторией движения по ней. А поезда разной массы, движущиеся под различными тяговыми усилиями на сцепных крюках локомотивов и потому с разной скоростью, будут двигаться по одной и той же траектории, определяемой формой рельсового пути, налагающего на движение несвободного тела (поезда) конкретные связи, интенсивность которых будет в каждом случае различной
-
Так, Луна обращается вокруг Земли только в системе отсчёта, связанной с их общим центром гравитации (находится внутри Земного шар). В системе же отсчёта, началом которой является Солнце, Луна обращается вокруг него по той же эллиптической орбите, что и Земля, но с периодическими отклонениями от неё на величину расстояния от Луны до Земли. Никакого взаимного обращения этих небесных тел в этом случае просто нет.
Наличие земного притяжения для объяснения формы траектории Луны в системе координат, связанной с Солнцем, вообще не обязательно. Так, исчезни Земля, Луна могла бы продолжать двигаться, как самостоятельное небесное тело, по той же самой старой траектории, а её периодические возмущения можно было бы тогда в качестве гипотезы объяснить изменением силы тяготения, скажем, за счёт вариации массы Солнца по причине пульсации его светимости (что, кстати, и наблюдается в определённых пределах в действительности).
И обе упомянутые формы траектории истинны и оба объяснения их формы на основании правильно проведённого анализа действующих сил справедливы. Но они исключают друг друга, как исключается возможность одновременного рассмотрения при выборе той или иной системы координат.
- ↑ С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука». Главная редакция физико-математической литературы.
- Физический энциклопедический словарь/ Гл. ред. А. М. Прохоров. Ред.кол. Д. М. Алексеев, А. М. Бонч-Бруевич,А. С. Боровик-Романов и др. М.: Сов.энциклопедия, 1983. — 323 с.,ил, 2 л.цв.ил. страница 282.
В физике есть ещё одна формула измерения траектории (пути): s=4Atv, где A — амплитуда, t — время, v — частота колебаний
Что строим?
А раз так, основным в образовании получается освоенное (траектория), а не программа (маршрут)! Но учителя проектную логику все равно вынуждены вести, даже если подготовленные планы приходится все время корректировать, т.е. будут продолжать строить программы (с учетом возрастающей гибкости), а ученики и родители — траекторию: учителя проективно, а ученики с родителями — ситуативно, по факту, на один-два шага «здесь и сейчас», в тьюторском понимании программы.
Из этого совсем не следует хаотичность образовательного процесса и ненужность учителей, тьюторов, консультантов: они действуют проективно, их предложения по построению и реализации образовательных маршрутов важны именно внятностью перспектив. Именно это дает разумный выбор ученикам и их родителям. Но с их стороны выбор происходит не раз и навсегда, а итерационно, шаг за шагом. И никто не знает, будет ли следующий шаг продолжением прошлого выбора или он окажется на новом образовательном маршруте.
Описание траектории
Рис. 2. Прямолинейное равномерно ускоряющееся движение в одной инерциальной системе в общем случае будет параболическим в другой равномерно двигающейся инерциальной системе отсчёта.
Принято описывать траекторию материальной точки в наперёд заданной системе координат при помощи радиус-вектора, направление, длина и начальная точка которого зависят от времени. При этом кривая, описываемая концом радиус-вектора в пространстве может быть представлена в виде сопряжённых дуг различной кривизны, находящихся в общем случае в пересекающихся плоскостях. При этом кривизна каждой дуги определяется её радиусом кривизны, направленном к дуге из мгновенного центра поворота, находящегося в той же плоскости, что и сама дуга. При том прямая линия рассматривается как предельный случай кривой, радиус кривизны которой может считаться равным бесконечности. И потому траектория в общем случае может быть представлена как совокупность сопряжённых дуг.
Существенно, что форма траектории зависит от системы отсчёта, избранной для описания движения материальной точки. Так, прямолинейное равномерно ускоряющееся движение в одной инерциальной системе в общем случае будет параболическим в другой равномерно двигающейся инерциальной системе отсчёта.
Участок траектории материальной точки в физике обычно называют путём и обычно обозначают символом S — от итал. spostamento (перемещение).
Связь со скоростью и нормальным ускорением
Рис. 3. Суточное движение светил в системе отсчёта, связанной с фотоаппаратом в проекции на плоскость рисунка
Скорость материальной точки всегда направлена по касательной к дуге, используемой для описания траектории точки. При этом существует связь между величиной скорости v{\displaystyle v}, an{\displaystyle a_{n}} и радиусом кривизны траектории R{\displaystyle R} в данной точке:
- an=v2R{\displaystyle a_{n}={\frac {v^{2}}{R}}}
Однако, не всякое движение с известной скоростью по кривой известного радиуса и найденное по приведённой выше формуле нормальное (центростремительное) ускорение связано с проявлением силы, направленной по нормали к траектории (центростремительной силы). Так, найденное по данным фотографии суточного движения светил ускорение любой из звёзд отнюдь не говорит о существовании вызывающей это ускорение силы, притягивающей её к Полярной звезде, как центру вращения.
Примечания
- Понятие траектории достаточно наглядно может быть проиллюстрировано трассой бобслея. (Если по условиям задачи можно пренебречь её шириной). И именно трассой, а не самим бобом.
- Так улица, в начале которой висит знак «кирпич» останется в принципе траекторией движения по ней. А поезда разной массы, движущиеся под различными тяговыми усилиями на сцепных крюках локомотивов и потому с разной скоростью, будут двигаться по одной и той же траектории, определяемой формой рельсового пути, налагающего на движение несвободного тела (поезда) конкретные связи, интенсивность которых будет в каждом случае различной
-
Так, Луна обращается вокруг Земли только в системе отсчёта, связанной с их общим центром гравитации (находится внутри Земного шар). В системе же отсчёта, началом которой является Солнце, Луна обращается вокруг него по той же эллиптической орбите, что и Земля, но с периодическими отклонениями от неё на величину расстояния от Луны до Земли. Никакого взаимного обращения этих небесных тел в этом случае просто нет.
Наличие земного притяжения для объяснения формы траектории Луны в системе координат, связанной с Солнцем, вообще не обязательно. Так, исчезни Земля, Луна могла бы продолжать двигаться, как самостоятельное небесное тело, по той же самой старой траектории, а её периодические возмущения можно было бы тогда в качестве гипотезы объяснить изменением силы тяготения, скажем, за счёт вариации массы Солнца по причине пульсации его светимости (что, кстати, и наблюдается в определённых пределах в действительности).
И обе упомянутые формы траектории истинны и оба объяснения их формы на основании правильно проведённого анализа действующих сил справедливы. Но они исключают друг друга, как исключается возможность одновременного рассмотрения при выборе той или иной системы координат.
- ↑ С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука». Главная редакция физико-математической литературы.
- Физический энциклопедический словарь/ Гл. ред. А. М. Прохоров. Ред.кол. Д. М. Алексеев, А. М. Бонч-Бруевич,А. С. Боровик-Романов и др. М.: Сов.энциклопедия, 1983. — 323 с.,ил, 2 л.цв.ил. страница 282.
В физике есть ещё одна формула измерения траектории (пути): s=4Atv, где A — амплитуда, t — время, v — частота колебаний
Связь со скоростью и нормальным ускорением
Рис. 3. Суточное движение светил в системе отсчёта, связанной с фотоаппаратом в проекции на плоскость рисунка
Скорость материальной точки всегда направлена по касательной к дуге, используемой для описания траектории точки. При этом существует связь между величиной скорости v{\displaystyle v}, an{\displaystyle a_{n}} и радиусом кривизны траектории R{\displaystyle R} в данной точке:
- an=v2R{\displaystyle a_{n}={\frac {v^{2}}{R}}}
Однако, не всякое движение с известной скоростью по кривой известного радиуса и найденное по приведённой выше формуле нормальное (центростремительное) ускорение связано с проявлением силы, направленной по нормали к траектории (центростремительной силы). Так, найденное по данным фотографии суточного движения светил ускорение любой из звёзд отнюдь не говорит о существовании вызывающей это ускорение силы, притягивающей её к Полярной звезде, как центру вращения.
Примечания
- Понятие траектории достаточно наглядно может быть проиллюстрировано трассой бобслея. (Если по условиям задачи можно пренебречь её шириной). И именно трассой, а не самим бобом.
- Так улица, в начале которой висит знак «кирпич» останется в принципе траекторией движения по ней. А поезда разной массы, движущиеся под различными тяговыми усилиями на сцепных крюках локомотивов и потому с разной скоростью, будут двигаться по одной и той же траектории, определяемой формой рельсового пути, налагающего на движение несвободного тела (поезда) конкретные связи, интенсивность которых будет в каждом случае различной
-
Так, Луна обращается вокруг Земли только в системе отсчёта, связанной с их общим центром гравитации (находится внутри Земного шар). В системе же отсчёта, началом которой является Солнце, Луна обращается вокруг него по той же эллиптической орбите, что и Земля, но с периодическими отклонениями от неё на величину расстояния от Луны до Земли. Никакого взаимного обращения этих небесных тел в этом случае просто нет.
Наличие земного притяжения для объяснения формы траектории Луны в системе координат, связанной с Солнцем, вообще не обязательно. Так, исчезни Земля, Луна могла бы продолжать двигаться, как самостоятельное небесное тело, по той же самой старой траектории, а её периодические возмущения можно было бы тогда в качестве гипотезы объяснить изменением силы тяготения, скажем, за счёт вариации массы Солнца по причине пульсации его светимости (что, кстати, и наблюдается в определённых пределах в действительности).
И обе упомянутые формы траектории истинны и оба объяснения их формы на основании правильно проведённого анализа действующих сил справедливы. Но они исключают друг друга, как исключается возможность одновременного рассмотрения при выборе той или иной системы координат.
- ↑ С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука». Главная редакция физико-математической литературы.
- Физический энциклопедический словарь/ Гл. ред. А. М. Прохоров. Ред.кол. Д. М. Алексеев, А. М. Бонч-Бруевич,А. С. Боровик-Романов и др. М.: Сов.энциклопедия, 1983. — 323 с.,ил, 2 л.цв.ил. страница 282.
В физике есть ещё одна формула измерения траектории (пути): s=4Atv, где A — амплитуда, t — время, v — частота колебаний
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. В состав системы отсчёта входят
1) только тело отсчёта
2) только тело отсчёта и система координат
3) только тело отсчёта и часы
4) тело отсчёта, система координат, часы
2. Относительной величиной является: А. Путь; Б. Перемещение. Правильный ответ
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
3. Пассажир метро стоит на движущемся вверх эскалаторе. Он неподвижен относительно
1) пассажиров, стоящих на другом эскалаторе, движущемся вниз
2) других пассажиров, стоящих на этом же эскалаторе
3) пассажиров, шагающих вверх по этому же эскалатору
4) светильников на баллюстраде эскалатора
4. Относительно какого тела покоится автомобиль, движущийся по автостраде?
1) относительно другого автомобиля, движущегося с такой же скоростью в противоположную сторону
2) относительно другого автомобиля, движущегося с такой же скоростью в ту же сторону
3) относительно светофора
4) относительно идущего вдоль дороги пешехода
5. Два автомобиля движутся с одинаковой скоростью 20 м/с относительно Земли в одном направлении. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?
1) 0
2) 20 м/с
3) 40 м/с
4) -20 м/с
6. Два автомобиля движутся с одинаковой скоростью 15 м/с относительно Земли навстречу друг другу. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?
1) 0
2) 15 м/с
3) 30 м/с
4) -15 м/с
7. Какова относительно Земли траектория точки лопасти винта летящего вертолёта?
1) прямая
2) окружность
3) дуга
4) винтовая линия
8. Мяч падает с высоты 2 м и после удара о пол поднимается на высоту 1,3 м. Чему равны путь \( l \) и модуль перемещения \( s \) мяча за всё время движения?
1) \( l \)= 3,3 м, \( s \) = 3,3 м
2) \( l \) = 3,3 м, \( s \) = 0,7 м
3) \( l \)= 0,7 м, \( s \) = 0,7 м
4) \( l \)= 0,7 м, \( s \) = 3,3 м
9. Решают две задачи. 1. Рассчитывают скорость движения поезда между двумя станциями. 2. Определяют силу трения, действующую на поезд. При решении какой задачи поезд можно считать материальной точкой?
1) только первой
2) только второй
3) и первой, и второй
4) ни первой, ни второй
10. Точка обода колеса при движении велосипеда описывает половину окружности радиуса \( R \). Чему равны при этом путь \( l \) и модуль перемещения \( s \) точки обода?
1)\( l=2R \), \( s=2R \)
2)\( l=\pi R \),\( s=2R \)
3)\( l=2R \),\( s=\pi R \)
4) \( l=\pi R \), \( s=\pi R \).
11. Установите соответствие между элементами знаний в левом столбце и понятиями в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.
ЭЛЕМЕНТ ЗНАНИЙ
A) физическая величина
Б) единица величины
B) измерительный прибор
ПОНЯТИЕ
1) траектория
2) путь
3) секундомер
4) километр
5) система отсчёта
12. Установите соответствие между величинами в левом столбце и характером величины в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.
ВЕЛИЧИНА
A) путь
Б) перемещение
B) проекция перемещения
ХАРАКТЕР ВЕЛИЧИНЫ
1) скалярная
2) векторная
Часть 2
13. Автомобиль свернул на дорогу, составляющую угол 30° с главной дорогой, и совершил по ней перемещение, модуль которого равен 20 м. Определите проекцию перемещения автомобиля на главную дорогу и на дорогу, перпендикулярную главной дороге.
Вчера — не сегодня
Почему мы все время говорим о программах? Потому что воспитаны в культуре стабильного общества, привыкшего и считающего правильным обстоятельное планирование и проектирование будущего. Обучение и воспитание, которые в совокупности мы привыкли называть образованием, тоже выстроены в логике социального проектирования: мы, взрослые, знаем, что и как правильно делать, и научаем этому неумелых детей. В логике проектирования образовательного процесса образовательная программа абсолютно органична. Особенно в логике традиционного для классической школы образовательного конвейера, когда все одновременно обучаются по единой программе.
Однако с некоторого момента в середине прошлого века этот конвейер начал давать сбои: общество, повысив уровень грамотности, стало постепенно требовать большей гибкости. Это выразилось в появлении спецшкол, расширении сети дополнительного образования. Потом и этого перестало хватать — опыт педагогов-новаторов вылился в новый закон «Об образовании», дающий право школе самой создавать образовательную программу, ориентируясь на своих детей и педагогов. С этим не справилась устаревшая система управления образованием, начались попытки ограничивать свободу школ по созданию индивидуальных программ, но полностью кран перекрыть уже невозможно. Аналогичные процессы идут и в обществе —традиционные процессы проектирования перестали удовлетворять разработчиков, так как при таком подходе проект устаревает к моменту окончания проектирования. Благодаря Грефу, название одного из новых гибких проектных подходов Agile стало известно широкому кругу.
Самое важное, что всем, включая детей, стало ясно, что никаким сакральным знанием «правильности» взрослые не обладают. Раз так, возникает вопрос: чему они могут научить? Почему дети должны прислушиваться к их мнению и учиться по их программам? Они прекрасно знают от своих родителей и старших родственников, друзей, что школьная «галиматья» практически никому не нужна, а в новых устройствах эти горделивые учителя и вовсе «не копенгаген»
Чем они могут быть полезны? Что они пасут их на время отсутствия родителей на работе?
К такому свержению с пьедестала учителя не готовы: они привыкли почитать своих Учителей (с большой буквы) и надеялись на такой же пиетет по отношению к себе, а их даже Председатель Правительства послал заниматься бизнесом, если что-то не устраивает в школе. Если образовательная программа перестает работать или работает исключительно при подавлении воли учеников, что можно делать?
Связь со скоростью и нормальным ускорением
Рис. 3. Суточное движение светил в системе отсчёта, связанной с фотоаппаратом в проекции на плоскость рисунка
Скорость материальной точки всегда направлена по касательной к дуге, используемой для описания траектории точки. При этом существует связь между величиной скорости v{\displaystyle v}, an{\displaystyle a_{n}} и радиусом кривизны траектории R{\displaystyle R} в данной точке:
- an=v2R{\displaystyle a_{n}={\frac {v^{2}}{R}}}
Однако, не всякое движение с известной скоростью по кривой известного радиуса и найденное по приведённой выше формуле нормальное (центростремительное) ускорение связано с проявлением силы, направленной по нормали к траектории (центростремительной силы). Так, найденное по данным фотографии суточного движения светил ускорение любой из звёзд отнюдь не говорит о существовании вызывающей это ускорение силы, притягивающей её к Полярной звезде, как центру вращения.
«Механическое движение. Траектория и путь»
Механическое движение — это изменение положения тела или его частей относительно других тел с течением времени. Механическое движение — это изменение положения тела или его частей относительно других тел с течением времени. Изучение механики традиционно начинают с кинематики.
Кинематика — раздел механики, в котором рассматривают способы описания механического движения тел без выяснения причин изменения характера их движения. Сами причины рассматриваются в других разделах механики.

Траектория движения — это линия, вдоль которой движется тело.
Перемещением точки за промежуток времени называют направленный отрезок прямой, начало которого совпадает с начальным положением точки, а конец — с конечным положением точки. Перемещение точечного тела определяется только конечной и начальной координатами тела и не зависит от того, как двигалось тело в течение рассматриваемого промежутка времени.

Путь — это длина траектории, пройденной телом. Путь — всё расстояние, пройденное точечным телом за рассматриваемый промежуток времени.
Если тело в процессе движения не меняло направления движения, то пройденный этим телом путь равен модулю его перемещения. Если тело в течение рассматриваемого промежутка времени меняло направление своего движения, путь больше и модуля перемещения тела, и модуля изменения координаты тела.
Путь всегда величина неотрицательная. Он равен нулю только в том случае, если в течение всего рассматриваемого промежутка времени тело покоилось (стояло на месте).
Виды траекторий. Если тело движется вдоль прямой, движение называют прямолинейным. Траектория в этом случае — отрезок прямой. Если же траектория — кривая линия, движение называют криволинейным.

Относительность движения
Для того чтобы описать положение данного тела в пространстве, необходимо:
- выбрать тело отсчёта и начало отсчёта на нём;
- связать с ним координатную ось, проходящую через начало отсчёта в нужном направлении, и указать единицу длины.
При этом расстояние от начала отсчёта до данного тела, выраженное в выбранных единицах длины и взятое с соответствующим знаком, называют координатой этого тела.
Система отсчета
Поступив так, мы будем говорить, что описали положение данного тела относительно выбранного тела отсчёта. Если мы выберем в качестве тела отсчёта другое тело или другую ось координат, то и координата данного тела может стать другой. Совокупность тела отсчёта, с которым связана ось координат, и часов называют системой отсчёта.

Если координата тела не изменяется с течением времени в выбранной системе отсчёта, то говорят, что это тело в данной системе отсчёта неподвижно, или покоится.
Если координата тела выбранной системы отсчёта увеличивается со временем, то говорят, что тело движется в положительном направлении координатной оси. Напротив, если координата тела в выбранной системе отсчёта со временем уменьшается, то говорят, что тело движется в отрицательном направлении координатной оси.
Нельзя сказать, как движется тело, если не сказать, в какой системе отсчёта рассматривается это тело. Иначе говоря, одно и то же тело в разных системах отсчёта может двигаться по-разному (в том числе и покоиться).
Конспект по физике в 7 классе по теме «Механическое движение. Траектория».
Следующая тема: Прямолинейное равномерное движение