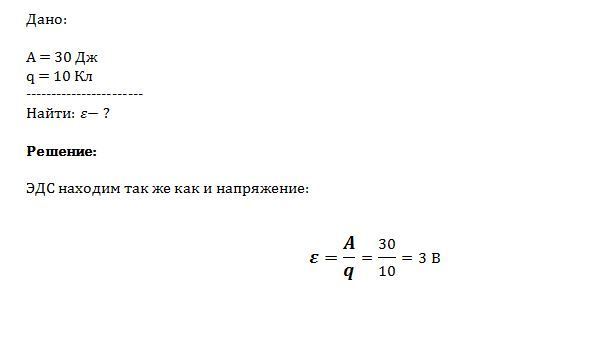Сторонние силы и эдс

ЭДС и закон Ома

Электродвижущая сила источника связана с электрическим током, протекающим в цепи, соотношениями закона Ома. Закон Ома для неоднородного участка цепи имеет вид:

φ1−φ2+E=IR,{\displaystyle \varphi _{1}-\varphi _{2}+{\mathcal {E}}=IR,}

где φ1−φ2{\displaystyle \varphi _{1}-\varphi _{2}} — разность между значениями потенциала в начале и в конце участка цепи, I{\displaystyle I} — сила тока, текущего по участку, а R{\displaystyle R} — сопротивление участка.

Если точки 1 и 2 совпадают (цепь замкнута), то φ1−φ2={\displaystyle \varphi _{1}-\varphi _{2}=0} и предыдущая формула переходит в формулу закона Ома для замкнутой цепи:

E=IR,{\displaystyle {\mathcal {E}}=IR,}

где теперь R{\displaystyle R} — полное сопротивление всей цепи.

В общем случае полное сопротивление цепи складывается из сопротивления внешнего по отношению к источнику тока участка цепи (Re{\displaystyle R_{e}}) и внутреннего сопротивления самого́ источника тока (r{\displaystyle r}). С учётом этого следует:

E=IRe+Ir.{\displaystyle {\mathcal {E}}=IR_{e}+Ir.}

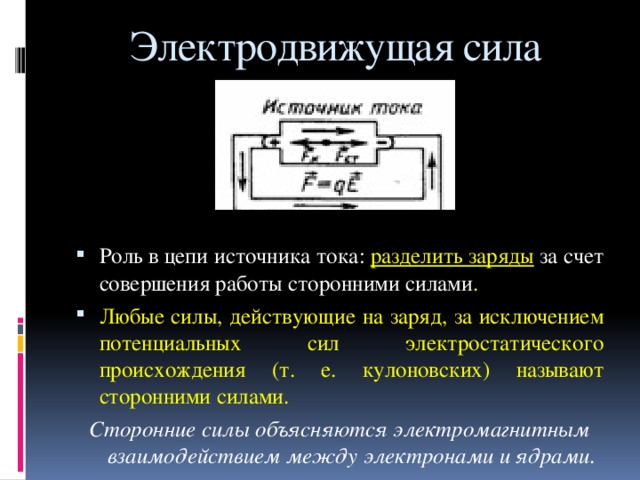
Сторонние силы

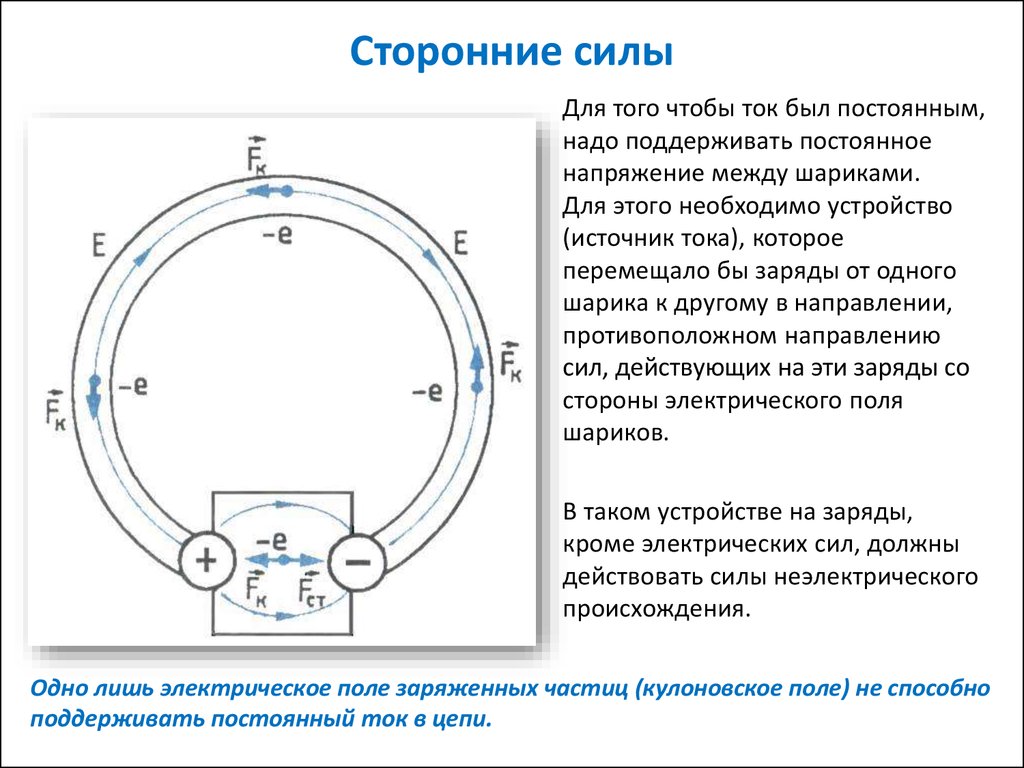
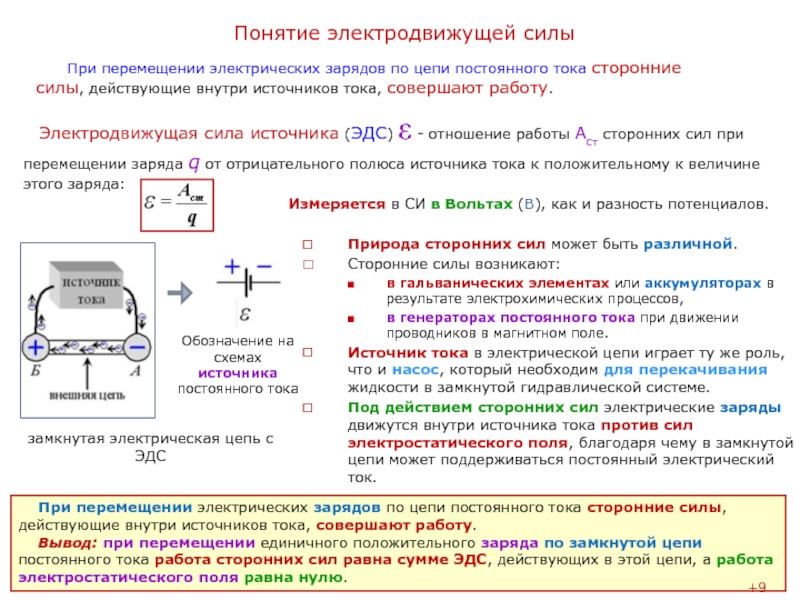
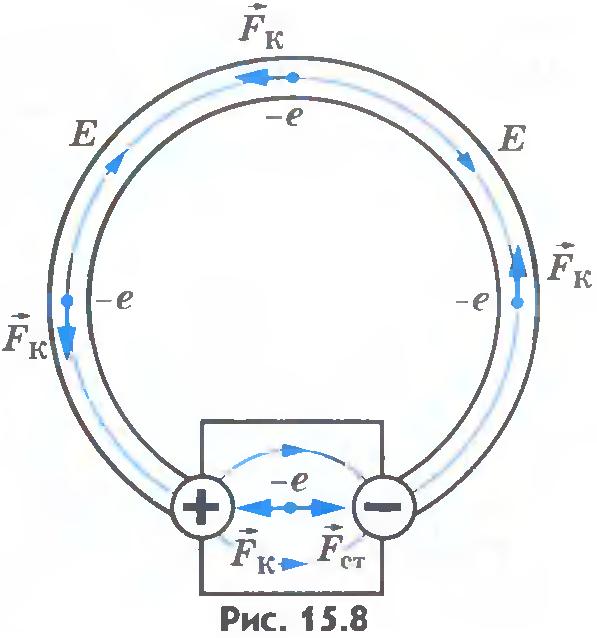
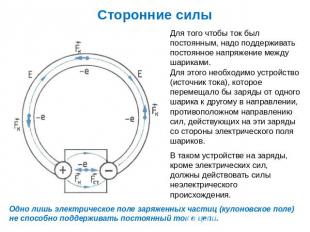
Для того, чтобы поддерживать разность потенциалов на полюсах источника тока, необходимо совершать работу по переносу зарядов между полюсами. Причем, этот перенос должен осуществляться против действия имеющегося электрического поля. В самом деле, если носитель заряда имеет отрицательный заряд (например, свободный электрон), то он, придя к положительному полюсу – должен быть перенесен внутри источника к отрицательному полюсу, несмотря на то, что поле будет двигать его по-прежнему к положительному.

Это значит, что перенос зарядов внутри источника электрического тока должен осуществляться силами, имеющими природу, отличную от электрической. Поэтому эти силы называются сторонними.

Природа сторонних сил может быть различной. В батарейках и аккумуляторах это силы химической природы. В промышленных генераторах природа сторонних сил механическая. В солнечных батареях – световая.

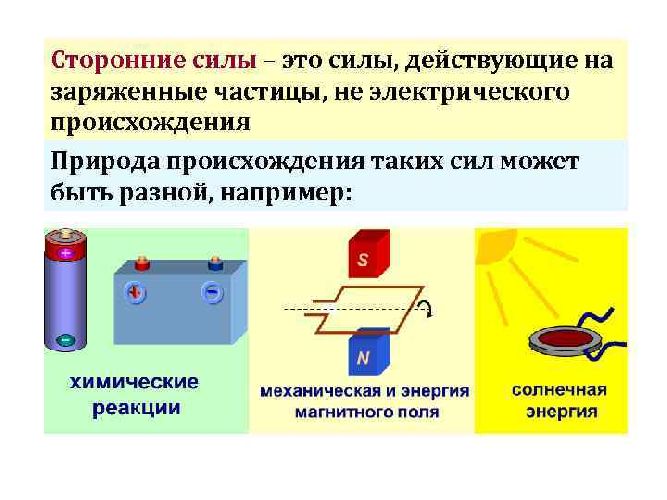
Рис. 2. Сторонние силы различной природы.

От электростатики к электрокинетике

Между концом XVIII и началом XIX века работы таких учёных, как Кулон, Лагранж и Пуассон, заложили математические основы определения электростатических величин. Прогресс в понимании электричества на этом историческом этапе очевиден. Франклин уже ввёл понятие «количество электрической субстанции», но пока ещё и он, ни его преемники не смогли его измерить.

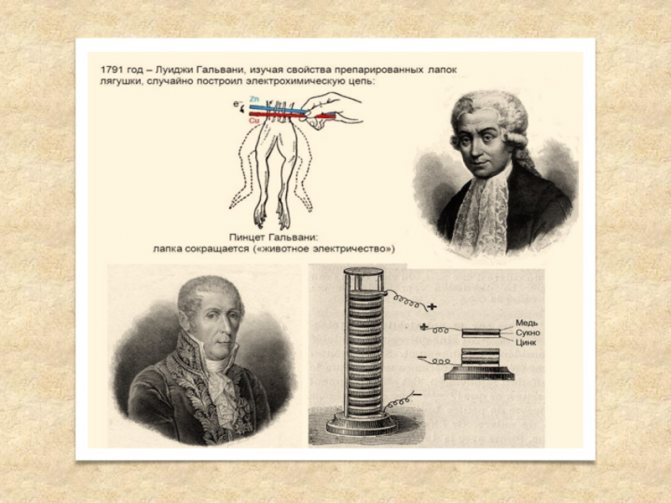
Следуя за экспериментами Гальвани, Вольта пытался найти подтверждения того, что «гальванические жидкости» животного были одной природы со статическим электричеством. В поисках истины он обнаружил, что когда два электрода из разных металлов контактируют через электролит, оба заряжаются и остаются заряженными несмотря на замыкание контура нагрузкой. Это явление не соответствовало существующим представлениям об электричестве потому, что электростатические заряды в подобном случае должны были рекомбинировать.

Вольта ввёл новое определение силы, действующей в направлении разделения зарядов и поддержании их в таком состоянии. Он назвал её электродвижущей. Подобное объяснение описания работы батареи не вписывалось в теоретические основы физики того времени. В Кулоновской парадигме первой трети XIX века э. д. с. Вольта определялась способностью одних тел вырабатывать электричество в других.

Важнейший вклад в объяснение работы электрических цепей внёс Ом. Результаты ряда экспериментов привели его к построению теории электропроводности. Он ввёл величину «напряжение» и определил её как разность потенциалов на контактах. Подобно Фурье, который в своей теории различал количество тепла и температуру в теплопередаче, Ом создал модель по аналогии, связывающую количество перемещаемого заряда, напряжение и электропроводность. Закон Ома не противоречил накопленным знаниям об электростатическом электричестве.

Вам это будет интересно Физика и последствия поражения электрическим током

Затем, благодаря Максвеллу и Фарадею, пояснительные модели тока получили новую теорию поля. Это позволило разработать связанную с полем концепцию энергии как для статических потенциалов, так и для электродвижущей силы. Основные даты эволюции понятия ЭДС:

1800 г. — создание Вольтой гальванической батареи;
1826 г. — Ом формулирует свой закон для полной цепи;
1831 г. — обнаружение электромагнитной индукции Фарадеем.

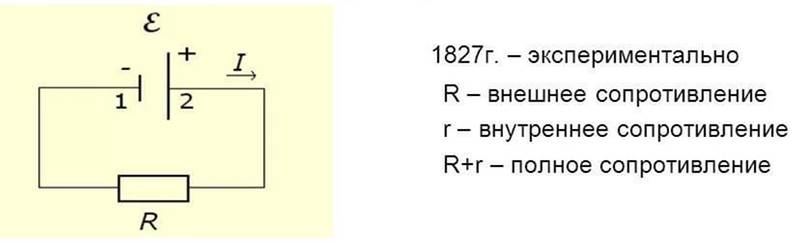
2.3. Закон Ома для участка и полной замкнутой цепи

В
1826 г. немецкий ученый Георг Ом
экспериментально установил прямую
пропорциональную зависимость между
силой тока I
в проводнике и напряжением U
на его концах:
,
гдеG
— электрическая
проводимость проводника.
Величина, обратная проводимости
называется электрическим
сопротивлением проводника R.
Таким образом, закон
Ома для участка цепи, не содержащего
источника э.д.с.,
имеет вид
. Учитывая,
что в общем случае участок цепи может
содержать и э.д.с.,закон
Ома
следует представить в виде
.

Сопротивление
проводника зависит от его размеров,
формы и материала, из которого он
изготовлен. Для
однородного линейного проводника
,
где l
— длина, S
— площадь поперечного сечения проводника,

— удельное электрическое
сопротивление, зависящее от материала,
из которого изготовлен проводник.
Единица сопротивления 1 Ом — это
сопротивление такого проводника, в
котором при напряжении 1В течет ток в
1А.

Если
цепь замкнута, то
,,
гдеR
— общее сопротивление всей цепи, включая
сопротивление источника э.д.с. Тогда
закон
Ома для замкнутой цепи
следует записать
,
где
— алгебраическая сумма всех э.д.с.,
имеющихся в этой цепи.

Принято
называть сопротивление источника тока
r
— внутренним,
а сопротивление всей остальной цепи
R
— внешним.
Окончательный
вид формулы закона Ома для замкнутой
цепи
. В системе
единиц СИ напряжение и э.д.с. измеряются
в Вольтах (В), сопротивление — в Омах
(Ом), удельное электрическое сопротивление
— в Ом-метрах (Омм),
электрическая проводимость в Сименсах (См).

Рис.2.1.
Отрезок проводника.

Закон Ома можно
записать и для плотности тока. Рассмотрим
участок электрической длиной dl
и поперечным сечением dS
(рис.2.1). Сила тока на этом участке
,
сопротивление,
падение напряжения,
где Е — напряженность
электрического поля в проводнике.
Подставив эти параметры в закон Ома
для участка цепи, получим
.
Отсюдаили,
где-удельная электрическая
проводимость проводника или
удельная электропроводность.
В векторном виде имеем
(единицей измерения
в системе СИ является сименс на метр
(См/м)). Полученное выражение есть закон
Ома в дифференциальной форме : плотность
тока в любой точке внутри проводника
прямо пропорциональна напряженности
поля в этой точке.

Огромные
различия в электропроводности веществ
позволили создать высокоэффективный
метод обработки пищевых продуктов,
называемый электростатическим
сепарированием. Например, при
производственной сушке желатина на
алюминиевых сетках в продукт попадают
мельчайшие частицы алюминия. Желатин
— диэлектрик с удельной проводимостью
=10-8-10-10
См/м, алюминий — проводник,=36106
См/м. Такое различие в электропроводности
позволяет разделять компоненты
посредством поля в электростатическом
сепараторе. Электрическая сепарация
применяется при очистке муки, подсолнечника,
крупы и др. от металлических примесей.

Установлена связь
между электропроводностью и качеством
некоторых овощей (содержание сахаров,
доли биологически активной воды и др.)
Поэтому электропроводность является
объективным показателем состояния
овощей и их устойчивости к
длительному хранению.

Обозначение источников тока

Чтобы при выборе не возникало вопроса относительно того, какой тип источника тока представлен, используются специальные обозначения. В физике существуют точные графические изображения, которые позволяют идентифицировать тип применяемого источника:

Обозначения

На каждой схеме условных обозначений можно увидеть следующие параметры:

Общее обозначение источника тока и движущей силы ЭДС;
Графическое изображение без ЭДС;
Химический тип;
Батарея;
Постоянное напряжение;
Переменное напряжение;
Генератор.

Благодаря графическим идентификаторам на схеме электрической цепи всегда можно определить, какой именно тип используется в конкретной ситуации, и как правильно его обозначать. Существуют также международные обозначения, которые встречаются немного реже, обычно при реализации интернациональных проектов.

Сколько же мы можем «взять» киловатт с С16А?

В первом столбце отношение токов, во втором ток в цепи, протекающий через автоматический выключатель, в третьем время отключения, в четвертом — мощность в однофазной нагрузке без учета коэффициента мощности и гармоник.

Время-Токовая Характеристика С — таблица с мощностью

Определение и физический смысл

Приложение некоторой разности потенциалов между двумя концами проводника создаст перетекание электронов от одного конца к другому. Но этого недостаточно для поддержания потока зарядов в проводнике. Дрейф электронов приводит к уменьшению потенциала до момента его уравновешивания (прекращение тока). Таким образом, для создания постоянного тока необходимы механизмы, непрерывно возвращающие описанную систему в первоначальную конфигурацию, то есть, препятствующие агрегации зарядов в результате их движения. Для этой цели используются специальные устройства, называемые источники питания.

В качестве иллюстрации их работы удобно рассматривать замкнутый контур из сопротивления и гальванического источника питания (батареи). Если предположить, что внутри батареи тока нет, то описанная проблема объединения зарядов остаётся неразрешённой. Но в цепи с реальным источником питания электроны перемещаются постоянно. Это происходит благодаря тому, что поток ионов протекает и внутри батареи от отрицательного электрода к положительному. Источник энергии, перемещающий эти заряды в батарее — химические реакции. Такая энергия называется электродвижущей силой.

ЭДС является характеристикой любого источника энергии, способного управлять движением электрических зарядов в цепи. В аналогии с замкнутым гидравлическим контуром работа источника э. д. с. соответствует работе насоса для создания давления воды. Поэтому значок, обозначающий эти устройства, неотличим на гидравлических и электрических схемах.

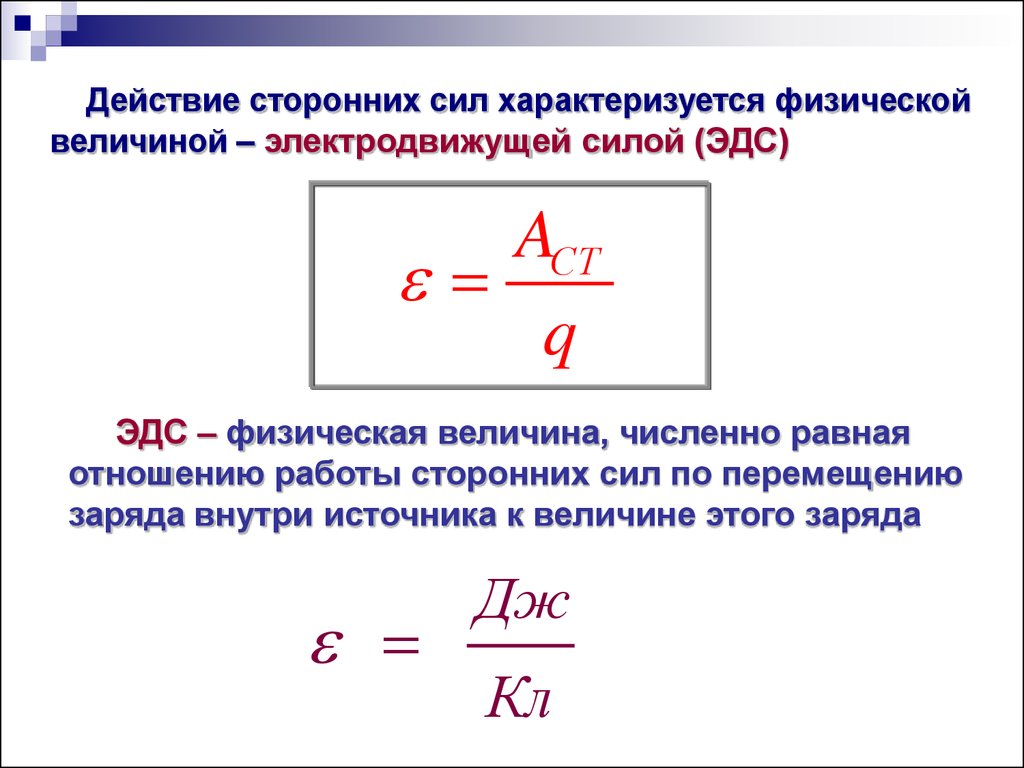
Несмотря на название, электродвижущая сила на самом деле не является силой и измеряется в вольтах. Её численное значение равно работе по перемещению заряда по замкнутой цепи. ЭДС источника выражается формулой E=A/q, в которой:

E — электродвижущая сила в вольтах;
A — работа сторонних сил по перемещению заряда в джоулях;
q — перемещённый заряд в кулонах.

Электрический ток. Работа и мощность в цепи постоянного тока. Закон Ома для полной цепи

Кристаллическая решётка Электрический ток. Все металлы являются проводниками электрического тока. Они состоят из пространственной кристаллической решетки, узлы которой совпадают с центрами положительных ионов. Вокруг ионов хаотически движутся свободные электроны.

В металлах электронная проводимость

Электрическим током в металлах называется упорядоченное движение свободных электронов. За направление тока принимают направление движения положительно заряженных частиц.

Электрические заряды могут двигаться упорядоченно под действием электрического поля, поэтому условием для существования эл. тока является наличие электрического поля и свободных носителей эл.заряда.

Сила тока численно равна заряду, протекающему через данное поперечное сечение проводника в единицу времени. Ток называется постоянным, если сила тока и его направление не изменяется с течением времени.

I = 1 Кл/с = 1 А

1 ампер (А) равен силе постоянного тока, при котором через любое поперечное сечение проводника за 1 с протекает 1 Кл электричества. I = q0 nvS Силу тока в цепи измеряют амперметром. Условное обозначение в цепи

Работа и мощность тока. Электрический ток снабжает нас энергией. Она возникает за счёт работы электрического поля по передвижению свободных зарядов в проводнике. Рассмотрим участок цепи, по которому течёт ток I. Напряжение на участке обозначим U, сопротивление участка равно R. При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном участке совершает работу. ΔA = U I Δt — эту работу называют работой электрического тока. За счёт работы на рассматриваемом участке может совершаться механическая работа; могут также протекать химические реакции. Если этого нет, то работа эл.поля приводит только к нагреванию проводника. Работа тока равна количеству теплоты, выделяемому проводником с током: — закон Джоуля — Ленца

Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена на данном участке: P = IU или . Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт).

Закон Ома для замкнутой цепи. Источник тока имеет ЭДС () и сопротивление (r), которое называют внутренним. Электродвижущей силой (ЭДС) называется отношение работы сторонних сил по перемещению заряда q вдоль цепи, к значению этого заряда (1В=1Дж/1Кл). Рассмотрим теперь замкнутую (полную) цепь постоянного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. (R+r) — полное сопротивление цепи. Закон Ома для полной цепи записывается в виде или

Сила тока в электрической цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи.

Особенности выращивания в регионах

Как мы уже упомянули, яблоня Услада, прежде всего, обитает в европейской части России.

В целом этот сорт довольно неприхотливый и выносливый, поэтому вырастить такое дерево под силу даже начинающим садоводам.

Чтобы избежать проблем при выращивании в регионах, важно учесть некоторые особенности сорта Услада. Услада хорошо адаптировалась в этом регионе, несмотря на большое количество осадков и небольшое число солнечных тёплых дней в летний период, благодаря её хорошей устойчивости к парше

Услада хорошо адаптировалась в этом регионе, несмотря на большое количество осадков и небольшое число солнечных тёплых дней в летний период, благодаря её хорошей устойчивости к парше.

Подмосковье

Условия в этом регионе подходят для выращивания сорта Услада. Она хорошо плодоносит на плодородных почвах, а её жизнеспособность помогает адаптироваться к местным погодным условиям.

Сибирь

Хотя сорт обладает зимоустойчивостью, но для выращивания в суровых условиях Сибири хорошо подойдёт карликовый морозоустойчивый вид яблони Услада.

Сибирский регион.

Сторонние силы

Сторонними силами называются силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля. Например, в гальваническом элементе или аккумуляторе сторонние силы возникают в результате электрохимических процессов, происходящих на границе соприкосновения электрода с электролитом; в электрическом генераторе постоянного тока сторонней силой является сила Лоренца.

Работа и мощность тока. Закон Джоуля – Ленца в интегральной и дифференциальной форме

При
протекании тока по однородному участку
цепи электрическое поле совершает
работу. За время Δt
по
цепи протекает заряд Δq
= I
Δt
.
Электрическое поле на выделенном учестке
совершает работу

выражающей закон
Ома для однородного участка цепи с
сопротивлением R
,
умножить на I
Δt
,
то получится соотношение

Закон
преобразования работы тока в тепло был
экспериментально установлен независимо
друг от друга Дж. Джоулем иЭ. Ленцем и
носит название закона
Джоуля–Ленца

.

Мощность
электрического тока равна отношению
работы тока ΔA
к
интервалу времени Δt
,
за которое эта работа была совершена:

Работа
электрического тока в СИ выражается
в джоулях

(Дж),
мощность – в ваттах

(Вт).

Закон
Джоуля-Ленца в дифференциальной форме
— удельная мощность тока равна скалярному
произведению векторов плотности тока
и напряженности электрического
поля:

где s —
удельная проводимость;

r —
удельное сопротивление среды.

Закон
Джоуля-Ленца в дифференциальной форме
носит совершенно общий характер, т. е.
не зависит от природы сил, возбуждающих
электрический ток. Закон Джоуля-Ленца,
как показывает опыт, справедлив и для
электролитов и для полупроводников.

17.
. Обобщенный закон Ома для неоднородного
участка цепи в интегральной и
дифференциальной форме. Анализ обобщенного
закона Ома. Замкнутая электрическая
цепь. Соединение сопротивлений:
последовательное и параллельное.

ЭДС источника тока

Если на участке цепи не действуют сторонние силы (однородный участок цепи) и, значит, источника тока на нём нет, то, как это следует из закона Ома для неоднородного участка цепи, выполняется:

φ1−φ2=IR.{\displaystyle \varphi _{1}-\varphi _{2}=IR.}

Значит, если в качестве точки 1 выбрать анод источника, а в качестве точки 2 — его катод, то для разности между потенциалами анода φa{\displaystyle \varphi _{a}} и катода φk{\displaystyle \varphi _{k}} можно записать:

φa−φk=IRe,{\displaystyle \varphi _{a}-\varphi _{k}=IR_{e},}

где как и ранее Re{\displaystyle R_{e}} — сопротивление внешнего участка цепи.

Из этого соотношения и закона Ома для замкнутой цепи, записанного в виде E=IRe+Ir{\displaystyle {\mathcal {E}}=IR_{e}+Ir} нетрудно получить

φa−φkE=ReRe+r{\displaystyle {\frac {\varphi _{a}-\varphi _{k}}{\mathcal {E}}}={\frac {R_{e}}{R_{e}+r}}} и затем φa−φk=ReRe+rE.{\displaystyle \varphi _{a}-\varphi _{k}={\frac {R_{e}}{R_{e}+r}}{\mathcal {E}}.}

Из полученного соотношения следуют два вывода:

Во всех случаях, когда по цепи течёт ток, разность потенциалов между клеммами источника тока φa−φk{\displaystyle \varphi _{a}-\varphi _{k}} меньше, чем ЭДС источника.
В предельном случае, когда Re{\displaystyle R_{e}} бесконечно (цепь разорвана), выполняется E=φa−φk.{\displaystyle {\mathcal {E}}=\varphi _{a}-\varphi _{k}.}

Таким образом, ЭДС источника тока равна разности потенциалов между его клеммами в состоянии, когда источник отключён от цепи.

Разность потенциалов

Напряжение
на неоднородном участке цепи

(где есть сторонние силы) равно сумме
ЭДС источника и разности потенциалов
на этом участке:

Для
однородного
участка цепи
,
где сторонние силы не действуют,

Т.е.
напряжение
совпадает с разностью потенциалов на
концах участка цепи
.

Закон
Ома для однородного участка

цепи в
интегральной

и дифференциальной форме
.
Сопротивление и его зависимость от
температуры. Сверхпроводимость.

Закон
Ома для однородного участка

цепи в
интегральной

и дифференциальной форме

Закон
Ома для однородного участка цепи:
н
емецкий
физик Георг Ом экспериментально
установил, чтосила тока в
цепи прямо пропорциональна приложенному
напряжению и обратно пропорциональна
сопротивлению проводника:.

Закон
Ома в дифференциальной форме (закон Ома
для плотности тока).
Закон
Ома в форме
относится ко всему проводнику. Представим
закон Ома в дифференциальной (т.е.
относящейся к элементу тока длиныdl
)
форме. Некоторая точка внутри проводника
характеризуется вектором плотности
тока
,
напряженностью электрического поляи свойствами материала проводника, т.е.
удельным сопротивлением.
Выделим мысленно малый объем вблизи
рассматриваемой точки и подставимв закон Ома,
получим:,
здесь
— разность потенциалов между сечениямиdS

отстоящими на расстоянии dl
.
Следовательно,.

Учтем,
что
— напряженность электростатического
поля;- плотность электрического поля;- удельная электрическая проводимость.

Тогда
из формулы (20) следует закон
Ома в дифференциальной форме
:
.

Практика

Мы уже упомянули о том, что в быту электрическое поле проявляется, когда вы снимаете шерстяную или синтетическую одежду с себя и проскакивают искорки между волосами и шерстью, когда натрете пластиковую линейку и проведете над мелкими бумажками, а они притягиваются и прочее. Но это не является нормальными техническими примерами.

В проводниках малейшее ЭП вызывает движение носителей зарядов и их перераспределение. В диэлектриках, так как ширина запрещенной зоны в этих веществах большая, ЭП вызовет движение носителей зарядов только в случае пробоя диэлектрика. В полупроводниках действие находится между диэлектриком и проводником, но нужно преодолеть небольшую ширину запрещенной зоны, передав энергию порядка 0.3…0.7 эВ (для германия и кремния).

Из того, что есть в каждом доме – это электронные бытовые приборы, в том числе и блоки питания. В них есть важная деталь, которая работает благодаря электрическому полю – это конденсатор. В нём заряды удерживаются на обкладках, разделенных диэлектриком, как раз таки благодаря работе электрического поля. На картинке ниже вы видите условное изображение зарядов на обкладках конденсатора.

Другое применение в электротехнике — это полевые транзисторы или МДП-транзисторы. В их названии уже упоминается принцип действия. В них принцип работы основан на изменении проводимости СТОК-ИСТОК под воздействием на полупроводник поперечного электрического поля, а в МДП (МОП, MOSFET – одно и то же) и вовсе затвор отделен диэлектрическим слоем (окислом) от проводящего канала, так что влияние токов ЗАТВОР-ИСТОК невозможно по определению.

Другое применение уже отошедшее в быту, но еще «живое» в промышленной и лабораторной технике – электроннолучевые трубки (ЭЛТ или т.н. кинескопы). Где одним из вариантов устройства для перемещения луча по экрану является электростатическая отклоняющая система.

Если рассказать простым языком, то есть пушка, которая излучает (эмитирует) электроны. Есть система, которая отклоняет этот электрон в нужную точку на экране, для получения необходимого изображения. Напряжение прикладывается к пластинам, а на эмитированный летящий электрон воздействуют кулоновские силы, соответственно и электрическое поле. Все описанное происходит в вакууме. Тогда к пластинам прикладывают высокое напряжение, а для его формирования устанавливают трансформатор строчной развертки и обратноходовой преобразователь.

На видео ниже кратко и понятно объясняется, что такое электрическое поле и какими свойствами обладает этот особый вид материи:

Материалы по теме:

Что такое диэлектрические потери
Зависимость сопротивления проводника от температуры
Закон Ома простыми словами
Книги для электриков

Ссылки

	Тамм И. Е. Основы теории электричества: Учеб. пособие для вузов. 11-е изд. М.: ФИЗМАТЛИТ, 2003. С. 181.
	Яворский Б. М. и Детлаф А. А. Справочник по физике (для инженеров и студентов вузов). М.: Госиздат физ.-мат. лит., 1963. С. 355.
	БЭС, Физика. М.: Научное изд. БРЭ, 1999. С. 903.
	Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля. М.: Гостехтеориздат, 1954. С. 301.
	Савельев И. В. Курс общей физики. Т. 2. М.: Наука. Главное изд. физ.-мат. лит., 1978. С. 20.
	Парселл Э. Берклиевский курс физики. Т. 2. Электричество и магнетизм. — М.: Наука, 1971. С. 181.
	Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Т. 5. Электричество и магнетизм. — М.: Мир, 1977. С. 267.
	Григорьев А. Н. О существовании магнитного поля. — http://www.sciteclibrary.ru/rus/catalog/pages/11737.html

2.3. Закон Ома для участка и полной замкнутой цепи

Рис.2.1.
Отрезок проводника.

ЭДС источника тока

φ1−φ2=IR.{\displaystyle \varphi _{1}-\varphi _{2}=IR.}

φa−φk=IRe,{\displaystyle \varphi _{a}-\varphi _{k}=IR_{e},}

где как и ранее Re{\displaystyle R_{e}} — сопротивление внешнего участка цепи.

Из полученного соотношения следуют два вывода:

Во всех случаях, когда по цепи течёт ток, разность потенциалов между клеммами источника тока φa−φk{\displaystyle \varphi _{a}-\varphi _{k}} меньше, чем ЭДС источника.
В предельном случае, когда Re{\displaystyle R_{e}} бесконечно (цепь разорвана), выполняется E=φa−φk.{\displaystyle {\mathcal {E}}=\varphi _{a}-\varphi _{k}.}

Механическая сторонняя электродвижущая сила

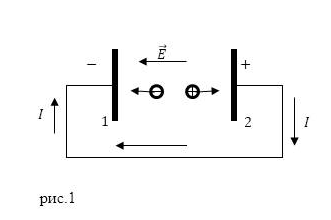Рисунок 1. Источник. тока. Автор24 — интернет-биржа студенческих работ

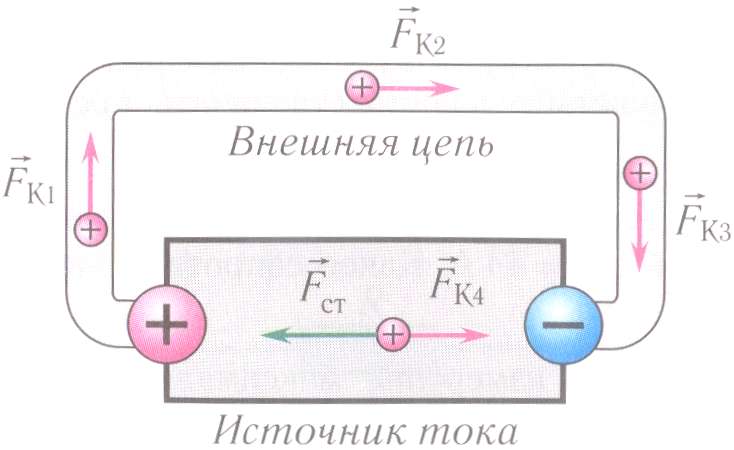
Рассмотрим схему самого простого источника тока, имеющего стороннюю электродвижущую силу механического происхождения (рис.1). Между электродами 1 и 2 находится нейтральное вещество, обладающее равным количеством положительных и отрицательных зарядов. Сторонняя сила неэлектростатической природы передвигает заряды со знаком плюс к электроду 2, а отрицательные частицы к электроду 1. В результате данного процесса электрод 1 несет отрицательный заряд, а электрод 2 имеет заряд больше нуля. Во внешней цепи от 2 к 1 идет электрический ток, который совершает работу. Требуемая для этого энергия передается системе сторонними силами. Эти силы разделяют заряды между нашими электродами и доставляют эти заряды на электроды против сил электрического поля, напряженность которого $\vec E$, которое находится между электродами. Электрический ток, текущий между электродами 1 и 2 внутри источника ЭДС замыкает ток во внешней цепи.

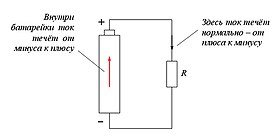
При этом:

во внешней цепи ток следует от положительного электрода к заряженному отрицательно;
во внутренней цепи (внутри источника) ток следует от электрода со знаком минус к электроду со знаком плюс.

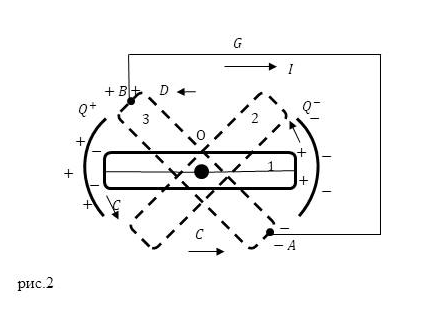Рисунок 2. Электростатическая машина. Автор24 — интернет-биржа студенческих работ

Практическим примером механической сторонней ЭДС может служить электростатическая машина. Схема такой машины изображена на рис.2. Заряды $Q^+$ и $Q^-$ создают электростатическое поле в пространстве между этими зарядами. Изолированные друг от друга проводящие пластинки перемещаются по окружности вокруг оси $О$ при воздействии сторонних механических сил. В положении 1 (рис.2) пластины соединяются друг с другом и становятся неподвижным проводником. Благодаря электростатической индукции пластины $C$ и $D$ в данном положении заряжаются:

$C$ заряжается отрицательно;
$D$ заряжается положительно.

При дальнейшем движении их контакт с проводником нарушается и в положении 2 пластины становятся изолированными друг от друга, но имеют заряды разного знака. В положении 3 пластины контактируют с электродами $A$ и $B$. На эти электроды переходит заряд с пластин. Между электродами по цепи $BGA$ идет электрический ток. При наличии только одной пары вращающихся проводников $C; D$, ток по цепи течет импульсами, по два импульса за один оборот.

Если иметь большое количество пар пластин, подобных $C$ и $D$, таких, чтобы они контактировали с нашими электродами последовательно с очень маленькими разрывами, то можно организовать почти постоянный ток во внешней цепи. Данная машина реализует стороннюю ЭДС механического происхождения, которая возникает за счет механических сил, которые обеспечивают перемещение пластин $C$ и $D$ по окружности.

Последовательность превращений энергии при таком действии выглядит так:

Сторонние механические силы, двигая пластины $C$ и $D$, выполняют работу против сил электрического поля, которое имеется между зарядами $Q^+$ и $Q^-$.
Эти силы переносят заряды на пластинах $C$ и $D$ к электродам $A$ и $B$. В результате изменяется энергия электрического поля, так происходит переход энергии из механической формы в энергию электрического поля.
После этого данная энергия при протекании тока по цепи трансформируется в джоулеву теплоту и другие формы энергии, которые обусловлены работой тока в цепи.

Действие источника электрического тока

В любой электрической цепи происходит движение носителей заряда через звенья цепи. Это движение возможно только под действием некоторого электрического поля. Следовательно, в любой электрической цепи должен существовать специальный элемент, который будет создавать электрическое поле, движущее заряды.

Такой элемент называется источником электрического тока. Источник тока имеет два контакта (полюса), с помощью которых и осуществляется поддержание электрического поля. Между полюсами всегда имеется некоторая разность электрических потенциалов. Теперь если к этим полюсам подключить электрическую цепь, то носители заряда под действием поля придут в движение, совершая полезную работу в цепи. При этом, в источнике тока должен постоянно происходить процесс, который бы поддерживал разность потенциалов на полюсах, несмотря на движение носителей заряда по цепи.

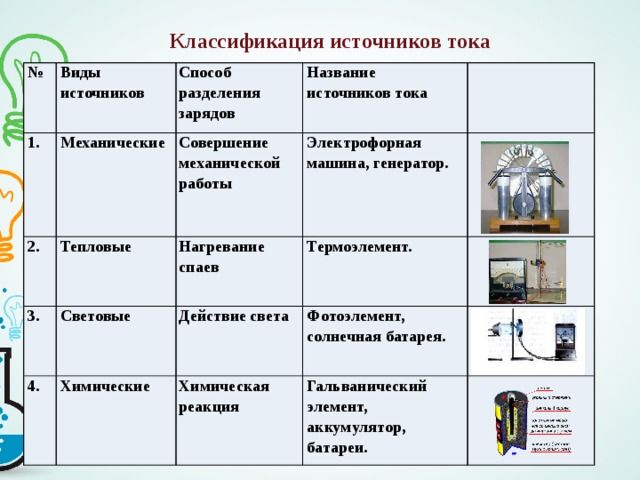
Рис. 1. Виды источников электрического тока.