Сопряжения - сопряжение окружностей, сопряжение углов, сопряжение линий, сопряжение дуг

Сопряжение окружностей(дуг) с прямой линией

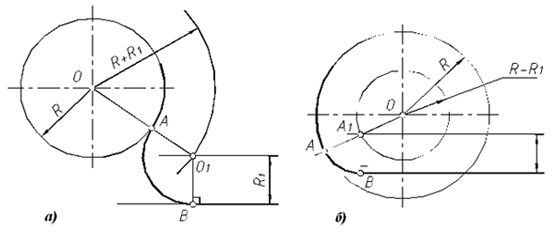
Внешнее сопряжение дуги и прямой линии

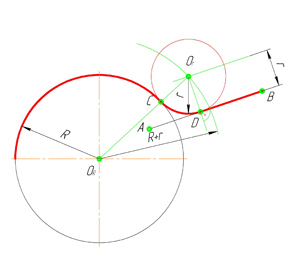
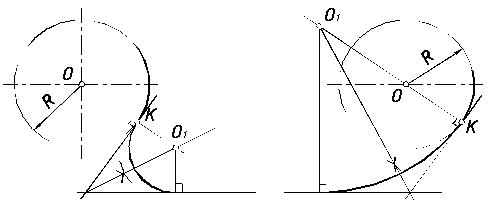
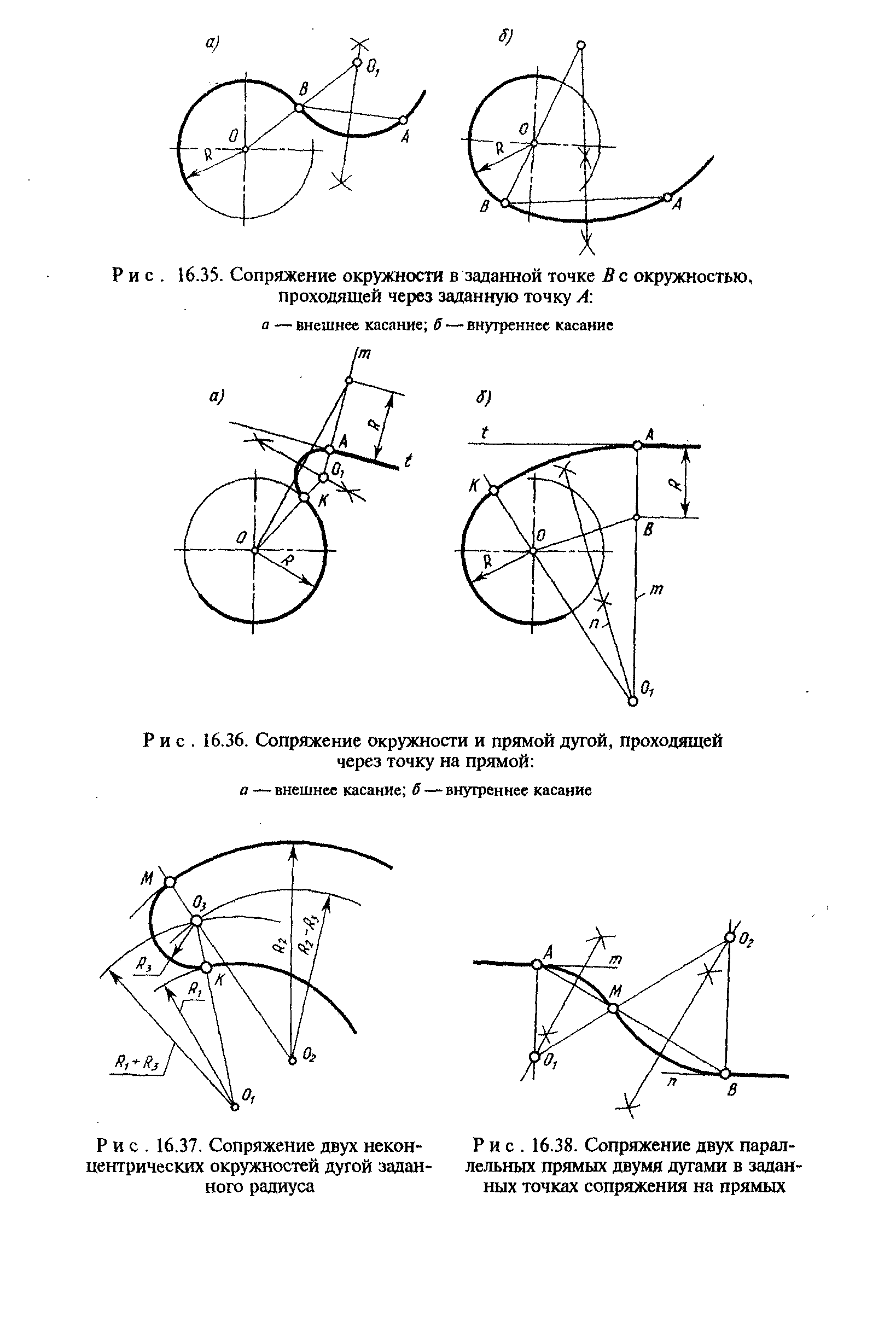
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

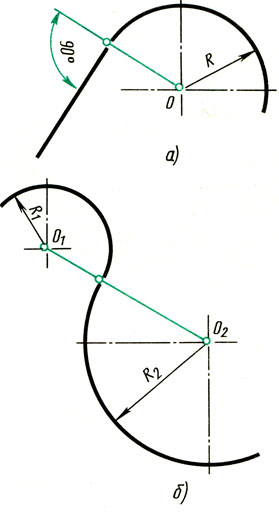
Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности OR радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой Оr.

Из центра сопряжения, точки Оr, опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности ОR и центр сопряжения Оr линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.

Внутреннее сопряжение прямой линии с дугой

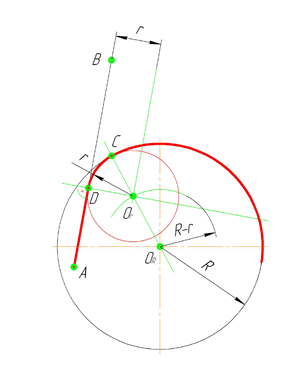
По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности OR радиусом R-r. Точка Оr, полученная на пересечении прямой и дуги, и будет центром сопряжения.

Из центра сопряжения(точка Оr) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности ОR прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки Оr, центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.

Определение

Точки P{\displaystyle P} и P∗{\displaystyle P^{*}} называются изогонально сопряжёнными (устаревшие названия — изогональными, обратными) в треугольнике △ABC{\displaystyle \triangle ABC}, если ∠ABP=∠CBP∗{\displaystyle \angle ABP=\angle CBP^{*}}, ∠BAP=∠CAP∗{\displaystyle \angle BAP=\angle CAP^{*}}, ∠BCP=∠ACP∗{\displaystyle \angle BCP=\angle ACP^{*}}. Корректность данного определения можно доказать через теорему Чевы в синусной форме, существует и чисто геометрическое доказательство корректности этого определения. Изогональное сопряжение — преобразование, ставящее точке в соответствие изогонально сопряжённую ей. На всей плоскости за исключением прямых, содержащих стороны треугольника, изогональное сопряжение является взаимно-однозначным отображением.

Сопряжение окружностей (дуг)

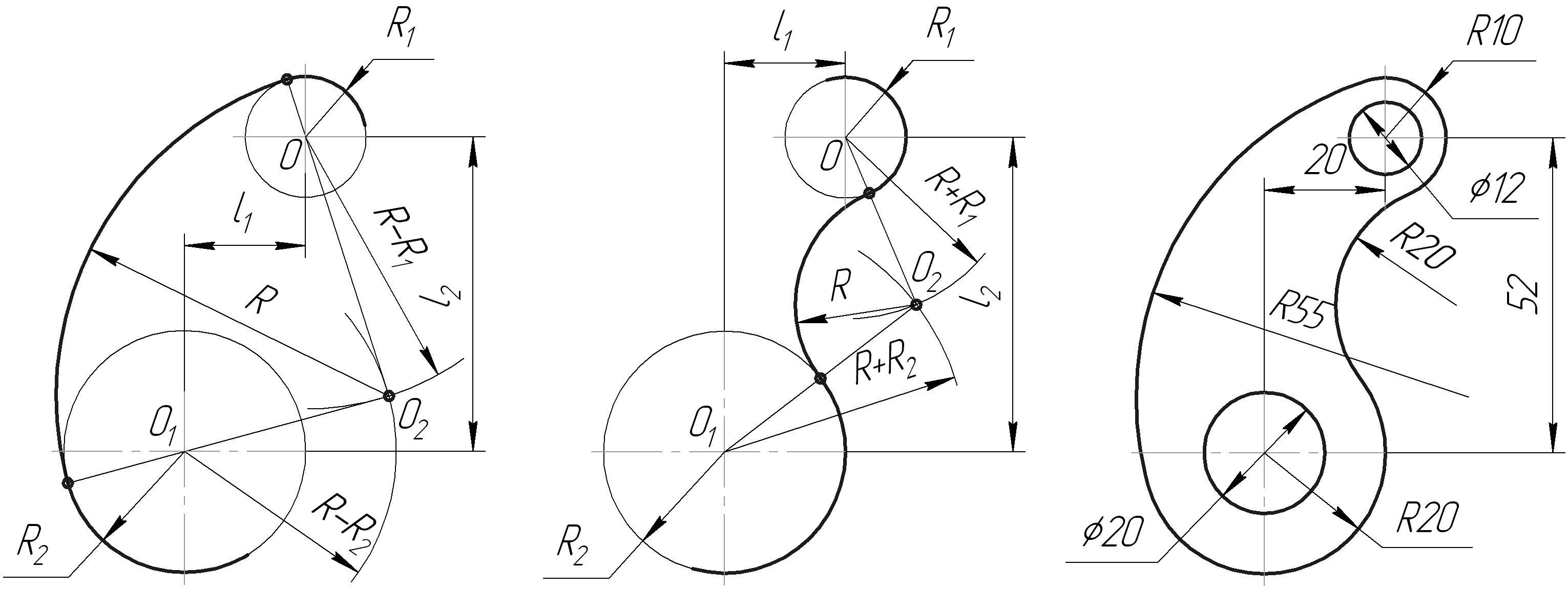
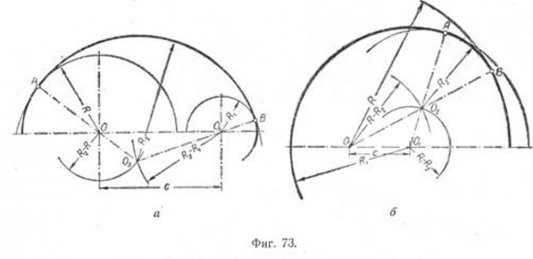
Внешнее сопряжение дуг окружностей

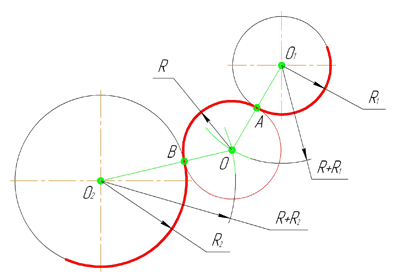
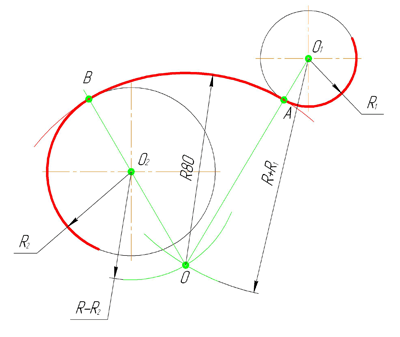
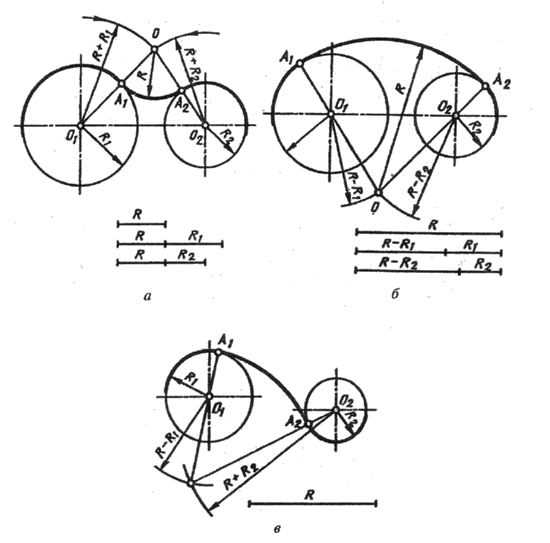
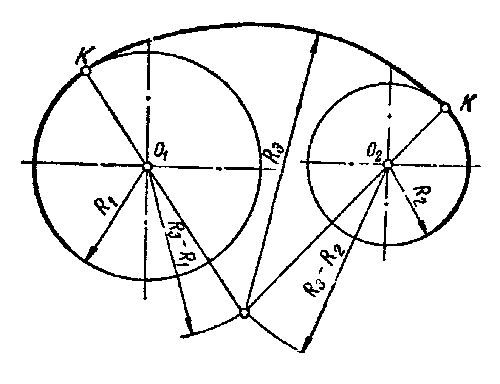
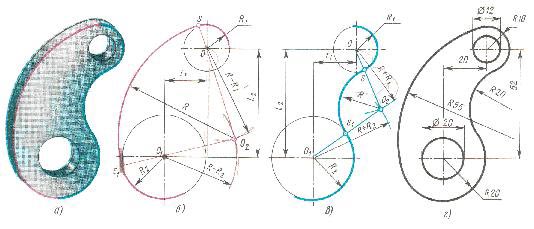
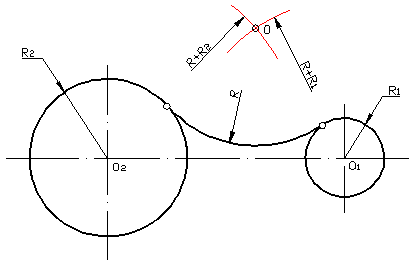
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Внутреннее сопряжение дуг окружностей

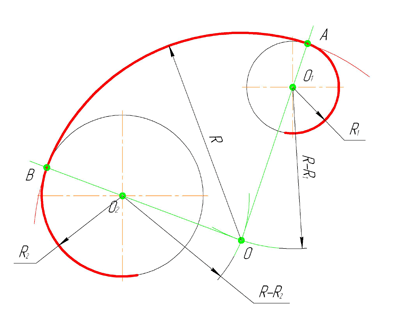
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

Смешанное сопряжение дуг окружностей

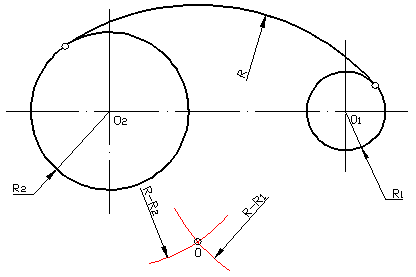
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

Сопряжение пк с внешними устройствами bluetooth

Мы уже в прошлый раз писали, как у нас появился мой bluetooth, поэтому здесь мы ещё раз не будем повторяться…

Мы будем сопрягать наш телефон и ноутбук. И + также разбирали тему передачи файлов , посмотрите, если вам интересно.

Открываем эту вкладку.

Попадаем в управление bluetooth устройствами.

Здесь мы видим, что мы ранее сопрягали нашу магнитолу.

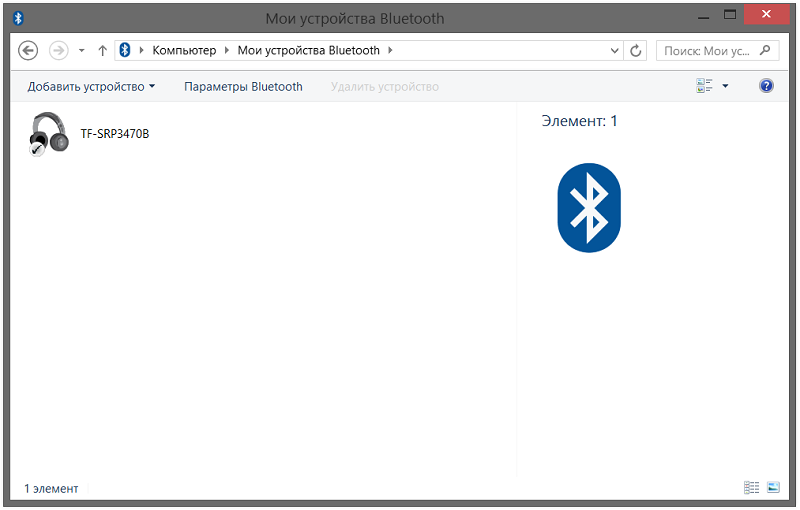
Далее, прежде чем искать наш телефон, на нем нужно включить bluetooth и включить режим видимости, если у вас есть такой.

У нас есть такая кнопка

Здесь мы видим строчку – тайм аут видимости – мы устанавливаем флажок на без тайм аута

Обратите внимание, что наш ПК нашелся в телефоне – это BIG

Если у вас Пк не находится идите в настройки – bluetooth там установите видимость для всех устройств.

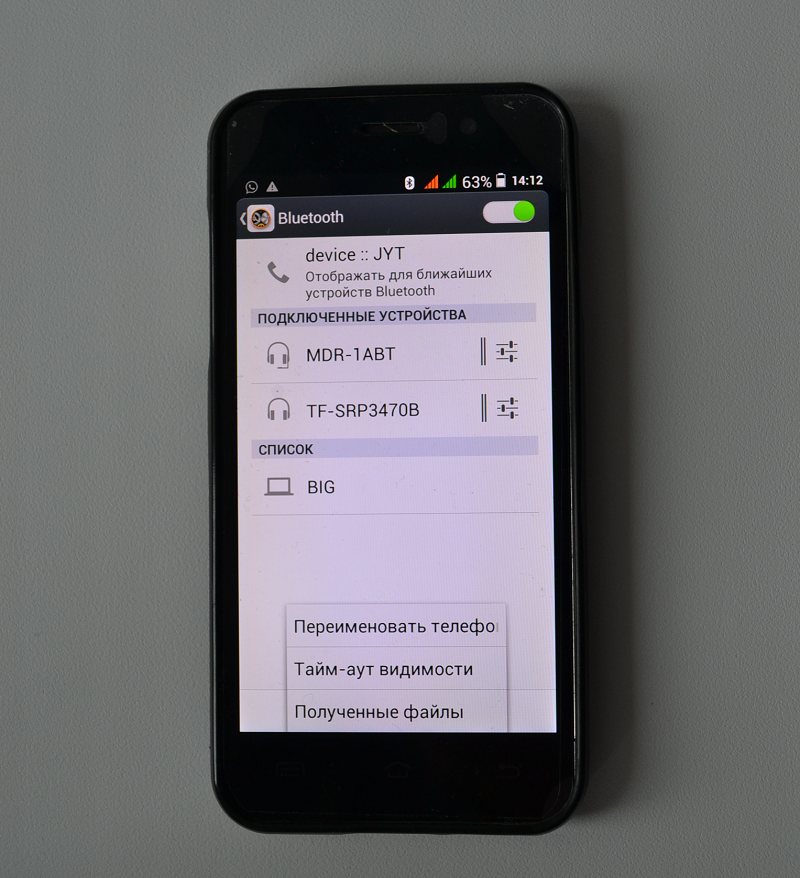
Далее на пк нажимаем добавить устройство.

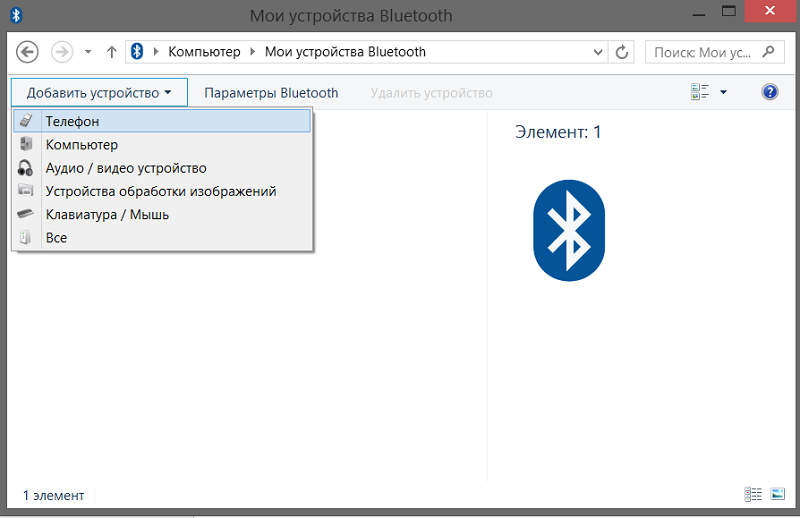
Далее – мы обнаружили устройство, с которым хотим соединиться. Нажимаем по найденному устройству.

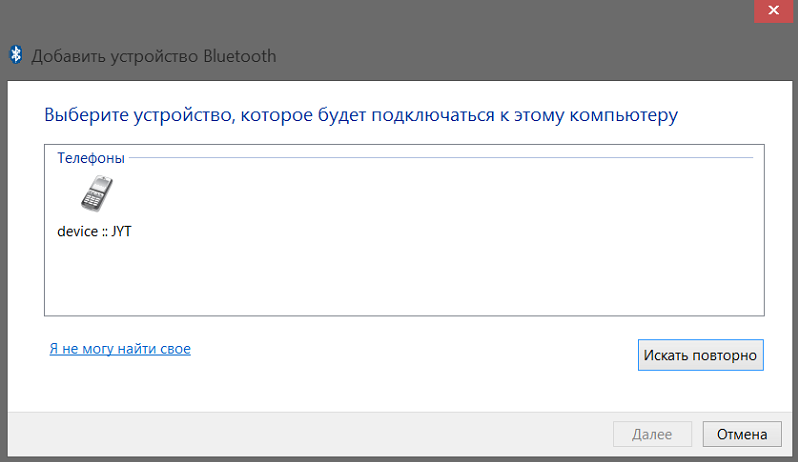
Ну и далее, как говорится дело в шляпе, вам только требуется потвердеть ваше сопряжение. На телефон отправляется сообщение, с кодом. Либо надо просто потвердеть!

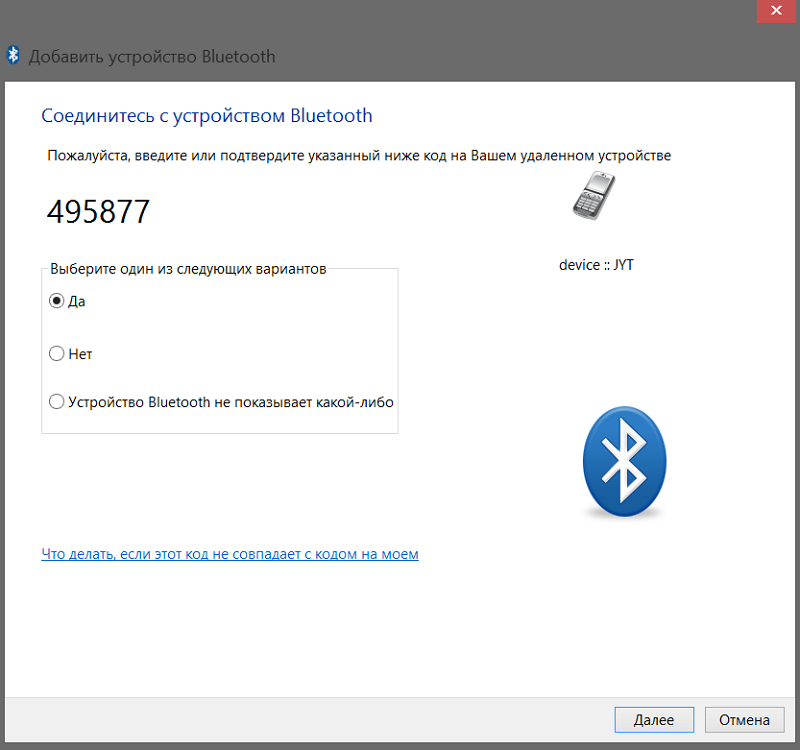
Всё! Наши устройства сопряжены!

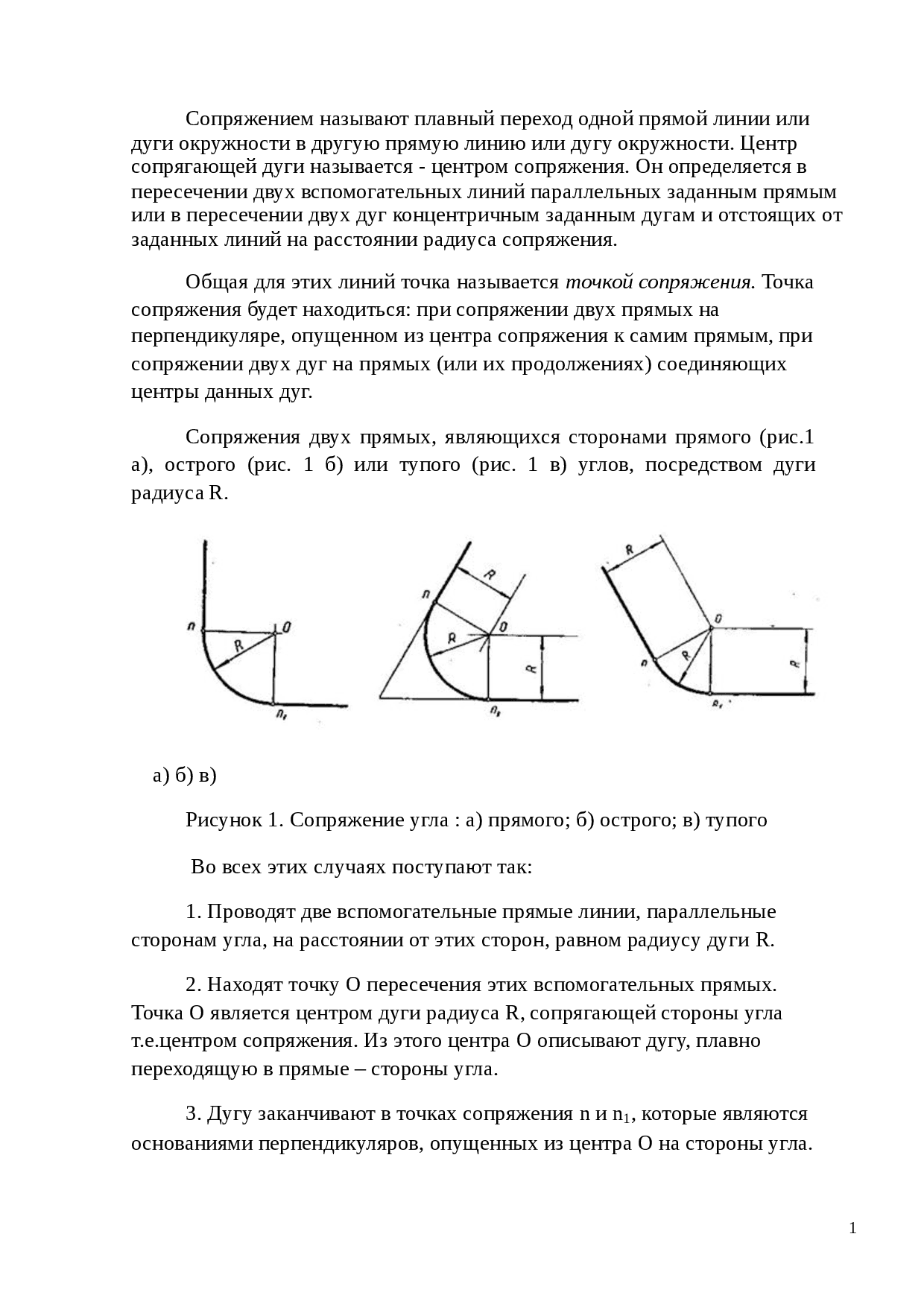
Сопряжение углов (Сопряжение пересекающихся прямых)

Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)

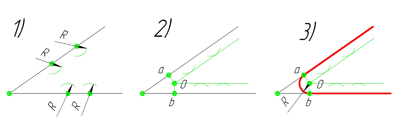
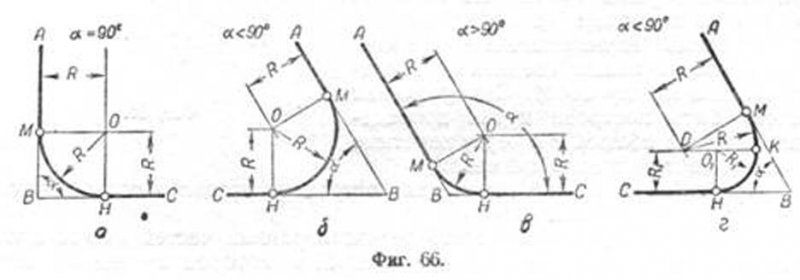
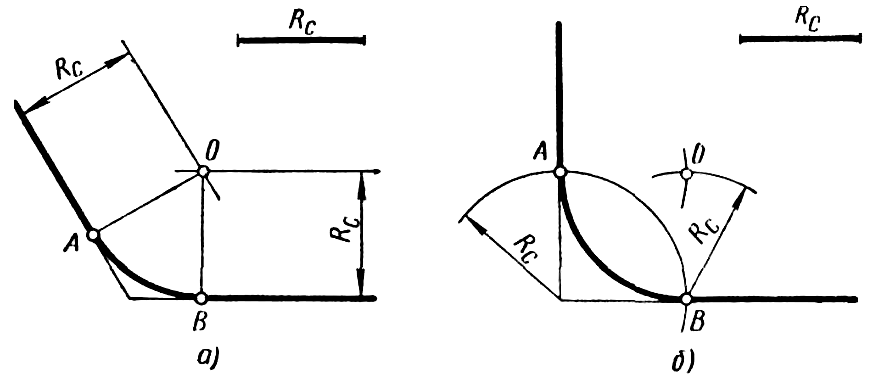
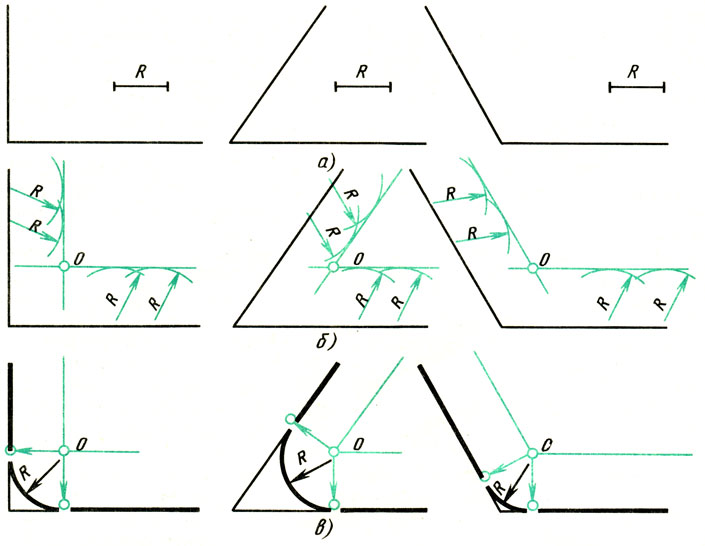
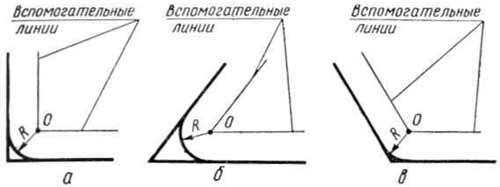
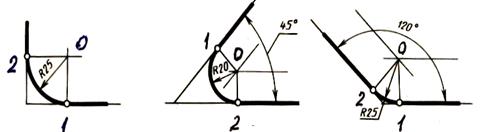
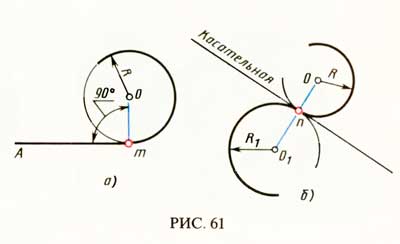
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.

Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)

Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

Что такое сопряжение!?

Когда между двумя и более устройствами произошло сопряжение, то данные устройства беспрепятственно могут обмениваться информацией между собой!

Под «обмениваться информацией» подразумевается, что вы можете отправлять, принимать файлы, слушать музыку, смотреть видео используя одно устройство в виде передатчика, а второе в качестве приемника.

А если данного сопряжения нет, то выше перечисленное невозможно!

Сопряжение может быть не только между техникой.

К примеру, в черчении, есть такое понятие : «сопряжение двух кривых», «сопряжение двух окружностей» и т.д.

В нашем случае, будем рассматривать сопряжение между компом и телефоном!

Определение

Свойства

Изогональное сопряжение оставляет на месте только центры вписанной и вневписанных окружностей.
Точка, изогонально сопряжённая точке на описанной окружности — бесконечно удалённая. Направление, задаваемое этой точкой, перпендикулярно прямой Симсона исходной точки.
Если точки Pa{\displaystyle P_{a}}, Pb{\displaystyle P_{b}}, Pc{\displaystyle P_{c}} симметричны точке P{\displaystyle P} относительно сторон треугольника, то центр описанной окружности PaPbPc{\displaystyle P_{a}P_{b}P_{c}} изогонально сопряжён точке P{\displaystyle P}.
Если в треугольник вписан эллипс, то его фокусы изогонально сопряжены.

Проекции двух изогонально сопряжённых точек на стороны лежат на одной окружности (верно и обратное) . Центр этой окружности — середина отрезка между сопряжёнными точками. Частный случай — окружность девяти точек.
Последнее означает, что подерные окружности двух изогонально сопряженных точек совпадают. В частности, подерной окружностью ортоцентра и центра описанной окружности является окружность Эйлера. Подерной или педальной окружностью называют описанную окружность подерного треугольника.
Две точки треугольника изогонально сопряжены тогда и только тогда, когда произведения трёх их расстояний до трёх сторон треугольника равны .

Пары изогонально сопряженных линий

Образ прямой при изогональном сопряжении — коника, описанная около треугольника. В частности, изогонально сопряжены бесконечно удалённая прямая и описанная окружность, прямая Эйлера и гипербола Енжабека, ось Брокара и гипербола Киперта, линия центров вписанной и описанной окружности и гипербола Фейербаха.
Если коника α{\displaystyle \alpha } изогонально сопряжена прямой l{\displaystyle l}, то трилинейные поляры всех точек на α{\displaystyle \alpha } будут проходить через точку, изогонально сопряжённую трилинейному полюсу l{\displaystyle l}.
Некоторые известные кубики, например, кубика Томпсона (Thompson cubic), кубика Дарбу (Darboux cubic), кубика Нейберга (Neuberg cubic) изогонально самосопряжены в том смысле, что при изогональном сопряжении всех их точек в треугольнике снова получаются кубики.