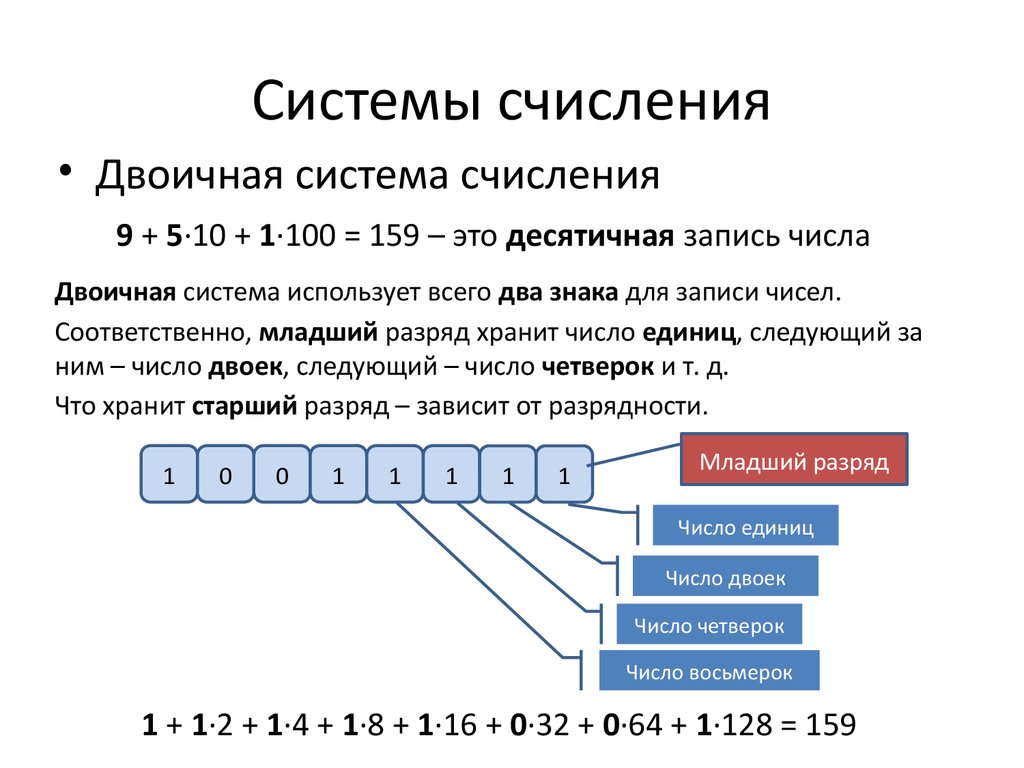
Арифметические операции
Вне зависимости от того, в каком виде представлено число, с ним можно проводить привычные для нас вычисления. Это может быть деление и умножение, вычитание и сложение в системе счисления, которую вы выбрали. Конечно, для каждой из них действуют свои правила.
Так для двоичной системы разработаны свои таблицы для каждой из операций. Такие же таблицы используются и в других позиционных системах.
Заучивать их необязательно – достаточно просто распечатать и иметь под рукой. Также можно воспользоваться калькулятором на ПК.

Одна из важнейших тем в информатике – система счисления. Знание этой темы, понимание алгоритмов перевода чисел из одной системы в другую – залог того, что вы сможете разобраться в более сложных темах, таких как алгоритмизация и программирование и сможете самостоятельно написать свою первую программу.
Примечания
- Н. А. Криницкий, Г. А. Миронов, Г. Д. Фролов, под ред. М. Р. Шура-Бура. Глава 10. Программно-управляемая машина «Сетунь» // Программирование. — М., 1963.
- ↑
- О. А. Акулов, Н. В. Медведев. Информатика и вычислительная техника. 4-е изд. — М.: Омега-Л, 2007. (Раздел I, Гл.3.3)
- Депман И. Я. Возникновение системы мер и способов измерения величин. Выпуск 1. (Москва: Государственное учебно-педагогическое издательство Министерства просвещения РСФСР (Учпедгиз), 1956. — Серия «Библиотека школьника»). Глава VIII. § Использование наиболее удобной системы гирь в России. Стр.118
- ↑ В Google Chrome после нажатия на PDF(333Kb) нужно стронуть одну из боковых сторон рамки браузера.
- Е. С. Давыдов, Наименьшие группы чисел для образования натуральных рядов, Спб., 1903, 36 стр.
- В. Ф. Гартц, Лучшая система для весовых гирь, Спб., 1910, 36 стр.
- Ф. А. Слудский, О свойствах степеней двух и трёх. «Математический сборник», ч. III, стр. 214.
- Юрий Ревич «Наследники Бэббиджа» // «Домашний компьютер», № 12, 1 декабря 2002 года.
- И. Я. Депман. «Меры и метрическая система», Учпедгиз, 1955.
- И. Я. Депман. «Возникновение системы мер и способов измерения величин», вып. 1, Учпедгиз, 1956.
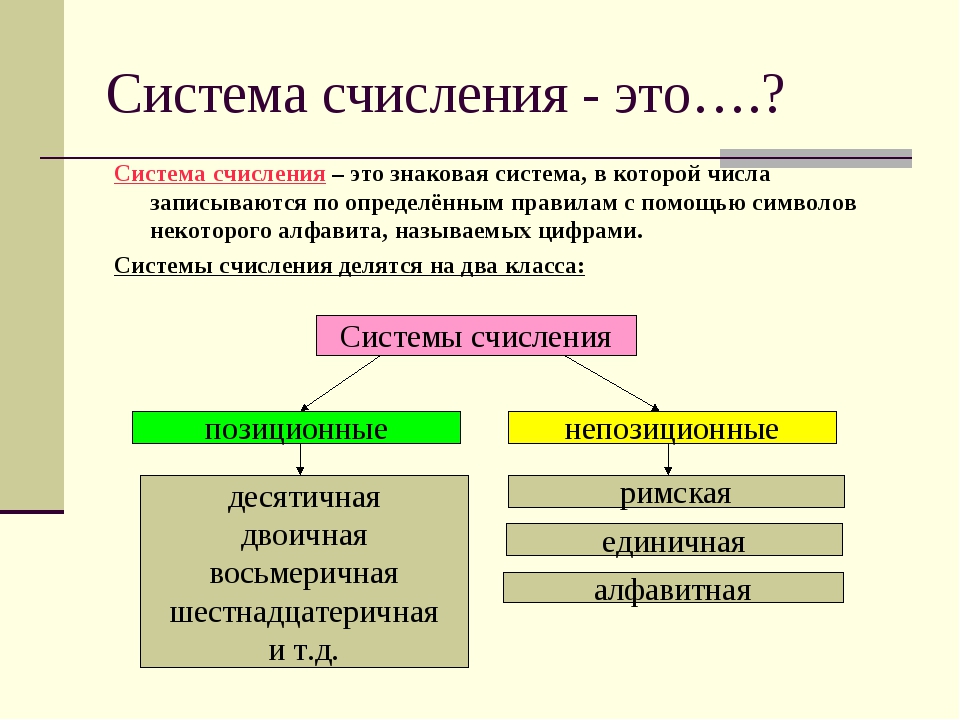
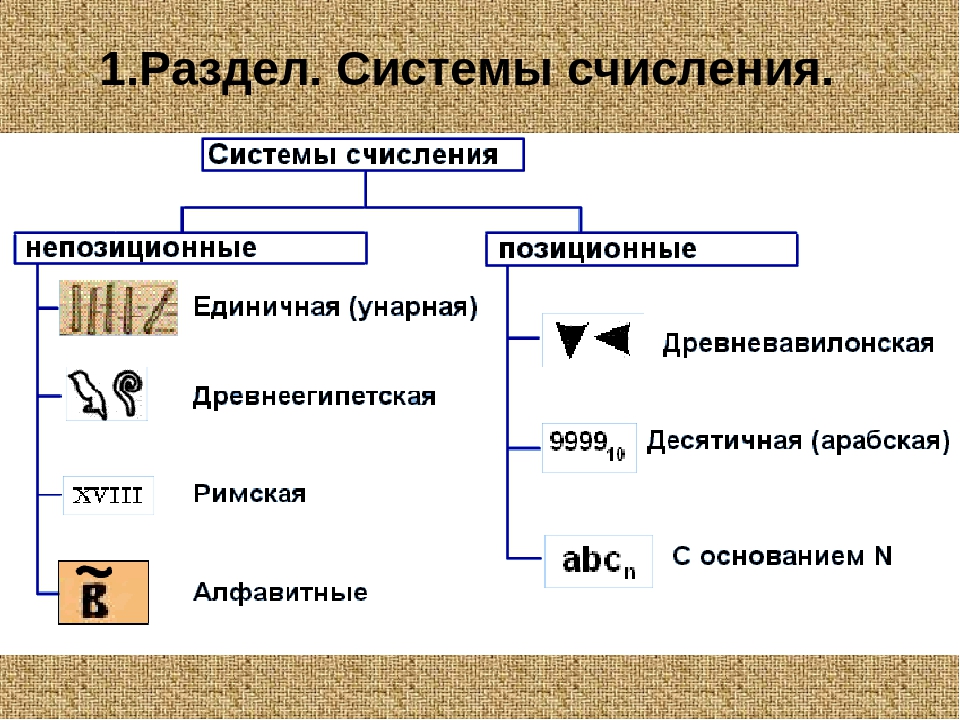
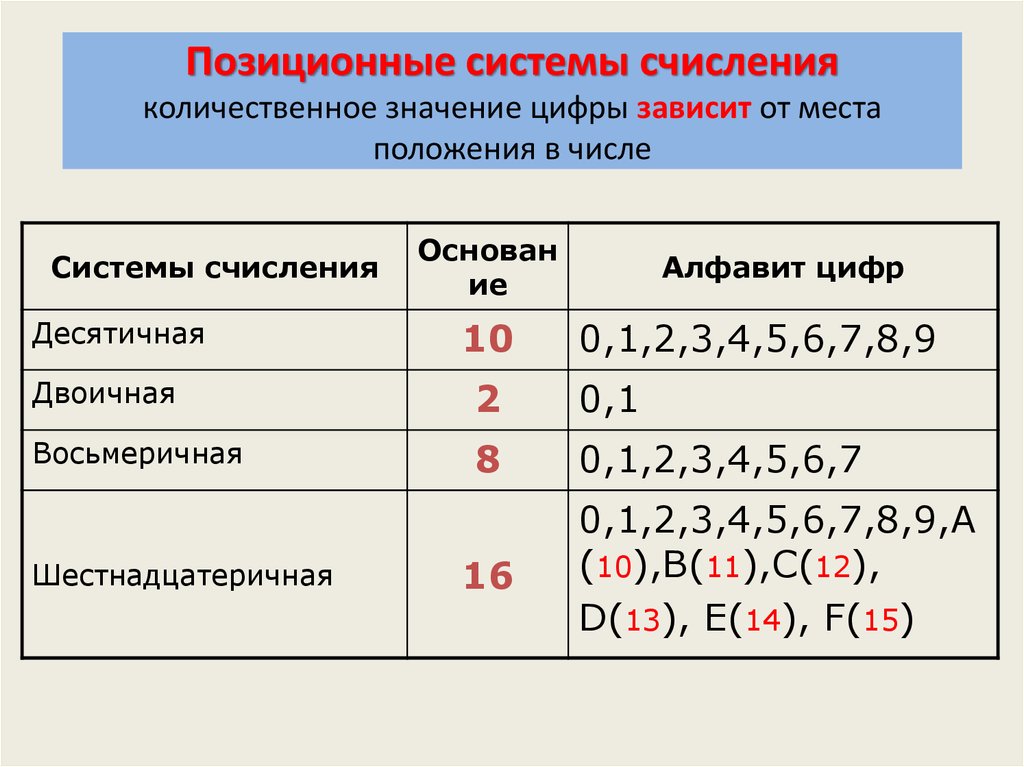
Системы счисления

Система счисления – одно из ключевых понятий в информатике, которое надо знать при изучении информационных технологий. Это основа, на базе которой строится всё остальное. Без понимания, что это такое, в будущем вам будет достаточно тяжело. Поэтому, самое время разобраться, что из себя представляет система счисления.
Что за зверь
Если говорить простыми словами, то система счисления – это способ записи чисел. Числа пишутся и
обозначаются через знаки. Эти знаки называются цифрами. Все мы их уже прекрасно
знаем – это 1, 2, 3, 4, 5 и так далее до бесконечности. Это арабские цифры, к
которым мы все привыкли. Но есть и римские. Чаще всего мы встречаем вот эти
римские цифры: I, V, X. Но есть ещё и вот такие: L, M. У нас они применяются, но гораздо
реже, чем арабские цифры. Отсюда мы делаем вывод, что числа систем счисления бывают двух видов:
- Арабские;
- Римские.
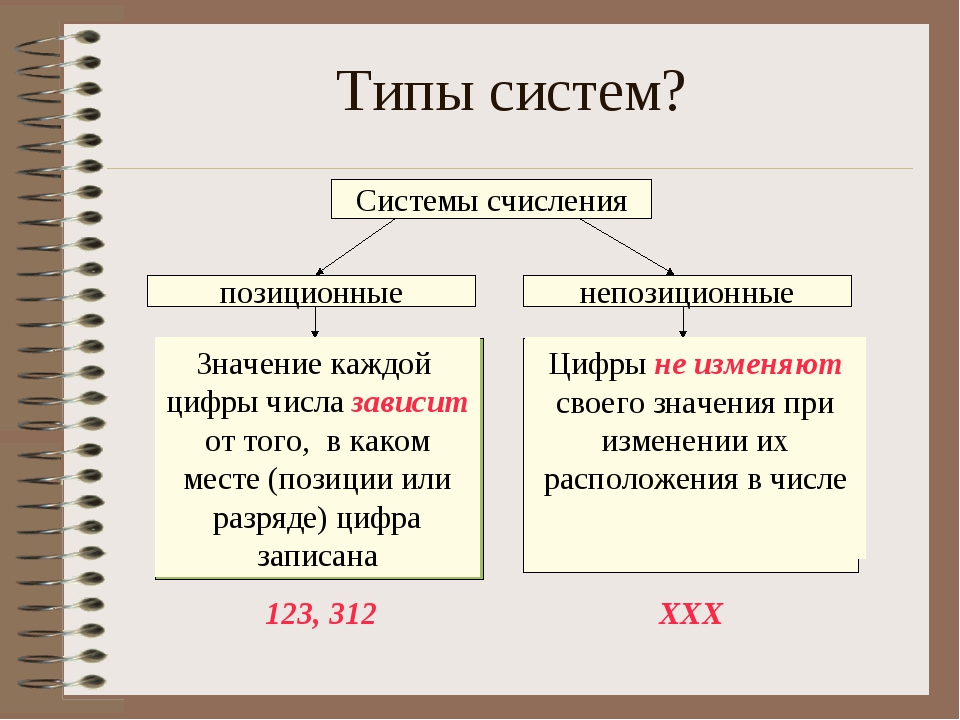
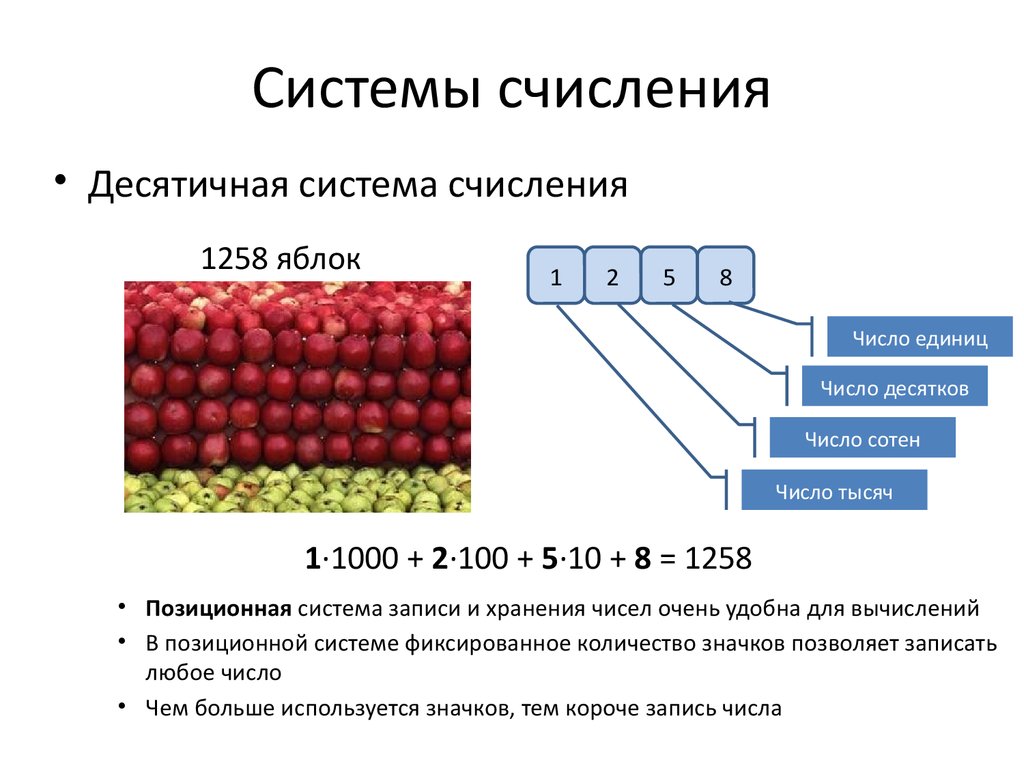
Также бывает позиционная и непозиционная система счисления. В первой итоговое количество чисел зависит от позиции, где стоит цифра. В непозиционной такого правила нет. Приведём пример. Возьмём число 11 и II. В первом случае мы используем арабские цифры, во втором – римские. 11 – это позиционная система счисления, где первая 1-ца показывает десятки, а вторая – единицу. В конце мы получаем итоговое число – одиннадцать. То есть, итог у нас зависит от того, на какой позиции стояли цифры. Поэтому такая система и называется позиционной.
Что же с II?
Это пример непозиционной системы. Здесь мы видим, что I – это один. А II означает два, так как стоят
две «палочки» и итоговое значение не зависит от позиции цифры в числе. Поэтому
система непозиционная.
Надеемся, здесь всё понятно. Время перейти к примерам
посложнее.
Возьмём числа 819, 595, 910. Рассматриваемой цифрой у нас
будет девятка. В первом варианте 819 она стоит на последней позиции, а значит
играет роль обычной девятки. В 595 девятка стоит на втором месте между
пятёрками. Здесь она играет роль десятых (90), обозначая 95 – девяносто пять. В
третьем числе 910 она стоит на первом месте, обозначая сотые (900), поэтому
читается как «девять сот». Это ещё один пример позиционной системы счисления.
Возьмём непозиционную систему. Например, XXV, XVI, XIV.
Рассматриваемое число – V.
Посмотрите внимательно. Куда бы мы не поставили нашу V, она всегда будет обозначать пять
единиц. А значит, итоговое значение не будет зависеть от позиции.
Возникает вопрос: как тогда удобнее
считать? Как вы заметили, при сложении, умножении, делении, вычитании, мы
применяем позиционные числа систем
счисления.То есть, 12, 492,
3123 и так далее. Это неспроста. Выполнять математические операции с такими
числами гораздо проще. Можно складывать и умножать в столбик, так проще делать
операции деления и вычитания. С римскими гораздо тяжелее. По этой причине римские
числа чаще применяются для обозначения времени. Например, XV лет до нашей
эры. Тут можете просто заглянуть в учебник по истории, где римские цифры будут
почти в каждой теме.
Слышал про разряд – что это такое
При работе с числами есть такое понятие, как разряд. Здесь
совсем всё просто. Разряд — это позиция цифры, которое оно занимается в числе.
А разрядность числа – то количество цифр, которые находятся в числе. Например,
48 – двухразрядное число, 987412 — шестиразрядное число, 127501750174 –
двенадцатиразрядное число. Как мы это определили? А вы посчитайте количество
цифр в числе и сами поймёте. В самих числах разряды считаются с правой стороны
налево. Например, число 841. Единица находится в первом разряде. Четвёрка – во
втором. Восьмёрка – в третьем. Думаем, принцип вы поняли.
Унитарная система счисления
Здесь все проще – она имеет только один цифровой знак – 1. В этой системе можно обрабатывать только целые числа, которые будут представлены набором единиц. Например, число 2 будет представлено как 11, а число 17 как 11111111111111111. Унитарная система счисления очень проста и легко реализуемая – это плюс, но уж очень громоздкая – это минус. Ранее ее активно использовали для записей нужного количества импульсов на барабанах и магнитных лентах. Но из-за громоздкости она не получила широкого применения, ведь необходимо очень много символов для представления числа 4552/10 – 1111…1111…1111…
Смешанные системы счисления
Смешанная система счисления является обобщением b{\displaystyle b}-ичной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы счисления является возрастающая последовательность чисел {bk}k=∞{\displaystyle \{b_{k}\}_{k=0}^{\infty }}, и каждое число x{\displaystyle x} в ней представляется как линейная комбинация:
- x=∑k=n−1akbk{\displaystyle x=\sum _{k=0}^{n-1}a_{k}b_{k}}, где на коэффициенты ak{\displaystyle a_{k}}, называемые как и прежде цифрами, накладываются некоторые ограничения.
Записью числа x{\displaystyle x} в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса k{\displaystyle k}, начиная с первого ненулевого.
В зависимости от вида bk{\displaystyle b_{k}} как функции от k{\displaystyle k} смешанные системы счисления могут быть степенными, показательными и т. п. Когда bk=bk{\displaystyle b_{k}=b^{k}} для некоторого b{\displaystyle b}, смешанная система счисления совпадает с показательной b{\displaystyle b}-ичной системой счисления.
Наиболее известным примером смешанной системы счисления является представление времени в виде количества суток, часов, минут и секунд. При этом величина «d{\displaystyle d} дней, h{\displaystyle h} часов, m{\displaystyle m} минут, s{\displaystyle s} секунд» соответствует значению d⋅24⋅60⋅60+h⋅60⋅60+m⋅60+s{\displaystyle d\cdot 24\cdot 60\cdot 60+h\cdot 60\cdot 60+m\cdot 60+s} секунд.
Факториальная система счисления
В факториальной системе счисления основаниями являются последовательность факториалов bk=k!{\displaystyle b_{k}=k!}, и каждое натуральное число x{\displaystyle x} представляется в виде:
- x=∑k=1ndkk!{\displaystyle x=\sum _{k=1}^{n}d_{k}k!}, где ≤dk≤k{\displaystyle 0\leq d_{k}\leq k}.
Факториальная система счисления используется при декодировании перестановок списками инверсий: имея номер перестановки, можно воспроизвести её саму следующим образом: номер перестановки (нумерация начинается с нуля) записывается в факториальной системе счисления, при этом коэффициент при числе i!{\displaystyle i!} будет обозначать число инверсий для элемента i+1{\displaystyle i+1} в том множестве, в котором производятся перестановки (число элементов меньших i+1{\displaystyle i+1}, но стоящих правее его в искомой перестановке).
Пример: рассмотрим множество перестановок из 5 элементов, всего их 5! = 120 (от перестановки с номером 0 — (1,2,3,4,5) до перестановки с номером 119 — (5,4,3,2,1)), найдём перестановку с номером 100:
- 100=4!⋅4+3!⋅+2!⋅2+1!⋅=96+4;{\displaystyle 100=4!\cdot 4+3!\cdot 0+2!\cdot 2+1!\cdot 0=96+4;}
положим ti{\displaystyle t_{i}} — коэффициент при числе i!{\displaystyle i!}, тогда t4=4{\displaystyle t_{4}=4}, t3={\displaystyle t_{3}=0}, t2=2{\displaystyle t_{2}=2}, t1={\displaystyle t_{1}=0}, тогда: число элементов меньших 5, но стоящих правее равно 4; число элементов меньших 4, но стоящих правее равно 0; число элементов меньших 3, но стоящих правее равно 2; число элементов меньших 2, но стоящих правее равно 0 (последний элемент в перестановке «ставится» на единственное оставшееся место) — таким образом, перестановка с номером 100 будет иметь вид: (5,3,1,2,4)
Проверка данного метода может быть осуществлена путём непосредственного подсчёта инверсий для каждого элемента перестановки.
Фибоначчиева система счисления
Фибоначчиева система счисления основывается на числах Фибоначчи. Каждое натуральное число n{\displaystyle n} в ней представляется в виде:
- n=∑kfkFk{\displaystyle n=\sum _{k}f_{k}F_{k}}, где Fk{\displaystyle F_{k}} — числа Фибоначчи, fk∈{,1}{\displaystyle f_{k}\in \{0,1\}}, при этом в коэффициентах fk{\displaystyle f_{k}} есть конечное количество единиц и не встречаются две единицы подряд.
Двоичная система счисления
Почти все электронные вычислительные устройства, в том числе компьютеры используют вовсе не привычную для нас десятичную, а двоичную систему счисления, где основанием системы является 2. В ее основе лежит использование всего двух чисел 0 и 1. Это очень удобно для электронных устройств в силу технических причин, поскольку соответствует всего двум состояниям включено (1) и выключено (0) или высокий и низкий сигнал или «истина» и «ложь» и так далее. Наличие всего двух состояний упрощает техническую реализацию, повышает надежность работы, уменьшает габариты и обеспечивает высокую помехоустойчивость цифровых схем, в сравнение с аналоговыми.
В итоге любые числа представлены в виде комбинаций нулей и единиц. Например, число 4 в двоичной системе счисления записывается как 100, но читается каждый символ в отдельности, то есть «один ноль ноль». Это может запутать, поскольку запись числа 4 в двоичной системе счисления внешне не отличается от числа 100 из десятичной. В некоторых ситуациях из-за этого может возникнуть путаница. В таких случаях справа от числа подстрочным шрифтом принято указывать систему счисления, к которой относится данной число в десятичном формате. Числа из нашего примера можно записать следующим образом 410 и соответственно 1002. Так же встречается вариант указания перед двоичным числом префиксов 0b или &, то есть 0b100 или &100.
Чтобы перевести десятичное число в двоичное, можно воспользоваться калькулятором расположенным ниже или применить метод Горнера. Для этого нужно десятичное число последовательно делить на основание системы, в данном случае 2. Если результат получается с остатком, то остаток отбрасываем, пишем 1 и снова делим на 2. Если результат получается без остатка, то пишем 0 и снова делим на 2. Запись нулей и единиц осуществляется справа налево, а деление продолжается пока в частном не получится ноль. Рассмотрим это на примере и преобразуем число 1110 в двоичный вид.
11/2=5 остаток 1 5/2=2 остаток 1 2/2=1 остаток 0 1/2=0 остаток 1
В частном получился ноль, осталось записать получившиеся цифры справа налево от первой к последней и в итоге получаем, что 1110=10112
Для обратной конвертации двоичных в десятичные, можно складывать последовательно цифры слева на право, умножая получившейся в предыдущем шаге результат на 2. Пересчитаем наш пример в обратную сторону.
Дано: &1011 1+0*2=1 (на первом шаге предыдущая сумма отсутствует, поэтому 0*2 ) 0+1*2=2 1+2*2=5 1+5*2=11 Результат: 1110
Чтобы окончательно вас запутать, стоит упомянуть, что для записи чисел может применяться двоичный код, а система счета при этом использоваться десятичная. Такая комбинация называется двоично-десятичное кодирование и так же находит применение в вычислительной технике.
Определение
Один десятичный разряд в десятичной системе счисления иногда называют декадой. В цифровой электронике одному десятичному разряду десятичной системы счисления соответствует один десятичный триггер.
Целое число x в десятичной системе счисления представляется в виде конечной линейной комбинации степеней числа 10:
- x=±∑k=n−1ak10k{\displaystyle x=\pm \sum _{k=0}^{n-1}a_{k}10^{k}}, где ak{\displaystyle \ a_{k}} — это целые числа, называемые цифрами, удовлетворяющие неравенству ≤ak≤9.{\displaystyle 0\leq a_{k}\leq 9.}
Обычно для ненулевого числа x требуют, чтобы старшая цифра an−1{\displaystyle a_{n-1}} в десятичном представлении x была также ненулевой.
Например, число сто три представляется в десятичной системе счисления в виде:
- 103=1⋅102+⋅101+3⋅10.{\displaystyle 103=1\cdot 10^{2}+0\cdot 10^{1}+3\cdot 10^{0}.}
С помощью n позиций в десятичной системе счисления можно записать целые числа от 0 до 10n−1{\displaystyle 10^{n}-1}, то есть, всего 10n{\displaystyle 10^{n}} различных чисел.
Дробные числа записываются в виде строки цифр с разделителем десятичная запятая, называемой десятичной дробью:
- an−1an−2…a1a,a−1a−2…a−(m−1)a−m=∑k=−mn−1ak10k,{\displaystyle a_{n-1}a_{n-2}\dots a_{1}a_{0},a_{-1}a_{-2}\dots a_{-(m-1)}a_{-m}=\sum _{k=-m}^{n-1}a_{k}10^{k},}
где n — число разрядов целой части числа, m — число разрядов дробной части числа.
Двоично-десятичное кодирование
В двоичных компьютерах применяют двоично-десятичное кодирование десятичных цифр, при этом для одной двоично-десятичной цифры отводится четыре двоичных разряда (двоичная тетрада). Двоично-десятичные числа требуют большего количества битов для своего хранения. Так, четыре двоичных разряда имеют 16 состояний, и при двоично-десятичном кодировании 6 из 16 состояний двоичной тетрады не используются.
Таблица сложения в десятичной системе счисления
| + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 10 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Таблица умножения в десятичной системе
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Смешанные системы счисления
Смешанная система счисления является обобщением b{\displaystyle b}-ичной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы счисления является возрастающая последовательность чисел {bk}k=∞{\displaystyle \{b_{k}\}_{k=0}^{\infty }}, и каждое число x{\displaystyle x} в ней представляется как линейная комбинация:
- x=∑k=n−1akbk{\displaystyle x=\sum _{k=0}^{n-1}a_{k}b_{k}}, где на коэффициенты ak{\displaystyle a_{k}}, называемые как и прежде цифрами, накладываются некоторые ограничения.
Записью числа x{\displaystyle x} в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса k{\displaystyle k}, начиная с первого ненулевого.
В зависимости от вида bk{\displaystyle b_{k}} как функции от k{\displaystyle k} смешанные системы счисления могут быть степенными, показательными и т. п. Когда bk=bk{\displaystyle b_{k}=b^{k}} для некоторого b{\displaystyle b}, смешанная система счисления совпадает с показательной b{\displaystyle b}-ичной системой счисления.
Наиболее известным примером смешанной системы счисления является представление времени в виде количества суток, часов, минут и секунд. При этом величина «d{\displaystyle d} дней, h{\displaystyle h} часов, m{\displaystyle m} минут, s{\displaystyle s} секунд» соответствует значению d⋅24⋅60⋅60+h⋅60⋅60+m⋅60+s{\displaystyle d\cdot 24\cdot 60\cdot 60+h\cdot 60\cdot 60+m\cdot 60+s} секунд.
Факториальная система счисления
В факториальной системе счисления основаниями являются последовательность факториалов bk=k!{\displaystyle b_{k}=k!}, и каждое натуральное число x{\displaystyle x} представляется в виде:
- x=∑k=1ndkk!{\displaystyle x=\sum _{k=1}^{n}d_{k}k!}, где ≤dk≤k{\displaystyle 0\leq d_{k}\leq k}.
Факториальная система счисления используется при декодировании перестановок списками инверсий: имея номер перестановки, можно воспроизвести её саму следующим образом: номер перестановки (нумерация начинается с нуля) записывается в факториальной системе счисления, при этом коэффициент при числе i!{\displaystyle i!} будет обозначать число инверсий для элемента i+1{\displaystyle i+1} в том множестве, в котором производятся перестановки (число элементов меньших i+1{\displaystyle i+1}, но стоящих правее его в искомой перестановке).
Пример: рассмотрим множество перестановок из 5 элементов, всего их 5! = 120 (от перестановки с номером 0 — (1,2,3,4,5) до перестановки с номером 119 — (5,4,3,2,1)), найдём перестановку с номером 100:
- 100=4!⋅4+3!⋅+2!⋅2+1!⋅=96+4;{\displaystyle 100=4!\cdot 4+3!\cdot 0+2!\cdot 2+1!\cdot 0=96+4;}
положим ti{\displaystyle t_{i}} — коэффициент при числе i!{\displaystyle i!}, тогда t4=4{\displaystyle t_{4}=4}, t3={\displaystyle t_{3}=0}, t2=2{\displaystyle t_{2}=2}, t1={\displaystyle t_{1}=0}, тогда: число элементов меньших 5, но стоящих правее равно 4; число элементов меньших 4, но стоящих правее равно 0; число элементов меньших 3, но стоящих правее равно 2; число элементов меньших 2, но стоящих правее равно 0 (последний элемент в перестановке «ставится» на единственное оставшееся место) — таким образом, перестановка с номером 100 будет иметь вид: (5,3,1,2,4)
Проверка данного метода может быть осуществлена путём непосредственного подсчёта инверсий для каждого элемента перестановки.
Фибоначчиева система счисления
Основная статья: Фибоначчиева система счисления
Фибоначчиева система счисления основывается на числах Фибоначчи. Каждое натуральное число n{\displaystyle n} в ней представляется в виде:
- n=∑kfkFk{\displaystyle n=\sum _{k}f_{k}F_{k}}, где Fk{\displaystyle F_{k}} — числа Фибоначчи, fk∈{,1}{\displaystyle f_{k}\in \{0,1\}}, при этом в коэффициентах fk{\displaystyle f_{k}} есть конечное количество единиц и не встречаются две единицы подряд.
Перевод чисел из одной системы счисления в другую.
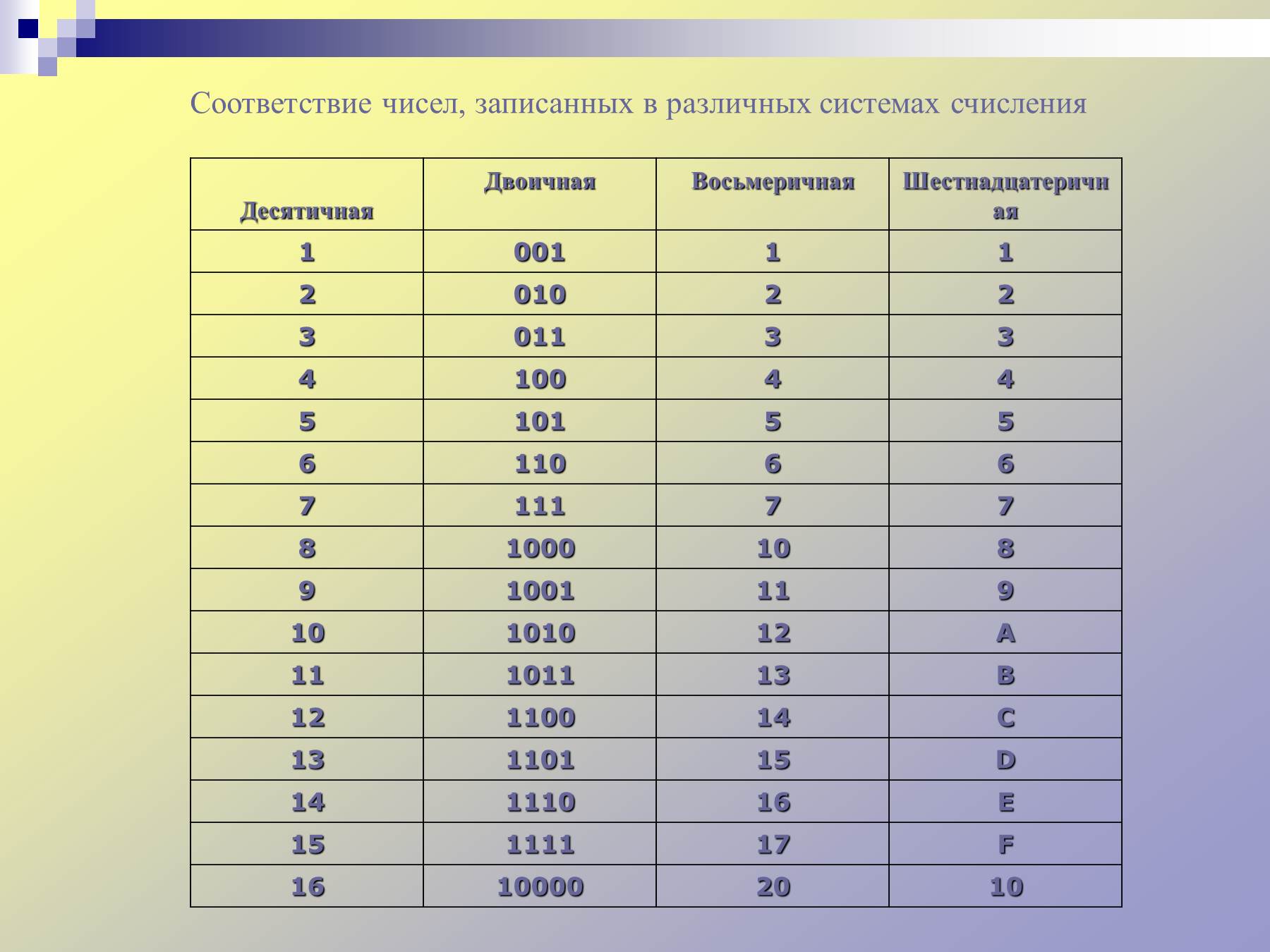
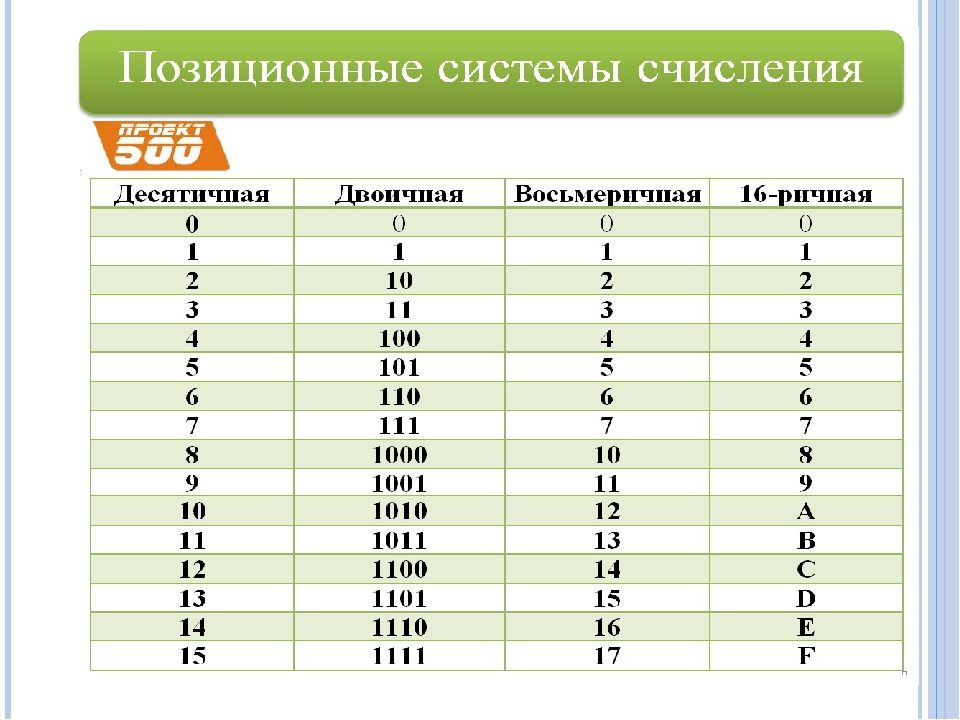
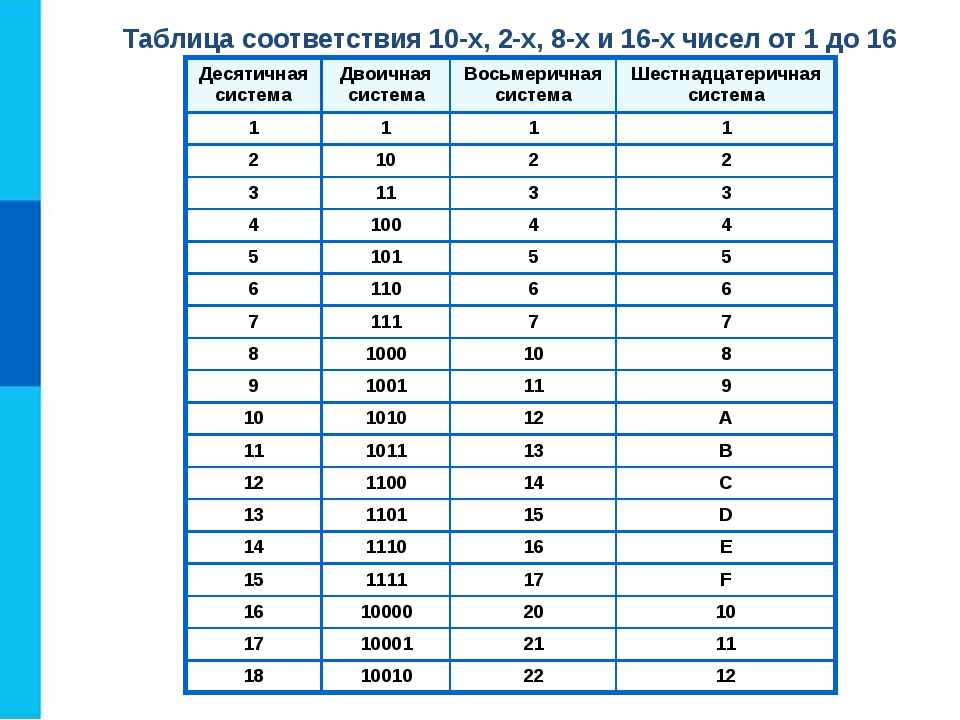
Наиболее часто встречающиеся системы счисления – это двоичная, шестнадцатеричная и десятичная. Как же связаны между собой представления числа в различных системах счисления? Есть различные способы перевода чисел из одной системы счисления в другую на конкретных примерах.
Пусть нужно перевести число 567 из десятичной в двоичную систему. Сначала определяется максимальная степень двойки, такая, чтобы два в этой степени было меньше или равно исходному числу. В данном случае это 9, т.к. 29 =512, а 210 = 1024, что больше начального числа. Таким образом получается число разрядов результата, оно равно 9 + 1 = 10, поэтому результат будет иметь вид 1ххххххххх, где вместо х могут стоять любые двоичные цифры. Вторая цифра результата находится так – двойка возводится в степень 9 и вычитается из исходного числа: 567 – 29 = 55. Остаток сравнивается с числом 28 = 256. Так как 55 меньше 256, то девятый разряд – нуль, т.е. результат имеет вид 10хххххххх. Рассмотрим восьмой разряд. Так как 27 = 128 > 55, то и он будет нулевым.
Седьмой разряд также оказывается нулевым. Искомая двоичная запись числа принимает вид 1000хххххх. 25 = 32 ххххх). Для остатка 55 – 32 = 23 справедливо неравенство 24 = 16
567 = 1·29 + 0·28 + 0·27 + 0·26 + 1·25 + 1·24 + 0·23 + 1·22 + 1·21 + 1·2
При другом способе перевода чисел используется операция деления в столбик. Если взять то же число 567 и разделить его на 2, получается частное 283 и остаток 1. Та же операция производится и с числом 283. Частное – 141, остаток – 1. Опять полученное частное делится на 2 и так до тех пор, пока частное не станет меньше делителя. Теперь, чтобы получить число в двоичной системе счисления, достаточно записать последнее частное, т.е. 1, и приписать к нему в обратном порядке все полученные в процессе деления остатки.
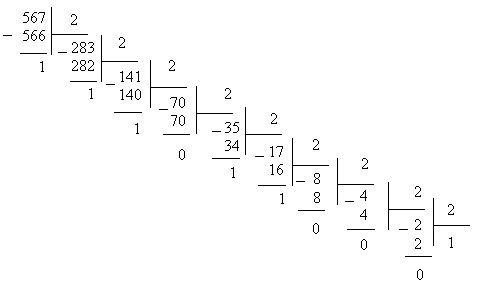
Результат, естественно, не изменился: 567 в двоичной системе счисления записывается как 1 000 110 111.
Эти два способа применимы при переводе числа из десятичной системы в систему с любым основанием. Например, при переводе числа 567 в систему счисления с основанием 16 число сначала разлагается по степеням основания. Искомое число состоит из трех цифр, т.к. 162 = 256 3 = 4096. Определяется цифра старшего разряда. 2·162 = 512 2 = 768, следовательно, искомое число имеет вид 2хх, где вместо х могут стоять любые шестнадцатеричные цифры. Остается распределить по следующим разрядам число 55 (567 – 512). 3·16 = 48
Второй способ состоит в последовательном делении в столбик, с единственным отличием в том, что делить надо не на 2, а на 16, и процесс деления заканчивается, когда частное становится строго меньше 16.
Конечно, для записи числа в шестнадцатеричной системе счисления, необходимо заменить 10 на A, 11 на B и так далее.
Операция перевода в десятичную систему выглядит гораздо проще, так как любое десятичное число можно представить в виде x = a0·pn + a1·pn–1 +… + an–1·p1 + an·p0, где a0 … an – это цифры данного числа в системе счисления с основанием p.
Например,так можно перевести число 4A3F в десятичную систему. По определению, 4A3F= 4·163 + A·162 + 3·16 + F. При замене A на 10, а F на 15, получается 4·163 + 10·162 + 3·16 + 15= 19007.
Проще всего переводить числа из двоичной системы в системы с основанием, равным степеням двойки (8 и 16), и наоборот. Для того чтобы целое двоичное число записать в системе счисления с основанием 2n, нужно данное двоичное число разбить справа налево на группы по n-цифр в каждой; если в последней левой группе окажется меньше n разрядов, то дополнить ее нулями до нужного числа разрядов; рассмотреть каждую группу, как n-разрядное двоичное число, и заменить ее соответствующей цифрой в системе счисления с основанием 2n.
| Таблица 1. ДВОИЧНО-ШЕСТНАДЦАТЕРИЧНАЯ ТАБЛИЦА | ||||||||
| 2-ная | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| 16-ная | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 2-ная | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 16-ная | 8 | 9 | A | B | C | D | E | F |
| Таблица 2. ДВОИЧНО-ВОСЬМЕРИЧНАЯ ТАБЛИЦА | ||||||||
| 2-ная | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 8-ная | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Известный французский астроном, математик и физик Пьер Симон Лаплас (1749–1827) писал об историческом развитии систем счисления, что «Мысль выражать все числа девятью знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна. Как нелегко было прийти к этому методу, мы видим на примере величайших гениев греческой учености Архимеда и Аполлония, от которых эта мысль осталась скрытой.»
Сравнение десятичной системы исчисления с иными позиционными системами позволило математикам и инженерам-конструкторам раскрыть удивительные возможности современных недесятичных систем счисления, обеспечившие развитие компьютерной техники.
Анна Чугайнова
Девятеричная форма представления команд
Представление команд троичным кодом при программировании и при вводе в машину неудобно и неэкономно, поэтому вне машины применяется девятеричная форма представления команд. Девятеричные цифры 4¯,3¯,2¯,1¯,,1,2,3,4{\displaystyle {\bar {4}},{\bar {3}},{\bar {2}},{\bar {1}},0,1,2,3,4} сопоставляются парам троичных цифр:
- 1¯1¯=4¯;1¯=3¯;1¯1=2¯;1¯=1¯;00=;{\displaystyle {\bar {1}}{\bar {1}}={\bar {4}};\quad {\bar {1}}0={\bar {3}};\quad {\bar {1}}1={\bar {2}};\quad 0{\bar {1}}={\bar {1}};\quad 00=0;}
- 11=4;10=3;11¯=2;01=1.{\displaystyle 11=4;\quad 10=3;\quad 1{\bar {1}}=2;\quad 01=1.}
При выводе из машины отрицательные девятеричные цифры обозначают буквами:
| Девятеричная цифра | 1¯{\displaystyle {\bar {1}}} | 2¯{\displaystyle {\bar {2}}} | 3¯{\displaystyle {\bar {3}}} | 4¯{\displaystyle {\bar {4}}} |
|---|---|---|---|---|
| Буква латинского алфавита | Z | Y | X | W |
| Буква русского алфавита | Ц | У | Х | Ж |
Двоично-кодированные системы счисления
Определенное неудобство двоичной кодировки заключается в ее громоздкости. Например, количество цифр двоичного кода примерно в 13,3 раза больше, чем такое же число в представлении десятичным кодом. Именно из-за этого в технике довольно часто используют смешанные системы кодирования, такие как двоично-шестнадцатеричную, двоично-восьмеричную, двоично-десятичную. При смешанном кодировании объединяют достоинства нескольких систем, а именно – емкость (для шестнадцатеричных, восьмеричных и десятичных) и двоичное изображение цифр при использовании двоичного кодирования.
В двоично-десятичном коде каждая цифра десятичного числа (0, 1, 2, …,9) записывается двоичным кодом. Для этого используют двоичные разряды – тетрады:

При использовании нормального значения (веса) каждого разряда двоичного кода, то значимость в тетраде разрядов (начинается с левого старшего разряда) составит 23 – 22 – 21 – 2, или же 8421. Исходя из этого, десятичные цифры будут представлены двоичным кодом: 1 — 0001; 2 – 0010, …, остальные коды представлены ниже:

Итак, двоично-десятичный код по существу является десятичным, а по форме двоичным. Ранее такие коды наиболее часто применялись для записи на перфоленты.
Рассмотренная выше двоично-десятичная система еще носит названия взвешенного двоично-десятичного кода 8421. Удобство данного кода хорошее, но имеется один недостаток, а именно – обрабатываться могут не только цифры 0…9, но и числа 10…15, которые используют не всегда и их приходится исключать.
Разработано большое количество кодов с другими наборами весов по разрядам – 2421, 5211, 7421 и многие другие. Также существуют коды, у которых присутствуют отрицательные веса в некоторых разрядах: (6)(4)(-2)(-1) и другие.
Также довольно часто используют для изображения в двоично-десятичных системах десятичных цифр комбинаторные коды, такие как – код Грея однопеременный, 2 из 5, 3 из 5 и другие.
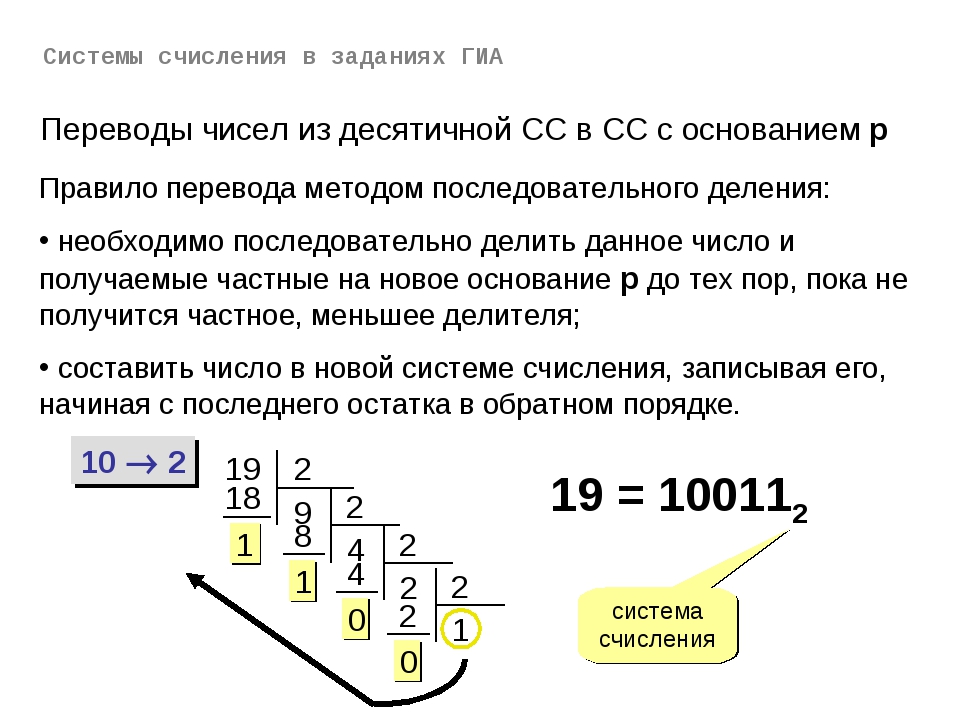
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4. Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 2 | 1 |
Рис. 1
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:
Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
Рис. 2
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Рис. 3
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | ||
| x | 2 | |
| 0.428 | ||
| x | 2 | |
| 0.856 | ||
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0.848 | ||
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Рис. 4
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011.
Следовательно можно записать:
Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0.25 | ||
| x | 2 | |
| 0.5 | ||
| x | 2 | |
| 1 | 0.0 |
Рис. 5
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Рис. 6
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0.768 | ||
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Рис. 7
Получили:
Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим: