Прямоугольная система координат

Примечания

Пархоменко А. С. Аффинная система координат. — Математическая энциклопедия. — М: Советская энциклопедия, 1977—1985.
Скляренко Е. Г. Барицентрические координаты. — Математическая энциклопедия. — М: Советская энциклопедия, 1977—1985.
Долгачев И. В., Псковских В. А. Биполярные координаты. — Математическая энциклопедия. — М: Советская энциклопедия, 1977—1985.
Соколов Д. Д. Бицилиндрические координаты. — Математическая энциклопедия. — М: Советская энциклопедия, 1977—1985.
Войцеховский М. И. Проективные координаты. — Математическая энциклопедия. — М: Советская энциклопедия, 1977—1985.
Соколов Д. Д. Эллипсоидальные координаты. — Математическая энциклопедия. — М: Советская энциклопедия, 1977—1985.

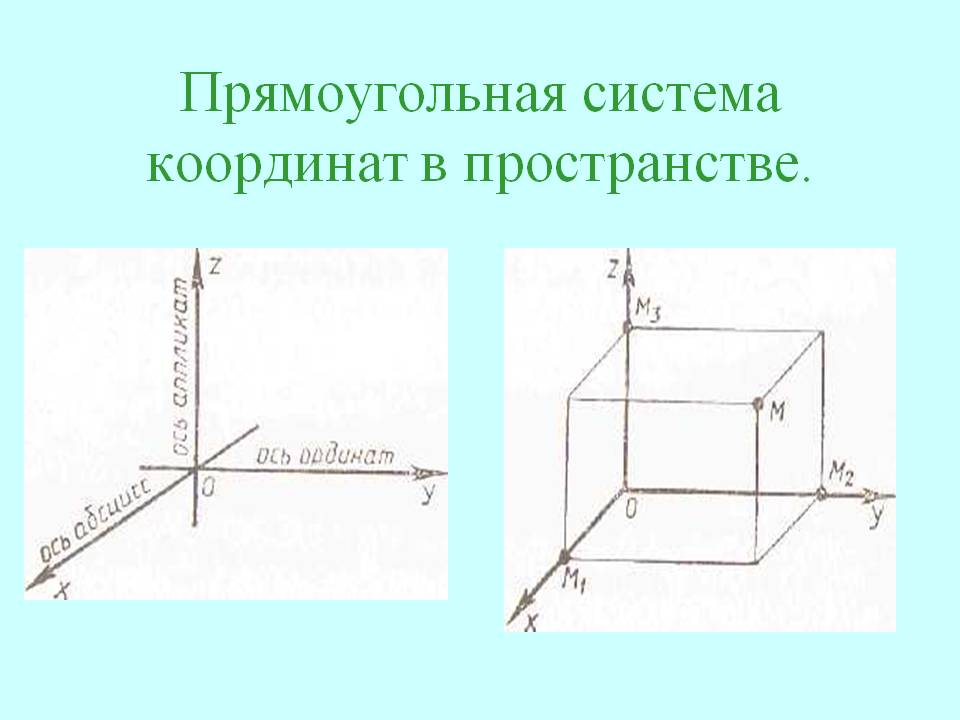
Прямоугольная система координат в пространстве

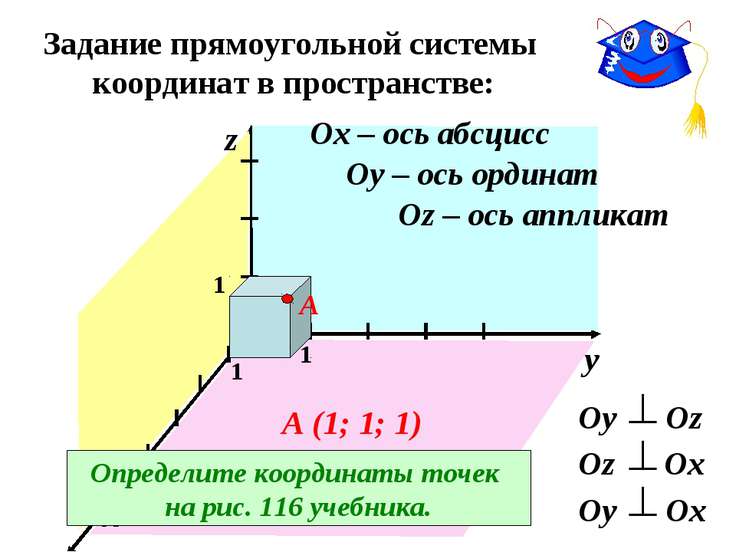
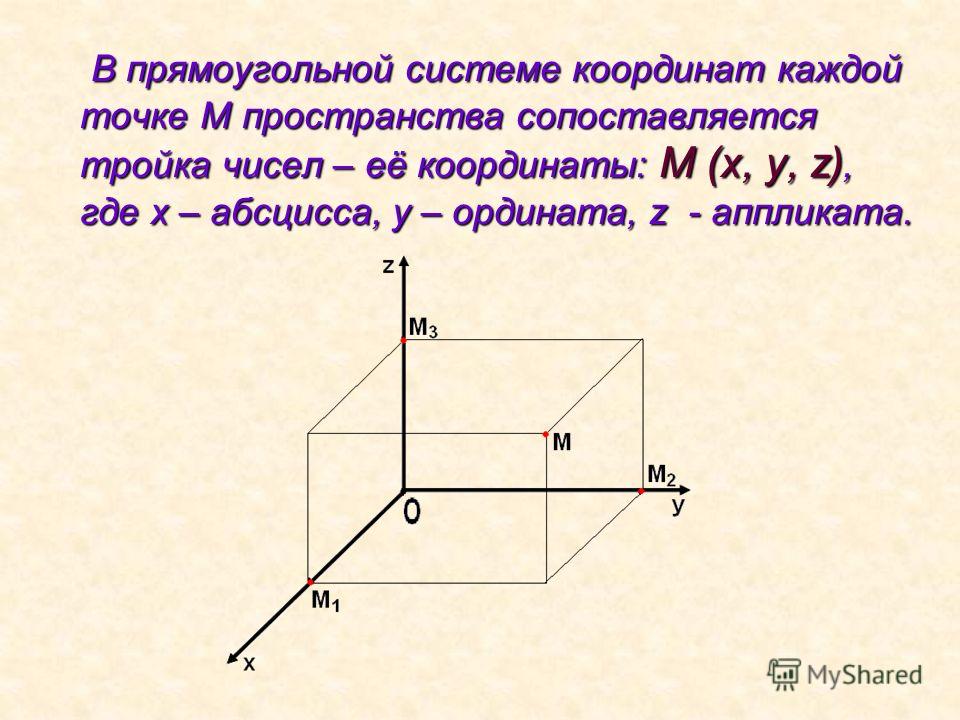
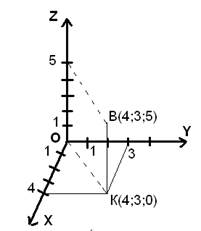
Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трёхмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат OX{\displaystyle OX}, OY{\displaystyle OY} и OZ{\displaystyle OZ}. Оси координат пересекаются в точке O{\displaystyle O}, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно) одинаковы для всех осей. OX{\displaystyle OX} — ось абсцисс, OY{\displaystyle OY} — ось ординат, OZ{\displaystyle OZ} — ось аппликат.

Рис. 2

Положение точки A{\displaystyle A} в пространстве определяется тремя координатами x{\displaystyle x}, y{\displaystyle y} и z{\displaystyle z}. Координата x{\displaystyle x} равна длине отрезка OB{\displaystyle OB}, координата y{\displaystyle y} — длине отрезка OC{\displaystyle OC}, координата z{\displaystyle z} — длине отрезка OD{\displaystyle OD} в выбранных единицах измерения. Отрезки OB{\displaystyle OB}, OC{\displaystyle OC} и OD{\displaystyle OD} определяются плоскостями, проведёнными из точки A{\displaystyle A} параллельно плоскостям YOZ{\displaystyle YOZ}, XOZ{\displaystyle XOZ} и XOY{\displaystyle XOY} соответственно.

Координата x{\displaystyle x} называется абсциссой точки A{\displaystyle A},

координата y{\displaystyle y} — ординатой точки A{\displaystyle A},

координата z{\displaystyle z} — аппликатой точки A{\displaystyle A}.

Символически это записывают так:

A(x,y,z){\displaystyle A(x,\;y,\;z)}

или

A=(x,y,z){\displaystyle A=(x,\;y,\;z)}

или привязывают запись координат к конкретной точке с помощью индекса:

xA,yA,zA{\displaystyle x_{A},\;y_{A},\;z_{A}}

и т. п.

Каждая ось рассматривается как числовая прямая, т. е. имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка B{\displaystyle B} лежала не как на рисунке — на луче OX{\displaystyle OX}, а на его продолжении в обратную сторону от точки O{\displaystyle O} (на отрицательной части оси OX{\displaystyle OX}), то абсцисса x{\displaystyle x} точки A{\displaystyle A} была бы отрицательной (минус расстоянию OB{\displaystyle OB}). Аналогично и для двух других осей.

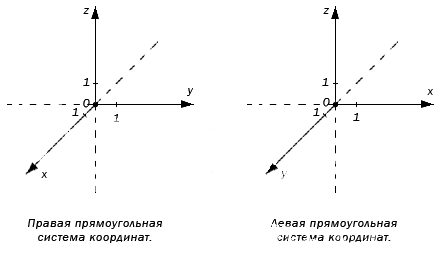
Все прямоугольные системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении еще и располагают их, если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат, можно, используя правило правой руки, правило винта и т. п. (положительное направление осей выбирают так, чтобы при повороте оси OX{\displaystyle OX} против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY{\displaystyle OY}, если этот поворот наблюдать со стороны положительного направления оси OZ{\displaystyle OZ}).

Любая из восьми областей, на которые пространство делится тремя взаимно перпендикулярными координатными плоскостями называться октант.

Переход из одной системы координат в другую

Декартовы и полярные

x=rcos⁡φ,{\displaystyle x=r\,\cos \varphi ,}

y=rsin⁡φ,{\displaystyle y=r\,\sin \varphi ,}

r=x2+y2,{\displaystyle r={\sqrt {x^{2}+y^{2}}},}

φ=arctg⁡yx+πu(−x)sgn⁡y,{\displaystyle \varphi =\operatorname {arctg} {\frac {y}{x}}+\pi u_{0}(-x)\,\operatorname {sgn} y,}

где u — функция Хевисайда с u()=,{\displaystyle u_{0}(0)=0,} а sgn — функция signum. Здесь функции u и sgn используются как «логические» переключатели, аналогичные по значению операторам «если .. то» (if…else) в языках программирования. Некоторые языки программирования имеют специальную функцию atan2 (y, x), которая возвращает правильный φ в необходимом квадранте, определённом координатами x и y.

Декартовы и цилиндрические

x=rcos⁡φ,{\displaystyle x=r\,\cos \varphi ,}

y=rsin⁡φ,{\displaystyle y=r\,\sin \varphi ,}

z=z.{\displaystyle z=z.\quad }

r=x2+y2,{\displaystyle r={\sqrt {x^{2}+y^{2}}},}

φ=arctg⁡yx+πu(−x)sgn⁡y,{\displaystyle \varphi =\operatorname {arctg} {\frac {y}{x}}+\pi u_{0}(-x)\,\operatorname {sgn} y,}

z=z.{\displaystyle z=z.\quad }

(dxdydz)=(rcos⁡θ−rsin⁡φrsin⁡θrcos⁡φ1)⋅(drdφdz),{\displaystyle {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}={\begin{pmatrix}r\cos \theta &-r\sin \varphi &0\\r\sin \theta &r\cos \varphi &0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}},}

(drdφdz)=(xx2+y2yx2+y2−yx2+y2xx2+y21)⋅(dxdydz).{\displaystyle {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}}={\begin{pmatrix}{\frac {x}{\sqrt {x^{2}+y^{2}}}}&{\frac {y}{\sqrt {x^{2}+y^{2}}}}&0\\{\frac {-y}{\sqrt {x^{2}+y^{2}}}}&{\frac {x}{\sqrt {x^{2}+y^{2}}}}&0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}.}

Декартовы и сферические

x=ρsin⁡θcos⁡φ,{\displaystyle {x}=\rho \,\sin \theta \,\cos \varphi ,\quad }

y=ρsin⁡θsin⁡φ,{\displaystyle {y}=\rho \,\sin \theta \,\sin \varphi ,\quad }

z=ρcos⁡θ;{\displaystyle {z}=\rho \,\cos \theta ;\quad }

ρ=x2+y2+z2,{\displaystyle {\rho }={\sqrt {x^{2}+y^{2}+z^{2}}},}

θ=arccos⁡zρ=arctg⁡x2+y2z,{\displaystyle {\theta }=\arccos {\frac {z}{\rho }}=\operatorname {arctg} {\frac {\sqrt {x^{2}+y^{2}}}{z}},}

φ=arctg⁡yx+πu(−x)sgn⁡y.{\displaystyle {\varphi }=\operatorname {arctg} {\frac {y}{x}}+\pi \,u_{0}(-x)\,\operatorname {sgn} y.}

(dxdydz)=(sin⁡θcos⁡φρcos⁡θcos⁡φ−ρsin⁡θsin⁡φsin⁡θsin⁡φρcos⁡θsin⁡φρsin⁡θcos⁡φcos⁡θ−ρsin⁡θ)⋅(dρdθdφ),{\displaystyle {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}={\begin{pmatrix}\sin \theta \cos \varphi &\rho \cos \theta \cos \varphi &-\rho \sin \theta \sin \varphi \\\sin \theta \sin \varphi &\rho \cos \theta \sin \varphi &\rho \sin \theta \cos \varphi \\\cos \theta &-\rho \sin \theta &0\end{pmatrix}}\cdot {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}},}

(dρdθdφ)=(xρyρzρxzρ2×2+y2yzρ2×2+y2−(x2+y2)ρ2×2+y2−yx2+y2xx2+y2)⋅(dxdydz).{\displaystyle {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}}={\begin{pmatrix}x/\rho &y/\rho &z/\rho \\{\frac {xz}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {yz}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {-(x^{2}+y^{2})}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}\\{\frac {-y}{x^{2}+y^{2}}}&{\frac {x}{x^{2}+y^{2}}}&0\end{pmatrix}}\cdot {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}.}

Цилиндрические и сферические

r=ρsin⁡θ,{\displaystyle {r}=\rho \,\sin \theta ,}

φ=φ,{\displaystyle {\varphi }=\varphi ,\quad }

z=ρcos⁡θ;{\displaystyle {z}=\rho \,\cos \theta ;}

ρ=r2+z2,{\displaystyle {\rho }={\sqrt {r^{2}+z^{2}}},}

θ=arctg⁡zr+πu(−r)sgn⁡z,{\displaystyle {\theta }=\operatorname {arctg} {\frac {z}{r}}+\pi \,u_{0}(-r)\,\operatorname {sgn} z,}

φ=φ.{\displaystyle {\varphi }=\varphi .\quad }

(drdφdh)=(sin⁡θρcos⁡θ1cos⁡θ−ρsin⁡θ)⋅(dρdθdφ),{\displaystyle {\begin{pmatrix}dr\\d\varphi \\dh\end{pmatrix}}={\begin{pmatrix}\sin \theta &\rho \cos \theta &0\\0&0&1\\\cos \theta &-\rho \sin \theta &0\end{pmatrix}}\cdot {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}},}

(dρdθdφ)=(rr2+z2zr2+z2−zr2+z2rr2+z21)⋅(drdφdz).{\displaystyle {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}}={\begin{pmatrix}{\frac {r}{\sqrt {r^{2}+z^{2}}}}&0&{\frac {z}{\sqrt {r^{2}+z^{2}}}}\\{\frac {-z}{r^{2}+z^{2}}}&0&{\frac {r}{r^{2}+z^{2}}}\\0&1&0\end{pmatrix}}\cdot {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}}.}

В ролях

Персонал мюзикла

Майкл Дуглас — хореограф Зак (дублирует Сергей Сазонтьев[источник не указан 252 дня])
Терренс Манн — Ларри, ассистент Зака
Шэрон Браун — Ким

Танцоры

Элисон Рид — Кэсси
Одри Лэндерс — Вэл Кларк (дублирует Марина Дюжева[источник не указан 252 дня])
Майкл Блевинс — Марк Тобори
Ямил Боргес — Диана Моралес (дублирует Наталья Гурзо[источник не указан 252 дня])
Жан Ган Бойд — Конни Вонг
Грэг Бурже — Ричи Уолтерс
Кэмерон Инглиш — Пол Сан Марко
Тони Филдс — Эл Делюка
Николь Фосси — Кристин Эвелин Эрлих-Делюка (дублирует Татьяна Божок[источник не указан 252 дня])
Вики Фредерик — Шейла Брайнт
Мишель Джонстон — Биби Бенсон
Джанет Джонс — Джуди Монро
Пэм Клингер — Мэгги Уинслоу
Чарльз МакГоуэн — Майк Кэсс (дублирует Вадим Андреев[источник не указан 252 дня])
Джастин Росс — Грэг Гарднер (дублирует Владимир Антоник[источник не указан 252 дня])
Блэйн Сэведж — Дон
Мэтт Уэст — Бобби

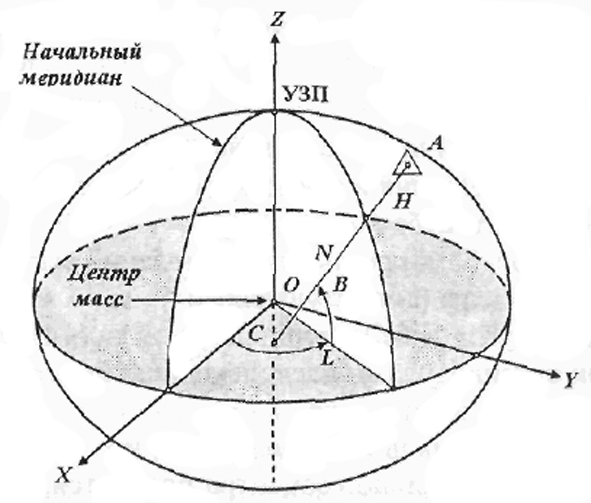
Вторая экваториальная система координат

Что интересно, главная плоскость и точка отчёта аналогичны предыдущей системе. Но её координатами выступают склонение и прямое восхождение. Подразумевается, что восхождение это дуга экватора неба, которая проходит от точки весеннего равноденствия до круга светила. Кроме того, измерение проходит в часовой мере. Однако, её отсчёт ведётся противоположно часовой стрелки. Между тем, вторая система координат, характеризуется постоянными координатами звёзд. В противовес первой системе, движение Земли за сутки не влияет на них. Применяется она для определения перемещения небесных тел за год.

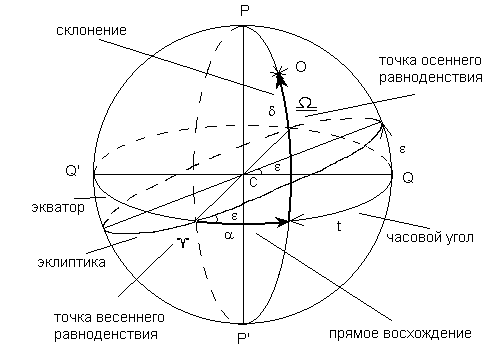Вторая экваториальная система координат

Важно понимать, что координаты могут быть всегда разными. Поэтому существует множество задач

Их решение возможно с применением, подходящей отдельной ситуации, системой. Вообще, для решения задач и определении координат, очень часто чередуют системы. Создание систем координат позволило учёным составить карту звёздного неба. Кроме того, обрисовалась определённая структура небесной системы. Что, в значительной мере, способствовало развитию астрономии и астрологии. Помимо того, экваториальные системы координат применяются во многих областях научной деятельности.

Звёздное небо

Очевидно, что разработка и внедрение определённых систем, составляет основу исследования космического пространства. Мы стараемся максимально приблизиться к его пониманию. Конечно, множество уже применяемых приёмов, расчётов и методов способствует расширению нашего кругозора.

3.2 Ориентирование линий по истинному и магнитному меридианам

Горизонтальный
угол (от 0 до 360°),
отсчитываемый по ходу часовой стрелки
от северного
направления
истинного
меридиана до данного направления,
называется
истинным азимутом А(рисунок.7,
а).
Направление истинного
меридиана
на местности может быть получено из
астрономических
наблюдений

Горизонтальный
угол(от
0 до 360°),
отсчитываемый по ходу часовой стрелки
от северного направления магнитного
меридиана
до данного направления, называется
магнитным
азимутом А_m(рисунок
7, а)
Направление магнитного
меридиана
определяется при помощи приборов с
магнитной
стрелкой
(компаса или буссоли).

Магнитный
меридиан,
как правило, не совпадает с истинным
в
данной точке земной поверхности, образуя
с ним некоторый уголδ,
называемый склонением
магнитной стрелки.

Угол
δ
отсчитывается от истинного меридиана
до магнитного и может быть восточным
(со знаком плюс) и западным (со знаком
минус).

Зная склонение
магнитной стрелки в данной точке, можно
осуществить переход от магнитного
азимута направления к истинному по
формуле А=Ам+(± δ)

Рисунок
7 -Истинный
и магнитный азимуты

В
различных точках земного шара склонение
магнитной стрелки имеет разные значения.
Так, на территории СНГ его величина
изменяется от +10,2 до —14,5°. Склонение
магнитной стрелки в одной и той же точке
существенно изменяется со временем.
Различают вековые
(на 22,5° за 500 лет), годовые
(до
±8′) и суточные
(порядка ±15″ и более) изменения
склонения
магнитной стрелки.

Вследствие
указанных причин положение
магнитного меридиана может быть
установлено лишь
приближенно,
и ориентирование линий с помощью
магнитных азимутов допускается только
при составлении планов
небольших участков местности.

В
геодезии принято различать прямое и
обратное направления линий местности.
Если направление линии MN
с точкиМ
на
точку N
(рисунок 7, б)
считать
прямым,
то NMбудет
обратным
направлением
той же линии. В соответствии с этим угол
Аi
является
прямым
азимутом MNв
точке М,
а
А₂
— обратным
азимутом
той же линии в точке N.

Вследствие
сферичности Земли меридианыв
различных точках, расположенных на
одной линии,не параллельнымежду собой. Поэтомуазимутлинии в каждой ее точке имеетразличное
значение. Угол между направлениями
меридианов в данных двух
точках линии называется сближением
меридиановγ.Зависимость
между прямым и обратными азимутами
линииMNопределится
выражением

А_пр=А_обр±
180˚+ γ;

γ
= Δλ sin
φ,

где
Δλ —
разность долгот меридианов, проходящих
через точки Ми N;
φ—
средняя широта ориентируемой линии
(для территории
СНГ величина сближения меридианов
достигает более минуты на 1 км дуги
параллели).

Прямоугольная система координат в пространстве

Рис. 2

Координата x{\displaystyle x} называется абсциссой точки A{\displaystyle A},

координата y{\displaystyle y} — ординатой точки A{\displaystyle A},

координата z{\displaystyle z} — аппликатой точки A{\displaystyle A}.

Символически это записывают так:

A(x,y,z){\displaystyle A(x,\;y,\;z)}

или

A=(x,y,z){\displaystyle A=(x,\;y,\;z)}

или привязывают запись координат к конкретной точке с помощью индекса:

xA,yA,zA{\displaystyle x_{A},\;y_{A},\;z_{A}}

и т. п.

Общие системы координат

Числовая строка

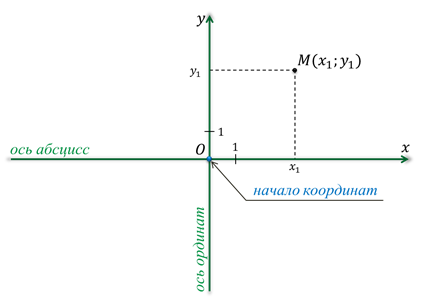
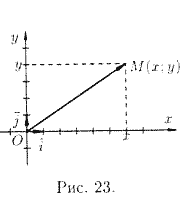
Самый простой пример системы координат — это идентификация точек на прямой с действительными числами с помощью числовой прямой . В этой системе на заданной прямой выбирается произвольная точка O (начало координат ). Координата точки P определяется как расстояние со знаком от O до P , где расстояние со знаком — это расстояние, принимаемое как положительное или отрицательное, в зависимости от того, с какой стороны лежит линия P. Каждой точке дается уникальная координата, и каждое действительное число является координатой уникальной точки.

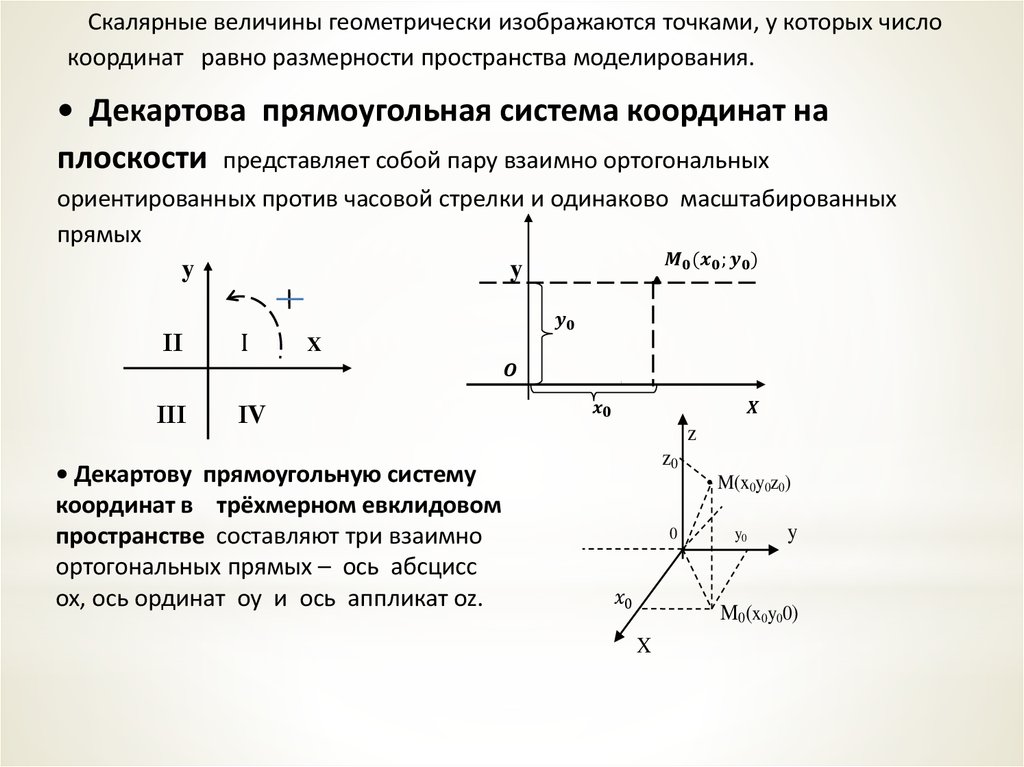
Декартова система координат

Декартова система координат на плоскости.

Прототипным примером системы координат является декартова система координат . На плоскости выбираются две перпендикулярные линии, и координаты точки принимаются в качестве расстояний до линий со знаком.

В трех измерениях выбираются три взаимно ортогональные плоскости, и три координаты точки являются расстояниями со знаком до каждой из плоскостей. Это можно обобщить, чтобы создать n координат для любой точки n- мерного евклидова пространства.

В зависимости от направления и порядка осей координат трехмерная система может быть правосторонней или левосторонней. Это одна из многих систем координат.

Полярная система координат

Другой распространенной системой координат для плоскости является полярная система координат . В качестве полюса выбирается точка, а луч из этой точки принимается за полярную ось . Для заданного угла θ через полюс проходит одна линия, угол которой с полярной осью равен θ (измеряется против часовой стрелки от оси к прямой). Тогда на этой линии есть единственная точка, расстояние со знаком которой от начала координат равно r для данного числа r . Для данной пары координат ( r , θ) существует одна точка, но любая точка представлена множеством пар координат. Например, ( r , θ), ( r , θ + 2π) и (- r , θ + π) — все полярные координаты для одной и той же точки. Полюс представлен как (0, θ) для любого значения θ.

Цилиндрическая и сферическая системы координат

Есть два распространенных метода расширения полярной системы координат до трех измерений. В системе цилиндрических координат , A г координата с тем же значением , как и в декартовой системе координат добавляется к г и & thetas ; в полярных координатах , давая тройную ( г , & thetas , г ). Сферические координаты делают еще один шаг вперед, преобразовывая пару цилиндрических координат ( r , z ) в полярные координаты ( ρ , φ ), давая тройку ( ρ , θ , φ ).

Однородная система координат

Точка на плоскости может быть представлена в однородных координатах тройкой ( x , y , z ), где x / z и y / z — декартовы координаты точки. Это вводит «дополнительную» координату, поскольку для определения точки на плоскости необходимы только две, но эта система полезна тем, что представляет любую точку на проективной плоскости без использования бесконечности . В общем, однородная система координат — это система, в которой важны только отношения координат, а не фактические значения.

Другие часто используемые системы

Вот некоторые другие общие системы координат:

Криволинейные координаты — это обобщение систем координат в целом; система основана на пересечении кривых.
- Ортогональные координаты : координатные поверхности пересекаются под прямым углом
- Наклонные координаты : координатные поверхности не ортогональны
Лог-полярная система координат представляет собой точку в плоскости по логарифму расстояния от начала координат и углом , измеренного от базисной линии , пересекающего начала координат.
Координаты Плюккера — это способ представления линий в трехмерном евклидовом пространстве с использованием набора из шести чисел в качестве однородных координат .
Обобщенные координаты используются в лагранжевой трактовке механики.
Канонические координаты используются в гамильтоновой трактовке механики.
Барицентрическая система координат, используемая для троичных графиков и в более общем плане при анализе треугольников .
Трилинейные координаты используются в контексте треугольников.

Существуют способы описания кривых без координат с использованием внутренних уравнений , в которых используются инвариантные величины, такие как кривизна и длина дуги . Это включает:

Уравнение Уивелла связывает длину дуги и тангенциальный угол .
Уравнение Чезаро связывает длину дуги и кривизну.

Определяем географические координаты

Градусная сеть поможет определить географические координаты. Поскольку мы имеем дело с дугами и окружностями, то все расчеты координат следует производить в градусах, минутах и секундах. Поэтому и сеть называется градусной.

Градусная сеть позволяет определять местоположение любой точки на земной поверхности с помощью географических координат – широты и долготы. При определении географических координат Земля принимается за шар, хотя мы помним, что она геоид.

Географическая широта φ – угол между плоскостью экватора и отвесной линией в данной точке, другими словами – это угловое расстояние точки от экватора по меридиану. Измеряется от 0 (экватор) до 90° (полюса). Различают северную (лежащую в Северном полушарии) и южную (расположенную в Южном полушарии) широту. Северную широту принято считать положительной, а южную – отрицательной. О широтах, близких к экватору, принято говорить как о низких, к полюсам – как о высоких.

Все точки, лежащие на одной параллели, имеют одинаковую широту. На глобусе параллели подписываются на 0° и 180° меридианах, на картах – на боковых рамках.

Определение географической широты

Все параллели – окружности, они содержат 360°. От экватора до каждого из полюсов градусное расстояние составляет 90°.

Ответьте на вопросы. По какой параллели можно быстрее совершить кругосветное путешествие – по 0° или по 66°? Почему кругосветные плавания нельзя считать доказательством шарообразности Земли?

«… 7июня 1862 г. трёхмачтовое судно «Британия» … Глазго потерпело крушение …гони … южн… берег… два матроса Капитан Гр… дости… контин… пл… жесток… инд… брошен этот документ … долготы и 37° … широты. Окажите им помощь… погибнут …» — это всё, что было известно о гибели судна капитана Гранта из романа Жюля Верна «Дети капитана Гранта». Но одной широты недостаточно, чтобы определить положение объекта на Земле. Ведь 37 параллель только в Южном полушарии пересекает и Южную Америку, и Австралию, и Новую Зеландию, и многочисленные острова.

Географическая долгота λ – двугранный угол, образованный плоскостью начального меридиана и плоскостью меридиана, проходящего через данную точку, иначе – угловое расстояние точки от начального меридиана.

Все меридианы – дуги и по длине они одинаковые. Поэтому люди договорились, от какого из них вести отсчёт. Долгое время каждая страна вела счёт долготы от своего начального меридиана, Франция – от Парижского, Россия – от Пулковского (с обсерваторией) у Санкт-Петербурга, США и Англия – от Гринвичского. С 1884 года нулевым и начальным меридианом для всех стран считается Гринвичский. Он проходит через пригород города Лондона Гринвич, где в 1637 г была основана одна из старейших в мире астрономических обсерваторий. Выбор начального меридиана очень важен, так как с ним связан и отсчёт времени.

От нулевого меридиана ведут счёт расстояния в градусах на восток от 0° до 180° и на запад 0° до 180°. Нулевой меридиан, продолжением которого является 180°, делит Землю на Западное и Восточное полушария. Меридианы показывают направление север-юг.

К востоку от Гринвичского меридиана долгота восточная, к западу – западная. От неё зависит местное солнечное время. Все точки, лежащие на одном меридиане, имеют одинаковую долготу. На глобусе меридианы подписываются на экваторе, на картах – на экваторе или на верхней и нижней рамках. На практике географическую долготу определяют по разнице местного времени между нулевым меридианом и меридианом пункта наблюдения.

Определение географической долготы

Любая точка на земле имеет свой «географический адрес». Теперь мы знаем, что этот адрес состоит из двух частей. Это как при игре в «морской бой», где тоже используется адрес. Две части географического адреса – широта и долгота, определить их нам помогает градусная сеть. Широта – место точки на определённой параллели, долгота – на меридиане. Место их пересечения и есть географический адрес – географические координаты.

Зная географические координаты можно найти любой объект на карте. И, наоборот, можно нанести новый объект на карту, определив его географические координаты, как это делали все первооткрыватели. Ошибки в этом стоили многих жизней.

До времени существования навигаторов, географические координаты в открытом море определяли сначала с помощью такого прибора, как астролябия, а затем его заменил секстант.

АстролябияСекстант

Проекции[править]

Пусть на плоскости дана прямая l{\displaystyle l} и прямая l′{\displaystyle l’}, непараллельная ей.
Тогда через произвольную точку A{\displaystyle A} плоскости можно провести прямую lA′{\displaystyle l’_{A}}, параллельную прямой l′{\displaystyle l’}.
Она пересекает прямую l{\displaystyle l} в точке Al{\displaystyle A_{l}}, которую называют проекцией точки A{\displaystyle A}на прямую l{\displaystyle l}вдоль прямой l′{\displaystyle l’}.
Если прямые l{\displaystyle l} и l′{\displaystyle l’} перпендикулярны, то проекцию называют прямоугольной.

Аналогично, пусть в пространстве даны прямая l{\displaystyle l} и плоскость λ′{\displaystyle \lambda ‘}, непараллельная ей.
Тогда для любой точки A{\displaystyle A} пространства определены:

проекция Al{\displaystyle A_{l}} на прямую l{\displaystyle l} вдоль плоскости λ′{\displaystyle \lambda ‘} — точка пересечения прямой l{\displaystyle l} с плоскостью λA′{\displaystyle \lambda ‘_{A}}, проведенной через точку A{\displaystyle A} параллельно плоскости λ′{\displaystyle \lambda ‘};
проекция Aλ′{\displaystyle A_{\lambda ‘}} на плоскость λ′{\displaystyle \lambda ‘} вдоль прямой l{\displaystyle l} — точка пересечения плоскости λ′{\displaystyle \lambda ‘} с прямой lA{\displaystyle l_{A}}, проведенной через точку A{\displaystyle A} параллельно прямой l{\displaystyle l}.

Если прямая l{\displaystyle l} перпендикулярна плоскости λ′{\displaystyle \lambda ‘}, то проекцию называют прямоугольной.

Пусть дан вектор a{\displaystyle \mathbf {a} }. Отложим его от некоторой точки O{\displaystyle O}, получится вектор a=OM→{\displaystyle \mathbf {a} ={\overrightarrow {OM}}}. Спроектируем начало и конец вектора на прямую l{\displaystyle l} вдоль прямой l′{\displaystyle l’} (плоскости λ′{\displaystyle \lambda ‘}), получим точки O′,M′{\displaystyle O’,M’}. Вектор a′=O′M′→{\displaystyle \mathbf {a} ‘={\overrightarrow {O’M’}}} называется проекцией вектора a{\displaystyle \mathbf {a} }на прямую l{\displaystyle l}вдоль прямой l′{\displaystyle l’} (плоскости λ′{\displaystyle \lambda ‘}), обозначается a′=prll′a{\displaystyle \mathbf {a} ‘=\mathrm {pr} _{l}^{l’}\mathbf {a} }.

Проверим корректность этого определения, то есть независимость вектора a′{\displaystyle \mathbf {a} ‘} от выбора точки O{\displaystyle O}.

Рассмотрим случай плоскости. Для этого спроектируем вектор OM→{\displaystyle {\overrightarrow {OM}}} на прямую l′{\displaystyle l’}. Получим вектор a″=O1′M1′→{\displaystyle \mathbf {a} »={\overrightarrow {O’_{1}M’_{1}}}}. Ясно, что по построению OM→=O′M′→+O1′M1′→{\displaystyle {\overrightarrow {OM}}={\overrightarrow {O’M’}}+{\overrightarrow {O’_{1}M’_{1}}}} или

a=a′+a″{\displaystyle \mathbf {a} =\mathbf {a} ‘+\mathbf {a} »}.

Чтобы определение проекции не зависело от точки O{\displaystyle O} достаточно показать, что разложение вектора >a{\displaystyle \mathbf {>} a} в виде суммы векторов, параллельных прямым l{\displaystyle l} и l′{\displaystyle l’} единственно. Возьмем другое такое представление:

a=b′+b″{\displaystyle \mathbf {a} =\mathbf {b} ‘+\mathbf {b} »}

Тогда

(a′−b′)+(a″−b″)={\displaystyle (\mathbf {a} ‘-\mathbf {b} ‘)+(\mathbf {a} »-\mathbf {b} »)=0}

Значит векторы a′−b′{\displaystyle \mathbf {a} ‘-\mathbf {b} ‘} и a″−b″{\displaystyle \mathbf {a} »-\mathbf {b} »} линейно зависимы, а значит коллинеарны. С другой стороны, первый из этих векторов параллелен прямой l{\displaystyle l}, а второй — прямой l′{\displaystyle l’}. Это возможно только тогда, когда оба эти вектора нулевые. Значит, разложение вектора на плоскости в виде суммы двух векторов, параллельных двум пересекающимся прямым, единственно.

Аналогично можно доказать, что в пространстве единственно разложение вектора в виде суммы двух векторов, один из которых параллелен прямой, а второй — плоскости, пересекающейся с данной прямой.

Точность картографических проекций¶

Картографические проекции никогда не дают абсолютно точное отображение сферической поверхности. В результате проецирования, карта получает искажения углов, площадей и расстояний. Проекции могут давать как несколько типов искажений, так и достаточно приемлемый результат, в котором искажения углов, площадей и расстояний находятся в допустимых пределах. Примером таких компромиссных проекций могут служить тройная проекция Винкеля и проекция Робинсона, часто используемые для карт мира (см. рисунок ).

Figure Robinson Projection 1:

Проекция Робинсона дает приемлемые искажения площади, расстояний и углов.

В большинстве случаев сохранить все характеристики исходных объектов при проецировании невозможно. Это значит, что когда вам требуется выполнить анализ, необходимо подбирать такую проекцию, которая даст наилучшие характеристики для анализа. Например, если требуется измерить расстояния, необходимо выбрать проекцию, которая обеспечит точные расстояния.

Равноугольные проекции

Когда мы работаем с глобусом, основные направления компаса (север, восток, юг и запад) всегда расположены под углом в 90 градусов друг к другу. Другими словами восток всегда будет находиться на 90 градусов от севера. Проекция может сохранять угловые направления, и такая проекция называется конморфной или равноугольной.

Проекции, сохраняющие угловые величины, очень важны. Они широко используются для навигационных и метеорологических задач. Необходимо помнить, что сохранять правильные углы на карте большой площади трудно, поэтому применять такие проекции лучше к небольшим участкам поверхности. Конформные проекции искажают площади, а значит измерения площадей, выполненные в такой проекции будут неправильными. Чем больше площадь, тем менее точными будут измерения. Примерами проекций могут служить проекция Меркатора (см. рисунок ) и равноугольная коническая проекция Ламберта. Геоологическая служба США использует конформные проекции для многих своих топографических карт.

Figure Mercator Projection 1:

Проекция Меркатора используется в тех случаях, когда важна правильность углов и допустимы искажения площади.

Равнопромежуточные проекции

Если необходимо получить точные расстояния, то для карты выбирается проекция, хорошо передающая расстояния. Такие проекции, их называют равнопромежуточными, требуют, чтобы масштаб карты был неизменным. Карта будет равновеликой, когда она правильно передает расстояние от центра проекции до любой точки. Равнопромежуточные проекции обеспечивают точные расстояни от центра проекции или заданой линии. Такие проекции используются для сейсмических карт, а также для навигации. Хорошим примером равнопромежуточных проекций могут быть равнопромежуточная цилиндрическая Плате-Карре (см. рисунок ) и цилиндрическая равнопромежуточная. На эмблеме ООН испльзуется азимутальная равнопромежуточная проекция (см. рисунок ).