I. механика

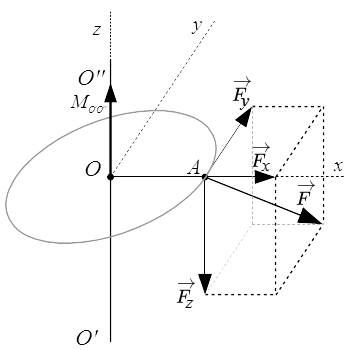
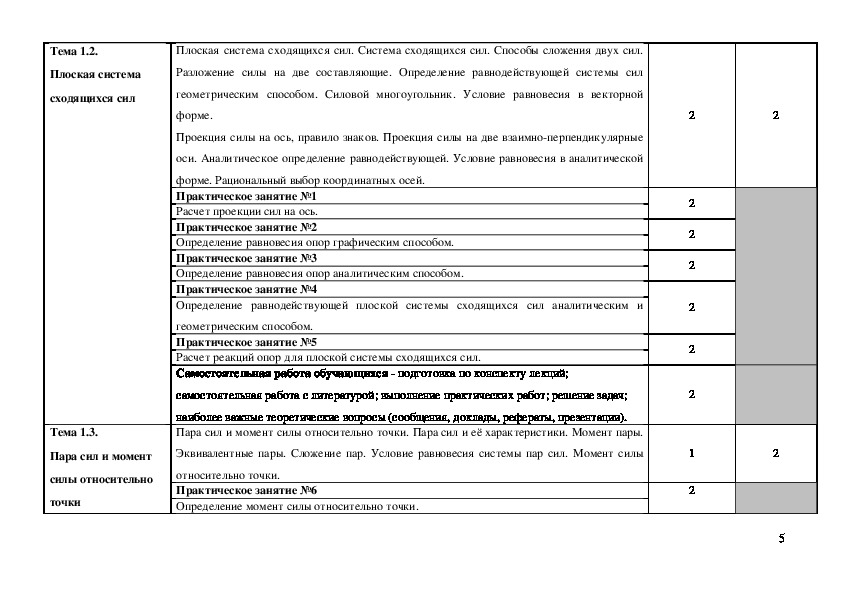
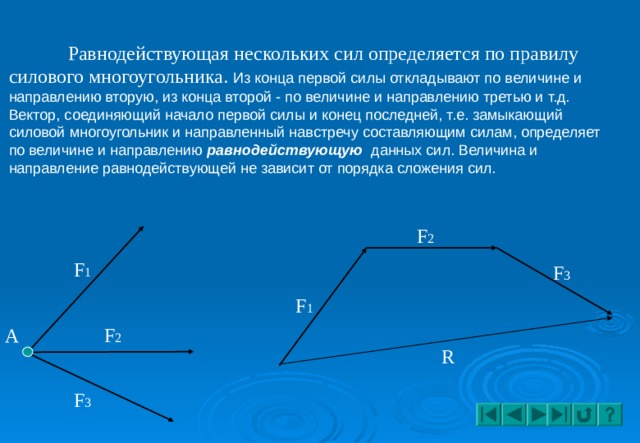
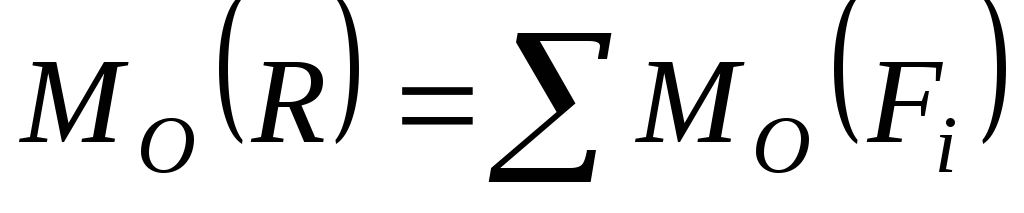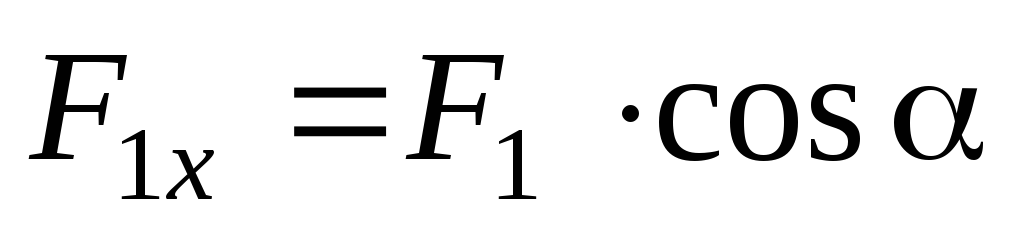Правило параллелограмма сложения сил

Сила известна как связанный вектор, что означает, что у нее есть направление, величина и точка приложения. Удобный способ для определения силы является отрезок прямой от точки A до точки B . Если мы обозначим координаты этих точек как A = (A _x , A _y , A _z ) и B = (B _x , B _y , B _z ), то вектор силы, приложенный в A, будет иметь вид

Fзнак равноB-Азнак равно(BИкс-АИкс,By-Аy,Bz-Аz).{\ displaystyle \ mathbf {F} = \ mathbf {B} — \ mathbf {A} = (B_ {x} -A_ {x}, B_ {y} -A_ {y}, B_ {z} -A_ {z) }).}

Длина вектора B — A определяет величину F и определяется выражением

|F|знак равно(BИкс-АИкс)2+(By-Аy)2+(Bz-Аz)2.{\ displaystyle | \ mathbf {F} | = {\ sqrt {(B_ {x} -A_ {x}) ^ {2} + (B_ {y} -A_ {y}) ^ {2} + (B_ { z} -A_ {z}) ^ {2}}}.}

Сумма двух сил F ₁ и F _2, приложенных к точке A, может быть вычислена из суммы сегментов, которые их определяют. Пусть F ₁ = B — A и F ₂ = D — A , тогда сумма этих двух векторов равна

Fзнак равноF1+F2знак равноB-А+D-А,{\ displaystyle \ mathbf {F} = \ mathbf {F} _ {1} + \ mathbf {F} _ {2} = \ mathbf {B} — \ mathbf {A} + \ mathbf {D} — \ mathbf { A},}

который можно записать как

Fзнак равноF1+F2знак равно2(B+D2-А)знак равно2(E-А),{\ displaystyle \ mathbf {F} = \ mathbf {F} _ {1} + \ mathbf {F} _ {2} = 2 ({\ frac {\ mathbf {B} + \ mathbf {D}} {2} } — \ mathbf {A}) = 2 (\ mathbf {E} — \ mathbf {A}),}

где Е является середина отрезка BD , который соединяет точки B и D .

Таким образом, сумма сил F ₁ и F ₂ равна удвоенному отрезку, соединяющему A со средней точкой E отрезка, соединяющего конечные точки B и D двух сил. Удвоение этой длины легко достигается путем определения отрезков BC и DC, параллельных AD и AB , соответственно, чтобы сформировать параллелограмм ABCD . Диагональ AC этого параллелограмма представляет собой сумму двух векторов силы. Это известно как правило параллелограмма для сложения сил.

Толкаем груз

Не такая уж и легкая работа — держать тяжелый груз, например большие гантели, на вытянутых вверх руках. Однако с точки зрения физики, несмотря на приложенную силу, здесь нет никакого перемещения, а значит, нет и работы. Хотя с точки зрения биологии здесь выполняется огромная работа, но с точки зрения физики работы нет, если нет перемещения. Даже с точки зрения химии наше тело поставляет огромное количество энергии нашим мышцам для удержания груза. Но, несмотря на очевидную физическую усталость, работа с точки зрения физики не выполняется.

Для работы необходимо движение. Представьте, что вы нашли огромный слиток золота и толкаете его домой, как показано на рис. 8.1. Какую работу придется при этом выполнить? Во-первых, нужно определить силу, которую нужно приложить к слитку.

Пусть коэффициент трения скольжения, ​\( \mu_c \)​ (подробнее об этом см. главу 6), между поверхностями слитка и дороги равен 0,25, а слиток имеет массу 1000 кг. Итак, какую силу нужно приложить к слитку, чтобы поддерживать его движение вопреки силе трения скольжения ​\( F_{трение} \)​? Начнем поиск ответа на этот вопрос со следующей формулы, известной нам из главы 6:

где ​\( F_н \)​ — это нормальная сила.

Предполагая, что поверхность дороги абсолютно плоская, получим, что нормальная сила \( F_н \) равна произведению массы слитка ​\( m \)​ на ускорение свободного падения ​\( g \)​ под действием силы гравитационного притяжения (силы тяжести) между слитком и Землей:

Подставляя численные значения, получим:

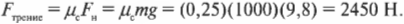
Итак, для преодоления силы кинетического трения нужно приложить силу 2450 Н. Допустим, что длина пути до вашего дома равна 3 км. Какую работу придется проделать, чтобы дотолкать этот слиток золота домой? Поскольку угол ​\( \theta \)​ между направлением прилагаемой силы ​\( \mathbf{F} \)​ и перемещением \( \mathbf{s} \), выполняемым под действием этой силы, равен нулю, то формула работы ​\( W=Fs\cos\theta \)​ упрощается, поскольку ​\( \cos\theta \)​ = 1. Подставляя численные значения, получим:

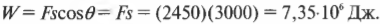
Работу измеряют также в калориях (или сокращенно кал), причем 1 кал = 4,186 Дж. Эту единицу измерения используют также для измерения энергии, и ее часто можно встретить на упаковках продуктов питания. Так вот, чтобы дотолкать слиток золота домой, вам потребуется потратить 1,755·106 калорий, или 1755 Ккал (т.е. килокалорий, где 1 килокалория = 1 Ккал). Забегая вперед, скажем, что в электротехнике для измерения работы и энергии используется единица “киловатт·час” (кВт·ч), которая равна 3,6·106 Дж. Итак, для выполнения этой работы потребуется около 2 кВт·ч. (Более подробно эти и другие единицы измерения описываются в конце этой главы и в главе 13.)

Физика. Законы силы (базовый уровень)

Материалы для подготовки к ЕГЭ. Тематический тренинг ФИЗИКА (базовый уровень). ЗАДАНИЕ № 2. Задачи на силы вокруг нас: Законы Ньютона, закон всемирного тяготения, закон Гука, сила трения. Вернуться к Списку заданий тренинга по физике.

ЗАДАНИЕ № 2.
Законы Ньютона, закон всемирного тяготения,
закон Гука, сила трения

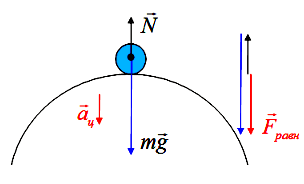
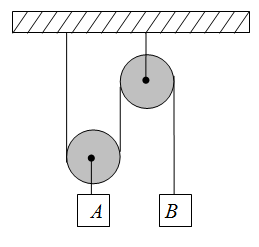
1. Тело движется по окружности с постоянной скоростью (см. рис.). Определите направление суммы сил, действующих на тело.

1. На тело действуют две силы F₁ и F₂, направленные на север и на юг соответственно. Если F₁ > F₂, то ускорение тела направлено на…

Ответ: ______.

1. Какое ускорение получит тело массой 5 кг, если на него действуют две силы по 5 Н, направленные под углом 120° друг к другу (см. рис.)?

Ответ: ______м/с2.

1. Если силы F₁ = F₂ = 3 Н направлены под углом a = 120° друг к другу (см. рис.), то модуль их равнодействующей равен…

Ответ: _______Н.

1. На тело действуют три силы (см. рис.): F₁ = F₂ = F₃ = 2 Н. Найдите, чему равна равнодействующая сил, действующая на тело в направлении оси х. Ответ округлите до десятых.

Ответ: _______Н.

1. Груз массой m = 2 кг подвешен на двух тросах, сила натяжения каждого из которых равна 20 Н. Найдите, чему равен угол а (см. рис.).

Ответ: ______°.

1. Груз массой 2 • 103 кг загружают по вертикали в трюм теплохода. График зависимости скорости движения груза от времени представлен на рисунке. Определите равнодействующую сил, действующих на груз в интервале времени 0—6 с.

Ответ: ______ кН.

1. В инерциальной системе отсчёта сила F сообщает телу массой m ускорение а. Ускорение тела массой 2m под действием силы 2F в этой системе отсчёта равно…

Ответ: ______ а.

1. На тело массой 5 кг действуют силы, как показано на рисунке, F₁ = 15 Н, F₂ = 20 Н. С каким ускорением будет двигаться тело?

Ответ: _______м/с2

1. На вертикально падающее тело массой 500 г действует сила сопротивления воздуха, равная 2 Н. Чему равно ускорение тела?

Ответ: ______м/с2.

1. На первоначально покоившееся тело массой 3 кг действуют две силы: F₁ = 5 Н, направленная влево, и F₂ = 2 Н, направленная вправо. На какое расстояние сдвинется тело за 2 секунды?

Ответ: ______м.

1. Какой путь пройдёт первоначально покоившееся тело массой 2 кг, если на него в течение 5 секунд будет действовать сила 10 Н?

Ответ: ______м.

1. Вес тела в лифте уменьшился в 4 раза. Чему равен модуль ускорения лифта?

Ответ: ______м/с2.

1. Санки съезжают с горки, образующей угол а с горизонтом, и проходят некоторый путь по горизонтальной поверхности до остановки (см. рис.). Сравните силы тяжести в точках траектории — А, В и С. Чему равно отношение наибольшей силы тяжести к наименьшей?

Ответ: ______.

1. Чему равно отношение силы гравитационного взаимодействия, действующей со стороны Луны на Землю, к силе гравитационного взаимодействия, действующей со стороны Земли на Луну, если масса Земли в 81 раз больше массы Луны?

Ответ: ______.

1. Если массу спутника, вращающегося по круговой орбите над поверхностью Земли на высоте h, увеличить в 2 раза, то во сколько раз изменится первая космическая скорость?

Ответ:______.

1. Чему равна максимальная сила трения покоя, действующая на человека массой 70 кг, бегущего по дороге, если коэффициент трения равен 0,5?

Ответ: ______Н.

1. На рисунке представлен график зависимости модуля силы упругости, возникающей при растяжении пружины, от значения её деформации. Чему равна жёсткость этой пружины?

Ответ: _____Н/м.

1. Чему равна жёсткость системы, состоящей из двух соединённых параллельно пружин жёсткостью 2 кН/м каждая?

Ответ: _____кН/м.

1. Тело массой m висит на пружине жёсткостью k, удлиняя её на величину х₁. Рядом на пружине жёсткостью 2k висит тело массой 3m, удлиняя её на величину х₂. Найдите, чему равно отношение x₂/x₁.

Ответ: _____.

Материалы для подготовки к ЕГЭ. Тематический тренинг ФИЗИКА (базовый уровень). ЗАДАНИЕ № 2. Задачи на силы вокруг нас: Законы Ньютона, закон всемирного тяготения, закон Гука, сила трения.

Вернуться к Списку заданий тренинга по физике.

Просмотров:
3 898

задачи

Что такое сила тяжести?

Сила тяжести — это сила, с которой Земля притягивает к себе тело. Эта сила всегда направлена вертикально вниз. Запомни: чем больше масса тела, тем больше сила тяжести, действующая на это тело. Именно поэтому нам трудно поднять или сдвинуть с места очень тяжелые предметы. И чем тяжелее предмет, тем больше сила тяжести и тем сложнее нам преодолеть эту силу. Сила тяжести, действующая на тело, несколько отдаленное от поверхности Земли, зависит от массы тела и расстояния.

«Космические» факты

Каждый космонавт переживает так называемую космическую болезнь: при отсутствии силы тяготения он привыкает к тому, что все окружающие предметы, да и он сам, летают, а не падают. Поэтому по возвращении на Землю космонавты в течение некоторого времени обращаются с вещами так, как привыкли это делать в космосе: просто отпускают их, при этом совершенно не задумываясь над тем, что они сразу упадут на землю или на пол.

В условиях невесомости в организме космонавта увеличивается объем циркулирующей крови, что, в свою очередь, может привести к повышению давления. Однако сердце космонавта очень интересно приспосабливается к данной ситуации: во избежание дополнительной нагрузки оно уменьшается в объеме и, соответственно, начинает перекачивать меньшее количество крови. Это своеобразная защитная реакция на увеличение объема крови.

Ученые выяснили, что в случае длительного пребывания в невесомости (состояние, при котором вес тела равен нулю) в организме человека происходят некоторые изменения. Например, рост космонавтов увеличивается почти на 5 см за счет расхождения позвоночных дисков. В течение 10 дней после возвращения на Землю рост становится прежним.

Общая сила

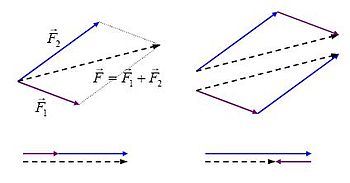
Схематический метод сложения сил.

Сила — это векторная величина, что означает, что она имеет величину и направление, и обычно обозначается жирным шрифтом, например F, или стрелкой над символом, например .
F→{\ displaystyle \ scriptstyle {\ vec {F}}}

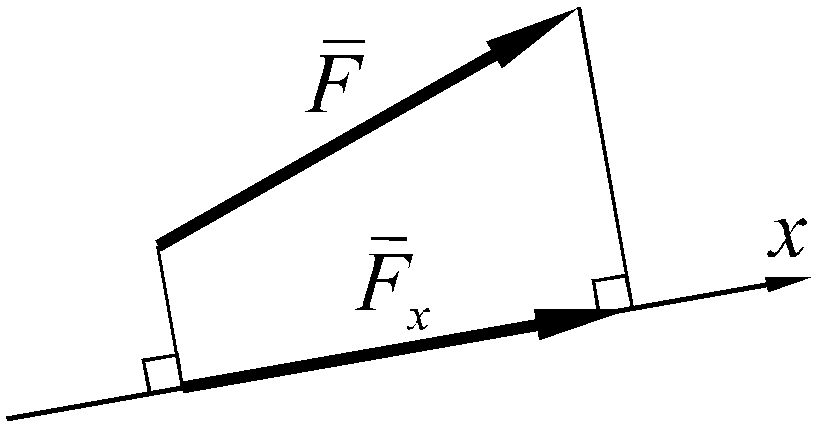
Графически сила представлена ​​в виде отрезка линии от точки ее приложения A до точки B , которая определяет ее направление и величину. Длина отрезка AB представляет величину силы.

Векторное исчисление было разработано в конце 1800-х — начале 1900-х годов. Однако правило параллелограмма, используемое для сложения сил, восходит к древности и явно отмечено Галилеем и Ньютоном.

На схеме показано сложение сил и . Сумма двух сил изображена в виде диагонали параллелограмма, определяемого двумя силами.
F→1{\ displaystyle \ scriptstyle {\ vec {F}} _ {1}}F→2{\ displaystyle \ scriptstyle {\ vec {F}} _ {2}}F→{\ displaystyle \ scriptstyle {\ vec {F}}}

Силы, приложенные к вытянутому телу, могут иметь разные точки приложения. Силы являются связанными векторами и могут добавляться только в том случае, если они применяются в одной и той же точке. Суммарная сила, полученная от всех сил, действующих на тело, не сохраняет его движения, если не прикладывается в той же точке и не определяется соответствующий крутящий момент, связанный с новой точкой приложения. Чистая сила, приложенная к телу в одной точке с соответствующим крутящим моментом, известна как результирующая сила и крутящий момент.

Как ни крути, а энергия сохраняется

Механической энергией называется сумма потенциальной и кинетической энергии объекта. Благодаря закону сохранения этой полной механической энергии, процедура решения задач по физике существенно упрощается. Рассмотрим поподробнее этот закон.

Пусть тележка на аттракционе “Американские горки” в разных точках 1 и 2 на разных высотах \( h_1 \) и \( h_2 \) имеет разные скорости \( v_1 \) и \( v_2 \). Полная механическая энергия тележки ​\( E_1 \)​ в точке 1 равна:

а полная механическая энергия тележки ​\( E_2 \)​ в точке 2 равна:

Чему равна разница между величинами \( E_1 \) и \( E_2 \). При наличии неконсервативных сил эта разница должна быть равна работе ​\( W_{неконс} \)​ этих сил

С другой стороны, если неконсервативные силы отсутствуют, т.е. \( W_{неконс} \) = 0, то:

или:

или:

Именно эти равенства представляют собой закон сохранения механической энергии. Если работа неконсервативных сил равна нулю, то полная механическая энергия сохраняется. (Закон сохранения механической энергии гласит, что при наличии консервативных сил полная энергия остается неизменной, а могут происходить только превращения потенциальной энергии в кинетическую и обратно. — Примеч. ред.)

и использовать более простую формулировку:

Определяем конечную скорость с помощью закона сохранения энергии

Совсем непросто проводить физические эксперименты на аттракционе “Американские горки”. Но ведь кто-то должен их делать! Представьте себе, что вы находитесь в тележке, которая практически без трения скользит по рельсам вниз с высоты ​\( h_1 \)​ = 400 м. Предположим, что где-то на полпути вниз выходит из строя спидометр и уже нельзя определить скорость тележки по приборам. Как вычислить скорость ​\( v_2 \)​ в самой нижней точке спуска \( h_2 \)? Нет проблем. Все, что нам нужно, это закон сохранения энергии. Согласно этому закону, полная механическая энергия объекта должна сохраняться, если равна нулю работа всех неконсервативных сил. Из предыдущего раздела нам уже знакома следующая сокращенная формулировка закона сохранения энергии:

Для простоты предположим, что начальная скорость ​\( v_1 \)​ = 0, а высота самой нижней точки спуска ​\( h_2 \)​ = 0. Тогда предыдущее уравнение существенно упрощается:

Откуда очень легко получить формулу для конечной скорости:

Подставляя численные значения, получим:

Итак, скорость тележки в самой нижней точке спуска на аттракционе “Американские горки” будет равна 89 м/с или около 320 км/ч. Довольно быстро: дух перехватит даже у самых отчаянных смельчаков!

Определяем максимальную высоту подъема с помощью закона сохранения энергии

Помимо определения конечной скорости, с помощью закона сохранения энергии можно также определить максимальную высоту подъема. Предположим, что Тарзан находится у кишащей крокодилами реки и хочет с помощью гибкой лианы перепрыгнуть с низкого берега на другой более высокий берег, высота которого на 9 м больше. Пусть максимальная скорость ​\( v_1 \)​, с которой он может разогнаться на низком берегу (т.е. в самой нижней точке траектории), равна 13 м/с. Достаточно ли этой скорости, чтобы запрыгнуть на противоположный высокий берег? Попробуем применить известную нам сокращенную формулировку закона сохранения энергии:

Предположим, что высота начального положения ​\( h_1 \)​ = 0. Чтобы определить максимально возможную высоту конечного положения на другом высоком берегу, следует предположить, что конечная скорость ​\( v_2 \)​ = 0. При таких условиях прежняя формула существенно упрощается:

Отсюда очень легко получить формулу для высоты конечного положения ​\( h_2 \)​ на другом берегу:

Подставляя численные значения, получим:

Итак, Тарзану не хватит 40 см, чтобы с максимальной скоростью разгона 13 м/с запрыгнуть на другой берег с помощью лианы.

Законы Ньютона

Влияние сил на тела впервые описал Исаак Ньютон — один из величайших физиков и математиков всех времен. Он сформировал три закона или аксиомы механики, благодаря которым мы знаем принципы работы сил. Законы Ньютона использовались при описании многих научных вопросов, например, движение спутников, влияние Луны на приливы и отливы или расчет орбит комет. Они открыли связь между силой и ускорением, что позволило ученым того времени сконструировать паровой двигатель, а позднее — двигатель внутреннего сгорания.

В 20-м веке Альберт Эйнштейн добавил правки к законам Ньютона, которые касались движения тел со скоростями, близкими к скорости света. Современные научные открытия в области теории относительности, квантовой теории и физики элементарных частиц показали, что в условиях бесконечно больших и бесконечно малых тел законы Ньютона не работают. Именно поэтому современные формулировки отличаются от законов, которые сформулирован лично сэр Исаак.

Несмотря на то, что все законы связаны, наш калькулятор в большей степени посвящен второму закону Ньютона. Рассмотрим их.

Первый закон Ньютона

Итак, если на тело не воздействуют силы, оно либо покоится, либо движется прямолинейно и равномерно. Это историческая формулировка первой аксиомы механики, которая сегодня считается неверной. Все дело в том, что Ньютон рассматривал тела в абсолютно неподвижной системе отсчета, следовательно, говорил об абсолютных пространстве и времени. Сегодняшняя физика учитывает постулаты теории относительности, поэтому определение звучит несколько иначе: есть такие системы отсчета, в которых при отсутствии сил физические объекты пребывают в состоянии покоя. Подобные системы отсчета носят название инерциальных.

Существуют и неинерциальные системы отсчета, которые сами перемещаются с ускорением или поворачиваются относительно инерциальных систем. Также возможны сопутствующие системы, связанные с самим рассматриваемым телом и движущиеся вместе с ним. Естественно, что в таких системах классическая механика не применима. Интересно, что на Земле невозможна ситуация, когда на объекты не воздействует никакая сила: гравитационное поле планеты создает постоянную силу тяжести.

Второй закон Ньютона

Авторское определение этого закона звучит непонятно: изменение количества движения пропорционально движущей силе и сонаправлено с ней. Школьная формулировка второй аксиомы механики куда проще:

F = m × a,

или сила — это произведение массы физического объекта на его ускорение.

Если же рассмотреть современную формулировку второй аксиомы, то становится ясно, что в инерциальной системе отсчета материальная точка получает ускорение прямо пропорциональное действующим силам и обратно пропорциональное своей массе или:

a = F / m.

При этом важно уточнить, что масса физического объекта не изменяется во времени. Это уточнение необходимо для релятивистской механики, в которой при достижении скоростей, близких к скорости света, масса тела начинает изменяться

Именно данный закон лежит в основе нашего калькулятора. Эта простая формула используется в большинстве задач по физике из курса «Механика». Но на повестке дня остался третий, последний закон Ньютона.

Третий закон Ньютона

Исторически закон звучит как «всякому действие существует противодействие». В современной физике такой закон не действует, и простыми словами постулат звучит так: силы возникают только попарно, и любая сила, воздействующая на тело, происходит от другого тела. Таким образом, сила — это всегда результат взаимодействия нескольких физических объектов. Не существует сил, которые возникают самостоятельно без взаимодействия тел.

Наша программа позволяет быстро определить силу, ускорение или массу тела, если известны два параметра из трех. Для использования калькулятора достаточно ввести любые два значения, после чего программа автоматически заполнит пустое поле. Калькулятор пригодится школьникам и студентам первых курсов, которые изучают механику.

Равнодействующая сила

Графическое изображение равнодействующей силы.

Результирующая сила и крутящий момент заменяют эффекты системы сил, действующих на движение твердого тела. Интересным частным случаем является результат без крутящего момента, который можно найти следующим образом:

1. Сложение векторов используется для нахождения чистой силы;
2. Используйте уравнение для определения точки приложения с нулевым крутящим моментом:

р→×F→рзнак равно∑язнак равно1N(р→я×F→я){\ displaystyle {\ vec {r}} \ times {\ vec {F}} _ {\ mathrm {R}} = \ sum _ {i = 1} ^ {N} ({\ vec {r}} _ { i} \ times {\ vec {F}} _ {i})}

где — результирующая сила, расположение точки ее приложения, а отдельные силы — точки приложения . Может оказаться, что нет точки приложения, которая дает результат без крутящего момента.
F→р{\ displaystyle {\ vec {F}} _ {\ mathrm {R}}}р→{\ displaystyle {\ vec {r}}}F→я{\ displaystyle {\ vec {F}} _ {i}}р→я{\ displaystyle {\ vec {r}} _ {я}}

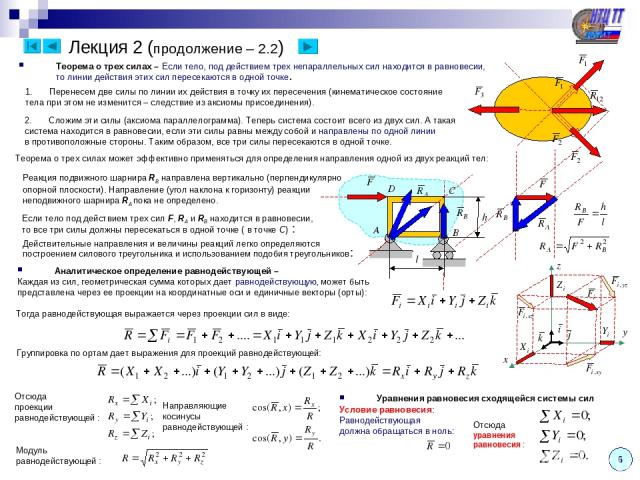
На диаграмме напротив показаны простые графические методы поиска линии приложения равнодействующей силы простых плоских систем:

1. Линии приложения действительных сил и на самом левом рисунке пересекаются. После того, как векторное сложение выполнено «в месте », полученная результирующая сила преобразуется так, что линия приложения проходит через общую точку пересечения. Относительно этой точки все крутящие моменты равны нулю, поэтому крутящий момент результирующей силы равен сумме крутящих моментов фактических сил.F→1{\ displaystyle {\ vec {F}} _ {1}}F→2{\ displaystyle {\ vec {F}} _ {2}}F→1{\ displaystyle {\ vec {F}} _ {1}}F→р{\ displaystyle {\ vec {F}} _ {\ mathrm {R}}}
2. На рисунке в середине диаграммы показаны две параллельные действительные силы. После сложения вектора «в месте » результирующая сила переводится в соответствующую линию приложения, где она становится равнодействующей . Процедура основана на разложении всех сил на составляющие, для которых линии приложения (бледные пунктирные линии) пересекаются в одной точке (так называемый полюс, произвольно установленный в правой части иллюстрации). Затем аргументы из предыдущего случая применяются к силам и их компонентам, чтобы продемонстрировать отношения крутящего момента.F→2{\ displaystyle {\ vec {F}} _ {2}}F→р{\ Displaystyle \ scriptstyle {\ vec {F}} _ {\ mathrm {R}}}
3. На крайнем правом рисунке показана пара , две равные, но противоположные силы, для которых величина результирующей силы равна нулю, но они создают чистый крутящий момент,    где   — расстояние между линиями их приложения. Поскольку нет равнодействующей силы, этот крутящий момент может быть описан как «чистый» крутящий момент.τзнак равноFd{\ Displaystyle \ scriptstyle \ tau = Fd} d{\ Displaystyle \ scriptstyle \ d}

Равнодействующая сила

С детства известна басня И.А. Крылова о том, как не могут сдвинуть воз с места три персонажа.

Предстоит выяснить, почему к телу приложены целых три силы, а скорость его не меняется.

Но сначала еще несколько случаев.

На репку в сказке «Репка» действовали силами одного направления дружные члены семьи и собачка Жучка. Силы не хватало совсем маленькой. Когда подбежала мышка, общие усилия оказались больше, и репку вытащили.

Итак, силы складываются, если они направлены в одну сторону по прямой. Их суммарная сила, называемая равнодействующей, имеет то же направление.

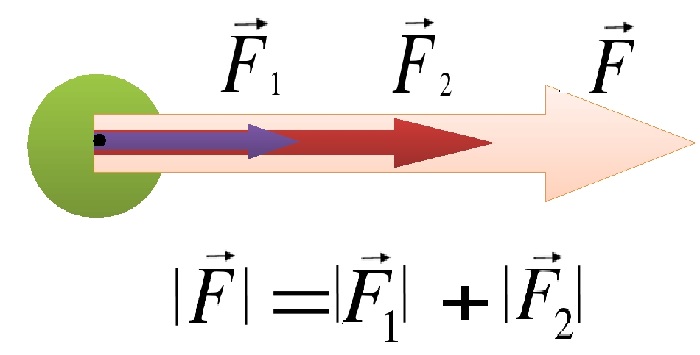
Теперь другой пример: состязание двух команд по перетягиванию каната. Каждая команда тянет канат в своем направлении. Некоторое время канат не движется. Вот одна из команд начинает перетягивать канат на свою сторону вместе с соперниками. Сильнейшая команда – победитель.

 

Сила ее оказалась по модулю больше. Равнодействующая сила находится как разность приложенных сил. Направление ее совпадает с направлением большей силы.

В истории про двух баранов, черного и белого, которые не уступили друг другу дорогу на мостике через речку, силы баранов противоположны, по величине равны. Результат ничейный.

Итак, равнодействующая сила – это результат общего действия всех приложенных к телу сил.                         

Теперь следует вернуться к проблеме трех персонажей басни Крылова. Действуя в разные стороны, они уравновесили свои силы. Совместные усилия дали нулевой результат. Поэтому воз стоит на месте.

Если две или более силы произвольно направлены, то они также имеют равнодействующую. И если эта равнодействующая  не равна нулю, то она изменяет скорость тела. Именно равнодействующая сила в конечном итоге определяет движение тел.

Направление — результирующая сила

Направление результирующей силы, действующей со стороны потока на тело, зависит от формы тела и его ориентировки в потоке.
 

Направление ускорения совпадает с направлением результирующей силы.
 

Математические операции, выполняемые прибором ПФ1. 1.

Развиваемые при этом усилия в зависимости от направления результирующей силы перемещают мембранный узел сумматора / / / в сторону либо сопла питания, либо сопла, сообщенного с атмосферой, в результате чего выходное давление элемента / / / изменяется. Это давление, усиленное по мощности в элементе IV, подается в камеру отрицательной обратной связи Б элемента / / / для уравновешивания его мембранного узла, а также направляется в выходную линию прибора.
 

Таким образом, в том случае, когда все направления результирующей силы при разных положениях тела не пересекаются в одной точке, но лежат в одной плоскости, можно считать, что результирующая сила приложена к определенной точке тела, но эта точка перемещается в теле при изменении его положения относительно потока. Такой способ определения точки приложения результирующей силы вполне законен, если мы рассматриваем только такие изменения положения тела, при которых результирующая сила все время лежит в одной плоскости.
 

Таким образом, даже в том случае, когда все направления результирующей силы при разных положениях тела не пересекаются в одной точке, но лежат в одной плоскости, все же можно считать, что результирующая сила приложена к определенной точке тела, но эта точка перемешается в теле при изменении его положения относительно потока.
 

Функцией этого же числа является и угол а, образуемый направлением результирующей силы с прямой, соединяющей центры цапфы и подшипника. Результирующая сила пересекает окружность подшипника в определенной точке, впереди которой по направлению вращения расположена та точка, которая ближе всего отстоит от цапфы.
 

Уравнение говорит также, что вектор ускорения должен совпадать с направлением результирующей силы. Коэффициент пропорциональности в этой формуле полагается равным единице, что накладывает известные из школьного курса условия на единицы измерения входящих в это уравнение величин.
 

Чтобы определить направление действия равнодействующей силы, можно пользоваться следующим правилом: направление результирующей силы, действующей на тело, получается путем поворота вектора скорости тела относительно жидкости на угол 90 в направлении циркуляции скорости.
 

При точении инструмент неподвижен и направление силы резания остается постоянным; при фрезеровании направление результирующей силы резания все время изменяется; кроме того силы все время меняются вследствие входа и выхода зубьев фрезы из детали. Поэтому коэффициенты направления при фрезеровании не являются константами, а описываются периодическими функциями с разрывами. Расчет устойчивости процесса с такими функциями сложен и требует затрат большого количества времени, поэтому данные функции заменяются их средними значениями. Как показывают сравнительные расчеты, эти упрощения вносят незначительную погрешность.
 

Если на тело действуют любые две неравные силы, то тело будет иметь ускорение в направлении результирующей силы, которая сообщает телу такое же ускорение, как и все одновременно действующие на него силы.
 

Так как рассматриваемое тело приходит в движение из состояния относительного покоя, то очевидно, что направление результирующей силы совпадет с направлением начального перемещения, которое, как следует из опыта, не совпадает с линией наибольшего ската опорной плоскости.
 

В нем, очевидно, заключен частный случай ( 90), выражающий условие обращения пары Р в нуль; направление пары Р совпадает с направлением результирующей силы.
 

Схематическое изображение деформированного при изгибе цилиндра с глубокой кольцевой трещиной.

В этом случае величина б упругого перемещения перешейка трещины ( см. 1 рис. 14, отрезок ОС) относительно плоскости ее поверхностей считается достаточно малой, так что направление результирующей силы Д практически перпендикулярно к поверхности трещины.
 

Работаем в разных системах единиц измерения

Работа является скалярной, а не векторной величиной, т.е. она имеет величину, но не имеет направления (подробнее скаляры и векторы рассматриваются в главе 4). Согласно формуле \( W=Fs\cos\theta \), работа измеряется в единицах “Н·м” в системе СИ или в единицах “г·см2/с2” — в системе СГС. Но с такими единицами не очень удобно работать, и физики для измерения работы используют специальную единицу измерения — джоуль (или сокращенно Дж) в системе СИ. Иначе говоря, в системе СИ 1 Дж = 1 Н · 1 м.

В системе СГС работа измеряется в единицах “г·см2/с2”. Вместо нее для удобства физики также используют специальную единицу измерения — эрг (неплохое название для единицы работы, поскольку очень похоже на энергичное междометие, произнесенное во время подъема тяжелого груза). Иначе говоря, 1 эрг = 1 дин · 1 см. В системе фут-фунт-секунда работа измеряется в единицах “фунт-фут”. (Эти системы единиц подробно описываются в главе 2 .)