Что такое регрессия: виды и примеры

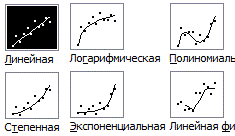
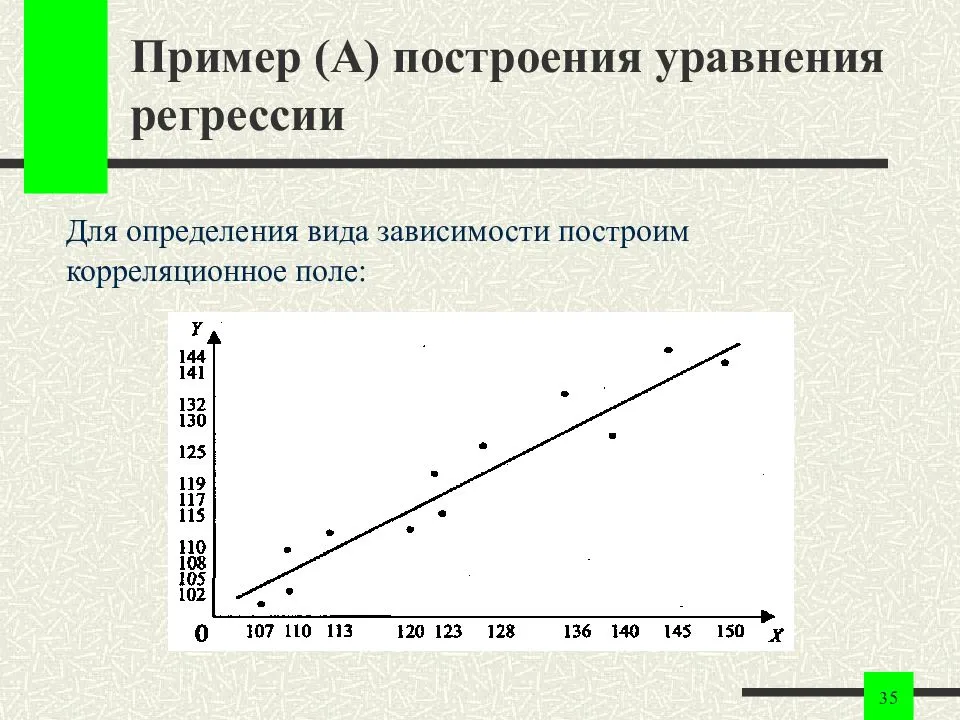
Введение в регрессионный анализ

Если имеется корреляционная зависимость между переменными и , возникает необходимость определить функциональную связь между двумя величинами. Зависимость среднего значения называется регрессией по .

Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей минимальна.

Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.

Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений вокруг регрессии является дисперсия.

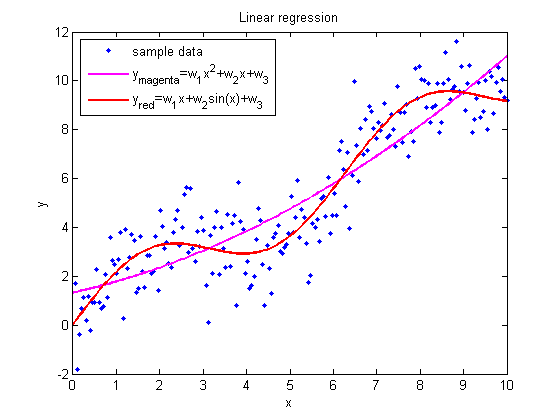
Чаще всего используется модель линейной регрессии, а все нелинейные зависимости приводят к линейному виду с помощью алгебраических ухищрений, различных преобразования переменных и .

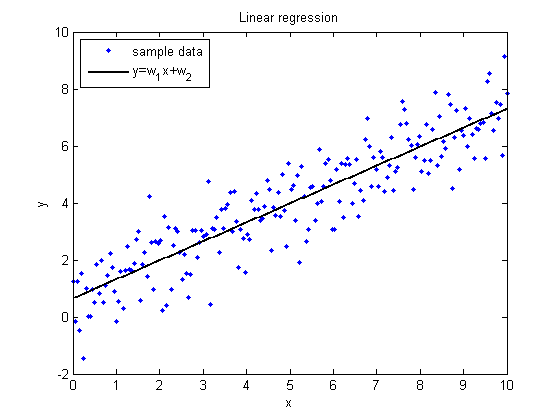
Линейная регрессия

Уравнения линейной регрессии можно записать в виде

В матричном виде это выгладит

y — зависимая переменная;
x — независимая переменная;
β — коэффициенты, которые необходимо найти с помощью МНК;
ε — погрешность, необъяснимая ошибка и отклонение от линейной зависимости;

Случайная величина может быть интерпретирована как сумма из двух слагаемых:

— полная дисперсия (TSS).
— объясненная часть дисперсии (ESS).
— остаточная часть дисперсии (RSS).

Еще одно ключевое понятие — коэффициент корреляции R2.

Что такое регрессия в психологии

Регрессия есть возвращение к своим более ранним формам поведения. Она происходит оттого, что нынешним, зрелым поведением человек не имеет возможности добиться желаемых целей. Например, девушка не может убедить своего мужчину в действительности какого-то факта

Что выбирает она? Часто это слезы, и плач, которые не являются рациональным способом в разрешении ситуации, это тот способ, которым она пользовалась в детстве, дабы привлечь внимание и добиться желаемого

Спортсмены, занимающиеся боевыми искусствами и изучающие множество приемов в зале, выходя на ринг, используют лишь несколько приемов регрессии, что происходит из-за фрустрации, стресса, в котором человеку свойственно возвращаться к наиболее эффективным ранним формам поведения, которые его никогда не подводили. Хотя их эффективность – очень спорный вопрос, на деле было бы уместнее использовать другие формы поведения. Но есть навыки, какие содержатся в основе психики, как говорят, «на подкорке», вернуться к которым легко, и это происходит бессознательно. Проблему это не решает, но временно успокаивает человека, снижает уровень его тревоги.

Каждый сохраняет из детства воспоминания о приятных моментах, легком разрешении проблем и хоть раз задумывался, чтобы вернуться в детство. Личности же, что используют регрессию как доминирующий механизм защиты, когда она становится стратегией жизни, называются инфантильными, такая длительная регрессия в психологии это синоним инфантилизма.

Регрессия как явление была описана впервые Фрейдом. Регрессия по Фрейду есть отказ от прогрессивного движения желания в сторону действий, возврат к образам или галлюцинациям. Также регрессия по Фрейду находит себя в сновидениях и неврозах, в каких он рассматривал возврат к архаическим формам жизни как индивидуальным, так и филогенетическим.

Кто больше всех склонен к регрессии

Чаще всего с регрессией сталкиваются дети, чья психика находится еще в стадии формирования и отличается неустойчивостью. Если им хочется больше внимания или нет желания что-то делать, они плачут и капризничают. А иногда ведут себя словно совсем маленькие, например, забывая попроситься на горшок или отказываясь самостоятельно кушать и одеваться. Особенно часто такие ситуации возникают в семьях, где рождается второй ребенок

Старший таким образом показывает свою ревность, требует вернуть утраченное внимание со стороны родителей

Регрессия у взрослых — признак слабости и инфантилизма. В группе риска находятся такие категории людей:

слабохарактерные, с нестабильным эмоциональным состоянием личности;
неуверенные в себе индивиды с низкой самооценкой;
те, кто легко поддается влиянию со стороны окружающих или СМИ;
люди, которым сложно жить в социуме, строить взаимоотношения с теми, кто находится вокруг них;
личности, склонные к повышенной тревожности, панике, неврозам и истерии.

Интересно, что иногда регрессия случается и у тех, кто уверен в себе. Это происходит в случаях, когда другие механизмы психологической защиты оказались малоэффективными или неэффективными вовсе. Иногда трудности отнимают все эмоциональные и физические силы, а желаемое при этом так и остается где-то вдалеке. В такие моменты, чтобы защитить себя от дальнейшего разочарования и депрессии, человек словно бы впадает в детство. Он плачет, всем жалуется, «заедает» стресс, всем своим видом показывает обиду и страдания.

Стоит отметить, что для сильных духом людей регрессия — это всего лишь временное явление, это слабость, которая нужна для того, чтобы снять эмоциональное напряжение. После он снова становится самим собой.

Как видно, в психологии регрессия имеет свои плюсы и минусы.

Регрессия в математике

В математических науках регрессия применяется как относительная величина, отражающая зависимость среднего показателя какой-то величины от другой или нескольких величин. Такой может быть «множественная регрессия».

Линейной регрессией называют статистическую модель, отражающую зависимость одной переменной у от различных факторов – одного или нескольких. Такие факторы – независимые переменные – называются регрессорами. Через линейную регрессию можно восстановить зависимость между двумя любыми переменными.

В математических расчетах также применяются другие типы регрессий: одномерная, полиномиальная, логистическая, множественная.

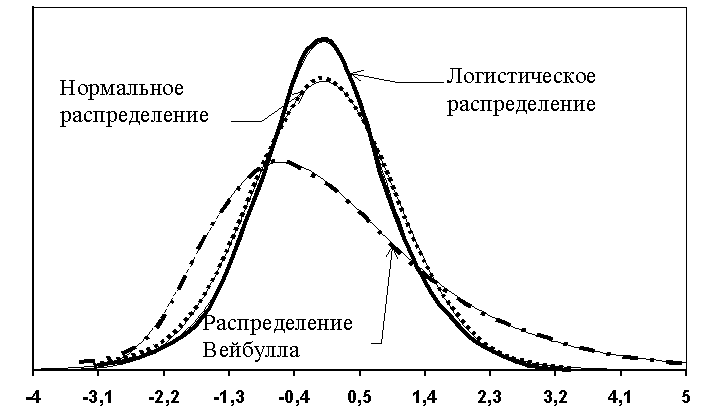
Логистическая регрессия рассматривает случаи связей между разными двумя классами, позволяет вывести обоснования и минимизировать эмпирический риск. Этот метод применяется в так называемой байесовской классификации, в методах настройки весов.

При помощи логистической регрессии (она же логит-регрессия, логит-модель) предсказывают степень вероятности наступления разных событий. Результат подгоняется к логистической кривой с использованием полученных модельных данных.

Виды регрессии

В каждом человеке присутствует регрессивная манера поведения, но ее проявление отличается и зависит от вида:

Кратковременная

Считается самой распространённой. Является обычной реакцией, вызывает слабость на фоне эмоционального или физического перенапряжения. Осуществляет помощь в расслаблении при стрессе. Подобный вид регрессии безобиден.

Частичная

Имеет более длительную продолжительность. В человеческом поведении происходят изменения, при осложнении развивается психическое расстройство. Для примера, погрузитесь в представление серьезно больного человека. Личность использует собственное заболевание для манипулирования родными и друзьями, ради получения выгоды. С течением времени подобное поведение станет ипохондрией. Что выражается в поведении, где человек постоянно ищет все новые проблемы со здоровьем, для получения дальнейшего манипулирования окружающими. Что и является проблемой с психическим состоянием.

Полная

Чаще всего выявляется при слабоумии и деменции. Думаю, вам приходилось слышать выражение, что старики впадают в детство. Но имеется такой нюанс, что подобное состояние наблюдается и у молодых людей, переживших тяжелую психологическую травму. Их сознание противится произошедшему и не хочет его признавать, вследствие чего происходит психологическая защита в виде закрытия от произошедшего, возвращая сознание в детство. Данная регрессия в психологии считается очень серьезным психическим заболеванием, с которым возможно справиться только с помощью психиатра.

Регрессия выступает в роли предохранителя, защищая психическое состояние от перенапряжения. Подобное работает на подсознательном уровне, следовательно, все происходит без контролирования человеческим разумом. Тревогу стоит поднимать при полной регрессии.

Регрессия — что это такое простыми словами

Регрессия в психологии — это один из описанных Зигмундом Фрейдом методов психологической защиты. Он условно разделил их на 2 большие группы:

Механизмы высокого уровня трансформируют неудовлетворенность и негативные переживания в активные действия. Наглядный пример — занятия творчеством.
Механизмы низшего уровня характеризуются искажением реальности. Они не помогают решить проблему, а, наоборот, усугубляют ее, переводя из сознания в подсознание. Человеку лишь кажется, что он ведет полноценную жизнь. На самом же деле он находится на прямом пути к развитию неврозов и других психических проблем.

Регрессия относится к низшим психологическим защитам. И это еще не все. Она по праву считается самой примитивной техникой.

Интересно, что существует несколько определений регрессии:

Регрессией в психологии называют такой механизм защиты психики, при котором индивид приспосабливается к конфликтной или тревожной ситуации, прибегая к ранним, но менее зрелым моделям поведения. Их он считает максимально безопасными и эффективными в данных обстоятельствах.
Согласно Глоссарию психологических терминов, регрессия — это состояние, для реализации которого происходит возврат к примитивным формам мышления и поведения, свойственным людям на более ранней стадии развития.
В словаре аналитической психологии сказано, что регрессия — это обратное движение либидо к ранним способам адаптации. Сопровождается инфантильными фантазиями и желаниями.
Р. Комер (профессор кафедры психологии Принстонского университета с более чем 25-летним стажем) называл регрессией защитный механизм внутреннего «Я», при котором человек возвращается к примитивным способам взаимодействия с окружающим миром.

Свое определение регрессии и регрессивному поведению дают различные направления психотерапии:

В психоанализе регрессия — это простой механизм защиты, относящийся к этапу воссоединения, когда при невозможности удовлетворить ту или иную потребность человек обращается к тем периодам прошлого, в которых он испытывал наслаждение и получал полное удовлетворение другими способами. Степень выраженности регрессии в этом случае зависит от колебаний между адаптацией к новому способу удовлетворения и силой привычки к старым способам.
В гештальт-терапии этим термином называют возврат к ранним уровням развития или манере самовыражения. Регрессия, по словам психологов, помогает уменьшить тревогу путем отказа от реальности в пользу той модели поведения, которая помогала справиться с негативными эмоциями в прошлом.
В бихевиоризме регрессия — это возвращение к раннему, более примитивному и простому способу реагирования. Так, человек оправдывается с позиции рассуждений маленького ребенка, отказывается от логического размышления, стоит на своем даже в тех случаях, когда собеседник абсолютно прав. У таких личностей сильно замедлилось или вовсе остановилось психическое развитие, в результате чего к ним часто возвращаются их детские привычки.

Регресс в развитии общества

Эволюция человечества – это сложный процесс развития, который характеризуется как движением вперед (прогрессом), так и движением назад (регрессом).

Пример: период с 20 века по сегодняшний день – это стремительный прогресс науки и техники. Человечество поднялось на новую ступень эволюционного развития. Но положительные результаты этого процесса затронули не все человечество.

В мире есть десятки регионов и даже целых стран, где людям недоступны элементарные медицинские услуги, где люди гибнут от различных инфекций, потому что у них нет антибиотиков. В этих странах налицо процесс регресса.

Допустим, эти страны не будут иметь возможность получать какую-либо помощь извне. В результате, с течением времени (возможно, через несколько сотен лет), население этих стран деградирует в умственном (отсутствие образования), физическом (голод) и нравственном развитии.

Наиболее значимые признаки регресса в обществе:

прекращение роста экономики → упадок экономики → кризис → развал экономики;
снижение уровня жизни населения → рост разницы благосостояния богатых и бедных слоев населения → обнищание основной массы населения;
(снижение рождаемости + рост смертности + рост заболеваемости) → уменьшение численности населения;
(падение уровня образованности + снижение актуальности моральных и духовных ценностей) → моральная деградация населения;
решение острых общественных вопросов мерами насилия;
снижение роли страны в международных отношениях.

Самое интересное, что человечество уже «проходило» тему регресса. В далеких 15 – 18 веках до н.э. существовала развитая микенская цивилизация (Греция). А примерно в 12 веке до н.э. данная цивилизация (это как?) перестала существовать.

По мнению ученых, упадок и гибель цивилизации произошли из-за регресса развития, который привел к миграции населения в другие регионы, утрате письменности, исчезновению технологий производства, прекращению торговых отношений с другими странами.

Склонность к регрессии

Регрессивное состояние чаще всего встречается у детей в период формирования психики. Обычно проявляется, когда ребенок желает внимания к себе и начинает устраивать истерику и плакать на глазах. Бывает, что начинает себя вести как годовалые дети, ходить под себя, переставать питаться самостоятельно и так далее… Обычно подобное поведение у ребенка наблюдается, когда в семье появляется еще одно чадо

У старшего ребенка подобным поведением проявляется ревность, попытка вернуть к себе внимание родителей

У взрослого человека регрессия характеризуется признаком слабости и инфантилизма. Примером служат следующие индивиды:

Слабохарактерность, нестабильное эмоциональное состояние.
Неуверенность в себе, заниженная самооценка.
Люди, поддающиеся под манипулирование от других людей.
Социопаты.
Имеющие повышенную тревожность, панику, неврозы и истерию.

Бывают случаи, что регрессия может наблюдаться и у уверенных в себе индивидах. Это происходит, когда все остальные психологические защиты не привели к результату. Трудности могут отнимать всю эмоциональность и ухудшать физическое состояние, а желаемое так и не достигается. При подобных ситуациях организм включает защиту для недопущения разочарования, и недопуская погружения в депрессивное состояние. Личность словно впадает в детство. У нее проявляется плаксивость, жалобность, заедание стресса, демонстрируется обида и страдания.

Что такое регрессия

Регрессия – что это такое простыми словами? Зигмунд Фрейд относил ее к психологической защитной реакции. Так же разделяя ее на 2 группы:

Регрессия

Высокий уровень. Трансформирует неудовлетворенность и отрицательные мысли в активные действия. Одним из примеров послужит занятие творчеством.
Низший уровень. Связано с искажением реальности. Нет помощи в решении проблем. Напротив, происходит усугубление ситуации, переводя ее из сознания в подсознание. Личность только мысленно живет полноценной жизнью. В действительности личность находится на развитии нервозного состояния и остальных психических недугов.

Регрессия в психологии выступает низшим уровнем психологической защиты. Она считается самой примитивной защитой.

Регрессия в психологии имеет несколько определений:

Защитный механизм в психике человека называется регрессией, при котором происходит приспосабливание к конфликтной или иной неприятной ситуации, производя более ранние, менее зрелые модели поведения. Личность считает, что данное поведение наиболее безопасное и эффективное при сложившихся обстоятельствах.
С позиции психологических терминов Глоссария, регрессия воспринимается, как состояние возвращающая к примитивной форме мышления и манере поведения, свойственным личностям на ранних стадиях развития.
Аналитическая психология рассматривает регрессию как обратное движение либидо к раннему способу адаптации. Наблюдаются инфантильные фантазии и желания.

Психотерапия также имеет собственные определения регрессивному поведению:

Психоанализ рассматривает регрессию как простейший механизм защиты, удовлетворяющий потребности. Человек погружается в те периоды прошлого, когда чувствовалось наслаждение и был удовлетворен иными способами. В данном случае сила выражения регрессии зависит от адаптации к новому удовлетворению и силы привычки к прошлым способам.
Гештальт-терапия в медицине рассматривает ситуацию с ранним развитием или манерой самовыражения. При помощи регрессии уменьшается тревога пациента, благодаря отказу от реальной жизни, прикрываясь манерой поведения из прошлого, для избегания негативной эмоции.
Бихевиоризм регрессию рассматривает как возвращение к ранней, более примитивной и простой манере реагирования. Происходит оправдывание по манере ребенка, будет детская упертость, даже при осознании, что оппонент полностью прав. Считается, что у человека наблюдается остановка психического развития, впоследствии чего происходит воспроизведение детских привычек.

Реинкарнация ребенка

Считается, что у детей открыта память души примерно до 3-5 лет. Они помнят и рассказывают о вещах, которые было бы невозможно другим способом узнать о людях. Как подтверждение, Джимом Такером были найдены семьи, в которых жили эти дети в прежнем воплощении: подтверждены адреса, профессии и различные другие подробности жизни людей, которыми они были раньше.

Американский психиатр Ян Стивенсон был главой отделения неврологии и психиатрии в медицинском колледже Университета Вирджинии и заинтересовался рассказами некоторых детей об их “прошлой жизни”. Все эти истории Стивенсон записывал, и потом проверял их достоверность.

Команда Стивенсона досконально изучила 895 случаев, и оказалось, что число совпадений с реальными фактами можно объяснить только теорией реинкарнации. Дети в возрасте от трех до пяти лет могли подробно описать и страну, и среду, в которой они никогда не находились, детально охарактеризовать место гибели человека, факты чьей биографии они вспоминали.

Занимаясь почти тридцать лет этой проблемой, Стивенсон опубликовал “Свидетельства о выживании сознания, почерпнутые из воспоминаний о Предыдущих воплощениях”. Эта работа вызвала огромный резонанс во всем мире.

В наше время благодаря работам американских психологов и гипнотерапевтов был доказан факт возможности регрессии в предыдущие жизни. Майкл Ньютон, Долорес Кэннон, Реймонд Моуди, Сел Рейчел исследовали множество людей в регрессиях и после клинической смерти.

Для чего нужно знать прошлые жизни

То, что запомнили и описывали эти пациенты доказывает существование жизни после смерти и возможность посещения своих предыдущих жизней, Мира Душ и общения со своими Наставниками. Более подробно о этой теме можно прочесть в книгах перечисленных авторов.

В ходе погружения вы осознаете все, что происходит, все помните, слышите, ощущаете. Состояние похоже на то, как будто вы только что проснулись или погружаетесь в сон. По желанию, вы можете остановить сеанс. Никакие манипуляции с вами невозможны. У Вас есть право сказать: «Стоп!», если вы не хотите рассказывать консультанту то, что видите на данный момент. Кроме того, Вы получаете запись погружения и имеете возможность пересмотреть ее.

Преимущество метода в том, что вы сами видите, проживаете этот опыт. С помощью техники “Альтернанивное планирование” можно просмотреть возможные варианты развития событий. Особенно это актуально, когда нужно сделать выбор. Например: куда пойти учиться, поехать на отдых, с кем связать свою дальнейшую судьбу.

Вспомните:

раннее детство;
младенческий период;
внутриутробное развитие. Узнайте Как обстоятельства появления на свет влияют на вашу жизнь и установки;
ощутить мышление богатого человека;
воплощения между жизнями;
ресурсные состояния, таланты, способности;
нечеловеческие воплощения на других планетах.

В удивительном пространстве между жизнями можно узнать какие задачи ваша душа ставила на это воплощение, познакомиться со своими наставниками, чтобы напрямую от них получать для себя интересующую информацию.

Освойте метод. Регистрируйтесь на беслатный мастер класс и получите БОНУС медитацию в прошлые жизни под моим руководством.

Регрессия в статистике

Для точности результатов в статистике важна корректная постановка задачи – таким путем можно правильно восстановить структуру логит-модели. Выработка правильного алгоритма обеспечит отыскание правильных параметров.

В статистике применяется линейный дискриминант Фишера на основе логистической регрессии. Он основан на байесовских правилах (байесовская сеть). Применяется принцип максимального правдоподобия, но на практике достигаются очень разные результаты.

Множественная регрессия используется для многомерного анализа, где наблюдаются взаимосвязи между зависимой переменной у и совокупности предикторов – независимых переменных х, расчет делается на базе линейного уравнения.

В виде регрессии обычно также представлен исходный код в основе компьютерной программы.

История

Этот термин в статистике впервые был использован Френсисом Гальтоном (1886) в связи с исследованием вопросов наследования физических характеристик человека. В качестве одной из характеристик был взят рост человека; при этом было обнаружено, что в целом сыновья высоких отцов, что не удивительно, оказались более высокими, чем сыновья отцов с низким ростом. Более интересным было то, что разброс в росте сыновей был меньшим, чем разброс в росте отцов. Так проявлялась тенденция возвращения роста сыновей к среднему (regression to mediocrity), то есть «регресс». Этот факт был продемонстрирован вычислением среднего роста сыновей отцов, рост которых равен 56 дюймам, вычислением среднего роста сыновей отцов, рост которых равен 58 дюймам, и т. д. После этого результаты были изображены на плоскости, по оси ординат которой откладывались значения среднего роста сыновей, а по оси абсцисс — значения среднего роста отцов

Точки (приближённо) легли на прямую с положительным углом наклона меньше 45°; важно, что регрессия была линейной.

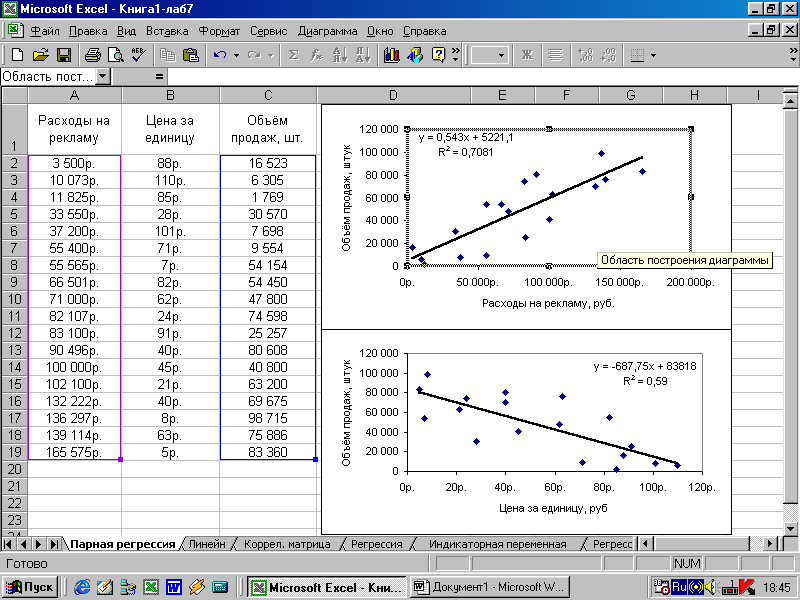
Линейная регрессия плюсов на Хабре

Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.

Загружает данные из файла.

Проверка мультиколлинеарности.

Теперь собственно сама модель, используем функцию .

В первой строке мы задаем параметры линейной регрессии. Строка определяет зависимую переменную и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через , набор переменных — .

Перейдем теперь к расшифровке полученных результатов.

— Если у нас модель представлена в виде , то тогда — точка пересечения прямой с осью координат, или .
— Коэффициент детерминации указывает насколько тесной является связь между факторами регрессии и зависимой переменной, это соотношение объясненных сумм квадратов возмущений, к необъясненным. Чем ближе к 1, тем ярче выражена зависимость.
— Проблема с в том, что он по любому растет с числом факторов, поэтому высокое значение данного коэффициента может быть обманчивым, когда в модели присутствует множество факторов. Для того, чтобы изъять из коэффициента корреляции данное свойство был придуман .
— Используется для оценки значимости модели регрессии в целом, является соотношением объяснимой дисперсии, к необъяснимой. Если модель линейной регрессии построена удачно, то она объясняет значительную часть дисперсии, оставляя в знаменателе малую часть. Чем больше значение параметра — тем лучше.
— Критерий, основанный на . Значение параметра в линейной регрессии указывает на значимость фактора, принято считать, что при фактор является значимым для модели.
— Это вероятность истинности нуль гипотезы, которая гласит, что независимые переменные не объясняют динамику зависимой переменной. Если значение ниже порогового уровня (.05 или .01 для самых взыскательных), то нуль гипотеза ложная. Чем ниже — тем лучше.

Проверим значения параметров линейной регрессии.

Как видим в целом отзывчивость модели возросла, параметры подтянулись ~~и стали более шелковистыми~~, выросла, так же как и .

Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.

И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.

Регрессия в психологии

В психоанализе применяется термин «регрессия», где таким образом маркируют возврат от более высокой ступени психологической организации к низкой. Например, в ходе психоаналитической сессии пациент может вернуться к предыдущим этапам своего эмоционального, сексуального развития, к более примитивным и упрощенным вариантам поведения, мышления, реагирования.

Регрессией называют и сам процесс движения психики пациента в новый формат. Иногда регрессия необходима как один из этапов преодоления комплексов, зависимости, раскрытия причин психотравм и душевных ран. Это необходимо для адаптации человека к переменам во внутреннем мире и внешней среде.

Психологическая регрессия может сопровождаться необычными фантазиями, детскими и примитивными желаниями. В регрессивной форме может проявляться либидо, отношение к родителям.

Человек возвращается на прошедшую стадию развития, чтобы облегчить собственное состояние, перенести разные по силе переживания.

Метод наименьших квадратов (расчёт коэффициентов)

На практике линия регрессии чаще всего ищется в виде линейной функции Y=b+b1X1+b2X2+…+bNXN{\displaystyle Y=b_{0}+b_{1}X_{1}+b_{2}X_{2}+…+b_{N}X_{N}} (линейная регрессия), наилучшим образом приближающей искомую кривую. Делается это с помощью метода наименьших квадратов, когда минимизируется сумма квадратов отклонений реально наблюдаемых Y{\displaystyle {Y}} от их оценок Y^{\displaystyle {\hat {Y}}} (имеются в виду оценки с помощью прямой линии, претендующей на то, чтобы представлять искомую регрессионную зависимость):

∑k=1M(Yk−Yk^)2→min{\displaystyle \sum _{k=1}^{M}(Y_{k}-{\hat {Y_{k}}})^{2}\to \min }

(M{\displaystyle M} — объём выборки). Этот подход основан на том известном факте, что фигурирующая в приведённом выражении сумма принимает минимальное значение именно для того случая, когда Y=y(x1,x2,…xN){\displaystyle Y=y(x_{1},x_{2},…x_{N})}.

Для решения задачи регрессионного анализа методом наименьших квадратов вводится понятие функции невязки:

σ(b¯)=12∑k=1M(Yk−Y^k)2{\displaystyle \sigma ({\bar {b}})={\frac {1}{2}}\sum _{k=1}^{M}{(Y_{k}-{\hat {Y}}_{k})^{2}}}

Условие минимума функции невязки:

{∂σ(b¯)∂bi=i=N⇔{∑i=1Myi=∑i=1M∑j=1Nbjxi,j+bM∑i=1Myixi,k=∑i=1M∑j=1Nbjxi,jxi,k+b∑i=1Mxi,kk=1,…,N{\displaystyle \left\{{\begin{matrix}{\frac {\partial \sigma ({\bar {b}})}{\partial b_{i}}}=0\\i=0…N\end{matrix}}\right.\Leftrightarrow {\begin{cases}\sum \limits _{i=1}^{M}{y_{i}}=\sum \limits _{i=1}^{M}{\sum \limits _{j=1}^{N}{b_{j}x_{i,j}}}+b_{0}M\\\sum \limits _{i=1}^{M}{y_{i}x_{i,k}}=\sum \limits _{i=1}^{M}{\sum \limits _{j=1}^{N}{b_{j}x_{i,j}x_{i,k}}}+b_{0}\sum \limits _{i=1}^{M}{x_{i,k}}\\k=1,\ldots ,N\end{cases}}}

Полученная система является системой N+1{\displaystyle N+1} линейных уравнений с N+1{\displaystyle N+1} неизвестными b,…,bN{\displaystyle b_{0},\ldots ,b_{N}}.

Если представить свободные члены левой части уравнений матрицей

B=(∑i=1Myi∑i=1Myixi,1⋮∑i=1Myixi,N),{\displaystyle B=\left({\begin{matrix}\sum \limits _{i=1}^{M}{y_{i}}\\\sum \limits _{i=1}^{M}{y_{i}x_{i,1}}\\\vdots \\\sum \limits _{i=1}^{M}{y_{i}x_{i,N}}\end{matrix}}\right),}

а коэффициенты при неизвестных в правой части — матрицей

A=(M∑i=1Mxi,1∑i=1Mxi,2…∑i=1Mxi,N∑i=1Mxi,1∑i=1Mxi,1xi,1∑i=1Mxi,2xi,1…∑i=1Mxi,Nxi,1∑i=1Mxi,2∑i=1Mxi,1xi,2∑i=1Mxi,2xi,2…∑i=1Mxi,Nxi,2⋮⋮⋮⋱⋮∑i=1Mxi,N∑i=1Mxi,1xi,N∑i=1Mxi,2xi,N…∑i=1Mxi,Nxi,N),{\displaystyle A=\left({\begin{matrix}M&\sum \limits _{i=1}^{M}{x_{i,1}}&\sum \limits _{i=1}^{M}{x_{i,2}}&…&\sum \limits _{i=1}^{M}{x_{i,N}}\\\sum \limits _{i=1}^{M}{x_{i,1}}&\sum \limits _{i=1}^{M}{x_{i,1}x_{i,1}}&\sum \limits _{i=1}^{M}{x_{i,2}x_{i,1}}&…&\sum \limits _{i=1}^{M}{x_{i,N}x_{i,1}}\\\sum \limits _{i=1}^{M}{x_{i,2}}&\sum \limits _{i=1}^{M}{x_{i,1}x_{i,2}}&\sum \limits _{i=1}^{M}{x_{i,2}x_{i,2}}&…&\sum \limits _{i=1}^{M}{x_{i,N}x_{i,2}}\\\vdots &\vdots &\vdots &\ddots &\vdots \\\sum \limits _{i=1}^{M}{x_{i,N}}&\sum \limits _{i=1}^{M}{x_{i,1}x_{i,N}}&\sum \limits _{i=1}^{M}{x_{i,2}x_{i,N}}&…&\sum \limits _{i=1}^{M}{x_{i,N}x_{i,N}}\end{matrix}}\right),}

то получаем матричное уравнение: A×X=B{\displaystyle A\times X=B}, которое легко решается методом Гаусса. Полученная матрица будет матрицей, содержащей коэффициенты уравнения линии регрессии:

X=(bb1⋮bN){\displaystyle X=\left({\begin{matrix}b_{0}\\b_{1}\\\vdots \\b_{N}\end{matrix}}\right)}

Для получения наилучших оценок необходимо выполнение предпосылок МНК (условий Гаусса — Маркова). В англоязычной литературе такие оценки называются BLUE (Best Linear Unbiased Estimators — «наилучшие линейные несмещенные оценки»).
Большинство исследуемых зависимостей может быть представлено с помощью МНК нелинейными математическими функциями.

Математическое определение регрессии

Строго регрессионную зависимость можно определить следующим образом. Пусть Y,X1,X2,…,Xp{\displaystyle Y,X_{1},X_{2},\ldots ,X_{p}} — случайные величины с заданным совместным распределением вероятностей. Если для каждого набора значений X1=x1,X2=x2,…,Xp=xp{\displaystyle X_{1}=x_{1},X_{2}=x_{2},\ldots ,X_{p}=x_{p}} определено условное математическое ожидание

y(x1,x2,…,xp)=E(Y∣X1=x1,X2=x2,…,Xp=xp){\displaystyle y(x_{1},x_{2},\ldots ,x_{p})=\mathbb {E} (Y\mid X_{1}=x_{1},X_{2}=x_{2},\ldots ,X_{p}=x_{p})} (уравнение регрессии в общем виде),

то функция y(x1,x2,…,xp){\displaystyle y(x_{1},x_{2},\ldots ,x_{p})} называется регрессией величины Y{\displaystyle Y} по величинам X1,X2,…,Xp{\displaystyle X_{1},X_{2},\ldots ,X_{p}}, а её график — линией регрессии Y{\displaystyle Y} по X1,X2,…,Xp{\displaystyle X_{1},X_{2},\ldots ,X_{p}}, или уравнением регрессии.

Зависимость Y{\displaystyle Y} от X1,X2,…,Xp{\displaystyle X_{1},X_{2},\ldots ,X_{p}} проявляется в изменении средних значений Y{\displaystyle Y} при изменении X1,X2,…,Xp{\displaystyle X_{1},X_{2},\ldots ,X_{p}}. Хотя при каждом фиксированном наборе значений X1=x1,X2=x2,…,Xp=xp{\displaystyle X_{1}=x_{1},X_{2}=x_{2},\ldots ,X_{p}=x_{p}} величина Y{\displaystyle Y} остаётся случайной величиной с определённым распределением.

Для выяснения вопроса, насколько точно регрессионный анализ оценивает изменение Y{\displaystyle Y} при изменении X1,X2,…,Xp{\displaystyle X_{1},X_{2},…,X_{p}}, используется средняя величина дисперсии Y{\displaystyle Y} при разных наборах значений X1,X2,…,Xp{\displaystyle X_{1},X_{2},…,X_{p}} (фактически речь идет о мере рассеяния зависимой переменной вокруг линии регрессии).

В матричной форме уравнение регрессии (УР) записывается в виде: Y=BX+U{\displaystyle Y=BX+U}, где U{\displaystyle U} — матрица ошибок. При обратимой матрице X◤X получается вектор-столбец коэффициентов B с учётом U◤U=min(B). В частном случае для Х=(±1) матрица X◤X является рототабельной, и УР может быть использовано при анализе временны́х рядов и обработке технических данных.

Линейная регрессия

Регрессия — это метод, используемый для моделирования и анализа отношений между переменными, а также для того, чтобы увидеть, как эти переменные вместе влияют на получение определенного результата. Линейная регрессия относится к такому виду регрессионной модели, который состоит из взаимосвязанных переменных. Начнем с простого. Парная (простая) линейная регрессия — это модель, позволяющая моделировать взаимосвязь между значениями одной входной независимой и одной выходной зависимой переменными с помощью линейной модели, например, прямой.

Более распространенной моделью является множественная линейная регрессия, которая предполагает установление линейной зависимости между множеством входных независимых и одной выходной зависимой переменных. Такая модель остается линейной по той причине, что выход является линейной комбинацией входных переменных. Мы можем построить модель множественной линейной регрессии следующим образом:

Y = a_1*X_1 + a_2*X_2 + a_3*X_3 ……. a_n*X_n + b

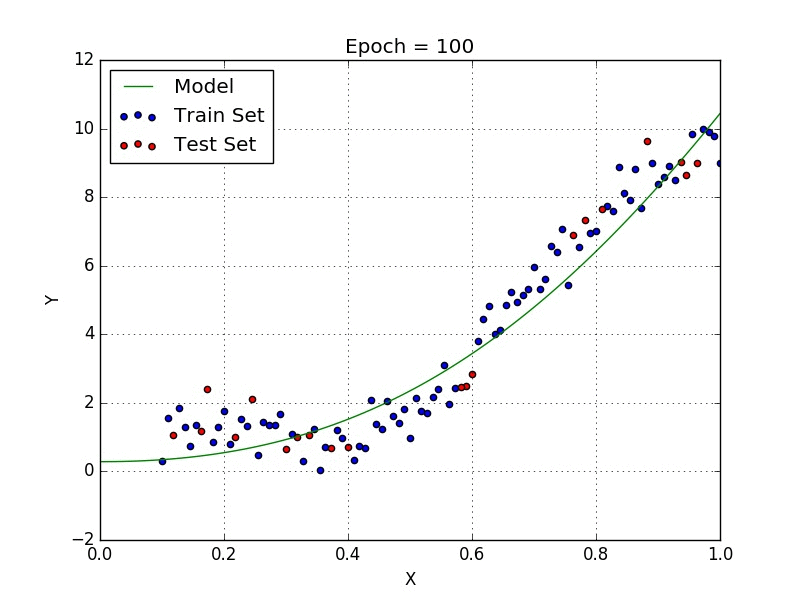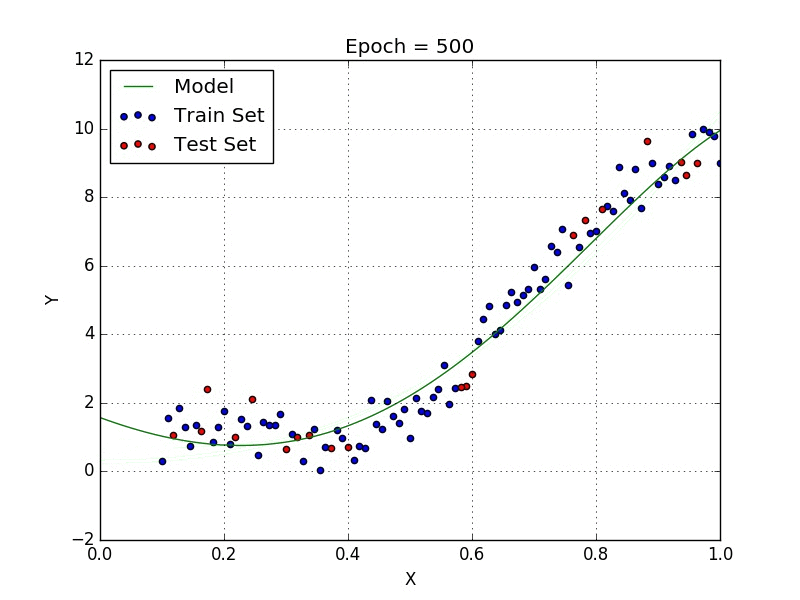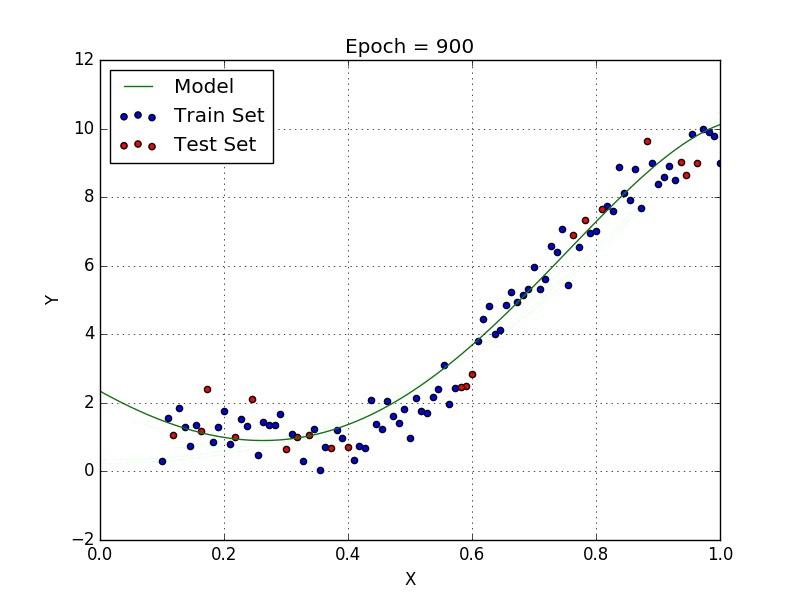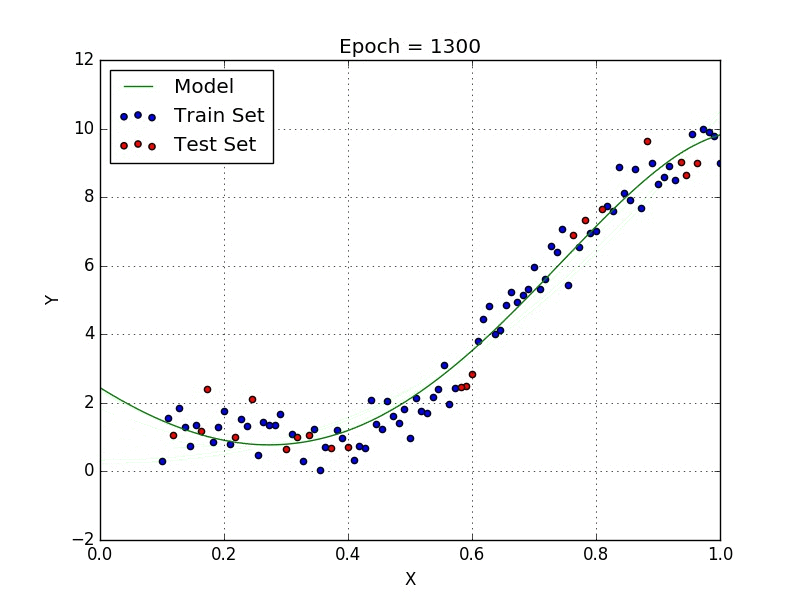
Где a_n — это коэффициенты, X_n — переменные и b — смещение. Как видим, данная функция не содержит нелинейных коэффициентов и, таким образом, подходит только для моделирования линейных сепарабельных данных. Все очень просто: мы взвешиваем значение каждой переменной X_n с помощью весового коэффициента a_n. Данные весовые коэффициенты a_n, а также смещение b вычисляются с применением стохастического градиентного спуска. Посмотрите на график ниже в качестве иллюстрации!

Иллюстрация поиска оптимальных параметром для линейной регрессии с помощью градиентного спуска

Несколько важных пунктов о линейной регрессии:

Она легко моделируется и является особенно полезной при создании не очень сложной зависимости, а также при небольшом количестве данных.
Обозначения интуитивно-понятны.
Чувствительна к выбросам.