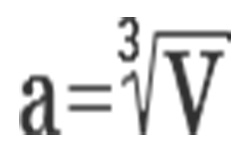Как найти ребро куба | Сделай все сам

Зная некоторые параметры куба, дозволено легко обнаружить его ребро. Для этого довольно лишь иметь информацию о его объеме, площади грани либо длине диагонали грани либо куба.
Вам понадобится
Инструкция
1. В основном встречаются четыре типа задач, в которых нужно обнаружить ребро куба. Это определение длины ребра куба по площади грани куба, по объему куба, по диагонали грани куба и по диагонали куба. Разглядим все четыре варианта таких задач.
(Остальные задания, как водится, являются вариациями вышеперечисленных либо задачами по тригонометрии, имеющими крайне косвенное отношение к рассматриваемому вопросу)Если вестима площадь грани куба, то обнаружить ребро куба дюже легко. Потому что грань куба представляет собой квадрат со стороной, равной ребру куба, то ее площадь равняется квадрату ребра куба.
Следственно длина ребра куба равняется корню квадратному из площади его грани, то есть:а=?S, гдеа – длина ребра куба,S – площадь грани куба.
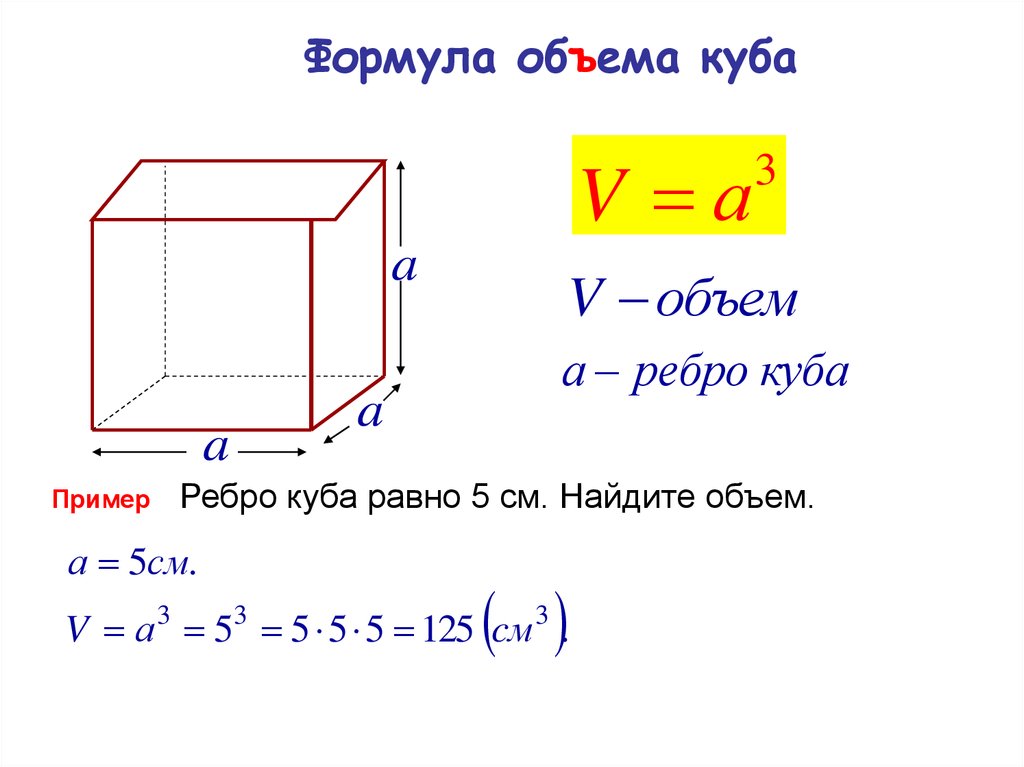
2. Нахождение грани куба по его объему еще проще. Рассматривая, что объем куба равен кубу (третьей степени) длины ребра куба, получаем что длина ребра куба равняется корню кубическому (третьей степени) из его объема, т.е.:а=?V (кубический корень), гдеа – длина ребра куба,V – объем куба.
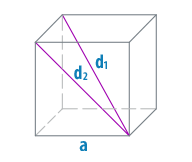
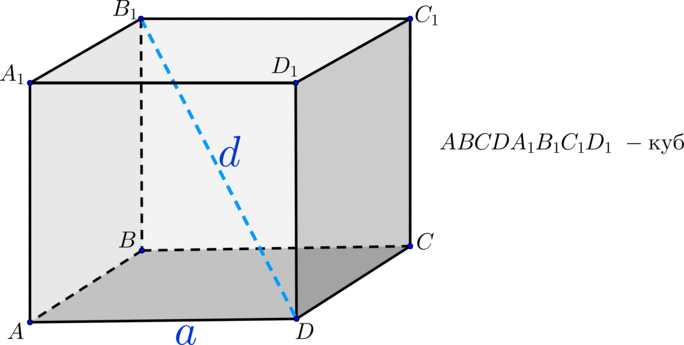
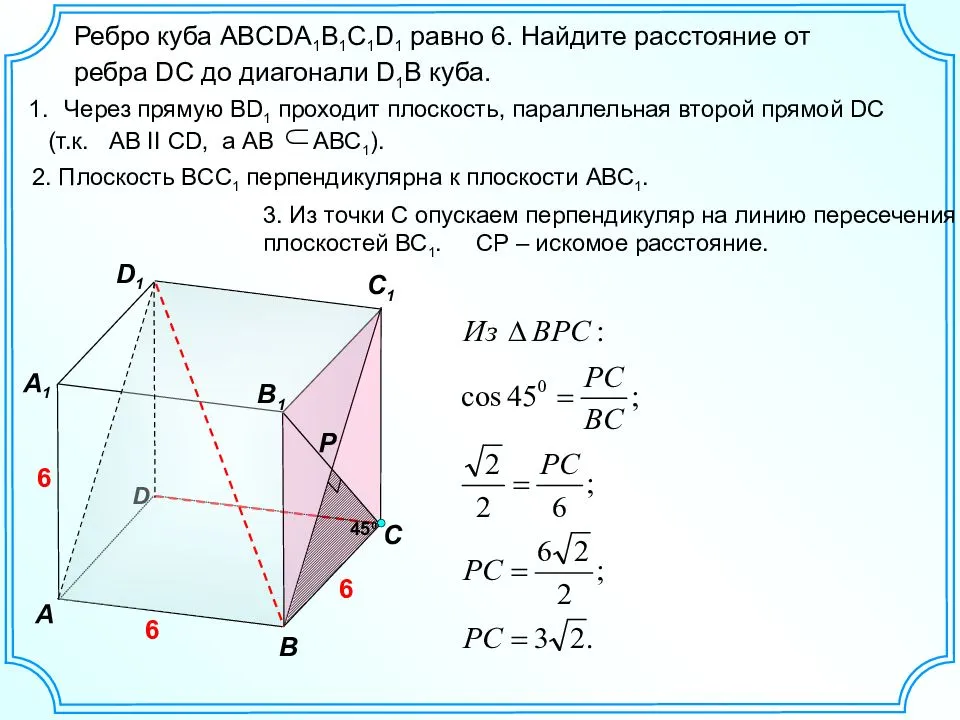
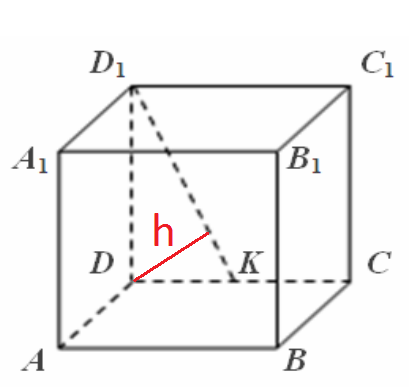
3. Немногим труднее нахождение длины ребра куба по знаменитым длинам диагоналей. Обозначим через:а – длину ребра куба;b – длину диагонали грани куба;c – длину диагонали куба.
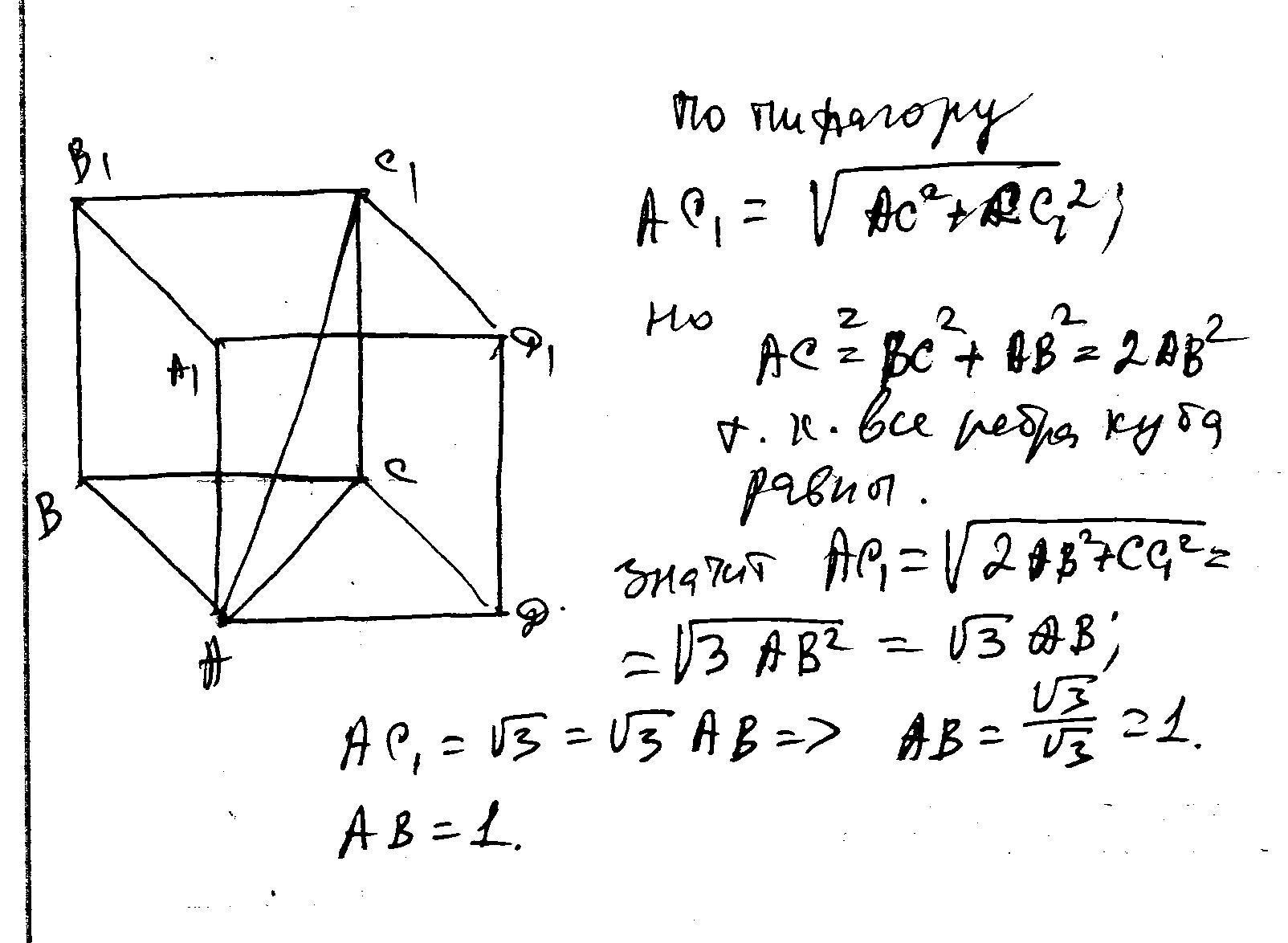
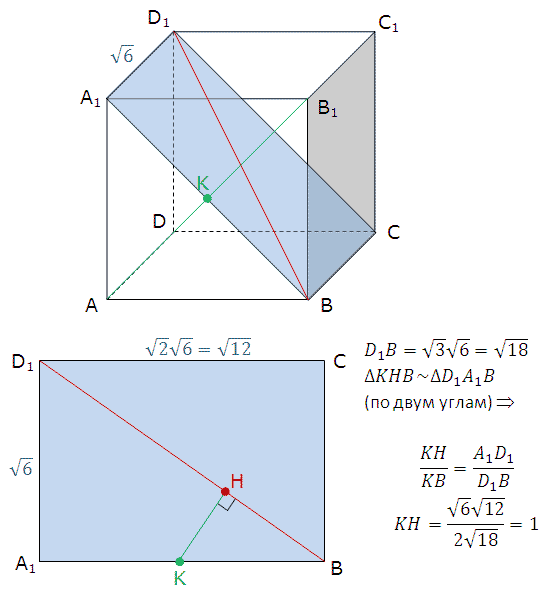
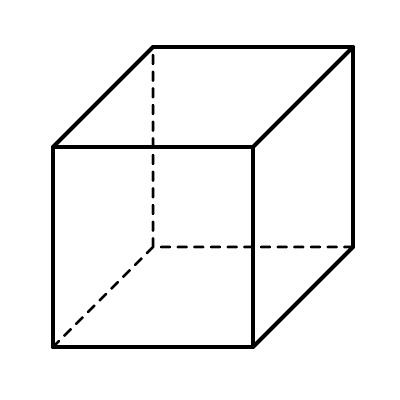
Как видно из рисунка, диагональ грани и ребра куба образуют прямоугольный равносторонний треугольник. Следственно, по теореме Пифагора:a2+a2=b2( – значок возведения в степень).
Отсель находим:a=?(b2/2)(дабы обнаружить ребро куба надобно извлечь квадратный корень из половины квадрата диагонали грани).
4. Дабы обнаружить ребро куба по его диагонали, вновь воспользуемся рисунком. Диагональ куба (с), диагональ грани (b) и ребро куба (а) образуют прямоугольный треугольник. Значит, согласно теореме Пифагора:a2+b2=c2.Воспользуемся вышеустановленной зависимостью между a и b и подставим в формулуb2=a2+a2. Получаем:a2+a2+a2=c2, откуда находим:3*a2=c2, следственно:a=?(c2/3).
Совет 2: Как обнаружить площадь и объем куба
Куб – это прямоугольный параллелепипед, все ребра которого равны. Следственно всеобщая формула для объема прямоугольного параллелепипеда и формула для площади его поверхности в случае куба упрощаются. Также объем куба и его площадь поверхности дозволено обнаружить, зная объем шара, вписанного в него, либо шара, описанного вокруг него.
Вам понадобится
длина стороны куба, радиус вписанного и описанного шара
Совет 3: Как обнаружить обьём куба
Кубом называют объемный многоугольник с шестью гранями положительной формы – верный гексаэдр. Число положительных граней определяет форму всякой из них – это квадраты.
Это, вероятно, самая комфортная из многогранных фигур с точки зрения определения ее геометрических свойств в привычной нам трехмерной системе координат.
Все ее параметры дозволено вычислить, зная каждого лишь длину одного ребра.
Куб – свойства, виды и формулы

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
- многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
- прямая призма, все грани которой есть квадраты;
- прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
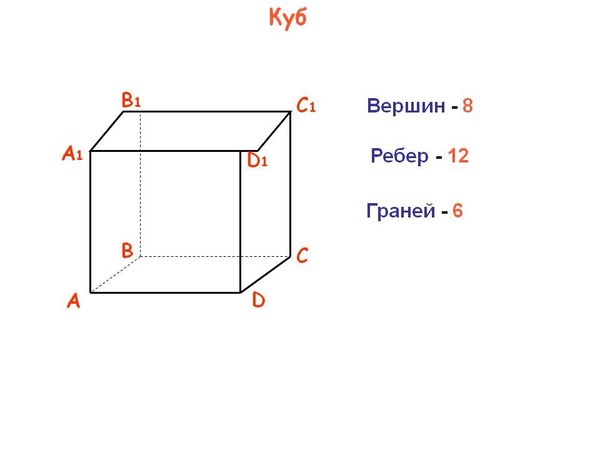
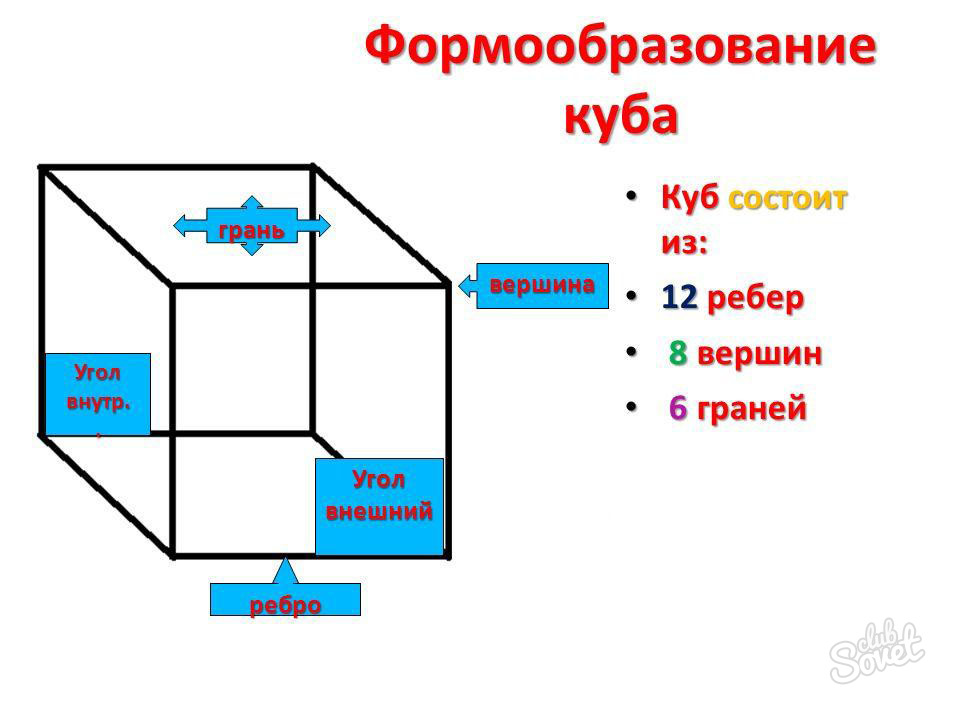
Грань
Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
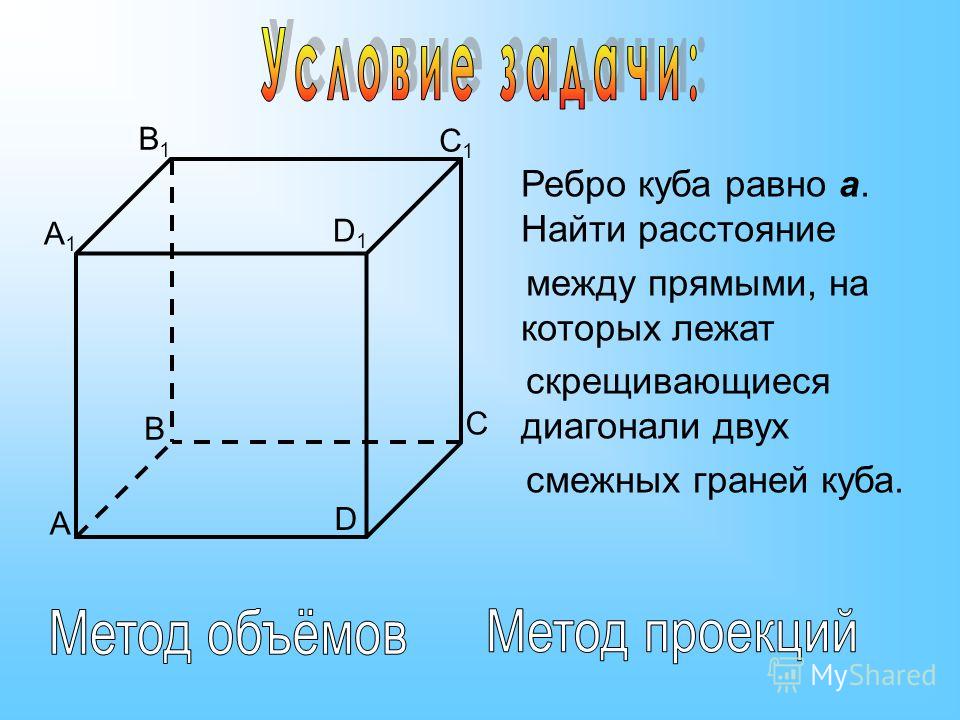
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
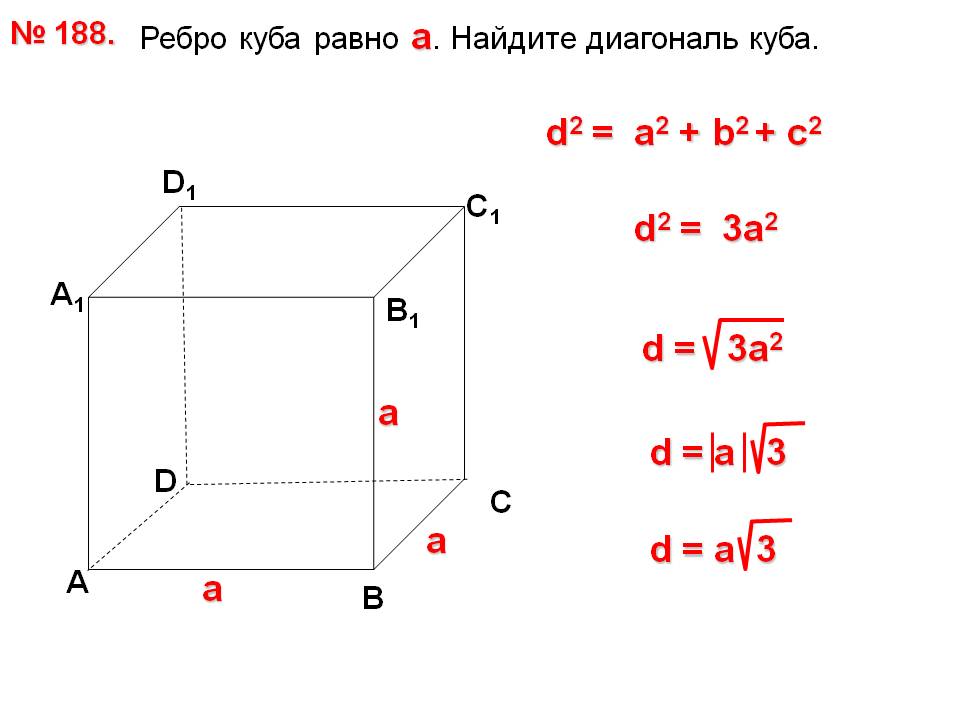
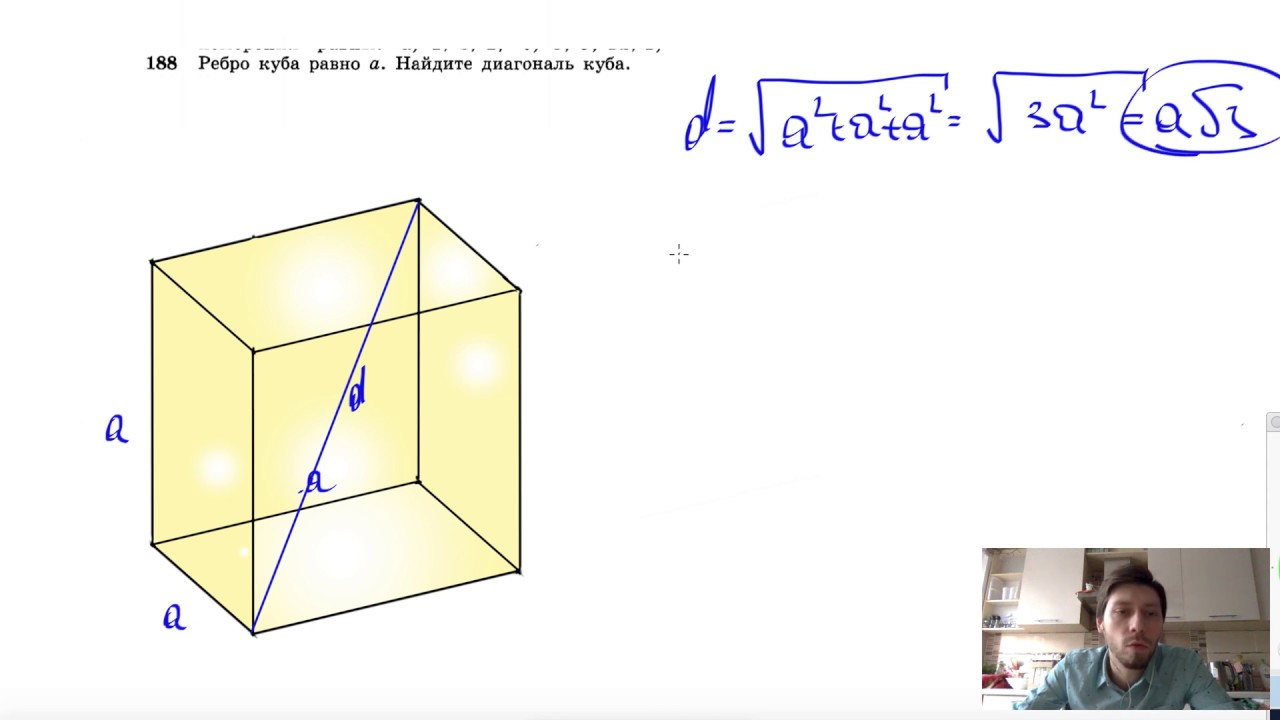
Диагональ куба
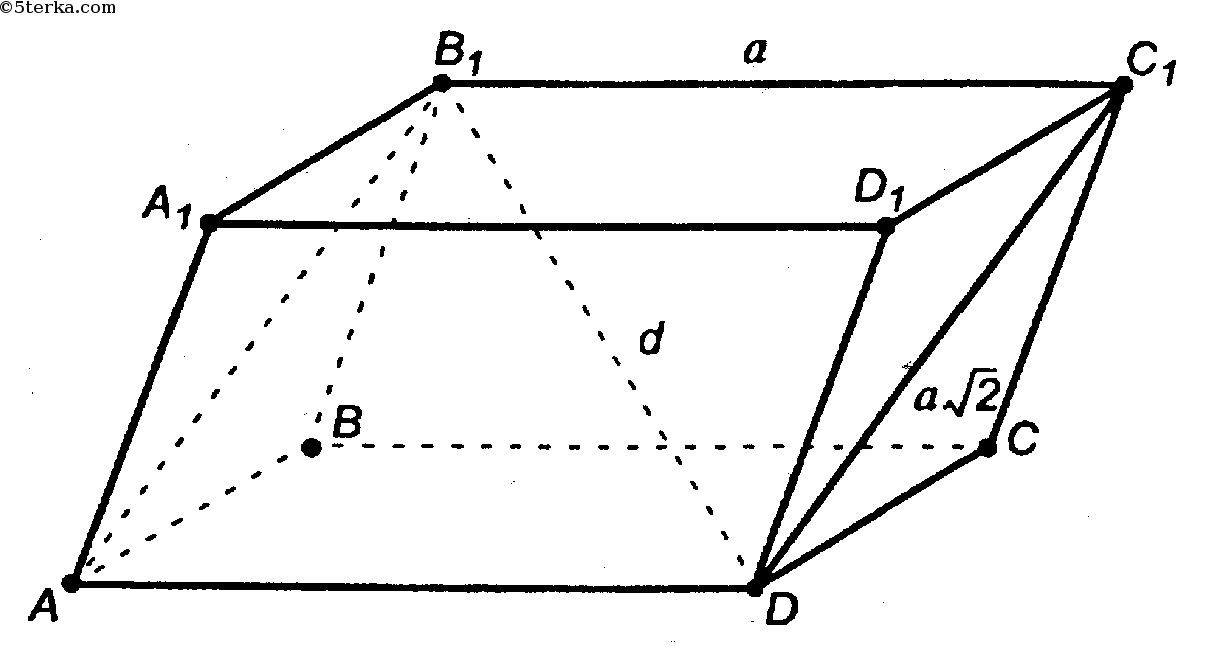
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Диагональ куба – одна из осей симметрии.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Такая сфера имеет центр, совпадающий с центром куба.
Радиус равен половине ребра:
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.
Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
Прочие свойства:
- у куба все грани равны, являются квадратами;
- у куба все рёбра равны;
- один центр и несколько осей симметрии.
Геометрия 10 класс
«Аксиомы стереометрии 10 класс» — Аксиомы стереометрии. А, В, С ? одной прямой А, В, С ? ? ? — единственная плоскость. 1. Лежат ли на плоскости ? точки В и С? 2. Найдите длину отрезка CF и площадь треугольника АВС. 2. Объясните, как построить линию пересечения плоскостей (AB1K) и (ADD1)? В любой плоскости пространства справедливы все аксиомы и теоремы планиметрии. 3. Назовите линию пересечения плоскостей (МОВ) и (ADO). Через две пересекающиеся прямые проходит плоскость, и притом только одна.
«Основные аксиомы стереометрии» — Древняя китайская пословица. Аксиомы стереометрии. Источники и ссылки. Изображения пространственных фигур. Геометрические тела. Геометрия. Пирамида Хеопса. Основные фигуры в пространстве. Следствия из аксиом стереометрии. Предмет стереометрии. Плоскость. Первые уроки стереометрии. Следствия из аксиом. Плоскости имеют общую точку. Аксиома. Четыре равносторонних треугольника. Точки прямой лежат в плоскости.
«Сечения фигур» — Пирамида. Значение. Многогранники в архитектуре. Точка. Воздух. Проведем прямую МК. Прямые в плоскостях. Пчёлы. Точка пересечения прямых. Построить сечение куба. Сечение куба плоскостью. Точки, лежащие в плоскости сечения. Мир многогранников. Построение сечений многогранника. Земля. Определение. Сечение куба. Искомое сечение. Сечение. Глубины различных наук. Сечение пирамид. Решение. Отметим точки.
«Сечение призмы» — Сечение призмы. Плоскость сечения параллельна боковому ребру призмы. Построение методом «следов». Определение сечения призмы. Плоскость сечения. Определение сечения. Диагональное сечение. Построение. Виды сечений. Построение сечений. Самостоятельная работа. Сечение призмы плоскостью. Сечения призмы.
«Предмет стереометрии» — Теорема Пифагора. Невидимая сторона. Неопределяемые понятия. Наглядные представления. Планиметрия. Стереометрия. Из истории. Вселенная. Сегодня на уроке. Геометрия. Пространственные представления. Египетские пирамиды. Помните ли вы теорему Пифагора. Точки. Пифагор. Аксиомы стереометрии. Пентаграмма. Понятие науки стереометрии. Указания. Правильные многогранники. Евклид. Философская школа. Основные понятия стереометрии.
«Декартова система» — Декартова система координат. Вопросы для заполнения. Прямоугольная система координат. Понятие системы координат. Введение декартовых координат в пространстве. Определение декартовой системы. Координаты точки. Координаты любой точки. Координаты вектора. Рене Декарт.
«Геометрия 10 класс»
Калькулятор площади куба
Куб — это правильный шестигранник, каждая грань которого является квадратом. Кубические фигуры часто встречаются в реальной жизни, поэтому на работе или в быту вам может понадобиться вычислить объем или площадь поверхности объекта, который имеет форму кубика.
Геометрия куба
Куб или правильный гексаэдр — это частный случай шестигранной прямоугольной призмы, все грани которой представляют собой квадраты. Кроме того, куб — это и частный случай прямоугольного параллелепипеда, у которого длина, ширина и высота абсолютно равны.
Куб — уникальная фигура, существующая в разных многомерных пространствах. К примеру, нульмерный куб — это точка, одномерный — отрезок, двухмерный — квадрат, а четырехмерный — тессеракт.
В нашем родном трехмерном пространстве куб встречается повсеместно, к примеру, в форме детских кубиков, рафинированного сахара, картонных коробок, газетных киосков или предметов интерьера.
Кубы широко используются в программировании, аналитике, научных изысканиях и прочих высоких материях.
Идеальная форма геометрической фигуры позволяет при помощи разномерных кубов выражать массивы данных, измерять объемы или визуализировать данные.
Кубические фигуры часто встречаются в реальности и абстрактных задачах, поэтому вам может понадобиться рассчитать объем или площадь поверхности кубика для решения самых разных проблем.
Площадь поверхности куба
Площадь кубической фигуры — это сумма площадей всех граней. Каждая грань куба — это квадрат. Площадь квадрата, то есть одной грани, определяется по простой формуле как:
Sg = a2
Куб — это гексаэдр, то есть шестигранник. Таким образом, площадь поверхности кубической фигуры представляет собой сумму шести квадратов:
S = 6 Sg = 6 a2
Определить площадь куба можно не только при помощи длины его ребра: для расчета площади поверхности вы можете использовать диагональ самого куба или диагональ одной грани.
Диагональ куба — это отрезок, который находится внутри пространства куба и соединяет две противоположные вершины. Проведенная диагональ разделяет куб на два прямоугольных треугольника. Согласно теореме Пифагора квадрат ребра куба равен одной трети от квадрата диагонали D, следовательно, формула площади полной поверхности приобретает вид:
- S = 2 D2
Площадь поверхности куба легко определить и с помощью диагонали одной грани. Площадь квадрата через диагональ равна:
- S = 0,5 d2.
Так как у куба 6 граней, общая площадь поверхности составит сумму шести граней куба, то есть:
- S = 6 × 0,5 d2 = 3 d2
Таким образом, чтобы определить площадь поверхности кубической фигуры вам достаточно ввести в форму-онлайн калькулятора всего один параметр на выбор:
- длину ребра;
- диагональ куба;
- диагональ квадрата.
Рассмотрим примеры использования данных формул в реальной жизни.
Ящик
Представьте, что вы хотите соорудить из листов ДСП ящик для хранения инструментов в форме куба. Вы знаете, что он отлично впишется в пространство на чердаке высотой 50 см.
Сколько же квадратных метров ДСП вам понадобится для создания такого контейнера? Зная высоту, равную a = 0,5 м вы можете легко подсчитать площадь общей поверхности куба, введя данный параметр в онлайн-калькулятор. Вы получите ответ в виде:
S = 1,5
Таким образом, вам понадобится всего 1,5 квадратных метра ДСП для создания ящика для инструментов. Зная всего один параметр, вы без труда порежете листы на грани куба и соорудите нужную конструкцию.
Контейнер
Допустим, вы хотите обработать антикоррозионным покрытием грузовые контейнеры, которые имеют кубическую форму. Для правильного расчета параметров покрытия вам необходимо знать площадь обрабатываемой поверхности. Вы знаете, что диагональ грани стандартного контейнера равняется d = 3 м. Зная этот параметр, вы легко рассчитаете площадь кубической поверхности, которая равна:
S = 18
Зная общую площадь покрытия, вы без проблем определите необходимое количество антикоррозионной жидкости.
Заключение
Куб встречается в реальной жизни не так часто, как призматические фигуры или параллелепипеды, однако в любом случае вам может понадобиться удобный калькулятор, при помощи которого вы определите площадь полной поверхности кубического объекта. Наш сервис поможет решить вам бытовые, производственные или школьные задачи мгновенно и без ошибок.