Ложные и истинные ребра: строение и расположение у женщин и мужчин

Представление графов[править]

Матрица и списки смежностиправить

Граф можно представить в виде матрицы смежности (англ. adjacency matrix), где . Также в ячейке матрицы можно хранить вес ребра или их количество (если в графе разрешены параллельные рёбра).
Для матрицы смежности существует теорема, позволяющая связать степень матрицы и количество путей из вершины в вершину .

Если граф разрежен (англ. sparse graph), , то есть, неформально говоря, в нем не очень много рёбер. Формально говорить не получается, потому что везде разреженные графы определяются по-разному, его лучше представить в виде списков смежности, где список для вершины будет содержать вершины . Данный способ позволит сэкономить память, так как не придется хранить много нулей.

Пути в графахправить

Определение:

Путём (маршрутом,англ. path) в графе называется последовательность вида , где — длина (англ. length) пути.

Определение:

Длина пути — количество рёбер, входящих в последовательность, задающую этот путь.

Определение:

Циклическим путём (англ. closed walk) в ориентированном графе называется путь, в котором .

Определение:

Циклическим путём в неориентированном графе называется путь, в котором , а также .

Определение:

Цикл (англ. integral cycle) — это циклических путей на отношении эквивалентности таком, что два пути эквивалентны, если ; где и — это две последовательности рёбер в циклическом пути.

Определение:

Простой (вершинно-простой) путь (англ. simple path) — путь, в котором каждая из вершин графа встречается не более одного раза.

Определение:

Рёберно-простой путь — путь, в котором каждое из рёбер графа встречается не более одного раза.

Д

• Двойственный граф. Граф А называется двойственным к планарному графу В, если вершины графа А соответствуют графа В, и две вершины графа A соединены ребром тогда и только тогда, когда соответствующие грани графа B имеют хотя бы одно общее ребро.
• Двудольный граф (или биграф, или чётный граф) — такой граф G(V,E){\displaystyle G(V,E)}, что множество вершин V разбито на два непересекающихся подмножества V1{\displaystyle V_{1}} и V2{\displaystyle V_{2}}, причём всякое ребро E инцидентно вершине из V1{\displaystyle V_{1}} и вершине из V2{\displaystyle V_{2}} (то есть соединяет вершину из V1{\displaystyle V_{1}} с вершиной из V2{\displaystyle V_{2}}). То есть двумя цветами. Множества V1{\displaystyle V_{1}} и V2{\displaystyle V_{2}} называются «долями» двудольного графа. Двудольный граф называется «полным», если любые две вершины из V1{\displaystyle V_{1}} и V2{\displaystyle V_{2}} являются смежными. Если |V1|=a{\displaystyle \left|V_{1}\right|=a}, |V2|=b{\displaystyle \left|V_{2}\right|=b}, то полный двудольный граф обозначается Ka,b{\displaystyle K_{a,b}}.
• Двусвязный граф — , в котором нет .
• Дерево — , не содержащий .
• Диаметр графа diam(G){\displaystyle \mathrm {diam} (G)} — максимум расстояния между вершинами для всех пар вершин. Расстояние между вершинами — наименьшее число рёбер , соединяющего две вершины.
• Длина  — количество рёбер в маршруте (с повторениями). Если маршрут M=v,e1,v1,e2,v2,…,ek,vk{\displaystyle M=v_{0},e_{1},v_{1},e_{2},v_{2},…,e_{k},v_{k}}, то длина M равна k (обозначается |M|=k{\displaystyle \left|M\right|=k}).
• Длина  — число дуг пути (или сумма длин его дуг, если последние заданы). Так для пути v₁, v₂, …, v_n длина равна n-1.
• Дуга — ориентированное .
• Дополнение графа — граф над тем же множеством вершин, что и исходный, но вершины соединены ребром тогда и только тогда, когда в исходном графе ребра нет.

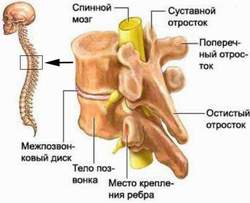
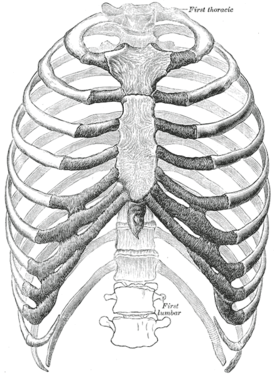
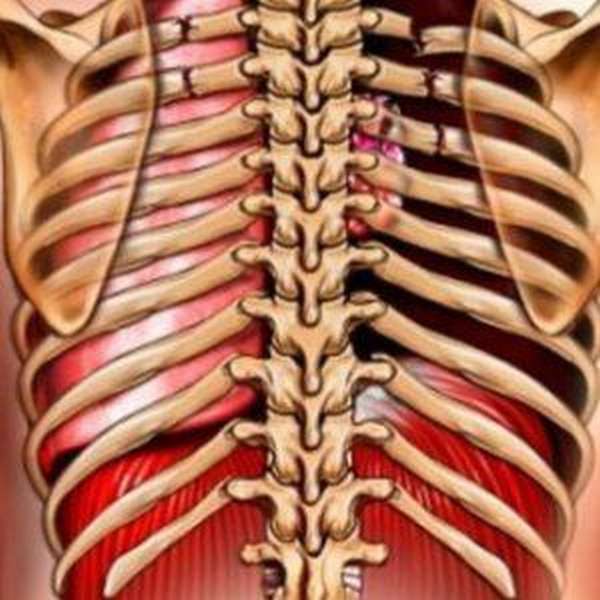
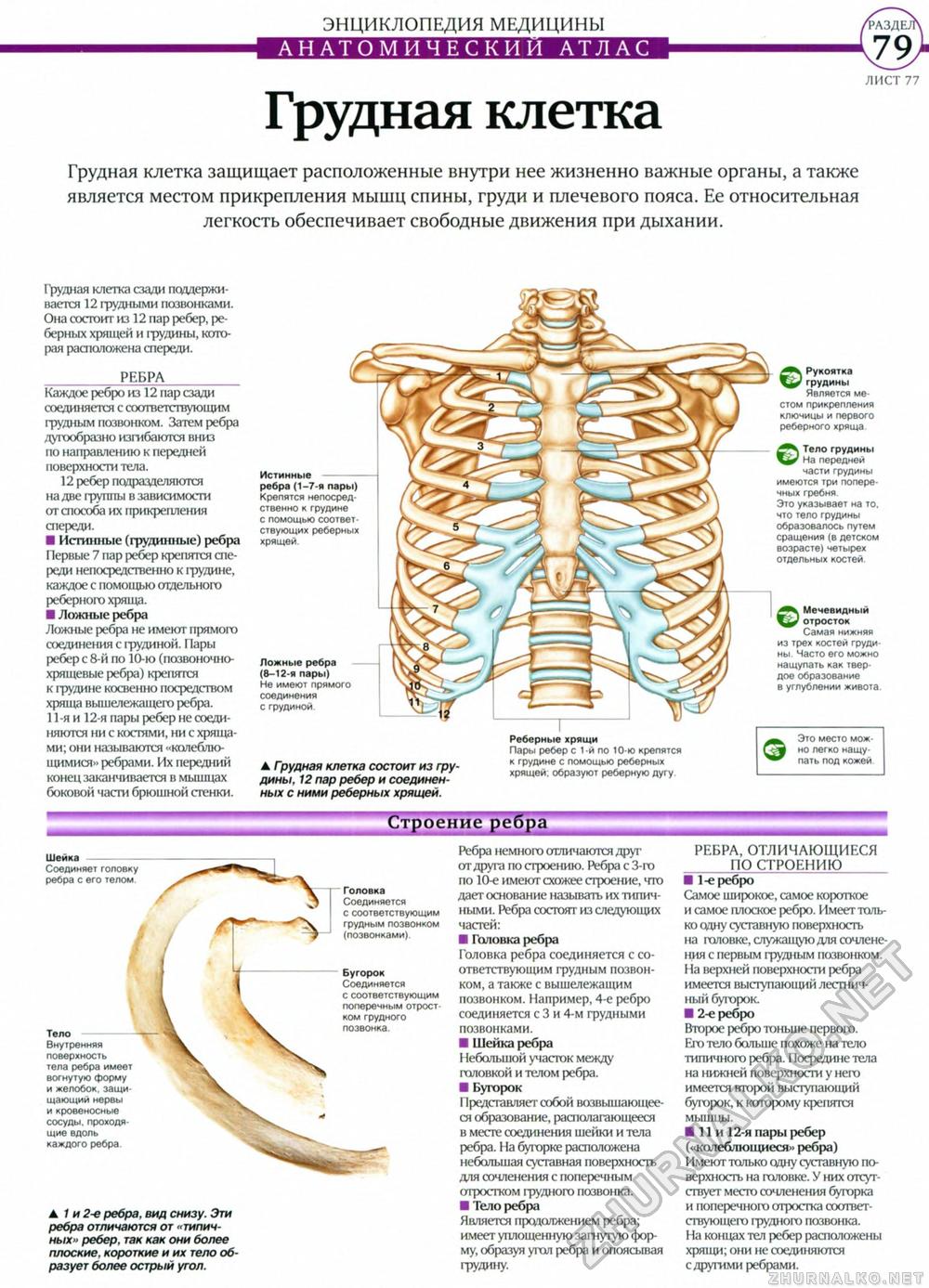
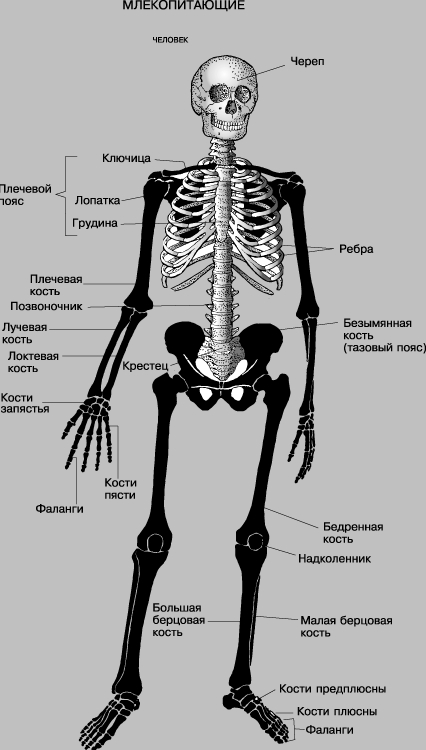
Костная часть ребра

Костная часть ребра имеет головку, шейку и тело. Головка ребра, caput costae, располагается на его позвоночном конце. На ней имеется суставная поверхность головки ребра, facies articularis capitis costae. Эту поверхность на II-X ребрах разделяет горизонтально идущий гребень головки ребра, crista capitis costae, на верхнюю, меньшую, и нижнюю, большую, части, каждая из которых соответственно сочленяется с реберными ямками двух соседних позвонков.

рис. 36. Рёбра, costae, правые; вид сверху. А — I ребро; Б — II ребро.

Шейка ребра, collum costae, – наиболее суженная и округлая часть ребра, несет на верхнем крае гребень шейки ребра, crista colli costae, (I и XII ребра этого гребня не имеют).

На границе с телом у 10 верхних пар ребер на шейке имеется небольшой бугорок ребра, tuberculum costae, на котором находится суставная поверхность бугорка ребра, facies articularis tuberculi costae, сочленяющаяся с поперечной реберной ямкой соответствующего позвонка.

Между задней поверхностью шейки ребра и передней поверхностью поперечного отростка соответствующего позвонка образуется реберно-поперечное отверстие, foramen costotransversarium (см. рис. ).

рис. 37. Восьмое (VIII) ребро, costa VIII) правое. (Внутренняя поверхность.)

Тело ребра, corpus costae, простираясь от бугорка до грудинного конца ребра, является наиболее длинным отделом костной части ребра. На некотором расстоянии от бугорка тело ребра, сильно изгибаясь, образует угол ребра, angulus costae. У I ребра (см. рис. ) он совпадает с бугорком, а на остальных ребрах расстояние между этими образованиями увеличивается (вплоть до XI ребра); тело XII ребра угла не образует. На всем протяжении тело ребра уплощено. Это позволяет различать в нем две поверхности: внутреннюю, вогнутую, и наружную, выпуклую, и два края: верхний, округлый, и нижний, острый. На внутренней поверхности вдоль нижнего края проходит борозда ребра, sulcus costae (см. рис. ) , где залегают межреберные артерия, вена и нерв. Края ребер описывают спираль, поэтому ребро перекручено вокруг своей длинной оси.

рис. 38. Двенадцатое (XII) ребро, costa XII) правое. (Наружная поверхность.)

На переднем грудинном конце костной части ребра имеется ямка с небольшой шероховатостью; к ней прикрепляется реберный хрящ.

Как действует кинезио пластырь

Мышцы в организме человека не только выполняют опорно-двигательную функцию, но принимают активное участие в венозном кровообращении и движении лимфы. Поэтому любые повреждения мышечной ткани приводят к проблемам с кровообращением. Именно в связи с этим необходимо использовать такие методы лечения, которые бы гарантировали скорейшее восстановление после травмы.

Кинезио тейп — это эластичный пластырь для спортсменов, который изготавливают из натурального хлопка. Он имеет волнообразную структуру, и в дополнение есть слой который не вызывает аллергической реакции. Клей активируется только под воздействием температуры тела человека. Уникальная структура пластырей делает их очень похожими на человеческую кожу.

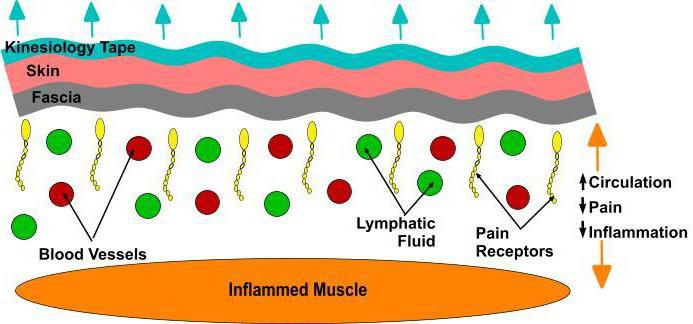
Воздействует тейп на микроскопическом уровне — он как бы приподнимает кожу над поврежденным участком, что существенно снижает давление и уменьшает болевой синдром. В результате воздействия улучшается кровообращение и лимфоток, что приводит к более быстрому рассасыванию гематом и опухолей.

После того как нанесен кинезио тейп, инструкция разрешает сохранять подвижный образ жизни, так как гарантируется интенсивная поддержка мышц. Все это при условии правильного нанесения, но с этим, как правило, сложностей не бывает.

Способы представления графа в информатике

Матрица смежности

Основная статья: Матрица смежности

Таблица, где как столбцы, так и строки соответствуют вершинам графа.
В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).

Это наиболее удобный способ представления плотных графов.

Недостатком являются требования к памяти, прямо пропорциональные квадрату количества вершин.

• Двумерный массив;
• Матрица с пропусками;
• Неявное задание (при помощи функции).

Матрица инцидентности

Основная статья: Матрица инцидентности

Таблица, где строки соответствуют вершинам графа, а столбцы соответствуют связям (рёбрам) графа.
В ячейку матрицы на пересечении строки i{\displaystyle i} со столбцом j{\displaystyle j} записывается:

1

в случае, если связь j{\displaystyle j} «выходит» из вершины i{\displaystyle i},

−1,

если связь «входит» в вершину,

во всех остальных случаях (то есть если связь является петлёй или связь не инцидентна вершине)

Данный способ является довольно ёмким (размер пропорционален |V||E|{\displaystyle |V||E|}) для хранения, поэтому применяется очень редко, в особых случаях (например, для быстрого нахождения циклов в графе).

Список смежности

Основная статья: Список смежности

Список, где каждой вершине графа соответствует строка, в которой хранится список смежных вершин. Такая структура данных не является таблицей в обычном понимании, а представляет собой «список списков».

Размер занимаемой памяти: O(|V|+|E|){\displaystyle O(|V|+|E|)}.

Это наиболее удобный способ для представления разреженных графов, а также при реализации базовых алгоритмов обхода графа в ширину или глубину, где нужно быстро получать «соседей» текущей просматриваемой вершины.

Список рёбер

Список, где каждому ребру графа соответствует строка, в которой хранятся две вершины, инцидентные ребру.

Размер занимаемой памяти: O(|E|){\displaystyle O(|E|)}.

Это наиболее компактный способ представления графов, поэтому часто применяется для внешнего хранения или обмена данными.

Языки описания

Для описания графов, пригодного для машинной обработки и одновременно удобного для человеческого восприятия, используется несколько стандартизированных языков, среди которых:

• DOT
• GraphML
• Trivial Graph Format
• GML
• GXL
• XGMML
• DGML

Программы для построения

Разработана серия коммерческих программ для построения графов, так, построение графов лежит в основе прикладных программных пакетов фирмы ILOG (с 2009 года принадлежит корпорации IBM), среди других программ — GoView, Lassalle AddFlow, LEDA (есть бесплатная редакция).

Также существует свободная программа для построения графов igraph и свободная библиотека Boost.

Программы для визуализации

Для визуализации графов применяются следующие программные средства:

• Graphviz (Eclipse Public License)
• LION Graph Visualizer.
• Графоанализатор — русскоязычная программа, с простым пользовательским интерфейсом (GNU LGPL; только для Windows).
• Gephi — графическая оболочка для представления и изучения графов (GNU GPL, CDDL).
• Библиотека GraphX — свободная библиотека для .NET для расчёта и отрисовки графов, использует WPF 4.0.
• Библиотека MSAGL — свободная библиотека для .NET.

М

• Макси-код μmax{\displaystyle \mu _{max}} — трудновычислимый полный инвариант графа, получаемый путём выписывания двоичных значений матрицы смежности в строчку с последующим переводом полученного двоичного числа в десятичную форму. Макси-коду соответствует такой порядок следования строк и столбцов, при котором полученное значение является максимально возможным.
• Максимальное паросочетание в графе. Паросочетание называется максимальным, если любое другое паросочетание содержит меньшее число рёбер.
• Маршрут в графе — чередующаяся последовательность вершин и рёбер v,e1,v1,e2,v2,…,ek,vk{\displaystyle v_{0},e_{1},v_{1},e_{2},v_{2},…,e_{k},v_{k}}, в которой любые два соседних элемента . Если v=vk{\displaystyle v_{0}=v_{k}}, то маршрут замкнут, иначе открыт.
• Матрица достижимости орграфа — матрица, содержащая информацию о существовании путей между вершинами в орграфе.
• Матрица инцидентности графа — матрица, значения элементов которой характеризуется инцидентностью соответствующих вершин графа (по вертикали) и его рёбер (по горизонтали). Для неориентированного графа элемент принимает значение 1, если соответствующие ему вершина и ребро инцидентны. Для графа элемент принимает значение 1, если инцидентная вершина является началом ребра, значение -1, если инцидентная вершина является концом ребра; в остальных случаях (в том числе и для ) значению элемента присваивается .
• Матрица смежности графа — матрица, значения элементов которой характеризуются смежностью вершин графа. При этом значению элемента матрицы присваивается количество рёбер, которые соединяют соответствующие вершины (то есть которые обоим вершинам). считается сразу двумя соединениями для вершины, то есть к значению элемента матрицы в таком случае следует прибавлять 2.
• Мини-код μmin{\displaystyle \mu _{min}} — трудновычислимый полный инвариант графа, получаемый путём выписывания двоичных значений матрицы смежности в строчку с последующим переводом полученного двоичного числа в десятичную форму. Мини-коду соответствует такой порядок следования строк и столбцов, при котором полученное значение является минимально возможным.
• Минимальный каркас (или каркас минимального веса, минимальное остовное дерево) графа — ациклическое (не имеющее циклов) множество рёбер в связном, взвешенном и неориентированном графе, соединяющих между собой все вершины данного графа, при этом сумма весов всех рёбер в нём минимальна.
• Множество смежности вершины v — множество вершин, смежных с вершиной v. Обозначается Γ+(v){\displaystyle \Gamma ^{+}(v)}.
• Минором графа называется граф, который можно получить из исходного путём удаления и стягивания дуг.
• Мост — , удаление которого увеличивает количество в графе.
• Мультиграф — граф, в котором может быть пара вершин, которая соединена более чем одним ребром (ненаправленным), либо более чем двумя дугами противоположных направлений.

Литература

• Оре О. Теория графов. — М.: Наука, 1968. — 336 с.
• Уилсон Р. Введение в теорию графов. — М.: Мир, 1977. — 208 с.
• Харари Ф. Теория графов. — М.: Мир, 1973.
• Кормен Т. М. и др. Часть VI. Алгоритмы для работы с графами // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: Вильямс, 2006. — С. 1296. — ISBN 0-07-013151-1.
• Салий В. Н., Богомолов А. М. Алгебраические основы теории дискретных систем. — М.: Физико-математическая литература, 1997. — ISBN 5-02-015033-9.
• Касьянов В. Н., Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение. — СПб.: БХВ-Петербург, 2003. — С. 1104. — ISBN 5-94157-184-4.
• Емеличев В. А., Мельников О. И., Сарванов В. И., Тышкевич Р. И. Лекции по теории графов. М.: Наука, 1990. 384с. (Изд.2, испр. М.: УРСС, 2009. 392 с.)
• Кирсанов М. Н. Графы в Maple. — М.: Физматлит, 2007. — 168 с. — ISBN 978-5-9221-0745-7.
• Графы // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 86-88. — 352 с.

Особенности двух первых и последних пар ребер

Некоторые особенности имеют две первые и две последние пары ребер. Первое ребро, costa prima (I) (см. рис. , А), короче, но шире остальных, имеет почти горизонтально расположенные верхнюю и нижнюю поверхности (вместо наружной и внутренней у других ребер). На верхней поверхности ребра, в переднем отделе, имеется бугорок передней лестничной мышцы, tuberculum m. scaleni anterioris. Кнаружи и сзади от бугорка лежит неглубокая борозда подключичной артерии, sulcus a. subclaviae, (след пролегающей здесь одноименной артерии, a. subclavia, кзади от которой находится небольшая шероховатость (место прикрепления средней лестничной мышцы, m. scalenus medius. Кпереди и кнутри от бугорка имеется слабо выраженная борозда подключичной вены, sulcus v. subclaviae. Суставная поверхность головки I ребра не разделена гребнем; шейка длинная и тонкая; реберный угол совпадает с бугорком ребра.

рис. 44. Грудной сегмент. Отношение рёбер к позвонку (IV) и грудине.

Второе ребро, costa secunda (II)) (см. рис. , Б), имеет на наружной поверхности шероховатость – бугристость передней зубчатой мышцы, tuberositas m. serrati anterioris, (место прикрепления зубца указанной мышцы).

Одиннадцатое и двенадцатое ребра, costa II et costa XII (см. рис. ), имеют не разделенные гребнем суставные поверхности головки. На XI ребре угол, шейка, бугорок и реберная борозда выражены слабо, а на III они отсутствуют.

Заболевания ребер

Существует не менее сотни различных видов и подвидов болезней, которые так или иначе затрагивают костную систему и грудную клетку. Но самый распространенный фактор повреждения – переломы.

Перелом ребер

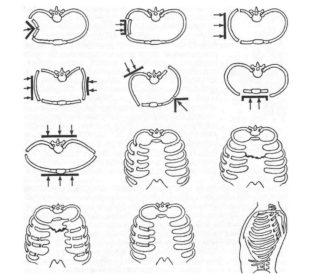Механизмы переломов ребер

Чаще всего от перелома страдают люди пожилого возраста, так как кости к старости изнашиваются, становятся пористыми, а хрящи утрачивают смягчающие функции. Провоцируют переломы падения, удары, сильные сдавливания грудной клетки.

Перелом обычно происходит в боковой поверхности грудной клетки, в точке наибольшего изгиба. Именно в этой зоне возникает болезненность. Если была получена травма, симптомы могут проявиться через некоторое время, когда обломки костей начинают тереться о внутренние органы.

Иногда происходит надлом костей, который провоцируют некоторые заболевания, уменьшающие прочность тканей:

• опухоли грудной клетки;
• остеопороз, при котором из костей вымываются соли кальция;
• туберкулез ребер;
• хроническое воспаление тканей;
• заболевания крови.

Часто происходит неосложненный перелом, при котором кости просто ломаются, не образуя осколков. Однако опасность для организма все еще сохраняется:

• нарушается дыхание;
• повреждаются органы, расположенные в зоне перелома;
• развиваются осложнения, в том числе в виде защемления нервных окончаний.

Аномалии развития

Патологией, которой подверженная реберная система, является наличие шейного ребра с обеих или одной стороны. Они крепятся к 6 шейному позвонку, что провоцирует боли, головокружения и другие симптомы, связанные с работой головного мозга и нервной системы. Также к аномалиям относятся врожденные костные островки, но они реже вызывают неблагоприятные симптомы.

Хондрит и остеомиелит

Симптомы хондрита схожи с проявлением остеомиелита

Остеомиелит относится к тяжелым инфекционным воспалениям, которые переносятся током крови. Развивается на фоне травм в детском возрасте, когда повреждаются первые 3 реберные пары. Сопровождается воспаление острыми симптомами:

• потливостью и ознобом;
• бледностью;
• слабостью;
• температурой.

Хондрит также относится к воспалительным заболеваниям, его симптомы нередко схожи с проявлением остеомиелита.

Туберкулез костей и сифилис

Туберкулезное поражение грудины

Туберкулез реберной системы обычно развивается на фоне аналогичного заболевания в легких. Обнаруживается припухлость в области поврежденных участков, болезненность, формируются свищи. По мере прогрессирования на костях нарастают кисты, начинается разрушение тканей.

Сифилис в ребрах встречается очень редко и сопровождается аналогичными туберкулезу симптомами. Подтвердить наличие болезней можно путем рентгена грудной клетки и бактериологического исследования.

Паразиты и грибки

Ребра могут сильно пострадать от паразитных заболеваний и грибков. Наиболее распространенный грибок – актиномикоз, распространяющийся вглубь тканей с органов или снаружи. Происходит деформация ребер, развиваются симптомы периостита – воспаляется надкостница. Все это сопровождается сильной болью и дискомфортом в верхней части туловища.

Заболевание Титца

Торакохондралгия, или болезнь Титца сопровождается формированием веретенообразных уплотнений на первых 6 парах ребер. Болезнь поражает хрящевые окончания костных структур. Возникает острая боль, усиливающаяся при кашле или глубоком дыхании. Также при заболевании могут встречаться небольшие изолированные очаги и припухлости.

Коарктация аорты и рахит

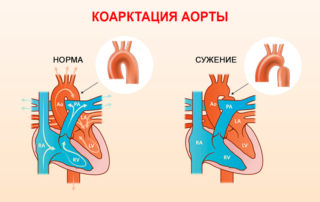Рахит возникает из-за недостатка витамина Д, а также при нарушениях обмена веществ, вызванных дефицитом этого микроэлемента. Патологические изменения затрагивают нижние конечности и череп. Дополнительно у пациента диагностируется потливость, недостаток кальция и фосфора в крови. У детей астенического телосложения в реберных частях могут пальпироваться уплотнения, где кости переходят в хрящи.

При коарктации аорты диагностируется врожденная аномалия сосуда, выходящего из сердца. Нисходящая часть аорты будет суженной, из-за чего нижний край ребер становится неровным, так как артерии приобретают расширенный вид и извилистость.

Злокачественные процессы

Онкологические заболевания ребер встречаются очень редко и выступают следствием распространения метастазов из других органов. Однако в некоторых случаях болезнь может протекать без первичных признаков. К онкологическим заболеваниям относят остеомы, остеобластомы и остеосаркомы. Сопровождаются злокачественные процессы периодическими сильными болями, внезапными переломами. Пациент чувствует себя плохо, возникает апатия и сильная слабость.

Перелом ребра: симптомы и лечение, как спать

Перелом ребра вызывается физическим воздействием на грудную клетку.

По данным статистики такие травмы наблюдаются у 70% людей, обращающихся к травматологу по поводу подозрения на повреждение грудной клетки, и у 16% пациентов с переломами.

Чаще нарушается целостность IV-VII ребра и этот факт объясняется тем, что в области их расположения нет корсета из мышц, который защищает остальные ребра, и они не обладают такой гибкостью как нижерасположенные.

Тяжесть травм ребер во многом зависит от разновидности перелома и наличия повреждений окружающих его тканей и органов. Почти в 60% случаев такие травмы сопровождаются поражениями легких, плевры, пищевода, печени, сосудов и сердца. Они являются наиболее тяжелыми и могут вызывать летальный исход.

Опасными считаются и такие переломы, которые сопровождаются нарушением целостности нескольких ребер или множественными разломами. В таких случаях вероятность развития тяжелых осложнений значительно увеличивается.

Простые травмы ребер обычно срастаются самостоятельно и не представляют опасности для здоровья и жизни больного.

Повреждения ребер чаще наблюдаются у взрослых (особенно у пожилых людей), т. к. детская грудная клетка более эластична и менее подвержена таким травмам. В этой статье мы ознакомим вас с причинами, разновидностями, симптомами, способами оказания первой помощи пострадавшему, методами лечения переломов ребер и особенностями постельного режима и сна при таких травмах.

П

• Паросочетание — набор попарно несмежных рёбер.
• Петля — ребро, начало и конец которого находятся в одной и той же вершине.
• Пересечение графов (помеченных графов G1=(X1,U1){\displaystyle G_{1}=(X_{1},U_{1})} и G2=(X2,U2){\displaystyle G_{2}=(X_{2},U_{2})}) — граф G1∩G2{\displaystyle G_{1}\cap G_{2}}, множеством вершин которого является X1∩X2{\displaystyle X_{1}\cap X_{2}}, а множеством рёбер — U=U1∩U2{\displaystyle U=U_{1}\cap U_{2}}.
• Перечисление графов — подсчёт числа неизоморфных графов в заданном классе (с заданными характеристиками).
• Периферийная вершина — вершина, эксцентриситет которой равен диаметру графа.
• Планарный граф — граф, который может быть изображён () на плоскости без пересечения рёбер. плоскому графу, то есть является графом с пересечениями, но допускающий его плоскую укладку, поэтому может отличаться от изображением на плоскости. Таким образом, может быть разница между плоским графом и планарным графом при изображении на плоскости.
• Плоский граф — , в котором никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершины (не пересекаются). Является графом на плоскости.
• Подграф исходного графа — граф, содержащий некое подмножество вершин данного графа и некое подмножество им рёбер. (ср. .) По отношению к подграфу исходный граф называется
• Полный граф — граф, в котором для каждой пары вершин v1,v2{\displaystyle v_{1},v_{2}}, существует ребро, инцидентное v1{\displaystyle v_{1}} и инцидентное v2{\displaystyle v_{2}} (каждая вершина соединена ребром с любой другой вершиной).
• Полный инвариант графа — числовая характеристика графа или их упорядоченный вектор, значения которой необходимо и достаточно для установления графов.
• Полным двудольным называется , в котором каждая вершина одного подмножества соединена ребром с каждой вершиной другого подмножества
• Полустепень захода в для вершины v{\displaystyle v} — число дуг, входящих в вершину. Обозначается d+(v){\displaystyle d^{+}(v)}, deg+(v){\displaystyle \mathrm {deg} ^{+}(v)}, indeg(v){\displaystyle \mathrm {indeg} (v)} или dt(v){\displaystyle d_{t}(v)}.
• Полустепень исхода в для вершины v{\displaystyle v} — число дуг, исходящих из вершины. Обозначается d−(v){\displaystyle d^{-}(v)}, deg−(v){\displaystyle \mathrm {deg} ^{-}(v)}, outdeg(v){\displaystyle \mathrm {outdeg} (v)} или do(v){\displaystyle d_{o}(v)}.
• Помеченный граф — граф, вершинам или дугам которого присвоены какие-либо метки, например, натуральные числа или символы какого-нибудь алфавита.
• Порождённый подграф — подграф, порождённый множеством рёбер исходного графа. Содержит не обязательно все вершины графа, но эти вершины соединены такими же рёбрами, как в графе.
• Порядок графа — количество вершин графа.
• Правильная раскраска графа — раскраска, при которой каждый цветной класс является независимым множеством. Иначе говоря, в правильной раскраске любые две смежные вершины должны иметь разные цвета.
• Произведение графов — для данных графов G1=(V1,E1){\displaystyle G_{1}=(V_{1},E_{1})} и G2=(V2,E2){\displaystyle G_{2}=(V_{2},E_{2})} произведением называется граф G=(V,E){\displaystyle G=(V,E)}, вершины которого V(G)=V1×V2{\displaystyle V(G)=V_{1}\times V_{2}} — декартово произведение множеств вершин исходных графов.
• Простая цепь — , в котором все вершины различны.
• Простой граф — , в котором нет и .
• Простой путь — , все вершины которого попарно различны

  Простой цикл — цикл, не проходящий дважды через одну вершину.

  . Другими словами, простой путь не проходит дважды через одну вершину.

• Псевдограф — граф, который может содержать и/или кратные рёбра.
• Пустой граф (вполне несвязный граф, нуль-граф) — степени 0, то есть граф, не содержащий .
• Путь — последовательность (в неориентированном графе) и/или дуг (в ориентированном графе), такая, что конец одной дуги (ребра) является началом другой дуги (ребра). Или последовательность вершин и дуг (рёбер), в которой каждый элемент инцидентен предыдущему и последующему. Может рассматриваться как частный случай .
• Путь в орграфе — последовательность вершин v₁, v₂, …, v_n, для которой существуют дуги v₁ → v₂, v₂ → v₃, …, v_n-1 → v_n. Говорят, что этот путь начинается в вершине v₁, проходит через вершины v₂, v₃, …, v_n-1, и заканчивается в вершине v_n.

В словаре Ожегова

РЕБРО, -а, мн. ребра, ребер, ребрам, ср. 1. Одна из нескольких парных дугообразных плоских костей, идущих от позвоночника к грудной кости и составляющих грудную клетку. Грудинные ребра. Шейное р. Поясничное р. Одни ребра остались у кого-н. (перен.: очень исхудал; разг.). Пересчитать ребра кому-н. (перен.: поколотить;прост.). 2. В геометрии: отрезок прямой, лежащий на пересечении двух граней многогранника. 3. Узкий край или сторона предмета. Поставить доску на р. 4. Дугообразно изогнутая скрепляющая часть остова какого-н. сооружения (спец.). 4- Поставить вопрос ребром (разг.) — заявить о чем-н. со всей решительностью. || умелый. ребрышко, -а, ср. (к 1 знач.). || прил. реберный, -ая, -ое (к 1 знач.) и ребровый, -ая, -ое (ко 2 и 3 знач.; спец.).

Возрастные изменения

Врожденная патология искривления грудной клетки

С рождения и до старости ребра человека претерпевают множество изменений. У младенцев задний и боковой размер грудины гораздо больше фронтального, что обеспечивает удобство при передвижении ползком. В младенчестве кости грудины расположены горизонтально, и меняются они только с возрастом почти до вертикального положения.

Наиболее уязвимый отдел позвоночника – грудной. Это и сказывается на некоторых патологиях ребер, связанных с деформацией каркаса. Избежать возрастных изменений невозможно в полной мере, но можно сохранить здоровье позвоночника, если умеренно работать и отдыхать, вести здоровый образ жизни и делать зарядку. Сюда же относится отказ от вредных привычек и правильное питание.

Что такое ребра и вершины куба ? Определение.

Срооочно пж Сравните a и –b, если a и b отрицательные числа. 15+26:54 як це порахувати ​ Пж сроооочноо Найдите наибольшее целое число, при котором выполняется неравенство: x ≤ −64,4 Срочно!!! Оба задания! Помогите, пожалуйста!!! Вася записал пример (смотри рисунок).Петя придумал,как превратить этот пример в верное равенство. Он решил отразить весь пример целиком зеркально (сим метрично).Как следует отражать?а)один раз по горизонтали,б)один раз по вертикали в)сначала по горизонтали,а потом-по вертикали г)сначала по вертикали,а затем-по горизонтали. Д)два раза подряд по вертикали Это не школьный вопрос,но кто нибудь может знает ответ.. Короче,я боюсь лазить по разным сайтам,что бы не подключить не дай бог какую нибудь подписку Так вот,каждый раз когда мне дожили деньги на телефон,через минуту деньги куда-то пропали,причём какая только это сумма не была,снимались деньги,и оставались ровно 3 рубля Так я потеряла 169 рубле, оказалось,деньги списывал номер 9836,кого нибудь знает как вернуть деньги*подписку мне отключили* Помогите пожалуйста Укажите слово, где неверно выделен корень.Варианты ответов•ВОДяной•УЧЕНИК•БЕЛизна•СЛОН​ Знайдіть відстань між точками а (-2;3) і В (4;5) Помогите пожалуйста​ Помогите решить пож 1) tg72-ctg48/1+tg72*ctg48 2)cos 20 (градус.)-sin 20 (град.)

Р

• Радиус графа — минимальный из эксцентриситетов вершин связного графа; вершина, на которой достигается этот минимум, называется центральной вершиной.
• Разбиение графа — представление исходного графа в виде множества подмножеств вершин по определённым правилам.
• Разделяющая вершина — то же, что и и .
• Развёртка графа — функция, заданная на вершинах ориентированного графа.
• Размеченный граф — граф, для которого задано множество меток S, функция разметки вершин f : A → S и функция разметки дуг g : R → S. Графически эти функции представляются надписыванием меток на вершинах и дугах. Множество меток может разделяться на два непересекающихся подмножества меток вершин и меток дуг. См. Размеченный граф.
• Разрез — множество , удаление которого делает граф .
• Рамочный граф — граф, который можно нарисовать на плоскости таким способом, что любая ограниченная грань является четырёхугольником и любая вершина с тремя и менее соседями инцидентна неограниченной грани.
• Раскраска графа — разбиение вершин на множества (называемые цветами). Если при этом нет двух смежных вершин, принадлежащих одному и тому же множеству (то есть две смежные вершины всегда разного цвета), то такая раскраска называется правильной.
• Расстояние между вершинами — длина кратчайшей цепи (в орграфе пути), соединяющей заданные вершины. Если такой цепи (пути) не существует, расстояние полагается равным бесконечности.
• Рёберное покрытие — множество рёбер графа такое, что каждая вершина инцидентна хотя бы одному ребру из этого множества.
• Рёберный граф неориентированного графа — это граф, представляющий соседство рёбер графа.
• Ребро — базовое понятие. Ребро соединяет две графа.
• Регулярный граф — граф, всех вершин которого равны. Степень регулярности является инвариантом графа и обозначается r(G){\displaystyle r(G)}. Для нерегулярных графов r(G){\displaystyle r(G)}

  Регулярный граф степени 0 (вполне несвязный граф, пустой граф, нуль-граф) — граф без рёбер.

  не определено. Регулярные графы представляют особую сложность для многих алгоритмов.

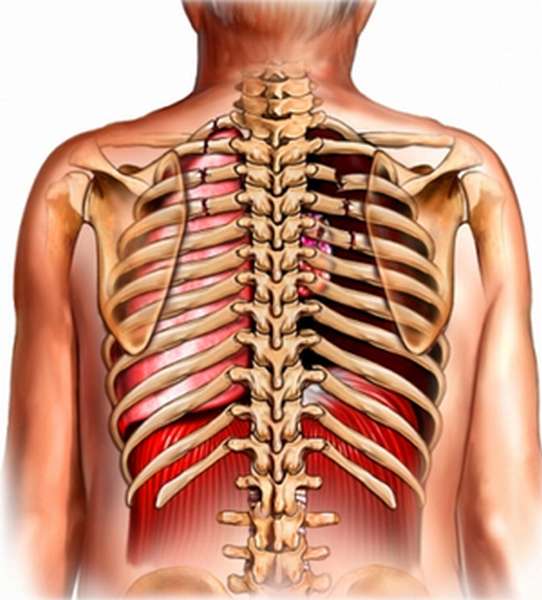
Строение и функции ребер

Согласно утверждениям анатомов, ребра – это изогнутые узкие пластинки, тело которых имеет наружную (выпуклую) и внутреннюю (вогнутую) поверхности, ограниченные острым и закругленным краями. Нервы и сосуды находятся в борозде, находящейся на внутренней поверхности нижнего края.

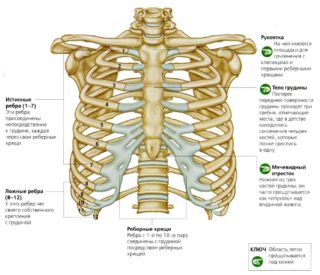
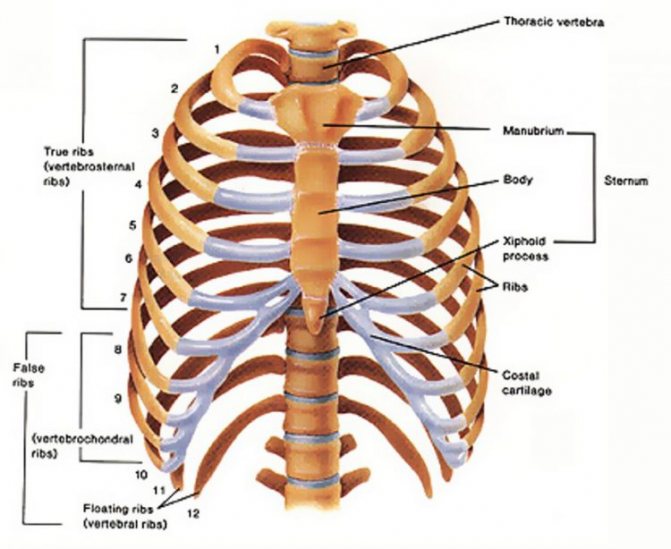
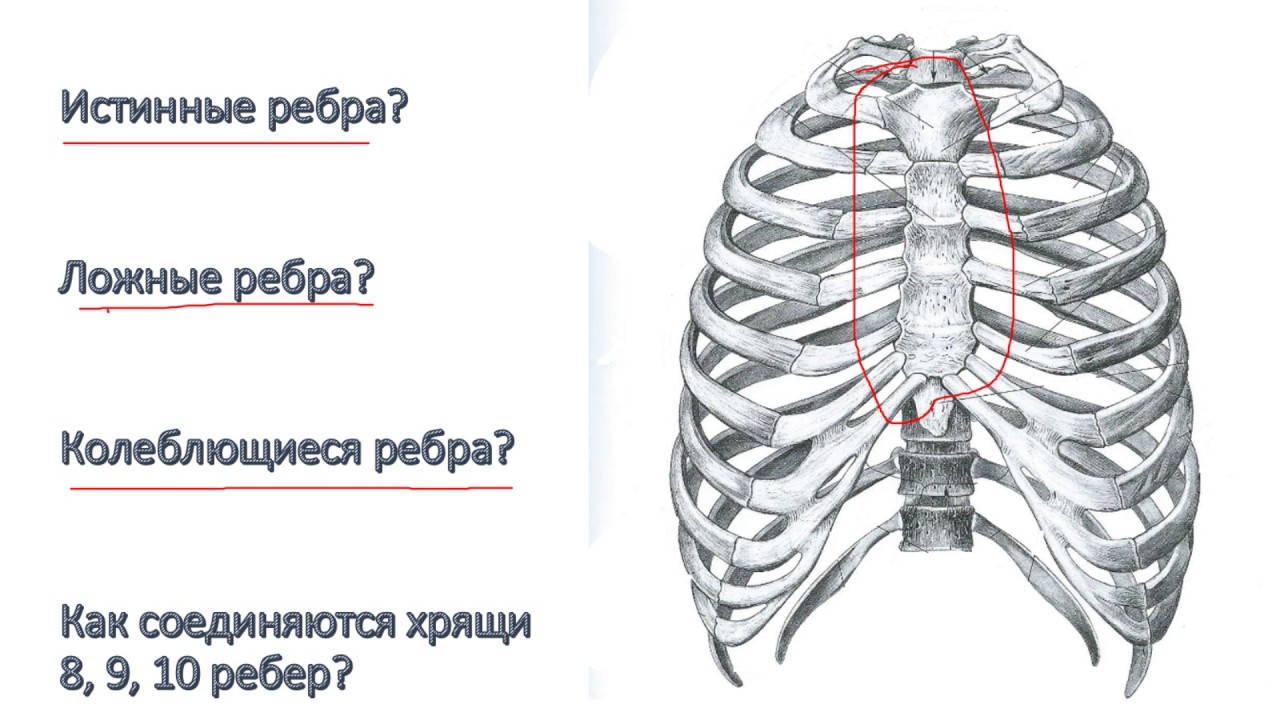
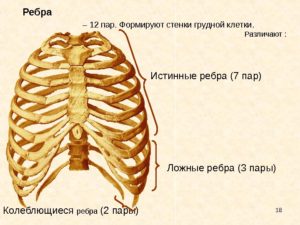
Человеческий организм имеет двадцать четыре ребра (по двенадцать на каждой стороне). По способу крепления эти кости разделяются на 3 группы:

• 2 нижних (колеблющихся) ребра, передние концы которых лежат свободно;
• 3 ложных ребра, которые своими хрящами соединены с хрящом последнего верхнего ребра;
• 7 верхних (истинных) ребер, которые передними концами крепятся к грудине.

Главными функциями ребер являются:

• Каркасная функция. С помощью грудной клетки, легкие и сердце на протяжении всей жизни находятся в одном и том же положении.
• Защитная функция. Вышеуказанные пластинки, образуя грудную клетку, защищают крупные сосуды, легкие и сердце от внешних воздействий и травм.

Н

• Направленный граф —

  Направленный ациклический граф — ориентированный граф без контуров.

  , в котором две вершины соединяются не более чем одной дугой.

• Независимое множество вершин (известное также как внутренне устойчивое множество) — множество вершин графа G, в котором любые две вершины несмежны (никакая пара вершин не соединена ребром).
  • Независимое множество называется максимальным, когда нет другого независимого множества, в которое оно бы входило. Дополнение наибольшего независимого множества называется минимальным вершинным покрытием графа.
  • Наибольшим независимым множеством называется независимое множество наибольшего размера.
• Независимые вершины — попарно несмежные вершины графа.
• Неразделимый граф — связный, непустой, не имеющий точек сочленения граф..
• Нормированный граф — без .
• Нуль-граф (вполне несвязный граф, пустой граф) — степени 0, то есть граф, не содержащий .