Механическое движение. траектория. путь. перемещение

Вектор перемещения

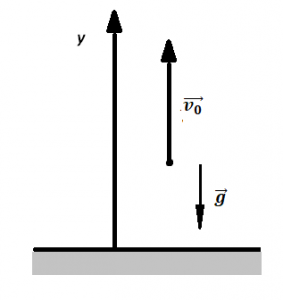
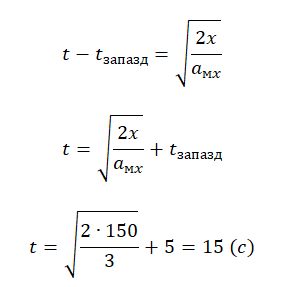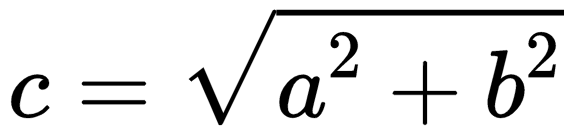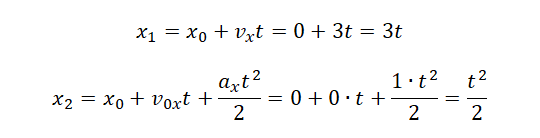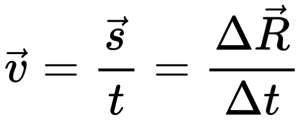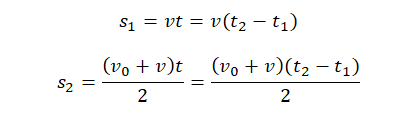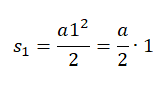Вектор перемещения (или просто перемещение) – это
направленный отрезок прямой, соединяющий начальное положение тела с его последующим
положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен
от начальной точки движения к конечной.

Модуль вектора перемещения (то есть длина отрезка, который соединяет
начальную и конечную точки движения) может быть равен пройденному пути или быть
меньше пройденного пути. Но никогда модуль вектора перемещения не может быть
больше пройденного пути.

Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией
(см. разделы Траектория и
), например,
если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора
перемещения меньше пройденного пути, когда материальная точка движется по
криволинейной траектории (рис. 1.1).

Рис. 1.1. Вектор перемещения и пройденный путь.

На рис. 1.1:

Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка
начала движения совпадёт с точкой конца движения и тогда вектор перемещения
будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом,
путь и перемещение – это два разных понятия.

Правило сложения векторов

Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).

Рис. 1.2. Сложение векторов перемещений.

На рис 1.2 показаны правила сложения векторов S1 и S2:

а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма

Траектория. Путь. Перемещение

Подробности

Просмотров: 469

«Физика — 10 класс»

Чем отличаются векторные величины от скалярных?

Линия, по которой движется точка в пространстве, называется траекторией.

В зависимости от формы траектории все движения точки делятся на прямолинейные и криволинейные.

Если траекторией является прямая линия, движение точки называется прямолинейным, а если кривая — криволинейным.

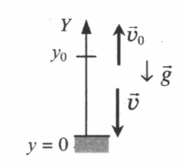
Пусть в какой-то момент времени движущаяся точка занимает положение М₁ (рис. 1.7, а). Как найти её положение спустя некоторый промежуток времени после этого момента?

Допустим, известно, что точка находится на расстоянии l относительно своего начального положения. Сможем ли мы в этом случае однозначно определить новое положение точки? Очевидно, нет, поскольку есть бесчисленное множество точек, которые удалены от точки М₁ на расстояние l. Чтобы однозначно определить новое положение точки, надо ещё знать, в каком направлении от точки М₁ следует отложить отрезок длиной l.

Таким образом, если известно положение точки в какой-то момент времени, то найти её новое положение можно с помощью определённого вектора (рис. 1.7, б).

Вектор, проведённый из начального положения точки в её конечное положение, называется вектором перемещения или просто перемещением точки

Поскольку перемещение — величина векторная, то перемещение, показанное на рисунке (1.7, б), можно обозначить

Покажем, что при векторном способе задания движения перемещение можно рассматривать как изменение радиус-вектора движущейся точки.

Пусть радиус-вектор ₁ задаёт положение точки в момент времени t₁, а радиус-вектор ₂ — в момент времени t₂ (рис. 1.8). Чтобы найти изменение радиус-вектора за промежуток времени Δt = t₂ — t₁, надо из конечного вектора ₂ вычесть начальный вектор ₁. Из рисунка 1.8 видно, что перемещение, совершённое точкой за промежуток времени Δt, есть изменение её радиус-вектора за это время. Следовательно, обозначив изменение радиус-вектора через Δ , можно записать: Δ = ₁ — ₂.

Путь s — длина траектории при перемещении точки из положения М₁ в положение М₂.

Модуль перемещения может быть не равен пути, пройденному точкой.

Например, на рисунке 1.8 длина линии, соединяющей точки М₁ и М₂, больше модуля перемещения: s > |Δ|. Путь равен перемещению только в случае прямолинейного однонаправленного движения.

Перемещение тела Δ — вектор, путь s — скаляр, |Δ| ≤ s.

Следующая страница «Равномерное прямолинейное движение. Скорость. Уравнение движения»

Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»

Кинематика — Физика, учебник для 10 класса — Класс!ная физика

Физика и познание мира —
Что такое механика —
Механическое движение. Система отсчёта —
Способы описания движения —
Траектория. Путь. Перемещение —
Равномерное прямолинейное движение. Скорость. Уравнение движения —
Примеры решения задач по теме «Равномерное прямолинейное движение» —
Сложение скоростей —
Примеры решения задач по теме «Сложение скоростей» —
Мгновенная и средняя скорости —
Ускорение —
Движение с постоянным ускорением —
Определение кинематических характеристик движения с помощью графиков —
Примеры решения задач по теме «Движение с постоянным ускорением» —
Движение с постоянным ускорением свободного падения —
Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» —
Равномерное движение точки по окружности —
Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение —
Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями —
Примеры решения задач по теме «Кинематика твёрдого тела»

Проекции вектора перемещения

При решении задач по физике часто используют проекции вектора перемещения на координатные оси.
Проекции вектора перемещения на координатные оси могут быть выражены через разности
координат его конца и начала. Например, если материальная точка переместилась из точки
А в точку В, то при этом вектор перемещения

(рис. 1.3).

Выберем ось ОХ так, чтобы вектор

лежал с этой осью в одной плоскости.
Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения)
до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х.
Обозначим проекции точек А и В соответственно А_x и В_x. Длина отрезка
А_xВ_x на оси
ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть

Sx = AxBx

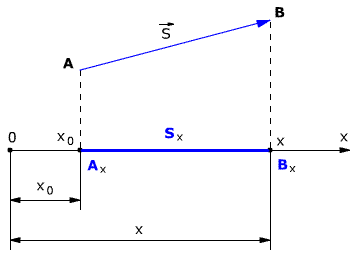Рис. 1.3. Проекция вектора перемещения.

Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть

Sx = x – x

Sy = y – y
Sz = z – z

Здесь x, y, z — начальные координаты, или координаты начального
положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего
положения тела (материальной точки).

Проекция вектора перемещения считается положительной, если направление вектора и
направление координатной оси совпадают (как на рис 1.3). Если направление вектора и
направление координатной оси не совпадают (противоположны), то проекция вектора
отрицательна (рис. 1.4).

Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого
Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен
нулю (рис. 1.4).

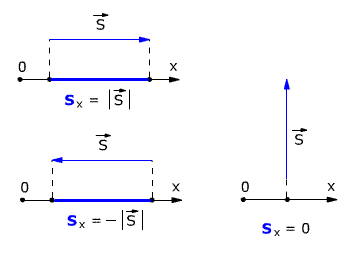Рис. 1.4. Модули проекции вектора перемещения.

Разность между последующим и начальным значениями какой-нибудь величины называется
изменением этой величины. То есть проекция вектора перемещения на координатную ось
равна изменению соответствующей координаты. Например, для случая, когда тело перемещается
перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело
НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.

Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с
координатами х и у, то есть А(х, у).
Конечное положение тела – точка В с координатами х и у, то есть В(х, у).
Найдём модуль перемещения тела.

Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).

Рис. 1.5. Движение тела на плоскости.

Определим проекции вектора перемещения на осях ОХ и OY:

Sx = x – x
Sy = y – y

На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при
решении задачи может использоваться теорема Пифагора, с помощью которой
можно найти модуль вектора перемещения, так как

АС = sx
CB = sy

По теореме Пифагора

S2 = Sx2 + Sy2

Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:

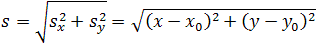
Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько
примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат
и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев
(скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках
вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и
дробная части должны разделяться точкой, например, 10.5.

Вектор перемещения

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.

Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.

Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и ), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).

Рис. 1.1. Вектор перемещения и пройденный путь.

На рис. 1.1:

Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.

Правило сложения векторов

Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).

Рис. 1.2. Сложение векторов перемещений.

На рис 1.2 показаны правила сложения векторов S1 и S2:

а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма

Понятие о пути

Что такое путь в физике? Это величина, равная длине отрезка в пространстве, который преодолело в ходе своего движения изучаемое тело. Чтобы вычислить путь, необходимо знать не только начальное и конечное положения тела, но и траекторию его перемещения. На вопрос о том, что такое путь в физике, можно ответить иначе. Под этой величиной понимают длину траектории, то есть воображаемой линии, по которой тело перемещалось.

Для обозначения пути используют разные символы. Так, если речь идет об одномерном перемещении, то могут использовать символ Δx, где Δ означает изменение координаты x. Кроме этого символа, часто для обозначения рассматриваемой величины пользуются буквами s, l и h, причем две последние означают длину и высоту соответственно. Таким образом, в кинематике чаще всего для обозначения пути можно встретить букву s.

Если известно, что тело перемещается по прямой в трехмерном пространстве, а также известны координаты его положения начального (x; y; z) и конечного (x₁; y₁; z₁), тогда путь можно определить по формуле:

Формулы кинематики

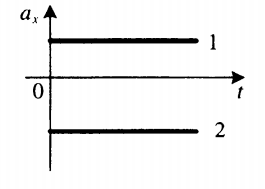
Рассмотрев, как обозначается путь в физике и что собой эта величина представляет, приведем пару формул кинематики, которые применяются для вычисления изучаемой характеристики движения. Это следующие формулы:

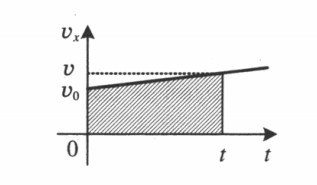
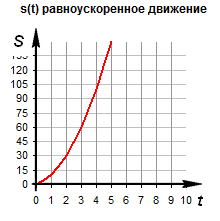
Здесь первое выражение соответствует ситуации, когда тело равномерно прямолинейно перемещается со скоростью v в течение времени t. Второе выражение справедливо для равноускоренного перемещения, где символами v и a обозначены начальная скорость и ускорение соответственно. Знак «плюс» следует использовать, если тело ускоряется, а знак «минус» — если оно замедляет свою скорость.

Сходство и различие.

Путь и перемещение – это не одно и то же. Если движение происходит на плоскости или в пространстве и криволинейно, то длина траектории всегда будет больше модуля перемещения. Происходит этот потому, что вектор является прямой, то есть, кратчайшим расстоянием между двумя точками. Криволинейная траектория же прямой не является.

Более того, перемещение может быть равно нулю, несмотря на то, что путь будет иметь большую длину. Например, планеты, двигаясь по окружностям, проходят за каждый оборот большой путь, однако, перемещение при этом никогда не превышает диаметра орбиты, и может быть равно нулю, если планета делает полный оборот.

Рис. 3. Орбиты планет.

Однако, и перемещение и траектория пути служат одной и той же цели – описанию движения. Обе этих величины измеряются в единицах длины, к обоим могут быть применены формулы движения.

Но, если траектория описывает весь путь, пройденный телом, то перемещение акцентирует внимание на разнице положения тела между первым и последним моментами движения. Поэтому большинство формул в кинематике, в которые входит время, работают именно с перемещением

Единственный случай, когда путь и перемещение равны – это случай прямолинейного движения, при условии, что скорость движения не меняла знак.

Что мы узнали?

Траектория пути – это линия, вдоль которой перемещалось тело во время своего движения. Перемещение – это вектор, направленный из точки начала движения в точку конца движения. Длина пути всегда равна или больше, чем длина перемещения.

Тест по теме

1. Вопрос 1 из 5

Начать тест(новая вкладка)

Понятие о пути

Что такое путь в физике? Это величина, равная длине отрезка в пространстве, который преодолело в ходе своего движения изучаемое тело. Чтобы вычислить путь, необходимо знать не только начальное и конечное положения тела, но и траекторию его перемещения. На вопрос о том, что такое путь в физике, можно ответить иначе. Под этой величиной понимают длину траектории, то есть воображаемой линии, по которой тело перемещалось.

Для обозначения пути используют разные символы. Так, если речь идет об одномерном перемещении, то могут использовать символ Δx, где Δ означает изменение координаты x. Кроме этого символа, часто для обозначения рассматриваемой величины пользуются буквами s, l и h, причем две последние означают длину и высоту соответственно. Таким образом, в кинематике чаще всего для обозначения пути можно встретить букву s.

Если известно, что тело перемещается по прямой в трехмерном пространстве, а также известны координаты его положения начального (x; y; z) и конечного (x₁; y₁; z₁), тогда путь можно определить по формуле:

Формулы кинематики

Рассмотрев, как обозначается путь в физике и что собой эта величина представляет, приведем пару формул кинематики, которые применяются для вычисления изучаемой характеристики движения. Это следующие формулы:

Здесь первое выражение соответствует ситуации, когда тело равномерно прямолинейно перемещается со скоростью v в течение времени t. Второе выражение справедливо для равноускоренного перемещения, где символами v и a обозначены начальная скорость и ускорение соответственно. Знак «плюс» следует использовать, если тело ускоряется, а знак «минус» — если оно замедляет свою скорость.

Проекции вектора перемещения

При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения (см.рис. 1.3).

Выберем ось ОХ так, чтобы вектор лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно А_x и В_x. Длина отрезка А_xВ_x на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть

Sx = AxBx

Рис. 1.3. Проекция вектора перемещения.

Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть

Sx = x – x

Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:

Sy = y – y
Sz = z – z

Здесь x, y, z — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).

Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).

Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).

Рис. 1.4. Модули проекции вектора перемещения.

Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.

Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х и у, то есть А(х, у). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.

Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).

Рис. 1.5. Движение тела на плоскости.

Определим проекции вектора перемещения на осях ОХ и OY:

Sx = x – x
Sy = y – y

На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как

АС = sx
CB = sy

По теореме Пифагора

S2 = Sx2 + Sy2

Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:

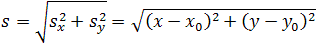
Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.

Что такое точка отсчета? Что такое механическое движение?

Andreus-папа-ndrey

Механи́ческим движе́нием тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики. Раздел механики, описывающий геометрические свойства движения без учёта причин, его вызывающих, называется кинематикой
В более общем значении движением называется любое пространственное или временное изменение состояния физической системы. Например, можно говорить о движении волны в среде.
Механическое движение можно рассматривать для разных механических объектов:
* Движение материальной точки полностью определяется изменением её координат во времени (например, двух на плоскости) . Изучением этого занимается кинематика точки.
o Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна эта прямой)
o Криволинейное движение это движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности) .
* Движение твёрдого тела складывается из движения какой-либо его точки (например, центра масс) и вращательного движения вокруг этой точки. Изучается кинематикой твёрдого тела.
o Если вращение отсутствует, то движение называется поступательным и полностью определяется движением выбранной точки. Заметим, что при этом оно не обязательно является прямолинейным.
o Для описания вращательного движения — движения тела относительно выбранной точки, например закреплённого в точке, используют Углы Эйлера. Их количество в случае трёхмерного пространства равно трём.
o Также для твёрдого тела выделяют плоское движение — движение, при котором траектории всех точек лежат в параллельных плоскостях, при этом оно полностью определяется одним из сечений тела, а сечение тела положением любых двух точек.
* Движение сплошной среды. Здесь предполагается, что движение отдельных частиц среды довольно независимо друг от друга (обычно ограничено лишь условиями непрерывности полей скорости) , поэтому число определяющих координат бесконечно (неизестными становятся функции) .
Относительность — зависимость механического движения тела от системы отсчёта, не указав систему отсчёта — не имеет смысла говорить о движении.

Даниил юрьев

Виды механического движения
Механическое движение можно рассматривать для разных механических объектов:
Движение материальной точки полностью определяется изменением её координат во времени (например, для плоскости — изменением абсциссы и ординаты). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.
Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна этой прямой)
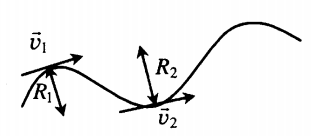
Криволинейное движение — движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности).
Движение твёрдого тела складывается из движения какой-либо его точки (например, центра масс) и вращательного движения вокруг этой точки. Изучается кинематикой твёрдого тела.
Если вращение отсутствует, то движение называется поступательным и полностью определяется движением выбранной точки. Движение при этом не обязательно является прямолинейным.
Для описания вращательного движения — движения тела относительно выбранной точки, например закреплённого в точке, — используют Углы Эйлера. Их количество в случае трёхмерного пространства равно трём.
Также для твёрдого тела выделяют плоское движение — движение, при котором траектории всех точек лежат в параллельных плоскостях, при этом оно полностью определяется одним из сечений тела, а сечение тела — положением любых двух точек.
Движение сплошной среды. Здесь предполагается, что движение отдельных частиц среды довольно независимо друг от друга (обычно ограничено лишь условиями непрерывности полей скорости), поэтому число определяющих координат бесконечно (неизвестными становятся функции).