Производная в других разделах математики
Производные в комплексном анализе
Основная статья: Моногенная функция
В комплексном анализе (анализе функций комплексных переменных), центральными объектами изучения являются голоморфные функции, которые являются комплекснозначными функциями на плоскости комплексных чисел и удовлетворяющие соответственно расширенному определению дифференцируемости.
Основная статья: Инвариант Шварца
Производная Шварца описывает, как комплексная функция аппроксимируется дробно-линейным отображением, аналогично тому, как обычная производная описывает, как функция аппроксимируется линейным отображением.
Производные в алгебре и алгебраической геометрии
Дифференцирование в общей алгебре — это линейное отображение на кольце или алгебре, которое удовлетворяет закону Лейбница (правилу произведения). Они изучаются в чистой алгебраической постановке в дифференциальной теории Галуа, но также появляются во многих других областях, где они часто употребляются с менее строгими алгебраическими определениями производных.
В алгебраической геометрии кэлеров дифференциал позволяет расширить определение внешней производной на произвольные алгебраические многообразия, вместо просто гладких многообразий.
Другие обобщения
Вполне можно скомбинировать два или больше различных понятий расширения или абстракции простой производной. Например, в геометрии Финслера изучаются пространства, которые локально выглядят как банаховы пространства. Таким образом можно создать производную с некоторыми особенностями функциональной производной и ковариантной производной.
В области квантовых групп q{\displaystyle q}-производная — это <span class=»mwe-math-element»><span class=»mwe-math-mathml-inline mwe-math-mathml-a11y» style=»display: none;»><math alttext=»{\displaystyle q}» xmlns=»http://www.w3.org/1998/Math/MathML»>
<semantics>
<mrow class=»MJX-TeXAtom-ORD»>
<mstyle displaystyle=»true» scriptlevel=»0″>
<mi>q</mi>
</mstyle>
</mrow>
<annotation encoding=»application/x-tex»>{\displaystyle q}</annotation>
</semantics>
</math></span><img alt=»q» aria-hidden=»true» class=»mwe-math-fallback-image-inline» src=»https://wikimedia.org/api/rest_v1/media/math/render/svg/06809d64fa7c817ffc7e323f85997f783dbdf71d» style=»vertical-align: -0.671ex; width:1.07ex; height:2.009ex;»/></span>-деформация обычной производной функции.
История
В классическом дифференциальном исчислении производная чаще всего определяется через понятие предела, однако исторически теория пределов появилась позже дифференциального исчисления. Исторически производная вводилась кинематически (как скорость) или геометрически (определяясь по сути наклоном касательной, в разных конкретных формулировках). Ньютон называл производную флюксией, обозначая точкой над символом функции, школа Лейбница предпочитала в качестве базового понятия дифференциал.
Русский термин в форме «производная функция» впервые употребил В. И. Висковатов, переведя на русский язык соответствующий французский термин dérivée, используемый Лагранжем.
Производная вектор-функции по параметру
Определим производную вектор-функции r(t){\displaystyle \mathbf {r} (t)} по параметру:
- ddtr(t)=limh→r(t+h)−r(t)h{\displaystyle {\frac {d}{dt}}\mathbf {r} (t)=\lim _{h\to 0}{\frac {\mathbf {r} (t+h)-\mathbf {r} (t)}{h}}}.
Если производная в точке t{\displaystyle t} существует, вектор-функция называется дифференцируемой в этой точке. Координатными функциями для производной будут x′(t), y′(t), z′(t){\displaystyle x'(t),\ y'(t),\ z'(t)}.
Свойства производной вектор-функции (всюду предполагается, что производные существуют):
- ddt(r1(t)+r2(t))=dr1(t)dt+dr2(t)dt{\displaystyle {\frac {d}{dt}}(\mathbf {r_{1}} (t)+\mathbf {r_{2}} (t))={\frac {d\mathbf {r_{1}} (t)}{dt}}+{\frac {d\mathbf {r_{2}} (t)}{dt}}} — производная суммы есть сумма производных.
- ddt(f(t)r(t))=df(t)dtr(t)+f(t)dr(t)dt{\displaystyle {\frac {d}{dt}}(f(t)\mathbf {r} (t))={\frac {df(t)}{dt}}\mathbf {r} (t)+f(t){\frac {d\mathbf {r} (t)}{dt}}} — здесь f(t){\displaystyle f(t)} — дифференцируемая скалярная функция.
- ddt(r1(t)r2(t))=dr1(t)dtr2(t)+r1(t)dr2(t)dt{\displaystyle {\frac {d}{dt}}(\mathbf {r_{1}} (t)\mathbf {r_{2}} (t))={\frac {d\mathbf {r_{1}} (t)}{dt}}\mathbf {r_{2}} (t)+\mathbf {r_{1}} (t){\frac {d\mathbf {r_{2}} (t)}{dt}}} — дифференцирование скалярного произведения.
- ddtr1(t),r2(t)=dr1(t)dt,r2(t)+r1(t),dr2(t)dt{\displaystyle {\frac {d}{dt}}=\left+\left} — дифференцирование векторного произведения.
- ddt(a(t),b(t),c(t))=(da(t)dt,b(t),c(t))+(a(t),db(t)dt,c(t))+(a(t),b(t),dc(t)dt){\displaystyle {\frac {d}{dt}}(\mathbf {a} (t),\mathbf {b} (t),\mathbf {c} (t))=\left({\frac {d\mathbf {a} (t)}{dt}},\mathbf {b} (t),\mathbf {c} (t)\right)+\left(\mathbf {a} (t),{\frac {d\mathbf {b} (t)}{dt}},\mathbf {c} (t)\right)+\left(\mathbf {a} (t),\mathbf {b} (t),{\frac {d\mathbf {c} (t)}{dt}}\right)} — дифференцирование смешанного произведения.
Таблица производных
| Производные степенных функций | Производные тригонометрических функций | Производные обратных тригонометрических функций | Производные гиперболических функций |
|---|---|---|---|
| (c)′={\displaystyle \left(c\right)’=0} | (sinx)′=cosx{\displaystyle \left(\sin x\right)’=\cos x} | (arcsinx)′=11−x2{\displaystyle \left(\arcsin x\right)’={\dfrac {1}{\sqrt {1-x^{2}}}}} | (sinhx)′=coshx{\displaystyle (\sinh x)’=\cosh x} |
| (xa)′=axa−1{\displaystyle \left(x^{a}\right)’=ax^{a-1}} | (cosx)′=−sinx{\displaystyle \left(\cos x\right)’=-\sin x} | (arccosx)′=−11−x2{\displaystyle \left(\arccos x\right)’=-{\dfrac {1}{\sqrt {1-x^{2}}}}} | (coshx)′=sinhx{\displaystyle (\cosh x)’=\sinh x} |
| (ax)′=axlna{\displaystyle \left(a^{x}\right)’=a^{x}\ln a} | (tgx)′=1cos2x{\displaystyle \left(\operatorname {tg} x\right)’={\dfrac {1}{\cos ^{2}x}}} | (arctgx)′=11+x2{\displaystyle \left(\operatorname {arctg} x\right)’={\dfrac {1}{1+x^{2}}}} | (tanh)′=1cosh2x{\displaystyle (\tanh )’={\frac {1}{\cosh ^{2}x}}} |
| (logax)′=1xlna{\displaystyle \left(\log _{a}x\right)’={\dfrac {1}{x\ln a}}} | (ctgx)′=−1sin2x{\displaystyle \left(\operatorname {ctg} x\right)’=-{\dfrac {1}{\sin ^{2}x}}} | (arcctgx)′=−11+x2{\displaystyle \left(\operatorname {arcctg} x\right)’=-{\dfrac {1}{1+x^{2}}}} | (coth)′=−1sinh2x{\displaystyle (\coth )’=-{\frac {1}{\sinh ^{2}x}}} |
(c)=(const){\displaystyle \left(c\right)=\left(\mathrm {const} \right)}(ex)(n)=ex{\displaystyle \left(e^{x}\right)^{\left(n\right)}=e^{x}}
Способы записи производных
В зависимости от целей, области применения и используемого математического аппарата используют различные способы записи производных. Так, производная n-го порядка может быть записана в нотациях:
Лагранжа f(n)(x0){\displaystyle f^{(n)}(x_{0})}, при этом для малых n часто используют штрихи и римские цифры:
- f(1)(x)=f′(x)=fI(x),{\displaystyle f^{(1)}(x_{0})=f'(x_{0})=f^{I}(x_{0}),}
- f(2)(x)=f″(x)=fII(x),{\displaystyle f^{(2)}(x_{0})=f»(x_{0})=f^{II}(x_{0}),}
- f(3)(x)=f‴(x)=fIII(x),{\displaystyle f^{(3)}(x_{0})=f»'(x_{0})=f^{III}(x_{0}),}
- f(4)(x)=fIV(x),{\displaystyle f^{(4)}(x_{0})=f^{IV}(x_{0}),} и т. д.
Такая запись удобна своей краткостью и широко распространена; однако штрихами разрешается обозначать не выше третьей производной.
Лейбница, удобная наглядной записью отношения бесконечно малых (только в случае, если x{\displaystyle x} — независимая переменная; в противном случае обозначение верно лишь для производной первого порядка):
- dnfdxn(x){\displaystyle {\frac {d^{n}\!f}{dx^{n}}}(x_{0})}
Ньютона, которая часто используется в механике для производной по времени функции координаты (для пространственной производной чаще используют запись Лагранжа). Порядок производной обозначается числом точек над функцией, например:
- x˙(t){\displaystyle {\dot {x}}(t_{0})} — производная первого порядка x{\displaystyle x} по t{\displaystyle t} при t=t{\displaystyle t=t_{0}}, или f¨(x){\displaystyle {\ddot {f}}(x_{0})} — вторая производная f{\displaystyle f} по x{\displaystyle x} в точке x{\displaystyle x_{0}} и т. д.
Эйлера, использующая дифференциальный оператор (строго говоря, дифференциальное выражение, пока не введено соответствующее функциональное пространство), и потому удобная в вопросах, связанных с функциональным анализом:
- Dnf(x){\displaystyle \mathrm {D} ^{n}\!f(x_{0})}, или иногда ∂nf(x){\displaystyle \partial ^{n}\!f(x_{0})}.
В вариационном исчислении и математической физике часто применяется обозначение fx{\displaystyle f_{x}}, fxx{\displaystyle f_{xx}}; для значения производной в точке — fx|x=x0{\displaystyle f_{x}\vert _{x=x_{0}}}. Для частных производных обозначение то же, поэтому смысл обозначения определяют из контекста.
Конечно, при этом необходимо не забывать, что служат все они для обозначения одних и тех же объектов:
- f(n)(x)=dnfdxn(x)=f⋅⋅…⋅⏞n PA3(x)=Dnf(x)=fxx…x⏟n PA3|x=x.{\displaystyle f^{(n)}(x_{0})={\frac {d^{n}\!f}{dx^{n}}}(x_{0})={\overset {\overbrace {\cdot \cdot …\cdot } ^{n\ \mathrm {PA} 3}}{f}}(x_{0})=\mathrm {D} ^{n}\!f(x_{0})=f{\underbrace {_{xx\ldots x}} _{n\ \mathrm {PA} 3}}\vert _{x=x_{0}}.}
Замечания
- Назовём Δx=x−x{\displaystyle \Delta x=x-x_{0}} приращением аргумента функции, а Δy=f(x)−f(x){\displaystyle \Delta y=f(x)-f(x_{0})} или Δy=f(x+Δx)−f(x){\displaystyle \Delta y=f(x_{0}+\Delta x)-f(x_{0})} приращением значения функции в точке x.{\displaystyle x_{0}.} Тогда
- f′(x)=limΔx→ΔyΔx.{\displaystyle f'(x_{0})=\lim \limits _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}.}
- Пусть функция f(a,b)→R{\displaystyle f\colon (a,b)\to \mathbb {R} } имеет конечную производную в каждой точке x∈(a,b).{\displaystyle x_{0}\in (a,b).} Тогда определена произво́дная фу́нкция
- f′(a,b)→R.{\displaystyle f’\colon (a,b)\to \mathbb {R} .}
- Функция, имеющая производную в точке, непрерывна в ней. Обратное не всегда верно.
- Если производная функция сама является непрерывной, то функцию f{\displaystyle f} называют непреры́вно дифференци́руемой и пишут: f∈C(1)((a,b)).{\displaystyle f\in C^{(1)}{\bigl (}(a,b){\bigr )}.}
Таблица производных.
В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п.
Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.)
Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная.
| Функция y |
Производная функции y y’ |
|
| 1 | C (постоянная величина) | C’ = 0 |
| 2 | x | x’ = 1 |
| 3 | xn (n — любое число) | (xn)’ = nxn-1 |
| x2 (n = 2) | (x2)’ = 2x | |
| 4 | sin x | (sin x)’ = cosx |
| cos x | (cos x)’ = — sin x | |
| tg x | ||
| ctg x | ||
| 5 | arcsin x | |
| arccos x | ||
| arctg x | ||
| arcctg x | ||
| 4 | ax | |
| ex | ||
| 5 | loga x | |
| ln x (a = e) |
Рекомендую обратить внимание на третью группу функций в этой таблице производных. Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть
Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)
Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету…
Рассмотрим несколько примеров:
1. Найти производную функции y = x3
Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат:
(x3)’ = 3·x3-1 = 3×2
Вот и все дела.
Ответ: y’ = 3×2
2. Найти значение производной функции y = sinx в точке х = 0.
Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию… Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция.
По табличке находим синус и соответствующую производную:
y’ = (sin x)’ = cosx
Подставляем ноль в производную:
y'(0) = cos 0 = 1
Это и будет ответ.
3. Продифференцировать функцию:
Что, внушает? ) Такой функции в таблице производных и близко нет.
Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает…
Но если увидеть, что наша функция — это косинус двойного угла, то всё сразу налаживается!
Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. По формуле косинуса двойного угла:
Т.е. наша хитрая функция есть не что иное, как y = cosx. А это — табличная функция. Сразу получаем:
Ответ: y’ = — sin x.
Пример для продвинутых выпускников и студентов:
4. Найти производную функции:
Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями… То вполне можно упростить эту функцию. Вот так:
А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем:
Вот и всё. Это будет ответ.
Надеюсь, что с первым китом дифференцирования — таблицей производных — всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования.
Примеры
Пусть f(x)=x2{\displaystyle f(x)=x^{2}}. Тогда
- f′(x)=limx→xx2−x2x−x=limx→x(x−x)(x+x)x−x=limx→x(x+x)=2x.{\displaystyle f'(x_{0})=\lim \limits _{x\to x_{0}}{\frac {x^{2}-x_{0}^{2}}{x-x_{0}}}=\lim \limits _{x\to x_{0}}{\frac {(x-x_{0})(x+x_{0})}{x-x_{0}}}=\lim \limits _{x\to x_{0}}(x+x_{0})=2x_{0}.}
Пусть f(x)=|x|{\displaystyle f(x)=|x|}. Тогда если x0≠0,{\displaystyle x_{0}\neq 0,} то
- f′(x)=sgnx,{\displaystyle f'(x_{0})=\operatorname {sgn} x_{0},}
где sgn{\displaystyle \operatorname {sgn} } обозначает функцию знака. А если x=,{\displaystyle x_{0}=0,} то
f+′(x)=1,f−′(x)=−1,{\displaystyle f’_{+}(x_{0})=1,\;f’_{-}(x_{0})=-1,}
а следовательно f′(x){\displaystyle f'(x_{0})} не существует.
Уравнение касательной к графику функции
Чтобы закрепить предыдущий параграф, рассмотрим задачу нахождения касательной к графику функции в данной точке. Это задание встречалось нам в школе, и оно же встречается в курсе высшей математики.
Рассмотрим «демонстрационный» простейший пример.
Составить уравнение касательной к графику функции в точке с абсциссой . Я сразу приведу готовое графическое решение задачи (на практике этого делать в большинстве случаев не надо):

Строгое определение касательной даётся с помощью определения производной функции, но пока мы освоим техническую часть вопроса. Наверняка практически всем интуитивно понятно, что такое касательная. Если объяснять «на пальцах», то касательная к графику функции – это прямая, которая касается графика функции в единственной точке. При этом все близлежащие точки прямой расположены максимально близко к графику функции.
Применительно к нашему случаю: при касательная (стандартное обозначение) касается графика функции в единственной точке .
И наша задача состоит в том, чтобы найти уравнение прямой .
Как составить уравнение касательной в точке с абсциссой ?
Общая формула знакома нам еще со школы:
Значение нам уже дано в условии.
Теперь нужно вычислить, чему равна сама функция в точке :
На следующем этапе находим производную:
Находим производную в точке (задание, которое мы недавно рассмотрели):
Подставляем значения , и в формулу :
Таким образом, уравнение касательной:
Это «школьный» вид уравнения прямой с угловым коэффициентом. В высшей математике уравнение прямой на плоскости принято записывать в так называемой общей форме , поэтому перепишем найденное уравнение касательной в соответствии с традицией:
Очевидно, что точка должна удовлетворять данному уравнению: – верное равенство.
Следует отметить, что такая проверка является лишь частичной. Если мы неправильно вычислили производную в точке , то выполненная подстановка нам ничем не поможет.
Рассмотрим еще два примера.
Пример 5
Составить уравнение касательной к графику функции в точке с абсциссой
Уравнение касательной составим по формуле
1) Вычислим значение функции в точке :
2) Найдем производную. Дважды используем правило дифференцирования сложной функции: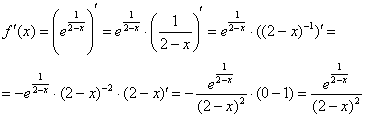
3) Вычислим значение производной в точке :
4) Подставим значения , и в формулу :
Готово.
Выполним частичную проверку:
Подставим точку в найденное уравнение: – верное равенство.
Пример 6
Составить уравнение касательной к графику функции в точке с абсциссой
Полное решение и образец оформления в конце урока.
В задаче на нахождение уравнения касательной очень важно ВНИМАТЕЛЬНО и аккуратно выполнить вычисления, привести уравнение прямой к общему виду. И, конечно же, ознакомьтесь со строгим определением касательной, после чего закрепите материал на уроке Уравнение нормали, где есть дополнительные примеры с касательной
Производная по-простому
Где применяется
Немного о твоей будущей зарплате
Попробую объяснить несколько иначе, чем в школе.
Вы заканчиваете школу, поступаете в университет и начинаете подрабатывать:
В первый год после школы вы зарабатываете 0,5 у.е. (условных единиц).
Вы хорошо учитесь, устраиваетесь по специальности или находите свое призвание, и ваши дела постепенно, но идут в гору!

Какой молодец! Заработок растет не по годам, а по часам!
Если посмотреть на этот график внимательнее, то можно увидеть сходство с ветвью параболлы, которая в самом простом случае задается уравнением y = x². Если это понятно, то дальше все проще!
Интересно, а на сколько увеличивался заработок из года в год:
I год: 0,5 − 0 = 0,5 .
II год: 2 − 0,5 = 1,5.
III год: 4,5 − 2 = 2,5.
IV год: 8 − 4,5 = 3,5.
…
Получается, что наш доход каждый год возрастал равномерно. Вот что выйдет, если построить график:
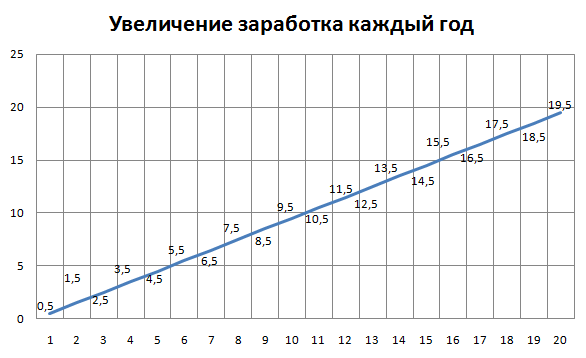
Получается прямая!
То есть все наши старания каждый год были постоянными, достаточно было ежегодно улучшать свой доход на 1 у.е.
Нетрудно заметить, что график заработка задается уравнением y = 0,5x².
А график увеличения заработка залается прямой y = x − 0,5.
Кто знает толк в производных, скажет Неверно!Конечно, производная от 0,5x² не будет равна x − 0,5, и это мы обсудим ближе к концу статьи.
Изменение заработка для нескольких лет
Для того, чтобы посчитать скорость изменения заработка, нужно взять один из «треугольников» с графика, например первый, и разделить длину вертикального катета (Δy) (в данном случае это 12,5 − 8 = 4,5) на длину горизонтального (Δx) (тут он равен 1).
Получится 4,5 / 1 = 4,5.
Таким образом, разделив вертикальный катет на горизонтальный, мы получаем скорость изменения функции, что показывает второй график.

Но как же это все относится к производным?
А так, что производная показывает «скорость» изменения функции!
Функция заработка предсталяет из себя график параболы (график функции) .
В тоже время функция увеличения заработка каждый год представляет прямую (график производной функции).
Однако прежде, чем ты расскажешь это своим друзьям, давай проверим, а если мы возьмем другой треугольник (в этот раз второй).
Вертикальный катет: 24,5 − 18 = 6,5.
Горизонтальный катет: 1.
Разделим: 6,5 / 1 = 6,5 — не сходится с первым треугольником!
А если объединить второй и третий треугольник?
Вертикальный катет: 40,5 − 18 = 22,5.
Горизонтальный катет: 9 − 6 = 3.
Разделим: 22,5 / 3 = 7,5 — опять не сходится!
Какая же тогда производная правильная?
Для того, чтобы верно найти производную, нужно взять как можно меньший горизонтальный катет — максимальное приближение (Δх)!
Сам график задается уравнением y = 0,5x².
Тогда возьмем x₁ = 4 => y₁ = 0,5 × 4² = 8, а при x₂ = 4,001 => y₂ = 0,5 × 4,001² ≈ 8,004.
Получается: Δy = 8,004 − 8 = 0,004, Δх= 4,001 − 4 = 0,001.
Производная: Δy / Δх = 0,004 / 0,001 = 4.
И что же тогда производная?
Производная — это скорость изменения функции при самых маленьких значениях Δх (наименьших значениях горизонтального катета).
Именно поэтому производную и называют тангенсом (отношение противолежащего катета к прилежащему) угла наклона этой функции.
Если же мы посчитаем производную для каждой точки, получится такой график функции:

А это уже похоже на правду!
Производная от y = 0,5x² будет равна y = х (именно такой график получился у нас).
Погрешность в данном графике вызвана плохим приближением по оси х (в данном случае Δх = 1), из-за чего появляется неточность.
Конечно, можно не делать такое большое количество действий, проверяя точки.
Есть готовые формулы для базовых функций, пользуйтесь ими, если хотите облегчить себе жизнь.
Выводы:
- Производные встречаются почти во всех областях: от медицины до финансов, по сути дела производная, показывая скорость изменения функции, предсказывает дальнейшее поведение функции.
- Представьте матрешку, так же как в каждой матрешке внутри есть следующая, так и функция скрывает в себе производную. У каждой функции есть своя производная функции. Так же можно брать от производной функции еще одну производную и повторять действие до бесконечности.
- Производная функции показывает скорость изменения самой функции. Так же, как у вас есть родители и предки (предыдущии поколения), которые вам передали какие-то отличительные особенности, так и у функции есть производная, которая передает ей скорость ее изменения.
Будь в курсе новых статеек, видео и легкого математического юмора.
Определение
Пусть в некоторой окрестности точки x∈R{\displaystyle x_{0}\in \mathbb {R} } определена функция fU(x)⊂R→R.{\displaystyle f\colon U(x_{0})\subset \mathbb {R} \to \mathbb {R} .} Производной функции называется такое число A{\displaystyle A}, что функцию в окрестности U(x){\displaystyle U(x_{0})} можно представить в виде
- f(x+h)=f(x)+Ah+o(h){\displaystyle f(x_{0}+h)=f(x_{0})+Ah+o(h)}
если A{\displaystyle A} существует.
Определение производной функции через предел
Пусть в некоторой окрестности точки x∈R{\displaystyle x_{0}\in \mathbb {R} } определена функция fU(x)⊂R→R.{\displaystyle f\colon U(x_{0})\subset \mathbb {R} \to \mathbb {R} .} Производной функции f{\displaystyle f} в точке x{\displaystyle x_{0}} называется предел, если он существует,
- f′(x)=limx→xf(x)−f(x)x−x=limΔx→f(x+Δx)−f(x)Δx=limΔx→Δf(x)Δx.{\displaystyle f'(x_{0})=\lim \limits _{x\to x_{0}}{\frac {f(x)-f(x_{0})}{x-x_{0}}}=\lim _{\Delta x\to 0}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}=\lim \limits _{{\Delta x}\to 0}{\frac {\Delta {f(x)}}{\Delta x}}.}