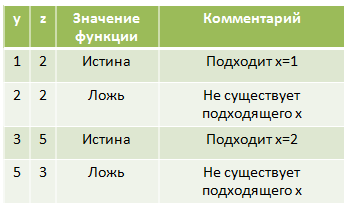
Предикат

Структура

Итак, структура предиката может быть поверхностной и исходной. Однако состав синтаксических групп не отражает ни порядка слов, ни залога — пассивного или активного. Например: дуб растёт тысячу лет; тысячу лет растёт дуб; растёт дуб тысячу лет. Все эти предложения имеют тождественные составляющие предиката в их исходной структуре.

Однако исходные структуры со всей их близостью не всегда бывают связаны с поверхностными структурами семантической эквивалентностью. Логику предиката не всякий раз можно сводить к одной интерпретации, даже если составляющие соотносятся по залогу. Например:

Новые деревья выращены в старом саду.
В старом саду были выращены новые деревья.

Не правда ли, в одни и те же слова при ближайшем рассмотрении вкладывается несколько разный смысл?

Предикат в грамматике

Существует два конкурирующих понятия предиката в теориях грамматики. Конкуренция между этими двумя концепциями породила путаницу в отношении использования термина «предикат» в теориях грамматики. Так что такое предикат? В этой статье рассматриваются оба эти понятия.

Первое понятие относится к традиционной грамматике, которая имеет тенденцию рассматривать предикат как одну из двух основных частей предложения, другая часть является предметом. Цель предиката состоит в том, чтобы завершить представление о предмете, например, что он делает или что из себя представляет.

Второе понятие было получено из работы в исчислении предикатов (логика предикатов, логика первого порядка) и является заметным в современных теориях синтаксиса и грамматики. В этом подходе предикат предложения в основном соответствует главному глаголу и любым вспомогательным средствам, которые сопровождают главный глагол. В то же время его аргументы (например, фразы существительные) находятся за пределами предиката.

Что такое предикат

Предикат (с латинского praedicatum означает «заявленное, упомянутое, сказанное») — понятие в логике, которым называют утверждение, высказанное о том или ином субъекте. Субъект высказывания — это та вещь или явление, о котором или которой делается утверждение.

Одна из важнейших особенности логики предикатов в том, что все общие имена (такие, как «цветок», «деревня»), знаки свойств («розовый», «большая») и знаки отношений («красивее», «роднее») рассматриваются как относящиеся к одной категории знаков: категории предикаторов (иначе говоря, предметно-истинных функторов).

Предикаторы, в свою очередь, показывают функции, у которых вероятные аргументы — это универсальные в рассмотрении объекты, а значения — истинные оценки. В классической логике они называются «истина» и «ложь». К примеру, возьмем предикатор «человек», который представляет функцию, определяемую как истина каждым отдельным человеком, а каждым отличным от человека существом — как ложь.

Другой пример: функция, которая соответствует предикатору «больше», сопоставляет истину каждой паре объектов или субъектов, один из которых больше. Например, такая пара, как «слон, мышь». Но всем остальным парам, по типу «мышь, слон» и «мышь, мышь», такая функци будет сопоставлять оценку «ложь».

Предикаторы могут быть:

Одноместные. Те, которые представляют предметно-истинные функции от одного аргумента. Например, «человек».
Двухместные. Те, которым соответствуют функции двух аргументов. Например, «больше».
Другие, в зависимости от количества соответствующих аргументов.

Типы предикатов

Среди семантических типов выделяют таксономические, реляционные, оценочные, характеризующие. Таксономические указывают на класс предмета. Например: любимая обувь — лапти; выросшее дерево — кедр; новое кино — фэнтези. Реляционный предикат — значение указания на то, каким образом один объект относится к другим. Например: на лапти идёт лыко; кедр — из семейства сосновых; фэнтези — жанр фантастики. Характеризующие предикаты указывают на признаки объекта статические или динамические, преходящие или постоянные. Например: лапти износились; кедр растёт; фэнтези увлекает.

Особое внимание нужно уделить типу, который называется предикатом оценочным. Например: лапти — обувь экологичная; кедры очень красивы; фэнтези погружают зрителя в сказку

Существуют и слова-предикаты, относящиеся к типу пространственной и временно́й локализации. Например: лапти в ящике; кедровые шишки будут в сентябре; фэнтези читаю дома. Нужно помнить, что определить тип предиката не так просто именно потому, что в языке разные типы их представлены чаще всего синкретически. То есть одним глаголом может быть выражено не только одно отношение предметов друг к другу, но одновременно и характеристики, и локализации.

Предикат в грамматике

Кванторные операции над предикатами

Прежде чем изучить квантовые операции, нужно разобраться, что из себя представляет сам квантор.

Квантор — общее название для логических операций, ограничивающих область истинности какого-либо предиката и создающих высказывание.

Кванторы впервые были определены немецким математиком Готлобом Фреге. Он упомянул их в своей работе «Begriffsschrift» («Исчисление понятий», 1879 года). Однако сам термин был изобретен английским логиком Чарльзом Пирсом в 1885 году. Вместе со словом «квантор» он ввел также и термин «квантификация», который означает измерение качеств признаков.

Обозначение кванторов

Символическое обозначение кванторов придумал итальянский математик Дж. Пеано в 90-е годы XIX века. Выглядят эти символы так:

\(\forall\) — «для любого», «для каждого», «для всех»;

\(\exists\) — «существует», «найдётся».

Кроме самих кванторов и вместе с ними используют обозначения \(«!», «:», «|»\), которые являются сокращениями:

! – «единственный»;

– «такой, что»;

| – «такой, что».

Знак «:» обычно используется в формулировках определений или теорем, которые записываются с помощью кванторов. Знак «|» применяется в определениях множеств.

Квантор общности \(\forall\)

Операция связывания квантором общности — это правило, в соответствии с которым каждому одноместному предикату P(x) во множестве N сопоставляется высказывание \((\forall x)(P(x))\), которое произносится, как «для всякого \(x — P(x)\) ».

Оно истинно только в том случае, когда \(P(x)\) — тождественно истинен. В ином случае данное высказывание ложно.

Операция связывания квантором общности по переменной \(x_1\) — это правило, в соответствии с которым каждому n-местному \((n\geqslant2)\) предикату \(P(x, x_2, …, x_n)\), на множествах \(N_1, N_2, …, N_n\), в соответствие ставится новый \((n-1)\) — местный предикат. Он обозначается как \((\forall x)(P(x, x_2, …, x_n)).\)

Оно истинно только в том случае, когда одноместный предикат \(P(x, a_2, …, a_n)\) на множестве \(N_1\) тождественно истинен. В противном случае оно ложно.

Квантор существования \( \exists\)

Операция связывания квантором существования — это правило, по которому каждому одноместному утверждению \(P(x)\) на множестве N соответствует высказывание \( (\exists)(P(x))\), которое звучит так: « существует \( x\), такое, что \( P(x)\), »).

Это высказывание ложно только, когда \(P(x)\), тождественно ложен. В противном случае оно истинно.

Операция связывания квантором существования по переменной \(x_1\) — это правило, в соответствие с которым каждому n-местному \((n\geqslant2)\) высказыванию \(P(x_1, x_2, …, x_n)\) на множествах \(N_1, N_2, …, N_n\) соответствует новый (n-1-местный предикат. Он обозначается как \((\exists)(P(x_1, x_2, …, x_n)\). Это высказывание ложно только в том случае, если одноместный предикат \((P(x_1, a_2, …, a_n)\) на множестве \(N_1\) тождественно ложен. В противном случае данное высказывание истинно.

Компоненты

В семантической структуре предложения имеются собственные категории. Это предикаты, передающие состояние или конкретное действие, актанты — субъекты действия или объекты разного рода (прямые, косвенные, результативы и так далее), сирконстанты — различные обстоятельства как поле совершения действий.

Например: Ночью в окно стучало дерево ветками. Детализация здесь, можно сказать, максимальная. Предикатом активного действия будет слово «стучало». Далее идут актанты: субъект — «дерево», объект — «в окно», инструментатив — «ветками». Сирконстантой (или темпоративом, или обстоятельством времени) выступает слово «ночью». Но может появиться и вторая, локативная — «с улицы», например.

В синтаксисе

Синтаксический П указывает синтаксическую обоснованность применения произведения в формальной грамматике и аналогичен семантическому предикату, который определяет семантическую действительность применения произведения. В своей первоначальной реализации синтаксические предикаты имели форму «(α)?» и могли появляться только на левом краю произведения. Необходимым синтаксическим условием α может быть любой допустимый контекстно-свободный фрагмент грамматики.

Более формально синтаксический предикат представляет собой форму производственного пересечения, используемого в спецификациях парсера или в формальных грамматиках. В этом смысле термин имеет значение математической функции индикатора. Если p1 и p2 являются производственными правилами, язык, сгенерированный как p1, так и p2, является их заданным пересечением.

Размышляющие грамматики выражений (PEGs), изобретенные Брайаном Фордом, расширяют эти простые П, позволяя им появляться где угодно в пределах производства наравне с «не предикатами». Более того, Форд изобрел процедуру разбора для обработки этих грамматик в линейном времени.

Этот подход реализуется в ANTLR версии 3, которая использует детерминированные конечные автоматы для просмотра. Это может потребовать тестирования предиката для выбора между синтаксическими переходами (так называемый «пред-LL (*)» синтаксический анализ).

В традиционной грамматике

Предикат в традиционной грамматике вдохновлен пропозициональной логикой древности (в отличие от более современной логики предикатов ). Предикат рассматривается как свойство, которым обладает субъект или которым он характеризуется. Следовательно, предикат — это выражение, которое может относиться к чему-либо. Таким образом, выражение «движется» применимо ко всему, что движется. Это классическое понимание предикатов было более или менее прямо заимствовано в латинских и греческих грамматиках; а оттуда он проник в грамматики английского языка, где применяется непосредственно к анализу структуры предложения. Это также понимание предикатов, как они определены в англоязычных словарях. Предикат — это одна из двух основных частей предложения (другая — подлежащее , которое предикат модифицирует ). Предикат должен содержать глагол , а глагол требует или разрешает другим элементам завершать сказуемое, либо запрещает им это делать. Этими элементами являются объекты (прямые, косвенные, предложные), предикативы и дополнения :

Она танцует . — предикат, состоящий только из глагола

Бен читает книгу . — предикат глагол плюс прямой объект

Мать Бена, Фелисити, подарила мне подарок . — предикат глагол-плюс-косвенный-объект-плюс-прямой-объект

Она слушала радио . — предикат глагол-плюс-предложный-объект

Они выбрали ее президентом . — предикат глагол-плюс-объект-плюс-предикатив-существительное

Она встретила его в парке . — предикат глагол-плюс-объект-плюс-дополнение

Она в парке . — предикат глагол-плюс-предикатив-предложная-фраза

Предикат предоставляет информацию о субъекте, например, что это за субъект, что субъект делает или каков субъект. Отношение между субъектом и его предикатом иногда называют связью . Предикативные номинальный является именным , например, в предложении « Георг III король Англии », фраза « король Англии » является предикативным номинальной. Подлежащее и предикативное именное должны быть связаны глаголом-связкой , также называемым связкой . Предикативное прилагательное является прилагательное , например, в Ивано является привлекательным , привлекательным являются предикативной прилагательное. Подлежащее и предикативное прилагательное также должны быть связаны связкой.

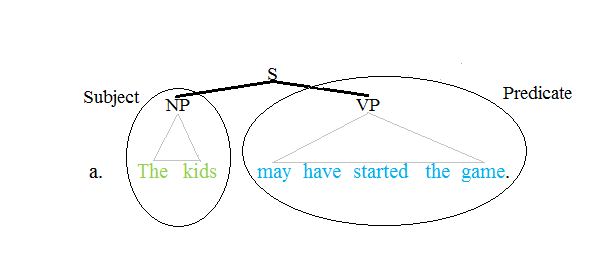
Это традиционное понимание предикатов находит конкретный отражение во многих синтаксических теориях структуры фраз . Эти теории делят повествовательное предложение английского языка (S) на именную фразу (NP) и глагольную фразу (VP), например

Подлежащее NP показано зеленым, а предикат VP — синим. Эта концепция структуры предложения резко контрастирует с теориями грамматики о структуре зависимостей , которые ставят конечный глагол (= спряганный глагол) как корень всей структуры предложения и, таким образом, отвергают это бинарное деление NP-VP даже для английского языка. Языки с более гибким порядком слов (часто называемые неконфигурационными языками ) часто по-разному обрабатываются также в подходах к структуре фраз.

Предикат в математике

В математической логике предикат обычно понимается как функция P: X → {правда, ложь}, называемая предикатом X. Однако предикаты имеют много разных применений и интерпретаций в математике и логике, и их точное определение, смысл и использование будут варьироваться от теории к теории. Так, например, если теория определяет понятие отношения, то предикат является просто характеристической функцией, иначе известной как индикаторная функция отношения. Однако не все теории имеют отношения или основаны на теории множеств, поэтому нужно быть осторожным с правильным определением и семантической интерпретацией предиката.

Формальное определение

Точная семантическая интерпретация атомной формулы и атомного предложения будет варьироваться от теории к теории.
В пропозициональной логике атомные формулы называются пропозициональными переменными. В некотором смысле это предикаты с нулевыми значениями.
В логике первого порядка атомная формула состоит из предикатного символа, применяемого к соответствующему числу членов.
В теории множеств предикаты понимаются как характерные функции или задают функции индикатора, т. е. функции от заданного элемента до значения истины.
Метод построения видов суждений использует предикаты для их определения.
В автоэпистемической логике, которая отвергает закон исключенного среднего, предикаты могут быть истинными, ложными или просто неизвестными, т. е. данный набор фактов может быть недостаточным для определения истины или ложности предиката.
В нечеткой логике предикаты являются характерными функциями распределения вероятностей. То есть строгая истинная / ложная оценка предиката заменяется величиной, интерпретируемой как степень правды.

Monoid (моноид)

Объект с функцией, которая «комбинирует» объект с другим объектом того же типа. Простой пример моноида это сложение чисел:

В этом случае число — это объект, а это функция.

Должен существовать нейтральный элемент (identity), так, чтобы комбинирование значения с ним не изменяло значение. В случае сложения таким элементом является .

Также необходимо, чтобы группировка операций не влияла на результат (ассоциативность):

Конкатенация массивов — это тоже моноид:

Нейтральный элемент — это пустой массив

Если существуют функции нейтрального элемента и композиции, то функции в целом формируют моноид:

— это любая функция с одним аргументом.

В современных теориях синтаксиса

Большинство современных теорий синтаксиса и грамматики берут свое начало в теории исчисления предикатов, связанных с Готлобом Фреге. Это понимание видит предикаты как отношения или функции, стоящие над аргументами. Они служат либо для назначения свойства одному аргументу, либо для связи двух или более аргументов друг с другом. Предложения состоят из предикатов и их аргументов (и дополнений) и являются, таким образом, структурами предикатного аргумента. В соответствии с ними данный П рассматривается как связывание его аргументов с большей структурой.

Предикаты помещаются слева за пределами скобок, тогда как их аргументы помещаются внутри скобок. Один признает валентность предикатов, в соответствии с которым он может быть доступен (не показан), моновалентный, двухвалентный или трехвалентный. Эти типы представлений аналогичны формальным семантическим анализам, где речь идет о надлежащем учете фактов кванторов и логических операторов. Однако в отношении основной структуры предложения эти представления предполагают прежде всего, что глаголы являются предикатами, а фразы существительных, с которыми они появляются, являются их аргументами. При таком понимании предложения двоичное деление предложения на предмет NP и предикат VP вряд ли возможно. Вместо этого глагол является предикатом, а существительные — его аргументами.

Операции над предикатами

Предикаты, так же, как высказывания, принимают два значения: истинное и ложное, поэтому к ним применимы все операции логики высказываний.
Рассмотрим применение операций логики высказываний к предикатам на примерах одноместных предикатов.

Логические операции

Конъюнкцией двух предикатов A(x) и B(x) называется новый предикат A(x)∧B(x){\displaystyle A\left(x\right)\wedge B\left(x\right)}, который принимает значение «истина» при тех и только тех значениях х из Т, при которых каждый из предикатов принимает значение «истина», и принимает значение «ложь» во всех остальных случаях.
Множеством истинности Т предиката A(x)∧B(x){\displaystyle A\left(x\right)\wedge B\left(x\right)} является пересечение множеств истинности предикатов A(x) — T1 и B(x) — T2, то есть T = T1 ∩ T2.
Например: A(x): «x — чётное число», B(x): «x кратно 3».
A(x) B(x) — «x — чётное число и x кратно 3».
То есть предикат «x делится на 6».

Дизъюнкцией двух предикатов A(x) и B(x) называется новый предикат A(x)∨B(x){\displaystyle A\left(x\right)\vee B\left(x\right)}, который принимает значение «ложь» при тех и только тех значениях x из T, при которых каждый из предикатов принимает значение «ложь» и принимает значение «истина» во всех остальных случаях.
Областью истинности предиката A(x)∨B(x){\displaystyle A\left(x\right)\vee B\left(x\right)} является объединение областей истинности предикатов A(x) и B(x).

Отрицанием предиката A(x) называется новый предикат, который принимает значение «истина» при всех значениях x из T, при которых предикат A(x) принимает значение «ложь», если A(x) принимает значение «истина».

Множеством истинности предиката x X является дополнение T’ к множеству T в множестве X.

Импликацией предикатов A(x) и B(x) называется новый предикат A(x)⇒B(x){\displaystyle A\left(x\right)\Rightarrow B\left(x\right)}, который является ложным при тех и только тех значениях x из T, при которых A(x) принимает значение «истина», а B(x) — значение «ложь», и принимает значение «истина» во всех остальных случаях.
Читают: «Если A(x), то B(x)».

Например. A(x): «Натуральное число x делится на 3». B(x): «Натуральное число x делится на 4», можно составить предикат: «Если натуральное число x делится на 3, то оно делится и на 4».
Множеством истинности предиката A(x)⇒B(x){\displaystyle A\left(x\right)\Rightarrow B\left(x\right)} является объединение множества T2 — истинности предиката B(x) и дополнения к множеству T1 истинности предиката A(x).

Кванторные операции

Квантор всеобщности ∀{\displaystyle \forall }
Квантор существования ∃{\displaystyle \exists }
Квантор существования по переменной x{\displaystyle x}₁

Определение

Предика́т (n-местный, или n-арный) — это функция с множеством значений {,1}{\displaystyle \{0,1\}} (или {ложь, истина}), определённая на множестве M=M1×M2×…×Mn{\displaystyle M={{M}_{1}}\times {{M}_{2}}\times \ldots \times {{M}_{n}}}. Таким образом, каждый набор элементов множества M характеризуется либо как «истинный», либо как «ложный».

Предикат можно связать с математическим отношением: если (m₁,m₂,…,m_n) принадлежит отношению, то предикат будет возвращать на ней 1. В частности, одноместный предикат определяет отношение принадлежности некоторому множеству.

Предикат — один из элементов логики первого и высших порядков. Начиная с логики второго порядка, в формулах можно ставить кванторы по предикатам.

Предикат называют тождественно-истинным и пишут:

P(x1,…,xn)≡1{\displaystyle P\left(x_{1},…,x_{n}\right)\equiv 1}

если на любом наборе аргументов он принимает значение 1.

Предикат называют тождественно-ложным и пишут:

P(x1,…,xn)≡{\displaystyle P\left(x_{1},…,x_{n}\right)\equiv 0}

если на любом наборе аргументов он принимает значение 0.

Предикат называют выполнимым, если хотя бы на одном наборе аргументов он принимает значение 1.

Так как предикаты принимают только два значения, то к ним применимы все операции булевой алгебры, например: отрицание, импликация, конъюнкция, дизъюнкция и т. д.

В традиционной грамматике

Понятие П в традиционной грамматике вдохновлено пропозициональной логикой древности (в отличие от более современной логики предикатов). Предикат рассматривается как свойство, которое субъект имеет. Следовательно, предикат является выражением, которое может быть истинным. Таким образом, выражение «движется» верно для всего, что движется. Это дает ответ на вопрос, что такое предикат.

Такое классическое понимание предикатов было принято более или менее непосредственно в латинской и греческой грамматиках, и оттуда оно попало в грамматику английского и русского языков, где применяется непосредственно к анализу структуры предложения. Это понимание П также используется в англоязычных словарях.

Составляющие

Предикаты составлены по семантическому принципу таким образом: собственно предикаты (например — состояния) и актанты (участники события). Семантически актанты тоже имеют разделение на типы:

Субъект (иначе — агенс) — это субъектного типа актант или активное действующее лицо. Например: дерево растёт.
Объект — это адресат прямого или косвенного действия, подвергающийся или нет прямому воздействию. Например: кошка ловит мышку.
Инстументатив — предмет, без которого ситуация не может осуществиться. Например: наелись супом.
Результатив — обозначение результата совершённых действий. Например: весной выросла трава.

Кроме того, не обойтись и без сирконстант — обстоятельств совершения действий. Они тоже разделяются на группы. Две самые частые и основные — темпоратив и локатив. Например: весной становится тепло. Слово «весной» — темпоратив. Повсюду расцветает сирень. Слово «повсюду» — локатив.

Другая классификация

Можно классифицировать данные слова и на других основаниях. Тип субъекта играет определяющую роль: низшего порядка предикаты относятся к сущностям материальным, а высшего — характеризуют разнообразные виды объектов нематериальных. Здесь резко противопоставляются два вида: относящиеся к событию и характеризующие пропозицию, инвариант. Например: лапти порвались только вчера — лапти порвались, но вчера — очень сомнительно.

Далее, по этой классификации, нужно делить предикаты по количеству актантов. Одноместные: лапти — легки; кедр — мощный; двухместные: лапти легки на ногах; кедр закрыл солнце; трёхместные: лапти легки на ногах при ходьбе; кедр закрыл солнце для подлеска. Другим образом можно разделить предикаты на первопорядковые (непроизводные — кедр стоит); второго порядка (являющиеся производными от первых — кедр стойкий); третьего порядка (производные от вторых) и так далее.

Правда или ложь

Если вам все еще непонятно, что такое предикат в математике, то стоит остановиться на этом подробнее. Неформально предикат — это утверждение, которое может быть истинным или ложным в зависимости от значений его переменных. Его можно рассматривать как оператора или функцию, которая возвращает значение, являющееся истинным или ложным. Например, предикаты иногда используются для указания набора элементов: при разговоре о наборах иногда бывает неудобно или невозможно описать набор, перечисляя все его элементы. Таким образом, предикат P (x) будет истинным или ложным, в зависимости от того, принадлежит ли x множеству.

Теоретическая часть

Существует много дедуктивных систем для видов суждений и логики первого порядка, которые являются как звуковыми (все доказуемые утверждения верны во всех моделях), так и полными (утверждения, которые верны для всех моделей, являются доказуемыми). Хотя отношение логического следствия разрешимо лишь наполовину, в автоматизированной теореме, доказанной в логике первого порядка, достигнут значительный прогресс. Логика первого порядка также удовлетворяет нескольким металогическим теоремам, которые делают ее пригодной для анализа в теории доказательств, такой как теорема Левенхайма-Сколема и теорема о компактности.

Логика первого порядка является стандартом для формализации математики в аксиомах и изучается в основах математики. Арифметика Пеано и теория множеств Цермело-Френкеля являются аксиоматизациями теории чисел и теории множеств, соответственно, являются частью логики первого порядка. Однако теория первого порядка не имеет возможности однозначно описывать структуру с бесконечной областью, например натуральные числа. Системы аксиом, которые полностью описывают эти две структуры (то есть системы категориальной аксиомы), могут быть получены в более сильных формах логики, таких как логика второго порядка.

Основы логики первого порядка были разработаны независимо Готлобом Фреге и Чарльзом Сандерсом Пирсом.

Формальное определение

Точная семантическая интерпретация атомной формулы и атомного предложения будет варьироваться от теории к теории.
В пропозициональной логике атомные формулы называются пропозициональными переменными. В некотором смысле это предикаты с нулевыми значениями.
В логике первого порядка атомная формула состоит из предикатного символа, применяемого к соответствующему числу членов.
В теории множеств предикаты понимаются как характерные функции или задают функции индикатора, т. е. функции от заданного элемента до значения истины.
Метод построения видов суждений использует предикаты для их определения.
В автоэпистемической логике, которая отвергает закон исключенного среднего, предикаты могут быть истинными, ложными или просто неизвестными, т. е. данный набор фактов может быть недостаточным для определения истины или ложности предиката.
В нечеткой логике предикаты являются характерными функциями распределения вероятностей. То есть строгая истинная / ложная оценка предиката заменяется величиной, интерпретируемой как степень правды.

Определение

В логике и лингвистике предикат — это сказуемое суждения, то есть то, что высказано с отрицанием или утверждением о субъекте. Такие слова показывают отсутствие или наличие у предмета того или иного признака. С точки зрения лингвистики, говорится о семантических и синтаксических предикатах. Последний — элемент поверхности структуры, то есть сказуемое, а первый является ядром семантической конфигурации, отображающей ситуацию вне языка, то есть её ядерную семантему.

Таким же образом семантический предикат представляется самыми разными способами и на уровне поверхности структуры. Взаимного однозначного соответствия между этими двумя типами предикатов нет, поскольку любым из них можно отразить одну и ту же ситуацию. Например: я ставлю лапти в угол; я поставила лапти в угол; поставленные в угол лапти. Традиционно не имеющая решения задача языкознания относится к определению понятия предиката. Положительный ответ был бы существенным для развития концепции — семантической или синтаксической, однако предикат пока не получил однозначного определения.