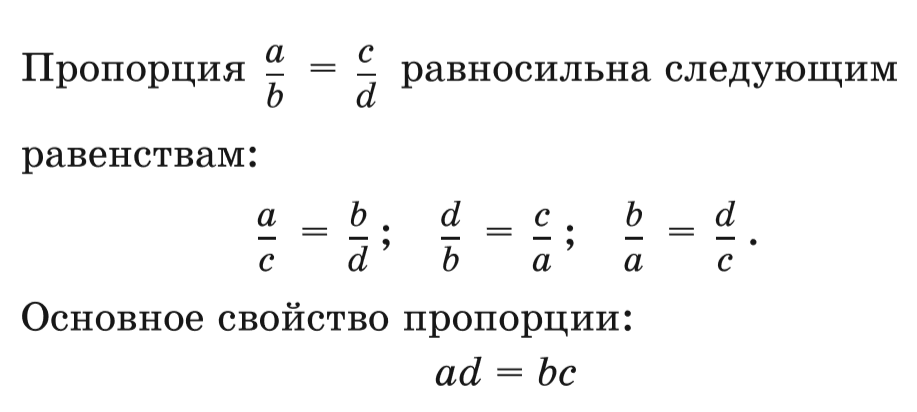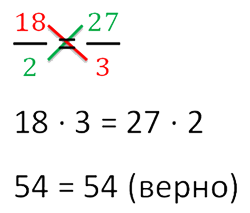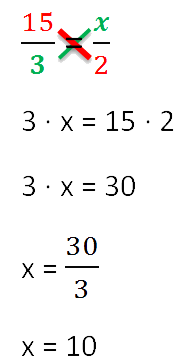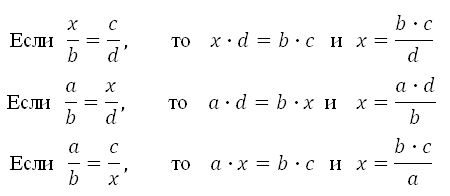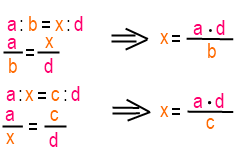Пропорция

Прямая пропорция

Прямая пропорция это взаимоотношение величин при котором, увеличивая одну величину, мы автоматически увеличим другую. Самый простой пример это булочки в магазине и цена на них. Булочка в любом случае стоит 30 руб. Покупая одну штуку мы платим 30 руб.

Если увеличим размер покупки, то соразмерно возрастет и цена. Она не может не возрасти, ведь булочник не будет отдавать свой товар просто так. За 2 булочки мы заплатим 60 рублей, за 3 – 90 и так далее.

Если устанавливать зависимость между количеством булочек и ценой на них, то получится следующее отношение:

Цена булочек/количество=30/1=60/2 и так далее. Заметим, что всегда это отношение равно одному и тому же числу. В данном примере это число 30. Оно будет постоянным для любого варианта данной пропорции. Конкретно в данном примере это число является одновременно и ценой одной булочки.

Иными словами, для приведенного примера пропорциональность можно объяснить так: сколько бы булочек мы ни купили, все равно цена одной будет 30 рублей. Вот и все. В рамках математики говорят, что если коэффициент пропорциональности не меняется, то числа пропорциональны.

Для того, чтобы понять, изменяется коэффициент или нет, нужно просто поделить друг на друга числа этой пропорции и сравнить результат. То есть, взять сначала отношение цены одной булочки к ее количеству, а затем цены 30 булочек к их количеству. Коэффициент сохранит свое значение, значит эти числа прямопропорциональны.

Задачи на обратную пропорциональность

Чтобы стало понятнее, давайте разберем несколько задач. Они не слишком сложные, а их решение поможет вам наглядно представить, что такое обратная пропорциональность и как эти знания могут пригодиться в вашей обычной жизни.

Задача №1.
Автомобиль движется со скоростью 60 км/ч. Чтобы доехать до места назначения, ему потребовалось 6 часов. Сколько времени ему потребуется, чтобы преодолеть такое же расстояние, если он будет двигаться со скоростью в 2 раза выше?

Можем начать с того, что запишем формулу, которая описывает отношения времени, расстояния и скорости: t = S/V. Согласитесь, она очень напоминает нам функцию обратной пропорциональности. И свидетельствует о том, что время, которое автомобиль проводит в пути, и скорость, с которой он движется, находятся в обратной пропорциональности.

Чтобы убедиться в этом, давайте найдем V 2 , которая по условию выше в 2 раза: V 2 = 60 * 2 = 120 км/ч. Затем рассчитаем расстояние по формуле S = V * t = 60 * 6 = 360 км. Теперь совсем несложно узнать время t 2 , которое требуется от нас по условию задачи: t 2 = 360/120 = 3 ч.

Как видите время в пути и скорость движения действительно обратно пропорциональны: со скоростью в 2 раза выше изначальной автомобиль потратит в 2 раза меньше времени на дорогу.

Решение этой задачи можно записать и в виде пропорции. Для чего сначала составим такую схему:

↓ 60 км/ч – 6 ч

↓120 км/ч – х ч

Стрелки обозначают обратно пропорциональную зависимость. А также подсказывают, что при составлении пропорции правую часть записи надо перевернуть: 60/120 = х/6. Откуда получаем х = 60 * 6/120 = 3 ч.

Задача №2.
В мастерской трудятся 6 рабочих, которые с заданным объемом работы справляются за 4 часа. Если количество рабочих сократить в 2 раза, сколько времени потребуется оставшимся, чтобы выполнить тот же объем работы?

Запишем условия задачи в виде наглядной схемы:

↓ 6 рабочих – 4 ч

↓ 3 рабочих – х ч

Запишем это в виде пропорции: 6/3 = х/4. И получим х = 6 * 4/3 = 8 ч. Если рабочих станет в 2 раза меньше, оставшиеся затратят на выполнение всей работы в 2 раза больше времени.

Задача №3.
В бассейн ведут две трубы. Через одну трубу вода поступает со скоростью 2 л/с и наполняет бассейн за 45 минут. Через другую трубу бассейн наполнится за 75 минут. С какой скоростью вода поступает в бассейн через эту трубу?

Для начала приведем все данные нам по условию задачи величины к одинаковым единицам измерения. Для этого выразим скорость наполнения бассейна в литрах в минуту: 2 л/с = 2 * 60 = 120 л/мин.

Поскольку из условия следует, что через вторую трубу бассейн заполняется медленнее, значит, и скорость поступления воды ниже. На лицо обратная пропорциональность. Неизвестную нам скорость выразим через х и составим такую схему:

↓ 120 л/мин – 45 мин

↓ х л/мин – 75 мин

А затем составим пропорцию: 120/х = 75/45, откуда х = 120 * 45/75 = 72 л/мин.

В задаче скорость наполнения бассейна выражена в литрах в секунду, приведем полученный нами ответ к такому же виду: 72/60 = 1,2 л/с.

Задача №4.
В небольшой частной типографии печатают визитки. Сотрудник типографии работает со скоростью 42 визитки в час и трудится полный рабочий день – 8 часов. Если бы он работал быстрее и печатал 48 визиток за час, насколько раньше он смог бы уйти домой?

Идем проверенным путем и составляем по условию задачи схему, обозначив искомую величину как х:

↓ 42 визитки/ч – 8 ч

↓ 48 визитки/ч – х ч

Перед нами обратно пропорциональная зависимость: во сколько раз больше визиток в час напечатает сотрудник типографии, во столько же раз меньше времени ему потребуется на выполнение одной и той же работы. Зная это, составим пропорцию:

42/48 = х/8, х = 42 * 8/48 = 7ч.

Таким образом, справившись с работой за 7 часов, сотрудник типографии смогу бы уйти домой на час раньше.

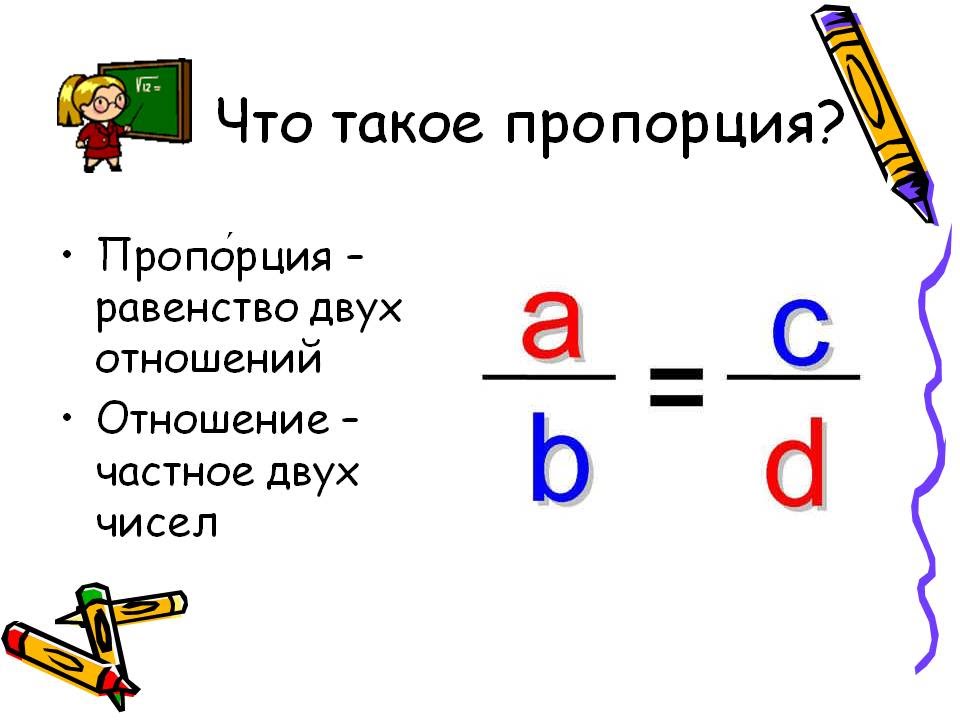
Что такое пропорция?

Пропорцией называют равенство двух отношений. Например, отношение  равно отношению 

Данная пропорция читается следующим образом:

Десять так относится к пяти, как два относится к одному

Дроби, из которых составлена пропорция, всегда равны. Например, если в пропорции выполнить деление в обеих дробях, то получится число 2 в обеих частях:

Предположим, что в классе 10 девочек и 5 мальчиков

Запишем отношение десяти девочек к пяти мальчикам:

10 : 5

Преобразуем данное отношение в дробь

Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки

Теперь рассмотрим другой класс в котором две девочки и один мальчик

Запишем отношение двух девочек к одному мальчику:

2 : 1

Преобразуем данное отношение в дробь:

Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:

Можно сделать вывод, что отношение  пропорционально отношению . Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».

В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.

Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам

а также отношение 12 девочек к 2 мальчикам

Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что , поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.

Поэтому отношение  не пропорционально отношению .

Из рассмотренных примеров видно, что пропорция составляется из дробей. Первая рассмотренная нами пропорция  состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.

Вторая рассмотренная нами пропорция была . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями  и  знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.

Рассмотрим пропорцию . Данная пропорция составлена правильно, поскольку отношения    и    равны между собой:

Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2

2 = 2

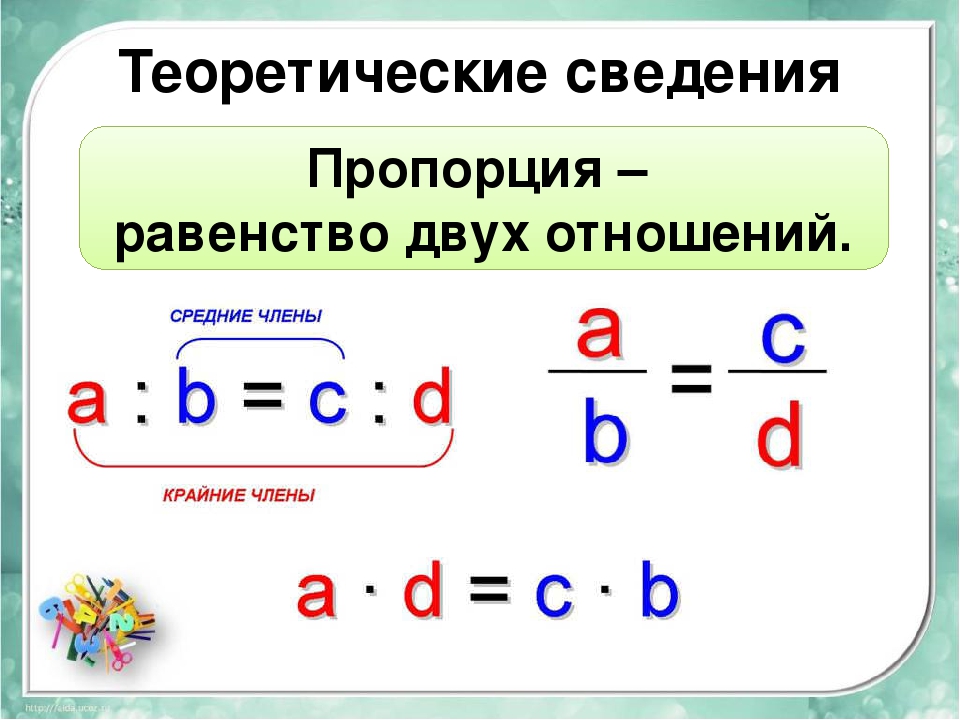
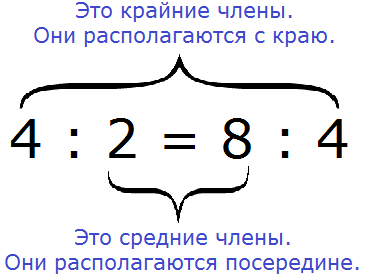
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.

В нашей пропорции    крайние члены это 4 и 4, а средние члены это 2 и 8

Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:

4 : 2 = 8 : 4

Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:

С помощью переменных пропорцию можно записать так:

Данное выражение можно прочесть следующим образом:

a так относится к b, как c относится к d

Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.

Функция и ее график

Функцию обратной пропорциональности можно описать как y = k/x. В котором x ≠ 0 и k ≠ 0.

Эта функция обладает следующими свойствами:

1. Областью ее определения является множество всех действительных чисел, кроме x = 0. D(y): (-∞; 0) U (0; +∞).
2. Областью значений являются все действительные числа, кроме y = 0. Е(у): (-∞; 0) U (0; +∞).
3. Не имеет наибольших и наименьших значений.
4. Является нечетной и ее график симметричен относительно начала координат.
5. Непериодическая.
6. Ее график не пересекает оси координат.
7. Не имеет нулей.
8. Если k > 0 (т.е. аргумент возрастает), функция пропорционально убывает на каждом из своих промежутков. Если k < 0 (т.е. аргумент убывает), функция пропорционально возрастает на каждом из своих промежутков.
9. При возрастании аргумента (k > 0) отрицательные значения функции находятся в промежутке (-∞; 0), а положительные – (0; +∞). При убывании аргумента (k < 0) отрицательные значения расположены на промежутке (0; +∞), положительные – (-∞; 0).

График функции обратной пропорциональности называется гиперболой. Изображается следующим образом:

Рассмотрим пример, который поможет разобраться в понятии прямой пропорциональности.

Скорость мотоциклиста 30 км/ч. Какое расстояние он проедет за 2 часа, за 4 часа, за 6 часов, за 8 часов?

Чтобы данные были наглядными составим таблицу.

Чтобы найти расстояние, нужно скорость умножить на время:

Заполним таблицу, подставляя вместо времени 2 ч, 4 ч, 6 ч и 8 ч.

Из таблицы видно, что если скорость остается неизменной, то при увеличении времени в 2 раза, расстояние увеличивается также 2 раза.

Время в пути было 2 ч – мотоциклист проехал 60 км.

Увеличиваем время в 2 раза, и теперь оно 4 ч (2*2=4) – расстояние увеличивается также в 2 раза и становится равным 120 км (60*2=120).

Увеличиваем время в 3 раза, и теперь оно 6 ч (2*3=6) – расстояние увеличивается также в 3 раза и становится равным 180 км (60*3=180).

Увеличиваем время в 4 раза, и теперь оно 8 ч (2*4=8) – расстояние увеличивается также в 4 раза и становится равным 240 км (60*4=240).

Исследование функции прямой пропорциональности $f(x)=kx$ и её график

Вначале рассмотрим функцию $f\left(x\right)=kx$, где $k > 0$.

1. Область определения — все числа.
2. Область значения — все числа.
3. $f\left(-x\right)=-kx=-f(x)$. Функция прямой пропорциональности нечетна.
4. Функция проходит через начало координат.
5. $f’\left(x\right)={\left(kx\right)}’=k>0$. Следовательно, данная функция возрастает на всей области определения. Точек экстремума нет.
6. $f^{»}\left(x\right)=k’=0$. Следовательно, функция не имеет точек перегиба.
7. ${\mathop{lim}_{x\to -\infty } kx\ }=-\infty $, ${\mathop{lim}_{x\to +\infty } kx\ }=+\infty $
8. График (рис. 1).

Рис. 1. График функции $y=kx$, при $k>0$

Теперь рассмотрим функцию $f\left(x\right)=kx$, где $k

1. Область определения — все числа.
2. Область значения — все числа.
3. $f\left(-x\right)=-kx=-f(x)$. Функция прямой пропорциональности нечетна.
4. Функция проходит через начало координат.

5. $f’\left(x\right)={\left(kx\right)}’=k

6. $f^{»}\left(x\right)=k’=0$. Следовательно, функция не имеет точек перегиба.
7. ${\mathop{lim}_{x\to -\infty } kx\ }=+\infty $, ${\mathop{lim}_{x\to +\infty } kx\ }=-\infty $
8. График (рис. 2).

Рис. 2. График функции $y=kx$, при $k

Важно: для построения графика функции $y=kx$ достаточно найти одну, отличную от начала координат точку $\left(x_0,\ y_0\right)$ и провести прямую через эту точку и начало координат

Примеры задач

А теперь решим пару задач на прямую пропорциональность

Начнем с простого.

Задача 1: Представьте, что 5 куриц за 5 дней снесли 5 яиц. А если будет 20 куриц, сколько яиц они снесут за 20 дней?

Решение: Обозначим неизвестное какх. И рассуждать будем следующим образом: во сколько раз больше куриц стало? Разделим 20 на 5 и узнаем, что в 4 раза. А во сколько раз больше яиц снесут 20 куриц за те же 5 дней? Тоже в 4 раза больше. Значит, находим нашх так: 5*4*4 = 80 яиц снесут 20 куриц за 20 дней.

Теперь пример чуть сложнее, перефразируем задачу из «Всеобщей арифметики» Ньютона. Задача 2: Писатель за 8 дней может сочинить 14 страниц новой книги. Если бы у него были помощники, сколько бы человек понадобилось, чтобы написать 420 страниц за 12 дней?

Решение: Рассуждаем, что количество человек (писатель + помощники) увеличивается с увеличением объема работы, если бы ее пришлось сделать за то же количество времени. Но во сколько раз? Разделив 420 на 14, узнаем, что увеличивается в 30 раз. Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз, а таким образом: х = 1 (писатель) * 30 (раз) : 12/8 (дней). Преобразуем и выясним, что х = 20 человек напишут 420 страниц за 12 дней.

Решим еще задачу, похожую на те, что были у нас в примерах.

Задача 3: В одно и то же путешествие отправилось два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найдите скорость второго автомобиля.

Решение: Как вы помните, путь определяется через скорость и время – S = V *t. Поскольку путь оба автомобиля проделали одинаковый, мы можем приравнять два выражения: 70*2 = V*7. Откуда найдем, что скорость второго автомобиля, это V = 70*2/7 = 20 км/ч.

И еще пару примеров заданий с функциями прямой пропорциональности. Иногда в задачах требуется найти коэффициент k.

Задача 4: Даны функции у = — х/16 и у = 5х/2, определите их коэффициенты пропорциональности.

Решение: Как вы помните, k = у/х. Значит, для первой функции коэффициент равен -1/16, а для второй k = 5/2.

А еще вам может встретиться задание, как Задача 5: Запишите формулой прямую пропорциональность. Ее график и график функции у = -5х + 3 расположены параллельно.

Решение: Функция, которая дана нам в условии, – линейная. Нам известно, что прямая пропорциональность – частный случай линейной функции. А также мы знаем, что если коэффициенты k функций равны, их графики параллельны. Значит, все, что требуется – это вычислить коэффициент известной функции и задать прямую пропорциональность по знакомой нам формуле: y = k*x. Коэффициент k = -5, прямая пропорциональность: у = -5*х.

Прямая пропорциональность

При наличии два переменных х и у , у находится прямо пропорционально к й , если существует ненулевая константа K такой , что

yзнак равноkИкс.{\ displaystyle y = kx.}

Unicode символы

U + 221D ∝ ПРОПОРЦИОНАЛЬНО (HTML   · ) U + 007E ~ ТИЛЬДА (HTML ) U + 223C ∼ ТИЛЬДНЫЙ ОПЕРАТОР (HTML   · ) U + 223A ∺ ГЕОМЕТРИЧЕСКАЯ ПРОПОРЦИЯ (HTML   · ) См. Также: знак равенства

Отношение часто обозначается символами «∝» (не путать с греческой буквой альфа ) или «~»:

y∝Икс,{\ displaystyle y \ propto x,} или y∼Икс.{\ displaystyle y \ sim x.}

Для получения от константы пропорциональности может быть выражена как отношение
Икс≠{\ Displaystyle х \ neq 0}

kзнак равноyИкс.{\ displaystyle k = {\ frac {y} {x}}.}

Ее также называют постоянной вариации или постоянной пропорциональности .

Прямая пропорциональность также можно рассматривать в качестве линейного уравнения в двух переменных с у -intercept из и наклон от к . Это соответствует линейному росту .

Примеры

• Если объект движется с постоянной скоростью , то пройденное расстояние прямо пропорционально времени, затраченному на путешествие, а скорость является константой пропорциональности.
• Окружность из круга прямо пропорциональна его диаметр , с константой пропорциональности , равная П .
• На карте достаточно небольшой географической области, нарисованной в масштабе расстояний, расстояние между любыми двумя точками на карте прямо пропорционально прямому расстоянию между двумя местоположениями, представленными этими точками; константа пропорциональности — это масштаб карты.
• Сила , действующая на небольшой объект с небольшой массой по близлежащей большой расширенной массы за счет силы тяжести , прямо пропорциональна массе объекта; константа пропорциональности между силой и массой известна как ускорение свободного падения .
• Суммарная сила, действующая на объект, пропорциональна ускорению этого объекта относительно инерциальной системы отсчета. Константа пропорциональности в этом втором законе Ньютона — это классическая масса объекта.

Обратная пропорциональность.

И прямую и обратную пропорциональность проще рассматривать на задачах движения. Представим себе автомобиль, который едет со скоростью 90 км в час. Если примем расстояние между двумя городами за 180 км, то такой путь машина должна проехать за 2 часа. Пока все понятно.

Но что будет, если водитель поспешит и увеличит скорость до 180 км/ч, то требуемый отрезок пути он проедет быстрее. То есть на тоже расстояние водитель потратит не 2 часа, а 1. То есть, увеличение скорости привело к уменьшению времени в дороге.

А что будет, если водитель уменьши скорость в два раза? Со 120 км/ч до 60 км/ч? Значит, время в пути увеличится так же в два раза и будет составлять не 2, а 4 ч. Так уменьшение скорости привело к увеличению времени в пути.

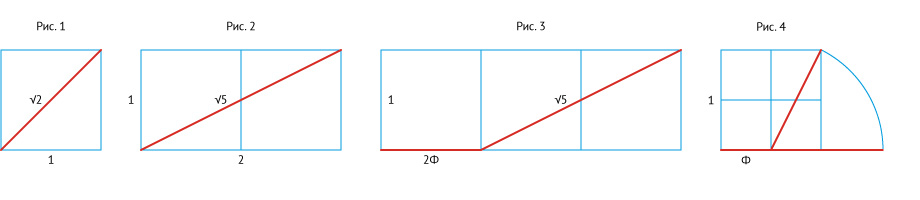
Геометрическая иллюстрация

Когда дублирование данного прямоугольника сохраняет свою форму, отношение большого измерения к маленькому измерению — постоянное число во всех копиях, и в оригинальном прямоугольнике. Самый большой прямоугольник рисунка подобен одному или другому прямоугольнику с полосами. От их ширины до их высоты коэффициент — отношение их размеров, горизонтально написанных в пределах изображения, наверху или основания, определяет общую форму трех подобных прямоугольников.

Общая диагональ подобных прямоугольников делит каждый прямоугольник на два superposable треугольника с двумя различными видами полос. У четырех полосатых треугольников и двух полосатых прямоугольников есть общая вершина: центр homothetic преобразования с отрицательным отношением −k или, который преобразовывает один треугольник и его полосы в другой треугольник с теми же самыми полосами, увеличенными или уменьшенными. Масштаб дублирования полосатого треугольника — пропорциональность, постоянная между соответствующими длинами сторон треугольников, равных положительному отношению, косвенно написанному в пределах изображения: или

В пропорции условия a и d называют крайностями, в то время как b и c — средства, потому что a и d — чрезвычайные условия списка, в то время как b и c посреди списка. От любой пропорции мы получаем другую пропорцию, инвертируя крайности или средства. И продукт крайностей равняется продукту средств. В пределах изображения двойная стрелка указывает на два перевернутых условия первой пропорции.

Рассмотрите деление самого большого прямоугольника в двух треугольниках, сокращающихся вдоль диагонали. Если мы удаляем два треугольника из любой половины прямоугольника, мы получаем один из простых серых прямоугольников. Выше и ниже этой диагонали, области двух самых больших треугольников рисунка равны, потому что эти треугольники superposable. Выше и ниже вычтенных областей равны по той же самой причине. Поэтому, у двух простых серых прямоугольников есть та же самая область:

Прямая пропорциональность

Учитывая две переменные x и y, y ‘непосредственно пропорционален x (x, и y варьируются непосредственно, или x, y находится в прямом изменении), если есть постоянный k отличный от нуля, таким образом что

Отношение часто обозначается, используя ∝ символ, как

и постоянное отношение

назван пропорциональностью, постоянной, постоянной из изменения или постоянной из пропорциональности.

Примеры

• Если объект едет на постоянной скорости, то расстояние поехало, непосредственно пропорционально времени, проведенному, путешествуя, со скоростью, являющейся константой пропорциональности.
• Окружность круга непосредственно пропорциональна его диаметру с константой пропорциональности, равной π.
• На чертившей в масштабе карте расстояние между любыми двумя пунктами на карте непосредственно пропорционально расстоянию между двумя местоположениями, которые пункты представляют с константой пропорциональности, являющейся масштабом карты.
• Сила, действующая на определенный объект из-за силы тяжести, непосредственно пропорциональна массе объекта; константа пропорциональности между массой и силой известна как гравитационное ускорение.

Свойства

С тех пор

эквивалентно

из этого следует, что, если y непосредственно пропорционален x с пропорциональностью (отличной от нуля) постоянный k, то x также непосредственно пропорционален y с пропорциональностью постоянный 1/К.

Если y будет непосредственно пропорционален x, то граф y как функция x будет прямой линией, проходящей через происхождение с наклоном линии, равной константе пропорциональности: это соответствует линейному росту.

Источники

Wikimedia Foundation
.
2010
.

• Второй закон Ньютона
• Кулоновский барьер

Смотреть что такое «Прямая пропорциональность» в других словарях:

прямая пропорциональность
— — Тематики энергетика в целом EN direct ratio … Справочник технического переводчика

прямая пропорциональность
— tiesioginis proporcingumas statusas T sritis fizika atitikmenys: angl. direct proportionality vok. direkte Proportionalität, f rus. прямая пропорциональность, f pranc. proportionnalité directe, f … Fizikos terminų žodynas

ПРОПОРЦИОНАЛЬНОСТЬ
— (от лат. proportionalis соразмерный, пропорциональный). Соразмерность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПРОПОРЦИОНАЛЬНОСТЬ отлат. proportionalis, пропорциональный. Соразмерность. Объяснение 25000… … Словарь иностранных слов русского языка

ПРОПОРЦИОНАЛЬНОСТЬ
— ПРОПОРЦИОНАЛЬНОСТЬ, пропорциональности, мн. нет, жен. (книжн.). 1. отвлеч. сущ. к пропорциональный. Пропорциональность частей. Пропорциональность телосложения. 2. Такая зависимость между величинами, когда они пропорционально (см. пропорциональный … Толковый словарь Ушакова

Пропорциональность
— Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.. Содержание 1 Пример 2 Коэффициент пропорциональности … Википедия

ПРОПОРЦИОНАЛЬНОСТЬ
— ПРОПОРЦИОНАЛЬНОСТЬ, и, жен. 1. см. пропорциональный. 2. В математике: такая зависимость между величинами, при к рой увеличение одной из них влечёт за собой изменение другой во столько же раз. Прямая п. (при к рой с увеличением одной величины… … Толковый словарь Ожегова

пропорциональность
— и; ж. 1. к Пропорциональный (1 зн.); соразмерность. П. частей. П. телосложения. П. представительства в парламенте. 2. Матем. Зависимость между пропорционально изменяющимися величинами. Коэффициент пропорциональности. Прямая п. (при которой с… … Энциклопедический словарь

Две величины называются прямо пропорциональными
, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз. Соответственно, при уменьшении одной из них в несколько раз, другая уменьшается во столько же раз.

Зависимость между такими величинами — прямая пропорциональная зависимость. Примеры прямой пропорциональной зависимости:

1) при постоянной скорости пройденный путь прямо пропорционально зависит от времени;

2) периметр квадрата и его сторона — прямо пропорциональные величины;

3) стоимость товара, купленного по одной цене, прямо пропорционально зависит от его количества.

Чтобы отличить прямую пропорциональную зависимость от обратной можно использовать пословицу: «Чем дальше в лес, тем больше дров».

Задачи на прямо пропорциональные величины удобно решать с помощью пропорции.

1) Для изготовления 10 деталей нужно 3,5 кг металла. Сколько металла пойдет на изготовление 12 таких деталей?

(Рассуждаем так:

1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

2. Чем больше
деталей, тем больше
металла нужно для их изготовления. Значит, это прямо пропорциональная зависимость.

Пусть х кг металла нужно для изготовления 12 деталей. Составляем пропорцию (в направлении от начала стрелки к ее концу):

12:10=х:3,5

Чтобы найти , надо произведение крайних членов разделить на известный средний член:

Значит, потребуется 4,2 кг металла.

Ответ: 4,2 кг.

2) За 15 метров ткани заплатили 1680 рублей. Сколько стоят 12 метров такой ткани?

(1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

2. Чем меньше ткани покупают, тем меньше за нее надо заплатить. Значит, это прямо пропорциональная зависимость.

3. Поэтому вторая стрелка одинаково направлена с первой).

Пусть х рублей стоят 12 метров ткани. Составляем пропорцию (от начала стрелки к ее концу):

15:12=1680:х

Чтобы найти неизвестный крайний член пропорции, произведение средних членов делим на известный крайний член пропорции:

Значит, 12 метров стоят 1344 рубля.

Ответ: 1344 рубля.

Сегодня мы рассмотрим, какие величины называются обратно пропорциональными, как выглядит график обратной пропорциональности и как все это может вам пригодится не только на уроках математики, но и вне школьных стен.