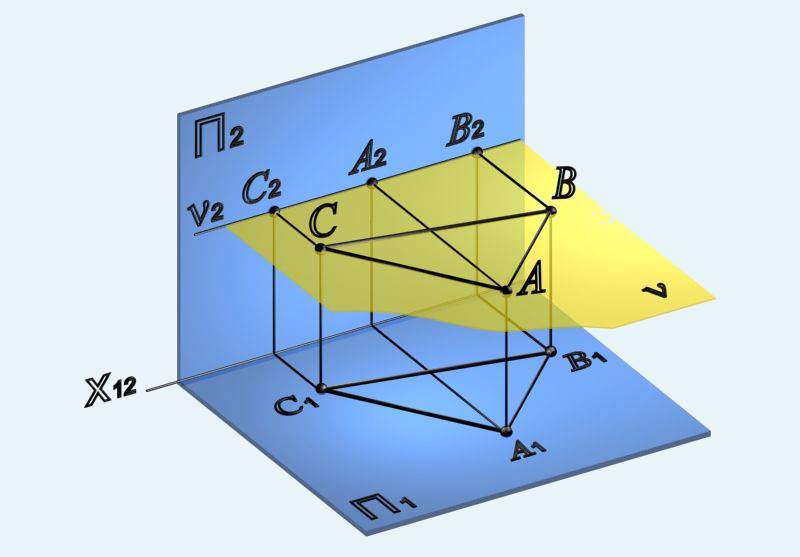
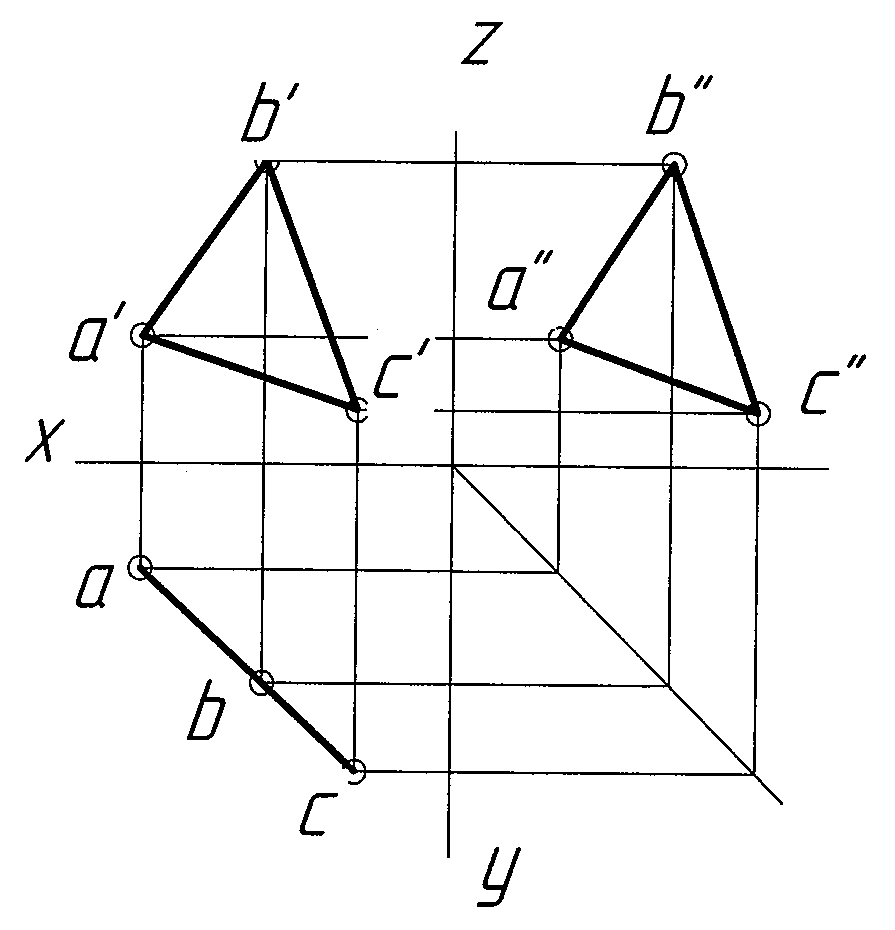Плоскость

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π₁ или π₂.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.

Необходимо отдельно определить видимость на каждой плоскости проекций.

Видимость на π₂ (рис. 3.15)

Выберем точки, конкурирующие на π₂ – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.

Чтобы определить видимость точек на плоскости проекций π₂надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π₂.

Направление взгляда на π₂ показано стрелкой.

По горизонтальным проекциям точек 3 и 4, при взгляде на π₂, видно, что точка 4₁ располагается ближе к наблюдателю, чем 3₁.

4₁∈E₁F₁ ⇒ 4∈EF ⇒ на π₂будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.

Видимость на π₁.

Для определения видимости выберем точки, конкурирующие на π₁ – точки 2 и 5.

Чтобы определить видимость точек на плоскости проекций π₁надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π₁.

Направление взгляда на π₁ показано стрелкой.

По фронтальным проекциям точек 2 и 5, при взгляде на π₁, видно, что точка 2₂ располагается ближе к наблюдателю, чем 5₂.

2₂∈А₂В₂ ⇒ 2∈АВ ⇒ на π₁будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.

Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

Вариации и обобщения

Плоскости в неевклидовом пространстве

Метрика плоскости не обязана быть евклидовой. В зависимости от введенных отношений инцидентности точек и прямых, различают проективные, аффинные, гиперболические и эллиптические плоскости.

Многомерные плоскости

Пусть дано n-мерное аффинное-конечномерное пространство Kn(V,P){\displaystyle K^{n}(V,P)}, над полем действительных чисел. В нём выбрана прямоугольная система координат O,e1→,…,en→{\displaystyle O,{\vec {e_{1}}},…,{\vec {e_{n}}}}. m-плоскостью называется множество точек α{\displaystyle \alpha }, радиус векторы которых удовлетворяют следующему соотношению α={x∣x=Anmtm→+d→}.{\displaystyle \alpha =\{x\mid x=A_{nm}{\vec {t_{m}}}+{\vec {d}}\}.} Anm{\displaystyle A_{nm}} — матрица, столбцы которой образует направляющие подпространство плоскости, t→{\displaystyle {\vec {t}}} — вектор переменных, d→{\displaystyle {\vec {d}}} — радиус-вектор одной из точек плоскости.
Указанное соотношение можно из матрично-векторного вида перевести в векторный:x=a1→t1+…+am→tm+d,ai→∈V{\displaystyle x={\vec {a_{1}}}t_{1}+\ldots +{\vec {a_{m}}}t_{m}+d,{\vec {a_{i}}}\in V} — векторное уравнение m-плоскости.
Вектора ai→{\displaystyle {\vec {a_{i}}}} образуют направляющее подпространство. Две m-плоскости α,β{\displaystyle \alpha ,\beta } называются параллельными, если их направляющие пространства совпадают и ∃x∈αx∉β{\displaystyle \exists x\in \alpha :x\notin \beta }.

(n-1)-плоскость в n-мерном пространстве называется гиперплоскостью или просто плоскостью. Для гиперплоскости существует общее уравнение плоскости. Пусть n→{\displaystyle {\vec {n}}} — нормальный вектор плоскости, r→=(x1,…,xn){\displaystyle {\vec {r}}=(x^{1},…,x^{n})} — вектор переменных, r→{\displaystyle {\vec {r_{0}}}} — радиус вектор точки, принадлежащей плоскости, тогда:(r→−r→,n→)={\displaystyle ({\vec {r}}-{\vec {r_{0}}},{\vec {n}})=0} — общее уравнение плоскости.
Имея матрицу направляющих векторов, уравнение можно записать так: det(r→−r→|An,n−1)={\displaystyle \det({\vec {r}}-{\vec {r_{0}}}|A_{n,n-1})=0}, или:|x1−x1a11a21…an−11×2−x2a12a21…an−12…………xn−xna1na2n…an−1n|={\displaystyle {\begin{vmatrix}x^{1}-x_{0}^{1}&a_{1}^{1}&a_{2}^{1}&…&a_{n-1}^{1}\\x^{2}-x_{0}^{2}&a_{1}^{2}&a_{2}^{1}&…&a_{n-1}^{2}\\…&…&…&…\\x^{n}-x_{0}^{n}&a_{1}^{n}&a_{2}^{n}&…&a_{n-1}^{n}\end{vmatrix}}=0}.Углом между плоскостями называется наименьший угол между их нормальными векторами.

Примером 1-плоскости в трёхмерном пространстве (n=3) служит прямая. Её векторное уравнение имеет вид: α={ax,ay,az}t+{bx,by,bz}{\displaystyle \alpha =\{a_{x},a_{y},a_{z}\}t+\{b_{x},b_{y},b_{z}\}}. В случае n = 2 прямая является гиперплоскостью.

Гиперплоскость в трёхмерном пространстве соответствует привычному понятию плоскости.

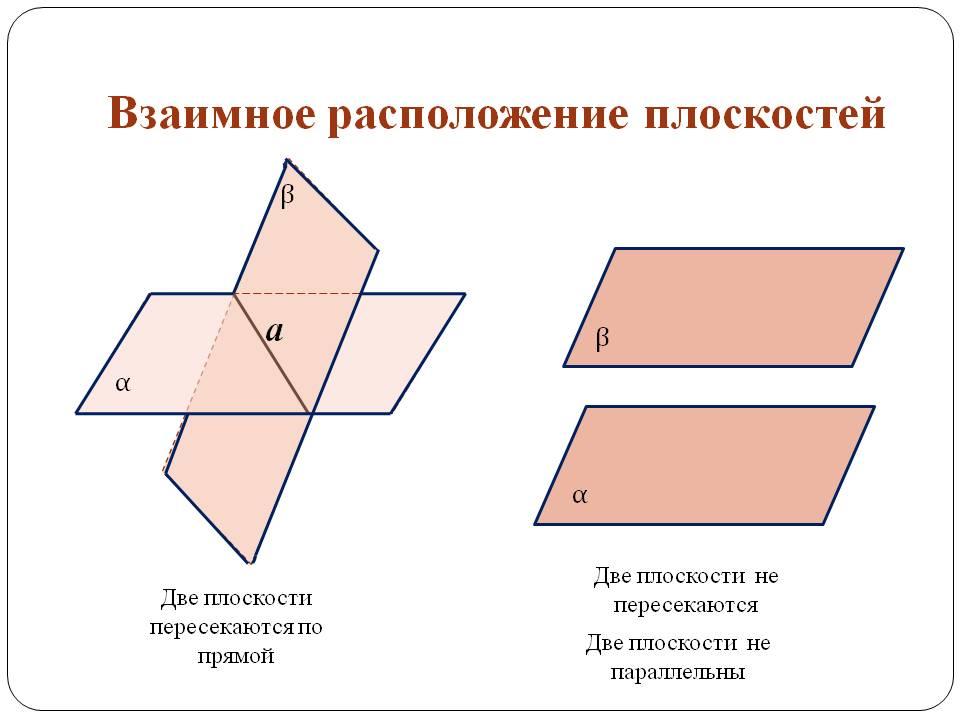
Взаимное расположение плоскостей

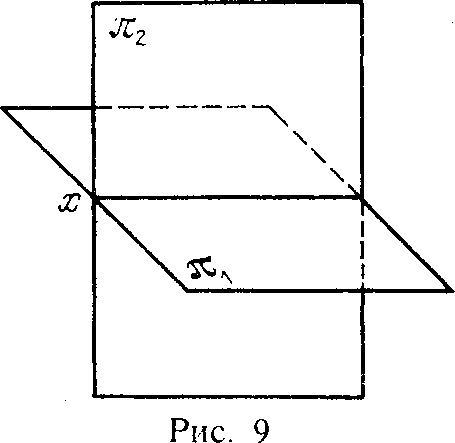
Плоскости в пространстве могут совпадать, пересекаться или быть параллельными.

Плоскости параллельны, если попарно параллельны две пересекающиеся прямые в каждой из плоскостей.

Пересекаться плоскости могут только по прямой. В этом случае плоскости образуют угол. Чтобы найти его численные значения нужно в каждой из плоскостей провести прямую перпендикулярную прямой пересечения плоскостей. Эти две прямые и образуют угол плоскостей. Эти свойства иногда называют правилами плоскостей.

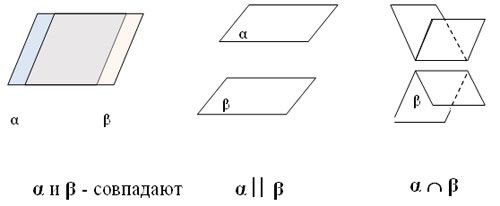
Рис. 3. Расположение плоскостей.

Что мы узнали?

Мы дали определение и привели примеры плоскости. Выделили варианты пересечения прямой и плоскости и пересечения плоскостей. Привели несколько признаков, относящихся с плоскостям и разобрали все случаи существования плоскостей в пространстве.

Тест по теме

Вопрос 1 из 5

Выбрать неверное утверждение:
- Геометрия состоит из двух разделов: планометрия и стереометрия
- Плоскость — это основная единица планометрии
- Плоскость представляет поверхность, содержащую прямые, соединяющие любые ее точки
- Планометрия – это геометрия объемных фигур

Начать тест(новая вкладка)

Связанные понятия

cos⁡φ=A1A2+B1B2+C1C2(A12+B12+C12)(A22+B22+C22);{\displaystyle \cos \varphi ={\frac {A_{1}A_{2}+B_{1}B_{2}+C_{1}C_{2}}{\sqrt {(A_{1}^{2}+B_{1}^{2}+C_{1}^{2})(A_{2}^{2}+B_{2}^{2}+C_{2}^{2})}}};}

Если в векторной форме, то

cos⁡φ=(N1,N2)|N1||N2|.{\displaystyle \cos \varphi ={\frac {(\mathbf {N_{1}} ,\mathbf {N_{2}} )}{|\mathbf {N_{1}} ||\mathbf {N_{2}} |}}.}

Плоскости параллельны, если

A1A2=B1B2=C1C2{\displaystyle {\frac {A_{1}}{A_{2}}}={\frac {B_{1}}{B_{2}}}={\frac {C_{1}}{C_{2}}}} или N1,N2={\displaystyle =0.} (Векторное произведение)

Плоскости перпендикулярны, если

A1A2+B1B2+C1C2={\displaystyle A_{1}A_{2}+B_{1}B_{2}+C_{1}C_{2}=0} или (N1,N2)={\displaystyle (\mathbf {N_{1}} ,\mathbf {N_{2}} )=0}. (Скалярное произведение)

Пучок плоскостей — все плоскости, проходящие через линию пересечения двух плоскостей. Уравнение пучка плоскостей, то есть любой плоскости, проходящей через линию пересечения двух плоскостей, имеет вид:222:

α(A1x+B1y+C1z+D1)+β(A2x+B2y+C2z+D2)=,{\displaystyle \alpha (A_{1}x+B_{1}y+C_{1}z+D_{1})+\beta (A_{2}x+B_{2}y+C_{2}z+D_{2})=0,}

где α{\displaystyle \alpha } и β{\displaystyle \beta } — любые числа, не равные одновременно нулю. Уравнение самой этой линии можно найти из уравнения пучка, подставляя α=1, β=0 и α=0, β=1.

Связка плоскостей — все плоскости, проходящие через точку пересечения трёх плоскостей:224. Уравнение связки плоскостей, то есть любой плоскости, проходящей через точку пересечения трёх плоскостей, имеет вид:

α(A1x+B1y+C1z+D1)+β(A2x+B2y+C2z+D2)+γ(A3x+B3y+C3z+D3)=,{\displaystyle \alpha (A_{1}x+B_{1}y+C_{1}z+D_{1})+\beta (A_{2}x+B_{2}y+C_{2}z+D_{2})+\gamma (A_{3}x+B_{3}y+C_{3}z+D_{3})=0,}

где α{\displaystyle \alpha }, β{\displaystyle \beta } и γ{\displaystyle \gamma } — любые числа, не равные одновременно нулю. Саму эту точку можно найти из уравнения связки, подставляя α=1, β=0, γ=0; α=0, β=1, γ=0 и α=0, β=0, γ=1 и решая получившуюся систему уравнений.

3.1. Способы задания плоскости на ортогональных чертежах

тремя точками, не лежащими на одной прямой;
прямой и точкой, взятой вне прямой;
двумя пересекающимися прямыми;
двумя параллельными прямыми;
плоской фигурой.

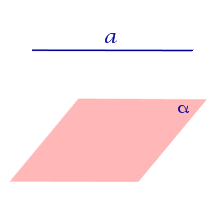
проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
проекциями точки и прямой (Рисунок 3.1,б);
проекциями двух пересекающихся прямых (Рисунок 3.1,в);
проекциями двух параллельных прямых (Рисунок 3.1,г);
плоской фигурой (Рисунок 3.1,д);
следами плоскости;
линией наибольшего ската плоскости.

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

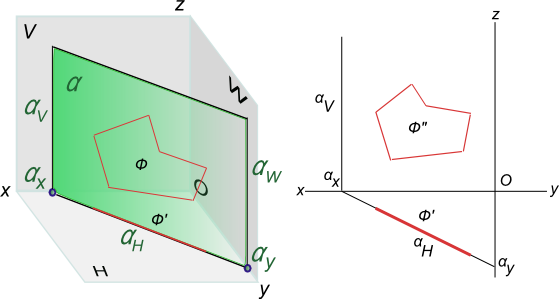
Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

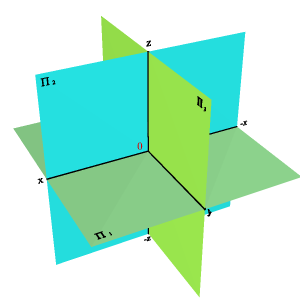
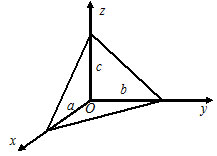
Плоскость общего положения может иметь три следа: горизонтальный – απ₁, фронтальный – απ₂и профильный – απ₃, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π₁, фронтальной π₂и профильной π₃ (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

В словаре Д.Н. Ушакова

ПЛО́СКОСТЬ, плоскости, мн. плоскости, плоскостей, ·жен.1. только ед. ·отвлеч. сущ. к плоский (·книж. ). Плоскость груди. Плоскость острот.2. Поверхность, имеющая только два измерения, так что между любыми двумя точками ее можно провести прямую, которая целиком сольется с этой поверхностью (мат.). Пересечение плоскостей.| Предмет, представляющий собою такую поверхность, имеющий плоскую форму (спец.). Верхняя и нижняя пплоскость биплана.3. перен. Область, сфера, круг каких-нибудь явлений, отношений (·книж. ). Эти вопросы лежат в разных плоскостях.| Точка зрения на что-нибудь, способ рассмотрения, обсуждения чего-нибудь (неол. ·книж. ). Изучить какой-нибудь вопрос в плоскости его экономического значения.4. Плоское замечание (см. плоский в 3 ·знач.), плоская шутка. Говорить плоскости.• Наклонная плоскость (мех.) — простейшая машина, приспособление для облегчения поднятия тяжести. По наклонной плоскости (пойти, катиться) — перен. о неуклонном ухудшении положения (политического, экономического и т.п.), о стремительном, быстром нравственном падении, разложении.

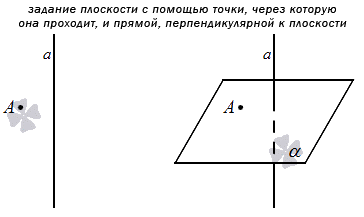
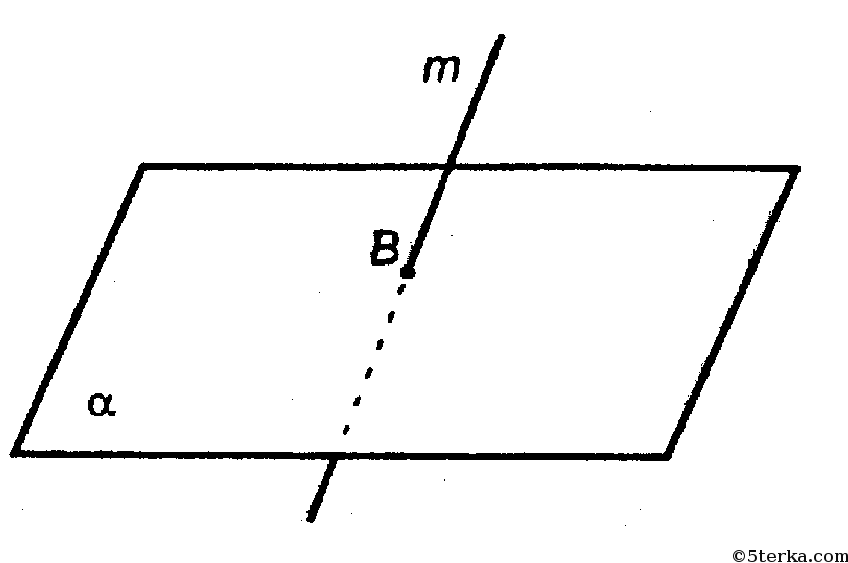
3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

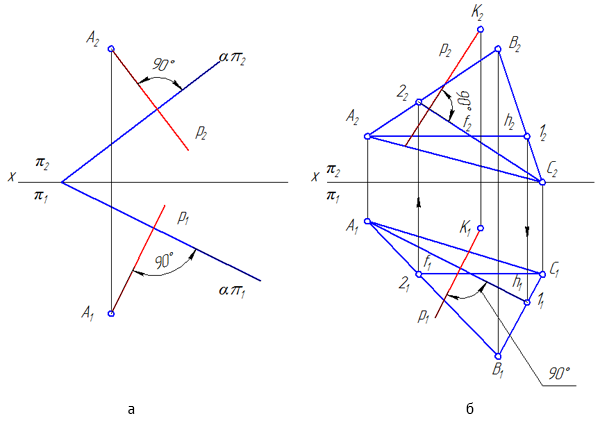
Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.

Построим горизонталь и фронталь в плоскости σ=ΔАВС : σ=ΔАВС : A-1∈σ; A-1//π₁; С-2∈σ; С-2//π₂.
Восстановим из точки K перпендикуляр к заданной плоскости: p₁⊥h₁ и p₂⊥f₂, или p₁⊥απ₁ и p₂⊥απ_2.

Определение плоскости

Плоскость представляет поверхность, содержащую прямые, соединяющие две любые ее точки. Это определение звучит достаточно запутанно, поэтому лучше его запомнить. А для понимания стоит запомнить, что плоскость это прямая поверхность. Любая грань пирамиды это плоскость, так же как стена, поверхность стола или лист бумаги.

Стена является частью плоскости, так как любой другой пример плоскости из реальной жизни это ограниченное пространство, а плоскость безгранична, так же как и линия.

Из плоскостей в планометрии составляются фигуры, как в стереометрии из линий. Яркий пример: четырехугольная пирамида, которая состоит из пяти граней, каждая из которых является частью отдельной плоскости.

Геометрия состоит из двух разделов: планометрия и стереометрия. Фигуры на плоскости, состоящие из линий и точек это раздел стереометрии. Планометрия изучает фигуры из плоскостей, прямых и точек. Проще говоря, планометрия – это геометрия объемных фигур.

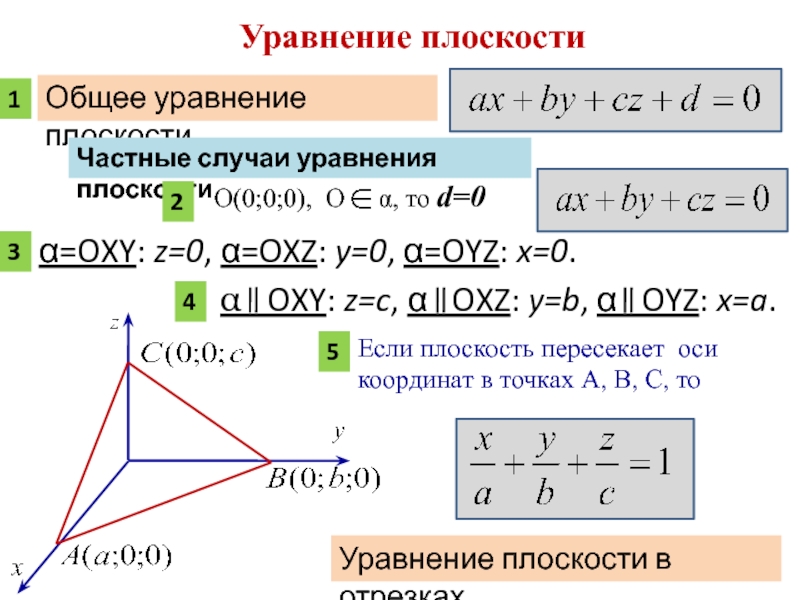
Уравнения плоскости

Впервые встречается у А. К. Клеро ().

Уравнение плоскости в отрезках, по-видимому, впервые встречается у Г. Ламе (—).

Нормальное уравнение ввёл Л. О. Гессе ().

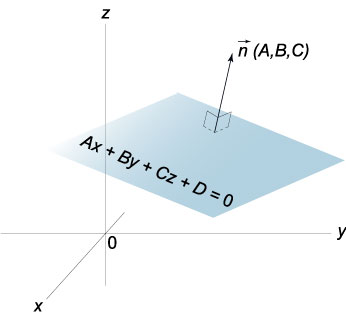
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.

Общее уравнение (полное) плоскости

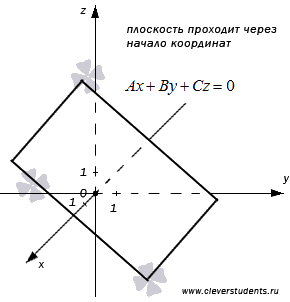
Ax+By+Cz+D=(1){\displaystyle Ax+By+Cz+D=0\qquad (1)}

где A,B,C{\displaystyle A,B,C} и D{\displaystyle D} — постоянные, причём A,B{\displaystyle A,B} и C{\displaystyle C} одновременно не равны нулю; в векторной форме:

(r,N)+D={\displaystyle (\mathbf {r} ,\mathbf {N} )+D=0}

где r{\displaystyle \mathbf {r} } — радиус-вектор точки M(x,y,z){\displaystyle M(x,y,z)}, вектор N=(A,B,C){\displaystyle \mathbf {N} =(A,B,C)} перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора N{\displaystyle \mathbf {N} }:

cos⁡α=AA2+B2+C2,{\displaystyle \cos \alpha ={\frac {A}{\sqrt {A^{2}+B^{2}+C^{2}}}},}

cos⁡β=BA2+B2+C2,{\displaystyle \cos \beta ={\frac {B}{\sqrt {A^{2}+B^{2}+C^{2}}}},}

cos⁡γ=CA2+B2+C2.{\displaystyle \cos \gamma ={\frac {C}{\sqrt {A^{2}+B^{2}+C^{2}}}}.}

Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При D={\displaystyle D=0} плоскость проходит через начало координат, при A={\displaystyle A=0} (или B={\displaystyle B=0}, C={\displaystyle C=0}) плоскость параллельна оси Ox{\displaystyle Ox} (соответственно Oy{\displaystyle Oy} или Oz{\displaystyle Oz}). При A=B={\displaystyle A=B=0} (A=C={\displaystyle A=C=0}, или B=C={\displaystyle B=C=0}) плоскость параллельна плоскости Oxy{\displaystyle Oxy} (соответственно Oxz{\displaystyle Oxz} или Oyz{\displaystyle Oyz}).

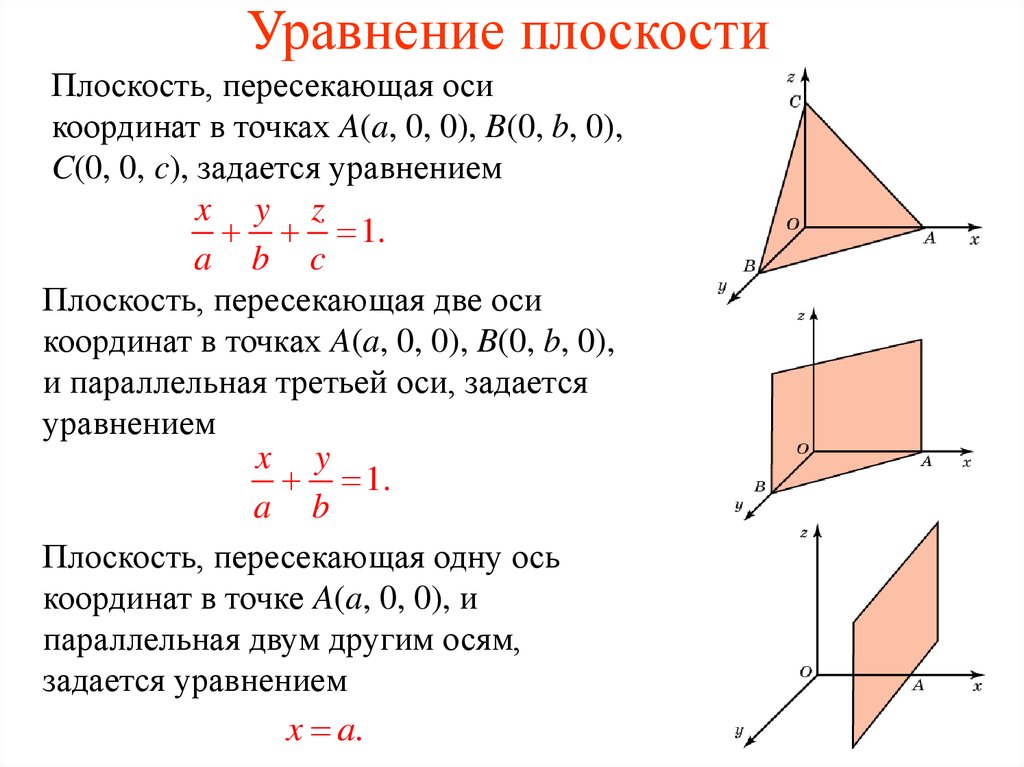
Уравнение плоскости в отрезках:

xa+yb+zc=1,{\displaystyle {\frac {x}{a}}+{\frac {y}{b}}+{\frac {z}{c}}=1,}

где a=−DA{\displaystyle a=-D/A}, b=−DB{\displaystyle b=-D/B}, c=−DC{\displaystyle c=-D/C} — отрезки, отсекаемые плоскостью на осях Ox,Oy{\displaystyle Ox,Oy} и Oz{\displaystyle Oz}.

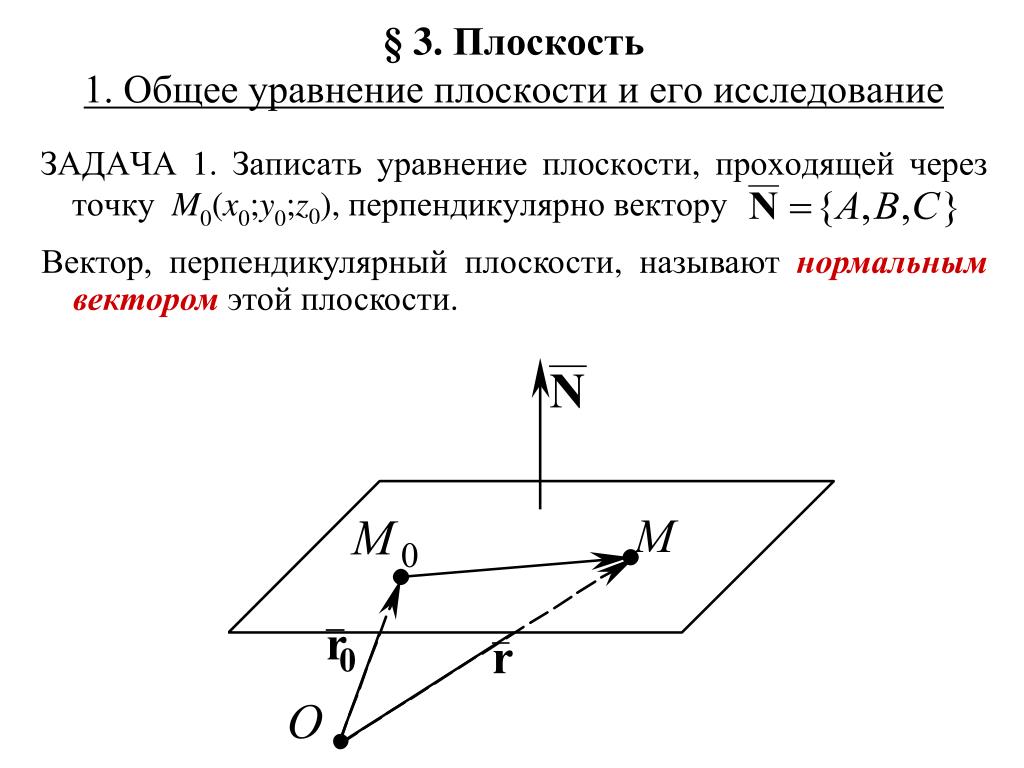
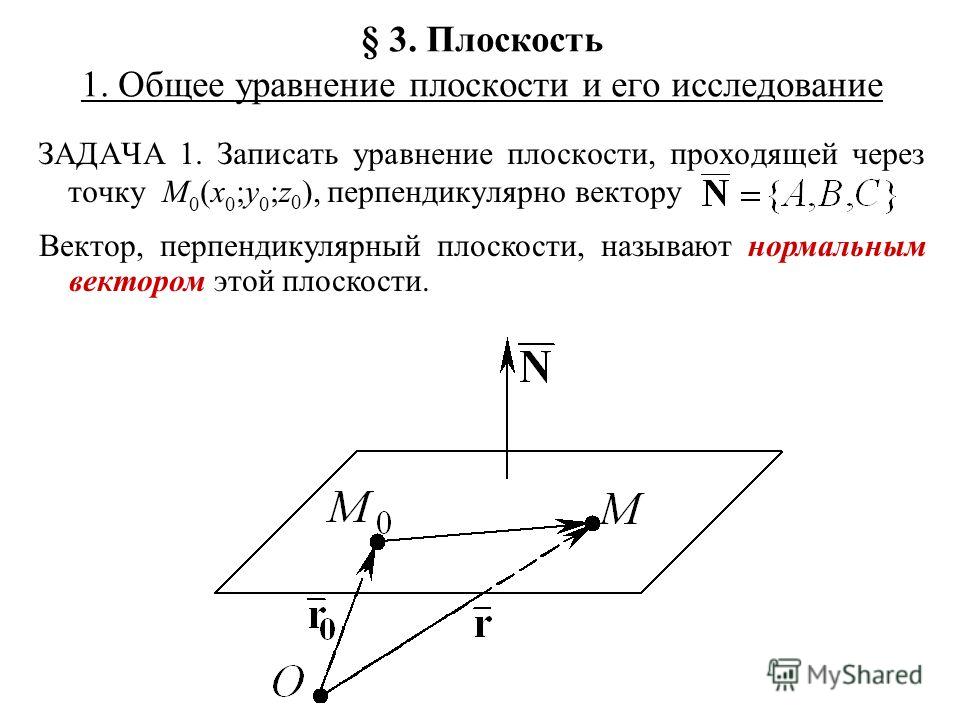
Уравнение плоскости, проходящей через точку M(x0,y0,z0){\displaystyle M(x_{0},y_{0},z_{0})} ,перпендикулярной вектору нормали N(A,B,C){\displaystyle \mathbf {N} (A,B,C)}:

A(x−x)+B(y−y)+C(z−z)=;{\displaystyle A(x-x_{0})+B(y-y_{0})+C(z-z_{0})=0;}

в векторной форме:

((r−r),N)={\displaystyle ((\mathbf {r} -\mathbf {r_{0}} ),\mathbf {N} )=0.}

Уравнение плоскости, проходящей через три заданные точки M(xi,yi,zi){\displaystyle M(x_{i},y_{i},z_{i})}, не лежащие на одной прямой:

((r−r1),(r2−r1),(r3−r1))={\displaystyle ((\mathbf {r} -\mathbf {r_{1}} ),(\mathbf {r_{2}} -\mathbf {r_{1}} ),(\mathbf {r_{3}} -\mathbf {r_{1}} ))=0}

(смешанное произведение векторов), иначе

|x−x1y−y1z−z1x2−x1y2−y1z2−z1x3−x1y3−y1z3−z1|={\displaystyle \left|{\begin{matrix}x-x_{1}&y-y_{1}&z-z_{1}\\x_{2}-x_{1}&y_{2}-y_{1}&z_{2}-z_{1}\\x_{3}-x_{1}&y_{3}-y_{1}&z_{3}-z_{1}\\\end{matrix}}\right|=0.}

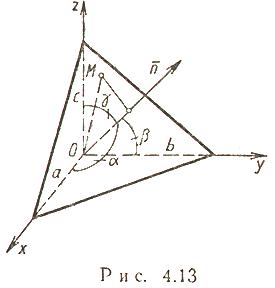
Нормальное (нормированное) уравнение плоскости

xcos⁡α+ycos⁡β+zcos⁡γ−p=(2){\displaystyle x\cos \alpha +y\cos \beta +z\cos \gamma -p=0\qquad (2)}