Первообразная функции и общий вид

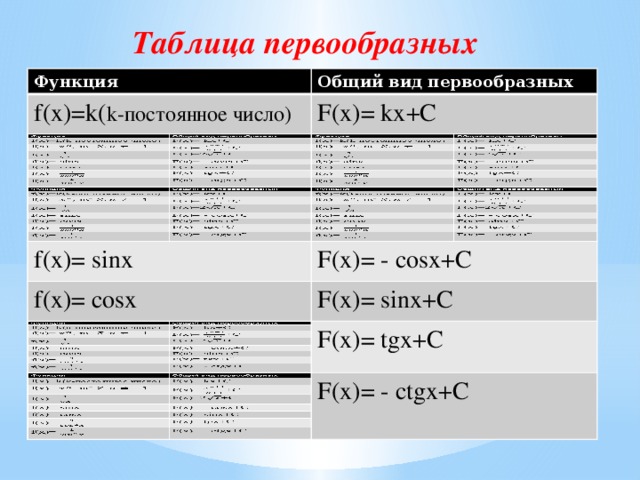
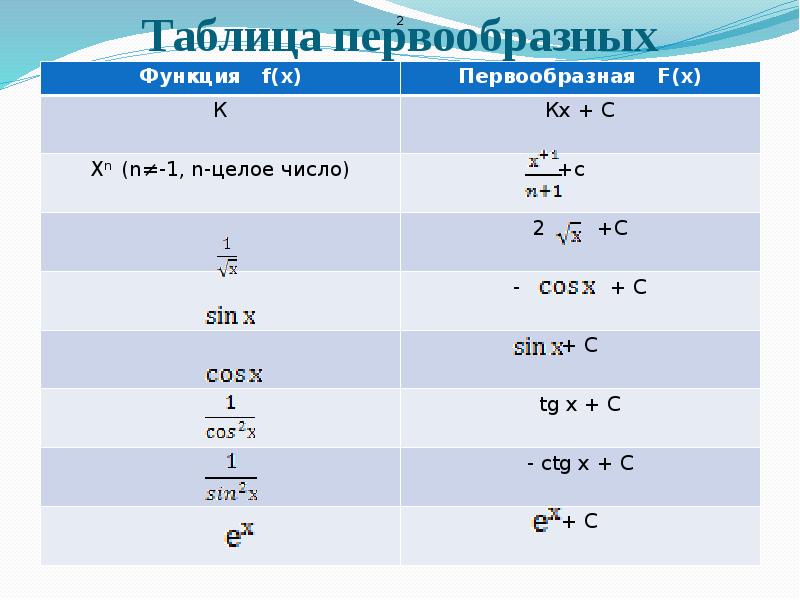
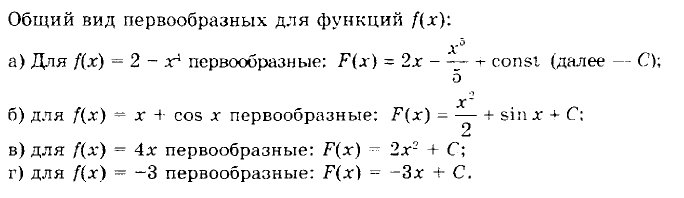Базовые понятия для понимания темы

Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.

Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.

Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.

Приращение – количественное изменение функции при некотором изменении аргумента.

Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.

Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.

Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.

Использование «секретного» приема

В заключение хотелось бы разобрать еще один интересный прием, который, с одной стороны выходит за рамки того, что мы сегодня в основном разбирали, но, с другой стороны, он, во-первых, отнюдь не сложный, т.е. его могут освоить даже начинающие ученики, а, во-вторых, он довольно часто встречается на всевозможных контрольных и самостоятельных работах, т.е. знание его будет очень полезно в дополнение к знанию таблицы первообразных.

Задача № 1

\

Очевидно, что перед нами что-то очень похожее на степенную функцию. Как нам поступить в этом случае? Давайте задумаемся: $x-5$ отличается от $x$ не так уж и сильно — просто добавили $-5$. Запишем так:

\

\

Давайте попробуем найти производную от ${{\left( x-5 \right)}^{5}}$:

\

Отсюда следует:

\

В таблице нет такого значения, поэтому мы сейчас сами вывели эту формулу, используя стандартную формулу первообразной для степенной функции. Давайте так и запишем ответ:

\

Задача № 2

\

Многим ученикам, которые посмотрят на первое решение, может показаться, что все очень просто: достаточно заменить в степенной функции $x$ на линейное выражение, и все станет на свои места. К сожалению, все не так просто, и сейчас мы в этом убедимся.

По аналогии с первым выражением запишем следующее:

\

\

\

Возвращаясь к нашей производной, мы можем записать:

\

\

Отсюда сразу следует:

\

Нюансы решения

Обратите внимание: если в прошлый раз по сути ничего не поменялось, то во втором случае вместо $-10$ появилось $-30$. На что отличается $-10$ и $-30$? Очевидно, что на множитель $-3$

Вопрос: откуда он взялся? Присмотревшись можно увидеть, что она взялась в результате вычислений производной сложной функции — тот коэффициент, который стоял при $x$, появляется в первообразной внизу

Это очень важное правило, которое я изначально вообще не планировал разбирать в сегодняшнем видеоуроке, но без него изложение табличных первообразных было бы неполным

Итак, давайте еще раз. Пусть есть наша основная степенная функция:

\

А теперь вместо $x$ давайте подставим выражение $kx+b$. Что тогда произойдет? Нам нужно найти следующее:

\

На каком основании мы это утверждаем? Очень просто. Давайте найдем производную написанной выше конструкции:

\

Это то самое выражение, которое изначально и было. Таким образом, эта формула тоже верна, и ею можно дополнить таблицу первообразных, а лучше просто запомнить всю таблицу.

Выводы из «секретного: приема:

• Обе функции, которые мы только что рассмотрели, на самом деле, могут быть сведены к первообразным, указанным в таблице, путем раскрытия степеней, но если с четвертой степенью мы еще более-менее как-то справимся, то вот девятую степень я бы вообще не рискнул раскрывать.
• Если бы мы раскрыли степени, то мы бы получили такой объем вычислений, что простая задача заняла бы у нас неадекватно большое количество времени.
• Именно поэтому такие задачи, внутри которых стоят линейные выражения, не нужно решать «напролом». Как только вы встречаете первообразную, которая отличается от той, что в таблице, лишь наличием выражения $kx+b$ внутри, сразу вспоминайте написанную выше формулу, подставляйте ее в вашу табличную первообразную, и все у вас получится намного быстрее и проще.

Естественно, в силу сложности и серьезности этого приема мы еще неоднократно вернемся к его рассмотрению в будущих видеоуроках, но на сегодня у меня все. Надеюсь, этот урок действительно поможет тем ученикам, которые хотят разобраться в первообразных и в интегрировании.

До новых встреч!

1. Первообразная функции
2. Интегрирование по частям
3. Пробный ЕГЭ 2012. Вариант 3 (без логарифмов)
4. Что такое ЕГЭ по математике 2011 и как его сдавать
5. Что такое ЕГЭ по математике 2012
6. Быстрое возведение чисел в квадрат без калькулятора

Правила вычисления интегралов

Что делать в том случае, если надо вычислить интеграл, которого нет в таблице? Существует три несложных правила интегрирования, которые могут помочь в такой ситуации.

Докажем это правило. Для этого просто продифференцируем правую часть равенства:

Получили именно то выражение, которое стоит под знаком интеграла в левой части равенства. Это значит, что формула справедлива.

Рассмотрим пример использования этого правила. Пусть надо найти первообразную функции

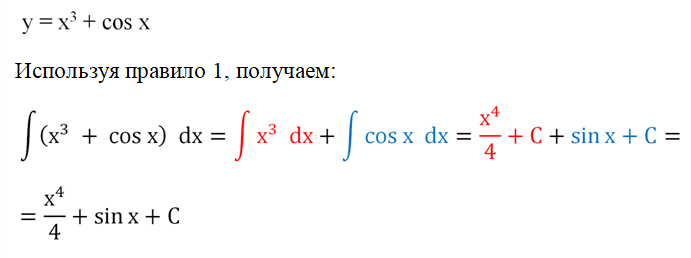
Здесь мы представили исходный интеграл как сумму двух более простых интегралов, которые являются табличными

Обратите внимание, что мы не стали складывать константы интегрирования С как подобные слагаемые и писать 2С. Дело в том, что С – это некоторое произвольное число

Но если сложить два произвольных числа, то в итоге получится третье произвольное число, которое также будет обозначаться как С! Поэтому обычно константу С просто дописывают в самом конце решаемого примера.

Естественно, что правило сложения интегралов работает и в случае суммы не двух, а большего количества слагаемых.

Задание. Вычислите неопределенный интеграл

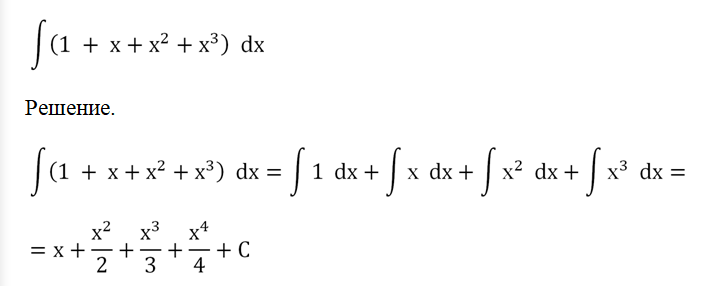
Возможна ситуация, когда мы не уверены в правильности полученного решения. В таком случае можно легко проверить себя, просто продифференцировав получившийся интеграл. В итоге мы должны получить исходную функцию (подынтегральное выражение):

Следующее правило позволяет выносить множитель из-под знака интеграла.

Для доказательства тождества снова продифференцируем его левую часть:

Получили как раз то выражение, которое стоит под интегралом справа. Следовательно, формула верна.

Рассмотрим несколько простейших примеров использования этого метода интегрирования неопределенных интегралов:

Естественно, что правила 1 и 2 можно комбинировать друг с другом, решая более сложные примеры.

Задание. Вычислите неопределенный интеграл от квадратичной функции

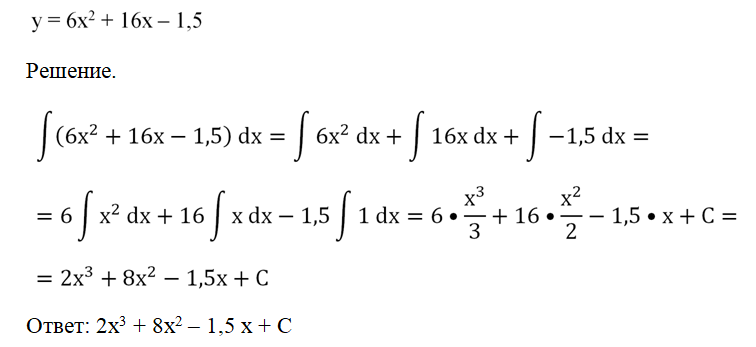
Первые два правила достаточно просты и напоминают . А вот третий метод вычисления неопределенного интеграла более сложный.

Проиллюстрируем его на примере. Пусть надо найти первообразную для функции

Но в нашем случае под знаком косинуса стоит не х, а выражение 5х + 7, являющееся линейной функцией. Поэтому, согласно правилу, мы должны написать впервообразной не sinx, а sin (5x + 7), то есть изменить аргумент. Также надо добавить перед синусом «поправочный множитель», равный 1/k, то есть в нашем случае 1/5:

Проверим себя. Продифференцируем получившуюся первообразную. При этом мы используем правило дифференцирования сложной функции:

Получили ту самую функцию, которую и надо было проинтегрировать.

Приведем ещё несколько примеров использования правила 3:

Напомним, что при изучении производной мы познакомились также с произведения, дроби и сложной функции. Используя их, мы могли найти производную для почти любой функции, которую только могли записать. С решением неопределенных интегралов ситуация значительно сложнее. С помощью приведенных трех правил не получится вычислить такие интегралы, как

Более того, в записанной нами таблице интегралов отсутствует ряд элементарных функций, поэтому мы не сможем даже проинтегрировать такую простую функцию, как

Дело в том, что задача интегрирования является значительно более сложной, чем задача дифференцирования. Отметим три момента. Во-первых, в нашей школьной таблице интегралов, содержащей всего 11 формул, указаны лишь самые простые элементарные функции. Существуют справочники, где в качестве табличных указаны интегралы десятков, а то и сотен функций. Во-вторых, есть и более сложные правила интегрирования, которые изучаются уже в институте. В-третьих, существуют такие элементарные функции, первообразную которых в принципе невозможно записать, используя элементарные функции (синус, косинус, логарифм и т.п.). В связи с этим приходится вводить в рассмотрение новые специальные функции, а также использовать приближенные методы вычислений.

Неопределенный интеграл

      Определение 2. Множество всех функции   f (x)   называют неопределенным интегралом от функции   f (x)   и обозначают

(1)

      Обозначение (1) читается так: «Неопределенный интеграл от функции   f (x)   по   dx» .

      Если   F (x)   является первообразной   f (x) ,   то в силу смысл формулы (1) заключается в следующем:

(2)

      Однако для упрощения формулу (2) принято записывать в виде

(3)

подразумевая, но не указывая специально, что   c   – любое число.

      В формуле (3) функцию   f (x)   называют подынтегральной функцией, выражение   f (x) dx   нызывают подынтегральным выражением, а число   c   называют постоянной интегрирования.

      Операцию вычисления (взятия) интеграла по известной подынтегральной функции называют интегрированием функции.

Метод интегрирования по частям.

Пусть функции \(u(x)\) и \(v(x)\) имеют непрерывные производные на промежутке \(\Delta\). Тогда функция \(uv\) также имеет непрерывную производную на \(\Delta\) и согласно правилу дифференцирования произведения выполняется равенство
$$
uv’=(uv)’-vu’.\nonumber
$$

Интегрируя это равенство и учитывая, что
$$
\int (uv)’dx=uv + C,\nonumber
$$
получаем
$$
\int uv’dx = uv + C — \int vu’ dx.\nonumber
$$

Относя произвольную постоянную \(C\) к интегралу \(\displaystyle \int vu’dx\), находим
$$
\int uv’dx = uv-\int vu’dx,\label{ref21}
$$
или
$$
\int udv = uv-\int vdu,\label{ref22}
$$

Формула \eqref{ref21} или \eqref{ref22} называется формулой интегрирования по частям. Она сводит вычисление интеграла \(\displaystyle udv\) к вычислению интеграла \(\displaystyle vdu\).

Пример 15.

$$
\int x\cos x dx=\int x d(\sin x)=x\sin x-\int \sin xdx=x\sin x-\cos x+C.\ \blacktriangle\nonumber
$$

Пример 16.

Вычислить интеграл
$$
J=\int \sqrt{x^2+a}dx.\nonumber
$$

\(\triangle\) Полагая \(u=\displaystyle\sqrt{x^2+a},\ v=x\), по формуле \eqref{ref21} находим
$$
J=x\sqrt{x^2+a}-\int \frac{x^2}{\sqrt{x^2+a}}dx,\nonumber
$$
где
$$
\int \frac{x^2}{\sqrt{x^2+a}}dx=\int \frac{x^2+a-a}{\sqrt{x^2+a}}dx=J-a\int \frac{dx}{\sqrt{x^2+a}}.\nonumber
$$

Отсюда получаем уравнение относительно \(J\):
$$
J=x\sqrt{x^2+a}-J+a\int \frac{dx}{\sqrt{x^2+a}}.\nonumber
$$

Используя результат , находим
$$
\int \sqrt{x^2+a}dx=\frac{x}{2}\sqrt{x^2+a}+\frac{a}{2}\operatorname{ln}|x+\sqrt{x^2+a}|+C.\ \blacktriangle\nonumber
$$

Пример 17.

Пусть
$$
J_n=\int \frac{dx}{(x^2+a^2)^n},\quad n\in\mathbb{N},\quad a\neq 0.\nonumber
$$
Выведем рекуррентную формулу для вычисления интеграла \(J_n\).

\(\triangle\) Пусть \(u=(x^2+a^2)^{-n},\ v=x\). Тогда \(u’=-2nx(x^2 + a^2)^{-n-1},\ v’=1\) и по формуле \eqref{ref21} получаем
$$
J_n=\frac{x}{(x^2+a^2)^n}+2n\int \frac{x^2}{(x^2+a^2)^{n+1}}dx,\nonumber
$$
где
$$
\int \frac{x^2}{(x^2+a^2)^{n+1}}dx=\int \frac{(x^2+a^2)-a^2}{(x^2+a^2)^{n+1}}dx=J_n-a^2J_{n+1}.\nonumber
$$
Следовательно,
$$
J_n=\frac{x}{(x^2+a^2)^n}+2nJ_n-2na^2J_{n+1},\nonumber
$$
откуда
$$
J_{n+1}=\frac{x}{2na^2(x^2+a^2)^n}+\frac{2n-1}{2na^2}J_n.\ \blacktriangle\label{ref23}
$$

Замечание 7.

Так как
$$
J_1=\int \frac{dx}{x^2+a^2}=\frac{1}{a}\operatorname{arctg}\frac{x}{a}+C,\nonumber
$$
то из формулы \eqref{ref23} находим
$$
J_2=\int \frac{dx}{(x^2+a^2)^2}=\frac{x}{2a^2(x^2+a^2)}+\frac{1}{2a^3}\operatorname{arctg}\frac{x}{a}+C.\nonumber
$$

Замечание 8.

Повторное применение формулы \eqref{ref21} позволяет получить обобщенную формулу интегрирования по частям
$$
\int uv^{(n+1)}dx=\\=uv^{(n)}-u’v^{(n-1)}+u″v^{(n-2)}+…+(-1)^n u^{(n)}v+(-1)^{n+1}\int u^{(n+1)}vdx\label{ref24}
$$
в предположении, что существуют непрерывные производные \(u^{(n+1)},\ v^{(n+1)}\) на рассматриваемом промежутке. При \(n=1\) формула \eqref{ref24} принимает вид
$$
\int uv″dx=uv’-u’v+\int u″vdx.\label{ref25}
$$

Пример 18.

Вычислить интеграл
$$
J = \int x^2 e^x dx.\nonumber
$$

\(\triangle\) Полагая \(u=x^2,\ v = e^x\) и учитывая, что \(u’=2x,\ u″ = 2,\ v’=v″=e^x\), получаем по формуле \eqref{ref25}
$$
J = x^2 e^x-2x e^x+2\int e^x dx,\nonumber
$$
откуда
$$
\int x^2 e^x dx=(x^2-2x+2)e^x+C.\ \blacktriangle\nonumber
$$

Пример 19.

Вычислить интеграл
$$
J=\int e^{\alpha x}\cos \beta x dx,\quad \alpha\beta\neq 0.\nonumber
$$

\(\triangle\) Положим \(u= \cos \beta x,\ v=\displaystyle\frac{e^{\alpha x}}{\alpha^2}\). Тогда \(u’=-\beta \sin\beta x,\ u″=-\beta^2\cos\beta x,\ v’=\displaystyle\frac{e^{\alpha x}}{\alpha},\ v″=e^{\alpha x}\). По формуле \eqref{ref25} находим
$$
J =\frac{e^{\alpha x}}{\alpha}\cos\beta x+\frac{\beta}{\alpha^2}e^{\alpha x}\sin \beta x-\frac{\beta^2}{\alpha^2}J + C,
$$
откуда
$$
J=\frac{\alpha \cos\beta x+\beta\sin \beta x}{\alpha^2+\beta^2}e^{\alpha x}+C_1.\ \blacktriangle\nonumber
$$

Неопределенный интеграл

Определение:

Неопределённым интегралом от функции f(x) называется выражение F(x) + С, то есть совокупность всех первообразных данной функции f(x). Обозначается неопределённый интеграл так: \int f(x) dx = F(x) + C

где

• f(x) — называют подынтегральной функцией;
• f(x) dx — называют подынтегральным выражением;
• x — называют переменной интегрирования;
• F(x) — одна из первообразных функции f(x);
• С — произвольная постоянная.

Свойства неопределённого интеграла

1. Производная неопределённого интеграла равна подынтегральной функции: .
2. Постоянный множитель подынтегрального выражения можно выносить за знак интеграла:.
3. Интеграл от суммы (разности) функций равен сумме (разности) интегралов от этих функций:.
4. Если k, b — постоянные, причём k ≠ 0, то .

Решение выражений со степенью с рациональным показателем

Пример № 1

\{x}\]

Посчитаем каждый корень отдельно:

\

\

\{x}={{x}^{\frac{1}{4}}}\to \frac{{{x}^{\frac{1}{4}}}}{\frac{1}{4}+1}=\frac{{{x}^{\frac{5}{4}}}}{\frac{5}{4}}=\frac{4\cdot {{x}^{\frac{5}{4}}}}{5}\]

Итого всю нашу конструкцию можно записать следующим образом:

\

Пример № 2

\

Запишем:

\

Следовательно, мы получим:

\

\

Итого, собирая все в одно выражение, можно записать:

\

Пример № 3

\{x}-x\sqrt{x}+1\]

Для начала заметим, что $\sqrt{x}$ мы уже считали:

\{x}\to \frac{4{{x}^{\frac{5}{4}}}}{5}\]

\

\

\

Перепишем:

\

Надеюсь, я никого не удивлю, если скажу, что то, что мы только что изучали — это лишь самые простые вычисления первообразных, самые элементарные конструкции. Давайте сейчас рассмотрим чуть более сложные примеры, в которых помимо табличных первообразных еще потребуется вспомнить школьную программу, а именно, формулы сокращенного умножения.

Вопросы о первообразной функции

Казалось бы, довольно простое и понятное определение. Однако, услышав его, у внимательного ученика сразу возникнет несколько вопросов:

1. Допустим, хорошо, эта формула верна. Однако в этом случае при $n=1$ у нас возникают проблемы: в знаменателе появляется «ноль», а на «ноль» делить нельзя.
2. Формула ограничивается только степенями. Как считать первообразную, например, синуса, косинуса и любой другой тригонометрии, а также констант.
3. Экзистенциальный вопрос: а всегда ли вообще можно найти первообразную? Если да, то как быть с первообразной суммы, разности, произведения и т.д.?

На последний вопрос я отвечу сразу. К сожалению, первообразная, в отличие от производной, считается не всегда. Нет такой универсальной формулы, по которой из любой исходной конструкции мы получим функцию, которая будет равна этой сходной конструкции. А что касается степеней и констант — сейчас мы об этом поговорим.

Почему вы не знаете, как решать интегралы

Внимание!

Если вам нужна помощь с академической работой, то рекомендуем обратиться к профессионалам. Более 70 000 экспертов готовы помочь вам прямо сейчас.

Расчет стоимости Гарантии Отзывы

А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.

Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:

• вычисление площади фигуры.
• вычисление массы тела с неравномерной плотностью.
• определение пройденного пути при движении с непостоянной скоростью.
• и др.

Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.

Главная причина незнания – отсутствие понимания практической значимости интегралов.

Интеграл – что это?

Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.

Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.

Метод исчерпывания для определения площади круга

В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.

Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.

Существование

Каждая непрерывная функция f{\displaystyle f} имеет первообразную F{\displaystyle F}, одна из которых представляется в виде интеграла от f{\displaystyle f} с переменным верхним пределом:

F(x)=∫axf(t)dt.{\displaystyle F(x)=\int \limits _{a}^{x}f(t)\,dt.}

Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например, f(x)=2xsin⁡1x−cos⁡1x{\displaystyle f(x)=2x\sin {\frac {1}{x}}-\cos {\frac {1}{x}}} с f()={\displaystyle f(0)=0} не непрерывна при x={\displaystyle x=0}, но имеет первообразную F(x)=x2sin1x{\displaystyle F(x)=x^{2}sin{\frac {1}{x}}} с F()={\displaystyle F(0)=0}. Для разрывных ограниченных функций вместо интеграла Римана удобно использовать более общий интеграл Лебега. Необходимыми условиями существования первообразной являются принадлежность функции f{\displaystyle f} первому классу Бэра и выполнение для неё свойства Дарбу.

Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:

∫e−x2dx,∫sin⁡(x)xdx,∫1ln⁡xdx{\displaystyle \int e^{-x^{2}}\,dx,\qquad \int {\frac {\sin(x)}{x}}\,dx,\qquad \int {\frac {1}{\ln x}}\,dx}.

Решение задач, содержащих показательную функцию

Для начала запишем такие формулы:

\

\

Давайте посмотрим, как это все работает на практике.

Пример № 1

\

Если мы посмотрим на содержимое скобок, то заметим, что в таблице первообразных нет такого выражения, чтобы ${{e}^{x}}$ стояло в квадрате, поэтому этот квадрат необходимо раскрыть. Для этого воспользуемся формулами сокращенного умножения:

\

\

Давайте найдем первообразную для каждого из слагаемых:

\

\

\

А теперь соберем все слагаемые в единое выражение и получим общую первообразную:

\

Пример № 2

\

На этот раз степень уже побольше, поэтому формула сокращенного умножения будет довольно сложной. Итак раскроем скобки:

\

\

\

Теперь от этой конструкции попробуем взять первообразную от нашей формулы:

\

\

Как видите, в первообразных показательной функции нет ничего сложного и сверхъестественного. Все один считаются через таблицы, однако внимательные ученики наверняка заметят, что первообразная ${{e}^{2x}}$ намного ближе просто к ${{e}^{x}}$ нежели к ${{a}^{x}}$. Так, может быть, существует какой-то более специальное правило, позволяющее, зная первообразную ${{e}^{x}}$, найти ${{e}^{2x}}$? Да, такое правило существует. И, более того, оно является неотъемлемой частью работы с таблицей первообразных. Его мы сейчас разберем на примере тех же самых выражений, с которыми мы только что работали.

Решение реальных задач

Задача № 1

\

Давайте каждую из степенных функций посчитаем отдельно:

\

\

Возвращаясь к нашему выражению, мы запишем общую конструкцию:

\

Задача № 2

\

Как я уже говорил, первообразные произведений и частного «напролом» не считаются. Однако здесь можно поступить следующим образом:

\

Мы разбили дробь на сумму двух дробей.

Посчитаем:

\

\

Хорошая новость состоит в том, что зная формулы вычисления первообразных, вы уже способны считать более сложные конструкции. Однако давайте пойдем дальше и расширим наши знания еще чуть-чуть. Дело в том, что многие конструкции и выражения, которые, на первый взгляд, не имеют никакого отношения к ${{x}^{n}}$, могут быть представлены в виде степени с рациональным показателем, а именно:

\

\{x}={{x}^{\frac{1}{n}}}\]

\

Все эти приемы можно и нужно комбинировать. Степенные выражения можно

• умножать (степени складываются);
• делить (степени вычитаются);
• умножать на константу;
• и т.д.

Решение задач: находим первообразную функции

Пример № 1

\

Давайте сумму, которая стоит в числители, разложи на три отдельных дроби:

\

Это довольно естественный и понятный переход — у большинства учеников проблем с ним не возникает. Перепишем наше выражение следующим образом:

\

\

А теперь вспомним такую формулу:

\

В нашем случае мы получим следующее:

\

\

Чтобы избавиться от всех этих трехэтажных дробей, предлагаю поступить следующим образом:

\

\

Пример № 2

\

В отличие от предыдущей дроби в знаменателе стоит не произведение, а сумма. В этом случае мы уже не можем разделить нашу дробь на сумму нескольких простых дробей, а нужно каким-то образом постараться сделать так, чтобы в числителе стояло примерно такое же выражение как в знаменателе. В данном случае сделать это довольно просто:

\

Такая запись, которая на языке математики называется «добавление нуля», позволит нам вновь разделить дробь на два кусочка:

\

Теперь найдем то, что искали:

\

Вот и все вычисления. Несмотря на кажущуюся большую сложность, чем в предыдущей задаче, объем вычислений получился даже меньшим.

Нюансы решения

И вот в этом кроется основная сложность работы с табличными первообразными, особенно это заметно на второй задаче. Дело в том, что для того чтобы выделить какие-то элементы, которые легко считаются через таблицу, нам нужно знать, что конкретно мы ищем, и именно в поиске этих элементов и состоит все вычисление первообразных.

Другими словами, недостаточно просто зазубрить таблицу первообразных — нужно уметь видеть что-то, чего пока еще нет, но что подразумевал автор и составитель этой задачи. Именно поэтому многие математики, учителя и профессора постоянно спорят: «А что такое взятие первообразных или интегрирование — это просто инструмент либо это настоящее искусство?» На самом деле, лично на мой взгляд, интегрирование — это никакое не искусство — в нем нет ничего возвышенного, это просто практика и еще раз практика. И чтобы попрактиковаться, давайте решим еще три более серьезных примера.