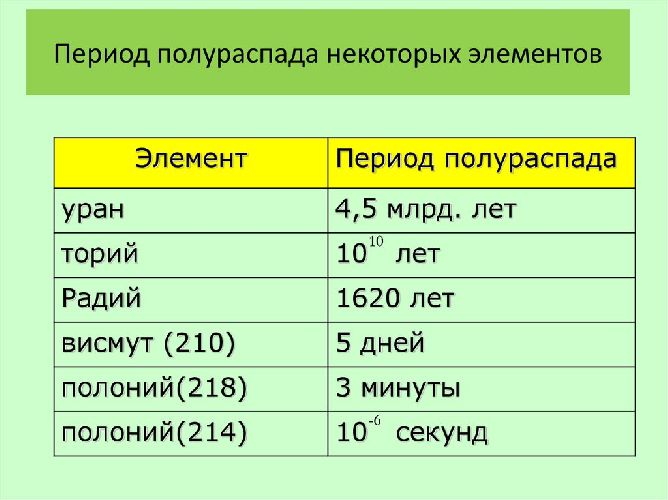
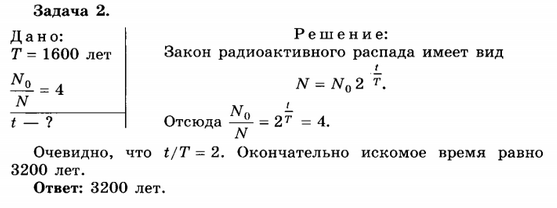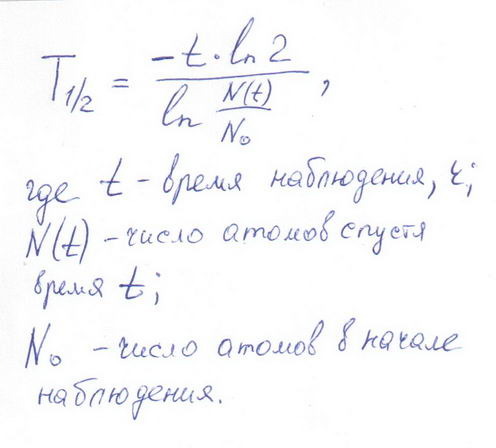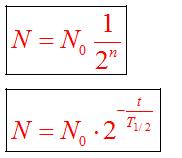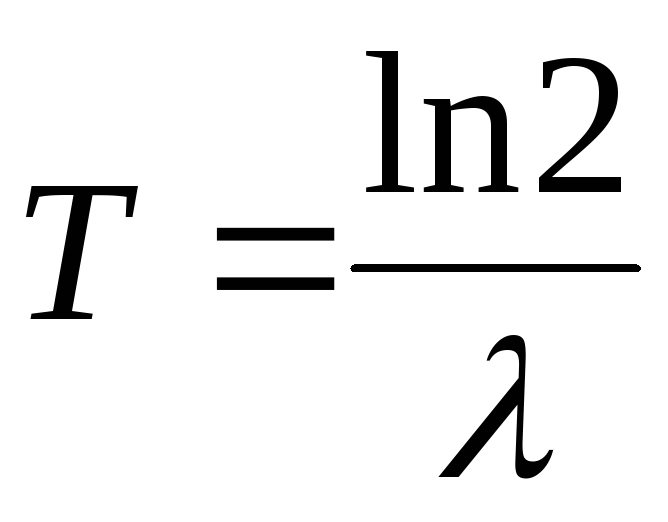Период полураспада

Таблица: «Полупериод распада отдельных изотопов»

Название	Обозначение	Вид распада	Период полураспада
Радий	₈₈Ra219	альфа	0,001 секунд
Магний	₁₂Mg27	бета	10 минут
Радон	₈₆Rn222	альфа	3,8 суток
Кобальт	₂₇Co60	бета, гамма	5,3 года
Радий	₈₈Ra226	альфа, гамма	1620 лет
Уран	₉₂U238	альфа, гамма	4,5 млрд лет

Определение периода полураспада выполнено экспериментально. В ходе лабораторных исследований многократно проводится измерение активности. Поскольку лабораторные образцы минимальных размеров (безопасность исследователя превыше всего), эксперимент проводится с различным интервалом времени, многократно повторяясь. В его основу положена закономерность изменения активности веществ.

С целью определения периода полураспада производится измерение активности данного образца в определенные промежутки времени. С учетом того, что данный параметр связан с количеством распавшихся атомов, используя закон радиоактивного распада, определяют период полураспада.

Примечания

↑
↑
↑
↑
↑ Carl R. (Rod) Nave. . . Georgia State University (2016). Дата обращения 22 ноября 2019.
↑
Такой же вид имеет зависимость от времени интенсивности (скорости) распада, то есть активности образца, и аналогичным образом через неё определяется период полураспада как промежуток времени, по истечении которого интенсивность распада снизится вдвое
Фиалков Ю. Я. Применение изотопов в химии и химической промышленности. — К.: Техніка, 1975. — С. 52. — 240 с. — 2000 экз.
↑ . infotables.ru — Справочные таблицы. Дата обращения 6 ноября 2019.
↑ . periodictable.com. Дата обращения 11 ноября 2019.
↑
↑ . Caltech Astronomy Department. Дата обращения 10 ноября 2019.
↑ . Калькулятор – справочный портал. Дата обращения 7 ноября 2019.
↑ M. P. Unterweger, D. D. Hoppes, F. J. Schima, and J. S. Coursey. (англ.). NIST (6 September 2009). Дата обращения 26 ноября 2019.

Цепочки радиоактивного превращения

Исследования радиоактивности проводились в лабораторных условиях. Удивительная способность радиоактивных элементов сохранять активность в течение часов, суток и даже лет не могла не вызывать удивления у физиков начала ХХ столетия. Исследования, к примеру, тория, сопровождались неожиданным результатом: в закрытой ампуле активность его была значительной. При малейшем дуновении она падала. Вывод оказался прост: превращение тория сопровождается выделением радона (газ). Все элементы в процессе радиоактивности превращаются в совершенно иное вещество, отличающееся и физическими, и химическими свойствами. Это вещество, в свою очередь, также нестабильно. В настоящее время известно три ряда аналогичных превращений.

Знания о подобных превращениях крайне важны при определении времени недоступности зон, зараженных в процессе атомных и ядерных исследований или катастроф. Период полураспада плутония — в зависимости от его изотопа — лежит в интервале от 86 лет (Pu 238) до 80 млн лет (Pu 244). Концентрация каждого изотопа дает представление о периоде обеззараживания территории.

Временной интервал в радиоактивности

Момент развала частицы невозможно установить для данного конкретного атома. Для него это скорее «несчастный случай», нежели закономерность. Выделение энергии, характеризующее этот процесс, определяют как активность образца.

Замечено, что она с течением времени меняется. Хотя отдельные элементы демонстрируют удивительное постоянство степени излучения, существуют вещества, активность которых уменьшается в несколько раз за достаточно короткий промежуток времени. Удивительное разнообразие! Возможно ли найти закономерность в этих процессах?

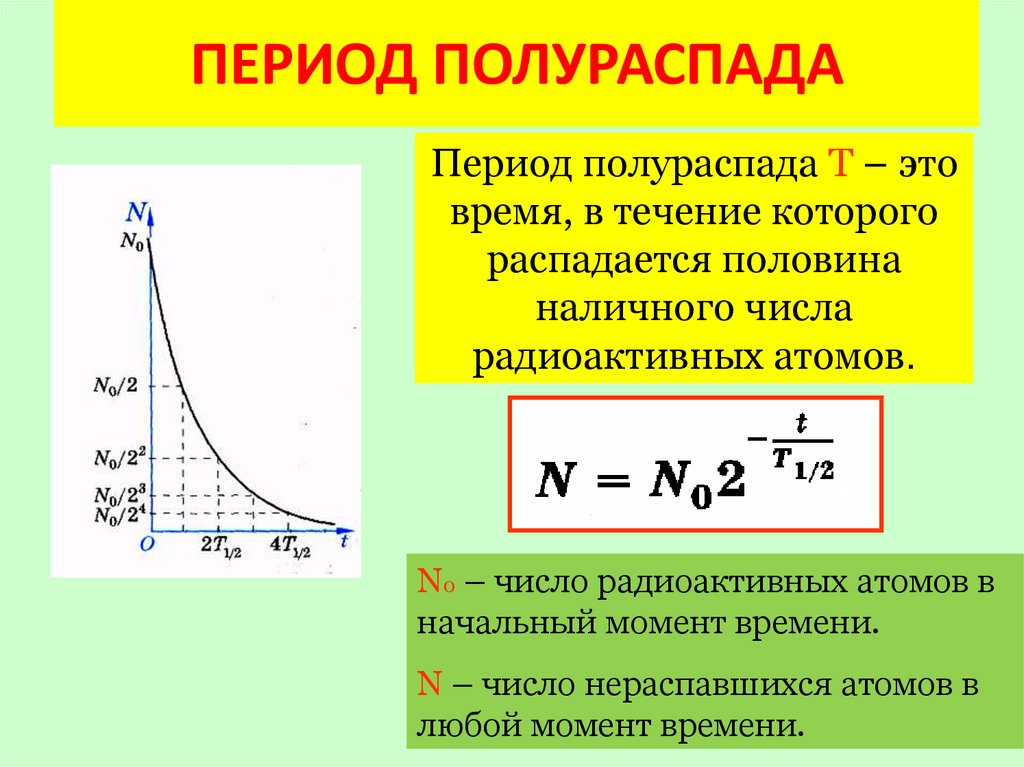
Установлено, что существует время, в течение которого ровно половина атомов данного образца претерпевает распад. Этот интервал времени получил название «период полураспада». В чем смысл введения этого понятия?

Вводим характеристики радиоактивности

Данный процесс – самопроизвольное превращение атома изотопа элемента в иной изотоп с одновременным выделением элементарных частиц (электронов, ядер атомов гелия). Превращение атомов оказалось самопроизвольным, не требующим поглощения энергии извне. Основной величиной, характеризующей процесс выделения энергии в ходе радиоактивного распада, называют активность.

СИ (Системе

А=λN, где λ- постоянная распада, N – число активных атомов в образце.

Выделяют α, β, γ-распады. Соответствующие уравнения называют правилами смещения:

название	Что происходит	Уравнение реакции
α –распад	превращение атомного ядра Х в ядро Y с выделением ядра атома гелия	_ZАХ→_Z-2YА-4+₂He4
β — распад	превращение атомного ядра Х в ядро Y с выделением электрона	_ZАХ→_Z+1YА+_-1eА
γ — распад	не сопровождается изменением ядра, энергия выделяется в виде электромагнитной волны	_ZХА→_ZXА+γ

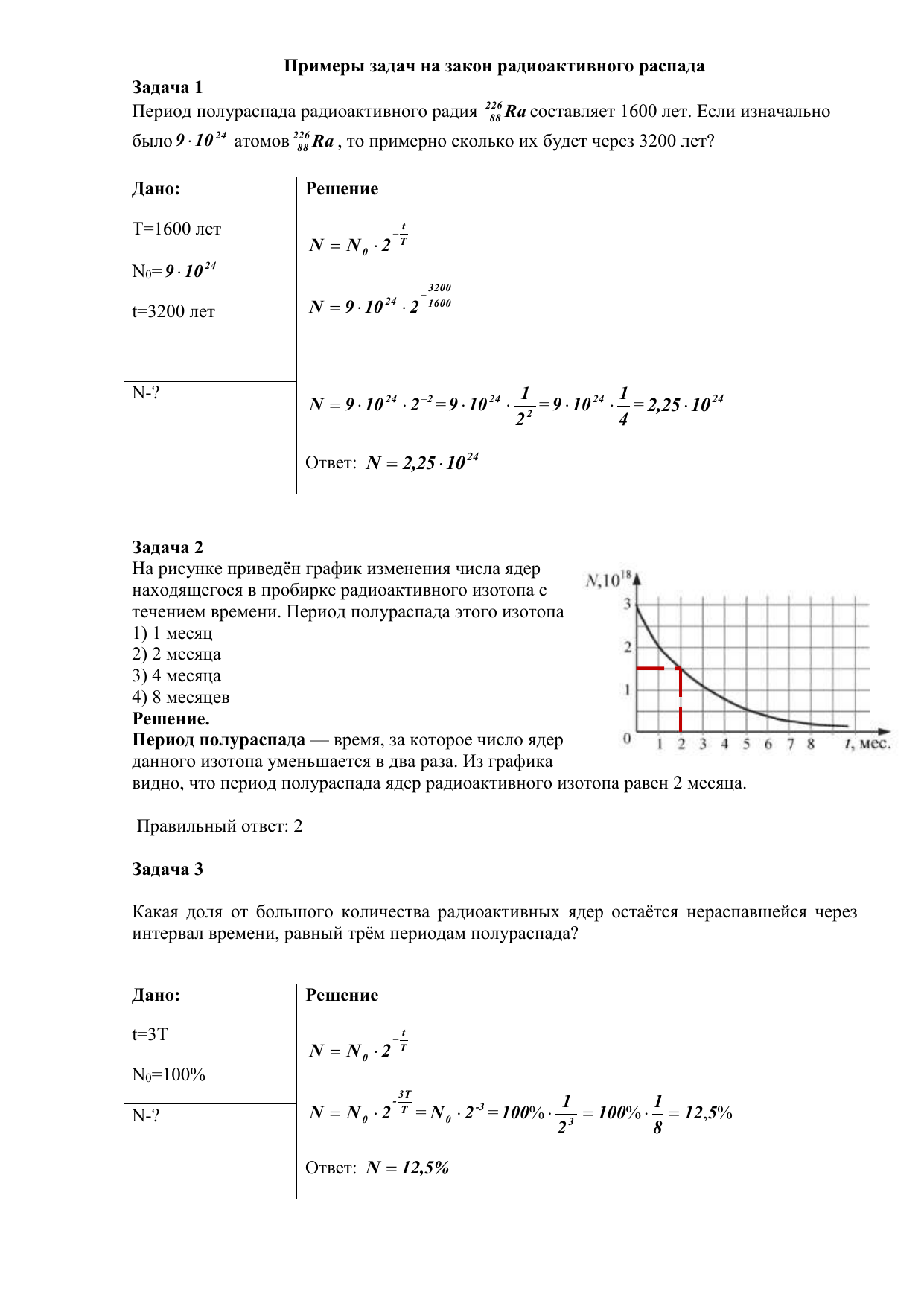
Примеры расчётов

Пример 1

Если рассматривать достаточно близкие моменты времени t1{\displaystyle t_{1}} и t2{\displaystyle t_{2}}, то число ядер, распавшихся за этот промежуток времени t2−t1≪λ{\displaystyle t_{2}-t_{1}\ll \lambda }, можно приближённо записать как ΔN≈λN(t2−t1){\displaystyle \Delta N\approx \lambda N_{0}(t_{2}-t_{1})}.

С её помощью легко оценить число атомов урана-238, имеющего период полураспада T12=4,498⋅109{\displaystyle T_{1/2}=4,498\cdot 10^{9}} лет, испытывающих превращение в данном количестве урана, например, в одном килограмме в течение одной секунды. Имея в виду, что количество любого элемента в граммах, численно равное атомному весу, содержит, как известно, 6,02⋅1023 атомов, а в году 365⋅24⋅60⋅60{\displaystyle 365\cdot 24\cdot 60\cdot 60} секунд, можно получить, что

ΔN≈,6934,498⋅109⋅365⋅24⋅60⋅606,02⋅1023238⋅1000=12⋅106.{\displaystyle \Delta N\approx {\frac {0,693}{4,498\cdot 10^{9}\cdot 365\cdot 24\cdot 60\cdot 60}}{\frac {6,02\cdot 10^{23}}{238}}\cdot 1000=12\cdot 10^{6}.}

Вычисления приводят к тому, что в одном килограмме урана в течение одной секунды распадается двенадцать миллионов атомов. Несмотря на такое огромное число, всё же скорость превращения ничтожно мала. Действительно, в секунду из наличного количества урана распадается его доля, равная

12⋅106⋅2386,02⋅1023⋅1000=47⋅10−19.{\displaystyle {\frac {12\cdot 10^{6}\cdot 238}{6,02\cdot 10^{23}\cdot 1000}}=47\cdot 10^{-19}.}

Пример 2

Образец содержит 10 г изотопа плутония Pu-239 с периодом полураспада 24 400 лет. Сколько атомов плутония распадается ежесекундно?

Поскольку рассматриваемое время (1 с) намного меньше периода полураспада, можно применить ту же, что и в предыдущем примере, приближённую формулу:

ΔN≈Δt⋅Nln⁡2T12=Δt⋅mμNAln⁡2T12{\displaystyle \Delta N\approx \Delta t\cdot N_{0}{\frac {\ln 2}{T_{1/2}}}=\Delta t\cdot {\frac {{\frac {m}{\mu }}N_{A}\ln 2}{T_{1/2}}}}

Подстановка численных значений даёт
ΔN≈1⋅,693⋅10239⋅6⋅102324400⋅365⋅24⋅60⋅60=,693⋅2,5⋅10227,7⋅1011=2,25⋅1010.{\displaystyle \Delta N\approx 1\cdot {\frac {0,693\cdot {\frac {10}{239}}\cdot 6\cdot 10^{23}}{24400\cdot 365\cdot 24\cdot 60\cdot 60}}={\frac {0,693\cdot 2,5\cdot 10^{22}}{7,7\cdot 10^{11}}}=2,25\cdot 10^{10}.}

Когда рассматриваемый период времени сравним с периодом полураспада, следует пользоваться точной формулой

ΔN=N−N(t)=N(1−2−tT12).{\displaystyle \Delta N=N_{0}-N(t)=N_{0}\left(1-2^{-t/T_{1/2}}\right).}

Она пригодна в любом случае, однако для малых периодов времени требует вычислений с очень большой точностью. Так, для данной задачи:

ΔN=N(1−2−tT12)=2.5⋅1022(1−2−17.7⋅1011)=2.5⋅1022(1−0.99999999999910)=2.25⋅1010.{\displaystyle \Delta N=N_{0}\left(1-2^{-t/T_{1/2}}\right)=2.5\cdot 10^{22}\left(1-2^{-1/7.7\cdot 10^{11}}\right)=2.5\cdot 10^{22}\left(1-0.99999999999910\right)=2.25\cdot 10^{10}.}

Примечания

↑
↑
↑
↑
↑ Carl R. (Rod) Nave. . . Georgia State University (2016). Дата обращения 22 ноября 2019.
↑
Такой же вид имеет зависимость от времени интенсивности (скорости) распада, то есть активности образца, и аналогичным образом через неё определяется период полураспада как промежуток времени, по истечении которого интенсивность распада снизится вдвое
Фиалков Ю. Я. Применение изотопов в химии и химической промышленности. — К.: Техніка, 1975. — С. 52. — 240 с. — 2000 экз.
↑ . infotables.ru — Справочные таблицы. Дата обращения 6 ноября 2019.
↑ . periodictable.com. Дата обращения 11 ноября 2019.
↑
↑ . Caltech Astronomy Department. Дата обращения 10 ноября 2019.
↑ . Калькулятор – справочный портал. Дата обращения 7 ноября 2019.
↑ M. P. Unterweger, D. D. Hoppes, F. J. Schima, and J. S. Coursey. (англ.). NIST (6 September 2009). Дата обращения 26 ноября 2019.

Определение и основные соотношения

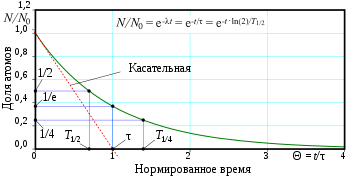
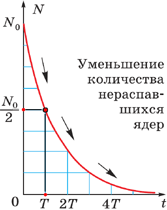
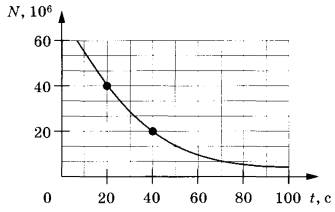
Зависимость числа выживших частиц от времени при экспоненциальном распаде

Понятие периода полураспада применяется как к испытывающим распад элементарным частицам, так и к радиоактивным ядрам. Поскольку событие распада имеет квантовую вероятностную природу, то если рассматривать одну структурную единицу материи (частицу, атом радиоактивного изотопа), можно говорить о периоде полураспада как промежутке времени, по истечении которого средняя вероятность распада рассматриваемой частицы будет равна 1/2.

Если же рассматривать экспоненциально распадающиеся системы частиц, то периодом полураспада T12{\displaystyle T_{1/2}} будет называться время, в течение которого распадается в среднем половина радиоактивных ядер. Согласно закону радиоактивного распада, число нераспавшихся атомов в момент времени t{\displaystyle t} связано с начальным (в момент t={\displaystyle t=0}) числом атомов N{\displaystyle N_{0}} соотношением

N(t)N=e−λt,{\displaystyle {\frac {N(t)}{N_{0}}}=e^{-\lambda t},}

где λ{\displaystyle \lambda } — постоянная распада.

По определению, N(T12)N=12,{\displaystyle {\frac {N(T_{1/2})}{N_{0}}}={\frac {1}{2}},} следовательно, e−λT12=12,{\displaystyle e^{-\lambda T_{1/2}}={\frac {1}{2}},} откуда

T12=ln⁡2λ≈,693λ.{\displaystyle T_{1/2}={\frac {\ln 2}{\lambda }}\approx {\frac {0,693}{\lambda }}.}

Далее, поскольку среднее время жизни τ=1λ{\displaystyle \tau ={\frac {1}{\lambda }}}, то

T12=τln⁡2≈,693τ,{\displaystyle T_{1/2}=\tau \ln 2\approx 0,693\tau ,}

то есть период полураспада примерно на 30,7 % короче, чем среднее время жизни. Например, для свободного нейтрона T12{\displaystyle T_{1/2}} = 10,3 минуты, а τ{\displaystyle \tau } = 14,9 минуты.

Не следует считать, что за два периода полураспада распадутся все частицы, взятые в начальный момент. Поскольку каждый период полураспада уменьшает число выживших частиц вдвое, за время 2T12{\displaystyle 2T_{1/2}} останется четверть от начального числа частиц, за 3T12{\displaystyle 3T_{1/2}} — одна восьмая и т. д.. При этом для каждой конкретной отдельной частицы по прошествии времени T12{\displaystyle T_{1/2}} ожидаемая средняя продолжительность жизни (соответственно, и вероятность распада, и период полураспада) не изменится — этот контринтуитивный факт является следствием квантовой природы явления распада

Парциальный период полураспада

Если система с периодом полураспада T12{\displaystyle T_{1/2}} может распадаться по нескольким каналам, для каждого из них можно определить парциальный период полураспада. Пусть вероятность распада по i-му каналу (коэффициент ветвления) равна pi{\displaystyle p_{i}}. Тогда парциальный период полураспада по i-му каналу равен

T12(i)=T12pi.{\displaystyle T_{1/2}^{(i)}={\frac {T_{1/2}}{p_{i}}}.}

Парциальный T12(i){\displaystyle T_{1/2}^{(i)}} имеет смысл периода полураспада, который был бы у данной системы, если «выключить» все каналы распада, кроме i-го. Так как по определению pi≤1{\displaystyle p_{i}\leq 1}, то T12(i)≥T12{\displaystyle T_{1/2}^{(i)}\geq T_{1/2}} для любого канала распада.

Вероятностный характер

Моделирование множества идентичных атомов, подвергающихся радиоактивному распаду, начиная с 4 атомов в коробке (слева) или 400 (справа). Число вверху показывает, сколько периодов полураспада прошло

Обратите внимание на следствие закона больших чисел : чем больше атомов, тем общий распад более регулярный и более предсказуемый.

Период полураспада обычно описывает распад дискретных объектов, таких как радиоактивные атомы. В этом случае нельзя использовать определение, которое гласит, что «период полураспада — это время, необходимое для распада ровно половины объектов». Например, если есть только один радиоактивный атом, а его период полураспада составляет одну секунду, то через одну секунду не останется «половины атома».

Вместо этого период полураспада определяется с точки зрения вероятности : «Период полураспада — это время, необходимое для разложения ровно половины объектов в среднем ». Другими словами, вероятность распада радиоактивного атома в период полураспада составляет 50%.

Например, изображение справа представляет собой симуляцию множества идентичных атомов, подвергающихся радиоактивному распаду

Обратите внимание, что после одного периода полураспада остается не ровно половина атомов, только приблизительно , из-за случайного изменения в процессе. Тем не менее, когда распадается много идентичных атомов (правые прямоугольники), закон больших чисел предполагает, что это очень хорошее приближение, чтобы сказать, что половина атомов остается после одного периода полураспада.

Различные простые упражнения могут продемонстрировать вероятностный распад, например, с помощью подбрасывания монет или запуска статистической компьютерной программы .

Стабильность периода полураспада

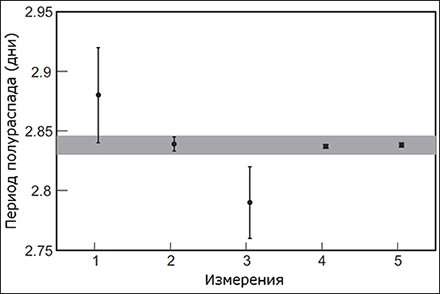
Во всех наблюдавшихся случаях (кроме некоторых изотопов, распадающихся путём электронного захвата) период полураспада был постоянным (отдельные сообщения об изменении периода были вызваны недостаточной точностью эксперимента, в частности, неполной очисткой от высокоактивных изотопов). В связи с этим период полураспада считается неизменным. На этом основании строится определение абсолютного геологического возраста горных пород, а также радиоуглеродный метод определения возраста биологических останков: зная концентрацию радиоизотопа в настоящее время и в прошлом, можно рассчитать, сколько точно времени прошло с тех пор.

Предположение об изменяемости периода полураспада используется креационистами, а также представителями т. н. «альтернативной науки» для опровержения научной датировки горных пород, остатков живых существ и исторических находок, с целью дальнейшего опровержения научных теорий, построенных с использованием такой датировки. (См., например, статьи Креационизм, Научный креационизм, Критика эволюционизма, Туринская плащаница).

Вариабельность постоянной распада для электронного захвата наблюдалась в эксперименте, но она лежит в пределах процента во всём доступном в лаборатории диапазоне давлений и температур. Период полураспада в этом случае изменяется в связи с некоторой (довольно слабой) зависимостью плотности волновой функции орбитальных электронов в окрестности ядра от давления и температуры. Существенные изменения постоянной распада наблюдались также для сильно ионизованных атомов (так, в предельном случае полностью ионизованного ядра электронный захват может происходить только при взаимодействии ядра со свободными электронами плазмы; кроме того, распад, разрешённый для нейтральных атомов, в некоторых случаях для сильно ионизованных атомов может быть запрещён кинематически). Все эти варианты изменения постоянных распада, очевидно, не могут быть привлечены для «опровержения» радиохронологических датировок, поскольку погрешность самого радиохронометрического метода для большинства изотопов-хронометров составляет более процента, а высокоионизованные атомы в природных объектах на Земле не могут существовать сколько-нибудь длительное время.

Поиск возможных вариаций периодов полураспада радиоактивных изотопов, как в настоящее время, так и в течение миллиардов лет, интересен в связи с гипотезой о вариациях значений фундаментальных констант в физике (постоянной тонкой структуры, константы Ферми и т. д.). Однако тщательные измерения пока не принесли результата — в пределах погрешности эксперимента изменения периодов полураспада не были найдены. Так, было показано, что за 4,6 млрд лет константа α-распада самария-147 изменилась не более чем на 0,75 %, а для β-распада рения-187 изменение за это же время не превышает 0,5 %; в обоих случаях результаты совместимы с отсутствием таких изменений вообще.

Стабильность периода полураспада

Самый дорогой металл

Известно, что в наше время есть металлы значительно более дорогие, чем золото, серебро и платина. К ним относится и плутоний. Интересно, что в природе созданный в процессе эволюции плутоний не встречается. Большинство элементов получены в лабораторных условиях. Эксплуатация плутония-239 в ядерных реакторах дала возможность ему стать чрезвычайно популярным в наши дни. Получение достаточного для использования в реакторах количества данного изотопа делает его практически бесценным.

Плутоний-239 получается в естественных условиях как следствие цепочки превращений урана-239 в нептуний-239 (период полураспада — 56 часов). Аналогичная цепочка позволяет накопить плутоний в ядерных реакторах. Скорость появления необходимого количества превосходит естественную в миллиарды раз.

Закон радиоактивного распада (ЗРР)

Период полураспада положен в основу ЗРР. Закономерность выведена Фредерико Содди и Эрнестом Резерфордом на основе результатов экспериментальных исследований в 1903 году. Удивительно, что многократные измерения, выполненные при помощи приборов, далеких от совершенства, в условиях начала ХХ столетия, привели к точному и обоснованному результату. Он стал основой теории радиоактивности. Выведем математическую запись закона радиоактивного распада.

— Пусть N– количество активных атомов в данный момент времени. По истечении интервала времени t нераспавшимися останутся N элементов.

— К моменту времени, равному периоду полураспада, останется ровно половина активных элементов: N=N/2.

— По прошествии еще одного периода полураспада в образце остаются: N=N/4=N/22 активных атомов.

— По прошествии времени, равному еще одному периоду полураспада, образец сохранит только: N=N/8=N/23.

— К моменту времени, когда пройдет n периодов полураспада, в образце останется N=N/2n активных частиц. В этом выражении n=t/T½: отношение времени исследования к периоду полураспада.

— ЗРР имеет несколько иное математическое выражение, более удобное в решении задач: N=N2-t/T½_.

Закономерность позволяет определить, помимо периода полураспада, число атомов активного изотопа, нераспавшихся в данный момент времени. Зная число атомов образца в начале наблюдения, через некоторое время можно определить время жизни данного препарата.

Определить период полураспада формула закона радиоактивного распада помогает лишь при наличии определенных параметров: числа активных изотопов в образце, что узнать достаточно сложно.

Радиоактивность

В природе встречаются как стабильные, так и не стабильные изотопы. Ядра некоторых нуклидов нестабильны, в них число нейтронов превосходит число протонов. Ядра таких нестабильных изотопов обладают способностью самопроизвольно превращаться в другие ядра или переходить из возбужденного состояния в основное. Этот процесс называется радиоактивным распадом. Он может сопровождаться испусканием альфа-частиц, бета-частиц, нейтронов или излучением гамма-квантов. Нуклиды (изотопы), способные к радиоактивному распаду, называется радионуклидами (радиоизотопами).

Явление радиоактивного распада — самопроизвольное (спонтанное) превращение атомных ядер некоторых элементов (например, урана, тория, радия и др.) в ядра атомов других элементов с испусканием α (альфа) — частиц, или β (бета) — частиц, сопровождающееся γ (гамма) — излучением называется радиоактивностью.☛ α — частицы представляют собой ядра атома гелия,
☛ β — частицы — электроны или позитроны (антиэлектроны),
☛ γ — лучи — это коротковолновое электромагнитное излучение, обладающее в большей степени корпускулярными, чем волновыми свойствами.

Радиоактивные изотопы характеризуются величиной активности, видом излучения, энергией излучаемых частиц и периодом полураспада.

Активность

Радиоактивное вещество характеризуется, среди других свойств, своей активностью, то есть количеством распадов в единицу времени, или числом ядер, которые распадаются в секунду.

Значение величины радиоактивности, выраженной в Беккерелях, может быть очень большим, так как даже в маленьком количестве вещества имеется огромное количество атомов. Страшно прозвучит сообщение, что в центре Вильнюса увеличилась радиоактивность до 20 миллионов Беккерель. Но так ли это страшно? Все, что требуется для такого «увеличения активности» — это 5000 зрителей, выходящих со стадиона. Поскольку каждое человеческое тело содержит приблизительно 4000 Беккерель естественного (природного) радиоактивного вещества калий-40.

Период Полураспада

Период полураспада — мера скорости распада вещества — время, которое требуется для того, чтобы радиоактивность вещества уменьшилась наполовину, или, время, которое требуется для того, чтобы распалась половина ядер.

После одного периода полураспада активность будет уменьшена в два раза от первоначальной, после двух периодов полураспада — в 4 раза и так далее.

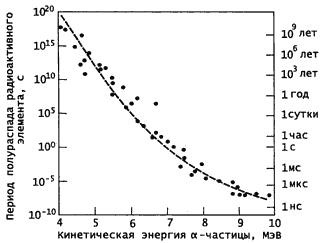
Рисунок 1.8 Период полураспада разных элементов

Периоды полураспада различных радиоактивных изотопов имеют значение от долей секунды до милионов лет.

Следует также отметить, что скорость радиоактивного распада для каждого радионуклида — строго определенной величина, и никакие температурные воздействия, давление или катализаторы не в силах ее изменить. Чем короче период полураспада, тем быстрее идет распад. В зависимости от скорости распада радионуклиды делятся (в достаточной мере условно) на:- короткоживущие, период полураспада которых исчисляется секундами, минутами, часами, днями, неделями;
— среднеживущие (месяцы, годы);
— долгоживущие, чьи периоды полураспада составляют от десятков до миллиардов лет.

Самый короткоживущий из известных нуклидов — 5Li: время его жизни составляет 4,4-10 с. За это время даже свет пройдет всего 10-11 см, т.е. расстояние, лишь в несколько десятков раз превышающее диаметр ядра и значительно меньшее размера любого атома. Самый долгоживущий — 128Te (содержится в природном теллуре в количестве 31,7%) с периодом полураспада восемь септиллионов (8-1024) лет — его даже трудно назвать радиоактивным; для сравнения — нашей Вселенной по оценкам «всего» 1010 лет.

Время жизни атома

Существование атома в его первоначальном состоянии может длиться секунду, а может и миллионы лет. Говорить о времени жизни данной частицы также не приходится. Введя величину, равную среднему значению времени жизни атомов, можно вести разговор о существовании атомов радиоактивного изотопа, последствиях радиоактивного распада. Период полураспада ядра атома зависит от свойств данного атома и не зависит от других величин.

Можно ли решить проблему: как найти период полураспада, зная среднее время жизни?

Определить период полураспада формула связи среднего времени жизни атома и постоянной распада помогает не меньше.

τ= T_1/2/ln2= T_1/2/0,693=1/ λ.

В этой записи τ – среднее время жизни, λ – постоянная распада.